the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel generalized sliding mode controller for uncertain robot manipulators based on motion constraints
Zhaodong Wang
Lixue Mei
Xiaoqun Ma
To improve the trajectory tracking performance and robustness for uncertain robot manipulators, a generalized sliding mode controller (GSMC) including an ideal controller and a continuous sliding mode controller (SMC) is proposed from the standpoint of motion constraints. First, the trajectory tracking requirements are formulated as the motion constraints, based on which an ideal controller is proposed to satisfy the motion constraints for robot manipulators whose dynamics are precisely known. Second, an additional continuous SMC is presented to compensate for the effects of uncertainty, and the chattering phenomenon that commonly exists in the SMC can be avoided by the introduction of a smoothing function. Third, Lyapunov analysis is conducted to verify that the proposed GSMC enables the tracking error restricted to a small region around zero. Finally, the numerical simulation and experiment are performed to verify the effectiveness and superiority of the proposed GSMC.
- Article
(5230 KB) - Full-text XML
- BibTeX
- EndNote
Recently, with the development of technology, robot manipulators have been widely applied in industrial manufacturing, aerospace, medical treatment, military, and other fields. Despite the different application scenarios, achieving fast and high-accuracy trajectory tracking is one of the common requirements for these tasks. However, acquiring a desirable trajectory tracking performance for robot manipulators remains a challenge, since robot manipulators have multiple variables, strong coupling, and nonlinear systems (Khalil and Dombre, 2004). Moreover, uncertainty (such as parameter uncertainty and external disturbances) may exist in robot manipulators, which can also deteriorate the system's performance. Some effective control schemes like computed torque control (CTC) (Perumalsamy et al., 2023) and backstepping control (Brahmi et al., 2018; Pan et al., 2018) are proposed. However, these schemes are model-based, which means that the tracking performance relies on the system dynamic model. In practice, due to the complex structure of robot manipulators, accurate dynamics models are difficult to obtain. Besides, the dynamics of robot manipulators may change; for example, if the end effector grasps loads, the inertia matrix will change (Kim et al., 2019). To cope with the uncertainty, many advanced control methods have been proposed, such as adaptive control (Slotine and Li, 1988; Wang, 2017), fuzzy control (Li et al., 2015), robust control (Mahmoud, 1993; Del Prete and Mansard, 2016; Liu and Abdel-Malek, 2000; Chen et al., 2022), neural-network control (Khan et al., 2021), and sliding mode controller (SMC) methods (Fang et al., 2022).
Owing to its strong robustness, the SMC has attracted much attention (Jing et al., 2019; Zhai et al., 2021). Conventional SMC schemes essentially have discontinuous control, which endeavors to force the system trajectory to follow the predefined sliding surface (Wang et al., 2019). However, the chattering problem caused by the use of the switching function will result in high control gains, high-frequency dynamics, and actuator deterioration. To reduce the chattering, the boundary layer method is proposed in Cupertino et al. (2009). However, since the boundary layer method is a continuous approximation, the control accuracy of the system will reduced. In Du et al. (2018), the terminal SMC (TSMC) method is proposed to attenuate the chattering and can ensure that the system is stable in finite time. Although the TSMC can achieve finite-time convergence, it suffers from the singularity problem. To avoid the singularity problem, the nonsingular TSMC (NTSMC) method is proposed (Van et al., 2016; Wang et al., 2020). However, the proposed NTSMC cannot eliminate the chattering, and the convergence rate is slow. To realize the faster convergence rate, a fast TSMC (FTSMC) is proposed in Amirkhani et al. (2019). However, the chattering in control still exists in the proposed FTSMC. A super-twisting SMC (STSMC) is presented in Mobayen et al. (2017), in which the control input is continuous to avoid chattering. However, this method assumes that the initial error is zero since the robustness of the system can only be ensured if the system states reach the sliding surface. The scheme proposed in this paper, on the other hand, does not require such an assumption.
To realize the precision control of robot manipulators with uncertainty, a two-step control scheme is proposed. In the first step, consider the control of the “ideal” robot manipulator system whose dynamics model is precisely known. An exact closed-form ideal controller is designed from a novel standpoint, where the control requirements are taken as a set of constraints exerted on the controlled system, and based on the analytical dynamics theory (Udwadia and Kalaba, 1996), the control inputs that enable the ideal system to meet these requirements are obtained. It is noted that the control inputs can be obtained without performing any approximations or linearizations for the system dynamic model. Moreover, the proposed control inputs can minimize a quadratic control cost at each moment; this means that the control inputs are modest (Udwadia, 2008; Udwadia and Koganti, 2015b). In the second step, the ideal controller is augmented by an additional continuous SMC to realize the precision control for robot manipulators whose dynamics model is not precisely known. This additional controller is developed on the basis of the notion of a generalized sliding surface, where the smoothing function is applied to replace the sign function to avoid chattering. Moreover, the proposed controller can track the desired trajectory within the expected error range even in the presence of uncertainty.
The main contributions are summarized below.
- 1.
Based on the analytical dynamics theory, an ideal controller that can enable the ideal system to meet the desired control requirements is presented in closed form. Moreover, the ideal control input is optimal since it renders the quadratic control cost minimized at each moment.
- 2.
By the introduction of the notion of the generalized sliding surface, an additional controller is designed to augment the ideal controller. The proposed controller can drive the system to meet the expected control requirements in the presence of initial condition deviations and uncertainty while avoiding the chattering problem.
Consider an n-link serial robot manipulator as follows (Zhu et al., 2023):
where Θ is the joint position, and D(Θ), , and G(Θ) represent the inertia matrix, Coriolis torque matrix, and gravitation torque, respectively. Notice that matrix D is positive definite. τ and are the control input and unknown disturbance, respectively. In the following, D(Θ), , G(Θ), and are abbreviated as D, V, G, and f for convenience.
Since uncertainty inevitably exists in the robot manipulator, we assume that (Su et al., 2020; Deng et al., 2023)
where denotes the ideal portions, and Δ(⋅) denotes the uncertain portions.
The control objective of this paper is to design a suitable controller that causes the tracking error to converge to zero as t→∞. To quantify the control objective, we have
where Θid denotes the desired trajectory of the ith joint.
In this paper, the control design is split into two steps. The first step is to design an ideal controller for the ideal system (i.e., whose dynamic model is precisely known and has no external disturbances imposed on it). The second step is to design a GSMC to enhance the robustness.
3.1 Ideal controller
Firstly, we suppose that the robot manipulator dynamic model parameters are all known and without load disturbances imposed on the robot manipulator. Then, we can obtain the ideal dynamic model of the robot manipulator as
In this paper, the control objective is reformatted as the form of motion constraint
where .
Generally, the motion constraint (Eq. 5) can be modified as
where is a positive user-defined matrix.
Differentiating Eq. (6) with respect to time t, one has
Rewriting Eqs. (6) and (7) in matrix form, one can obtain (Udwadia, 2005)
where M=I, , and .
According to Kalaba and Udwadia (1993) and Udwadia and Kalaba (2002), the control input that drives the motion constraints (Eq. 8) to be satisfied can be given by
In a sense, the control input (Eq. 9) is optimal since it renders the control cost minimized at each moment (Udwadia, 2003).
3.2 GSMC
In the previous section, the control input that drives the motion constraints satisfied is deduced based on the condition that the model parameters of robot manipulator are precisely known. However, precise knowledge of the system is difficult or even impossible to achieve. Therefore, in this section, we will explore the control of robot manipulator whose parameters are not perfectly known.
Define the auxiliary error variable as
where Θi(t) and Θia(t) are the ith joint position of the ideal and real robot manipulator, respectively.
According to Eq. (10), we have
where .
The generalized sliding surface is defined as
where is a positive user-defined matrix. One can see that e can asymptotically converge to zero once the controlled system is restricted on the hyperplane σ=0. However, the methods that can maneuver the systems to reach σ=0 in a limited time are generally discontinuous (Udwadia and Wanichanon, 2014; Udwadia and Koganti, 2015a). To avoid the problems caused by the usage of the discontinuous function, this paper intends to use a smooth function that can only guarantee that the system be restricted to a small region Ωζ close to zero, defined as
where ζ>0 is a arbitrarily small constant.
Notice that the generalized displacement and velocity at the initial time are the same for the ideal system and the real system (i.e., ), which means that the system is within the region Ωζ at the initial time.
Define
and suppose that the following estimates,
and
can be obtained. Based on these properties, the closed-form expression for the GSMC is given as
with
where ζ>0 is a user-defined parameter to satisfy desired tracking tolerances.
3.3 Stability analysis
Select the Lyapunov candidate as
Differentiating Eq. (19) along the sliding variable trajectory σ, one has
Differentiating Eq. (12) with respect to time, one has
By Eqs. (1), (4), (11), and (17), one has
Substituting Eq. (22) into Eq. (21) yields
Then, one has
Substituting Eq. (18) into Eq. (24) yields
Moreover, when , by Eq. (16), one has
According to Lyapunov’s stability theorem, the region Ωζ can be an attracting region for the real system. Since the tracking errors of the real system start inside the region Ωζ, they can always remain in the region Ωζ using the proposed controller (Eq. 17).
4.1 Numerical simulation results
To illustrate the effectiveness of the proposed controller, some simulations and experiments are conducted with a two-link robot manipulator. The dynamics of the manipulator is given as (Wu et al., 2019)
with
where mi and li () denote the actual mass and length of the ith link, respectively. The ideal parameter values of the manipulator dynamics (Eq. 27) are assigned as kg ⋅ m2, kg ⋅ m2, kg, kg, m, and m. To validate the robustness of the proposed GSMC, the system uncertainty is chosen as and , and the external disturbance is chosen as Nm. In the simulation, the desired trajectory is set as . The initial conditions are set as and . The control parameters of the proposed controller are set as , , and ζ=0.5.
To assess the superiority of the proposed controller, the comparison with a conventional SMC and robust control (Huang et al., 2021) is conducted. The expression of the conventional SMC is given as
where is the sliding surface, , , and η=50.
The expression of the robust control is given as
where , , , σ=0.1, and ν=2.
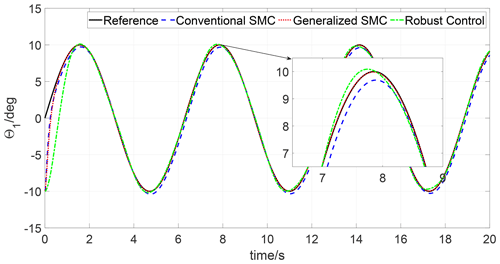
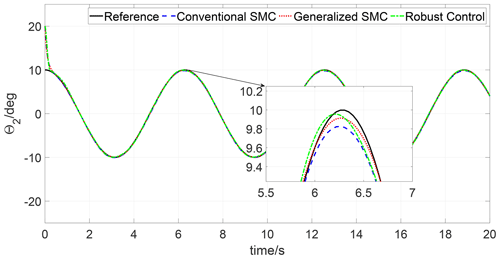
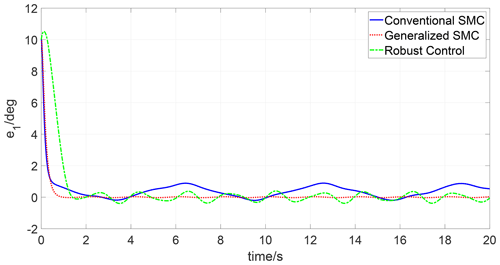
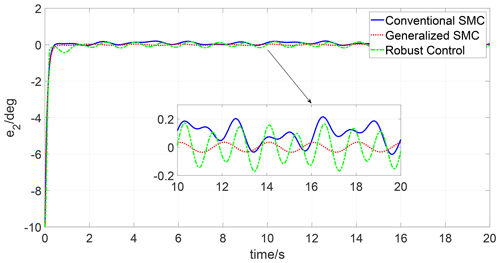
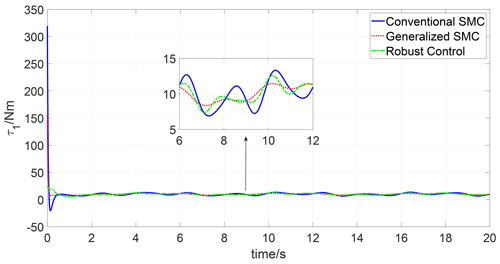
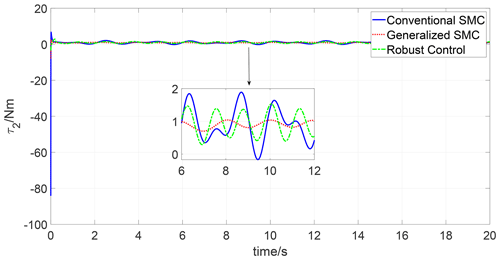
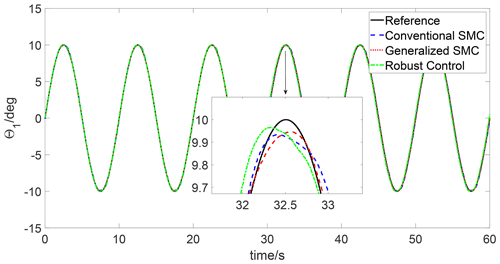
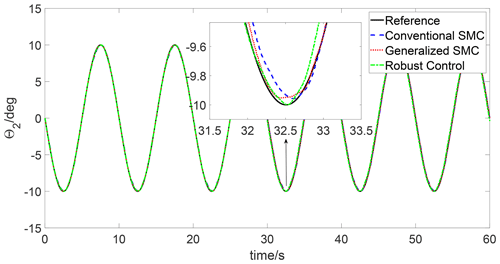
The simulations are carried out in the MATLAB environment, employing a variable time step ode15i solver. The simulation results are depicted in Figs. 1–6. Figures 1 and 2 present the trajectory tracking response of joints 1 and 2 under three different controls. As seen in Figs. 1 and 2, both the three controls can track the reference trajectory. To compare the tracking performance of three algorithms, the trajectory tracking errors of joints 1 and 2 are depicted in Figs. 3 and 4. It can be observed that both the transient response and steady-state tracking performance of the generalized SMC are superior to those of the conventional SMC and robust control. In addition, the control input of joints 1 and 2 under the three algorithms is illustrated in Figs. 5 and 6; one can see that the control inputs of the conventional SMC and robust control are higher than the generalized SMC for both joint 1 and joint 2.
4.2 Experimental results
To further validate the proposed control algorithm, the experimental validation on the robot manipulator experimental platform (see Fig. 7) is conducted. The experimental platform adopts the rapid control prototyping method, which enables users to establish the control algorithm model in the MATLAB/Simulink environment and then use the automatic code generation tool to automatically generate the C code, thus facilitating users to complete the algorithm validation in a fast and efficient way.
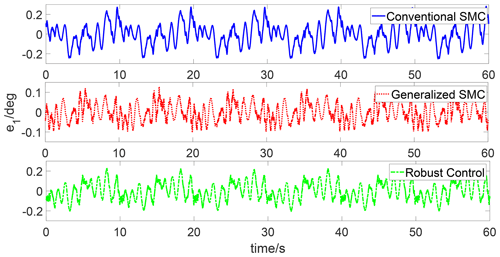
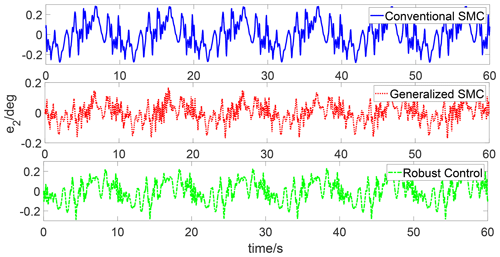
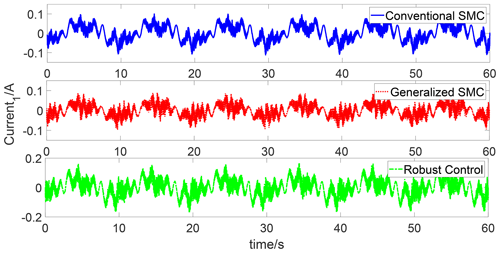
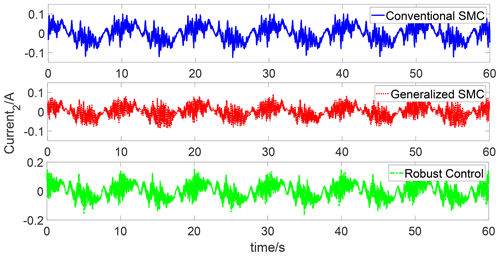
Figures 8 and 9 show the trajectory tracking responses of the conventional SMC algorithm, robust control algorithm, and generalized SMC algorithm, respectively. One can see that the generalized SMC algorithm provides better tracking performance than the conventional SMC algorithm and robust control algorithm. Figures 10 and 11 compare the tracking errors of the two joints under three different algorithms. The tracking errors of the two joints under the generalized SMC algorithm are below 0.2∘, while the tracking errors of the two joints under the conventional SMC algorithm and robust control algorithm are close to 0.3∘. Figures 12 and 13 compare the control inputs of the two joints under three different algorithms. For both joint 1 and joint 2, the control inputs of the conventional SMC algorithm and robust control algorithm are larger than those of the generalized SMC algorithm.
In this study, to improve the trajectory tracking control performance for robot manipulators subject to uncertainty, a generalized SMC is designed. The design procedure of the proposed generalized SMC contains two steps. In the first step, it is assumed that the dynamic model of robot manipulators is precisely known, and there are no external disturbances; an ideal control is designed based on analytical dynamics by reformulating the trajectory tracking as a problem of constrained motion. In the second step, a smooth-function-based SMC is designed to prevent the chattering phenomenon caused by discontinuous function and further enhance the robustness performance. Numerical simulations and experimental results simultaneously validate the effectiveness of the proposed generalized SMC algorithm. In the future, this method will be modified and applied to robotic manipulators with actuator saturation and output constraints.
All of the code used in this paper can be obtained from the corresponding author upon request.
No data sets were used in this article.
ZW designed the study and wrote the paper, LM provided guidance on the writing, and XM conducted the simulation research.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors acknowledge the financial support of the Jiangxi Provincial Department of Education.
This research has been supported by the Science and Technology Project of the Jiangxi Provincial Department of Education (grant no. GJJ2202403).
This paper was edited by Daniel Condurache and reviewed by four anonymous referees.
Amirkhani, S., Mobayen, S., Iliaee, N., Boubaker, O., and Hosseinnia, S. H.: Fast terminal sliding mode tracking control of nonlinear uncertain mass–spring system with experimental verifications, Int. J. Adv. Robot. Syst., 16, 1–10, https://doi.org/10.1177/1729881419828176, 2019. a
Brahmi, B., Saad, M., Ochoa-Luna, C., Rahman, M. H., and Brahmi, A.: Adaptive tracking control of an exoskeleton robot with uncertain dynamics based on estimated time-delay control, IEEE-ASME T. Mech., 23, 575–585, https://doi.org/10.1109/tmech.2018.2808235, 2018. a
Chen, X., Zhao, H., and Zhen, S.: Constraint-following control design for the position tracking of a permanent magnet linear motor with inequality constraints, Mech. Sci., 13, 297–310, https://doi.org/10.5194/ms-13-297-2022, 2022. a
Cupertino, F., Naso, D., Mininno, E., and Turchiano, B.: Sliding-mode control with double boundary layer for robust compensation of payload mass and friction in linear motors, IEEE T. Ind. Appl., 45, 1688–1696, https://doi.org/10.1109/tia.2009.2027521, 2009. a
Del Prete, A., and Mansard, N.: Robustness to joint-torque-tracking errors in task-space inverse dynamics, IEEE T. Robot., 32, 1091–1105, https://doi.org/10.1109/tro.2016.2593027, 2016. a
Deng, W., Zhou, H., Zhou, J., and Yao, J.: Neural network-based adaptive asymptotic prescribed performance tracking control of hydraulic manipulators, IEEE T. Syst. Man Cy.-S., 53, 285–295, https://doi.org/10.1109/TSMC.2022.3178626, 2023. a
Du, M., Zhao, D., Yang, B., and Wang, L.: Terminal sliding mode control for full vehicle active suspension systems, J. Mech. Sci. Technol., 32, 2851–2866, https://doi.org/10.1007/s12206-018-0541-x, 2018. a
Fang, H., Wu, Y., Xu, T., and Wan, F.: Adaptive neural sliding mode control of uncertain robotic manipulators with predefined time convergence, Int. J. Robust Nonlin., 32, 9213–9238, https://doi.org/10.1002/rnc.6333, 2022. a
Huang, K., Xian, Y., Zhen, S., and Sun, H.: Robust control design for a planar humanoid robot arm with high strength composite gear and experimental validation, Mech. Syst. Signal Process., 155, 107442, https://doi.org/10.1016/j.ymssp.2020.107442, 2021. a
Jing, C., Xu, H., and Niu, X.: Adaptive sliding mode disturbance rejection control with prescribed performance for robotic manipulators, ISA T., 91, 41–51, https://doi.org/10.1016/j.isatra.2019.01.017, 2019. a
Kalaba, R. E. and Udwadia, F. E.: Equations of motion for nonholonomic, constrained dynamical systems via Gauss’s principle, J. Appl. Mech., 60, 662–668, https://doi.org/10.1115/1.2900855, 1993 a
Khalil, W. and Dombre, E.: Modeling, identification and control of robots, Butterworth-Heinemann, Oxford, https://doi.org/10.1016/B978-1-903996-66-9.X5000-3, ISBN: 978-1-903996-66-9, 2004. a
Khan, A. T., Li, S., and Cao, X.: Control framework for cooperative robots in smart home using bio-inspired neural network, Measurement, 167, 108253, https://doi.org/10.1016/j.measurement.2020.108253, 2021. a
Kim, M. J., Lee, W., Choi, J. Y., Chung, G., Han, K. L., Choi, I. S., Ott, C., and Chung, W. K.: A passivity-based nonlinear admittance control with application to powered upper-limb control under unknown environmental interactions, IEEE-ASME T. Mech., 24, 1473–1484, https://doi.org/10.1109/tmech.2019.2912488, 2019. a
Li, Z., Yang, C., Su, C. Y., Deng, S., Sun, F., and Zhang, W.: Decentralized fuzzy control of multiple cooperating robotic manipulators with impedance interaction, IEEE T. Fuzzy Syst., 23, 1044–1056, https://doi.org/10.1109/tfuzz.2014.2337932, 2015. a
Liu, J. F. and Abdel-Malek, K.: Robust control of planar dual-arm cooperative manipulators, Robot. Cim.-Int. Manuf., 16, 109–119, https://doi.org/10.1016/S0736-5845(99)00043-5, 2000. a
Mahmoud, M. S.: Robust control of robot arms including motor dynamics, Int. J. Control, 58, 853–873, https://doi.org/10.1080/00207179308923032, 1993. a
Mobayen, S., Tchier, F., and Ragoub, L.: Design of an adaptive tracker for n-link rigid robotic manipulators based on super-twisting global nonlinear sliding mode control, Int. J. Syst. Sci., 48, 1990–2002, https://doi.org/10.1080/00207721.2017.1299812, 2017. a
Pan, Y., Wang, H., Li, X., and Yu, H.: Adaptive command-filtered backstepping control of robot arms with compliant actuators, IEEE T. Contr. Syst. T., 26, 1149–1156, https://doi.org/10.1109/tcst.2017.2695600, 2018. a
Perumalsamy, G., Kumar, D., Jose, J., Joseph Winston, S., and Murugan, S.: Computed torque control method for two-axis planar serial robotic arm, IETE J. Res., 69, 1437–1445, https://doi.org/10.1080/03772063.2020.1869595, 2023. a
Slotine, J. J. and Li, W.: Adaptive manipulator control: A case study, IEEE T. Automat. Contr., 33, 995–1003, https://doi.org/10.1109/9.14411, 1988. a
Su, Y., Zheng, C., and Mercorelli, P.: Robust approximate fixed-time tracking control for uncertain robot manipulators, Mech. Syst. Signal Process., 135, 106379, https://doi.org/10.1016/j.ymssp.2019.106379, 2020. a
Udwadia, F. E.: A new perspective on the tracking control of nonlinear structural and mechanical systems, P. Roy. Soc. A-Math. Phy., 459, 1783–1800, https://doi.org/10.1098/rspa.2002.1062, 2003. a
Udwadia, F. E.: Equations of motion for constrained multibody systems and their control, J. Optimiz. Theory App., 127, 627–638, https://doi.org/10.1007/s10957-005-7507-8, 2005. a
Udwadia, F. E.: Optimal Tracking Control of Nonlinear Dynamical Systems, P. Roy. Soc. A-Math. Phy., 464, 341–2363, https://doi.org/10.1098/rspa.2008.0040, 2008. a
Udwadia, F. E. and Kalaba, R. E.: On the foundations of analytical dynamics, Int. J. Nonlin. Mech., 37, 1079–1090, https://doi.org/10.1016/s0020-7462(01)00033-6, 2002. a
Udwadia, F. E., Kalaba, R. E.: Analytical Dynamics: a New Approach, Cambridge University Press, New York, https://doi.org/10.1017/CBO9780511665479, ISBN: 9780511665479, 1996. a
Udwadia, F. E. and Koganti, P. B.: Dynamics and control of a multi-body planar pendulum, Nonlinear Dynam., 81, 845–866, https://doi.org/10.1007/s11071-015-2034-0, 2015a. a
Udwadia, F. E. and Koganti, P. B.: Optimal stable control for nonlinear dynamical systems: an analytical dynamics based approach, Nonlinear Dynam., 82, 547–562, https://doi.org/10.1007/s11071-015-2175-1, 2015b. a
Udwadia, F. E. and Wanichanon, T.: Control of uncertain nonlinear multibody mechanical systems, J. Appl. Mech., 81, 1–11, https://doi.org/10.1115/1.4025399, 2014. a
Van, M., Ge, S. S., and Ren, H.: Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control, IEEE T. Cybernetics, 47, 1681–1693, https://doi.org/10.1109/tcyb.2016.2555307, 2016. a
Wang, H.: Adaptive control of robot manipulators with uncertain kinematics and dynamics, IEEE T. Automat. Contr., 62, 948–954, https://doi.org/10.1109/tac.2016.2575827, 2017. a
Wang, Y., Karimi, H. R., Shen, H., Fang, Z., and Liu, M.: Fuzzy-model-based sliding mode control of nonlinear descriptor systems, IEEE T. Cybernetics, 49, 3409–3419, https://doi.org/10.1109/tcyb.2018.2842920, 2019. a
Wang, Y., Li, S., Wang, D., Ju, F., Chen, B., and Wu, H.: Adaptive time-delay control for cable-driven manipulators with enhanced nonsingular fast terminal sliding mode, IEEE T. Ind. Electron., 68, 2356–2367, https://doi.org/10.1109/tie.2020.2975473, 2020. a
Wu, Y., Huang, R., Li, X., and Liu, S.: Adaptive neural network control of uncertain robotic manipulators with external disturbance and time-varying output constraints, Neurocomputing, 323, 108-116, https://doi.org/10.1016/j.neucom.2018.09.072, 2019. a
Zhai, J. and Li, Z.: Fast-exponential sliding mode control of robotic manipulator with super-twisting method, IEEE T. Circuit-II, 69, 489–493, https://doi.org/10.1109/tcsii.2021.3081147, 2021. a
Zhu, C., Yang, C., Jiang, Y., and Zhang, H.: Fixed-time fuzzy control of uncertain robots with guaranteed transient performance, IEEE T. Fuzzy Syst., 31, 1041–1051, https://doi.org/10.1109/tfuzz.2022.3194373, 2023. a