Decoupling active disturbance rejection trajectory-tracking control strategy for X-by-wire chassis system

Due to the inherent dynamic coupling between mechanical components such as the steering system and suspension system, the vertical external input will affect the lateral movement of the chassis, which makes it difficult to track the ideal trajectory when complex excitation conditions exist. To solve the abovementioned problems, the X-by-wire chassis is taken as the research object in this work, and the coupling dynamic model is established. Then, based on proving the reversibility of the coupling dynamic model, a pseudo-linear composite system is proposed to decouple the lateral and vertical signals of the chassis system. Next, the decoupling active disturbance rejection (DADR) trajectory-tracking control strategy is proposed. And a multi-objective optimization method of the bandwidth parameters of the DADR trajectory-tracking controller is proposed according to its convergence conditions. Experiments show that the proposed control strategy can effectively suppress the vehicle roll and yaw motion caused by the lateral–vertical dynamic coupling in the process of trajectory tracking to realize the accurate tracking of the ideal trajectory.

1 Introduction

Automatic lane-change maneuvers and obstacle-avoidance systems can effectively reduce the incidence of vehicle collision accidents caused by human behavior to further improve traffic safety (Liu et al., 2020; Ji et al., 2019). The achievements of automatic lane-change maneuvers and obstacle-avoidance depend on the high-precision tracking of ideal signals in chassis steering, braking, and other subsystems. However, when tracking obstacle avoidance trajectories in complex traffic environments, the trajectory-tracking accuracy and response speed will be affected by both sides of external factors, including random road input, lateral wind, etc., and internal factors, such as vertical and lateral dynamic coupling characteristics. Because of these factors, it is difficult to provide accurate and fast actuator responses in the process of vehicle trajectory tracking (Wang et al., 2017). Therefore, how to design the lane-change trajectory-tracking control strategy, considering the external disturbance of the vehicle in complex traffic environments and the vehicle chassis dynamic coupling, is the key point for the intelligent vehicle to ensure safety and stability for lane-change maneuvers.

Existing research on trajectory-tracking control mainly focuses on local trajectory replanning and hierarchical control under random disturbances (Yue et al., 2019; Wang et al., 2019). In Yue et al. (2019), aiming at a highway tire burst, a hierarchical control framework for vehicle automatic risk-avoidance trajectory planning and tracking is proposed. Wang et al. (2019) solve the problem of the full-state regulation control of asymmetric under-actuated surface vehicles under disturbance. The above studies effectively suppress fluctuations in the trajectory-tracking process under disturbance. However, due to lateral and vertical dynamic coupling, signal disturbance on lateral or vertical motion cannot be suppressed independently, and active inputs of steering and suspension systems will simultaneously affect vehicle lateral and vertical dynamics (Wang et al., 2018). For instance, the active roll control moments from the chassis controller will not only affect the vertical signals, such as the roll angular velocity, but also change the lateral dynamic parameters, such as yaw angular velocity. Besides, disturbance compensation in trajectory-tracking control has been widely studied (Fiengo et al., 2019; Wang et al., 2019). However, if the compensation control signal changes rapidly, then it is difficult to achieve desired control performance due to lateral and vertical dynamic coupling.

Compared with conventional chassis technology without active control, the advanced X-by-wire chassis enables the active control of roll torque, yaw torque, and front wheel angle. Therefore, the trajectory-tracking control of the X-by-wire chassis system is a typical multivariable control system (Ni et al., 2019). Specifically, when the vehicle equipped with an X-by-wire chassis tracks the curve trajectory, then the dynamic coupling on the signal layer will cause interference in the mechanical layer. For example, the road excitation signal will affect the yaw motion and roll motion of the vehicle with the X-by-wire chassis system. To eliminate the coupling between inputs and outputs, decoupling methods, such as artificial neural network decoupling, robust decoupling, fuzzy decoupling, and inverse system decoupling, are commonly used in multivariable control systems (Zhao et al., 2019; Wu et al., 2020). In Zhao et al. (2019), to solve the vibration problems caused by the nonlinear coupling of longitudinal, lateral, and vertical dynamics, a hierarchical integrated controller for distributed electric vehicles is proposed to improve driving safety. Wu et al. (2020) propose a sliding-mode decoupling control strategy for an electric wheel vehicle based on the inverse system method. However, the abovementioned decoupling control strategies are not applicable for curve trajectory-tracking problems in real complex traffic environments. Because these strategies do not take the trajectory-tracking accuracy and response speed into account in the lane-change obstacle-avoidance process, the disturbance suppression of excitation signals under uncertain environmental conditions is also excluded. In recent years, active disturbance rejection control (ADRC) has been proposed and applied to the tracking problem of multivariable control systems. In Luo et al. (2018), a feed-forward coupling compensation decoupling control method based on ADRC is proposed to solve the cross-coupling problem caused by variable wind disturbance in the system. In Zhang and Chen (2016), based on ADRC feedback linearization, a feed-forward controller based on an equivalent error model is designed to further improve the tracking performance of the system. In Xia et al. (2016), a tracking control method of an automatic land vehicle (ALV) lateral motion is proposed, and the ADRC is used to ensure the control accuracy and robustness. To some extent, the above methods have solved the performance robustness of the controller in the presence of disturbances and the coupling problem caused by the disturbance input but cannot solve the problem of the internal dynamic coupling of the system, so it needs to be further studied.

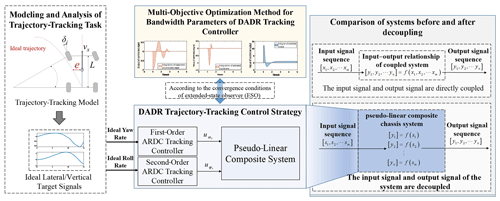
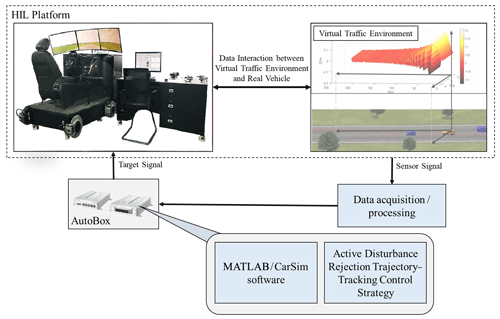
To solve the above problems, a decoupling active disturbance rejection (DADR) trajectory-tracking control strategy is proposed. First, based on the inverse system theory, the decoupled pseudo-linear composite system is constructed to decouple the input and output signals of the original system. Then, for the decoupled pseudo-linear system, independent lateral motion and vertical motion DADR trajectory-tracking controllers are used. And a multi-objective optimization method of bandwidth parameters of the DADR trajectory-tracking controller is proposed according to its convergence conditions. Finally, through the experimental verification on the hardware-in-the-loop test platform, it is proved that the strategy proposed in this work not only can effectively improve the trajectory-tracking performance under road excitation but also significantly inhibits the roll motion of the vehicle when tracking the curve trajectory in order to improve the ride comfort. The decoupling active disturbance rejection (DADR) trajectory-tracking control strategy proposed in this work and its hardware in the loop (HIL) test platform are shown in Fig. 1.

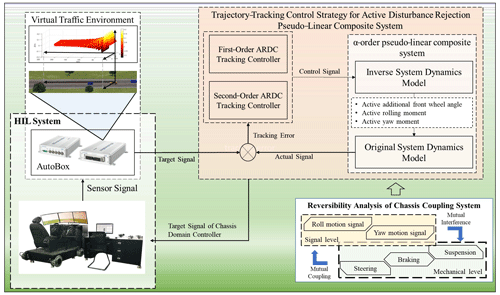
Figure 1 The decoupling active disturbance rejection (DADR) trajectory-tracking control strategy proposed in this work and its hardware in the loop (HIL) test platform.

The main contributions of this paper are as follows:

1. The chassis system's yaw signal and roll signal are decoupled on the signal layer so that the yaw motion or roll motion of the chassis system can be compensated and controlled independently. Furthermore, in the mechanical layer, the cooperative control of the chassis mechanical components in the steering-by-wire system, braking-by-wire system, and active suspension system can be realized.

2. The system reversibility is analyzed and verified based on the coupled lateral and vertical dynamic model, and the α-order chassis pseudo-linear composite system is obtained to decouple the lateral and vertical signals of the chassis system.

3. A decoupling active disturbance rejection (DADR) trajectory-tracking control strategy is proposed, and a multi-objective optimization method of bandwidth parameters of the DADR trajectory-tracking controller is proposed according to its convergence conditions.

The rest of this paper is arranged as follows: Sect. 2 is the modeling of the X-by-wire chassis and its analysis in the trajectory-tracking task. Section 3 proposes the decoupling active disturbance rejection (DADR) trajectory-tracking control strategy. Section 4 presents the results and discussion. Section 5 is the conclusion.

2 Modeling and analysis of X-by-wire chassis trajectory-tracking task

To analyze the mechanism of lateral and vertical dynamic coupling, this section first establishes the X-by-wire 3 DOF (degrees of freedom) coupled dynamic model, including the input signals of the active roll torque, yaw torque, and front wheel angle, as shown in Eq. (1).

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}m{v}_x(\dot{\mathit{\beta }}+{\mathit{\omega }}_r)+m_{\mathrm{s}}h\ddot{\mathit{\varphi }}r\\ =\mathrm{2}{k}_{\mathrm{f}}\left(\mathit{\delta }+{\mathit{\delta }}_{\mathrm{d}}+E_{\mathrm{f}}{\mathit{\varphi }}_r-\frac{a{\mathit{\omega }}_r}{v_x}-\mathit{\beta }\right)\\ +\mathrm{2}{k}_{\mathrm{r}}\left(\frac{b{\mathit{\omega }}_r}{v_x}+E_{\mathrm{r}}{\mathit{\varphi }}_r-\mathit{\beta }\right)+(b{m}_r-a{m}_{\mathrm{f}}){\dot{\mathit{\omega }}}_r\\ I_z{\dot{\mathit{\omega }}}_r+I_{xz}{\ddot{\mathit{\varphi }}}_r=\mathrm{2}a{k}_{\mathrm{f}}\left(\mathit{\delta }+{\mathit{\delta }}_{\mathrm{d}}+E_{\mathrm{f}}{\mathit{\varphi }}_r-\frac{a{\mathit{\omega }}_r}{v_x}-\mathit{\beta }\right)\\ -\mathrm{2}b{k}_r\left(\frac{b{\mathit{\omega }}_r}{v_x}+E_{\mathrm{r}}{\mathit{\varphi }}_r-\mathit{\beta }\right)\\ +(b{m}_r-a{m}_{\mathrm{f}})v_x(\dot{\mathit{\beta }}+{\mathit{\omega }}_r)+T_z\\ I_x{\ddot{\mathit{\varphi }}}_r+I_{xz}{\dot{\mathit{\omega }}}_r=m_{\mathrm{s}}gh{\mathit{\varphi }}_r-m_{\mathrm{s}}{v}_{x}h(\dot{\mathit{\beta }}+{\mathit{\omega }}_r)\\ -(K_{\mathit{\varphi }}{\mathit{\varphi }}_r+D_{\mathit{\varphi }}{\dot{\mathit{\varphi }}}_r)+T_{\mathit{\varphi }}\end{array},\right.\end{array}$$

where δ is the differential steering compensation angle signal of the front wheel, T_z is the yaw torque signal, and T_ϕ is the roll torque signal of the suspension system. m is the vehicle mass, m_s is the sprung mass, m_f is the front unsprung mass, and m_r is the rear unsprung mass. a is the distance from the center of mass to the front axle, b is the distance from the center of mass to the rear axle, I_z is the yaw moment of inertia, I_x is the roll moment of inertia, I_xz is the inertia product of the yaw motion, h is the roll center height, k_f is the front wheel yaw stiffness, k_r is the rear wheel yaw stiffness, E_f is the front roll steering coefficient, E_r is the rear roll steering coefficient, v_x is the longitudinal speed of the vehicle, β is the sideslip angle of the centroid, ω_r is the yaw rate, ϕ_r is the roll angle, K_ϕ is the suspension roll stiffness coefficient, D_ϕ is the suspension roll damping coefficient, and δ_d is the front wheel angle applied by the driver.

The state variable of the coupled chassis system is $x=[\mathit{\beta },{\mathit{\omega }}_r,{\mathit{\varphi }}_r,{\dot{\mathit{\varphi }}}_r{]}^{\mathrm{T}}$, the control input signal is $u=[\mathit{\delta },T_z,T_{\mathit{\varphi }}{]}^{\mathrm{T}}$, and the system output signal is $y=[\mathit{\beta },{\mathit{\omega }}_r,{\mathit{\varphi }}_r{]}^{\mathrm{T}}$. The state space of the system is shown in Eq. (2).

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{l}\mathbf{M}\dot{x}=\mathbf{A}x+\mathbf{B}u+\mathbf{P}{\mathit{\delta }}_{\mathrm{d}}\\ y=\mathbf{C}x\end{array}\right.\end{array}$$

$$\begin{array}{rl}& \mathbf{M}=\left[\begin{array}{cccc}m{v}_x& a{m}_{\mathrm{f}}-b{m}_r& \mathrm{0}& m_{\mathrm{s}}h\\ (a{m}_{\mathrm{f}}-b{m}_r)v_x& I_z& \mathrm{0}& I_{xz}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ m_{\mathrm{s}}{v}_{x}h& I_{xz}& \mathrm{0}& I_x\end{array}\right],\\ & \mathbf{B}=\left[\begin{array}{ccc}\mathrm{2}{k}_{\mathrm{f}}& \mathrm{0}& \mathrm{0}\\ \mathrm{2}a{k}_{\mathrm{f}}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\mathbf{P}=\left[\begin{array}{c}\mathrm{2}{k}_{\mathrm{f}}\\ \mathrm{2}a{k}_{\mathrm{f}}\\ \mathrm{0}\\ \mathrm{0}\end{array}\right],\\ & \mathbf{C}=\left[\begin{array}{cccc}\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}\end{array}\right],\\ & \mathbf{A}=\left[\begin{array}{cccc}-\mathrm{2}(k_{\mathrm{f}}+k_{\mathrm{r}})& \frac{\mathrm{2}(b{k}_r-a{k}_{\mathrm{f}})}{v_x}-m{v}_x& \mathrm{2}{k}_{\mathrm{f}}{E}_{\mathrm{f}}+\mathrm{2}{k}_{\mathrm{r}}{E}_{\mathrm{r}}& \mathrm{0}\\ \mathrm{2}(b{k}_r-a{k}_{\mathrm{f}})& (b{m}_r-a{m}_{\mathrm{f}})v_x-\frac{\mathrm{2}(a^{\mathrm{2}}{k}_{\mathrm{f}}+b^{\mathrm{2}}{k}_{\mathrm{r}})}{v_x}& \mathrm{2}a{k}_{\mathrm{f}}{E}_{\mathrm{f}}-\mathrm{2}b{k}_r{E}_{\mathrm{r}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\\ \mathrm{0}& -m_{\mathrm{s}}{v}_{x}h& m_{\mathrm{s}}gh-K_{\mathit{\varphi }}& -D_{\mathit{\varphi }}\end{array}\right].\end{array}$$

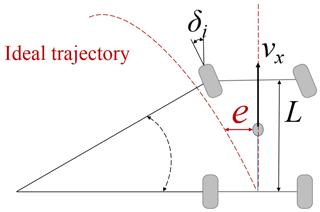
Then, the trajectory-tracking task is analyzed based on the above dynamic model, which is shown in Eq. (2). For the trajectory-tracking task, the goal is to eliminate the error between the actual trajectory and the ideal trajectory e. For the chassis motion control task, the goal is to eliminate the error between the ideal front wheel angle and the actual front wheel angle. Therefore, it is necessary to establish the relationship between the trajectory-tracking error and the ideal front wheel angle.

Figure 2 Trajectory-tracking task analysis.

The required front wheel angle to track a given path is calculated based on a pure pursuit algorithm (Yamasaki and Balakrishnan, 2010), as shown in Eq. (3).

$$\begin{array}{}\text{(3)}& {\mathit{\delta }}_i={\tan }^{-\mathrm{1}}\left({\displaystyle \frac{\mathrm{2}L}{{\left(k_v{v}_x\right)}^{\mathrm{2}}}}e\right),\end{array}$$

where δ_i is the ideal front wheel angle, L is the wheelbase, e is the lateral error between the current vehicle attitude and the target waypoint, v_x is the longitudinal speed of the vehicle, and k_v is the adjustment factor for the tracking process.

Next, ideal signals for the trajectory-tracking task are analyzed and listed as follows: tracking the desired trajectory is done by controlling the front wheel rotation angle and maintaining the roll angle as 0. For the X-by-wire chassis system, the target trajectory should be converted into the target yaw angle, as shown in Eq. (4) (Wang et al., 2018).

$$\begin{array}{}\text{(4)}& \left\{\begin{array}{l}{\mathit{\omega }}_{\mathrm{rd}}=\frac{v_x}{L(\mathrm{1}+K{v}_x^{\mathrm{2}})}{\mathit{\delta }}_{\mathrm{d}}\\ {\mathit{\varphi }}_{\mathrm{rd}}=\mathrm{0}\end{array}\right.\end{array}$$

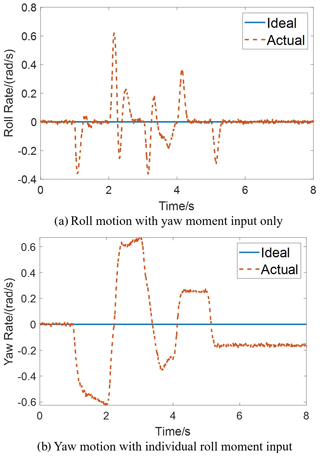
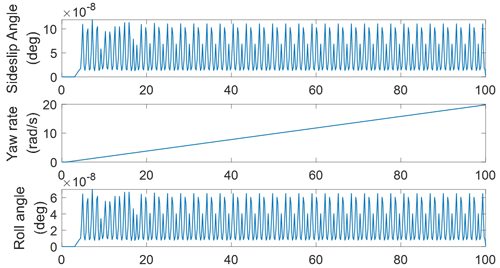
Based on the dynamic model without any decoupling transformation, the above trajectory-tracking control tasks are analyzed, and the results are shown in Fig. 3. It can be seen that the lateral motion and vertical motion of the chassis system cannot be controlled separately and are coupled with each other. In other words, the lateral motion cannot be corrected separately without affecting the vertical motion, and vice versa.

Figure 3 Analysis of coupling characteristics of the trajectory-tracking process.

3 Decoupling active disturbance rejection (DADR) trajectory-tracking control strategy

In this section, to suppress the random roll motion caused by the coupling of lateral and vertical dynamic signals during the trajectory tracking, a decoupling active disturbance rejection (DADR) trajectory-tracking control strategy is proposed. The control strategy is shown in Fig. 4. First, the α-order pseudo-linear composite chassis system is obtained, which decouples the input signal and output signal of the coupling system. Then, a trajectory-tracking control strategy with DADR for the pseudo-linear composite system is proposed, which can realize the independent anti-interference control of the lateral or vertical motion of the chassis system. Next, the convergence of extended-state observer (ESO) is verified, and a multi-objective optimization method based on bandwidth parameters of the DADR trajectory-tracking controller is proposed according to its convergence conditions, which can demonstrate that the system has better anti-interference performance in the process of trajectory tracking.

Figure 4 Decoupling active disturbance rejection (DADR) trajectory-tracking control strategy.

3.1 DADR trajectory-tracking control strategy for the pseudo-linear composite system

To complete the abovementioned control tasks, a pseudo-linear composite system is established by constructing an inverse system, which realizes the decoupling of lateral and vertical input and output. To build the inverse system, the system reversibility is first proved by introducing the following definitions and lemmas.

Definition 1 (Wu et al., 2020) is that nonlinear systems will be reversible if the system has a relative order vector, as in Eq. (5).

$$\begin{array}{}\text{(5)}& \sum _{i=\mathrm{1}}^{i=q}{\mathit{\alpha }}_i,\end{array}$$

where α_i is the relative order vector of the original system, and i is the ith output signal of the system.

If $\sum _{i=\mathrm{1}}^{i=q}{\mathit{\alpha }}_i\le n$, then the system is reversible. n is the matrix order of the original system.

Lemma 1 (Wang et al., 2018) is created, for which the existence condition of the relative order vector is presented. We continuously derive the system output variable $y=h(x,u)$ until each component in ${\mathit{Y}}_{\mathit{q}}=[y_{\mathrm{1}}^{{(}^{{\mathit{\alpha }}^{\mathrm{1}}})},y_{\mathrm{2}}^{{(}^{{\mathit{\alpha }}^{\mathrm{2}}})},\mathrm{\dots },y_q^{{(}^{{\mathit{\alpha }}^q})}{]}^{\mathrm{T}}$ can contain the input u, and ${\mathit{Y}}_{\mathit{q}}=[y_{\mathrm{1}}^{{(}^{{\mathit{\alpha }}^{\mathrm{1}}})},y_{\mathrm{2}}^{{(}^{{\mathit{\alpha }}^{\mathrm{2}}})},\mathrm{\dots },y_q^{{(}^{{\mathit{\alpha }}^q})}{]}^{\mathrm{T}}$ is the full rank of the Jacobian matrix of the input u; then, the system has a relative order vector, as in Eq. (6).

$$\begin{array}{}\text{(6)}& \mathit{\alpha }={\left[{\mathit{\alpha }}_{\mathrm{1}},{\mathit{\alpha }}_{\mathrm{2}},\mathrm{\dots },{\mathit{\alpha }}_q\right]}^{\mathrm{T}}\end{array}$$

Based on Definition 1 and Lemma 1, the system reversibility of the coupled chassis system is proved.

First, the output signal of the lateral and vertical coupled chassis system is obtained from Eq. (2). According to Lemma 1, the derivative of the output vector $\mathit{y}=[\mathit{\beta },{\mathit{\omega }}_r,{\mathit{\varphi }}_r{]}^{\mathrm{T}}$, with the input vector u, is calculated, as shown in Eq. (7).

$$\begin{array}{rl}& \left[\begin{array}{c}{\dot{y}}_{\mathrm{1}}\\ {\dot{y}}_{\mathrm{2}}\\ {\ddot{y}}_{\mathrm{3}}\end{array}\right]=\left[\begin{array}{c}\dot{\mathit{\beta }}\\ {\dot{\mathit{\omega }}}_r\\ {\ddot{\mathit{\varphi }}}_r\end{array}\right]=\left[\begin{array}{c}\frac{-(\mathrm{2}{k}_{\mathrm{f}}+\mathrm{2}{k}_{\mathrm{r}})}{m{v}_x}\\ \frac{\mathrm{2}b{k}_r-\mathrm{2}a{k}_{\mathrm{f}}}{I_z}\\ \mathrm{0}\end{array}\right]\mathit{\beta }\\ & +\left[\begin{array}{c}\mathrm{0}\\ \frac{(b{m}_r-a{m}_{\mathrm{f}})v_x}{I_z}\\ -\frac{m_{\mathrm{s}}{v}_{x}h}{I_x}\end{array}\right]\dot{\mathit{\beta }}+\left[\begin{array}{c}\frac{\mathrm{2}b{k}_r-\mathrm{2}a{k}_{\mathrm{f}}}{m{v}_x^{\mathrm{2}}}-\mathrm{1}\\ \frac{-\mathrm{2}{a}^{\mathrm{2}}{k}_{\mathrm{f}}-\mathrm{2}{b}^{\mathrm{2}}{k}_{\mathrm{r}}+(b{m}_r-a{m}_{\mathrm{f}})v_x^{\mathrm{2}}}{v_x{I}_z}\\ \frac{-ms{v}_{x}h}{Ix}\end{array}\right]{\mathit{\omega }}_r\end{array}$$

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& +\left[\begin{array}{c}\frac{(b{m}_r-a{m}_{\mathrm{f}})}{m{v}_x}\\ \mathrm{0}\\ -\frac{I_{xz}}{I_x}\end{array}\right]{\dot{\mathit{\omega }}}_r+\left[\begin{array}{c}\frac{\mathrm{2}{k}_{\mathrm{f}}{E}_{\mathrm{f}}+\mathrm{2}{k}_{\mathrm{r}}{E}_{\mathrm{r}}}{m{v}_x}\\ \frac{\mathrm{2}a{k}_{\mathrm{f}}{E}_{\mathrm{f}}-\mathrm{2}b{k}_r{E}_{\mathrm{r}}}{I_z}\\ \frac{m_{\mathrm{s}}gh-K_{\mathit{\varphi }}}{I_x}\end{array}\right]{\mathit{\varphi }}_r\\ & +\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ -\frac{D_{\mathit{\varphi }}}{I_x}\end{array}\right]{\dot{\mathit{\varphi }}}_r+\left[\begin{array}{c}-\frac{m_{\mathrm{s}}h}{m{v}_x}\\ -\frac{I_{xz}}{I_z}\\ \mathrm{0}\end{array}\right]\ddot{\mathit{\varphi }}r\\ & +\left[\begin{array}{c}\frac{\mathrm{2}{k}_{\mathrm{f}}}{m{v}_x}\\ \frac{\mathrm{2}a{k}_{\mathrm{f}}}{I_z}\\ \mathrm{0}\end{array}\right](\mathit{\delta }+{\mathit{\delta }}_{\mathrm{d}})+\left[\begin{array}{c}\mathrm{0}\\ \frac{\mathrm{1}}{I_z}\\ \mathrm{0}\end{array}\right]T_z+\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \frac{\mathrm{1}}{I_x}\end{array}\right]T_{\mathit{\varphi }}\end{array}\end{array}$$

The relative order vector is discussed according to Lemma 1. Assuming $Y_{\mathrm{1}}={\dot{y}}_{\mathrm{1}}$, the rank to the Jacobian matrix of the control input u is shown in Eq. (8). The first derivative equation of y₁ contains the control input u for the first time, and the Jacobian matrix of Y₁ to u is full rank, so that α₁=1.

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{t}_{\mathrm{1}}& =\text{rank}\left[{\displaystyle \frac{\partial Y_{\mathrm{1}}}{\partial u^{\mathrm{T}}}}\right]=\text{rank}\left[{\displaystyle \frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial \mathit{\delta }}},{\displaystyle \frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial T_z}},{\displaystyle \frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial T_{\mathit{\varphi }}}}\right]\\ & =\text{rank}\left[{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{f}}}{m{v}_x}},\mathrm{0},\mathrm{0}\right]=\mathrm{1}\end{array}\end{array}$$

Next, assuming $Y_{\mathrm{2}}=[{\dot{y}}_{\mathrm{1}},{\dot{y}}_{\mathrm{2}}{]}^{\mathrm{T}}$, the rank of the Jacobian matrix of u is shown in Eq. (9). The first derivative equation of y₂ contains the input u for the first time, and the Jacobian matrix of Y₂ to u is full rank, so that α₂=1.

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{t}_{\mathrm{2}}& =\text{rank}\left[{\displaystyle \frac{\partial Y_{\mathrm{2}}}{\partial u^{\mathrm{T}}}}\right]=\text{rank}\left[\begin{array}{ccc}\frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial \mathit{\delta }}& \frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial T_z}& \frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial T_{\mathit{\varphi }}}\\ \frac{\partial {\dot{y}}_{\mathrm{2}}}{\partial \mathit{\delta }}& \frac{\partial {\dot{y}}_{\mathrm{2}}}{\partial T_z}& \frac{\partial {\dot{y}}_{\mathrm{2}}}{\partial T_{\mathit{\varphi }}}\end{array}\right]\\ & =\text{rank}\left[\begin{array}{ccc}\frac{\mathrm{2}{k}_{\mathrm{f}}}{m{v}_x}& \mathrm{0}& \mathrm{0}\\ \frac{\mathrm{2}a{k}_{\mathrm{f}}}{I_z}& \frac{\mathrm{1}}{I_z}& \mathrm{0}\end{array}\right]=\mathrm{2}\end{array}\end{array}$$

Assuming $Y_{\mathrm{3}}=[{\dot{y}}_{\mathrm{1}},{\dot{y}}_{\mathrm{2}},{\ddot{y}}_{\mathrm{3}}{]}^{\mathrm{T}}$, the rank of the Jacobian matrix to u is shown in Eq. (10). The second derivative equation of y₃ contains the input u for the first time, and the Jacobian matrix of Y₃ has full rank to u, so that α₃=2.

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{t}_{\mathrm{3}}& =\text{rank}\left[{\displaystyle \frac{\partial Y_{\mathrm{3}}}{\partial u^{\mathrm{T}}}}\right]=\text{rank}\left[\begin{array}{ccc}\frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial \mathit{\delta }}& \frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial T_z}& \frac{\partial {\dot{y}}_{\mathrm{1}}}{\partial T_{\mathit{\varphi }}}\\ \frac{\partial {\dot{y}}_{\mathrm{2}}}{\partial \mathit{\delta }}& \frac{\partial {\dot{y}}_{\mathrm{2}}}{\partial T_z}& \frac{\partial {\dot{y}}_{\mathrm{2}}}{\partial T_{\mathit{\varphi }}}\\ \frac{\partial {\dot{y}}_{\mathrm{3}}}{\partial \mathit{\delta }}& \frac{\partial {\dot{y}}_{\mathrm{3}}}{\partial T_z}& \frac{\partial {\dot{y}}_{\mathrm{3}}}{\partial T_{\mathit{\varphi }}}\end{array}\right]\\ & =\text{rank}\left[\begin{array}{ccc}\frac{\mathrm{2}{k}_{\mathrm{f}}}{m{v}_x}& \mathrm{0}& \mathrm{0}\\ \frac{\mathrm{2}a{k}_{\mathrm{f}}}{I_z}& \frac{\mathrm{1}}{I_z}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \frac{\mathrm{1}}{I_x}\end{array}\right]=\mathrm{3}\end{array}\end{array}$$

From Lemma 1, since the Jacobian matrix of $Y_{\mathrm{3}}=[{\dot{y}}_{\mathrm{1}},{\dot{y}}_{\mathrm{2}},{\ddot{y}}_{\mathrm{3}}{]}^{\mathrm{T}}$ to u is full rank, the system has a relative order vector, as shown in Eq. (11).

$$\begin{array}{}\text{(11)}& \mathit{\alpha }={\left[{\mathit{\alpha }}_{\mathrm{1}},{\mathit{\alpha }}_{\mathrm{2}},{\mathit{\alpha }}_{\mathrm{3}}\right]}^{\mathrm{T}}=[\mathrm{1},\mathrm{1},\mathrm{2}{]}^{\mathrm{T}}\end{array}$$

According to Definition 1, ${\mathit{\alpha }}_{\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}+{\mathit{\alpha }}_{\mathrm{3}}=\mathrm{4}=n$. Therefore, the original integrated chassis system is reversible. The decoupling of the coupled signals in the original chassis system can be achieved by establishing an inverse system.

According to the above analysis, the coupled chassis system is reversible, which means the input and output signals of the original system can be decoupled by establishing a pseudo-linear composite system to achieve the compensation control for trajectory tracking. Then, the inverse system model of the coupled chassis system and the α-order pseudo-linear composite system will be established and analyzed. The following definitions and lemmas are introduced to present the derivation process.

For Lemma 2, in the α-order inverse system, the operator θ is used to represent the input–output relationship of a nonlinear system Σ with p-dimensional input and q-dimensional output, as shown in Eq. (12).

$$\begin{array}{}\text{(12)}& y=\mathit{\theta }u,\end{array}$$

where u is the control input of the original system, and y is the control output of the original system.

Assuming Π_α is a system with q input and p output, the mapping relationship between input and output is shown in Eq. (13).

$$\begin{array}{}\text{(13)}& u={\stackrel{\mathrm{‾}}{\mathit{\theta }}}_{\mathit{\alpha }}{\left[{\mathit{\phi }}_{\mathrm{1}},{\mathit{\phi }}_{\mathrm{2}},\mathrm{\dots },{\mathit{\phi }}_q\right]}^{\mathrm{T}},\end{array}$$

where $[{\mathit{\phi }}_{\mathrm{1}},{\mathit{\phi }}_{\mathrm{2}},\mathrm{\dots },{\mathit{\phi }}_q{]}^{\mathrm{T}}$ is a differentiable function vector whose initial value satisfies the initial value condition of the original nonlinear system Σ, and φ_i is defined as the α_i-order derivative of y_di, as Eq. (14).

$$\begin{array}{}\text{(14)}& \mathit{\phi }\left(t\right)=y_d^{\left(\mathit{\alpha }\right)}\left(t\right),\mathit{\alpha }={\left[{\mathit{\alpha }}_{\mathrm{1}},{\mathit{\alpha }}_{\mathrm{2}},\mathrm{\dots },{\mathit{\alpha }}_q\right]}^{\mathrm{T}}\end{array}$$

And if the operator ${\stackrel{\mathrm{‾}}{\mathit{\theta }}}_{\mathit{\alpha }}$ in Eq. (11) satisfies the condition in Eq. (15), then the following applies:

$$\begin{array}{}\text{(15)}& \mathit{\theta }{\stackrel{\mathrm{‾}}{\mathit{\theta }}}_{\mathit{\alpha }}\mathit{\phi }=\mathit{\theta }{\stackrel{\mathrm{‾}}{\mathit{\theta }}}_{\mathit{\alpha }}\left(y_d^{\left(\mathit{\alpha }\right)}\right)=\mathit{\theta }u=y_d.\end{array}$$

Then, the system Π_α is regarded as the α-order inverse system of the original nonlinear system Σ.

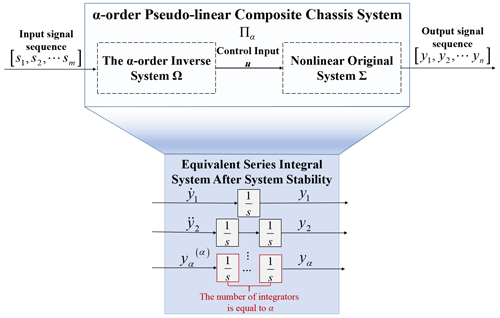
Definition 2 is the α-order pseudo-linear composite system. If the system Ω is a composite system $\mathit{\theta }{\stackrel{\mathrm{‾}}{\mathit{\theta }}}_{\mathit{\alpha }}$, with a similar linear transfer relationship composed of the α-order inverse system and the nonlinear original system Σ in series, then the system Ω is called the α-order pseudo-linear composite system.

The original multi-input–multi-output nonlinear system has been linearized and decoupled into q independent linear integral systems. The composite system $\mathit{\theta }{\stackrel{\mathrm{‾}}{\mathit{\theta }}}_{\mathit{\alpha }}$ is equivalent to several connected integrators in series, and its input and output are shown in Eq. (16).

$$\begin{array}{}\text{(16)}& y^{\left(\mathit{\alpha }\right)}=\mathit{\phi }\end{array}$$

Based on Definition 2 and Lemma 2, the inverse system model of the coupled chassis system is deduced, and then the input and output characteristics of the α-order pseudo-linear composite system are analyzed.

As shown in Eq. (2), the output of the nonlinear original system Σ is $y\left(u\right)=[v_{\mathrm{1}},v_{\mathrm{2}},v_{\mathrm{3}}{]}^{\mathrm{T}}={\left[\dot{\mathit{\beta }},{\dot{\mathit{\omega }}}_r,{\ddot{\mathit{\varphi }}}_r\right]}^{\mathrm{T}}$. From Lemma 2, the output of the α-order inverse system Π_α is the control input u of the original system, as shown in Eq. (17).

$$\begin{array}{}\text{(17)}& u=\mathit{\phi }\left(\mathit{\beta },{\mathit{\omega }}_r,{\mathit{\varphi }}_r,{\dot{\mathit{\varphi }}}_r,x,{\mathit{\delta }}_{\mathrm{d}},\dot{\mathit{\beta }},{\dot{\mathit{\omega }}}_r,{\ddot{\mathit{\varphi }}}_r\right),\end{array}$$

where

$$\begin{array}{rl}& \left[\begin{array}{c}{u}_{\mathrm{1}}\\ u_{\mathrm{2}}\\ u_{\mathrm{3}}\end{array}\right]=\left[\begin{array}{c}\mathit{\delta }\\ T_z\\ T_{\mathit{\varphi }}\end{array}\right]=\left[\begin{array}{c}\frac{(k_{\mathrm{f}}+k_{\mathrm{r}})}{k_{\mathrm{f}}}\\ -\left(\mathrm{2}b{k}_r+\mathrm{2}a{k}_r\right)\\ \mathrm{0}\end{array}\right]\mathit{\beta }\\ & +\left[\begin{array}{c}\frac{m{v}_x}{\mathrm{2}{k}_{\mathrm{f}}}\\ a\left(m_{\mathrm{f}}-m\right)v_x-b{m}_r{v}_x\\ m_{\mathrm{s}}{v}_{x}h\end{array}\right]\dot{\mathit{\beta }}\\ & +\left[\begin{array}{c}\frac{a}{v_x}-\frac{b{k}_r}{v_x{k}_{\mathrm{f}}}+\frac{m{v}_x}{\mathrm{2}{k}_{\mathrm{f}}}\\ {\displaystyle \frac{\mathrm{2}{a}^{\mathrm{2}}{k}_{\mathrm{f}}+\mathrm{2}{b}^{\mathrm{2}}{k}_{\mathrm{r}}}{v_x}}-b{v}_x{m}_{\mathrm{r}}+a{v}_x\left(m_{\mathrm{f}}-m\right)+\mathrm{4}amb{k}_r-\mathrm{4}{a}^{\mathrm{2}}m{k}_{\mathrm{f}}\\ ms{v}_{x}h\end{array}\right]{\mathit{\omega }}_r\\ & +\left[\begin{array}{c}\frac{(a{m}_{\mathrm{f}}-b{m}_r)}{\mathrm{2}{k}_{\mathrm{f}}}\\ I_z+ab{m}_r-a^{\mathrm{2}}{m}_{\mathrm{f}}\\ I_{xz}\end{array}\right]{\dot{\mathit{\omega }}}_r+\left[\begin{array}{c}-\frac{k_{\mathrm{f}}{E}_{\mathrm{f}}+k_{\mathrm{r}}{E}_{\mathrm{r}}}{k_{\mathrm{f}}}\\ \mathrm{2}b{k}_r{E}_{\mathrm{r}}+\mathrm{2}a{k}_r{E}_{\mathrm{r}}\\ -m_{\mathrm{s}}gh+K_{\mathit{\varphi }}\end{array}\right]{\mathit{\varphi }}_r\\ & +\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ D_{\mathit{\varphi }}\end{array}\right]{\dot{\mathit{\varphi }}}_r\\ & +\left[\begin{array}{c}\frac{m_{\mathrm{s}}h}{\mathrm{2}{k}_{\mathrm{f}}}\\ I_{xz}-a{m}_{s}h\\ Ix\end{array}\right]\ddot{\mathit{\varphi }}r+\left[\begin{array}{c}-\mathrm{1}\\ -\mathrm{2}a{k}_{\mathrm{f}}+\mathrm{2}a{k}_{\mathrm{f}}\\ \mathrm{0}\end{array}\right]{\mathit{\delta }}_{\mathrm{d}}.\end{array}$$

Then the state space of the inverse system is shown as Eq. (18).

$$\begin{array}{}\text{(18)}& \left\{\begin{array}{l}\dot{x}=\mathbf{E}x+\mathbf{F}v\\ u=\mathbf{K}x+\mathbf{H}v+\mathbf{Q}{\mathit{\delta }}_{\mathrm{d}}\end{array},\right.\end{array}$$

where

$$\begin{array}{rl}& \mathbf{E}=\left[\begin{array}{cccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right],\mathbf{F}=\left[\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\\ & \mathbf{H}=\left[\begin{array}{ccc}\frac{m{v}_x}{\mathrm{2}{k}_{\mathrm{f}}}& \frac{a{m}_{\mathrm{f}}-b{m}_r}{\mathrm{2}{k}_{\mathrm{f}}}& \frac{m_{\mathrm{s}}h}{\mathrm{2}{k}_{\mathrm{f}}}\\ a{m}_{\mathrm{f}}{v}_x-b{m}_r{v}_x-am{v}_x& I_z+\left(ab{m}_r-a^{\mathrm{2}}{m}_{\mathrm{f}}\right)& I_{xz}-a{m}_{s}h\\ m_{\mathrm{s}}{v}_{x}h& I_{xz}& I_x\end{array}\right],\\ & \mathbf{Q}=\left[\begin{array}{c}-\mathrm{1}\\ \mathrm{0}\\ \mathrm{0}\end{array}\right],\\ & \mathbf{K}=\left[\begin{array}{cccc}\frac{k_{\mathrm{f}}+k_{\mathrm{r}}}{k_{\mathrm{f}}}& \frac{a{k}_{\mathrm{f}}-b{k}_r}{v_x{k}_{\mathrm{f}}}+\frac{m{v}_x}{\mathrm{2}{k}_{\mathrm{f}}}& -\frac{k_{\mathrm{f}}{E}_{\mathrm{f}}+k_{\mathrm{r}}{E}_{\mathrm{r}}}{k_{\mathrm{f}}}& \mathrm{0}\\ -\mathrm{2}(a{k}_r-b{k}_r)& \frac{\left[\mathrm{2}{b}^{\mathrm{2}}{k}_{\mathrm{r}}-(b{m}_r-a{m}_{\mathrm{f}})v_x^{\mathrm{2}}+\mathrm{2}ab{k}_r-am{v}_x^{\mathrm{2}}\right]}{v_x}& \mathrm{2}b{k}_r{E}_{\mathrm{r}}+\mathrm{2}a{k}_r{E}_{\mathrm{r}}& \mathrm{0}\\ \mathrm{0}& m_{\mathrm{s}}{v}_{x}h& K_{\mathit{\varphi }}-m_{\mathrm{s}}gh& D_{\mathit{\varphi }}\end{array}\right].\end{array}$$

Next, based on the inverse system derived above and the original coupling system, the decoupled pseudo-linear composite system is obtained. The input and output characteristics of the α-order pseudo-linear composite system Π_α are presented and analyzed, as shown in Fig. 8. As shown in Fig. 5, the α-order pseudo-linear composite system Π_α is composed of the α-order inverse system Ω and the nonlinear original system Σ in series. So the original system can be equivalent to the series integral system, which is easier to design the tracking controller.

Figure 5 Series integral system obtained by pseudo-linear composite system equivalence.

For instance, with a single yaw signal input in the α-order pseudo-linear composite system, only the corresponding output value changes accordingly, and the other outputs are not affected, as shown in Fig. 6. However, although the coupled system was decoupled, some fluctuations in the other outputs still exist. And such fluctuations will be worse under road disturbance, which should be should be taken into consideration in the controller design.

Figure 6 System response analysis when the ${\dot{\mathit{\omega }}}_r$ step signal is the single input.

Next, the trajectory-tracking control strategy is designed. The purpose of the trajectory-tracking control task is to track the desired trajectory by controlling the front wheel angle and suppressing the random roll motion caused by road disturbance. To realize the above control task, a trajectory-tracking control strategy with decoupling active disturbance rejection (DADR) for the pseudo-linear composite system is proposed, as shown in Fig. 7. The lateral and vertical tracking controllers are designed separately through an active disturbance rejection control algorithm to achieve anti-interference tracking of the ideal trajectory and suppress the vertical motion at the same time.

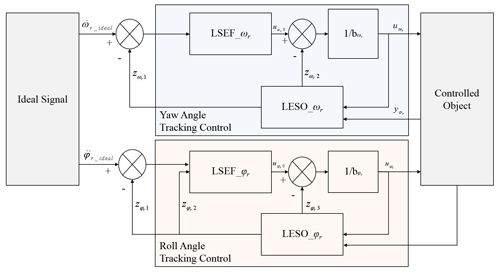
Figure 7 Trajectory-tracking controller with active disturbance rejection for a pseudo-linear system.

The standard form of the active disturbance rejection control algorithm for α-order systems is first discussed. As shown in Eq. (19),

$$\begin{array}{}\text{(19)}& y^{\left(\mathit{\alpha }\right)}=bu+f_{\mathrm{1}}\left(y,\mathit{\omega },t\right),\end{array}$$

where α is the order of the system, b is the control variable gain, y is the system output, w is system interference, and t is the time-varying state of the system. The interference sources are analyzed, including the external road input, crosswind, and other interference, as is the interference caused by the measurement error within the sensor inside the system.

Since the control variable gain b in Eq. (19) is difficult to obtain in the real control system, the estimated value b₀ is commonly used. And the disturbance caused by the inaccurate estimation is added to the total disturbance to realize the suppression of interference signals, such as road noise in the trajectory-tracking process, as shown in Eq. (20).

$$\begin{array}{}\text{(20)}& \begin{array}{rl}{y}^{\left(\mathit{\alpha }\right)}& =b_{\mathrm{0}}u+bu-b_{\mathrm{0}}u+f_{\mathrm{1}}(y,\mathit{\omega },t)\\ & =b_{\mathrm{0}}u+f(y,\mathit{\omega },t)\end{array}\end{array}$$

The state space of the α-order controlled object is shown in Eq. (21).

$$\begin{array}{}\text{(21)}& \left\{\begin{array}{rl}& \dot{x}=\mathbf{A}x+\mathbf{B}u+\mathbf{E}h\\ & y=\mathbf{C}x+\mathbf{D}u,\end{array}\right.\end{array}$$

where

$$\begin{array}{rl}& \mathbf{A}=\left[\begin{array}{cccc}\mathrm{0}& \mathrm{1}& \mathrm{\cdots }& \mathrm{0}\\ \mathrm{0}& & \mathrm{\ddots }& \mathrm{⋮}\\ \mathrm{⋮}& & & \mathrm{1}\\ \mathrm{0}& \mathrm{0}& \mathrm{\cdots }& \mathrm{0}\end{array}\right],\mathbf{B}=\left[\begin{array}{c}\mathrm{0}\\ \mathrm{⋮}\\ b_{\mathrm{0}}\\ \mathrm{0}\end{array}\right],\\ & \mathbf{C}=\left[\begin{array}{cccc}\mathrm{1}& \mathrm{0}& \mathrm{\cdots }& \mathrm{0}\end{array}\right],\mathbf{D}=\left[\mathrm{0}\right],\mathbf{E}=\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \mathrm{⋮}\\ \mathrm{1}\end{array}\right].\end{array}$$

The observer of the controlled object is shown in Eq. (22).

$$\begin{array}{}\text{(22)}& \left\{\begin{array}{l}\dot{z}=\mathbf{A}z+\mathbf{B}u+L\left(x_{\mathrm{1}}-z_{\mathrm{1}}\right)\\ y=\mathbf{C}z\end{array},\right.\end{array}$$

where L is an adjustable parameter in the state observer. A, B, L, and C are integrated into Eq. (20) to obtain the extended-state observer, as shown in Eq. (23).

$$\begin{array}{}\text{(23)}& \text{ESO}:\left\{\begin{array}{ll}\dot{z}& =\left[\begin{array}{cccc}-{\mathit{\beta }}_{\mathrm{1}}& \mathrm{1}& \mathrm{\cdots }& \mathrm{0}\\ -{\mathit{\beta }}_{\mathrm{2}}& & \mathrm{\ddots }& \mathrm{⋮}\\ \mathrm{⋮}& & & \mathrm{1}\\ -{\mathit{\beta }}_{\mathit{\alpha }}& \mathrm{0}& \mathrm{\cdots }& \mathrm{0}\end{array}\right]z\\ & +\left[\begin{array}{cc}\mathrm{0}& {\mathit{\beta }}_{\mathrm{1}}\\ \mathrm{⋮}& \mathrm{⋮}\\ b_{\mathrm{0}}& {\mathit{\beta }}_{\mathit{\alpha }-\mathrm{1}}\\ \mathrm{0}& {\mathit{\beta }}_{\mathit{\alpha }}\end{array}\right]\left[\begin{array}{c}u\\ y\end{array}\right]\\ \widehat{y}& =\left[\begin{array}{cccc}\mathrm{1}& \mathrm{0}& \mathrm{\cdots }& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& & \mathrm{0}\\ \mathrm{⋮}& & \mathrm{\ddots }& \mathrm{⋮}\\ \mathrm{0}& \mathrm{0}& & \mathrm{1}\end{array}\right]z\end{array}\right.\end{array}$$

As in Eq. (23), when ESO reaches the design goal, the last output of the extended-state observer z_α can track the real error f of the system. Therefore, the control law can be designed, as shown in Eq. (24), to achieve the control task.

$$\begin{array}{}\text{(24)}& u={\displaystyle \frac{u_{\mathrm{0}}-z_{\mathit{\alpha }}}{b_{\mathrm{0}}}}\end{array}$$

By substituting Eq. (24) into Eq. (20), Eq. (25) can be obtained.

$$\begin{array}{}\text{(25)}& y^{\left(\mathit{\alpha }\right)}=u_{\mathrm{0}}-z_{\mathit{\alpha }}+f_{\mathrm{1}}(y,\mathit{\omega },t)\end{array}$$

From the input–output relationship of the α-order pseudo-linear composite system Π_α, the yaw rate control can be regarded as the first-order system control, and the roll angle control is the second-order system control. Therefore, for the yaw rate control, the state error feedback (SEF) control law SEF_ω_r is shown in Eq. (26).

$$\begin{array}{}\text{(26)}& \text{SEF\_}{\mathit{\omega }}_r:u_{{\mathit{\omega }}_r}={\mathit{\omega }}_{\mathrm{c}}\left({\dot{\mathit{\omega }}}_{r\mathit{\_}\mathrm{ideal}}-z_{{\mathit{\omega }}_r\mathrm{1}}\right)\end{array}$$

The yaw rate control extended-state observer ESO_ω_r is shown in Eq. (27).

$$\begin{array}{}\text{(27)}& \text{ESO\_}{\mathit{\omega }}_r:\left\{\begin{array}{lcl}{\dot{z}}_{{\mathit{\omega }}_r}& =& \left[\begin{array}{cc}-{\mathit{\beta }}_{{\mathit{\omega }}_r\mathrm{1}}& \mathrm{1}\\ -{\mathit{\beta }}_{{\mathit{\omega }}_r\mathrm{2}}& \mathrm{0}\end{array}\right]z_{{\mathit{\omega }}_r}\\ & +& \left[\begin{array}{cc}{b}_{{\mathit{\omega }}_r}& {\mathit{\beta }}_{{\mathit{\omega }}_r\mathrm{1}}\\ \mathrm{0}& {\mathit{\beta }}_{{\mathit{\omega }}_r\mathrm{2}}\end{array}\right]\left[\begin{array}{c}{u}_{{\mathit{\omega }}_r}\\ y_{{\mathit{\omega }}_r}\end{array}\right]\\ {\widehat{y}}_{{\mathit{\omega }}_r}& =& \left[\begin{array}{cc}\mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}\end{array}\right]z_{{\mathit{\omega }}_r}\end{array}\right.\end{array}$$

For the roll angle control, the state error feedback control law SEF_φ_r is shown in Eq. (28).

$$\begin{array}{}\text{(28)}& \text{SEF\_}{\mathit{\phi }}_{\mathrm{r}}:u_{{\mathit{\phi }}_{\mathrm{r}}}=k_p\left({\ddot{\mathit{\varphi }}}_{r\mathit{\_}\mathrm{ideal}}-z_{{\mathit{\phi }}_{\mathrm{r}\mathrm{1}}}\right)-k_d{z}_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{2}}\end{array}$$

The roll angle control extended-state observer ESO_φ_r is shown in Eq. (29).

$$\begin{array}{}\text{(29)}& \text{ESO\_}{\mathit{\phi }}_{\mathrm{r}}:\left\{\begin{array}{lcl}{\dot{z}}_{{\mathit{\phi }}_{\mathrm{r}}}& =& \left[\begin{array}{ccc}-{\mathit{\beta }}_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{1}}& \mathrm{1}& \mathrm{0}\\ -{\mathit{\beta }}_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{2}}& \mathrm{0}& \mathrm{1}\\ -{\mathit{\beta }}_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{3}}& \mathrm{0}& \mathrm{0}\end{array}\right]z_{{\mathit{\phi }}_{\mathrm{r}}}\\ & +& \left[\begin{array}{cc}\mathrm{0}& {\mathit{\beta }}_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{1}}\\ b_{{\mathit{\phi }}_{\mathrm{r}}}& {\mathit{\beta }}_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{2}}\\ \mathrm{0}& {\mathit{\beta }}_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{3}}\end{array}\right]\left[\begin{array}{c}{u}_{{\mathit{\phi }}_{\mathrm{r}}}\\ y_{{\mathit{\phi }}_{\mathrm{r}}}\end{array}\right]\\ {\widehat{y}}_{{\mathit{\phi }}_{\mathrm{r}}}& =& \left[\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]z_{{\mathit{\phi }}_{\mathrm{r}}}\end{array}\right.\end{array}$$

When the roll angle control extended-state observer ESO_φ_r converges, then $z_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{1}}$ will converge to $y_{{\mathit{\phi }}_{\mathrm{r}}}$, and $z_{{\mathit{\phi }}_{\mathrm{r}}\mathrm{2}}$ will converge to ${\dot{y}}_{{\mathit{\phi }}_{\mathrm{r}}}$. The roll angle tracking control state error feedback control law SEF_φ_r and the stabilized controlled object are shown in Eq. (30).

$$\begin{array}{}\text{(30)}& \left\{\begin{array}{l}{u}_{\mathrm{0}}\left(s\right)=k_p\left(r\left(s\right)-y\left(s\right)\right)-k_{d}y\left(s\right)s\\ y\left(s\right)s^{\mathrm{2}}=u_{\mathrm{0}}\left(s\right)\end{array}\right.\end{array}$$

From Eq. (30), the closed-loop transfer function is shown in Eq. (31). The roll angle control extended-state observer ESO_φ_r works in an ideal state, so the transfer function between r and y is only related to the state error feedback control law. k_p and k_d directly determine the dynamic system response.

$$\begin{array}{}\text{(31)}& {\displaystyle \frac{y\left(s\right)}{r\left(s\right)}}={\displaystyle \frac{k_p}{s^{\mathrm{2}}+k_{d}s+k_p}}\end{array}$$

The controller is configured using the bandwidth method. For the controller parameters, the relationship between the bandwidth ω_c, k_p, and k_d is shown in Eq. (32).

$$\begin{array}{}\text{(32)}& {\displaystyle \frac{k_p}{s^{\mathrm{2}}+k_{d}s+k_p}}={\displaystyle \frac{{\mathit{\omega }}_{\mathrm{c}}^{\mathrm{2}}}{{\left(s+{\mathit{\omega }}_{\mathrm{c}}\right)}^{\mathrm{2}}}}={\displaystyle \frac{{\mathit{\omega }}_{\mathrm{c}}^{\mathrm{2}}}{s^{\mathrm{2}}+\mathrm{2}{\mathit{\omega }}_{\mathrm{c}}s+{\mathit{\omega }}_{\mathrm{c}}^{\mathrm{2}}}}\end{array}$$

It can be seen that ω_c corresponds to the cutoff frequency of the second-order system, since the closed-loop cutoff frequency can be applied to evaluate the closed-loop system transient response speed. A positive correlation is shown between the closed-loop cutoff frequency and dynamic system response speed. In addition, by adjusting the closed-loop cutoff frequency, the system is equivalent to a bandpass filter to remove road noise signals in specific frequency bands.

3.2 Extended-state observer (ESO) convergence proof

The DADR-based trajectory-tracking algorithm proposed in this paper has the ability of an anti-interference system because the error in the trajectory-tracking process can be estimated by the extended-state observers, ESO_ω_r and ESO_φ_r, and will be converted to an integrator series system, which is shown in Fig. 5, to achieve the control objectives of removing the interference. In this section, the convergence of ESO is proved, and a multi-objective optimization method of bandwidth parameters of the DADR trajectory-tracking controller is proposed according to its convergence conditions.

The following definitions are introduced to present the proposed controller derivation in detail.

For Definition 3 (Li and Lam, 2013), the linear time-invariant system is shown in Eq. (33).

$$\begin{array}{}\text{(33)}& \dot{X}=\mathbf{A}X\end{array}$$

The necessary and sufficient condition for a system to be asymptotically stable at the origin is that all the characteristic roots of matrix A have negative real parts, and the characteristic polynomial is shown in Eq. (34).

$$\begin{array}{}\text{(34)}& \left|SI-\mathbf{A}\right|=S^n+a_{\mathrm{1}}{S}^{n-\mathrm{1}}+\mathrm{\dots }{a}_{n-\mathrm{1}}S+a_n\end{array}$$

Its n-zero real points λ_i are completely located on the left half of the plane, as shown in Eq. (35).

$$\begin{array}{}\text{(35)}& \mathit{Re}{\mathit{\lambda }}_i<\mathrm{0}\end{array}$$

Taking the second-order system as an example, the convergence of the roll angle control extended-state observer ESO_φ_r is proved.

From the equation of the roll angle extended-state observer ESO_φ_r, the differential equation state estimation can be obtained, as in Eq. (36).

$$\begin{array}{}\text{(36)}& \dot{z}=\left(\mathbf{A}-L\mathbf{C}\right)z+\mathbf{B}u+Ly\end{array}$$

The state estimation error differential equation is established as Eq. (37). With increasing time, the estimation error value will tend to be 0.

$$\begin{array}{}\text{(37)}& \dot{x}-\dot{z}=\left(\mathbf{A}-L\mathbf{C}\right)(x-z)\end{array}$$

The state estimation error is defined as Eq. (38).

$$\begin{array}{}\text{(38)}& e=x-z\end{array}$$

From Eqs. (37) and (38), we obtain the following:

$$\begin{array}{}\text{(39)}& \dot{e}=\left(\mathbf{A}-L\mathbf{C}\right)e.\end{array}$$

The characteristic equation is obtained as Eq. (40). For the differential equation shown in Eq. (40), β₁, β₂, and β₃ are configured according to Definition 3. The eigenvalue can be less than 0 to ensure its convergence and system stability.

$$\begin{array}{}\text{(40)}& \left|\mathit{\lambda }\mathbf{I}-\left(\mathbf{A}-L\mathbf{C}\right)\right|={\mathit{\lambda }}^{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{1}}{\mathit{\lambda }}^{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{2}}\mathit{\lambda }+{\mathit{\beta }}_{\mathrm{3}}\end{array}$$

The controller parameters are configured using the bandwidth method (Fu and Tan, 2018), as shown in Eq. (41).

$$\begin{array}{}\text{(41)}& \begin{array}{rl}& {\mathit{\lambda }}^{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{1}}{\mathit{\lambda }}^{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{2}}\mathit{\lambda }+{\mathit{\beta }}_{\mathrm{3}}={\left(\mathit{\lambda }+{\mathit{\omega }}_{\mathrm{0}}\right)}^{\mathrm{3}}\\ & ={\mathit{\lambda }}^{\mathrm{3}}+\mathrm{3}{\mathit{\omega }}_{\mathrm{0}}{\mathit{\lambda }}^{\mathrm{2}}+\mathrm{3}{\mathit{\omega }}_{\mathrm{0}}^{\mathrm{2}}\mathit{\lambda }+{\mathit{\omega }}_{\mathrm{0}}^{\mathrm{3}}\end{array}\end{array}$$

The system will be stable if, and only if, ω₀>0.

According to Eq. (41), the relationship between the extended-state observer ESO parameter and the observer bandwidth ω_o is shown in Eq. (42).

$$\begin{array}{}\text{(42)}& {\mathit{\beta }}_{\mathrm{1}}=\mathrm{3}{\mathit{\omega }}_{\mathrm{0}};{\mathit{\beta }}_{\mathrm{2}}=\mathrm{3}{\mathit{\omega }}_{\mathrm{0}}^{\mathrm{2}};{\mathit{\beta }}_{\mathrm{3}}={\mathit{\omega }}_{\mathrm{0}}^{\mathrm{3}}\end{array}$$

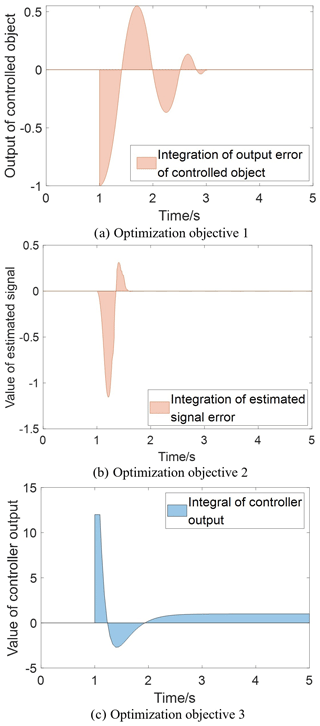
The extended-state observer bandwidth ω_o and the controller bandwidth ω_c are further discussed. ESO can convert the original problem into a series integrator control problem because the z_α of ESO can rapidly suppress the disturbance of the control object, which is equivalent to the inner loop of the controller, so the response speed is faster than the SEF of the outer loop. Therefore, the observer bandwidth ω_o should be larger than the controller bandwidth ω_c, but the excessive observer bandwidth is difficult to be realized in practical engineering and wastes the control output. In addition, for the controller bandwidth ω_c, the excessive bandwidth will also waste the control energy, and it is difficult to suppress the road noise signal of too small a bandwidth (Mosquera-Sánchez et al., 2017; Sahu et al., 2014). To sum up, the objective function in Eq. (43) is established to optimize the extended-state observer bandwidth ω_o.

$$\begin{array}{}\text{(43)}& \left\{\begin{array}{ll}min& \left\{f_{\mathrm{1}}\left({\mathit{\omega }}_{\mathrm{c}}\right),f_{\mathrm{2}}\left(a_c\right),f_{\mathrm{3}}\left(u\right)\right\}\\ \text{where}& f_{\mathrm{1}}\left({\mathit{\omega }}_{\mathrm{c}}\right)=\int y_{\mathrm{ideal}}\mathrm{d}t-\int y\mathrm{d}t\\ & f_{\mathrm{2}}\left(a_c\right)=\int f_{\mathrm{ideal}}\mathrm{d}t-\int z_{\mathit{\alpha }}\mathrm{d}t\\ & f_{\mathrm{3}}\left(u\right)=\int (u-\mathrm{0})\mathrm{d}t\\ & {\mathit{\omega }}_{\mathrm{o}}=a_c{\mathit{\omega }}_{\mathrm{c}}\\ \text{subject to}& {\mathit{\omega }}_{\mathrm{c}}\in \left[\mathrm{10},\mathrm{120}\right]\\ & a_c\in [\mathrm{2},\mathrm{8}]\\ & u\in \left[\mathrm{0},\mathrm{100}\right]\end{array},\right.\end{array}$$

where ω_c, a_c, and u are design variables to achieve the design goals so that the inner loop responds faster than the outer loop by adjusting the weight parameters. The objective function f₁(ω_c) represents the difference between the integral of the target signal and the integral of the actual system output. The objective function f₁(ω_c) is defined to evaluate the system response speed, overshoot, and steady-state error. The objective function f₂(a_c) is the difference between ∫f_ideal and ∫z_α, which represent the integral of the prior-known noise signal and the integral of the noise observation, respectively. The objective function f₂(a_c) is minimized to realize fast and accurate noise estimation. The objective function f₃(u) is defined as the integral of the controller output. The upper and lower bounds of the constraint are obtained through bench testing and then corrected through multiple tests. The schematic diagrams of these three objective functions are shown in Fig. 8. Due to the relative contradiction between the three objectives, the Pareto solution sets are obtained through iterative optimization, and then the required optimal solution is selected (Rodríguez-Molina et al., 2020; Wu et al., 2019).

Figure 8 Schematic diagram of optimization objectives.

The above analysis shows that it will inevitably lead to large controller output if the trajectory-tracking performance needs to be improved. Therefore, a multi-objective particle swarm optimization (PSO) algorithm is applied to optimize these contradictory objectives. The main steps are listed as follows (Zhao et al., 2018).

Step 1 – problem definition. This includes the model definition and algorithm parameters definition.

1. Model definition. This is the optimization objectives, constraints, and design variables.

2. Algorithm parameters definition. This includes the maximum iterations I_te, the number of particles n_ori, inertia weight w, weight descent rate w_damp, individual learning factor c₁, global learning factor c₂, and Pareto set threshold n_TPareto.

Step 2 – initialization. This is the position and velocity that are assigned for each particle, and the fitness function is calculated.

Step 3 – calculation cycle. This algorithm consists of a PSO module, decomposition module, and Pareto module. The particle velocity, position, and fitness functions are updated by the PSO module. The decomposition module is used to decompose and search the updated particles provided by the PSO module. Finally, the termination conditions are checked, and the Pareto set is obtained (Mac et al., 2018).

Step 4. If the termination conditions are not satisfied, then the iteration process will return to Step 3. Otherwise, the Pareto solution set will be obtained.

4 Results and discussion

The time–frequency domain analysis is conducted in multiple working conditions, and the system dynamic performance of the proposed control strategy is discussed. Then, a hardware-in-the-loop chassis test platform is designed based on dSPACE AutoBox and MATLAB/CarSim software. The proposed control strategy is verified for the lane-changing trajectory-tracking conditions in the established virtual traffic environment. And the simulation results are compared with the neural network proportional integral derivative (PID) control strategy in Wang et al. (2018). It proves that the proposed control strategy can effectively enhance trajectory-tracking accuracy and system anti-disturbance performance.

According to the analysis in Sect. 4, the system's dynamic response performance can be improved by optimizing controller bandwidth parameters and observer bandwidth parameters using a multi-objective optimization algorithm. The multi-objective optimization algorithm parameters are listed in Table 1.

Table 1 Initial setting of multi-objective particle swarm optimization algorithm.

The system dynamic behaviors are discussed in the time–frequency domain first. Then, based on the HIL test results, the system response of the proposed control strategy and the neural network PID method are compared and analyzed for the lane-changing trajectory-tracking conditions.

4.1 System dynamic performance simulation in the time–frequency domain

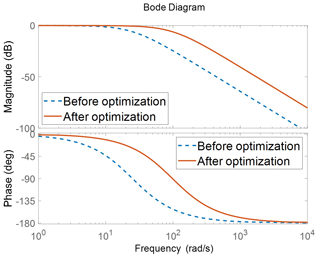
The trajectory-tracking performance and system robustness of the proposed control strategy are discussed based on the time–frequency simulation results. First, from the perspective of the frequency domain analysis, the natural frequencies of lateral vibration and vertical vibration are from 2 to 6 Hz (Morioka and Griffin, 2010; Arnold and Griffin, 2018). The road excitation within this frequency range will result in vehicle resonance, so the controller is required to suppress the signals within the natural frequencies. In this work, the bandwidth method is applied to design the controller's cutoff frequency. The original and optimum Bode diagrams are shown in Fig. 9.

Figure 9 Bode diagram of the system before and after optimization.

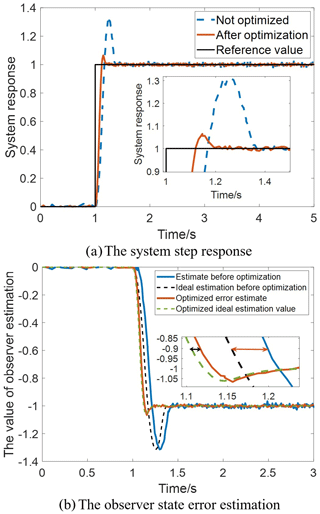
Figure 10 presents the system response in the time domain with the inputs of step signal and the prior-known interference, which verifies the improvement in the system's anti-interference performance. Compared with the benchmark, the dynamic system response speed is dramatically improved by 43.64 %. In addition, the accuracy of the observer state error estimation is improved by 11.93 %. The optimized system can estimate the interference signal faster, which is the foundation of the system simplification and the improvement of trajectory-tracking accuracy.

Figure 10 The dynamic system performance in the time domain.

As shown in Fig. 10, the baseline observer has a delay of 0.3 s compared with the target signal. Within 1 to 1.3 s, the system cannot be regarded as a multistage series system, so high-precision control performance is unlikely to be achieved in the baseline observer. However, the optimized system can effectively balance the contradiction of controller bandwidth, observer bandwidth, and control outputs to improve dynamic system performance.

4.2 Trajectory-tracking performance of the hardware-in-the-loop test

In this section, the hardwire-in-the-loop test platform for an X-by-wire chassis is established, based on the MicroAutoBox 1401/1501 (dSPACE GmbH). And the lane-changing trajectory-tracking conditions are established in the virtual traffic environment of MATLAB/CarSim. The effectiveness of the proposed trajectory-tracking control strategy is verified and compared with the neural network PID method in this test platform. The test platform is shown in Fig. 11. The chassis controller output of the platform is collected by the data acquisition card and is transmitted to the vehicle model in the virtual traffic environment. After that, the yaw rate and dynamic model parameters are calculated based on the vehicle model in the virtual traffic environment, which is transmitted to the chassis controller of the real vehicle in real time through the controller area network (CAN) network. This procedure realizes the closed-loop interaction between the real vehicle chassis controller and the virtual traffic environment.

Figure 11 The hardware-in-the-loop test platform.

The experimental results are analyzed below and compared with benchmarks. Figure 12 presents the performance of the proposed control strategy on decoupling with uncertain road interference. Both the benchmark and the proposed control strategy can realize the decoupling of lateral and vertical signals. However, in the case of interference, the variance between the actual signal and the ideal signal obtained by the proposed control strategy can be reduced by 51.61 % when compared with that of the benchmark. The mechanism of the above phenomenon is analyzed. The neural network PID inverse system requires a large number of prior-known training data. As for the model uncertainty from road interference, the training dataset is unlikely to cover all the working conditions. Therefore, the neural network PID inverse system cannot eliminate the coupling on the signal layer, which will result in the chassis system interference on the mechanical layer.

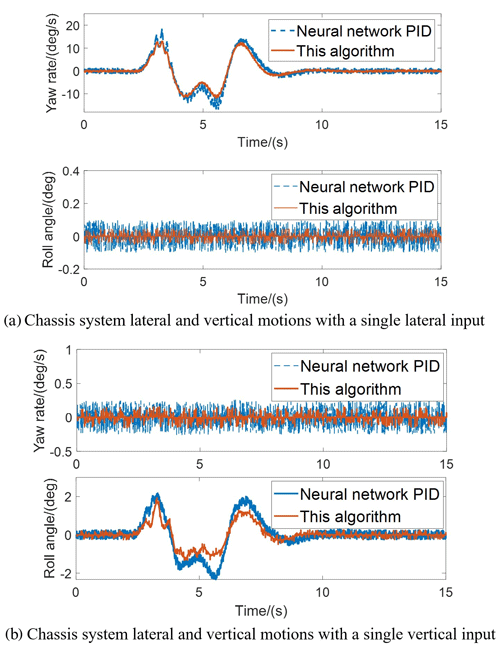
Figure 12 The performance of the proposed control strategy on decoupling with the uncertain road interference.

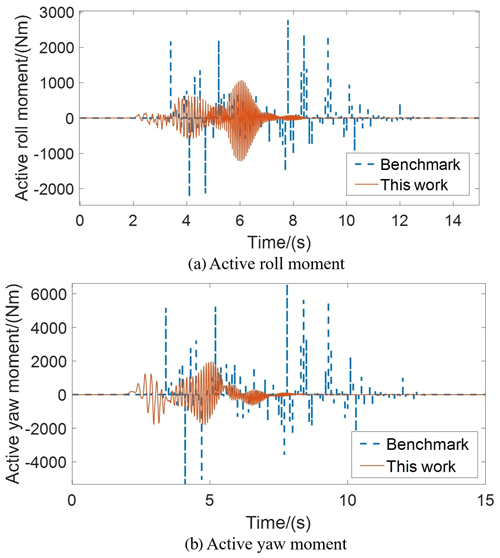
Then, the effectiveness of the proposed trajectory-tracking control strategy is discussed. The active control signals to the controlled object are shown in Fig. 13. The active yaw and roll moment can effectively resist road interferences and enhance the trajectory-tracking performance. Compared with the benchmark, the proposed control strategy can provide a faster response of active yaw moment and roll moment when road disturbances exist. The peak values of active yaw and roll moment obtained by the proposed control strategy can be reduced by 61.45 % and 70.49 %, respectively.

Figure 13 Control signals of active yaw torque and roll torque.

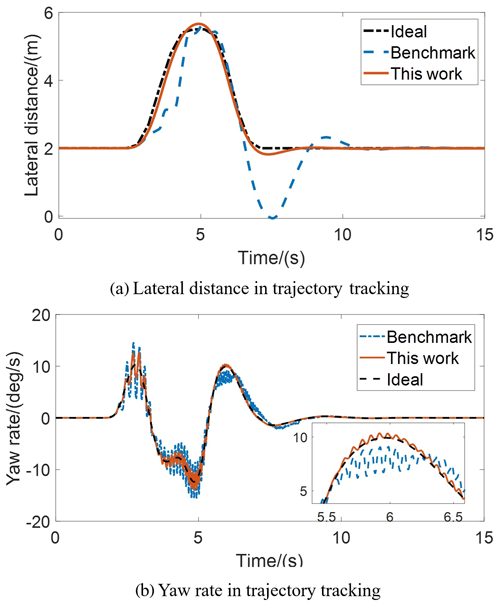
The benefits of the proposed control strategy on the anti-interference ability are compared from the perspectives of the lateral distance and yaw rate in trajectory tracking in Fig. 14. Compared with the benchmark, the proposed control strategy can reduce the trajectory-tracking error by 10.03 %, and the variance of the error within the yaw rate can be reduced by 34.54 %.

Figure 14 The lateral distance and yaw rate in trajectory tracking.

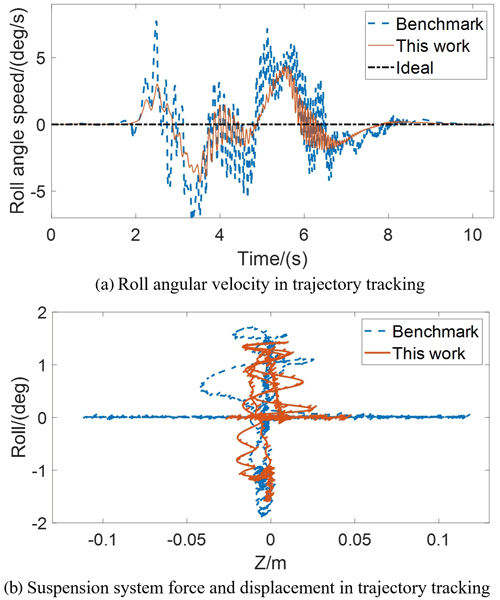
From the perspective of vertical motion control, compared with the benchmark, the proposed control strategy can reduce the peak roll angular velocity by 43.64 %. The trajectory-tracking performance on stability is further discussed. The suspension system force and displacement are shown in Fig. 15. The vertical relative displacement of the proposed control strategy is smaller compared with the benchmark. Therefore, the vehicle body behaves more stably with the proposed control strategy in the trajectory-tracking process.

Figure 15 Comparison of vertical output control effects in trajectory tracking.

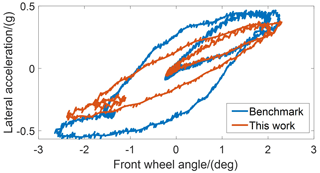
The conclusion can be further verified in Fig. 16. It shows the front wheel angle and lateral acceleration in trajectory tracking. With the same front wheel angle, the lateral acceleration obtained by the proposed control is relatively smaller compared to that of the benchmark. The proposed control strategy can effectively reduce the chassis system interference on the mechanical layer induced by the coupling on the signal layer.

Figure 16 Front wheel angle and lateral acceleration of chassis system in trajectory tracking.

5 Conclusion

In this paper, a coupled dynamic model of the X-by-wire chassis system is established, and the α-order chassis pseudo-linear composite system is obtained. On this basis, a decoupling active disturbance rejection (DADR) trajectory-tracking control strategy is proposed, and a multi-objective optimization method of bandwidth parameters of the DADR trajectory-tracking controller is proposed, according to its convergence conditions.

As far as the results of the simulation and hardware-in-the-loop test is concerned, the trajectory-tracking error within the proposed control strategy can be reduced by 10.03 %, compared with the benchmark, and the variance of the error within the yaw rate can be reduced by 34.54 %. In particular, when road interference existed, the chassis system with the proposed control strategy can track the target trajectory more stably. In addition, the peak value of vehicle roll angular velocity with the proposed strategy can be reduced by 43.64 %. And the relative vertical displacement is remarkably reduced, which demonstrates that the proposed strategy makes the vehicle body more stable.

In the future, first, the vehicle trajectory-tracking model with higher degrees of freedom should be studied, and the trajectory-tracking control method under the condition of actuator failure should be studied. Moreover, a large number of tests should be carried out through a hardware-in-the-loop test and real vehicle road tests to support the theoretical research.