Stiffness analysis of a 3-DOF parallel mechanism for engineering special machining

There are considerably rigorous requirements for accuracy and stability of the mechanism to accomplish large-scale and complex surface machining tasks in the aerospace field. In order to improve the stiffness performance of the parallel mechanism, this paper proposes a novel three degrees of freedom (DOF) redundantly actuated 2RPU-2SPR (where R, P, U and S stand for revolute, prismatic, universal and spherical joints, respectively) parallel mechanism. Firstly, the kinematics position inverse solution is derived and a dimensionless generalized Jacobian matrix is established through the driving Jacobian matrix and constraint Jacobian matrix. Secondly, the stiffness model of the parallel mechanism is deduced and the accuracy of the stiffness model is verified through finite-element analysis. Using eigenscrew decomposition to illustrate the physical interpretation of the stiffness matrix, the stiffness matrix is equivalent to six simple screw springs. Finally, the simulation experiment results demonstrate that redundantly actuated parallel mechanism has better stiffness performance compared to the traditional 2RPU-SPR parallel mechanism.

1 Introduction

In the field of industrial manufacturing, the processing equipment with the parallel mechanism has been widely used and researched because of its excellent performance. Tian et al. (2019) proposed a novel robot leg deformable parallel mechanism with the ability of reconstruction and motion change based on an innovative rotatable-axis revolute joint. Araujo-Gómez et al. (2019) carried out kinematic analysis and size optimization of 2R2T (where R and T stand for rotational and translational degrees of freedom, respectively) parallel mechanism. Wu et al. (2014) systematically introduced and discussed a series of 2-DOF parallel manipulators with equal–diameter spherical pure rotation. Three-DOF parallel mechanism is one of the most noticeable and widespread mechanisms and Li and Hervé (2010) synthesized a series of 3-DOF parallel mechanisms. The finite motions of 1T2R parallel mechanisms with parasitic motions were described and analyzed by Sun and Huo (2018) and their topologies were synthesized. Huang et al. (2019) proposed a simple and highly visual method for type synthesis of families of over-constrained parallel mechanisms with one translational and two rotational motion capabilities. In order to expand the application of parallel manipulators, Wu et al. (2018) created a 5-DOF hybrid machine and a mechatronics model was derived based on this parallel manipulator.

Stiffness design refers to optimization based on a certain stiffness analysis model with structural parameters as variables to improve the stiffness performance of the mechanism. A stiffness synthesis strategy was proposed for the desired elastic center of a 3-DOF parallel mechanism composed of 3RPR links (Wen et al., 2015). The Exechon parallel mechanism with over-constrained kinematic chain has attracted extensive attention in the research community and its stiffness has been studied by Zhang et al. (2016). Moosavian et al. (2016) introduced a method for designing variable geometry parallel mechanism with enhanced static properties. Generally, higher stiffness allows greater variable load and higher precision of the end–effector. There is no unified strategy to establish the stiffness model of the parallel mechanism and many experts have done relevant research on different types of parallel mechanisms. A new variable stiffness design method was proposed to optimize the geometric parameters of the parallel mechanism by Li et al. (2017). For the heavy-duty parallel robot manipulator, Wang et al. (2017) proposed a method to simultaneously optimize the size and structural parameters and introduced a stiffness performance evaluation index. This stiffness distribution index mainly focuses on the stiffness components of the manipulator. Moosavian et al. (2014) introduced a new method to enhance the stiffness of parallel mechanisms without redundant actuation. Chen et al. (2018) showed a negative stiffness criterion for active stiffness using the example of a redundantly actuated planar parallel mechanism. Ali et al. (2018) also studied the stiffness of the parallel mechanism. Moreover, the over-constrained parallel mechanism can also be more widely applied by combining with sliding rail such as the serial parallel hybrid 5-axis machining machine tool. In order to meet the requirements of the large workspace and high dexterity of aerospace industry processing equipment, Fang et al. (2020) and Jiang et al. (2021) proposed a new type of series–parallel hybrid processing robot mechanism. Portman (2020) presented a new method to define stiffness values for elastic support systems and demonstrated the effectiveness and generality of the method with examples of simulated applications. Cao et al. (2017) summarized a method for modeling stiffness of a 3R2T over-constrained parallel robot mechanism. The proposed method can be conveniently applied to build stiffness models with high accuracy for 3R2T over-constrained parallel mechanisms. Jiang et al. (2019) designed a 3T2R parallel mechanism with a large output rotation angle in terms of the Lie group theory and the integration of configuration, and analyzed various performance indices of the parallel mechanism.

The commonly used modeling methods at this stage can be roughly divided into two categories. One is the employ of some methods such as principle of virtual work, structural matrix, screw theory or a combination of them. Based on strain energy analysis and screw theory, Cao et al. (2017) proposed a systematic approach to a limb stiffness model that considers the coupling of constrained wrench stiffness and actuated wrench stiffness, and Sun et al. (2016) proposed a 2-DOF constrained rotating parallel mechanism with an articulated walking platform and established its stiffness model. Yan et al. (2016) performed a stiffness analysis using a strain energy method that considers compliance of the mobile platform. Wu et al. (2022) proposes a novel method to evaluate the dynamic performance of the robot along joint–space directions. Furthermore, a new stiffness index is proposed to evaluate stiffness properties. Fang et al. (2002) proposed a comprehensive method of 4-DOF parallel mechanism based on the screw theory and summarize a comprehensive method of 3R parallel mechanism. Gosselin and Schreiber (2018) considered two types of redundancy for parallel mechanisms, namely, actuation redundancy and motion redundancy. Then, each concept was mathematically formulated to clearly demonstrate their characteristics and properties. The other is with the help of commercial software. Combined with related theoretical and experimental research, a finite-element analysis model of mechanism stiffness was derived. A novel method for force analysis of the over-constrained parallel mechanisms was proposed by Xu et al. (2015) and the correctness of the proposed method for force analysis is effectively verified based on Adams simulation software. Zhang et al. (2019) verified the analytical results of kinematics and dynamics through the co-simulation solution of Simulink and Recurdyn. Cao and Ding (2018) proposed a general method for solving 3R2T parallel mechanisms with complex structures and multiple redundant constraints, and then verified the correctness of the established stiffness model through finite-element analysis.

The main contribution of this paper is as follows: a novel redundantly over constrained 2PRU-2SPR parallel mechanism is presented. What is more, the relationship between the pose of moving platform and external load is derived and the overall stiffness matrix of the mechanism is obtained. To have a deeper understanding of the internal structure of stiffness matrix, an eigenscrew decomposition method is utilized to illustrate the physical interpretation of stiffness matrix that can be expressed as linear superposition of simple springs based on the screw decomposition. Finally, the stiffness modeling and analysis methods are effective and correct after proving by finite-element software analysis, and the stiffness performances are compared with the traditional 2RPU-SPR parallel mechanism.

Table 1 Relevant concepts associated with stiffness analysis of parallel mechanism.

2 DOF analysis of 2RPU-2SPR parallel mechanism

2.1 Configuration of 2RPU-2SPR parallel mechanism

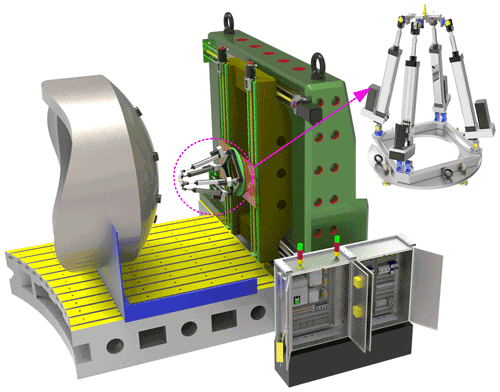
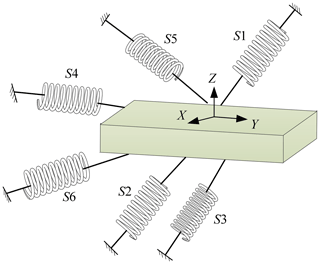
In order to meet the processing requirements of large complex special-shaped workpiece, an over-constrained 2RPU-2SPR redundantly actuated parallel mechanism is applied to the machine tool equipment combined with the characteristics of parallel mechanism and the purpose of machining complex curved surface. The over-constrained parallel mechanism not only has the characteristics of parallel mechanism but also has the advantages of high stiffness, high precision, strong carrying capacity and avoiding singularity. Wu et al. (2013) revealed the relationship between the stiffness performance index of the parallel manipulator and its natural frequency through the study of a 3-DOF parallel manipulator. And the simulation results demonstrate that additional redundant legs can increase the natural frequency of the parallel mechanism and improve the stiffness performance. As shown in Fig. 1, the 2RPU-2SPR parallel mechanism is mainly composed of a fixed platform, a moving platform, an end effector, and two joints of actuated branches with identical structures and symmetrically arranged. The fixed platform is connected with the moving platform through the two joints of actuated branches. One joint of branches is RPU moving branch chain including a revolute joint, a prismatic joint and a universal joint. The other joints of branches are SPR moving branches including a spherical joint, a prismatic joint and a revolute joint.

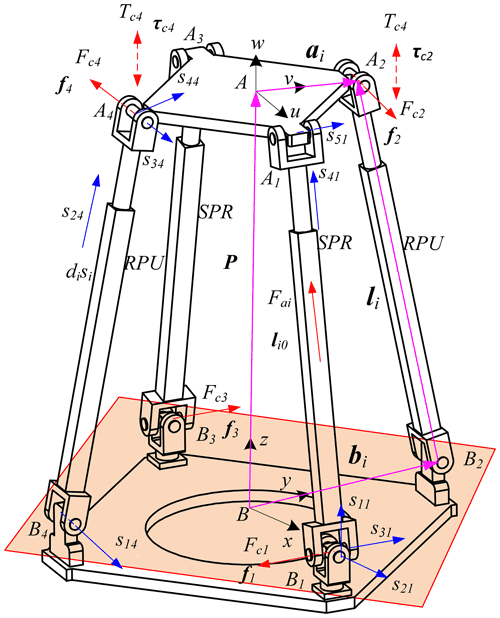
As shown in Fig. 2, the coordinate system is established on the structure diagram of the over-constrained parallel mechanism so as to facilitate the later modeling and optimization calculation. With B as the center, a fixed coordinate system B-xyz is established on the mechanism baseB₁B₂B₃B₄ in which the directions of the x axis and y axis are coincident to BB₁ and BB₂, and the direction of the z axis is determined according to the right-hand rule. The coordinate system A-uvw attached moving platform A₁A₂A₃A₄ is established with origin A as the geometric center of mechanism, and the directions of the u axis and v axis on the coordinate system are coincident to AA₁ and AA₂, and the w axis is determined according to the right-hand rule. s_ij indicates the direction of the rotation axis or the movement axis of the kinematic joints.

Figure 1 Five-axis linkage processing equipment.

Figure 2 2RPU-2SPR parallel mechanism.

2.2 Degree of freedom analysis

According to the screw theory, the constraint force and constraint moment on each kinematic branch chain do no work on the center of the moving platform, that is,

$$\begin{array}{}\text{(1)}& {\displaystyle }\left\{\begin{array}{c}{F}_{ci}\cdot {\mathit{f}}_i\cdot v+F_{ci}\cdot \left(\left({\mathit{a}}_i-{\mathit{l}}_i\right)\times {\mathit{f}}_i\right)\cdot w=\mathrm{0}(i=\mathrm{1},\mathrm{3})\\ F_{ci}\cdot {\mathit{f}}_i\cdot v+F_{ci}\cdot \left({\mathit{a}}_i\times {\mathit{f}}_i\right)\cdot w=\mathrm{0}(i=\mathrm{2},\mathrm{4})\end{array}\right.\text{(2)}& {\displaystyle }{T}_{ci}\cdot {\mathit{\tau }}_i\cdot w=\mathrm{0}(i=\mathrm{2},\mathrm{4}),\end{array}$$

where F_ci (i=1, 2, 3, 4) is the constraint force on each branch, f_i is its direction vector, v and w are the axis directions of the A–uvw coordinate system, l_i is the direction vector of the driving limb, a_i is the joint vector in the fixed coordinate system, and T_ci is the constraint moment on two and four branches whose direction vector is τ_i.

Equations (1) and (2) are written into matrix form and the relationship between constraints is as follows:

$$\begin{array}{}\text{(3)}& J_{\mathrm{c}}\left[\begin{array}{c}v\\ w\end{array}\right]=\left[\begin{array}{cc}{\mathit{f}}_i^T& {\left(\left({\mathit{a}}_i-{\mathit{l}}_i\right)\times {\mathit{f}}_i\right)}^T\\ {\mathit{f}}_i^T& {\mathit{a}}_i\times {\mathit{f}}_i^T\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^T& {\mathit{\tau }}_i^T\end{array}\right]\left[\begin{array}{c}v\\ w\end{array}\right]=\mathrm{0}.\end{array}$$

J_c is the constrained Jacobian matrix and the specific elements are as follows:

$$\begin{array}{}\text{(4)}& J_{\mathrm{c}}=\left[\begin{array}{cc}{\mathit{f}}_{\mathrm{1}}^T& {\left(\left({\mathit{a}}_{\mathrm{1}}-{\mathit{l}}_{\mathrm{1}}\right)\times {\mathit{f}}_{\mathrm{1}}\right)}^T\\ {\mathit{f}}_{\mathrm{2}}^T& {\mathit{a}}_{\mathrm{2}}\times {\mathit{f}}_{\mathrm{2}}^T\\ {\mathit{f}}_{\mathrm{3}}^T& {\left(\left({\mathit{a}}_{\mathrm{3}}-{\mathit{l}}_{\mathrm{3}}\right)\times {\mathit{f}}_{\mathrm{3}}\right)}^T\\ {\mathit{f}}_{\mathrm{4}}^T& {\mathit{a}}_{\mathrm{4}}\times {\mathit{f}}_{\mathrm{4}}^T\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^T& {\mathit{\tau }}_{\mathrm{2}}^T\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^T& {\mathit{\tau }}_{\mathrm{4}}^T\end{array}\right].\end{array}$$

It is known that the Kutzbach degree of freedom calculation formula is as follows:

$$\begin{array}{}\text{(5)}& F=d(n-g-\mathrm{1})+\sum _{i=\mathrm{1}}^g{f}_i+v-\mathit{\varsigma },\end{array}$$

where F represents the degree of freedom of the mechanism, n represents the number of mechanism components, g represents the number of kinematic joints, $d=\mathrm{6}-\mathit{\lambda }$ represents the order of the mechanism, f_i represents the degree of freedom of the i kinematic joint, v represents the redundant constraint of the mechanism and ς represents the local degree of freedom.

Since there is neither constraint couple with the same direction nor coaxial constraint force in the constraint screw of the mechanism, the mechanism has no common constraint, i.e., λ=0. Since the mechanism has no local degrees of freedom, i.e., ς=0, it is easy to know from Eq. (4) that the constrained Jacobian matrix J_c has three linearly independent terms so the mechanism has three redundant constraints, i.e., v=3. It can be seen from the mechanism diagram that the number of mechanism member n, kinematic joints g and relative degrees of freedom of all motion joints f_i are 10, 12 and 18, respectively.

The degree of freedom of the parallel mechanism can be obtained by substituting Eq. (5):

$$\begin{array}{}\text{(6)}& F=\mathrm{6}\times (\mathrm{10}-\mathrm{12}-\mathrm{1})+\mathrm{18}+\mathrm{3}-\mathrm{0}=\mathrm{3}.\end{array}$$

The parallel mechanism studied in this paper has three degrees of freedom which can rotate around two axes and move along one axis, namely, x axis, v axis and z axis, respectively. It is worth noting that the number of actuating joints of the parallel mechanism is four, resulting in the number of actuating joints of the parallel mechanism being greater than the number of DOF. Therefore, the mechanism is a redundantly actuated over-constrained parallel mechanism.

3 Kinematic analysis of parallel mechanism

3.1 Position inverse solution

Set R as the rotation matrix of the moving coordinate system relative to the fixed coordinate system:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}\mathbf{R}& =\mathbf{R}\left(\mathit{\gamma },z\right)\mathbf{R}\left(\mathit{\beta },y\right)\mathbf{R}\left(\mathit{\alpha },x\right)\\ & =\left[\begin{array}{ccc}c\mathit{\beta }c\mathit{\gamma }& s\mathit{\alpha }s\mathit{\beta }c\mathit{\gamma }-c\mathit{\alpha }s\mathit{\gamma }& c\mathit{\alpha }s\mathit{\beta }c\mathit{\gamma }+s\mathit{\alpha }s\mathit{\gamma }\\ c\mathit{\beta }s\mathit{\gamma }& s\mathit{\alpha }s\mathit{\beta }s\mathit{\gamma }+c\mathit{\alpha }c\mathit{\gamma }& c\mathit{\alpha }s\mathit{\beta }s\mathit{\gamma }-s\mathit{\alpha }c\mathit{\gamma }\\ -s\mathit{\beta }& s\mathit{\alpha }c\mathit{\beta }& c\mathit{\alpha }c\mathit{\beta }\end{array}\right],\end{array}\end{array}$$

where R(γ,z) represents rotation around z axis for γ, R(β,y) represents rotation around y axis forβ and R(α,x) represents rotation around x axis for α. Symbol c represents cos and s represents sin which will not be repeated later.

Assuming that the moving platform A₁A₂A₃A₄ and the fixed platform B₁B₂B₃B₄ are squares with circumscribed circle radii of r_a and r_b, respectively, the equation of A_iB_i vector in B-xyz is established by using the closed vector method as follows:

$$\begin{array}{}\text{(8)}& l_i=p+a_i-b_i,\end{array}$$

where $p={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T$ represents the position vector of the origin A of the moving platform coordinate system in the fixed coordinate system B-xyz, a_i and b_i are the position vectors of A_i and B_i hinge points in the fixed coordinate system, respectively, and their coordinates are respectively expressed as follows:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& a_i=R{\left(\begin{array}{ccc}{r}_{a}c{\mathit{\theta }}_i& r_{a}s{\mathit{\theta }}_i& \mathrm{0}\end{array}\right)}^T,\\ & b_i={\left(\begin{array}{ccc}{r}_{b}c{\mathit{\theta }}_i& r_{b}s{\mathit{\theta }}_i& \mathrm{0}\end{array}\right)}^T(i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}),\end{array}\end{array}$$

where ${\mathit{\theta }}_i=\frac{(i-\mathrm{1})\mathit{\pi }}{\mathrm{2}}$ $(i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4})$.

The inverse position solution of Eq. (8) can be expressed as follows:

$$\begin{array}{}\text{(10)}& l_i=\Vert p\mathbf{+}{a}_i\mathbf{-}{b}_i\Vert (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}).\end{array}$$

Equation $\Vert \mathrm{\dots }\Vert$ represents the Euclidean norm of the driving limb.

Due to the introduction of the rotating joint R, four constraint equations can be obtained, namely,

$$\begin{array}{}\text{(11)}& \left\{\begin{array}{c}{\left(p-b_i\right)}^T\cdot R{\left(\begin{array}{ccc}\mathrm{0}& \mathrm{1}& \mathrm{0}\end{array}\right)}^T=\mathrm{0}(i=\mathrm{1},\mathrm{3})\\ {\left(p\mathbf{+}{a}_i\right)}^T\cdot {\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\end{array}\right)}^T=\mathrm{0}(i=\mathrm{2},\mathrm{4})\end{array}\right.\end{array}$$

Equation (11) is organized as follows:

$$\begin{array}{}\text{(12)}& x=\mathrm{0},y=-{\displaystyle \frac{zs\mathit{\alpha }c\mathit{\beta }}{s\mathit{\alpha }s\mathit{\beta }s\mathit{\gamma }+c\mathit{\alpha }c\mathit{\gamma }}},\mathit{\gamma }=\arctan \left({\displaystyle \frac{s\mathit{\alpha }s\mathit{\beta }}{c\mathit{\alpha }}}\right).\end{array}$$

3.2 Jacobian matrix of parallel mechanism

Assuming that the velocity vector of the moving platform reference point A is v and the angular velocity vector of the moving platform is w, the hinge point between the driving limb and the moving platform is A_i and the velocity vector v_ai of the hinge point is expressed as follows:

$$\begin{array}{}\text{(13)}& {\mathit{v}}_{ai}=\mathit{v}+\mathit{\omega }\times a_i(i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}).\end{array}$$

Then, the axial speed ${\dot{\mathit{l}}}_i$ along the driving limb l_i0 can be expressed as follows:

$$\begin{array}{}\text{(14)}& {\dot{\mathit{l}}}_i={\mathit{v}}_{ai}\cdot l_{i\mathrm{0}}=(\mathit{v}+\mathit{\omega }\times a_i)\cdot l_{i\mathrm{0}}.\end{array}$$

In matrix form, it can be expressed as follows:

$$\begin{array}{}\text{(15)}& {\dot{\mathit{l}}}_i={\mathbf{J}}_{\mathrm{0}}\left[\begin{array}{c}v\\ w\end{array}\right],{\mathbf{J}}_{\mathrm{0}}=\left[\begin{array}{c}{\mathbf{J}}_{\mathrm{a}}\\ {\mathbf{J}}_{\mathrm{c}}\end{array}\right],\end{array}$$

where J₀ is the generalized Jacobian matrix, J_a is the actuated Jacobian matrix and J_c is the constrained Jacobian matrix of the mechanism.

Combining Eqs. (14) and (15), the generalized Jacobian matrix J₀ of the mechanism can be expressed as follows:

$$\begin{array}{}\text{(16)}& J_{\mathrm{0}}=\left[\begin{array}{cc}{l}_{i\mathrm{0}}^T& ({\mathit{a}}_i\cdot l_{i\mathrm{0}}{)}^T\end{array}\right].\end{array}$$

According to the dual relationship between velocity mapping and force mapping, the force mapping relationship between each branch of the mechanism and the moving platform can be obtained from Eq. (16).

$$\begin{array}{}\text{(17)}& \mathit{\tau }={\mathbf{J}}_{\mathrm{0}}^T\mathit{f},\end{array}$$

where $\mathit{\tau }={\left[\begin{array}{cc}{\mathit{F}}^T& {\mathit{M}}^T\end{array}\right]}^T$, $\mathit{f}={\left[\begin{array}{cc}{\mathit{f}}_{\mathrm{a}}^T& {\mathit{f}}_{\mathrm{c}}^T\end{array}\right]}^T$. Matrix τ is the external force F and external torque M acting on the reference point of the moving platform, and matrix f is the actuating force f_a and constraint force f_c on the branch chain.

4 Stiffness modeling of parallel mechanism

The five-coordinate hybrid machine tool has high requirements for the kinematic and static properties of the mechanism when performing high-speed milling tasks in the aerospace field, so the stiffness analysis and optimization design is the key content that must be considered in the mechanism design.

When constructing the stiffness analytical equation of 2RPU-2SPR over constrained parallel mechanism, it does not lose generality. Firstly, the moving and fixed platforms of the parallel mechanism are regarded as ideal rigid bodies and it is assumed that the deformation of other parts belongs to the category of linear elasticity and small deformation, ignoring the small deformation of revolute, spherical and universal joint. The unit actuating force screw and unit constraining force screw applied each branch at the center point A of the moving platform are represented by S_ai, S_ri, and their amplitudes are represented by f_ai, f_ri, i=1, 2, 3 and 4, respectively. The unit constraint couple screw and amplitude of the second and fourth branches to the moving platform are S_τi, f_τi (i=2, 4) but they can be decomposed into constraining couple helices along and perpendicular to the limb direction.

4.1 Modeling and analysis of branch stiffness

According to the basic knowledge of material mechanics, non-rigid parts will produce various deformations under different types of forces, so it is assumed that the tensile deformation of each branch under the driving screw S_ai, f_ai is δ_ai and the deflection along the binding axis under the wrench screw S_ri, f_ri is δ_ri. Under the restraining couple screw S_τj, f_τj, the branches 2 and 4 produce a torsional deformation of δθ_i1 along the limb axis l_i0 and a bending deformation of δθ_i2 along the direction l_i0 perpendicular to the limb axis.

The specific relationship between force and deformation and stiffness coefficient is as follows:

$$\begin{array}{}\text{(18)}& {\displaystyle }{f}_{ai}=k_{ai}{\mathit{\delta }}_{ai},k_{ai}={\displaystyle \frac{EA}{l_i}}\text{(19)}& {\displaystyle }{f}_{ri}=k_{ri}{\mathit{\delta }}_{ri},k_{ri}={\displaystyle \frac{\mathrm{3}E{I}_z}{l_i^{\mathrm{3}}}}\text{(20)}& {\displaystyle }{f}_{\mathit{\tau }i}{\mathit{\tau }}_i{l}_{i\mathrm{0}}=k_{ni}\mathit{\delta }{\mathit{\theta }}_{i\mathrm{1}},k_{ni}={\displaystyle \frac{G{I}_{\mathrm{p}}}{l_i}}\text{(21)}& {\displaystyle }{f}_i{\mathit{\tau }}_i\left(e_{\mathrm{1}}\times l_{i\mathrm{0}}\right)=k_{ti}\mathit{\delta }{\mathit{\theta }}_{i\mathrm{2}},k_{ti}={\displaystyle \frac{E{I}_z}{l_i}},\end{array}$$

where E is the elastic modulus, A is the cross-sectional area of the limb, k_ai is the tensile and compressive stiffness coefficient of the branch limb, I_z is the section moment of inertia, k_ri is the bending stiffness coefficient, G is the shear modulus and I_p is the polar inertia, ${\mathit{\tau }}_i=e_{\mathrm{1}}\times e_{\mathrm{2}}$, $e_{\mathrm{1}}={\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\end{array}\right)}^T$, $e_{\mathrm{2}}=\mathbf{R}{\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\end{array}\right)}^T$

The above formula is expressed in matrix form as follows:

$$\begin{array}{}\text{(22)}& \begin{array}{rl}{\left[\begin{array}{ccc}{f}_{ai}& f_{ri}& f_{\mathit{\tau }j}\end{array}\right]}^T=& {\mathbf{K}}_{\mathrm{0}}{\left[\begin{array}{cccc}{\mathit{\delta }}_{ai}& {\mathit{\delta }}_{ri}& {\mathit{\delta }}_{\mathit{\theta }j\mathrm{1}}& {\mathit{\delta }}_{\mathit{\theta }j\mathrm{2}}\end{array}\right]}^T\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},j=\mathrm{2},\mathrm{4})\end{array},\end{array}$$

where ${\mathbf{K}}_{\mathrm{0}}=\left[\begin{array}{ccc}{\mathbf{K}}_{\mathrm{a}}& {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}& {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}\\ {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}& {\mathbf{K}}_{\mathrm{c}}& {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}\\ {\mathrm{0}}_{\mathrm{2}\times \mathrm{4}}& {\mathrm{0}}_{\mathrm{2}\times \mathrm{4}}& {\mathbf{K}}_{\mathit{\tau }}\end{array}\right]$,
${\mathbf{K}}_{\mathrm{a}}=\mathrm{diag}\left[\begin{array}{cccc}{k}_{a\mathrm{1}}& k_{a\mathrm{2}}& k_{a\mathrm{3}}& k_{a\mathrm{4}}\end{array}\right]$,
${\mathbf{K}}_{\mathrm{c}}=\mathrm{diag}\left[\begin{array}{cccc}{k}_{r\mathrm{1}}& k_{r\mathrm{2}}& k_{r\mathrm{3}}& k_{r\mathrm{4}}\end{array}\right]$.

$$\begin{array}{rl}{\mathbf{K}}_{\mathit{\tau }}=& [\begin{array}{c}\frac{k}{\mathit{\tau }{l}_{\mathrm{20}}+\mathit{\tau }\left(e_{\mathrm{1}}\times l_{\mathrm{20}}\right)}\frac{k}{\mathit{\tau }{l}_{\mathrm{20}}+\mathit{\tau }\left(e_{\mathrm{1}}\times l_{\mathrm{20}}\right)}\\ {\mathrm{0}}_{\mathrm{1}\times \mathrm{2}}\end{array}\\ & \begin{array}{c}{\mathrm{0}}_{\mathrm{1}\times \mathrm{2}}\\ \frac{k}{\mathit{\tau }{l}_{\mathrm{40}}+\mathit{\tau }\left(e_{\mathrm{1}}\times l_{\mathrm{40}}\right)}\frac{k}{\mathit{\tau }{l}_{\mathrm{40}}+\mathit{\tau }\left(e_{\mathrm{1}}\times l_{\mathrm{40}}\right)}\end{array}]\end{array}.$$

4.2 Equivalent stiffness matrix of 2RPU-2SPR parallel mechanism

According to the above analysis, the elastic deformation vector generated by the actuating branch and moving platform under the constraint force and actuating force of each branch can be expressed as follows:

$$\begin{array}{}\text{(23)}& {\left[\begin{array}{cccc}{\mathit{\delta }}_{ai}& {\mathit{\delta }}_{ri}& {\mathit{\delta }}_{\mathit{\theta }j\mathrm{1}}& {\mathit{\delta }}_{\mathit{\theta }j\mathrm{2}}\end{array}\right]}^T={\mathbf{J}}_v\mathrm{\Delta }\mathit{X},\end{array}$$

where ΔX means the deformation of the end effector,
${\mathbf{J}}_v=\left[\begin{array}{c}{\mathbf{J}}_{\mathrm{a}}\\ {\mathbf{J}}_{rc}\\ {\mathbf{J}}_{\mathit{\tau }c}\end{array}\right]$,

$$\begin{array}{rl}& {\mathbf{J}}_{\mathrm{a}}=\left[\begin{array}{cc}{l}_{i\mathrm{0}}^T& {\left(a_i\times l_{i\mathrm{0}}\right)}^T\end{array}\right],{\mathbf{J}}_{rc}={\mathbf{J}}_{\mathrm{c}}(\mathrm{1}:\mathrm{4},\mathrm{1}:\mathrm{6}),\\ & {\mathbf{J}}_{\mathit{\tau }c}=\left[\begin{array}{cc}{\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^T& l_{\mathrm{20}}^T\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^T& {\left(e_{\mathrm{1}}\times l_{\mathrm{20}}\right)}^T\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^T& l_{\mathrm{40}}^T\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^T& {\left(e_{\mathrm{1}}\times l_{\mathrm{40}}\right)}^T\end{array}\right]\end{array}.$$

Substituting Eqs. (22) and (23) into Eq. (17)

$$\begin{array}{}\text{(24)}& \mathit{\tau }={\mathbf{J}}_{\mathrm{0}}^T{\mathbf{K}}_{\mathrm{0}}{\mathbf{J}}_v\mathrm{\Delta }\mathit{X}.\end{array}$$

Then, the stiffness matrix of the parallel mechanism is as follows:

$$\begin{array}{}\text{(25)}& \mathbf{K}={\mathbf{J}}_{\mathrm{0}}^T{\mathbf{K}}_{\mathrm{0}}{\mathbf{J}}_v.\end{array}$$

Figure 3 Deformation with force/moment imposed.

5 Stiffness analytical model of 2RPU-2SPR parallel mechanism

5.1 Linear stiffness and angular stiffness index

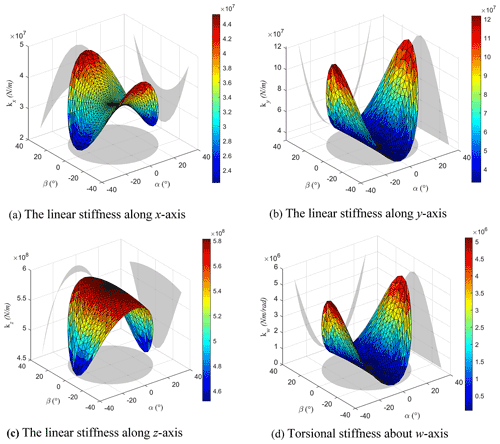
If the parameters and pose of the mechanism are given, the stiffness matrix of the mechanism will be determined and some stiffness indices can be defined to evaluate the stiffness characteristics of the mechanism. It should be noted that the parallel mechanism designed in this paper is mainly applied to the machine tool performing milling operation. Therefore, the linear stiffness and angular stiffness can be defined as follows:

$$\begin{array}{}\text{(26)}& \left\{\begin{array}{c}{k}_x=\mathbf{K}(\mathrm{1},\mathrm{1})\\ k_y=\mathbf{K}(\mathrm{2},\mathrm{2})\\ k_z=\mathbf{K}(\mathrm{3},\mathrm{3})\\ k_w=\mathbf{K}(\mathrm{6},\mathrm{6})\end{array}\right]\end{array}$$

k_x, k_y and k_z are the linear stiffness along the x, y and z axis, respectively; k_w is the torsional stiffness about w axis.

Table 2 Geometric parameters, configuration parameters and physical parameters.

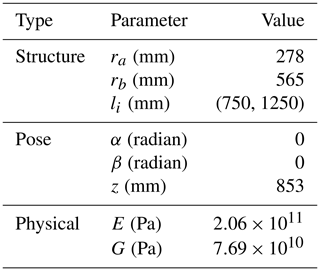
According to the structural parameters, position parameters and physical parameters given in Table 2, the stiffness matrix of the mechanism under this typical posture can be expressed as follows:

$$\begin{array}{}\text{(27)}& \mathbf{K}=\left[\begin{array}{cccccc}\mathrm{0.3297}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0.2719}& \mathrm{0}\\ \mathrm{0}& \mathrm{0.3297}& \mathrm{0}& -\mathrm{0.2713}& \mathrm{0}& -\mathrm{0.0006}\\ \mathrm{0}& \mathrm{0}& \mathrm{5.8136}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& -\mathrm{0.2713}& \mathrm{0}& \mathrm{0.2252}& \mathrm{0}& -\mathrm{0.0005}\\ \mathrm{0.2719}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0.2248}& \mathrm{0}\\ \mathrm{0}& -\mathrm{0.0006}& \mathrm{0}& -\mathrm{0.0005}& \mathrm{0}& \mathrm{0.0008}\end{array}\right]\times {\mathrm{10}}^{\mathrm{8}},\end{array}$$

where the units of terms are N m⁻¹ for K₁₁, K₂₂ and K₃₃, and Nm rad⁻¹ for K₄₄, K₅₅ and K₆₆.

5.2 Static stiffness finite-element simulation

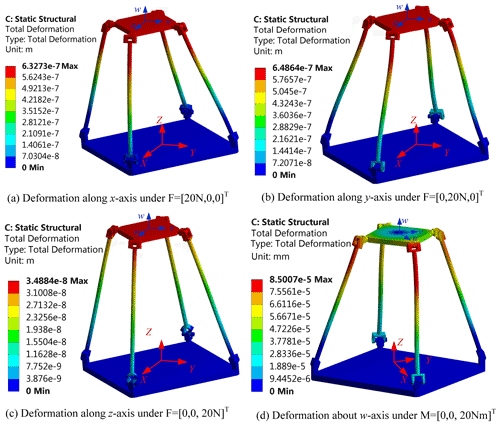
In order to testify the correctness and effectiveness of the stiffness model, finite-element analysis of the parallel mechanism is also conducted. The finite-element analysis of the parallel mechanism is carried out by employing the Ansys Workbench software. Figure 3a–c show the deformation of the parallel manipulator under force along the direction of x axis, y axis and z axis, respectively. Figure 3d is the deformation of the parallel manipulator under the moment about the direction of z axis.

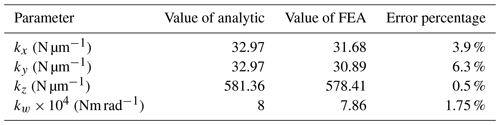
The results obtained by the analysis calculation and finite-element analysis are listed in Table 3. Clearly, the results obtained by the finite-element analysis are very consistent with the results of analysis calculation. FEA is the abbreviation of finite-element analysis.

Table 3 The results of calculation and finite-element analysis.

Under the premise of ignoring the deformation of the kinematic joint, the calculation results of the analytical model and the finite-element analysis model are very similar. The error of k_x is 3.9 %, the error of k_y is 6.3 %, the error of k_z is 0.5 %, the error of k_w is 1.75 % and the error range is within 0.5 %–6.3 %. Therefore, the established analytical model for the stiffness of the whole machine is effective and can be used for the study of the static stiffness characteristics of the parallel mechanism.

Assuming that the dynamic and static platforms are rigid bodies and ignoring the deformation of the moving pair, the calculation results of the analytical model and the finite-element model are very close. Therefore, the established stiffness analytical model is effective and it can be used for static stiffness analysis. In addition, the workspace is defined as $-\mathrm{40}{}^{\circ }\le \mathit{\alpha }\le \mathrm{40}{}^{\circ }$, $-\mathrm{40}{}^{\circ }\le \mathit{\beta }\le \mathrm{40}{}^{\circ }$. The anisotropic deformation cloud diagram of the virtual prototype under the initial pose is depicted in Fig. 4.

Figure 4 Stiffness distributions in the workspace when z=853 mm.

5.3 Eigenvalue decomposition of stiffness matrix

Normally, the end deformation ΔX is expressed in the axis coordinate system while the eigenscrew is generally expressed in the ray coordinate system. In order to ensure the consistency of coordinate system, the Δ matrix is required to convert the axis coordinate system to the ray coordinate system, i.e.,

$$\begin{array}{}\text{(28)}& \mathbf{\Delta }=\left[\begin{array}{cc}{\mathrm{0}}_{\mathrm{3}\times \mathrm{3}}& \mathbf{E}\\ \mathbf{E}& {\mathrm{0}}_{\mathrm{3}\times \mathrm{3}}\end{array}\right],\end{array}$$

where E is the identity matrix.

Therefore, the decomposition of the stiffness matrix is transformed into the decomposition of the KΔ matrix, i.e.,

$$\begin{array}{}\text{(29)}& \mathbf{K}\mathrm{\Delta }e=\mathit{\lambda }e,\end{array}$$

where λ and e represent the eigenvalues and eigenvectors of KΔ, respectively. So, the stiffness matrix can be expressed as follows:

$$\begin{array}{}\text{(30)}& \mathbf{K}=\sum _{m=\mathrm{1}}^{\mathrm{6}}{k}_m{\mathit{w}}_m{\mathit{w}}_m^T,\end{array}$$

where ${\mathit{w}}_m=\left[\begin{array}{c}{\mathit{n}}_m\\ {\mathit{\rho }}_m\times {\mathit{n}}_m+h_m{\mathit{n}}_m\end{array}\right]$, $h_m=\frac{\mathrm{1}}{\mathrm{2}}{\mathit{w}}_m^T\mathrm{\Delta }{\mathit{w}}_m$, $k_m=\frac{{\mathit{\lambda }}_m}{\mathrm{2}{h}_m}$, e_m is eigenvector of KΔ, w_m is unit screw of e_m, h_m represents the pitch of w_m, n_m is direction vector of w_m and ρ_m is position vector of w_m relative to the original coordinate system.

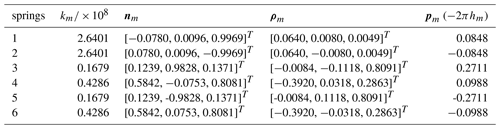
The eigenscrew decomposition is applied to the stiffness matrix K as described in Eq. (30). By applying matrix transformation for solving the eigenscrew problem, the six eigen stiffness λ_m, the eigenscrew pitches h_m and the eigenscrew w_m are derived as shown in Eq. (31):

$$\begin{array}{}\text{(31)}& \begin{array}{l}{\mathit{\lambda }}_m=\mathrm{diag}\left(\left[\begin{array}{cccccc}-\mathrm{7.1231}& \mathrm{7.1231}& -\mathrm{1.4493}& -\mathrm{1.3614}& \mathrm{1.4493}& \mathrm{1.3614}\end{array}\right]\right)\times {\mathrm{10}}^{\mathrm{6}}\\ h_m=\mathrm{diag}\left(\left[\begin{array}{cccccc}-\mathrm{0.0135}& \mathrm{0.0135}& -\mathrm{0.0431}& -\mathrm{0.0159}& \mathrm{0.0431}& \mathrm{0.0159}\end{array}\right]\right)\\ {\mathit{w}}_m=\left[\begin{array}{cccccc}-\mathrm{0.0780}& \mathrm{0.0780}& \mathrm{0.1239}& \mathrm{0.5842}& \mathrm{0.1239}& \mathrm{0.5842}\\ \mathrm{0.0096}& \mathrm{0.0096}& \mathrm{0.9828}& -\mathrm{0.0753}& -\mathrm{0.9828}& \mathrm{0.0753}\\ \mathrm{0.9969}& -\mathrm{0.9969}& \mathrm{0.1371}& \mathrm{0.8081}& \mathrm{0.1371}& \mathrm{0.8081}\\ \mathrm{0.0090}& \mathrm{0.0090}& -\mathrm{0.8158}& \mathrm{0.0379}& \mathrm{0.8158}& -\mathrm{0.0379}\\ -\mathrm{0.0644}& \mathrm{0.0644}& \mathrm{0.0590}& \mathrm{0.4852}& \mathrm{0.0590}& \mathrm{0.4852}\\ -\mathrm{0.0122}& -\mathrm{0.0122}& -\mathrm{0.003}& -\mathrm{0.0019}& \mathrm{0.003}& \mathrm{0.0019}\end{array}\right]\end{array}.\end{array}$$

The physical interpretation of stiffness matrix K based on eigenscrew decomposition is elaborated in Table 4, which indicates that K can be interpreted by six screw springs. The directions along the eigenscrew of K are shown in Fig. 5. p_m represents the pitch of the screw joint.

Table 4 Equivalent spring constants.

Figure 5 Stiffness matrix spring distribution diagram.

It can be seen from Table 4 and Fig. 5 that the stiffness matrix can be equivalent to a simple superposition of six springs. Six springs can be divided into three groups. Two springs in each group meet at one point which has the same spring stiffness and the pitches are opposite numbers. Since the mechanism has two branches that are not the same from each other, the mechanism does not show a certain symmetry and the resulting spring distribution is not regular.

5.4 Stiffness index at different heights

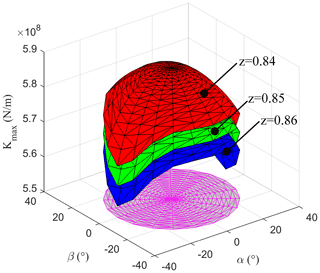
In order to evaluate the stiffness of some positions in the workspace, the maximum eigenvalues of the stiffness matrix K are employed as the evaluation index of the parallel machine tool.

Figure 6 Parallel mechanism stiffness surface.

It can be seen from Fig. 6 that the stiffness values of mechanism decrease with the increase of z value and the manipulator approaches singularity when approaching the workspace boundary. The lowest value of the maximum stiffness appears near the workspace boundary. Therefore, the minimum value of stiffness appears near the workspace boundary.

5.5 Stiffness comparison analysis

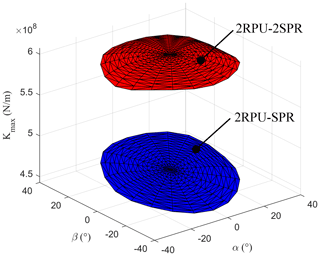
It is obvious from Fig. 7 that the kinematic performance of redundantly actuated 2RPU-2SPR parallel mechanism is better than traditional 2RPU-SPR parallel mechanism which has a bright engineering practical prospect. Therefore, the introduction of redundant branch chain can effectively improve the kinematic performance of 2RPU-SPR parallel mechanism which lays a theoretical foundation for later optimization design.

6 Discussions

Taking the 2RPU-2SPR over-constrained parallel mechanism applied to complex surface machining as the research object, it starts from the mechanism characteristic description and the DOF characteristics. The position mapping relationship between the input member and the output member is established and the Jacobian matrix representing the velocity mapping relationship between the input joint and the output joint of the mechanism is obtained. It is worth noting that the stiffness performance of the parallel mechanism directly determines the motion accuracy and stability of the system when the mechanism performs the surface machining task. Based on the screw theory, the stiffness of the 2RPU-2SPR over-constrained parallel mechanism is deduced. Then the eigenscrew decomposition method can be adopted to decompose the stiffness matrix.

Figure 7 Comparison of maximum stiffness.

7 Conclusions

In this study, aiming at the large-scale and complex surface machining tasks in the aerospace field, a novel over-constrained redundantly actuated parallel mechanism is proposed. Furthermore, the correctness of the derivation of the stiffness matrix through finite-element simulation analysis is verified which can be used to study the static stiffness characteristics of the parallel mechanism. Simultaneously, the stiffness matrix is equivalent to three groups of springs with more definite physical meanings. Finally, compared with the stiffness of the 2RPU-SPR parallel mechanism, the passive over-constrained parallel mechanism has higher stiffness, indicating that the introduction of the redundantly actuated over-constrained branch chain SPR can improve the stiffness performance of the mechanism and can also effectively improve the stiffness distribution of the mechanism.

In our future research, the mechanism proposed in this paper has great stiffness performance; it can be connected with x and y sliding rail to form a five-axis hybrid processing machine tool which has a wider range of applications. What is more, the theoretical design and analysis proposed in this paper mainly focus on the parallel mechanism. There is no complete digital virtual simulation and test prototype construction for the overall complex surface intelligent processing equipment. The control theory is limited to the parallel mechanism and further research is needed on the overall control of the hybrid mechanism.