Dynamic modeling of a metro vehicle considering the motor–gearbox transmission system under traction conditions

As a vital means of transportation to alleviate urban traffic congestion, the metro vehicle has been developing rapidly in China during recent years. For the violent vibration and shock under the frequent switches between traction and braking conditions, higher requirements are put forward in the drive system. The dynamic performance of the traction motor and gearbox, which are the key elements in the drive system of the metro vehicle, is worthy of attention. Based on the classical vehicle–track coupled dynamics and the gear dynamics theory, a vertical–longitudinal dynamics model for a metro vehicle with frame-hung motors and gearboxes is developed in this paper. This model enables the consideration of some complicated excitations, such as external excitations (the track vertical irregularity) and internal excitations (the mesh stiffness and the dynamic transmission error). The established dynamics model is then validated by comparing the simulated results with the field test results in both time domain and time–frequency domain under traction conditions. Consequently, the established dynamics model is demonstrated to be capable of revealing the dynamic performance of the metro vehicle effectively, especially for the traction and transmission system in the entire vehicle vibration environment of a metro. In turn, the results indicate that the gear transmission has a great and lasting effect on the force state of the traction motors and gearboxes compared to its effect on the axle load transfer.

1 Introduction

The metro can fundamentally improve the public transportation development problems that exist in the process of urban development due to its many advantages, such as large passenger capacity, high speed, high comfort, punctuality, high energy efficiency, and environmental protection. However, the metro vehicle needs to start and brake quickly and frequently in daily operation, during which the driving system is vulnerable to severe shock and vibration. As the traction motor and gearbox are the key elements of the metro vehicle driving system, their dynamic performance directly determines the running stability and safety of the metro vehicle. Therefore, it is self-evident for the development of urban rail transit to establish a vehicle–track coupled dynamics model for a metro vehicle, considering the traction motor and gear transmission, and analyze their coupling mechanism and dynamic interaction.

The gear transmission system plays the role of transmitting the force and motion in the mechanical transmission system of the metro vehicle, that is, the gearbox input is connected with the traction motor and the gearbox output is connected with the wheel axle, so the gear transmission system cooperates with the traction motor to transmit the traction torque to the wheel axle, and in turn, the longitudinal creep force generated at the wheel–rail contact interface drives the metro vehicle forward. Therefore, the gear transmission system should attract more significant attention. Since the gear mesh stiffness is one of the internal excitations of the gear transmission system, the methods, such as the finite element method (FEM) (Ma et al., 2015), the experimental method (Raghuwanshi and Anand, 2018), the analytical–FEM hybrid method (Chen et al., 2019), and the analytical method (Mohammed et al., 2015; Chen et al., 2017a) have been used to obtain the gear mesh stiffness. Generally, the advantage of the analytical method in computational efficiency makes it more popular and noteworthy. In addition, due to the wide reports of gear failure (Gu and Velex, 2013), wear (Brethee et al., 2017), and tooth profiles (Bahk and Parker, 2013), there are more and more researchers who have researched the vibration characteristics of gear transmission systems. A comprehensive method for simulating and analyzing the vibration of the gear transmission system was introduced by Choy et al. (1994). They established an analytical model to simulate the effects of pitting and wear on the surface of gear teeth through the phase and amplitude changes of gear meshing stiffness. Tamminana et al. (2007) developed a deformable-body model and a simplified discrete model to predict the dynamic performance of the gear pairs and quantify the impact of the nonlinear behavior. Using a multiple scale method, Moradi and Salarieh (2012) studied the nonlinear oscillations of spur gear pairs including the backlash nonlinearity under primary, super-, and subharmonic resonances. Chen et al. (2014) established a dynamic model that could consider the impact force and analyzed the effects of system parameters on the gear transmission system. By combining the dynamic loading with the elastohydrodynamic lubrication theory, Ouyang et al. (2018) proposed a tribo-dynamic model for spur gear pairs to validate the effect of coupling on the elastohydrodynamic lubrication behavior. Those works indicate that the gear transmission system is a complex nonlinear system.

A benefit of the contributions from researchers in the field of gear transmission systems, is that the coupling effect of gear transmission systems with the rail vehicle has been coming into focus in recent years. Based on the classical Zhai model (Zhai and Sun, 1994; Zhai et al., 2009), Chen et al. (2017b, c, 2018) established a locomotive–track coupled vertical (Chen et al., 2017b) and vertical–longitudinal (Chen et al., 2017c) dynamics model considering the gear transmission system, and analyzed the dynamic performance of the locomotive under traction and braking conditions (Chen et al., 2018). Wang et al. (2020) revealed the non-smooth dynamic characteristics of a gear–wheelset system under traction and braking conditions considering nonlinear meshing damping and piecewise continuous time-varying meshing stiffness. Furthermore, Jiang et al. (2020) studied the effect of tooth root crack fault on the locomotive dynamic performance, and in turn, Zhang et al. (2019a) established a spatial dynamics model for the locomotive–track coupled system and verified that the lateral vibrations of the bogie frame were not as significantly affected by the gear transmissions by discussing the different model with or without considering the gear transmission system (Zhang et al., 2019b). Liu et al. (2021a, b, c) comprehensively analyzed the interaction between the motor bearing and the locomotive model considering the gear transmission system. Particularly, Zhou et al. (2021a) proposed a co-simulation model to reveal the effect of the mechanical subsystem on the dynamic behavior of the electrical subsystem in a railway locomotive, and further, they preliminarily verified that the electromechanical coupling effect can be used to monitor the faults of rotating parts in the transfer path of the locomotive transmission system (Zhou et al., 2021b). In addition to the heavy-haul locomotive, similar works have been done in the field of the high-speed train (Huang et al., 2016; Wang et al., 2019, 2020). There are also some new developments in the field of wheel–rail contact and orbital dynamics. Marques et al. (2020) recently proposed a three-dimensional approach for contact detection to improve the railway dynamic analysis, and Urda et al. (2020) presented a computationally efficient method for the measurement of lateral wheel–rail contact force using artificial neural networks. Zhu et al. (2020) investigated the effect of the train–track interaction and environment loads on the mechanical characteristic variation of the ballastless track in the high-speed train. Metro vehicles assume a preponderant role on the equipment of urban rail transit, but its frequent and fast starting and braking conditions cause severe vibration and shock to the transmission system in the longitudinal and vertical direction of the vehicle. However, few studies involve the analysis of metro vehicle dynamics considering the traction motors and gearboxes.

In this paper, a vehicle–track vertical–longitudinal coupled dynamics model for a metro vehicle considering the traction motors and gearboxes is developed. The torsional movements of mechanical transmission systems composed of rotors, gear pairs, and wheelsets are coupled with the vertical–longitudinal movements of the traction motor–gearboxes and wheelsets through the wheel–rail contact interface and the gear meshing interface. The advantages of this model make it a practical model for metro vehicle dynamic simulation, especially for the dynamic characteristic research of the traction motors and gearboxes under rapid traction and braking conditions. Based on this model, the dynamic responses of the entire dynamics system under the excitations of the track irregularities and the time-varying gear mesh stiffness can be extracted. Additionally, the dynamic responses of the components obtained from the established coupled dynamics model are compared with the field test results for model validation.

2 Vehicle–track coupled dynamics model of a metro vehicle

Based on the classic vehicle-track coupled dynamics model proposed in Zhai et al. (2009) and Xu and Zhai (2020), and the development of the gear dynamics theory considering nonlinear factors in the last decades, a two-dimensional vehicle–track coupled with the vertical–longitudinal dynamics model for a typical metro vehicle used in China is developed with consideration of the motor–gearbox transmission system, and shown in Fig. 1. Here, the developed dynamics model for the metro vehicle with frame-hung traction motors is composed of three subsystems, namely the classical vehicle subsystem, the track subsystem, and the newly added motor–gearbox transmission subsystem, including the gear transmission.

In this model, the car body, bogie frames, wheelsets, gearboxes, and traction motors are individually regarded as rigid bodies, and their lumped masses and moments of inertia are concentrated at their respective centroids. As shown in Fig. 1, interactions between these rigid bodies are achieved by suspensions which are considered to be spring-damper elements. The primary suspension (K_pz, C_pz, K_px, and C_px) refers to the steel spring and the shock absorber between the bogie frame and the axle box. The secondary suspension (K_sz, C_sz, K_sx, and C_sx) denotes the air spring between the bogie frame and the car body. Gear transmission systems in gearboxes transmit the traction torques (T_mi) from traction motors to wheelsets, generating longitudinal creep force at the wheel–rail contact interface. The traction rods between the bogie frame and the car body are also seen as the spring elements that play a role to deliver the traction forces to move the car body longitudinally.

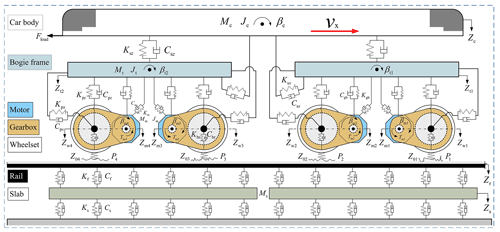
Figure 1 Vehicle–track coupled dynamics model of a metro vehicle with traction motors and gear transmissions.

As a typical type of non-ballasted track structure, composed of rails, rail pads, and slabs, the slab track has been widely used in China because of its advantages of high stability, less maintenance, and long service life. Thus, the track subsystem in this vehicle–track coupled dynamics model of the metro vehicle is modeled as a slab-track structure, as shown in Fig. 1. The rails that bear the enormous pressure from the wheelsets are modeled as continuous Bernoulli–Euler beams with vertical motion supported by slabs. The slabs are treated as a finite-length free beam supported on the viscoelastic foundation which can be viewed as a continuous linear spring-damping. Since the equations of motion of the slab-track subsystem, which are solved by the modal superposition method, are well recorded in Zhai et al. (2009), they are not presented here.

2.1 Interaction forces between the traction transmission components

The traction transmission system of a metro vehicle is shown in Fig. 2a. The traction motor is frame-hung, and its rotor and the pinion of the gearbox are connected by a coupling. One end of the gearbox is connected to the bogie frame through the steeve, and the other end is connected to the wheelset. Therefore, the longitudinal degree of freedom between the gearbox and the bogie frame is not directly constrained. In this dynamics model, the spring-damper elements are adopted to concatenate the different rigid components of the metro vehicle. Since the calculation method of internal forces conducted by the secondary suspension system between the car body and the bogie frames, as well as the method conducted by the primary suspension system between the bogie frames and the wheelsets, are well documented in Chen et al. (2017b, c), only the forces between the other components are listed here.

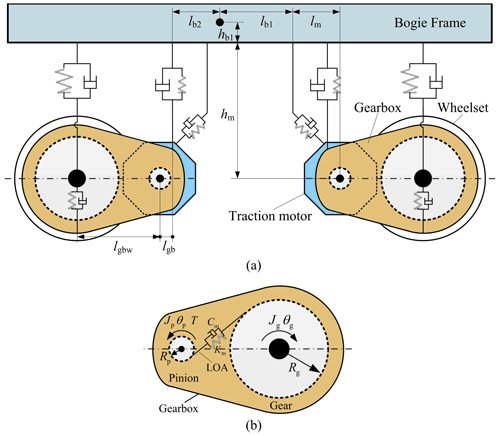
Figure 2 Traction and transmission system of a metro vehicle. Schematic representation of (a) the drive system and (b) the gearbox and transmission subsystem.

The interaction forces between the bogie frames and the traction motors can be derived as

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{F}_{\mathrm{tm}zi}& =K_{\mathrm{tm}z}[Z_{\mathrm{tround}(i/\mathrm{2})}-Z_{\mathrm{m}i}\\ & -(-\mathrm{1}{)}^i({\mathit{\beta }}_{\mathrm{tround}(i/\mathrm{2})}{l}_{\mathrm{b}\mathrm{1}}+{\mathit{\beta }}_{\mathrm{m}i}{l}_{\mathrm{m}}\left)\right]\\ & +C_{\mathrm{tm}z}[{\dot{Z}}_{\mathrm{tround}(i/\mathrm{2})}-{\dot{Z}}_{\mathrm{m}i}\\ & -(-\mathrm{1}{)}^i({\dot{\mathit{\beta }}}_{\mathrm{tround}(i/\mathrm{2})}{l}_{\mathrm{b}\mathrm{1}}+{\dot{\mathit{\beta }}}_{\mathrm{m}i}{l}_{\mathrm{m}}\left)\right]\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4})\\ F_{\mathrm{tm}xi}& =K_{\mathrm{tm}x}[X_{\mathrm{tround}(i/\mathrm{2})}-X_{\mathrm{m}i}\\ & -{\mathit{\beta }}_{\mathrm{tround}(i/\mathrm{2})}{h}_{\mathrm{b}\mathrm{1}}+{\mathit{\beta }}_{\mathrm{m}i}{h}_{\mathrm{m}}\left)\right]\\ & +C_{\mathrm{tm}x}[{\dot{X}}_{\mathrm{tround}(i/\mathrm{2})}-{\dot{X}}_{\mathrm{m}i}\\ & -{\dot{\mathit{\beta }}}_{\mathrm{tround}(i/\mathrm{2})}{h}_{\mathrm{b}\mathrm{1}}+{\dot{\mathit{\beta }}}_{\mathrm{m}i}{h}_{\mathrm{m}}\left)\right]\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}).\end{array}\end{array}$$

The interaction forces between the gearboxes and the traction motors can be calculated by

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{F}_{\mathrm{gbm}zi}& =K_{\mathrm{gbm}z}[Z_{\mathrm{gb}i}-Z_{\mathrm{m}i}]+C_{\mathrm{gbm}z}[{\dot{Z}}_{\mathrm{gb}i}-{\dot{Z}}_{\mathrm{m}i}]\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4})\\ F_{\mathrm{gbm}xi}& =K_{\mathrm{gbm}x}[X_{\mathrm{gb}i}-X_{\mathrm{m}i}]+C_{\mathrm{gbm}x}[{\dot{X}}_{\mathrm{gb}i}-{\dot{X}}_{\mathrm{m}i}]\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}).\end{array}\end{array}$$

Similarly, the frame-gearbox acting forces carried by the gearbox steeve can be calculated by

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{F}_{\mathrm{tgb}zi}& =K_{\mathrm{tgb}z}[Z_{\mathrm{tround}(i/\mathrm{2})}-Z_{\mathrm{gb}i}\\ & -(-\mathrm{1}{)}^i({\mathit{\beta }}_{\mathrm{tround}(i/\mathrm{2})}{l}_{\mathrm{b}\mathrm{2}}+{\mathit{\beta }}_{\mathrm{gb}i}{l}_{\mathrm{gb}}\left)\right]\\ & +C_{\mathrm{tgb}z}[{\dot{Z}}_{\mathrm{tround}(i/\mathrm{2})}-{\dot{Z}}_{\mathrm{gb}i}\\ & -(-\mathrm{1}{)}^i({\dot{\mathit{\beta }}}_{\mathrm{tround}(i/\mathrm{2})}{l}_{\mathrm{b}\mathrm{2}}+{\dot{\mathit{\beta }}}_{\mathrm{gb}i}{l}_{\mathrm{gb}}\left)\right]\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}).\end{array}\end{array}$$

The interaction forces between the gearbox and the wheelset are derived as

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{F}_{\mathrm{gbw}zi}& =K_{\mathrm{gbw}z}[Z_{\mathrm{gb}i}-Z_{\mathrm{w}i}+{\mathit{\beta }}_{\mathrm{gb}i}{l}_{\mathrm{gbw}}]\\ & +C_{\mathrm{gbw}z}[{\dot{Z}}_{\mathrm{gb}i}-{\dot{Z}}_{\mathrm{w}i}-{\dot{\mathit{\beta }}}_{\mathrm{gb}i}{l}_{\mathrm{gbw}}]\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4})\\ F_{\mathrm{gbw}xi}& =K_{\mathrm{gbw}x}[X_{\mathrm{gb}i}-X_{\mathrm{w}i}]+C_{\mathrm{gbw}x}[{\dot{X}}_{\mathrm{gb}i}-{\dot{X}}_{\mathrm{w}i}]\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}).\end{array}\end{array}$$

Through the gear teeth engagement, the forces and motions from the traction motors can be transmitted to the wheelsets. As shown in Fig. 2b, the mesh force along the line of action (LOA) between the pinion and the gear can be calculated as

$$\begin{array}{}\text{(5)}& F_{\mathrm{pg}}=K_{\mathrm{pg}}\mathit{\delta }+C_{\mathrm{pg}}\dot{\mathit{\delta }},\end{array}$$

where K_pg and C_pg are the gear mesh stiffness and the damping, respectively. The dynamic transmission error (DTE) is represented by δ, and the dot above the δ means the first-order differential.

In this paper, the time-varying mesh stiffness (K_pg) is calculated by the analytical model established by Chen et al. (2020) based on the potential energy principle, and it can be expressed as Eq. (6) where the notations of it have been explained in their works:

$$\begin{array}{}\text{(6)}& K_{\mathrm{pg}}={\displaystyle \frac{K_{\mathrm{1}}+K_{\mathrm{2}}-K_{\mathrm{1}}{K}_{\mathrm{2}}(\mathrm{1}/K_{\mathrm{12}}+\mathrm{1}/K_{\mathrm{21}})}{\mathrm{1}+K_{\mathrm{2}}{\stackrel{\mathrm{̃}}{E}}_{\mathrm{12}}(\mathrm{1}-K_{\mathrm{1}}/K_{\mathrm{12}})/F-K_{\mathrm{1}}{K}_{\mathrm{2}}/\left(K_{\mathrm{12}}{K}_{\mathrm{21}}\right)}},\end{array}$$

where the single-tooth mesh stiffness K_i can be described as

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{1}}{K_i}}& ={\displaystyle \frac{\mathrm{1}}{K_{\mathrm{ap}i}}}+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{bp}i}}}+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{sp}i}}}+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{ag}i}}}+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{bg}i}}}+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{ssg}i}}}\\ & +{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{ffp}i}}}+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{ffg}i}}}+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{h}i}}},i=\mathrm{1},\mathrm{2},\end{array}\end{array}$$

where the symbols K_a, K_b, K_ss, K_ff, K_h denote the bending stiffness, shear stiffness, axial compressive stiffness, tooth fillet-foundation deformation, and contact deformation of the tooth pair, respectively, and the subscripts p and g denote the pinion and the gear, respectively.

The DTE can be derived as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\mathit{\delta }}_i& =-R_{\mathrm{p}}{\mathit{\theta }}_{\mathrm{p}i}-R_{\mathrm{g}}{\mathit{\theta }}_{\mathrm{g}i}+(-\mathrm{1}{)}^k(Z_{\mathrm{gb}k}-Z_{\mathrm{w}k})\cos {\mathit{\alpha }}_{\mathrm{0}}\\ & -(-\mathrm{1}{)}^k(X_{\mathrm{gb}k}-X_{\mathrm{w}k})\sin {\mathit{\alpha }}_{\mathrm{0}}-b_{\mathrm{0}}-e_i,\end{array}\end{array}$$

where the subscripts i = p, g point to the pinion and gear, respectively. The base circle radius of the gears and their rotational displacements are denoted as R_i and θ_i, respectively. The symbols Z_gbk, Z_wk, X_gbk, and X_wk (k = 1–4) represent the vertical and longitudinal displacements of the gearbox and the wheelset, and the wheelset number k=1 represents the front-most position on the direction of metro vehicle operation. The gear error e_i may include the assembly and the manufacturing errors.

2.2 Nonlinear wheel–rail contact force

To calculate the wheel–rail contact force, the nonlinear Hertz elastic contact theory is used to calculate the vertical contact force on the wheel–rail interface, and the calculation formula is denoted as (Zhai and Sun, 1994; Zhai, 2020)

$$\begin{array}{}\text{(9)}& P\left(t\right)={\left[{\displaystyle \frac{\mathrm{1}}{G}}\mathit{\delta }Z\left(t\right)\right]}^{\mathrm{3}/\mathrm{2}},\end{array}$$

where G is the Hertz wheel–rail contact constant, for the worn profile tread used in the metro vehicle, $G=\mathrm{3.86}{R}_{\mathrm{0}}^{-\mathrm{0.115}}\times {\mathrm{10}}^{-\mathrm{8}}$ m N${}^{-\mathrm{2}/\mathrm{3}}$, where R₀ is the wheel radius. The elastic compressive deformation of the wheel–rail contact is denoted as δZ(t) and can be calculated as

$$\begin{array}{}\text{(10)}& \mathit{\delta }Z\left(t\right)=Z_{\mathrm{w}}\left(t\right)-Z_{\mathrm{r}}(x_{\mathrm{w}},t)-Z_{\mathrm{0}}\left(t\right),\end{array}$$

where Z_w and Z_r denote the vertical displacements of the wheelset and the rail at the wheel–rail contact point. The Z₀(t) denotes the geometrical irregularities on the surface of the wheel and rail, such as track irregularities, rail corrugation, wheel polygonization, etc.

When the metro vehicle operates under the action of the drive torques transmitted from the traction motors, the wheels will creep against the rails to generate the creep forces. The creep force is the link between the metro vehicle's longitudinal movement and the motor–gearbox transmission subsystem. It is also an important factor for studying the dynamic interaction between the wheelsets and the rails which can be given as

$$\begin{array}{}\text{(11)}& F_{\mathrm{creep}}=P\left(t\right)\cdot \mathit{\mu },\end{array}$$

where μ is the adhesion coefficient of the wheel–rail contact interface, which is determined by complicated factors. The formula for calculating the adhesion coefficient can refer to Chen et al. (2017b).

2.3 Dynamic equation of the motor–gearbox transmission components

Combining Figs. 1 and 2, based on the D'Alembert's principle, the corresponding dynamic equations of motion of the motor–gearbox transmission system are derived as follows:

Pitch, bounce, and longitudinal motions of traction motors

$$\begin{array}{}\text{(12)}& \begin{array}{rl}& \left\{\begin{array}{l}{J}_{\mathrm{m}i}{\ddot{\mathit{\beta }}}_{\mathrm{m}i}-(-\mathrm{1}{)}^i{F}_{\mathrm{tm}zi}{l}_{\mathrm{m}}+F_{\mathrm{tm}xi}{h}_{\mathrm{m}}+T_{\mathrm{m}i}=\mathrm{0}\\ M_{\mathrm{m}i}{\ddot{Z}}_{\mathrm{m}i}-F_{\mathrm{tm}zi}-F_{\mathrm{gbm}zi}-M_{\mathrm{m}i}g=\mathrm{0}\\ M_{\mathrm{m}i}{\ddot{X}}_{\mathrm{m}i}-F_{\mathrm{tm}xi}-F_{\mathrm{gbm}xi}=\mathrm{0}\end{array}\right.\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4})\end{array}\end{array}$$

Pitch, bounce, and longitudinal motions of gearboxes

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& \left\{\begin{array}{l}{J}_{\mathrm{gb}i}{\ddot{\mathit{\beta }}}_{\mathrm{gb}i}-(-\mathrm{1}{)}^i{F}_{\mathrm{gbw}zi}{l}_{\mathrm{gbw}}-(-\mathrm{1}{)}^i{F}_{\mathrm{tgb}zi}{l}_{\mathrm{gb}}=\mathrm{0}\\ M_{\mathrm{gb}i}{\ddot{Z}}_{\mathrm{gb}i}-F_{\mathrm{tgb}zi}+F_{\mathrm{gbw}zi}+F_{\mathrm{gbm}zi}\\ +(-\mathrm{1}{)}^i{F}_{\mathrm{pg}i}\cos {\mathit{\alpha }}_{\mathrm{0}}-M_{\mathrm{gb}i}g=\mathrm{0}\\ M_{\mathrm{gb}i}{\ddot{X}}_{\mathrm{gb}i}+F_{\mathrm{gbw}xi}+F_{\mathrm{gbm}xi}\\ -(-\mathrm{1}{)}^i\left|F_{\mathrm{pg}i}\right|\sin {\mathit{\alpha }}_{\mathrm{0}}=\mathrm{0}\end{array}\right.\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4})\end{array}\end{array}$$

Pitch, bounce, and longitudinal motions of the wheelsets

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& \left\{\begin{array}{l}{J}_{\mathrm{w}i}{\ddot{\mathit{\theta }}}_{\mathrm{w}i}-T_{\mathrm{gw}i}+\mathrm{2}{F}_{\mathrm{creep}i}{R}_{\mathrm{0}}=\mathrm{0}\\ M_{\mathrm{w}i}{\ddot{Z}}_{\mathrm{w}i}-F_{\mathrm{tw}zi}-F_{\mathrm{gbw}zi}-(-\mathrm{1}{)}^i{F}_{\mathrm{pg}i}\cos {\mathit{\alpha }}_{\mathrm{0}}\\ +\mathrm{2}{P}_i\left(t\right)-F_{\mathrm{pr}i}\sin {\mathit{\alpha }}_{\mathrm{pr}i}-M_{\mathrm{w}i}g=\mathrm{0}\\ M_{\mathrm{w}i}{\ddot{X}}_{\mathrm{w}i}-F_{\mathrm{creep}i}-F_{\mathrm{gbw}xi}+(-\mathrm{1}{)}^i{F}_{\mathrm{pg}i}\sin {\mathit{\alpha }}_{\mathrm{0}}\\ +(-\mathrm{1}{)}^i{F}_{\mathrm{pr}i}\cos {\mathit{\alpha }}_{\mathrm{pr}i}=\mathrm{0}\end{array}\right.\\ & (i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4})\end{array}\end{array}$$

Rotational motion of the rotor

$$\begin{array}{}\text{(15)}& J_{\mathrm{r}i}{\ddot{\mathit{\theta }}}_{\mathrm{r}i}+T_{\mathrm{rp}i}-T_{\mathrm{m}i}=\mathrm{0}\end{array}$$

Rotational motion of the pinion

$$\begin{array}{}\text{(16)}& J_{\mathrm{p}i}{\ddot{\mathit{\theta }}}_{\mathrm{p}i}-T_{\mathrm{rp}i}-F_{\mathrm{pg}i}{R}_{\mathrm{p}}=\mathrm{0}\end{array}$$

Rotational motion of the gear

$$\begin{array}{}\text{(17)}& J_{\mathrm{g}i}{\ddot{\mathit{\theta }}}_{\mathrm{g}i}+T_{\mathrm{gw}i}-F_{\mathrm{pg}i}{R}_{\mathrm{g}}=\mathrm{0}\end{array}$$

In Eqs. (12)–(17), the symbols J_i and θ_i denote the moment of inertia and the rotational displacement (the subscript i = t for bogie frame, m for traction motor, r for rotor, p for pinion, g for gear, gb for gearbox, and w for wheelset). The R_p, R_g, and R₀ are the base circle radius of the pinion, gear, and wheel radius, respectively. The T_m, T_rp, and T_gw are the output torque of the traction motor, the torque transmitted between the rotor and the pinion, and the torque transmitted between the gear and wheelset, respectively. The wheel–rail creep force is F_creep.

In order to improve the calculation efficiency for the whole dynamics model of metro vehicles with large-scale degrees of freedom (DOFs) and multiple nonlinear links, Zhai's integration algorithm is adopted here for the numerical solution (Zhai, 1996).

3 Analysis on dynamic responses of the metro vehicle under traction conditions

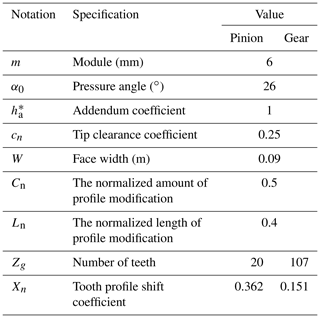
Owing to the fact that the gear is not as stable as the ideal involute gear in practical operation, the dynamic load caused by the meshing impact affects the bearing capacity. Tooth profile modification (TPM) is a means to reduce the impact vibration and noise, weaken the dynamic load, improve the lubrication state of the tooth surface, and in turn, slow down or prevent the gear scuffing. The TPM of both gear and pinion in this dynamics model is applied at the tooth tips because modifying the root or tip of one gear has the same effect (Lin et al., 1994). According to the relevant standards mentioned in Chen and Shao (2013) and the standard tip relief limitations (Li and Mao, 2008), the normalized amount and length of TPM for gear and pinion are set as 0.5 and 0.4, respectively. Based on the main parameters of the gear pair used in the metro vehicle dynamics model, as shown in Table 1, the time-varying mesh stiffness with TPM can be calculated through Eq. (6).

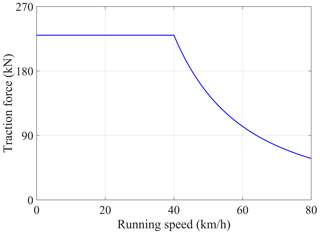
The traction characteristic curve of the metro vehicle without load (AW0) is shown in Fig. 3. To avoid applying too much traction force at the beginning of the simulation, the traction force can be set to increase linearly with the running speed less than 2 km h⁻¹ in the simulation process. Due to the good condition of the new track, the Association of American Railroads class 6 irregularity is adopted in all simulation processes. The main design parameters of the metro vehicle and slab-track structure are given in Tables 2 and 3.

Figure 3 Traction characteristic curve of the metro vehicle (AW0).

Table 1 Main parameters of the gear pair of the transmission system.

Table 2 Main parameters of the metro vehicle components.

Table 3 Main parameters of the slab-track structure.

3.1 Model validation

Based on the established coupled dynamics model, simulation analysis of the metro vehicle can be done under traction conditions.

The field test was carried out on the straight line of a Qingdao Metro Line in China. Prior to the test, accelerometer sensors were installed on the car body, bogie frame, traction motor, and axle box according to the relevant test standards, and the positions and testing photograph are shown in Fig. 4. Then, the vibration responses of the metro major components can be collected in traction conditions. According to the vibration responses acquired from the field tests in the first 7 s of the speed-up process, the same situation of the numerical simulations as field tests are also performed in the developed vehicle–track coupled dynamics model.

Figure 4 Accelerometer sensors on (a) the car body and bogie frame, (b) traction motor, and (c) axle box.

3.1.1 Model validation in the time domain

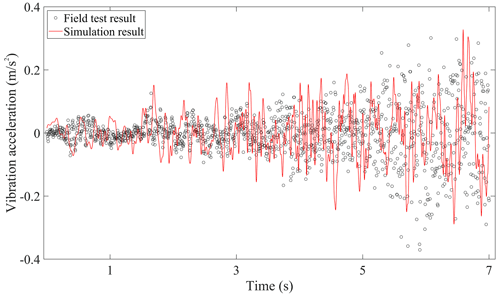
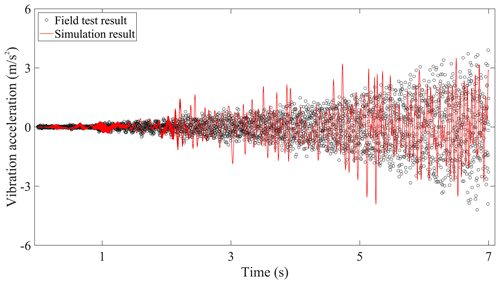
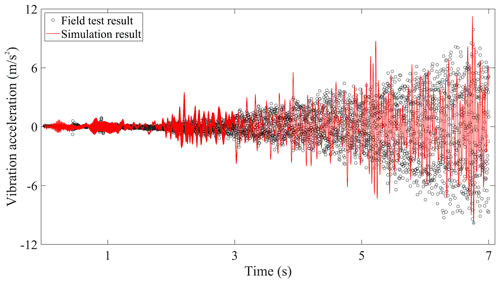
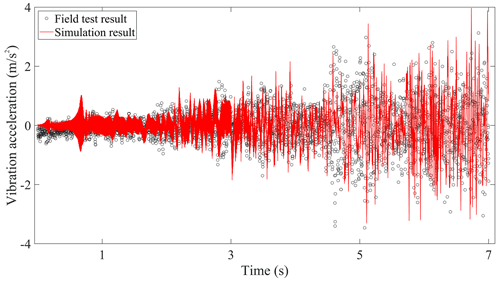
The comparisons of the vertical vibration responses in time histories on car body, bogie frame, traction motor, and wheelset between the field test results and simulation results are displayed in Figs. 5–8, respectively. Due to the dynamic interaction of the wheel–rail under track irregularity, the self-excited vibration of the driving system under the traction torque, and the gear mesh force that gradually intensifies with the speed-up process, it can be seen that the vibration intensity of these tested components increases gradually, and the same trend also occurs in the simulation results.

Figure 5 Comparison of vertical vibration responses of the car body.

Figure 6 Comparison of vertical vibration responses of the bogie frame.

Figure 5 compares the simulation results and field test vibration accelerations of the car body. The amplitude of vibration acceleration is relatively small, which is consistent with the high comfort requirements of the metro vehicle. Since the car body is regarded as rigid, the local flexible vibration of the car floor around the accelerometer sensor could not be revealed in the simulated results, so the field test results of the car body have much more high-frequency components than the simulation results. Furthermore, it should be noted that the vibration accelerations of the traction motor in Fig. 7 are generally greater than that of the bogie frame and the wheelset in Figs. 6 and 8 in amplitude, and the vibration amplitude of the bogie frame and wheelset is equivalent. The main reason is that the metro vehicle requires a fast start, which needs to reach high running speeds in a short time. The rotor rotates relative to the stator, and the huge traction torque causes the vibration of the driving system to intensify. However, the stator of the traction motor is fixedly connected to the bogie frame, namely the traction motor is frame-hung, so the vibration of the traction motor will seriously affect that of the bogie frame. Therefore, in the initial stage of metro vehicle speed-up, the vibration characteristics of the metro components are different from those of heavy-haul locomotive, which has the vibration decaying law during the down–up transmission of wheelset–motor–bogie frame–car body introduced in Chen et al. (2017c). Meanwhile, it just shows that the effect of the gear transmission systems on the vibration of the bogie frames in metro vehicles is more obvious than that of the locomotive, so it is necessary to carry out the coupling vibration study of the gear transmission system and the bogie frame in the future research.

In all, the simulation results are basically consistent with the field test data in the variation tendency and amplitude of vibration acceleration, which can verify the accuracy of the established vehicle–track coupled dynamics model.

Figure 7 Comparison of vertical vibration responses of the traction motor.

Figure 8 Comparison of vertical vibration responses of the wheelset.

3.1.2 Model validation in the time–frequency distribution

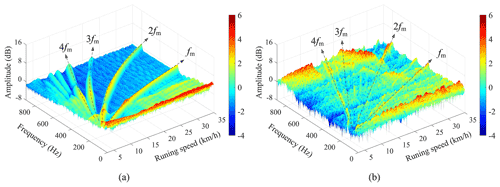
To further validate the established dynamics model, comparisons of the vibration responses in time–frequency distribution between the simulation results and the field test results have been made in this subsection. Although the previous papers (Chen et al., 2017c; Zhang et al., 2019a) verify that the excitations from the gearbox, mainly the gear mesh, can hardly affect the vibration responses of the car body and the bogie frame in the locomotive, considering the difference that the gearboxes of the metro vehicle are suspended on the bogie frames, the traction motors, wheelsets, and bogie frames are closely connected to the gear transmission systems. By using the short-time Fourier transform (STFT), the comparisons of vertical vibration responses in the time–frequency distribution of them are represented in Figs. 9–11, respectively. It can be seen that the gear mesh frequency and its harmonics are clearly visible, and their values and amplitudes increase with the vehicle running speed, both in the simulation results and the field test results, which coincide with the time-domain variation law introduced in Sect. 3.1.1. Due to the more complicated and unpredictable excitations from the wheel–rail contact interface, the frequency components of the field test results are much more complex than the simulation results.

The traction motor and wheelset are directly affected by the gear meshing. Figures 9 and 10 illustrate the time–frequency distributions of the vertical vibration responses of the traction motor and the wheelset. Compared to the vibration of the wheelset in the field test results, the gear mesh frequency and its harmonics of the traction motor vibration responses are more obvious under the whole speed-up process, especially at a higher speed. The main reason is that the wheelset is excited not only by the gear meshing, but also by the wheel–rail contact interface, which makes the periodic components submerged into the background noise to some extent. Similarly, a phenomenon similar to the time–frequency distribution of the traction motor can be seen in the vibration response of the bogie frame in Fig. 11. The difference is that the vibration amplitude of the wheelset and bogie frame is roughly the same, while the vibration amplitude of the traction motor is generally higher than that of both, which can also be seen from the time domain.

Consequently, the time–frequency distributions of the vibration responses of the key components by using the established vehicle–track coupled dynamics model are basically consistent with the field test results from the metro vehicle in terms of the main frequency components, amplitude, and variation trend. The accuracy of the established dynamics model is verified from the perspective of both time domain and time–frequency domain.

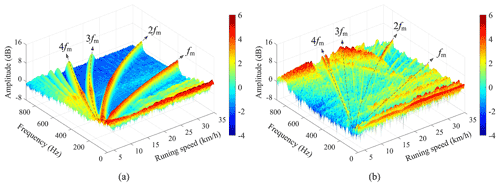
Figure 9 Time–frequency distribution of the traction motor vibration responses: (a) simulated results, (b) field test results.

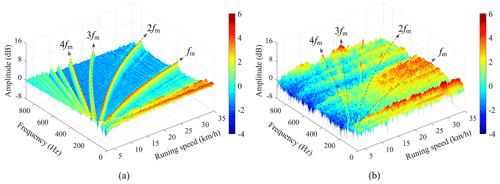
Figure 10 Time–frequency distribution of the wheelset vibration responses: (a) simulated results, (b) field test results.

Figure 11 Time–frequency distribution of the bogie frame vibration responses: (a) simulated results, (b) field test results.

3.2 Effect of the gear mesh force on the metro vehicle driving system

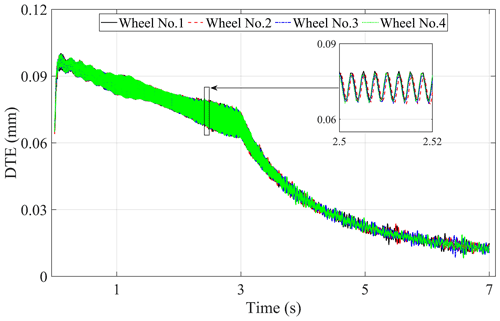
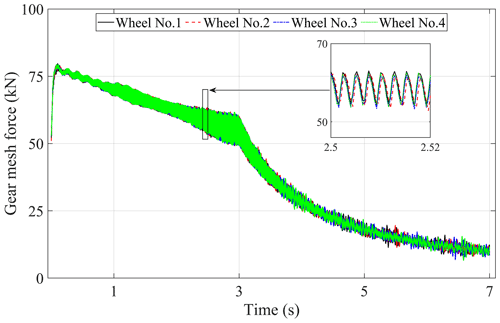
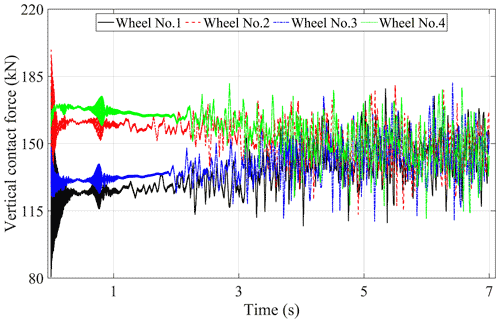
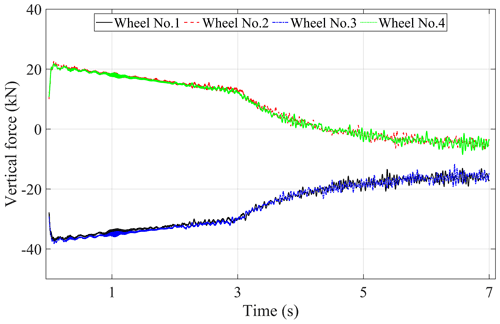
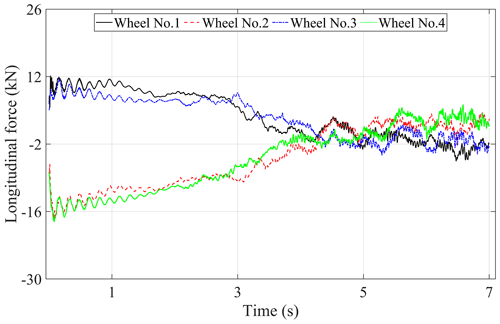
The gear dynamic mesh force is one of the main internal excitations of the driving system in the metro vehicle. Due to the frequent conversion of traction and braking conditions, the interaction between the components of the driveline will be more intense in the metro vehicle. To investigate the effect of the gear mesh forces on the dynamic responses of the metro vehicle driving system, some analysis has been done by using the time-varying mesh stiffness under traction conditions. The time histories of the DTEs, gear dynamic mesh forces, wheel–rail vertical contact forces, and the vertical and longitudinal interaction forces between the traction motors, gearboxes, and bogie frames are shown in Figs. 12–16, respectively. The legends of these figures (Wheel No. 1, Wheel No. 2, Wheel No. 3, Wheel No. 4) represent the relevant description in the corresponding position of the car body.

Figure 12 shows that the variation trend and value of DTEs of all gear pairs in the metro vehicle are basically the same in the process of acceleration. At the stage of low running speed with constant traction force, DTE tends to decrease linearly as time goes on. With the decrease of traction force, DTE decreases more obviously, indicating that the excitation from the gear transmission system gradually becomes weak at a higher running speed. It can be known that the gear dynamic mesh forces which are shown in Fig. 13 have similar variation law with the DTEs according to Eq. (6). Because there is an angle between the gear dynamic mesh force and the vertical–longitudinal direction which can be seen in Fig. 2b, and the opposite direction of the dynamic gear mesh force of the two gear pairs in the same bogie frame, the vertical component force of that in the opposite direction will produce the phenomenon of axle load transfer which can be seen in Fig. 14, and the detailed description can be found in Chen et al. (2018). It should be noted that the axle load transfer phenomenon becomes very weak because the static axle load is relatively large, which also supports the previous conclusion that the excitation of the gear transmission system becomes weak at a higher speed.

Figure 12 DTEs of the gear pairs under traction condition.

Figure 13 Dynamic mesh forces of the gear pairs under traction condition.

Figure 14 Wheel–rail vertical contact forces under traction condition.

In addition, Figs. 15 and 16 show the effect of the gear mesh forces on the traction motors and gearboxes. In Fig. 15, due to the effect of gear dynamic mesh forces, it can be seen that the suspension steeves located in “Wheel No. 1” and “Wheel No. 3” between the gearboxes and bogie frames are subjected to the stretch forces, while that located in “Wheel No. 2” and “Wheel No. 4” suffer the compressive forces at the lower-speed stage, but all of that will be in the stretch state when the effect of gear mesh force is less than the effect of gearbox gravity, and the gear mesh forces will continue to affect the force state of gearboxes because of the small weight. The same phenomenon can also be seen in Fig. 16, but the difference is that the gear mesh forces have little effect on the longitudinal interaction forces between the traction motors and the bogie frames because the longitudinal component of the gear mesh force is relatively small due to the small gear mesh angle, especially at the high running speed, so the longitudinal forces of the traction motors tend toward a stable positive value because the metro vehicle is in the traction condition. Therefore, compared to the influence on the axle load transfer, the gear mesh force has a great and lasting effect on the traction motors and gearboxes.

Figure 15 Forces of the suspension steeve between the gearboxes and bogie frames.

Figure 16 Longitudinal interaction forces between the traction motors and bogie frames.

4 Conclusions

According to the specific structure and the main parameters of the metro vehicle components, a vertical–longitudinal dynamics model which considers the frame-hung traction motor and gearbox is established in this paper. In particular, the vertical and longitudinal coupling effect of the gear transmission system is considered. Based on the established dynamics model, the corresponding vibration responses are extracted from the simulation with the effect of the gear time-varying mesh stiffness and the excitation from the track geometrical irregularity in traction. By comparing the simulation results and field test results in both time domain and time–frequency domain, the coupled model is validated to be reliable in the analysis of the metro vehicle dynamics characteristic. The analysis results indicate that the gear dynamic mesh force is the coupling link of the drive system in the vertical and longitudinal directions. Compared to the wheelset, the gear mesh force has a greater effect on the force state of the traction motor and gearbox. As a result, this dynamics model can be used to analyze the effect of the suspension stiffness and suspension position of the traction motor and gearbox on the dynamic characteristics of the metro vehicle, and in turn, it can help to optimize the suspension parameters of these components. Besides, further research works, such as the dynamic characteristics analysis of the traction motor–gearbox transmission system under the abnormal service conditions of the gear faults and wheel and rail defects, can be investigated.

Appendix A: Nomenclature

Notation	Specification
Mc	Car body mass
Mt	Bogie frame mass
Mw	Wheelset mass
Mm	Traction motor mass
Mgb	Gearbox mass
Jc	Mass moment of inertia of car body
Jt	Mass moment of inertia of bogie frame
Jw	Mass moment of inertia of wheelset
Jm	Mass moment of inertia of traction motor
Jgb	Mass moment of inertia of gearbox
Kpz	Stiffness of primary suspension
Ksz	Stiffness of secondary suspension
Kbmz	Vertical stiffness between traction motor and bogie frame
Kbmx	Longitudinal stiffness between traction motor and bogie frame
Kgbmz	Vertical stiffness between gearbox and traction motor
Kgbmx	Longitudinal stiffness between gearbox and traction motor
Kbgbz	Vertical stiffness between bogie frame and gearbox
Kgbwz	Vertical stiffness between gearbox and wheel axle
Kgbwx	Longitudinal stiffness between gearbox and wheel axle
Kpg	Gear mesh stiffness
Ki	Single-tooth mesh stiffness of the ith tooth pair
Ka	Bending stiffness
Kb	Shear stiffness
Kss	Axial compressive stiffness
Kff	Tooth fillet-foundation stiffness
Kh	Hertzian contact stiffness of gear teeth
Cpz	Damping coefficient of primary suspension
Csz	Damping coefficient of secondary suspension
Cbmz	Vertical damping coefficient of suspension connecting traction motor and bogie frame
Cbmx	Longitudinal damping coefficient of suspension connecting traction motor and bogie frame
Cgbmz	Vertical damping coefficient of suspension connecting gearbox and traction motor
Cgbmx	Longitudinal damping coefficient of suspension connecting gearbox and traction motor
Cbgbz	Vertical damping coefficient of suspension connecting bogie frame and gearbox
Cgbwz	Vertical damping coefficient of suspension connecting gearbox and wheel axle
Cgbwx	Longitudinal damping coefficient of suspension connecting gearbox and wheel axle
Cpg	Gear mesh damping coefficient

Lc	Semi-longitudinal distance between bogies
lt	Semi-longitudinal distance between wheelsets in bogie
$l_{\mathrm{m}}/h_{\mathrm{m}}$	Longitudinal/vertical distance between the center of the traction motor and its suspension point on the bogie frame
$l_{\mathrm{b}\mathrm{1}}/h_{\mathrm{b}\mathrm{1}}$	Longitudinal/vertical distance between the center of the bogie frame and the suspension point of the traction motor on the bogie frame
$l_{\mathrm{b}\mathrm{2}}/l_{\mathrm{gb}}$	Longitudinal distance between the center of bogie frame/gearbox and the suspension point of the gearbox on the bogie frame
lgbw	Distance between centers of pinion and gear
R0	Wheel radius
m	Module
α0	Pressure angle
$h_{\mathrm{a}}^{\ast }$	Addendum coefficient
cn	Tip clearance coefficient
W	Face width
Cn	The normalized amount of profile modification
Ln	The normalized length of profile modification
Zg	Number of teeth
Xn	Tooth profile shift coefficient
δ	Dynamic transmission error
Tm	The output torque of traction motor
Trp	The torque transmitted between the rotor and the pinion
Tgw	The torque transmitted between the gear and wheelset
E	Elastic modulus of rail
Iy	Rail second moment of area about y axis
mr	Rail mass per unit length
Kf	Fastener stiffness in vertical direction
Cf	Fastener damping coefficient in vertical direction
E1	Elastic modulus of slab
Iy1	Slab second moment of area about y axis
Ls	Slab length in longitudinal direction
Ks	Slab stiffness in vertical direction
Cs	Slab damping coefficient in vertical direction
Z	Vertical displacement
$X/x$	Longitudinal displacement
$\mathit{\beta }/\mathit{\theta }$	Rotation angle
P(t)	Vertical contact force on the wheel–rail interface
G	Hertz wheel–rail contact constant
δZ(t)	Elastic compressive deformation of the wheel–rail contact
μ	Adhesion coefficient of the wheel–rail contact interface
Subscript
c	Car body
t	Bogie frame
w	Wheelset
gb	Gearbox
p	Pinion
g	Gear
m	Traction motor
f	Fastener
s	Slab
z	Vertical direction
x	Longitudinal direction