Kinematic and dynamic analysis of an omnidirectional mobile platform driven by a spherical wheel

The increased use of spherical wheels has allowed mobile robots to have a higher degree of maneuverability, less complex path planning and less complex control schemes. The geometry and design of the mobile robot are the principal attributes that guarantee an omnidirectional motion. Furthermore, the platform uses an active spherical wheel and four passive spherical wheels to get the best stability when the robot uses a terminal element (Kärcher). The proposed model has been designed to improve the omnidirectional motion issues, such as vibration into the platform or lack of punctual contact between the wheel and the floor, compared to mobile robots using Mecanum wheels and more than one active wheel; due to the design concept, all the mathematical formulations, kinematics and dynamics presents how the models are validated with computer simulations.

1 Introduction

As mobile robotics continues to evolve, its application has diversified from service robots to space exploration robots. In the development of the mobile robot, the designer focuses on the novelty of the final element, leaving out the mobile platform evolution. The chief problem with wheeled mobile robots is the restricted movement in workspace due to the necessity for system reorientation. Our goal is to get a wheeled mobile robotic system that can generate an omnidirectional displacement without the need to redirect the wheels, thus guaranteeing continuous operation. Additionally, this would allow the mobile robotic to operate in small spaces without the need of reorientation (Doroftei et al., 2007).

The design of the mobile platform is mainly constituted by geometric model and by the type of wheels used (Muir and Neuman, 1986). These characteristics are strongly related to kinematic analysis. The odometry technique uses a geometric body in a general framework to locate it later in any point of our reference. This is the principle that uses the odometry technique (Agull et al., 1987) that provides important applications as satellite locations, trajectory assignment and even artificial intelligence applications. Subsequently, after we get the position analysis, the velocity analysis is included within the same reference frame. The acceleration is defined as the change in velocity within a time range (Muir and Neuman, 1987).

Besides, we consider the masses of each element in the platform and as well as external forces to generate a dynamic model that can predict the motor's behavior.

Although there are platforms that have solved the omnidirectional problem (redirection of the mobile platform), its implementation requires a high construction cost and much more complex control systems. In the case of the Seekur robot (Roland, 2004), it uses eight motors to steer four active wheels and thus generates the omnidirectional movement of the platform. The Institute of Technology of Leibniz University Hannover in Germany developed another solution which implements three spherical active wheels, each one driven by two motors (Runge et al., 2014). The Robot Development Engineering Laboratory of Tohoko Gakuin University in Japan developed a newer solution, one that has a spherical active wheel driven by three motors with Swedish-type rollers (Kumagai, 2010). The AZIMUT robot (Clavien et al., 2018) represents a decentralized omnidirectional system. The Massachusetts Institute of Technology (MIT) presented a mobile platform that was supported by spherical wheels (West and Ascada, 1995) using rollers to transmit the movement with three active wheels. The reports mentioned above relate the fact that the geometry and type of wheels used are fundamental components in the design (Muir and Neuman, 1986), i.e., from triangular geometry (Orozco et al., 2020) to dodecagonal geometry (Orozco, 2018), using standard wheels (Muñoz et al., 2007), Swedish wheels (Lee et al., 2007) or spherical wheels (Ishida and Miyamoto, 2010).

The use of actuated spherical wheels in mobile platforms drastically simplifies the control of the robot, as well as the reduction of costs in its manufacture (Zhao BeMent, 1992). Kinematic and dynamic analysis ensures the effectiveness in the spherical wheel implementation (Angeles and Lee, 1988). Kinematics also allows for implementing the use of odometry to program robot movements as satellite location applications (Agull et al., 1987).

This paper is based on the kinematic and dynamic model of an omnidirectional mobile platform (OMP) with an active spherical wheel driven by two motors and four passive wheels as support. The kinematic and dynamic conditions are strongly linked with the geometry, the location of the wheels and with the position analysis of each wheel.

The Sheth–Uicker convention is used in the contact point between the wheel and the ground as planar contact (Muir and Neuman, 1987). This method presents the forward kinematics in an analogous way to manipulative robots. For the dynamic analysis, the Lagrange method is used where the Lagrangian is composed only of kinetic energy, because this method considers that the platform only moves on flat surfaces. The holonomic restrictions, which are directly linked with the movement of the platform, are raised within the operating frame of the robot, which guarantees that the “sweep” condition is wholly rejected. This strategy allows energy optimization in the actuators; in the same way, a more straightforward control is implied to achieve the system's omnidirectional movement.

2 Platform design

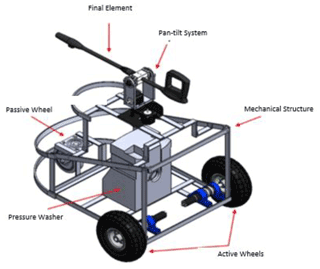
This paper presents the kinematic and dynamic model of a mobile platform driven by one active spherical wheel constructed of rubber and four passive wheels built of steel; see Fig. 1. The design will be used in a cleaning robot (Fig. 2) (Orozco et al., 2020). The dimensions and weight are shown in Table 1. Some of the principal details are the Kärcher pressure system (used as a terminal element), the pan–tilt rotation (used as the reorientation's Kärcher system) and the robot's energy conversion system.

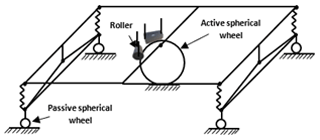
Figure 1 The main feature of the model is the omnidirectional platform displacement. This characteristic allows us to generate a kinematic and dynamic model (Muir and Neuman, 1987).

Figure 2 Pressure cleaning robot.

The kinematic analysis of a mobile robot is a direct analogy with the methodology used in manipulator robotics; the main differences between both systems are the restrictions and the type of joints used (d'Andrea-Novel et al., 1991).

In the manipulator model, most of the links are treated as solid bodies in the form of an open kinematic chain that generally uses rotational or prismatic joints (Angeles, 2007). When the modeling of the platform is presented, it is common to consider the system as n closed kinematic chains (the assign of the variable n is the number of wheels of the system with ground contact) (Yun and Yamamoto, 1993). The joint that generates the contact between the wheel and the ground is used as a contact of superior torque, which applies the Sheth–Uicker convention (Muir and Neuman, 1987). This allows us to consider the contact as a lower pair (planar contact).

Table 1 Features of pressure cleaning robot.

From the dynamic point of view, the analysis becomes more complex in that it becomes non-linear if the designer wants to contemplate all the system interaction effects (Zhao and BeMent, 1992). In this paper, the interactions that corrupt the linearity of the model are rejected. This is due to the movement of the platform, without any kind of interference, like vibration or any kind of external force. Figure 3 shows the elements that make up the mobile platform.

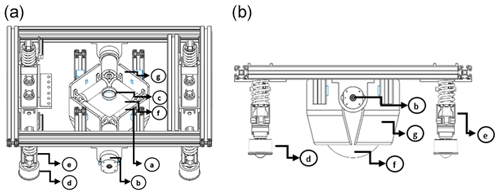
Figure 3 The platform elements, with (a) platform top view and (b) platform side view. Labels: (a) roller, (b) motor, (c) roller ball (transfer), (d) roller ball (support), (e) support base, (f) active spherical wheel, and (g) active spherical wheel support.

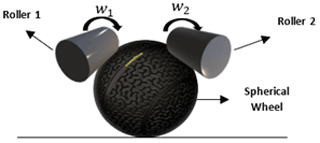
The platform has two DC (direct current) motors that by rollers (constructed of rubber) can transfer the angular velocity to the active spherical wheel; see Fig. 4. The platform also has a shock absorber system that guarantees the continuous actuated spherical wheel contact (Balkcom et al., 2009). The platform includes four roller-ball-type passive wheels implementing bearings as the mechanism of continuous contact with the ground.

Figure 4 Wheel driven by two motors.

3 Mobile platform proposal

3.1 Positional analysis

In this section, the coordinate system corresponding to the articulations of the mobile platform are assigned. As mentioned above, n closed kinematic chains are used where the variable n corresponds to the number of wheels that have contact with the ground; this contact is generated as a higher torque contact.

In this paper, the design implements the Sheth–Uicker convention (Muir and Neuman, 1987). The Sheth–Uicker convention model shows the high torque contact as a planar pair contact. See Fig. 5; as the result, we exclude the ambiguities of the transformation matrices.

Figure 5 (a) Planar contact and (b) point contact.

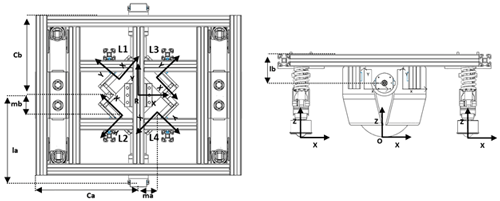
After considering this convention, we apply each link's coordinate system in the proposed model (Barraquand and Latombe, 1989). The result is illustrated in Fig. 6, and the corresponding matrices are given in Eqs. (1), (2), (3) and (4). Where L₁, L₂, L₃, L₄, and O are the roller coordinate axes, and C_b, C_a, m_a, m_b, l_a, and l_b are the dimensions of the platform (each letter indicates the dimension assignment). The matrices shown in Eqs. (1), (2), (3) and (4) describe the coordinate system from the central point R.

$$\begin{array}{}\text{(1)}& {}^R{T}_{L_{\mathrm{1}}}=\left[\begin{array}{llll}\cos \left(\frac{\mathit{\pi }}{\mathrm{4}}\right)& -\sin \left(\frac{\mathit{\pi }}{\mathrm{4}}\right)& \mathrm{0}& m_a\\ \sin \left(\frac{\mathit{\pi }}{\mathrm{4}}\right)& \cos \left(\frac{\mathit{\pi }}{\mathrm{4}}\right)& \mathrm{0}& m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& l_b\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\text{(2)}& {}^R{T}_{L_{\mathrm{2}}}=\left[\begin{array}{llll}\cos \left(\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}}\right)& -\sin \left(\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}}\right)& \mathrm{0}& m_a\\ \sin \left(\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}}\right)& \cos \left(\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}}\right)& \mathrm{0}& -m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& l_b\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\text{(3)}& {}^R{T}_{L_{\mathrm{3}}}=\left[\begin{array}{llll}\cos (-\frac{\mathit{\pi }}{\mathrm{4}})& -\sin (-\frac{\mathit{\pi }}{\mathrm{4}})& \mathrm{0}& -m_a\\ \sin (-\frac{\mathit{\pi }}{\mathrm{4}})& \cos (-\frac{\mathit{\pi }}{\mathrm{4}})& \mathrm{0}& -m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& l_b\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\text{(4)}& {}^R{T}_{L_{\mathrm{4}}}=\left[\begin{array}{cccc}\cos (-\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}})& -\sin (-\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}})& \mathrm{0}& -m_a\\ \sin (-\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}})& \cos (-\frac{\mathrm{3}\mathit{\pi }}{\mathrm{4}})& \mathrm{0}& m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& l_b\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right].\end{array}$$

The matrices are shown in Eqs. (5), (6), (7) and (8), which present the relationship that exists between point R and point of contact O.

$$\begin{array}{}\text{(5)}& {}^{L_{\mathrm{1}}}{T}_O=\left[\begin{array}{llll}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& m_a\\ -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& -m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& (l_a-l_b)\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\text{(6)}& {}^{L_{\mathrm{2}}}{T}_O=\left[\begin{array}{llll}-\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& m_a\\ -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& (l_a-l_b)\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\text{(7)}& {}^{L_{\mathrm{3}}}{T}_O=\left[\begin{array}{llll}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& -m_a\\ \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& -m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& (l_a-l_b)\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\text{(8)}& {}^{L_{\mathrm{4}}}{T}_O=\left[\begin{array}{llll}-\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& -m_a\\ \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}& \mathrm{0}& m_b\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& (l_a-l_b)\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right].\end{array}$$

Figure 6 Coordinate system assignment.

4 Kinematic and dynamic analysis

4.1 Kinematic analysis

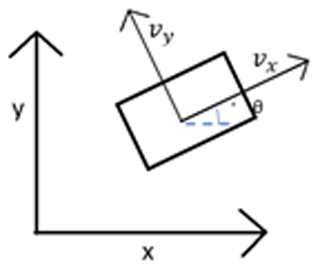
Now that the positional analysis of the mobile robot is known, Eqs. (9) and (10) present the velocity analysis. As mentioned above, an omnidirectional platform is contemplated in conjunction with the manipulator element. The corresponding equations are presented as

$$\begin{array}{}\text{(9)}& {\displaystyle }{V}_x=w_{\mathrm{1}}R\cos (-\mathit{\alpha })+w_{\mathrm{2}}R\cos \left(\mathit{\alpha }\right),\text{(10)}& {\displaystyle }{V}_y=-w_{\mathrm{1}}R\sin (-\mathit{\alpha })+w_{\mathrm{2}}R\sin \left(\mathit{\alpha }\right),\end{array}$$

where w is the angular velocities of the motors, R is the radius of the roller with spherical wheel contact, V_x is the linear velocity in the x-axis direction, V_y is the linear velocity in the y-axis direction, and α is the roll inclination angle with x-axis reference.

The spherical wheel contact with the roller is considered continuous contact with a constant relation in speeds, where the slip that may exist in them is neglected. (This is just a consideration to develop the dynamical model to guarantee the linear model in the platform.)

$$\begin{array}{c}{\displaystyle }{w}_{\mathrm{1}}R=w_{r}r,\\ {\displaystyle }{w}_r={\displaystyle \frac{w_{\mathrm{1}}R}{r}}.\end{array}$$

We know the linear speed of the wheel is

$$v=r{w}_r.$$

From the above equation, we obtain

$$\begin{array}{}\text{(11)}& \begin{array}{rl}& v=r{\displaystyle \frac{w_{\mathrm{1}}R}{r}},\\ & v=w_{\mathrm{1}}R,\end{array}\end{array}$$

where w_r is the angular spherical wheel velocity, and r is the spherical wheel radius.

After defining the relationships between the speed of the roller and the spherical wheel, we obtain

$$\begin{array}{}\text{(12)}& \left[\begin{array}{l}{v}_x\\ v_y\end{array}\right]=\left[\begin{array}{ll}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R\\ -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R\end{array}\right]\cdot \left[\begin{array}{l}{w}_{\mathrm{1}}\\ w_{\mathrm{2}}\end{array}\right].\end{array}$$

Considering the angular velocity obtained by the manipulator of the mobile robot, we get

$$\begin{array}{}\text{(13)}& \left[\begin{array}{l}{v}_x\\ v_y\\ w\end{array}\right]=\left[\begin{array}{lll}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \mathrm{0}\\ -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\cdot \left[\begin{array}{l}{w}_{\mathrm{1}}\\ w_{\mathrm{2}}\\ w_k\end{array}\right],\end{array}$$

where w_k is the mobile robot's angular velocity.

In this way, the Jacobian matrix is

$$\begin{array}{}\text{(14)}& J=\left[\begin{array}{lll}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \mathrm{0}\\ -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right].\end{array}$$

This analysis corresponds to the forward kinematics, and to obtain the inverse kinematics, we use

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& v=Jw,\\ & w=J^{-\mathrm{1}}v.\end{array}\end{array}$$

Equation (15) is justified by

$$\begin{array}{}\text{(16)}& \mathrm{Det}\left(J\right)=R^{\mathrm{2}}.\end{array}$$

As we can see from the Eq. (16) result, the J determinant is constant; it represents an advantage due to fact that the platform displacement does not present ambiguities.

4.2 Holonomic constraints

In this section, the restrictive dynamic equations are defined. We assumed the robot has one active wheel driven by two motors.

It is necessary to formulate an equation that guarantees that the mobile robot will roll and not slide.

Figure 7 shows the constraint diagram that guarantees the bearing, and we obtain

$$\begin{array}{c}{\displaystyle }{v}_x\cos \left(\mathit{\theta }\right)-v_y\sin \left(\mathit{\theta }\right)={\displaystyle \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}R{w}_{\mathrm{1}}+{\displaystyle \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}R{w}_{\mathrm{2}},\\ {\displaystyle }{v}_x\sin \left(\mathit{\theta }\right)+v_{y}cos\left(\mathit{\theta }\right)=-{\displaystyle \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}R{w}_{\mathrm{1}}+{\displaystyle \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}R{w}_{\mathrm{2}}.\end{array}$$

Restructuring the equations and representing them in a matrix way, we receive

$$\left[\begin{array}{ll}\cos \left(\mathit{\theta }\right)& -\sin \left(\mathit{\theta }\right)\\ \sin \left(\mathit{\theta }\right)& \cos \left(\mathit{\theta }\right)\end{array}\right]\left[\begin{array}{l}{v}_x\\ v_y\end{array}\right]=\left[\begin{array}{l}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R(w_{\mathrm{1}}+w_{\mathrm{2}})\\ \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R(w_{\mathrm{2}}-w_{\mathrm{1}})\end{array}\right].$$

From the previous equation, a solution condition can be proposed:

$$\begin{array}{}\text{(17)}& \begin{array}{rl}& \left[\begin{array}{ll}\cos \left(\mathit{\theta }\right)& -\sin \left(\mathit{\theta }\right)\\ \sin \left(\mathit{\theta }\right)& \cos \left(\mathit{\theta }\right)\end{array}\right]\left[\begin{array}{l}{v}_x\\ v_y\end{array}\right]-\left[\begin{array}{l}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R(w_{\mathrm{1}}+w_{\mathrm{2}})\\ \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R(w_{\mathrm{2}}-w_{\mathrm{1}})\end{array}\right]=\mathbf{0}\\ & \underset{R\left(\mathit{\theta }\right)}{\underbrace{\left[\begin{array}{llll}\cos \left(\mathit{\theta }\right)& -\sin \left(\mathit{\theta }\right)& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R\\ \sin \left(\mathit{\theta }\right)& \cos \left(\mathit{\theta }\right)& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R\end{array}\right]}}\underset{\dot{S}}{\underbrace{\left[\begin{array}{l}{v}_x\\ v_y\\ w_{\mathrm{1}}\\ w_{\mathrm{2}}\end{array}\right]}}=\left[\begin{array}{l}\mathrm{0}\\ \mathrm{0}\end{array}\right]\end{array}.\end{array}$$

Figure 7 Mobile platform path.

4.3 Dynamic analysis

In this section, the inverse dynamic equations are generated, where positions, speeds and motor accelerations are obtained. The Lagrange analysis is used in mobile robotic systems (Dhaouadi and Abu Hatab, 2013).

$$\begin{array}{}\text{(18)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial K}{\partial {\dot{S}}_i}}\right)-{\displaystyle \frac{\partial K}{\partial S_i}}={\mathit{\tau }}_i-r_{\mathrm{1}i}{\mathit{\lambda }}_{\mathrm{1}}-r_{\mathrm{2}i}{\mathit{\lambda }}_{\mathrm{2}},\end{array}$$

where i=1, 2, 3, 4; K is the total system's energy, τ_i is the generalized torque, λ₁ and λ₂ are Lagrange multipliers, r_ji represents the matrix R(θ) elements, S is the position vector, and $\dot{S}$ is the velocity vector.

$$\begin{array}{}\text{(19)}& \begin{array}{rl}& \left[\begin{array}{llll}\cos \left(\mathit{\theta }\right)& -\sin \left(\mathit{\theta }\right)& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R\\ \sin \left(\mathit{\theta }\right)& \cos \left(\mathit{\theta }\right)& \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R& -\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}R\end{array}\right]\\ & =\left[\begin{array}{llll}{r}_{\mathrm{11}}& r_{\mathrm{12}}& r_{\mathrm{13}}& r_{\mathrm{14}}\\ r_{\mathrm{21}}& r_{\mathrm{22}}& r_{\mathrm{23}}& r_{\mathrm{24}}\end{array}\right]\end{array}\end{array}$$

The total system's energy is given by

$$K=K_{\mathrm{T}}+K_{\mathrm{R}},$$

where K_T is the translational energy, and K_R is the rotational energy.

The potential energy is neglected because it is considered a horizontal not vertical displacement; therefore, U=0, (Li et al., 2015).

The translational energy is

$$\begin{array}{}\text{(20)}& K_{\mathrm{T}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}M(v_x^{\mathrm{2}}+v_y^{\mathrm{2}}),\end{array}$$

$$M=M_{\mathrm{p}}+M_{\mathrm{RA}}+M_{\mathrm{RP}},$$

where M_p is the platform mass, M_RA is the active wheel mass, and M_RP is the passive wheel mass.

On the other hand, the rotational energy is

$$\begin{array}{}\text{(21)}& K_{\mathrm{R}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(I_{\mathrm{R}}+I_{\mathrm{M}})w^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{I}_{\mathrm{W}}(w_{\mathrm{1}}^{\mathrm{2}}+w_{\mathrm{2}}^{\mathrm{2}}),\end{array}$$

where I_R is the robot inertia tensor, I_M is the spherical active wheel inertia tensor, and I_W is the roller ball inertial tensor.

In this way, the energy equation that represents the mobile platform is generated:

$$\begin{array}{}\text{(22)}& \begin{array}{rl}K& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(M_{\mathrm{p}}+M_{\mathrm{RA}}+M_{\mathrm{RP}})(v_x^{\mathrm{2}}+v_y^{\mathrm{2}})+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(I_{\mathrm{R}}+I_{\mathrm{M}})w^{\mathrm{2}}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{I}_{\mathrm{W}}(w_{\mathrm{1}}^{\mathrm{2}}+w_{\mathrm{2}}^{\mathrm{2}}),\end{array}\end{array}$$

Applying the Lagrange equation, we obtain

$$\begin{array}{}\text{(23)}& {\displaystyle }(M_{\mathrm{p}}+M_{\mathrm{RA}}+M_{\mathrm{RP}})\dot{v_x}=-{\mathit{\lambda }}_{\mathrm{1}}\cos \left(\mathit{\theta }\right)-{\mathit{\lambda }}_{\mathrm{2}}\sin \left(\mathit{\theta }\right),\text{(24)}& {\displaystyle }(M_{\mathrm{p}}+M_{\mathrm{RA}}+M_{\mathrm{RP}})\dot{v_y}={\mathit{\lambda }}_{\mathrm{1}}\sin \left(\mathit{\theta }\right)-{\mathit{\lambda }}_{\mathrm{2}}\cos \left(\mathit{\theta }\right),\text{(25)}& {\displaystyle }(I_{\mathrm{R}}+I_{\mathrm{M}})\dot{w}+I_w\dot{w_{\mathrm{1}}}={\displaystyle \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}R({\mathit{\lambda }}_{\mathrm{1}}-{\mathit{\lambda }}_{\mathrm{2}}),\text{(26)}& {\displaystyle }(I_{\mathrm{R}}+I_{\mathrm{M}})\dot{w}+I_w\dot{w_{\mathrm{2}}}={\displaystyle \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}R({\mathit{\lambda }}_{\mathrm{1}}+{\mathit{\lambda }}_{\mathrm{2}}).\end{array}$$

The dynamic model presented above describes the omnidirectional platform displacement considering the restrictions raised above. It is a single active wheel located in the platform mass center, which greatly simplifies the model.

5 Numerical kinematic and dynamic validation

5.1 Numerical kinematic validation

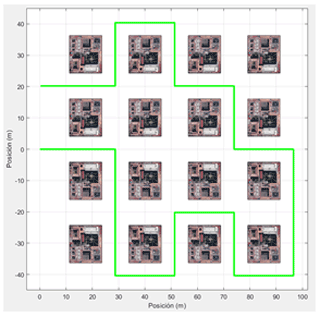
Validating the mobile platform kinematics consists of the linear velocity equation simulation (see Eqs. 9 and 10) to later integrate them and obtain the object's position, as shown below.

$$\begin{array}{c}{\displaystyle }{V}_x=w_{\mathrm{1}}R\cos (-\mathit{\alpha })+w_{\mathrm{2}}R\cos \left(\mathit{\alpha }\right),\\ {\displaystyle }{V}_y=-w_{\mathrm{1}}R\sin (-\mathit{\alpha })+w_{\mathrm{2}}R\sin \left(\mathit{\alpha }\right).\end{array}$$

Figure 8 describes the mobile platform path to follow, and Fig. 9 describes the platform displacement.

Figure 8 Mobile platform path.

Figure 9 Mobile platform displacement.

5.2 Numerical dynamic validation

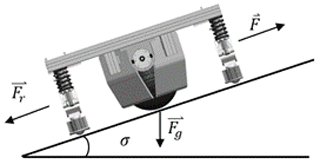
A scenario with a variable inclination slope is considered (Fig. 10). This gives the necessary torque to overcome the inclination force; the junction is considered a punctual rubber–concrete contact, and the friction coefficient is μ_T.

The mobile platform is considered to have a wheel activated by two motors, which implies the driven variable depends on w₁ and w₂.

Figure 10 Forces diagram.

Obtaining the necessary torque to overcome the F_r force and the F_g component that prevents the movement of the platform in the direction of F implies the use of Eqs. (20) and (21), considering the potential energy U, which is analytically expressed as

$$L=K-U,$$

where L is the Lagrangian.

Equation (18) becomes

$$\begin{array}{}\text{(27)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial L}{\partial {\dot{S}}_i}}\right)-{\displaystyle \frac{\partial L}{\partial S_i}}={\mathit{\tau }}_i-{\mathit{\tau }}_l,\end{array}$$

where τ_i −τ_l represents the generalized non-conservative forces (τ_i is the wheel torque, and τ_l is the friction contact torque), S is the position vector, and $\dot{S}$ is the velocity vector.

By substituting the kinetic and potential energy equations in L, we obtain

$$\begin{array}{c}{\displaystyle }L=K_T+K_R-U,\\ {\displaystyle }U=mgh,\end{array}$$

where m is mass, g is acceleration, and h is height.

Obtaining h implies considering the height of the object when both w₁ and w₂ are active (see Fig. 11).

Figure 11 Inclined displacement.

Therefore, we obtain

$$h=\sqrt{{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{X}_{\mathrm{1}}^{\mathrm{2}}+X_{\mathrm{1}}{X}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{X}_{\mathrm{2}}^{\mathrm{2}}-({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{X}_{\mathrm{1}}^{\mathrm{2}}+X_{\mathrm{1}}{X}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{X}_{\mathrm{2}}^{\mathrm{2}})(\cos \mathit{\alpha }{)}^{\mathrm{2}}}.$$

By replacing the values in L, we obtain

$$\begin{array}{}\text{(28)}& \begin{array}{rl}L& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(M_{\mathrm{p}}+M_{\mathrm{RA}}+M_{\mathrm{RP}})(v_x^{\mathrm{2}}+v_y^{\mathrm{2}})\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{I}_{\mathrm{W}}(w_{\mathrm{1}}^{\mathrm{2}}+w_{\mathrm{2}}^{\mathrm{2}})-mgh.\end{array}\end{array}$$

By substituting Eq. (28) into Eq. (27) and solving the Euler–Lagrange equation, we obtain

$$\begin{array}{c}{\displaystyle }{\mathit{\tau }}_{\mathrm{1}}=I_{\mathrm{W}}{\mathit{\alpha }}_{\mathrm{1}}+\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}mg\left({\displaystyle \frac{X_{\mathrm{1}}+X_{\mathrm{2}}-(X_{\mathrm{1}}+X_{\mathrm{2}})(\cos \mathit{\alpha }{)}^{\mathrm{2}}}{h}}\right)\right]+{\mathit{\mu }}_T{F}_{\mathrm{n}},\\ {\displaystyle }{\mathit{\tau }}_{\mathrm{2}}=I_{\mathrm{W}}{\mathit{\alpha }}_{\mathrm{2}}+\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}mg\left({\displaystyle \frac{X_{\mathrm{1}}+X_{\mathrm{2}}-(X_{\mathrm{1}}+X_{\mathrm{2}})(\cos \mathit{\alpha }{)}^{\mathrm{2}}}{h}}\right)\right]+{\mathit{\mu }}_T{F}_{\mathrm{n}},\end{array}$$

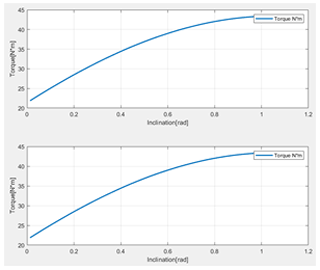
where α₁ and α₂ are the accelerations due to the rollers, X₁ and X₂ are the platform positions due to roller speed, μ_T is the dynamic friction coefficient, F_n is the normal force on the active wheel, and the equation simulations τ₁ and τ₂ are in Fig. 12.

Figure 12 Torque inclination.

By validating the dynamic part, the equations were simulated where the following values are considered: M_p=10.1 kg, M_RA=0.5 kg, M_RP=0.4 kg, I_R=diag (0.6895), and I_M and I_W=diag (0.0125). In this way the result in the dynamic model brings the congruence with the kinematic model. This reflects the Euler–Lagrange equation use with the omnidirectional mobile platforms.

6 Conclusion

Concluding, the design based on an active wheel and four passive wheels guarantees the omnidirectional displacement in the workspace with less complex design and construction.

In this paper, the kinematic and dynamic modeling of an omnidirectional mobile platform with an active wheel and four passive wheels was presented and validated. The active wheel uses two motors to generate its movement; the Sheth–Uicker convention was essential to locate each element of the mobile platform. In this way, the velocity analysis is summarized to simplify the position diagram and observe its change over time. The torque reflects the congruence with the kinematic equations, although the dynamic equation rejects the external forces.

The results generated in this article support the principle that a spherical wheel is the best option for a mobile platform when considering that the designer wants to build a land mobile robot. Due to the construction of this mobile platform, a smaller budget is required and less control in the programming of displacement is necessary.