A novel flying–walking power line inspection robot and stability analysis hanging on the line under wind loads

To address the problems of existing power line inspection robots (PLIRs), such as complex structural design, difficult landing on and off lines, short cruise times, and easy hitting lines, we propose a novel flying–walking power line inspection robot (FPLIR) with the ability to fly and walk. The structural design of an FPLIR is carried out, which mainly includes a flying mechanism and a walking mechanism. Compared with climbing PLIRs and unmanned aerial vehicles (UAVs), the FPLIR can quickly land on and off lines, easily cross obstacles, and have longer cruise times and steady inspection perspectives. In addition, a directing-push pressing component is designed to improve the walking stability along the line. We also investigate the walking stability of the FPLIR on the line when encountering working conditions with crossing wind. The dynamics model of the FPLIR on the power line using the Lagrangian equation is derived to analyze walking stability caused by wind loads, considering pressing force and walking speed. An optimized regression design with three factors (wind angle, walking speed, and pressing force) and five levels was adopted to reveal the effect of these factors on the walking stability of the FPLIR. The experimental results show that wind angle and pressing force significantly influence the walking stability of the FPLIR (P<0.05). The maximum swing displacement of the center of mass (COM) is 4.7 cm (when wind angle, walking speed, and pressing force are 90^∘, 7.2 m min⁻¹, and 0, respectively). The maximum swing displacement of the COM is 2.5 cm when the pressing force increasing to 39.4 N is reduced by 46.2 % (when wind angle and walking speed are 90^∘ and 5.1 m min⁻¹, respectively), which effectively reduces the influence of wind loads and improves the stability of the FPLIR. The proposed FPLIR significantly improves inspection stability, providing a theoretical basis for slipping control, collecting images of intelligence inspection robots in the future.

1 Introduction

Power lines exposed to the natural environment for a long time might have incurred some failures such as broken strands, vegetation encroachment, and damper slipping, affecting transmission capability and the safety of the power system. Therefore, it is essential to conduct regular inspections and maintenance to prevent power lines from losing transmitting power and causing security problems.

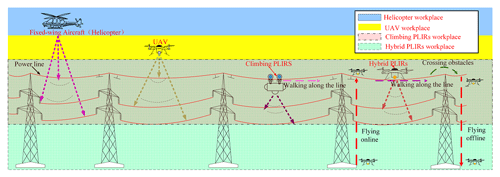
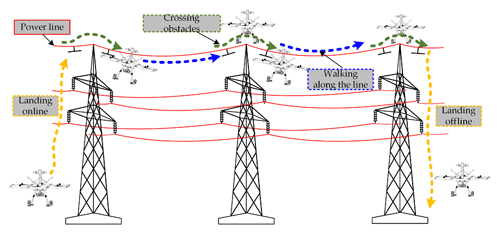
The original inspection method of power lines is manual inspection (Karjalainen et al., 2016). Manual inspection mainly relies on inspectors climbing line towers or using telescopes to inspect power lines. This method has heavy inspection intensity and low inspection accuracy (Wang et al., 2009). Therefore, people strive to develop all kinds of advanced power line inspection robots (PLIRs) to replace humans. Inspection robots have been widely used to reduce inspection intensity, improve inspection accuracy, and prevent accidents caused by manual inspection (Yang et al., 2020; Alhassan et al., 2019; Menendez et al., 2017; Seok and Kim, 2016; Luo and Tian, 2011; Jalal et al., 2013). At present, inspection robots can generally be classified into three categories, i.e., climbing PLIRs, flying PLIRs, and hybrid PLIRs (Alhassan et al., 2019). Their inspection features and workplaces are illustrated in Fig. 1.

Climbing PLIRs are typically characterized as two or more mechanical arms that climb and roll along the power line (Wang et al., 2011a, b). Paulo et al. (2008) developed a climbing robot that installed a telescopic adjustment mechanism to adjust the center of gravity to complete crossing of obstacles (Debenest and Guarnieri, 2010; Fonseca et al., 2008). Montambault and Pouliot (2015) designed the climbing inspection robot characterized as a clamping mechanism to cross obstacles (Pouliot and Montambault, 2012; Montambault and Pouliot, 2015). Wuhan University proposed a two-armed mobile robot to achieve autonomous motions (e.g., walking and crossing obstacles) on power lines (Wang et al., 2011b). Moreover, other types of climbing PLIRs include three-armed PLIRs (Yang et al., 2014; Tao and Fang, 2019), four-armed prototypes (Lima et al., 2018), five-armed structures (Tao et al., 2016; Shruthi et al., 2019), and snake-shaped mechanisms (Wei et al., 2013; Liu et al., 2019). Climbing PLIRs are more stable and reliable for performing inspection tasks, but their structural design is complicated, and they have more difficulty in crossing certain obstacles.

Flying PLIRs use unmanned aerial vehicles (UAVs) or helicopters to inspect power lines. Helicopters are initially used in the power transmission and distribution industry (Yan et al., 2008; Whitworth et al., 2001; Jones et al., 2000; Browne and Adam, 1988; Pelacchi, 1998). Helicopter inspection can quickly complete inspection tasks and dramatically reduce the inspection intensity. However, helicopter inspection is greatly affected by the complex operating environment and bad weather. For example, pilots need to be trained, and ground equipment needs to be maintained, meaning that this inspection method is costly and weather-dependent. Compared with helicopter inspection, UAV inspections have lower cost, excellent flight stability, and suspension capability (Hrabar et al., 2010; Wang et al., 2010; Zhang et al., 2012; Li et al., 2014; Luque-Vega et al., 2014; Qiu et al., 2018; Jiang et al., 2018). However, UAV inspections are highly vulnerable to the influence of wind and short cruise times. The short cruise time has limited its application to long-distance inspection tasks (Qin et al., 2018).

Hybrid PLIRs combined climbing and flying functions and were presented in Katrašnik et al. (2010), Chang et al. (2017), and Miralles et al. (2018). The flight ability is utilized to carry the PLIRs to the power line or to cross obstacles; the climbing mechanism moves the robot along the power line for the inspection task. Katrašnik et al. (2010) proposed a new climbing–flying robot and developed a walking mechanism installed under the flying mechanism (Buskey et al., 2001). Yu et al. (2015) designed a flying–sliding inspection robot with flying and sliding functions along the power line, achieving self-stabilization of the robot (Abd-Elaal et al., 2018). François et al. (2018) proposed a multi-rotor inspection robot, which can carry a payload (5 kg) and land semi-automatically on the power line (Eisenbeiss, 2009). Chang et al. (2017) designed a hybrid model inspection robot (Xie et al., 2019). Compared with other PLIRs, hybrid PLIRs integrate a walking mechanism and a flying mechanism to quickly land on and off lines and cross obstacles.

In addition, a power line is installed at a height of 50–65 m from the ground in western China, leading to the power line having lower structural damping and higher flexibility characteristics. Therefore, the power line is sensitive to the influence of environmental factors (e.g., wind, ice cover, and temperature difference). In addition, PLIRs on the power line are greatly affected by wind. Thus, it is crucial to study the impact of wind on the PLIRs. At present, Alhassan et al. (2019) have analyzed the impact of different wind angles on the walking vibration (Alhassan et al., 2019). Wang et al. (2009) analyzed wind load influence on robot structure and optimized the parameters (Wang et al., 2009). Fan et al. (2018) studied the speed and angle of the wind on the inspection robot, but the wind loads affecting its walking stability were not considered (Fan et al., 2018).

Our study proposes a novel flying–walking power line inspection robot (FPLIR) to analyze walking stability on the power line under wind loads. The main contributions of this paper are as follows. (1) A novel FPLIR with the ability to fly and walk is proposed to quickly land on and off the line, easily cross obstacles along the line, and get a steady inspection perspective of the line. (2) A directing-push pressing component is designed to improve the walking stability and inspection reliability along the line. (3) A dynamics model of the FPLIR hanging on the power line is derived to analyze the walking stability under wind loads. A three-factor, five-level test was designed to reveal the influence of each factor on the walking stability of the FPLIR.

The rest of the paper is organized as follows. The second section introduces the mechanism design and dynamics model of the walking mechanism. The third section focuses on the simulation analysis and dynamics model of the FPLIR on the power line. The experiment of the FPLIR walking stability is designed in the fourth section. The fifth section presents the experimental results and analysis. The summary and conclusion are given in the sixth section.

Figure 1 Illustration of the workspace of the different PLIRs.

2 Mechanical structure design and dynamics of the walking mechanism

2.1 Mechanical structure design

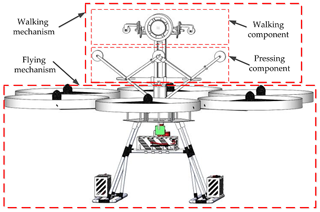
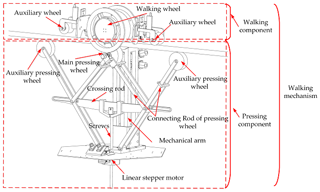
The mechanical structure of the FPLIR is shown in Fig. 2. The FPLIR has two mechanisms, i.e., a flying mechanism and a walking mechanism. The overall size of the FPLIR is 1.250 m × 1.250 m × 1.200 mm (length, width, and height). The flying mechanism is powered by the multi-rotor to land on and off power lines and cross obstacles. The walking mechanism is powered by a driving motor to walk along the power line. The walking mechanism includes a walking component and a pressing component. The walking component is shown in Fig. 3. The pressing component provides pressing force when the FPLIR walks along the power line.

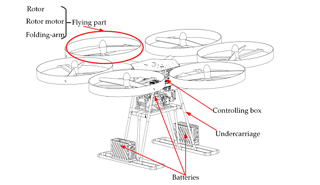
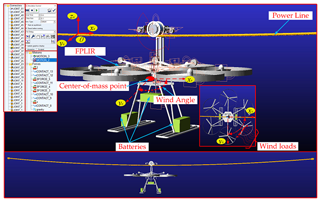
The schematic diagram of the flying mechanism is shown in Fig. 4, which mainly consists of a controlling box, a flying part, batteries, and an undercarriage. The controlling box is divided into two layers, which consist of three carbon fiber plates and aluminum columns.

The undercarriage assembled of carbon fiber tubes is installed at the bottom of the controlling box to bear the weight of the FPLIR and provide installing locations for three batteries. The function of the flying mechanism is to land on and off lines and to cross obstacles (e.g., tower and crossing wire clamp).

Figure 2 Structural design of the FPLIR.

Figure 3 The walking component of the FPLIR.

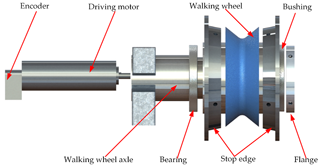
The walking component mainly includes a walking wheel, two auxiliary wheels, and a driving motor in Fig. 5.

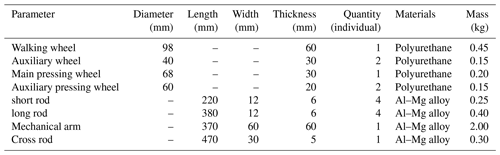
The pressing component mainly consists of three pressing wheels (a main pressing wheel and two auxiliary pressing wheels), a set of connecting rods, a screw, a crossing rod, and a linear stepper motor (42HD1403) in Fig. 5. The pressing wheels are installed on the connecting rod, the crossing rod with slots is installed on the connecting rod, the screw is installed at the center of the crossing rod, and all joints are connected by pins. The screw is powered by the linear stepper motor to push the crossing rod and connecting rods' installed pressing wheels to press the power line. The pressing component's function is to improve the FPLIR's walking stability and anti-interference ability along the power line. The specific design parameters and materials of the walking mechanism are listed in Table 1.

Figure 4 Schematic diagram of the flying mechanism.

Figure 5 Schematic diagram of the walking mechanism.

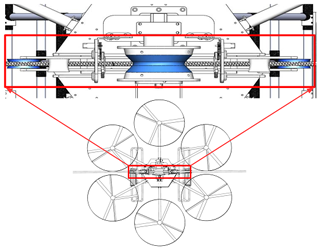
Figure 6 shows the top view of the FPLIR that illustrates the arrangement of the walking wheel, auxiliary wheels, and pressing wheels on the power line.

Figure 6 The top view of the FPLIR that illustrates the arrangement of the wheels on the power line.

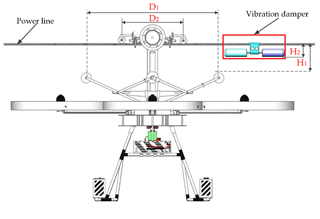
The process of crossing obstacles (e.g., the vibration damper) is shown in Fig. 7. When the obstacle is detected, the linear stepper motor pushes the screw to loosen the crossing rod's and connecting rod's installed pressing wheels away from the power line. When the FPLIR passes through the obstacle, the linear stepper motor pushes the screw to press the crossing rod and the pressing wheels on the power line. The crossing vibration damper should satisfy the following constraints:

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}{H}_{\mathrm{1}}\ge H_{\mathrm{2}}\\ D_{\mathrm{1}}>D_{\mathrm{2}}\end{array}\right.,\end{array}$$

where D₁ is the distance of two auxiliary pressing wheels, D₂ is the distance of two auxiliary wheels, H₁ is the distance between the line and the upper side of the pressing wheels, and H₂ is the maximum height of the vibration damper under the line.

The whole workflow of the FPLIR is shown in Fig. 8. First, the FPLIR lands online and walks along the power line for inspection. Then, the FPLIR crosses obstacles and continues inspection along the power line. Finally, the FPLIR lands offline when the inspection task is completed. Compared with climbing PLIRs, the FPLIR can quickly land on and off lines and easily cross obstacles. Compared with flying PLIRs, the FPLIR has a longer cruise time and a more stable inspection perspective.

Table 1 Design parameters of the walking mechanism.

2.2 The dynamics of the walking mechanism

The dynamics models of the walking mechanism are established to analyze the torque of the driving motor and the pressing force. The walking wheel has a middle groove in which sits the power line of radius r_c as shown in Fig. 9a, b. The walking wheel is a dual conical portion with an opening angle λ and a minimum radius r_min. The configuration describes the walking wheel steadily hanging on the power line and increases the available traction force because the reaction forces $F_{N\mathrm{1}}+F_{N\mathrm{2}}=\frac{F_N}{\cos \mathit{\lambda }}$ are greater than F_N. A simplified dynamics model of the walking mechanism on the power line is illustrated in Fig. 9c. An axis system is built at the O position as shown in Fig. 9c.

The torque equation of the driving motor is expressed as follows:

$$\begin{array}{}\text{(2)}& M-f_{\mathrm{r}}\times r=\mathrm{0},\end{array}$$

where r is the effective contact radius of the walking wheel, M is torques of the driving motor, and f_r is the driving force.

The balance of forces in the direction of the x axis is obtained as

$$\begin{array}{}\text{(3)}& f_{\mathrm{r}}-f_s-\sum _{i=\mathrm{1}}^{\mathrm{3}}{f}_{si}-m_{\mathrm{123}}g\sin \mathit{\theta }=m_{\mathrm{123}}{\ddot{x}}_{\mathrm{0}},\end{array}$$

where f_s represents the friction between the walking wheel and line contact, f_si represents the friction between the pressing wheels and line contact, θ represents the climbing slope in degrees, x₀ represents the distance of the FPLIR walking along the power line, m₁₂₃ represents the masses of the FPLIR, and g terms represent the gravitational accelerations.

The f_s is expressed as follows:

$$\begin{array}{}\text{(4)}& f_s-\mathit{\mu }\left(\sum _{i=\mathrm{1}}^{\mathrm{2}}{F}_{Ni}\right)=\mathrm{0},\end{array}$$

where F_Ni is the reaction force and μ is the friction coefficient.

The reaction force F_Ni is calculated as

$$\begin{array}{}\text{(5)}& \left(\sum _{i=\mathrm{1}}^{\mathrm{2}}{F}_{Ni}\right)={\displaystyle \frac{F_N}{\cos \mathit{\lambda }}}.\end{array}$$

The F_N is expressed as

$$\begin{array}{}\text{(6)}& F_N-m_{\mathrm{123}}\cos \mathit{\theta }=\mathrm{0}.\end{array}$$

The f_si is obtained as

$$\begin{array}{}\text{(7)}& \sum _{i=\mathrm{1}}^{\mathrm{3}}{f}_{si}-\mathit{\mu }\sum _{i=\mathrm{1}}^{\mathrm{3}}{N}_i=\mathrm{0},\end{array}$$

where N₁, N₂, and N₃ represent the pressing forces of the pressing wheels, respectively.

From the parameters of Tables 1 and 2, it can be seen that m₁₂₃=23.8 kg, λ=30^∘, r=0.098 m, and μ=0.3. To analyze the torque of the driving motor, some assumptions can be made for climbing slope in degrees and acceleration, assuming the climbing slope in degrees is 25^∘ (θ=25^∘) and the linear acceleration is 0 (${\ddot{x}}_{\mathrm{0}}=\mathrm{0}$). The pressing forces are 40 N (main pressing force) and 5 N (auxiliary pressing force), respectively. Finally, the torque of the driving motor can be calculated by Eqs. (2) to (7).

Figure 7 The process of crossing the obstacle (vibration damper).

Figure 8 The whole inspection process of the FPLIR.

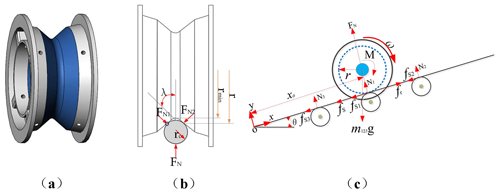
Figure 9 Dynamics model of the walking mechanism. (a) The structural design of the FPLIR with the walking wheel. (b) Schematic diagram of the FPLIR walking along the power line. (c) Schematic diagram of the FPLIR moving the whole robot along the power line for the dynamic model.

It was calculated that the maximum torque was enough to effectively perform the climbing slope of the FPLIR. Therefore, the maximum torque of the driving motor is 3.2 N m when the pressing force and climbing slope in degrees are 0. The maximum torque of the driving motor is 3.95 N m when the climbing slope in degrees is 0 and the pressing force is 50 N (the main pressing force is 40 N and the auxiliary pressing force is 10 N). The maximum torque of the driving motor is 7.38 N m when the climbing slope in degrees is 25^∘ and the pressing force is 0. The maximum torque of the driving motor is 8.12 N m when the pressing force is 50 N and the climbing slope in degrees is 25^∘.

The pressing force varies with the displacement of the screw and the torque of the linear stepper motor. Thus, the dynamics analysis of the pressing component is more necessary as the main load-bearing rod. A simplified dynamics model of the pressing component is shown in Fig. 10a. An axis system is created at the O position, with its x axis pointing in the horizontal direction and its y axis vertical to the x axis in Fig. 10a. The pressing component is symmetric about the y axis in Fig. 10a. Thus, it is analyzed to the right half of the y axis of the pressing component in Fig. 10b to e.

Take the rod O₁O₂ in Fig. 10a as a fixed rod to reduce the number of unknown forces in the moment equation. The forces are set in the tangential and normal directions in Fig. 10b to e.

The G_DE, $G_{O_{\mathrm{1}}C}$, and G_AE are the gravities of every rod, G_A and G_C are the gravities of the main pressing wheel and the auxiliary wheel, and F and y are thrust and displacement applied to the screw transforming from the torque of the linear stepper motor. M₁ and M₂ are the torques of rod O₁C and rod AE. The sizes of all unknown forces in Fig. 10b to e are arbitrary, and the actual values are determined by calculated results.

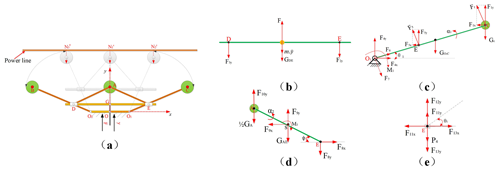
Figure 10 Schematic diagram of the pressing component. (a) Dynamics model of the pressing component. (b–e) Force analysis of rods.

Rod AE, rod DE, rod O₁C, and point E are separately considered as the research subjects. Assumptions are that the link points have negligible friction and that the center of mass is in the middle position of every rod. The dynamics equations are expressed as follows:

$$\begin{array}{}\text{(8)}& {\displaystyle }\sum F_x=\sum _{i=\mathrm{1}}^n{F}_{ix}=\mathrm{0},\text{(9)}& {\displaystyle }{F}_y=F\pm \sum _{i=\mathrm{1}}^n{F}_{iy}-m_{\mathrm{2}i}{\ddot{y}}_i-G_i=\mathrm{0},\text{(10)}& {\displaystyle }\begin{array}{rl}\sum M_O& =\sum _{j=\mathrm{1}}^n{F}_{jy}\left(x_{\mathrm{01}}-x_{\mathrm{0}}\right)-F_{jx}\left(y_{\mathrm{01}}-y_{\mathrm{0}}\right)\\ & -J_{Oi}\ddot{\mathit{\alpha }}-m_{\mathrm{2}i}\left(x_i-x_{\mathrm{0}}\right)-M_i=\mathrm{0},\end{array}\end{array}$$

where i, n, G_i, and m_2i are the serial number of the rod, the number of one research subject, gravity, and mass, respectively. J_Oi is the moment of inertia to one link joint. M_i and $\ddot{\mathit{\alpha }}$ are load moment and angular acceleration, respectively. F_ix is the force of the rod in the horizontal direction (x axis). F_iy is the force of the rod in the vertical direction (y axis), and $\ddot{y}$ is the acceleration of the rod mass in the vertical direction. x₀, y₀ is the coordinate center of the moment, x₀₁, y₀₁ is the coordinate of one end of the rod not being the center of the moment, and x_i, y_i is the coordinate of the rod mass center. The unknown forces in Fig. 10 can be solved from Eqs. (8) to (10).

The F_10y is calculated as follows:

$$\begin{array}{}\text{(11)}& F_{\mathrm{10}y}={\displaystyle \frac{\begin{array}{c}\frac{\mathrm{1}}{\mathrm{2}}{G}_A{l}_{\mathrm{AE}}\cos \mathit{\phi }+G_{\mathrm{AE}}{l}_{\mathrm{ES}}\cos \mathit{\phi }\\ -F_{\mathrm{9}y}{l}_{\mathrm{ES}}\cos \mathit{\phi }+F_{\mathrm{9}x}{l}_{\mathrm{ES}}\sin \mathit{\phi }-M_{\mathrm{2}}\end{array}}{l_{\mathrm{AE}}\cos \mathit{\phi }}}.\end{array}$$

The F₁ is calculated as follows:

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{F}_{\mathrm{1}}& ={\displaystyle \frac{M_{\mathrm{1}}{l}_{\mathrm{AE}}\cos {\mathit{\theta }}_{\mathrm{1}}\cos \mathit{\phi }-G_{\mathrm{DE}}{l}_{O_{\mathrm{1}}C}{l}_{\mathrm{AE}}{\cos }^{\mathrm{2}}{\mathit{\theta }}_{\mathrm{1}}\cos \mathit{\phi }}{l_{\mathrm{AE}}\times l_{O_{\mathrm{1}}C}\times \cos {\mathit{\theta }}_{\mathrm{1}}\cos \mathit{\phi }}}\\ & -{\displaystyle \frac{\frac{\mathrm{1}}{\mathrm{2}}{G}_{O_{\mathrm{1}}C}{l}_{O_{\mathrm{1}}C}{l}_{\mathrm{AE}}{\cos }^{\mathrm{2}}{\mathit{\theta }}_{\mathrm{1}}\cos \mathit{\phi }}{l_{\mathrm{AE}}\times l_{O_{\mathrm{1}}C}\times \cos {\mathit{\theta }}_{\mathrm{1}}\cos \mathit{\phi }}}\\ & -{\displaystyle \frac{\left[F_{\mathrm{2}y}{l}_{\mathrm{AE}}\cos \mathit{\phi }+\left(F_{\mathrm{9}y}-G_{\mathrm{AE}}\right)l_{\mathrm{AS}}\right]l_{O_{\mathrm{1}}E}}{l_{\mathrm{AE}}\times l_{O_{\mathrm{1}}C}\times \cos {\mathit{\theta }}_{\mathrm{1}}\cos \mathit{\phi }}}\\ & +{\displaystyle \frac{\left[F_{\mathrm{9}x}{l}_{\mathrm{ES}}\sin \mathit{\phi }-M_{\mathrm{2}}\right]l_{O_{\mathrm{1}}E}}{l_{\mathrm{AE}}\times l_{O_{\mathrm{1}}C}\times \cos {\mathit{\theta }}_{\mathrm{1}}\cos \mathit{\phi }}}.\end{array}\end{array}$$

Equations (11) and (12) are derived from Eqs. (8) to (10). The dynamics model of the pressing component is symmetric about the y axis. Thus, the main pressing force (N₁) is 2F_10y, and the auxiliary pressing force (N₂, N₃) is F₁cos θ₁. It was measured that the maximum angles of θ₁ and φ are 43 and 79^∘, respectively, to effectively perform the pressing task in Fig. 11a. Finally, the main pressing force and the auxiliary pressing force are 40 N and 5 N, conducted in ADAMS software in Fig. 11b, respectively.

Figure 11 The simulation analysis of the pressing force. (a) Maximum angle of the θ₁ and the φ. (b) Maximum force of the main pressing force and auxiliary pressing force.

3 Mechanism of wind loads on the FPLIR

3.1 Generalized wind loads

Figure 12a illustrates the wind loads on the FPLIR and power line model. However, the wind angle α on the FPLIR may not necessarily be perpendicular to the horizontal of the FPLIR. Thus, the schematics of the possible wind angle α are shown in Fig. 12b.

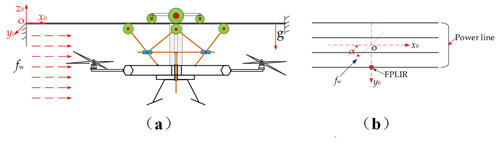
Figure 12 (a) The wind loads on the FPLIR and power line model in the x₀ direction. (b) Possible wind angle α on the FPLIR.

The dynamics of the wind load f_w is expressed as

$$\begin{array}{}\text{(13)}& f_{\mathrm{w}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{a}}{v}_{\mathrm{a}}^{\mathrm{2}}{C}_{\mathrm{d}}A,\end{array}$$

where C_d is the drag coefficient, A is the cross-sectional area, ρ_a is the air density, and v_a is the velocity of the wind.

C_d is a dimensionless quantity used to quantify the resistance of an object in a flow environment (air or liquid) (Qiu et al., 2018; Zhao et al., 2019).

It was seen that α changes from 0 to 90^∘. Thus, the general formulation of f_w is modified as follows (Alhassan et al., 2019):

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& f_{\mathrm{w}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{a}}{v}_{\mathrm{a}}^{\mathrm{2}}\\ & \sqrt{{\left(\sum _i^n{C}_{\mathrm{d}\mathit{\_}ix}{A}_{ix}\cos \mathit{\alpha }\right)}^{\mathrm{2}}+{\left(\sum _i^n{C}_{\mathrm{d}\mathit{\_}iy}{A}_{iy}\sin \mathit{\alpha }\right)}^{\mathrm{2}}},\end{array}\end{array}$$

where C_{d_ix} and A_ix are the drag coefficient and cross-sectional area of the ith components of the system on the x₀ axis, respectively. C_{d_iy} and A_iy are the drag coefficient and cross-sectional area of the ith components on the y₀ axis, respectively. Here, the number of components n is three, including the walking component, the pressing component, and the flying mechanism.

Table 2 Simulation parameters of the FPLIR.

3.2 Coupled dynamics model

The FPLIR–line coupled model under the influence of wind loads is shown in Fig. 13a. The dotted line represents the initial position of the FPLIR (there are no wind loads), and the solid line represents the position of the FPLIR when it is affected by wind in Fig. 13a. The FPLIR walking along the power line can be approximately considered a pendulum when it is affected by wind, leading to the angular displacements of the center of mass (COM) of the FPLIR on the x₀ axis (ϕ) and on the y₀ axis (β), respectively. The COM position of the FPLIR under the influence of wind loads can be illustrated in Fig. 13b. The horizontal displacement of the COM of the FPLIR is the δ₀ along the y₀ axis, and the vertical displacement of the COM of the FPLIR is δ₁ along the z₀ axis in Fig. 13c.

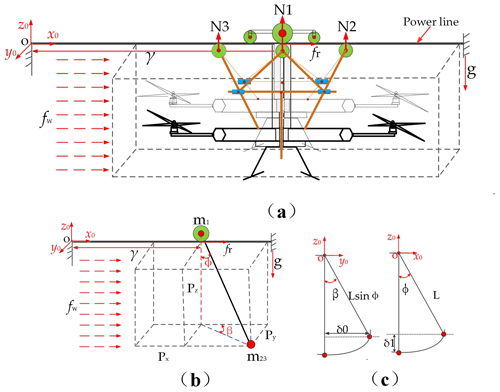
Figure 13 (a) Potential wind disturbance on the FPLIR–line coupled system. (b) The schematics of the FPLIR–line model under the influence of wind. (c) The schematics of the FPLIR showing its horizontal swing displacement on the y₀ axis (δ₀); the schematics of the robot showing its vertical swing displacement on the z₀ axis (δ₁).

The δ₀ can be expressed as

$$\begin{array}{}\text{(15)}& {\mathit{\delta }}_{\mathrm{0}}=L\sin \mathit{\varphi }\sin \mathit{\beta }.\end{array}$$

The δ₁ is expressed as

$$\begin{array}{}\text{(16)}& {\mathit{\delta }}_{\mathrm{1}}=-L+L\cos \mathit{\varphi },\end{array}$$

where L is the distance between the walking wheel and COM of the FPLIR.

The FPLIR generating the inertial moment J can be expressed as follows:

$$\begin{array}{}\text{(17)}& J={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{m}_{\mathrm{23}}{L}^{\mathrm{2}},\end{array}$$

where m₂₃ is the total mass of the pressing component and flying mechanism.

The general Lagrangian formulation is expressed as

$$\begin{array}{}\text{(18)}& {\displaystyle \frac{\mathrm{d}q}{\mathrm{d}t}}\left({\displaystyle \frac{\mathrm{d}T}{\mathrm{d}{\dot{q}}_i}}\right)-{\displaystyle \frac{\mathrm{d}T}{\mathrm{d}{q}_i}}+{\displaystyle \frac{\mathrm{d}U}{\mathrm{d}{\dot{q}}_i}}=Q_i,\text{(19)}& {\displaystyle }T=\sum _i^n{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{m}_i{\dot{q}}_i^{\mathrm{2}},\text{(20)}& {\displaystyle }U=\sum _i^n\left(m_{i}g{h}_i\right),\end{array}$$

where m_i is the mass of the ith coordinates, Q_i is the summation of the ith nonconservative forces, and q_i is the ith generalized independent point for n number of coordinates. T and U are the total kinetic and potential energies of the dynamics model, respectively. h_i is the vertical height from the center of the ith joint to the reference point, O. The total energies T and U are expressed in Eqs. (19) and (20), respectively.

The position P_t of the FPLIR in a 3D plane with reference to the fixed coordinate system O is given as follows:

$$\begin{array}{}\text{(21)}& P_t=\left\{\begin{array}{l}\left(\mathit{\gamma }+L\sin \mathit{\varphi }\cos \mathit{\beta }\right)\\ \left(L\sin \mathit{\varphi }\sin \mathit{\beta }\right)\\ \left(-L\cos \mathit{\varphi }\right)\end{array}\right.\end{array}$$

Therefore, the total kinetic T is calculated as follows:

$$\begin{array}{}\text{(22)}& \begin{array}{rl}T& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{m}_{\mathrm{123}}{\dot{\mathit{\gamma }}}^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{m}_{\mathrm{23}}({\dot{\mathit{\gamma }}}^{\mathrm{2}}+L^{\mathrm{2}}{\dot{\mathit{\varphi }}}^{\mathrm{2}}+L^{\mathrm{2}}{\dot{\mathit{\beta }}}^{\mathrm{2}}\sin \mathit{\varphi }\\ & +L\dot{\mathit{\gamma }}\dot{\mathit{\varphi }}\cos \mathit{\varphi }\cos \mathit{\beta }-L\dot{\mathit{\gamma }}\dot{\mathit{\varphi }}\sin \mathit{\varphi }\sin \mathit{\beta }).\end{array}\end{array}$$

The potential energy U is calculated as follows:

$$\begin{array}{}\text{(23)}& U=-m_{\mathrm{23}}L\cos \mathit{\varphi }.\end{array}$$

Moreover, γ is the distance where the FPLIR walks along the power line from a fixed reference point, O(x₀, y₀, and z₀). The external forces Q_i of the Lagrangian dynamics of Eq. (18) include the driving force f_r, the wind loads f_w, the sinusoidal force f_b that causes the flexible power line to swing along the y₀ axis, and the pressing forces $\sum _i^{\mathrm{3}}{N}_i$. Thus, the swing angle and swing displacement of the COM of the FPLIR under the influence of wind can be calculated by Eq. (18) using Eqs. (21) to (22).

The acceleration of the FPLIR on the line can be expressed as

$$\begin{array}{}\text{(24)}& \ddot{\mathit{\gamma }}={\displaystyle \frac{\mathrm{1}}{m_{\mathrm{123}}}}\left[\begin{array}{l}{f}_{\mathrm{r}}-m_{\mathrm{23}}L\ddot{\mathit{\varphi }}\cos \mathit{\varphi }\cos \mathit{\beta }\\ +L\ddot{\mathit{\beta }}\sin \mathit{\varphi }\sin \mathit{\beta }\\ +m_{\mathrm{23}}L{\dot{\mathit{\varphi }}}^{\mathrm{2}}\sin \mathit{\varphi }\cos \mathit{\beta }\\ +m_{\mathrm{23}}L{\dot{\mathit{\beta }}}^{\mathrm{2}}\sin \mathit{\varphi }\cos \mathit{\beta }\\ +m_{\mathrm{23}}L\dot{\mathit{\varphi }}\dot{\mathit{\beta }}\cos \mathit{\varphi }\sin \mathit{\beta }\end{array}\right].\end{array}$$

The angular acceleration of the FPLIR on the line on the z₀ axis can be expressed as

$$\begin{array}{}\text{(25)}& \begin{array}{rl}\ddot{\mathit{\varphi }}& ={\displaystyle \frac{\mathrm{1}}{\left(m_{\mathrm{23}}{L}^{\mathrm{2}}+J\right)}}\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{a}}{v}_{\mathrm{a}}^{\mathrm{2}}\right(\sum _i^n{C}_{\mathrm{d}\mathit{\_}ix}{A}_{ix}\cos \mathit{\alpha })\\ & -m_{\mathrm{23}}L\ddot{\mathit{\gamma }}\cos \mathit{\varphi }\cos \mathit{\beta }+m_{\mathrm{23}}{L}^{\mathrm{2}}{\dot{\mathit{\beta }}}^{\mathrm{2}}\cos \mathit{\varphi }\sin \mathit{\varphi }\\ & -m_{\mathrm{23}}gL\sin \mathit{\varphi }-\sum _i^n{N}_i\sin \mathit{\varphi }].\end{array}\end{array}$$

The angular acceleration of the FPLIR on the line on the y₀ axis can be expressed as

$$\begin{array}{}\text{(26)}& \begin{array}{rl}\ddot{\mathit{\beta }}& ={\displaystyle \frac{\mathrm{3}}{\left(m_{\mathrm{23}}{L}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\varphi }+J\right)}}[{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{a}}{v}_{\mathrm{a}}^{\mathrm{2}}\left(\sum _i^n{C}_{\mathrm{d}\mathit{\_}iy}{A}_{iy}\sin \mathit{\alpha }\right)\\ & +m_{\mathrm{23}}L\ddot{\mathit{\gamma }}\sin \mathit{\varphi }\sin \mathit{\beta }-m_{\mathrm{23}}{L}^{\mathrm{2}}\dot{\mathit{\beta }}\dot{\mathit{\varphi }}\sin \mathit{\varphi }\cos \mathit{\beta }+f_b\\ & -\sum _i^n{N}_i\sin \mathit{\beta }].\end{array}\end{array}$$

The δ₀ and δ₁ are modified by Eqs. (23) to (25). Thus, δ₀ and δ₁ are expressed as follows:

$$\begin{array}{}\text{(27)}& {\mathit{\delta }}_{\mathrm{0}}=L\times \sin \left(\int \int \ddot{\mathit{\varphi }}\right)\times \sin \left(\int \int \ddot{\mathit{\beta }}\right),\end{array}$$

$$\begin{array}{}\text{(28)}& {\mathit{\delta }}_{\mathrm{1}}=-L+L\cos \left(\int \int \ddot{\mathit{\varphi }}\right).\end{array}$$

3.3 Simulation analysis

These parameters, including wind speed (15.5 m s⁻¹), wind angle (0 to 90^∘), walking speed (0 to 12 m min⁻¹), and pressing force (0 or 48 N), were used to simulate δ₀ and δ₁ using ADAMS software. Figure 14 illustrates the simulation model of the FPLIR, where the kinematic pairs are added to the simulation model. The screw spiral movement (the screw and the linear stepper motor) is replaced by the moving pair in Fig. 14. In the simulation, the wind loads are loaded at the FPLIR's COM to test the δ₀ and δ₁. These parameters' used simulation is listed in Table 2, and the swing displacements of the FPLIR's COM (δ₀, δ₁) are shown in Fig. 15.

Figure 14 Simulation diagram of the FPLIR in the ADAMS software.

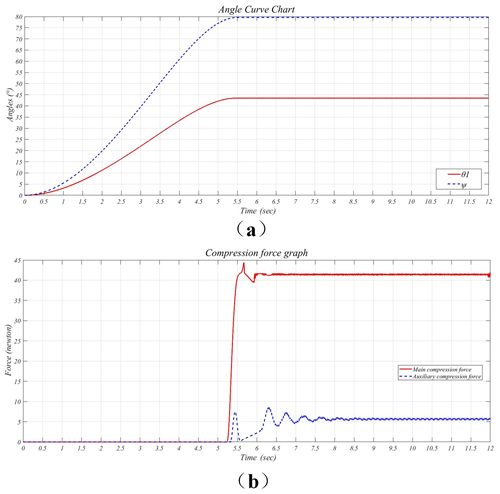
The walking speed along the power line is set to 12 m min⁻¹ to study the δ₀ and δ₁ under the influence of wind angles at 0, 30, 60, and 90^∘ on the y₀ axis and z₀ axis in Fig. 15a, respectively. The maximum value of the δ₀ is 5.9 cm when there is no pressing force and the wind angle is 90^∘. The maximum value of the δ₀ is 3.5 cm when there is a pressing force (48 N) and the wind angle of 90^∘ is reduced by 41 %. The δ₁ gradually reduces with the gradual increase in wind angle in Fig. 15b, and the maximum value of the δ₁ is measured when the wind angle is 0^∘.

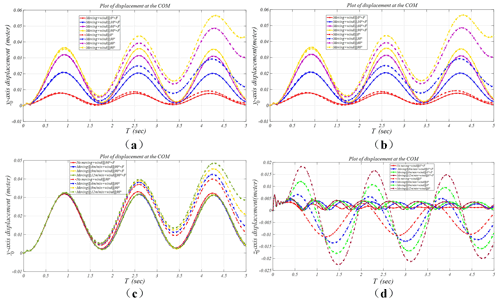
Figure 15 Swing displacement of the FPLIR's COM. (a) The swing displacement of the FPLIR's COM (δ₀) along the y₀ axis at a different wind angle. (b) The swing displacement of the FPLIR's COM (δ₁) along the z₀ axis at a different wind angle. (c) The swing displacement of the FPLIR's COM (δ₀) along the y₀ axis at a different walking speed. (d) The swing displacement of the FPLIR's COM (δ₁) along the z₀ axis at a different walking speed.

These factors influencing the walking stability of the FPLIR are the wind angles of 0 and 90^∘ in Fig. 15a and b. Thus, the walking speed along the power line is set (0 to 12 m min⁻¹) to further analyze the walking stability of the FPLIR under the influence of the wind angle at 0^∘ and 90^∘ on the z₀ axis and y₀ axis, respectively. The δ₀ remains constant, with the walking speed increasing when there is pressing force (48 N) and a wind angle of 90^∘, showing that the walking stability under the wind loads is less impacted by the walking speed in Fig. 15c. The maximum value of the δ₀ is 3.1 cm in Fig. 15c. The δ₁ gradually increases with the gradual increase in the walking speed in Fig. 15d. The maximum value of the δ₁ is measured when the walking speed is 12 m min⁻¹.

Moreover, the influence of wind loads on the FPLIR shows that wind load mainly affects the walking stability along the y₀ axis (wind angle is 90^∘), and the wind load has less impact on the FPLIR along the z₀ axis (wind angle is 0^∘) in the simulation. The main reasons for the swing displacement of the COM along the z₀ axis are analyzed as follows: the FPLIR is affected by inertia in the process of walking along the line, leading to the swing displacement of the COM along the z₀ axis gradually increasing. However, the simulation analysis shows that the pressing component can effectively reduce the influence of wind loads on the walking stability of the inspection robot.

4 The experiment

An experimental setup is used to verify the walking stability at different wind angles, walking speeds, and pressing forces in moderate gales (wind speed is 15.5 m s⁻¹) in Fig. 16. The following parameters are used for the experimental setup. (1) The length of the power line installed on the frame is 6 m. (2) The FPLIR is 0.8 m above the ground when it is suspended from the power line. (3) The wind angle acting on the COM of the FPLIR is set to change from 0 to 90^∘. (4) The mpu6050 gyroscope is installed on the surface of the control box to measure the swing displacement of the COM of the FPLIR on the three axes (x₀, y₀, and z₀). (5) An industrial fan (SF4-2, 1500 W, 2800 r min⁻¹, air volume 11000 m³ h⁻¹) is chosen as the wind source for simulating the moderate gale. (6) The wind speed is measured by a digital anemometer (AC826).

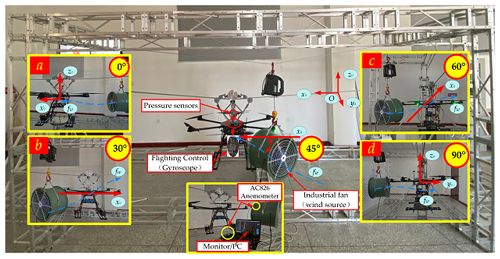
Figure 16 The experimental setup. (a) Position of the fan at a 0^∘ wind angle. (b) Position of the fan at a 30^∘ wind angle. (c) Position of the fan at a 60^∘ wind angle. (d) Position of the fan at a 90^∘ wind angle.

The walking stability of the FPLIR may be affected by many factors, but three factors (wind angle, walking speed, and pressing force) are selected as the main factors affecting the test according to the previous simulation.

Thus, the walking speed from 0 to 12 m min⁻¹, the pressing force from 0 to 48 N, and the wind angles from 0 to 90^∘ are selected to analyze the effects of these factors on the walking stability of the FPLIR adopting an optimized regression design with three factors (wind angle, walking speed, and pressing force) and five levels.

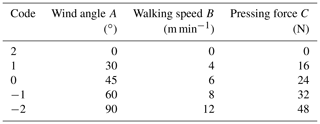
The level and code of variables in the test are listed in Table 3.

Table 3 Level and code of variables chosen for central composite design.

A three-factor, five-level test was designed according to the Box–Behnken test principle, including 20 test points (6 test points were zero estimation errors and the other 14 test points were analysis factors). The test results are listed in Table 4.

Table 4 Test design scheme and results.

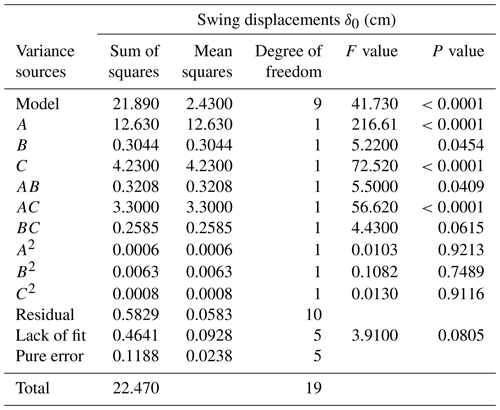
The Design-Expert software is used to perform regression analysis to find the optimal parameter combination in the test results. The regression equations between a test index and the factors are obtained, and the analysis of variance is shown in Table 5. The regression equation between the evaluation index and the three factors is derived as follows:

$$\begin{array}{}\text{(29)}& \begin{array}{rl}{\mathit{\delta }}_{\mathrm{0}}& =\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{5}}\times A^{\mathrm{2}}-\mathrm{0.01}\times B^{\mathrm{2}}-\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{4}}\times C^{\mathrm{2}}\\ & -\mathrm{7.42}\times {\mathrm{10}}^{-\mathrm{4}}\times AB-\mathrm{5.95}\times {\mathrm{10}}^{-\mathrm{4}}\times AC\\ & -\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{3}}\times BC+\mathrm{0.041}\times A+\mathrm{0.23}\times B\\ & +\mathrm{0.0163}\times C-\mathrm{0.097}.\end{array}\end{array}$$

Table 5 Analysis of variance.

Figure 17 Effect of interaction factors on the swing displacement δ₀.

5 Experimental results and discussion

Regression analysis is used to predict the quadratic equation and obtain a prediction model for the response variable δ₀. The result shows that the P value (< 0.0001) of the δ₀ is less than 0.01 from the analysis of variance (ANOVA) results in Table 5, showing that the regression model is highly significant. The absolute coefficient R² is 0.9741, demonstrating that the model can meet more than 97 % of the test results. Therefore, the regression model can analyze the parameters related to the influence of the FPLIR under the wind.

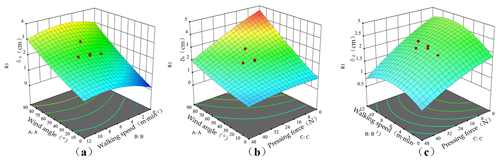
Table 5 shows the monomial coefficient of the δ₀, and F values of each factor are $F_A>F_C>F_B$; thus, the influence degree of the factors on the δ₀ is wind angle > pressing force > walking speed. The response surface was generated by Design-Expert software to analyze the influence of the interaction factors (wind angle, walking speed, and pressing force) in Fig. 17.

Figure 17a shows the response surface of the interaction between wind angle and walking speed when the pressing force is 24 N. The δ₀ gradually increases with increasing wind angle; the δ₀ gradually increases and then decreases with the gradually increasing walking speed; the δ₀ changes more quickly along the direction of the wind angle than along the direction of the walking speed in Fig. 17a, demonstrating that the influence of the wind angle on the δ₀ is more significant than the walking speed at zero levels.

Figure 17b shows the response surface of the interaction between wind angle and pressing force when the walking speed is 6 m min⁻¹. The δ₀ gradually decreases with the gradual increase in pressing force. The δ₀ is the minimum (when wind angle and walking speed are 0^∘ and 48 N, respectively), and the δ₀ is the maximum (when wind angle and walking speed are 90^∘ and 0 N, respectively). The δ₀ changes more quickly along the direction of the wind angle than along the direction of the pressing force in Fig. 17b, showing that the influence of the wind angle on the δ₀ is more significant than the pressing force at zero levels.

Figure 17c shows the response surface of the interaction between walking speed and pressing force when the wind angle is 45^∘. The δ₀ changes more quickly along the direction of the pressing force than along the direction of the walking force in Fig. 17c, showing that the influence of the pressing force on the δ₀ is more significant than the walking speed at zero levels.

It is necessary to further verify the impact of the three factors (wind angle, pressing force, and walking speed) on the walking stability of the FPLIR using Design-Expert to optimize and analyze the three factors and to get the maximum and minimum values of the δ₀ when the FPLIR is affected by wind loads. The optimization results of the three factors are as follows. (1) The maximum value of δ₀ is 4.7 cm (when wind angle, walking speed, and pressing force are 90^∘, 7.2 m min⁻¹, and 0, respectively). (2) The minimum value of δ₀ is 0 (when wind angle, walking speed, and pressing force are 0^∘, 0 m min⁻¹, and 3.4 N, respectively). (3) The maximum value of the δ₀ is 2.5 cm when pressing force increases to 39.4 N, reduced by 46.2 % (when wind angle and walking speed are 90^∘ and 5.1 m min⁻¹, respectively), which effectively reduces the influence of wind loads and improves the stability of the FPLIR.

6 Conclusions

The conclusions of this paper can be summarized as follows.

1. We propose a novel FPLIR with the ability to fly and walk, including a flying mechanism and a walking mechanism. The overall size of the FPLIR is 1250 mm × 1250 mm × 1200 mm, and the total weight is about 24 kg.

2. The dynamics model of the FPLIR on the power line using the Lagrangian equation is derived to analyze walking stability caused by wind, considering pressing force and walking speed.

3. In the simulation, the influence of wind on the walking stability of the FPLIR is studied to show that the wind angle of 90^∘ has the greatest influence on the walking stability. The δ₀ can be reduced by 41 % when using the pressing component, demonstrating that the directing-push pressing component effectively improves the walking instability of the FPLIR under the wind.

4. A three-factor, five-level test was designed to establish a response surface model with wind angle (0 to 90^∘), walking speed (0 to 12 m min⁻¹), and pressing force (0 to 48 N). The test results show that wind angle and pressing force have a significant influence (P<0.05) on the walking stability. The maximum value of δ₀ is 4.7 cm (when wind angle, walking speed, and pressing force are 90^∘, 7.2 m min⁻¹, and 0, respectively). The maximum value of δ₀ is 2.5 cm when the pressing force increasing to 39.4 N is reduced by 46.2 % (when wind angle and walking speed are 90^∘ and 5.1 m min⁻¹, respectively).

Therefore, it is proved that the FPLIR has been successfully designed and can be applied for power line inspection, providing a theoretical basis for slipping control, collecting images of intelligence inspection robots in the future.