Kinematic and dynamic accuracy of spherical mechanisms

Among parallel robots, spherical robots occupy an important place. Most applications of spherical manipulators can be found in orienting devices, such as camera orienting and medical instrument alignment. A spherical parallel robot is, in general, made up of the base platform and the moving platform. This mobile platform and base are connected by three equally spaced legs, each consisting of revolute joints only. The axes of all joints intersect at a common point, which is called the center of rotation. The motion of the moving platform is confined on the surface of a sphere centered at the rotation center. A spherical parallel robot provides 3 degrees of freedom of pure rotations. These robots have been the subject of many papers dealing with the structure, the problems of position and velocity, workspace modeling, singularity analysis, and some problems with the dynamic analysis. However, not all the important problems have been solved. These concern the problem of accuracy. This paper presents accuracy of the spherical parallel. In the considered spherical manipulator, each leg consists of five kinematic pairs. The kinematic accuracy is determined on the kinematic problem. The dynamic accuracy is estimated on the equation of motion. Examples of solving the problem of determining the positioning error of the output level are presented.

1 Introduction

Production automation is ensured by the use of robotic complexes and systems. One of the important characteristics of assessing the quality of functioning of robotic systems is the positioning accuracy. The task of ensuring this accuracy should be solved at the design stage of machinery and equipment.

Most of the production of light industry requires laser cutting and surface treatment, welding, and medical robotics.

The positioning error of the output link, when it is repeatedly withdrawn to a given point, is expressed for a spherical mechanism in angular units. The positioning error is determined by systematic (inaccuracy of the control system and deviations from the nominal dimensions of the links) and random components (gaps in the joints, loosening in fasteners, temperature fluctuations, robot vibrations caused by adjacent equipment, residual vibrations, and fatigue deformations of links). The positioning accuracy is determined by the positioning error of the output link (capture) when it is repeatedly brought to a given point and is expressed in angular or linear dimensions.

Systematic errors can be partially or completely compensated. Reducing random errors should be considered in design and operation. Most robotic systems consist of spatial mechanisms, including mechanisms of a parallel structure (Merlet, 2000; Kong and Gosselin, 2007; Gogu, 2008). Modern control systems allow for the introduction of appropriate amendments. Also, the negative impact of vibrations at the base of the robot on the positioning accuracy can be reduced by organizational measures (i.e., coordination of the manipulation cycle with the cycle of the equipment that caused the vibration). The purpose of cycle matching is to establish the time interval between the impact and the final stage of the manipulation cycle. This allows vibrations to dim before the positioning is complete. Residual oscillations of the output link, resulting from insufficient rigidity of the link drives and instability of the control system, have a significant effect on accuracy. The nature of the residual vibrations depends on the dynamic properties of the manipulator.

When creating robots, they strive to perform links with a uniform, constant cross section along the length. In this case, there is no need to describe the links through the distribution of length over mass, moments of inertia, and stiffness. In this case, the task of dynamic accuracy is simplified, since, in this case, the Lagrangian equations describe mechanical systems with lumped parameters.

In most cases, the positioning error is determined from solving problems on the position of the mechanism. However, this approach is not universal, since inaccuracies in the manufacture of links of mechanisms are inevitable, the temperature of the working environment is not constant, the mechanism can be located on a moving base, external influences can be present, and instability of motion occurs at a given law of motion.

An interesting approach is one that takes into account the determination of the accuracy of finding the executive body while taking into account the above restrictions and the possibility of their compensation. The paper shows a sequential approach to determining the kinematic, then dynamic, accuracy of the executive body and the positioning errors during control. Thus, an integrated approach to assessing the performance of the actuator is presented.

2 Kinematic accuracy of the spherical mechanism

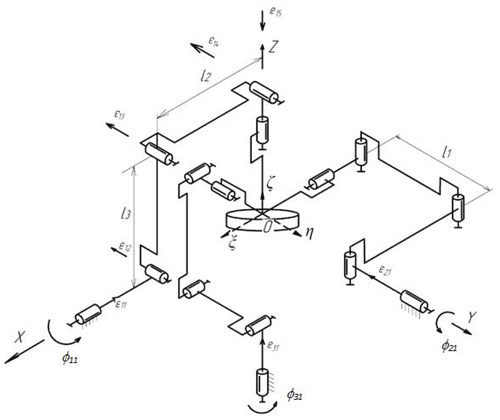
The article presents a solution to the problem of determining the positioning error of the working body, using the example of a spherical manipulator with 3 degrees of freedom of a parallel structure (Fig. 1). Such manipulators are used in orienting devices, in test benches, medical robotic complexes, for processing spherical surfaces, in mixers, and for performing rotational movements (Huda and Takeda, 2007; Mianovski, 2007; Leguay-Durand and Reboulet, 1997; Bai et al., 2016; Chaker et al., 2011; Nosova et al., 2018). The paper considers a spherical manipulator with 3 degrees of freedom and investigates the issues of the kinematic and dynamic accuracy of the positioning of the executive body.

In the considered mechanism, each input chain link is connected to a rotary motor. The output link is a platform rotating at point O around three coordinate axes. The output coordinates are the angles of rotation of the platform, with the angle α of rotation around the x axis, the angle β of rotation around the y axis, and the angle γ of rotation around the z axis. The generalized coordinates are the angles ϕ₁₁, ϕ₂₁, and ϕ₃₁ of rotation of the input links, respectively, of the first kinematic chain and second and third kinematic chain.

Figure 1 Mechanism of a parallel manipulator with 3 degrees of freedom.

The solution to the positioning problem determines the relationship between the input and output coordinates and is presented in the following form (Kheylo and Glazunov, 2016; Nhan et al., 2019):

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}{F}_{\mathrm{1}}=\mathrm{tg}{\mathit{\varphi }}_{\mathrm{11}}-\frac{\cos \mathit{\gamma }\cdot \sin \mathit{\gamma }\cdot \sin \mathit{\beta }+\cos \mathit{\gamma }\cdot \sin \mathit{\alpha }}{\cos \mathit{\alpha }\cdot \cos \mathit{\beta }}=\mathrm{0};\\ F_{\mathrm{2}}=\frac{\sin \mathit{\beta }}{\cos \mathit{\gamma }\cdot \cos \mathit{\beta }}-\mathrm{tg}{\mathit{\varphi }}_{\mathrm{21}}=\mathrm{0};\\ F_{\mathrm{3}}=\frac{\cos \mathit{\gamma }\cdot \sin \mathit{\beta }\cdot \sin \mathit{\alpha }-\cos \mathit{\alpha }\cdot \sin \mathit{\gamma }}{\cos \mathit{\alpha }\cdot \cos \mathit{\gamma }+\sin \mathit{\alpha }\cdot \sin \mathit{\beta }\cdot \sin \mathit{\gamma }}+\mathrm{tg}{\mathit{\varphi }}_{\mathrm{31}}=\mathrm{0}.\end{array}\right.\end{array}$$

In general, the positioning problem is specified in the form of implicit functions, as follows:

$$\begin{array}{}\text{(2)}& F_i=(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },{\mathit{\theta }}_{i\mathrm{1}},{\mathit{\theta }}_{i\mathrm{2}},{\mathit{\varphi }}_{i\mathrm{1}}),\end{array}$$

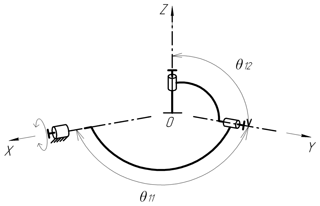
where θ_i1, θ_i2 is the angle between the axes of the kinematic pairs (Fig. 2).

Figure 2 Angles between the axes of kinematic pairs θ₁₁, θ₂₂ in the first kinematic chain.

The total differential of function (2) is written as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\displaystyle \frac{\partial F_i}{\partial \mathit{\alpha }}}\mathit{\delta }\mathit{\alpha }& +{\displaystyle \frac{\partial F_i}{\partial \mathit{\beta }}}\mathit{\delta }\mathit{\beta }+{\displaystyle \frac{\partial F_i}{\partial \mathit{\gamma }}}\mathit{\delta }\mathit{\gamma }+{\displaystyle \frac{\partial F_i}{\partial {\mathit{\theta }}_{i\mathrm{1}}}}\mathit{\delta }{\mathit{\theta }}_{i\mathrm{1}}\\ & +{\displaystyle \frac{\partial F_i}{\partial {\mathit{\theta }}_{i\mathrm{2}}}}\mathit{\delta }{\mathit{\theta }}_{i\mathrm{2}}+{\displaystyle \frac{\partial F_i}{\partial {\mathit{\varphi }}_{i\mathrm{1}}}}\mathit{\delta }{\mathit{\varphi }}_{i\mathrm{1}}=\mathrm{0}.\end{array}\end{array}$$

According to the linear accuracy theory, the increment in the drives is zero, where $\mathit{\delta }{\mathit{\varphi }}_{\mathrm{11}}=\mathit{\delta }{\mathit{\varphi }}_{\mathrm{21}}=\mathit{\delta }{\mathit{\varphi }}_{\mathrm{31}}=\mathrm{0}$.

The implicit function equations can be written as follows (Kheylo and Glazunov, 2014):

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& {\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}}\mathit{\delta }\mathit{\alpha }+{\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}}\mathit{\delta }\mathit{\beta }+{\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}}\mathit{\delta }\mathit{\gamma }=-\left({\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial {\mathit{\theta }}_{\mathrm{12}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{12}}+{\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial {\mathit{\theta }}_{\mathrm{11}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{11}}\right)\\ & {\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}}\mathit{\delta }\mathit{\alpha }+{\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}}\mathit{\delta }\mathit{\beta }+{\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}}\mathit{\delta }\mathit{\gamma }=-\left({\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial {\mathit{\theta }}_{\mathrm{22}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{22}}+{\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial {\mathit{\theta }}_{\mathrm{21}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{21}}\right)\\ & {\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}}\mathit{\delta }\mathit{\alpha }+{\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}}\mathit{\delta }\mathit{\beta }+{\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}}\mathit{\delta }\mathit{\gamma }=-\left({\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial {\mathit{\theta }}_{\mathrm{32}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{32}}+{\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial {\mathit{\theta }}_{\mathrm{31}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{31}}\right).\end{array}\end{array}$$

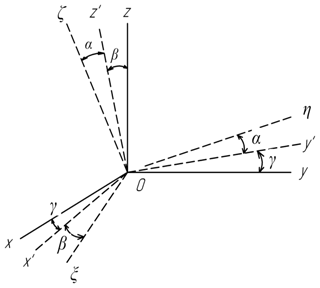
In the considered mechanism, the angles between the axes of the kinematic pairs θ_i1, θ_i2 are not equal to 90^∘. The sequence of rotations of the output link from a movable coordinate system to a fixed one is shown in Fig. 3.

Figure 3 Sequence of turns of the output link.

The transition matrix, from a moving coordinate system to a fixed one, will have the following form:

$${\mathbf{B}}_{\mathrm{1}}={\mathbf{F}}_z\cdot {\mathbf{F}}_x\cdot {\mathbf{B}}_x^{\prime }\cdot {\mathbf{C}}_y^{\prime }\cdot {\mathbf{B}}_y^{\prime }\cdot {\mathbf{C}}_x^{\prime }\cdot {\mathbf{B}}_z^{\prime },$$

where, in the following:

$$\begin{array}{rl}& {\mathbf{B}}_x^{\prime }=\left(\begin{array}{ccc}\cos {\mathit{\varphi }}_{\mathrm{11}}& -\sin {\mathit{\varphi }}_{\mathrm{11}}& \mathrm{0}\\ \sin {\mathit{\varphi }}_{\mathrm{11}}& \cos {\mathit{\varphi }}_{\mathrm{11}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right),\\ & {\mathbf{B}}_y^{\prime }=\left(\begin{array}{ccc}\cos {\mathit{\varphi }}_{\mathrm{12}}& -\sin {\mathit{\varphi }}_{\mathrm{12}}& \mathrm{0}\\ \sin {\mathit{\varphi }}_{\mathrm{12}}& \cos {\mathit{\varphi }}_{\mathrm{12}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right),\text{and}\\ & {\mathbf{B}}_z^{\prime }=\left(\begin{array}{ccc}\cos {\mathit{\varphi }}_{\mathrm{13}}& -\sin {\mathit{\varphi }}_{\mathrm{13}}& \mathrm{0}\\ \sin {\mathit{\varphi }}_{\mathrm{13}}& \cos {\mathit{\varphi }}_{\mathrm{13}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right),\end{array}$$

which are the rotation matrices of the first kinematic pairs and second and third kinematic pairs around the movable axis z by the angles φ₁₁, φ₁₂, and φ₁₃, respectively.

$$\begin{array}{rl}& {\mathbf{C}}_x^{\prime }=\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos {\mathit{\theta }}_{\mathrm{11}}& -\sin {\mathit{\theta }}_{\mathrm{11}}\\ \mathrm{0}& \sin {\mathit{\theta }}_{\mathrm{11}}& \cos {\mathit{\theta }}_{\mathrm{11}}\end{array}\right),\text{and}\\ & {\mathbf{C}}_y^{\prime }=\left(\begin{array}{ccc}\cos {\mathit{\theta }}_{\mathrm{12}}& \mathrm{0}& -\sin {\mathit{\theta }}_{\mathrm{12}}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \sin {\mathit{\theta }}_{\mathrm{12}}& \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{12}}\end{array}\right),\end{array}$$

which are the matrices of rotations around the x and y axes by the angles θ₁₁ and θ₁₂, respectively. θ₁₁ and θ₁₂ are the angles between the adjacent pairs.

$$\begin{array}{rl}& {\mathbf{F}}_z^{\prime }=\left(\begin{array}{ccc}\cos {\mathit{\xi }}_{\mathrm{12}}& \sin {\mathit{\xi }}_{\mathrm{12}}& \mathrm{0}\\ -\sin {\mathit{\xi }}_{\mathrm{12}}& \cos {\mathit{\xi }}_{\mathrm{12}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right),\text{and}\\ & {\mathbf{F}}_x^{\prime }=\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos {\mathit{\xi }}_{\mathrm{11}}& \sin {\mathit{\xi }}_{\mathrm{11}}\\ \mathrm{0}& -\sin {\mathit{\xi }}_{\mathrm{11}}& \cos {\mathit{\xi }}_{\mathrm{11}}\end{array}\right),\end{array}$$

which are matrices of additional rotations for aligning the moving and stationary coordinate system around the z and x axes by tje angles ξ₁₁, and ξ₁₂, respectively, with ξ₁₁=90^∘, and ξ₁₂=90^∘.

The unit vector of the axis of the pair of the output links of the first chain has the following coordinates: $\left(\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \mathrm{1}\end{array}\right),$ which are substituted into the following constraint equation $A\cdot \left(\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \mathrm{1}\end{array}\right)=B_{\mathrm{1}}\cdot \left(\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \mathrm{1}\end{array}\right)$. Using the found values of the matrices A and B^′, we obtain the following equation:

$$\begin{array}{rl}& \left(\begin{array}{l}\sin \mathit{\gamma }\cdot \sin \mathit{\alpha }+\cos \mathit{\alpha }\cdot \cos \mathit{\gamma }\cdot \sin \mathit{\beta }\\ \cos \mathit{\alpha }\cdot \sin \mathit{\gamma }\cdot \sin \mathit{\beta }-\cos \mathit{\gamma }\cdot \sin \mathit{\alpha }\\ \cos \mathit{\beta }\cdot \cos \mathit{\alpha }\end{array}\right)\\ & =\left(\begin{array}{l}\cos {\mathit{\theta }}_{\mathrm{12}}\cos {\mathit{\theta }}_{\mathrm{11}}+\sin {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{12}}\\ \cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}-\sin {\mathit{\theta }}_{\mathrm{12}}(\cos {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}\\ +\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{12}})\\ \sin {\mathit{\theta }}_{\mathrm{12}}\left(\cos {\mathit{\varphi }}_{\mathrm{11}}\cdot \cos {\mathit{\varphi }}_{\mathrm{12}}-\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{11}}\end{array}\right).\end{array}$$

For the second kinematic chain, the transition matrix from a moving coordinate system to a fixed one will have the following form:

$${\mathbf{B}}_{\mathrm{2}}={\mathbf{F}}_x\cdot {\mathbf{F}}_y\cdot {\mathbf{B}}_y^{\prime \prime }\cdot {\mathbf{C}}_z^{\prime \prime }\cdot {\mathbf{B}}_z^{\prime \prime }\cdot {\mathbf{C}}_y^{\prime \prime }\cdot {\mathbf{B}}_x^{\prime \prime },$$

where, in the following:

$$\begin{array}{rl}& {\mathbf{B}}_y^{\prime \prime }=\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{21}}& -\sin {\mathit{\varphi }}_{\mathrm{21}}\\ \mathrm{0}& \sin {\mathit{\varphi }}_{\mathrm{21}}& \cos {\mathit{\varphi }}_{\mathrm{21}}\end{array}\right),\\ & {\mathbf{B}}_z^{\prime \prime }=\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{22}}& -\sin {\mathit{\varphi }}_{\mathrm{22}}\\ \mathrm{0}& \sin {\mathit{\varphi }}_{\mathrm{22}}& \cos {\mathit{\varphi }}_{\mathrm{22}}\end{array}\right),\text{and}\\ & {\mathbf{B}}_x^{\prime \prime }=\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{21}}& -\sin {\mathit{\varphi }}_{\mathrm{21}}\\ \mathrm{0}& \sin {\mathit{\varphi }}_{\mathrm{21}}& \cos {\mathit{\varphi }}_{\mathrm{21}}\end{array}\right),\end{array}$$

which are rotation matrices of the first kinematic pairs and second and third kinematic pairs around the movable axis x by the angles φ₂₁, φ₂₂, and φ₂₃, respectively.

$$\begin{array}{rl}& {\mathbf{C}}_z^{\prime }=\left(\begin{array}{ccc}\cos {\mathit{\theta }}_{\mathrm{22}}& -\sin {\mathit{\theta }}_{\mathrm{22}}& \mathrm{0}\\ \cos {\mathit{\theta }}_{\mathrm{22}}& \sin {\mathit{\theta }}_{\mathrm{22}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right),\text{and}\\ & {\mathbf{C}}_y^{\prime }=\left(\begin{array}{ccc}\cos {\mathit{\theta }}_{\mathrm{21}}& \mathrm{0}& \sin {\mathit{\theta }}_{\mathrm{12}}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\sin {\mathit{\theta }}_{\mathrm{21}}& \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{12}}\end{array}\right),\end{array}$$

which are matrices of rotations around the z, y axes by the angles θ₂₂ and θ₂₁, respectively, and θ₂₁ and θ₂₂ are the angles between adjacent pairs.

$$\begin{array}{rl}& {\mathbf{F}}_y^{\prime \prime }=\left(\begin{array}{ccc}\cos {\mathit{\xi }}_{\mathrm{22}}& \mathrm{0}& \sin {\mathit{\xi }}_{\mathrm{22}}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \sin {\mathit{\xi }}_{\mathrm{22}}& \mathrm{0}& \cos {\mathit{\xi }}_{\mathrm{22}}\end{array}\right),\text{and}\\ & {\mathbf{F}}_x^{\prime \prime }=\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos {\mathit{\xi }}_{\mathrm{21}}& \sin {\mathit{\xi }}_{\mathrm{21}}\\ \mathrm{0}& -\sin {\mathit{\xi }}_{\mathrm{21}}& \cos {\mathit{\xi }}_{\mathrm{21}}\end{array}\right),\end{array}$$

which are matrices of additional rotations for aligning the moving and stationary coordinate systems around the z and x axes by the angles ξ₂₂ and ξ₂₁, respectively, with ξ₂₁=90^∘ and ξ₂₂=90^∘.

For the third kinematic chain, the transition matrix from a moving coordinate system to a fixed one will have the following form:

$$\begin{array}{rl}& {\mathbf{B}}_{\mathrm{3}}={\mathbf{F}}_y^{\prime \prime \prime }\cdot {\mathbf{F}}_z^{\prime \prime \prime }\cdot {\mathbf{B}}_z^{\prime \prime \prime }\cdot {\mathbf{C}}_x^{\prime \prime \prime }\cdot {\mathbf{B}}_x^{\prime \prime \prime }\cdot {\mathbf{C}}_z^{\prime \prime \prime }\cdot {\mathbf{B}}_y^{\prime \prime \prime }\\ & {\mathbf{B}}_z^{\prime \prime \prime }=\left(\begin{array}{ccc}\cos {\mathit{\varphi }}_{\mathrm{31}}& \mathrm{0}& \sin {\mathit{\varphi }}_{\mathrm{31}}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\sin {\mathit{\varphi }}_{\mathrm{31}}& \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{31}}\end{array}\right),\\ & {\mathbf{B}}_y^{\prime \prime \prime }=\left(\begin{array}{ccc}\cos {\mathit{\varphi }}_{\mathrm{32}}& \mathrm{0}& \sin {\mathit{\varphi }}_{\mathrm{32}}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\sin {\mathit{\varphi }}_{\mathrm{32}}& \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{32}}\end{array}\right),\text{and}\\ & {\mathbf{B}}_x^{\prime \prime \prime }=\left(\begin{array}{ccc}\cos {\mathit{\varphi }}_{\mathrm{33}}& \mathrm{0}& \sin {\mathit{\varphi }}_{\mathrm{33}}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\sin {\mathit{\varphi }}_{\mathrm{33}}& \mathrm{0}& \cos {\mathit{\varphi }}_{\mathrm{33}}\end{array}\right),\end{array}$$

which are matrices of rotations of the first kinematic pairs and second and third kinematic pairs around the movable axis y by the angles φ₃₁, φ₃₂, and φ₃₃, respectively.

$$\begin{array}{rl}& {\mathbf{C}}_z^{\prime \prime \prime }=\left(\begin{array}{ccc}\cos {\mathit{\theta }}_{\mathrm{31}}& -\sin {\mathit{\theta }}_{\mathrm{31}}& \mathrm{0}\\ \cos {\mathit{\theta }}_{\mathrm{31}}& \sin {\mathit{\theta }}_{\mathrm{31}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right),\text{and}\\ & {\mathbf{C}}_x^{\prime \prime \prime }=\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos {\mathit{\theta }}_{\mathrm{32}}& \sin {\mathit{\theta }}_{\mathrm{32}}\\ \mathrm{0}& -\sin {\mathit{\theta }}_{\mathrm{32}}& \cos {\mathit{\theta }}_{\mathrm{32}}\end{array}\right),\end{array}$$

which are matrices of rotations around the z and x axes by the angles θ₃₁ and θ₃₂, respectively. θ₃₁ and θ₃₂ are the angles between adjacent pairs.

$$\begin{array}{rl}& {\mathbf{F}}_y^{\prime \prime \prime }=\left(\begin{array}{ccc}\cos {\mathit{\xi }}_{\mathrm{32}}& \mathrm{0}& -\sin {\mathit{\xi }}_{\mathrm{32}}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \sin {\mathit{\xi }}_{\mathrm{32}}& \mathrm{0}& \cos {\mathit{\xi }}_{\mathrm{32}}\end{array}\right),\text{and}\\ & {\mathbf{F}}_z^{\prime \prime \prime }=\left(\begin{array}{ccc}\cos {\mathit{\xi }}_{\mathrm{31}}& \sin {\mathit{\xi }}_{\mathrm{31}}& \mathrm{0}\\ -\sin {\mathit{\xi }}_{\mathrm{31}}& \cos {\mathit{\xi }}_{\mathrm{31}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right),\end{array}$$

which are matrices of additional rotations for aligning the moving and stationary coordinate systems around the z and x axes by the angles ξ₃₁ and ξ₃₂, respectively, with ξ₃₁=90^∘ and ξ₃₂=90^∘.

Position function F₁ will look as follows:

$$\begin{array}{rl}& F_{\mathrm{1}}={\displaystyle \frac{\cos \mathit{\alpha }\sin \mathit{\gamma }\sin \mathit{\beta }-\cos \mathit{\gamma }\sin \mathit{\alpha }}{\cos \mathit{\beta }\cos \mathit{\alpha }}}\\ & -{\displaystyle \frac{\begin{array}{c}\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}-\sin {\mathit{\theta }}_{\mathrm{12}}(\cos {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}\\ +\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{12}})\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{12}}(\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\varphi }}_{\mathrm{12}}-\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}})\\ +\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{11}}\end{array}}}.\\ & F_{\mathrm{2}}={\displaystyle \frac{-\sin \mathit{\beta }}{\cos \mathit{\gamma }\cos \mathit{\beta }}}\\ & -{\displaystyle \frac{\begin{array}{c}\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}-\sin {\mathit{\theta }}_{\mathrm{21}}(\cos {\mathit{\varphi }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}\\ +\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{22}})\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{21}}(\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\varphi }}_{\mathrm{22}}-\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{22}})\\ +\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\end{array}}}.\\ & F_{\mathrm{3}}={\displaystyle \frac{\cos \mathit{\gamma }\sin \mathit{\beta }\sin \mathit{\alpha }-\cos \mathit{\alpha }\sin \mathit{\gamma }}{\cos \mathit{\gamma }\cos \mathit{\alpha }+\sin \mathit{\gamma }\sin \mathit{\beta }\sin \mathit{\alpha }}}\\ & -{\displaystyle \frac{\begin{array}{c}\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}-\sin {\mathit{\theta }}_{\mathrm{31}}(\cos {\mathit{\varphi }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}\\ +\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\theta }}_{\mathrm{32}})\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{31}}(\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\varphi }}_{\mathrm{32}}-\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{32}})\\ +\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}\end{array}}}.\end{array}$$

Partial derivatives will be equal to the following:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial {\mathit{\theta }}_{\mathrm{11}}}}=-{\displaystyle \frac{\begin{array}{c}\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{12}}\\ +\cos {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{12}}\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{12}}\left(\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\varphi }}_{\mathrm{12}}-\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}\end{array}}}\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\begin{array}{c}(\cos {\mathit{\theta }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}\\ +\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}\sin \mathit{\theta }{}_{\mathrm{12}})\end{array}}{\begin{array}{c}\left(\sin {\mathit{\theta }}_{\mathrm{12}}\right(\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\varphi }}_{\mathrm{12}}-\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}})\\ +\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{11}}{)}^{\mathrm{2}}\end{array}}}\\ {\displaystyle }& {\displaystyle }\times (\sin {\mathit{\theta }}_{\mathrm{12}}\left(\cos {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{12}}+\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\right)\\ {\displaystyle }& {\displaystyle }-\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}).\\ {\displaystyle }& {\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial {\mathit{\theta }}_{\mathrm{12}}}}=-{\displaystyle \frac{\begin{array}{c}\cos {\mathit{\theta }}_{\mathrm{12}}\left(\cos {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{12}}+\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\right)\\ +\cos {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{12}}\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{12}}\left(\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\varphi }}_{\mathrm{12}}-\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}\end{array}}}\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{12}}(\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}+\cos {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\cos {\mathit{\theta }}_{\mathrm{11}})\\ -\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}\end{array}}{\begin{array}{c}\left(\sin {\mathit{\theta }}_{\mathrm{12}}\right(\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\varphi }}_{\mathrm{12}}-\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}})\\ +\cos {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{11}}{)}^{\mathrm{2}}\end{array}}}\\ {\displaystyle }& {\displaystyle }\times (\cos {\mathit{\theta }}_{\mathrm{12}}\left(\cos {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\varphi }}_{\mathrm{12}}-\sin {\mathit{\varphi }}_{\mathrm{11}}\cos {\mathit{\theta }}_{\mathrm{11}}\sin {\mathit{\varphi }}_{\mathrm{12}}\right)\\ {\displaystyle }& {\displaystyle }-\sin {\mathit{\varphi }}_{\mathrm{11}}\sin {\mathit{\theta }}_{\mathrm{12}}\sin {\mathit{\theta }}_{\mathrm{11}}).\\ {\displaystyle }& {\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial {\mathit{\theta }}_{\mathrm{21}}}}=-{\displaystyle \frac{\begin{array}{c}\cos {\mathit{\theta }}_{\mathrm{21}}(\cos {\mathit{\varphi }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}+\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{22}})\\ +\cos {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{21}}\left(\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\varphi }}_{\mathrm{22}}-\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{22}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\end{array}}}\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{21}}\left(\cos {\mathit{\varphi }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}+\cos {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{22}}\right)\\ -\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\end{array}}{\begin{array}{c}(\sin {\mathit{\theta }}_{\mathrm{21}}\left(\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\varphi }}_{\mathrm{22}}-\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{22}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}{)}^{\mathrm{2}}\end{array}}}\\ {\displaystyle }& {\displaystyle }\times \left(\cos {\mathit{\theta }}_{\mathrm{21}}\right(\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\varphi }}_{\mathrm{22}}-\sin {\mathit{\varphi }}_{\mathrm{22}}\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{12}})\\ {\displaystyle }& {\displaystyle }-\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}).\\ {\displaystyle }& {\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial {\mathit{\theta }}_{\mathrm{22}}}}={\displaystyle \frac{\begin{array}{c}(\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{22}}\\ +\cos {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{22}}\sin {\mathit{\theta }}_{\mathrm{21}})\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{21}}\left(\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\varphi }}_{\mathrm{22}}-\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{22}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\end{array}}}\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\begin{array}{c}(\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{22}}\\ +\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{22}})\end{array}}{\begin{array}{c}(\sin {\mathit{\theta }}_{\mathrm{21}}\left(\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\varphi }}_{\mathrm{22}}-\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{22}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\varphi }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}{)}^{\mathrm{2}}\end{array}}}\\ {\displaystyle }& {\displaystyle }\times (\sin {\mathit{\theta }}_{\mathrm{21}}\left(\cos {\mathit{\varphi }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{21}}+\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{22}}\sin {\mathit{\varphi }}_{\mathrm{22}}\right)\\ {\displaystyle }& {\displaystyle }-\cos {\mathit{\varphi }}_{\mathrm{21}}\cos {\mathit{\theta }}_{\mathrm{21}}\sin {\mathit{\theta }}_{\mathrm{22}}).\\ {\displaystyle }& {\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial {\mathit{\theta }}_{\mathrm{31}}}}=-{\displaystyle \frac{\begin{array}{c}\cos {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}+\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{32}}\right)\\ +\cos {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\varphi }}_{\mathrm{32}}-\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{32}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}\end{array}}}\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}+\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{32}}\right)\\ -\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}\end{array}}{\begin{array}{c}(\sin {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\varphi }}_{\mathrm{32}}-\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{32}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}{)}^{\mathrm{2}}\end{array}}}\\ {\displaystyle }& {\displaystyle }\times (\cos {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\varphi }}_{\mathrm{32}}-\sin {\mathit{\varphi }}_{\mathrm{32}}\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}\right)\\ {\displaystyle }& {\displaystyle }-\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}).\\ {\displaystyle }& {\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial {\mathit{\theta }}_{\mathrm{32}}}}={\displaystyle \frac{\begin{array}{c}(\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{32}}\\ +\cos {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{32}})\end{array}}{\begin{array}{c}\sin {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\varphi }}_{\mathrm{32}}-\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{32}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}\end{array}}}\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\begin{array}{c}(\cos {\mathit{\theta }}_{\mathrm{32}}\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{31}}\\ +\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{32}})\end{array}}{\begin{array}{c}(\sin {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\varphi }}_{\mathrm{32}}-\cos {\mathit{\theta }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{32}}\right)\\ +\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\varphi }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}{)}^{\mathrm{2}}\end{array}}}\\ {\displaystyle }& {\displaystyle }\times (\sin {\mathit{\theta }}_{\mathrm{31}}\left(\cos {\mathit{\varphi }}_{\mathrm{32}}\sin {\mathit{\varphi }}_{\mathrm{31}}+\sin {\mathit{\varphi }}_{\mathrm{32}}\cos {\mathit{\theta }}_{\mathrm{32}}\cos {\mathit{\varphi }}_{\mathrm{31}}\right)\\ {\displaystyle }& {\displaystyle }-\cos {\mathit{\varphi }}_{\mathrm{31}}\cos {\mathit{\theta }}_{\mathrm{31}}\sin {\mathit{\theta }}_{\mathrm{32}}).\end{array}$$

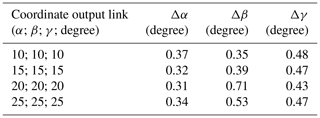
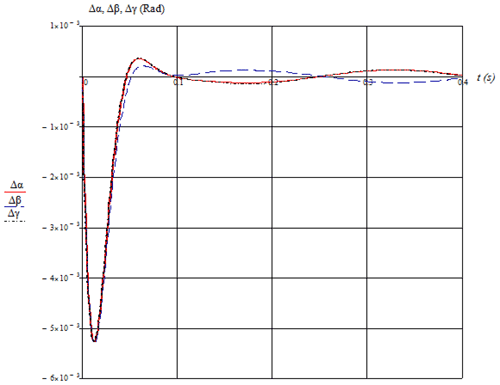
The values of the remaining partial derivatives are known from solving the positioning problem. Let us determine the positioning error of the output link in different positions with deviations of the angles between the axes equal to ${\mathit{\theta }}_{\mathrm{11}}={\mathit{\theta }}_{\mathrm{12}}={\mathit{\theta }}_{\mathrm{21}}={\mathrm{0.5}}^{\mathrm{0}}$ and ${\mathit{\theta }}_{\mathrm{22}}={\mathit{\theta }}_{\mathrm{31}}={\mathit{\theta }}_{\mathrm{32}}={\mathrm{0.4}}^{\mathrm{0}}$.

The deviations of the angles of the output link are expressed, from Eq. (4), as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\delta }\mathit{\alpha }={\displaystyle \frac{\begin{array}{c}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}{W}_{\mathrm{3}}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}{W}_{\mathrm{2}}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}{W}_{\mathrm{3}}\\ +\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}{W}_{\mathrm{2}}+\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}{W}_{\mathrm{1}}-\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}{W}_{\mathrm{1}}\end{array}}{\begin{array}{c}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}\\ +\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}+\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}\end{array}}},\\ {\displaystyle }& {\displaystyle }\\ {\displaystyle }& {\displaystyle }\mathit{\delta }\mathit{\beta }={\displaystyle \frac{\begin{array}{c}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}{W}_{\mathrm{3}}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}{W}_{\mathrm{2}}-\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}{W}_{\mathrm{3}}\\ +\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}{W}_{\mathrm{1}}+\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}{W}_{\mathrm{1}}-\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}{W}_{\mathrm{1}}\end{array}}{\begin{array}{c}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}\\ +\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}+\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}\end{array}}},\text{and}\\ {\displaystyle }& {\displaystyle }\\ {\displaystyle }& {\displaystyle }\mathit{\delta }\mathit{\alpha }={\displaystyle \frac{\begin{array}{c}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}{W}_{\mathrm{3}}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}{W}_{\mathrm{2}}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}{W}_{\mathrm{3}}\\ +\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}{W}_{\mathrm{2}}+\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\chi }}{W}_{\mathrm{1}}-\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}{W}_{\mathrm{1}}\end{array}}{\begin{array}{c}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\gamma }}\\ +\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\gamma }}+\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\alpha }}\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\beta }}-\frac{\partial F_{\mathrm{1}}}{\partial \mathit{\gamma }}\frac{\partial F_{\mathrm{2}}}{\partial \mathit{\beta }}\frac{\partial F_{\mathrm{3}}}{\partial \mathit{\alpha }}\end{array}}},\end{array}$$

where, in the following:

$$\begin{array}{rl}& W_{\mathrm{1}}=-\left({\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial {\mathit{\theta }}_{\mathrm{12}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{12}}+{\displaystyle \frac{\partial F_{\mathrm{1}}}{\partial {\mathit{\theta }}_{\mathrm{11}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{11}}\right),\\ & W_{\mathrm{2}}=-\left({\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial {\mathit{\theta }}_{\mathrm{22}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{22}}+{\displaystyle \frac{\partial F_{\mathrm{2}}}{\partial {\mathit{\theta }}_{\mathrm{21}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{21}}\right),\text{and}\\ & W_{\mathrm{3}}=-\left({\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial {\mathit{\theta }}_{\mathrm{32}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{32}}+{\displaystyle \frac{\partial F_{\mathrm{3}}}{\partial {\mathit{\theta }}_{\mathrm{31}}}}\mathit{\delta }{\mathit{\theta }}_{\mathrm{31}}\right).\end{array}$$

Thus, the solution to the problem of determining the deviation of the actuator of the mechanism in the case of the inaccuracy of its manufacture is presented. The values of the deviation of the coordinates of the output link at a given deviation between the axes are presented in Table 1.

Table 1 Output link angles deviation values.

3 Determination of dynamic accuracy

When assessing the dynamic positioning accuracy of the grip, small fluctuations around the stable equilibrium position are investigated.

The equations of motion for a manipulator with 3 degrees of freedom will be described by a system of differential equations (Kheylo and Glazunov, 2014; Nhan et al., 2019) as follows:

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial T}{\partial {\dot{\mathit{\varphi }}}_i}}\right)-{\displaystyle \frac{\partial T}{\partial {\mathit{\varphi }}_i}}=-{\displaystyle \frac{\partial \prod }{\partial {\mathit{\varphi }}_i}},i=\mathrm{1},\mathrm{\dots }\mathrm{3},\end{array}$$

where T is the kinetic energy of the system, and Π is potential energy of the system.

The potential energy of the system is defined as follows:

$$\prod ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{i=\mathrm{1}}^n{c}_i\cdot {\mathit{\varphi }}_i^{\mathrm{2}},$$

where c_i is the chain stiffness.

Kinetic energy is a quadratic function of generalized velocities.

$$\begin{array}{}\text{(6)}& T={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot J_x\cdot {\mathit{\omega }}_x^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot J_y\cdot {\mathit{\omega }}_y^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot J_z\cdot {\mathit{\omega }}_z^{\mathrm{2}},\end{array}$$

where ω_x, ω_y, and ω_z are the angular velocities of the output link around the x, y, and z axes, respectively. $J_z=\frac{\mathrm{1}}{\mathrm{2}}\cdot m\cdot r^{\mathrm{2}}$ and $J_y=J_z=\frac{\mathrm{1}}{\mathrm{12}}\cdot m\cdot r^{\mathrm{2}}$ are the moments of inertia of the output link around the axes x, y, and z, respectively. m is the mass of the output link (we take m=0.5 kg, and r=0.1 m). r is the radius of the platform of the output link. Then, Eq. (6) takes the following form:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}T& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}\cdot m\cdot r^{\mathrm{2}}\cdot {\mathit{\omega }}_x^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}\cdot m\cdot r^{\mathrm{2}}\cdot {\mathit{\omega }}_y^{\mathrm{2}}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot m\cdot r^{\mathrm{2}}\cdot {\mathit{\omega }}_z^{\mathrm{2}}.\end{array}\end{array}$$

The problem of determining the deviation of the coordinates of the input link when removing it from the equilibrium position is solved numerically (Fig. 4). Reducing the dynamic error can be achieved by increasing the rigidity of the drive or by introducing damping devices.

Automatic compensation of movements, using digital or pulse controllers, is also an effective method of damping the vibrations.

Figure 4 Deviation of the output link along the coordinates α, β, and γ.

4 Evaluation of the positioning of the output link when controlling the mechanism

The reduction of residual vibrations is possible by increasing the stiffness of the drives. This must also be taken into account when constructing a control algorithm (Nhan et al., 2019).

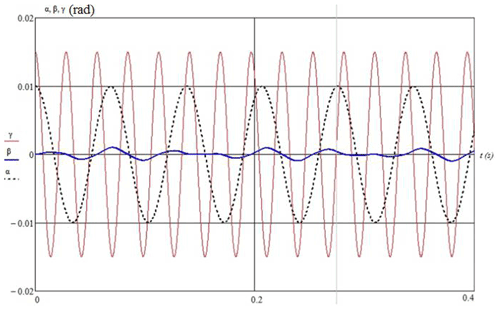
Let us set the required movement of the output link in the form of the law of coordinate change, i.e., α_T(t), β_T(t), and γ_T(t). The required speeds are ${\dot{\mathit{\alpha }}}_T\left(t\right)$, ${\dot{\mathit{\beta }}}_T\left(t\right)$, and ${\dot{\mathit{\gamma }}}_T\left(t\right)$, and acceleration is ${\ddot{\mathit{\alpha }}}_T\left(t\right)$, ${\ddot{\mathit{\beta }}}_T\left(t\right)$, and ${\ddot{\mathit{\gamma }}}_T\left(t\right)$, which we obtain after the differentiation.

The control problem is to minimize the coordinate error is as follows: ${\mathrm{\Delta }}_{\mathrm{1}}\left(t\right)={\mathit{\alpha }}_T\left(t\right)-\mathit{\alpha }\left(t\right)$, ${\mathrm{\Delta }}_{\mathrm{2}}\left(t\right)={\mathit{\beta }}_T\left(t\right)-\mathit{\beta }\left(t\right)$, ${\mathrm{\Delta }}_{\mathrm{3}}\left(t\right)={\mathit{\gamma }}_T\left(t\right)-\mathit{\gamma }\left(t\right)$, with the speed of ${\dot{\mathrm{\Delta }}}_{\mathrm{1}}\left(t\right)={\dot{\mathit{\alpha }}}_T\left(t\right)-\dot{\mathit{\alpha }}\left(t\right)$, ${\dot{\mathrm{\Delta }}}_{\mathrm{2}}\left(t\right)={\dot{\mathit{\beta }}}_T\left(t\right)-\dot{\mathit{\beta }}\left(t\right)$, and ${\dot{\mathrm{\Delta }}}_{\mathrm{3}}\left(t\right)={\dot{\mathit{\gamma }}}_T\left(t\right)-\dot{\mathit{\gamma }}\left(t\right)$, and acceleration of ${\ddot{\mathrm{\Delta }}}_{\mathrm{1}}\left(t\right)={\ddot{\mathit{\alpha }}}_T\left(t\right)-\ddot{\mathit{\alpha }}\left(t\right)$, ${\ddot{\mathrm{\Delta }}}_{\mathrm{2}}\left(t\right)={\ddot{\mathit{\beta }}}_T\left(t\right)-\ddot{\mathit{\beta }}\left(t\right)$, and ${\ddot{\mathrm{\Delta }}}_{\mathrm{3}}\left(t\right)={\ddot{\mathit{\gamma }}}_T\left(t\right)-\ddot{\mathit{\gamma }}\left(t\right)$, where α(t), β(t), and γ(t) are the actual values of the coordinates of the output link.

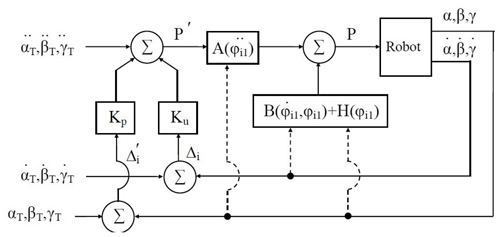
We then simulate the movement of the output link of the parallel structure mechanism along a given trajectory using the developed algorithm for optimal motion control (Fig. 5).

Figure 5 Control algorithm.

To measure the magnitude of the deviations, we use a quadratic integral assessment as follows:

$$J_S=\underset{t_{\mathrm{0}}}{\overset{T}{\int }}\left({\mathrm{\Delta }}_i^{\mathrm{2}}+k_{\mathrm{1}}\cdot {\dot{\mathrm{\Delta }}}_i^{\mathrm{2}}+k_{\mathrm{2}}\cdot {\ddot{\mathrm{\Delta }}}_i^{\mathrm{2}}\right)\mathrm{d}t.$$

There must be the following:

$$\begin{array}{}\text{(8)}& \ddot{\mathrm{\Delta }}+{\mathit{\gamma }}_{\mathrm{1}}\cdot \dot{\mathrm{\Delta }}+{\mathit{\gamma }}_{\mathrm{0}}\cdot \mathrm{\Delta }=\mathrm{0}.\end{array}$$

We then rewrite Eq. (8) in a form appropriate to the oscillatory link, as follows:

$$\left\{\begin{array}{l}{\mathit{\tau }}^{\mathrm{2}}\ddot{\mathrm{\Delta }}+\mathrm{2}\mathit{\zeta }\mathit{\tau }\cdot \dot{\mathrm{\Delta }}+\mathrm{\Delta }=\mathrm{0}\\ {\mathit{\tau }}^{\mathrm{2}}=\frac{\mathrm{1}}{{\mathit{\gamma }}_{\mathrm{0}}};\mathrm{2}\mathit{\zeta }\mathit{\tau }=\frac{{\mathit{\gamma }}_{\mathrm{1}}}{{\mathit{\gamma }}_{\mathrm{0}}},\end{array}\right.$$

where τ is time, and ζ is the damping ratio.

The law of acceleration change corresponds to the oscillatory link as follows:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& \ddot{\mathit{\alpha }}={\ddot{\mathit{\alpha }}}_T+{\mathit{\gamma }}_{\mathrm{1}}\cdot ({\dot{\mathit{\alpha }}}_T-\dot{\mathit{\alpha }})+{\mathit{\gamma }}_{\mathrm{0}}\cdot ({\mathit{\alpha }}_T-\mathit{\alpha })\\ & \ddot{\mathit{\beta }}={\ddot{\mathit{\beta }}}_T+{\mathit{\gamma }}_{\mathrm{1}}\cdot ({\dot{\mathit{\beta }}}_T-\dot{\mathit{\beta }})+{\mathit{\gamma }}_{\mathrm{0}}\cdot ({\mathit{\beta }}_T-\mathit{\beta })\\ & \ddot{\mathit{\gamma }}={\ddot{\mathit{\gamma }}}_T+{\mathit{\gamma }}_{\mathrm{1}}\cdot ({\dot{\mathit{\gamma }}}_T-\dot{\mathit{\gamma }})+{\mathit{\gamma }}_{\mathrm{0}}\cdot ({\mathit{\gamma }}_T-\mathit{\gamma }).\end{array}\end{array}$$

The equation of motion for a spherical mechanism with 3 degrees of freedom has the following form:

$$\left\{\begin{array}{l}{J}_{\mathit{\xi }}\cdot {\ddot{\mathit{\varphi }}}_{\mathit{\xi }}=M_{\mathrm{1}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{11}}}{\partial {\mathit{\varphi }}_{\mathit{\xi }}}+M_{\mathrm{2}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{21}}}{\partial {\mathit{\varphi }}_{\mathit{\xi }}}\\ +M_{\mathrm{3}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{31}}}{\partial {\mathit{\varphi }}_{\mathit{\xi }}}+{\dot{\mathit{\varphi }}}_{\mathit{\eta }}\cdot {\dot{\mathit{\varphi }}}_{\mathit{\zeta }}\cdot \left(J_{\mathit{\zeta }}-J_{\mathit{\eta }}\right)\\ J_{\mathit{\eta }}\cdot {\ddot{\mathit{\varphi }}}_{\mathit{\eta }}=M_{\mathrm{1}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{11}}}{\partial {\mathit{\varphi }}_{\mathit{\eta }}}+M_{\mathrm{2}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{21}}}{\partial {\mathit{\varphi }}_{\mathit{\eta }}}\\ +M_{\mathrm{3}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{31}}}{\partial {\mathit{\varphi }}_{\mathit{\eta }}}+{\dot{\mathit{\varphi }}}_{\mathit{\xi }}\cdot {\dot{\mathit{\varphi }}}_{\mathit{\zeta }}\cdot \left(J_{\mathit{\xi }}-J_{\mathit{\zeta }}\right)\\ J_{\mathit{\zeta }}\cdot {\ddot{\mathit{\varphi }}}_{\mathit{\zeta }}=M_{\mathrm{1}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{11}}}{\partial {\mathit{\varphi }}_{\mathit{\zeta }}}+M_{\mathrm{2}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{21}}}{\partial {\mathit{\varphi }}_{\mathit{\zeta }}}\\ +M_{\mathrm{3}}\cdot \frac{\partial {\mathit{\varphi }}_{\mathrm{31}}}{\partial {\mathit{\varphi }}_{\mathit{\zeta }}}+{\dot{\mathit{\varphi }}}_{\mathit{\xi }}\cdot {\dot{\mathit{\varphi }}}_{\mathit{\eta }}\cdot \left(J_{\mathit{\eta }}-J_{\mathit{\xi }}\right),\end{array}\right.$$

where $J_{\mathit{\xi }}=J_{\mathit{\eta }},J_{\mathit{\zeta }}$ are the moments of inertia about the axes ξ, η, and ζ. $M_{\mathrm{1}},M_{\mathrm{2}},$ and M₃ are the moments in drives. $\frac{\partial {\mathit{\varphi }}_{ij}}{\partial {\mathit{\varphi }}_{\mathit{\xi }}}$ are the variable coefficients.

${\ddot{\mathit{\varphi }}}_{\mathit{\xi }}$, ${\dot{\mathit{\varphi }}}_{\mathit{\xi }}$, ${\ddot{\mathit{\varphi }}}_{\mathit{\eta }}$, ${\dot{\mathit{\varphi }}}_{\mathit{\eta }}$, ${\ddot{\mathit{\varphi }}}_{\mathit{\zeta }}$, and ${\dot{\mathit{\varphi }}}_{\mathit{\zeta }}$ are the projection of accelerations and velocities on the moving axes of ξ, η, and ζ.

The dynamic properties of the system are determined by transient processes. Transient processes (the overshoot time and deviations of the output link from a given trajectory) are regulated by feedback coefficients γ₀ and γ₁.

Let us set the law of motion of the executive link, as follows:

$$\begin{array}{rl}& {\mathit{\alpha }}_T\left(t\right)=\mathrm{0},\mathrm{1}\cdot \sin \left(\mathit{\omega }t\right);\\ & {\mathit{\beta }}_T\left(t\right)=\mathrm{0},\mathrm{1}\cdot \sin \left(\mathit{\omega }t\right);\\ & {\mathit{\gamma }}_T\left(t\right)=\mathrm{0},\mathrm{1}\cdot \sin \left(\mathit{\omega }t\right).\end{array}$$

The differential acceleration in Eq. (9) takes the following form:

$$\begin{array}{rl}& \ddot{\mathit{\alpha }}={\ddot{\mathit{\alpha }}}_T+\mathrm{120}\cdot ({\dot{\mathit{\alpha }}}_T-\dot{\mathit{\alpha }})+\mathrm{7200}\cdot ({\mathit{\alpha }}_T-\mathit{\alpha })\\ & \ddot{\mathit{\beta }}={\ddot{\mathit{\beta }}}_T+\mathrm{120}\cdot ({\dot{\mathit{\beta }}}_T-\dot{\mathit{\beta }})+\mathrm{7200}\cdot ({\mathit{\beta }}_T-\mathit{\beta })\\ & \ddot{\mathit{\gamma }}={\ddot{\mathit{\gamma }}}_T+\mathrm{120}\cdot ({\dot{\mathit{\gamma }}}_T-\dot{\mathit{\gamma }})+\mathrm{7200}\cdot ({\mathit{\gamma }}_T-\mathit{\gamma }).\end{array}$$

When moving with feedback, the graph of the changes in the position error and the torque in the drive is shown in Fig. 6.

Figure 6 Graph of the changes in the position error Δα, Δβ, and Δγ of the output link.

Thus, by changing the feedback coefficients, it is possible to regulate the deviations of the output link from the desired trajectory, while the overshoot time τ changes.

5 Conclusion

An integrated approach allows one to evaluate and determine the positioning error of the output link from the standpoint of kinematics, dynamics, and control. This approach will allow, when synthesizing mechanisms, us to propose approaches to compensate for or completely eliminate errors.

So, with the kinematic estimate, the proposed approach to assessing the kinematic accuracy allows one to determine the deviations in the output link using the theory of accuracy. This allows one to determine the deviations in the output link at any point in the working area and propose constructive solutions for its compensation. This approach to determining the positioning error makes it possible to calculate the deviations in the output link for similar mechanisms of a parallel structure.

From the perspective of dynamics with free oscillations of the output link, or when it stops, a numerical estimate of the positioning error is given, which makes it possible to assess the technological requirements for the accuracy of operations and propose solutions to reduce it. In this case, an increase in the accuracy of the manipulation from the position of dynamics can be carried out by optimally selecting the rigidity of the drive or by introducing additional damping devices. In control, the minimization of the error during the transient process is ensured by the choice of feedback coefficients.