the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Mixed synthesis method of motion and path of planar four-bar linkages
Ruiqin Li
Hailong Liang
Fengping Ning
The mixed synthesis of motion and path generation, which is also known as the Alt–Burmester problem, is an attractive problem for study. However, such a problem for the four-bar linkages which possess more than M poses (M>5) and mixed N path points has not been well-solved. In this work, a mixed synthesis method is developed for planar four-bar linkages to cope with the above problem. The developed method can quickly select an optimal combination that contains five poses and N points by using the conic filtering algorithm, which is based on the similar characteristics of the value and direction between the conic and coupler curves in a certain neighborhood. Next, the selected five poses are substituted into a simplified equation system of motion synthesis which includes four equations and four variables to solve the parameters of the planar four-bar linkage. Finally, a case is provided to validate the effectiveness of the developed method in the mixed synthesis problem.
- Article
(1706 KB) - Full-text XML
- BibTeX
- EndNote
In general, kinematics problems are categorized into three kinds of problems that can be solved by three different solutions (Nolle, 1974; Li et al., 2020). Such a classification covers most kinematics synthesis problems. Some kinematic synthesis problems, however, fall into a class of problems that cannot be well-solved, such as the mixed synthesis problem with motion and path constraints. Therefore, further research on this kind of kinematics synthesis problem is needed. Tong et al. (2013) proposed naming such a mixed kinematics problem the Alt–Burmester problem and developed a combination of the geometric constraint programming (GCP) and numerical solutions of synthetic equations to solve such a problem. Brake et al. (2016) used a numerical algebraic geometry method to study all the Alt–Burmester problems with finite solutions under the case (M poses, N path points), where each solution set under the general case has dimensions and orders from zero to eight. Sharma et al. (2019) presented an analytical method based on the Fourier approximation to deal with the mixed synthesis problems, where the harmonic decomposition of the closed-loop equation represents the analytic relationship between the direction and the path. Then, the path points are converted to a back position to obtain the parameters of the motion synthesis problem. Zimmerman (2018) presented a graphical method for solving the mixed synthesis problems. However, this research only focused on the case of . Sharma et al. (2019) further generalized the research on the Alt–Burmester problem to the case under the constraint M≤5. In view of these, this paper proposes a mixed synthesis method for such a problem, namely the Alt–Burmester problem (), where M satisfies M>5.
Motion, path, and function generation are three categories of linkage synthesis problems that have three different synthesis equations (Zhao et al., 2016b; Pennestri and Valentini, 2018). In general, planar four-bar linkages can accurately visit up to five positions or nine path points (Zhao et al., 2016a; Sleesongsom and Bureerat, 2018). Bai et al. (2020) studied a single-degree-of-freedom 10-bar mechanism to track 10 exact positions. Among the above three kinds of mechanism synthesis problems, the path generation of four-bar linkages is the most challenging problem (Wampler et al., 1992; Khan et al., 2015; Buskiewicz, 2018) because of the complexity of the path synthesis equation. To solve path synthesis equations, various methods were attempted, such as the homotopy method, the evolutionary algorithm, and the Fourier algorithm (Morgan and Wampler, 1990; Cabrera et al., 2011; Guigue and Hayes, 2016). Also, another path synthesis problem, the coupler-curve synthesis, has been studied with a fully analytical method and a method that combines both the analytical and graphical methods (Wu et al., 2021; Bai et al., 2021). There are few reports on the study of equations for mixed synthesis problems. In this paper, a mixed synthesis method based on the equation of motion synthesis is proposed.
The studied mixed synthesis method is mainly for the Alt–Burmester problem with the case , M>5. The steps of the proposed method are roughly depicted as follows.
-
The conic filter algorithm is employed to transform the mixed synthesis problem into a motion synthesis problem.
-
A more easy-to-solve motion synthesis with four equations and four variables is governed for analysis.
-
More binary linkage groups can be obtained by solving the equations of motion synthesis.
-
The four-bar linkage synthesis is achieved by the optimal combination.
The remainder of this paper is organized as follows: Sect. 2 explains the theory of the filtering algorithm. Section 3 establishes a model and provides the derivation of the exact synthesis equation. Section 4 gives a case to validate the effectiveness of the proposed method. Section 5 summarizes the contribution of this paper.
The conic filtering algorithm uses a conic curve to fit the given pose and path points for finding the five-pose combinations that include the optimal combination. Under this algorithm, a mixed synthesis problem is turned into an exact motion synthesis problem. In this work, the over-constrained problem is transformed into a motion synthesis problem by quickly selecting the target design points. As there are many motion synthesis problems of the planar four-bar linkages, the mixed synthesis problem can be solved more elegantly after such a transformation.
To better explain the principle of the conic filtering algorithm, an important theorem, Taylor expansion, is reviewed. The mathematical form of the Taylor expansion on a binary function at point (xk,yk) is expressed as
Such an expansion approximates the value of a target function in the neighborhood of a certain point by constructing a polynomial that contains the derivatives of the target function as coefficients. The beauty of Taylor expansion is that a complex primitive function can be approximated by a simple polynomial, and the principle of the conic filtering algorithm has a similar idea.
Both Blechschmidt and Uicker (1986) and Bai and Angeles (2015) mentioned that a coupler curve is a sixth-order nonlinear equation. However, solving the coupler curve in such a sixth-order nonlinear equation is still a challenging problem. It is easier to use a five-pose composite to form a conic curve (which will be illustrated later) than to use a traditional nine-point for the path generation. Therefore, the developed conic filtering algorithm mainly uses five points on the coupler curve to synthesize a conic curve. The value of the synthesized conic curve in some specific ranges can be approximated to a value on the coupler curve.
The conic algebraic equation f(x,y) can be expressed as
where Ai is the coefficients of conic algebraic equation f(x,y) and A1≠0.
With the introduction of the new coefficients , the conic algebraic equation f(x,y) can be re-written by
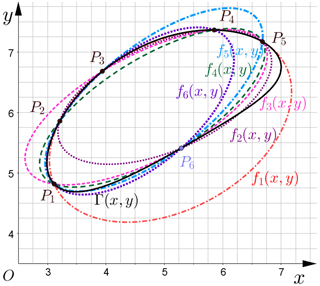
The conic filtering algorithm calculates errors by finding a conic curve in a given range to replace the coupler curve. Also, the use of the conic curve can reduce the computational complexity and computing cost in solving the mixed synthesis. Although there is no rigorous mathematical proof for the conic filtering algorithm, its principle is intuitive from the geometric point of view, as shown in Fig. 1.
In Fig. 1, all the points P1, P2, P3, P4, P5, and P6 are on the coupler curve Γ(x,y), where the form of the conic equation corresponds to Eq. (3). According to the formula, any five points can determine unique conic curves, and an additional point will determine five more conic curves (). The conic curve fi(x,y) and the coupler curve Γ(x,y) have highly similar curve properties within a certain range (or a large neighborhood). For example, the conic curve f1(x,y) within the range of (P1–P5) has a smaller error than the coupler curve, while the conic curve f4(x,y) within the range of (P1, P2, P4–P6) has a larger error than the coupler curve, though their shapes are similar.
The errors of both the conic curve and the coupler curve are smaller within a certain range. Therefore, the conic curve is used to select the optimal combination instead of the coupler curve. In this work, we believe that the most suitable point for the synthesis of the coupler curve is to select five points that correspond to the conic curve calculated by the optimization theory.
It should be emphasized that the angle problem is not considered in the filtering process. Because the curves in a certain range are highly similar, this work assumes that the properties of the curves are also similar.
The process of the filtering algorithm can be implemented by the following three steps.
-
Calculate all combinations of pose constraints.
-
Calculate the conic coefficients for solving the corresponding error.
-
Find the minimum error of the conic curve.
The objective function for minimizing the error can be expressed by
where fi(x) is the conic function and Piy is known.
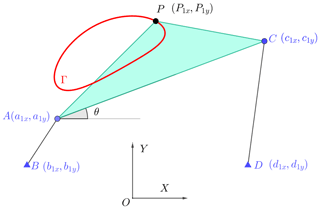
A typical four-bar linkage is shown in Fig. 2, where the origin of the fixed coordinate system is denoted by O–XY and can be arbitrarily selected. The position of the four-bar linkage can be uniquely determined by the five points, , and P. B(b1x,b1y) and D(d1x,d1y) are the coordinates of the fixed pivots. Herein, A(a1x,a1y), B(b1x,b1y), C(c1x,c1y), and D(d1x,d1y) are the coordinates described in O–XY. The position of the revolute joints (A and C) at the ith position are represented by A(aix,aiy) and C(cix,ciy). θ is the rotation angle between line AC and the horizontal axis. θi is the rotation angle of the ith pose.
The four-bar linkage can be divided into two dyads, namely PAB and PCD. These two links have the same motion synthesis because PAB and PCD have the same motion equation.
Because the dimension of the linkage AB is always fixed during the movement, there is a constraint equation on the linkage AB.
where aix and aiy in Eq. (5) can be expressed by the following matrix form:
where θ is the rotation angle of the four-bar linkage; θi is the rotation angles of the ith pose; (aix,aiy) are the coordinates of point A for the ith movement; (Pix,Piy) are the coordinates of point P for the ith movement. Substituting Eq. (6) into Eq. (5), the following equations are derived.
where is the function of each motion synthesis; (b1x,b1y) are the coordinates of point B for the first movement; (c1x,c1y) are the coordinates of point C for the first movement; (d1x,d1y) are the coordinates of point D for the first movement.
It is obvious that Eq. (7) is an equation system consisting of four equations and four parameters (a1x, a1y, b1x, and b1y). Because this equation system cannot be solved directly by the traditional equation solver, a classical elimination method is used to simplify it (Wen-Tsun, 1986). The resolved equations by such a method are composed of a set of triangular equations, which can be solved directly by the new equation solver. Besides, the resolved equation system improves computational efficiency and robustness. Due to the complexity of the expression of the resolved equations, a set of simplified expressions are derived:
Parameters a1x and a1y are eliminated in the operations in Eqs. (10)–(11). It is obvious that Eqs. (10)–(11) are the binary quadratic equations whose analytic solutions can be obtained by the symbolic calculation. The resulting solution is then substituted into Eqs. (8)–(9) to obtain all the solutions. Herein, the detailed steps are listed.
-
Give a mixed constraint in the plane coordinate system.
-
Calculate the value of the function f(x,y) and find the minimum value that corresponds to the five coordinates Pi(Pix,Piy).
-
Substitute the solved parameters Pi(Pix,Piy) into Eqs. (10)–(11); then the parameters, b1x and b1y, can be solved.
-
Substitute the solved parameters, b1x and b1y, into Eqs. (8)–(9); then the parameters, a1x and a1x, can be solved.
-
Find the combinations of two dyads that satisfy all the conditions in the motion synthesis.
Compared with other research on the Alt–Burmester problem, the differences between this work and the existing literature are depicted in Table 1.
Tong et al. (2013)Brake et al. (2016)Zimmerman (2018)Sharma et al. (2019)In this paper, a case is provided to illustrate how the developed method can find the parameters of a planar four-bar linkage from mixed constraints.
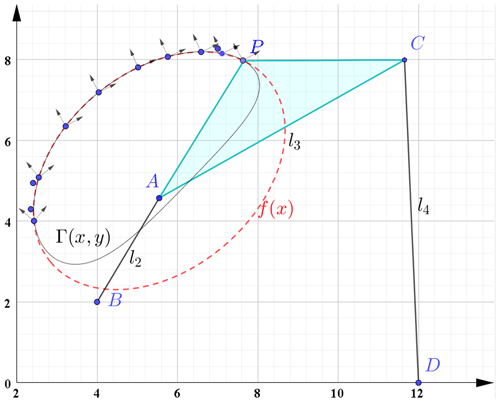
The case is presented in Table 2, where the problem is a classical mixed synthesis problem (nine poses and three points) to synthesizing the new coupler curve for tracing a set of poses and points.
There are nine pose constraints and three point constraints in Table 2, generating a total of 126 () combinations. Each combination consists of five poses and three path points. The first combination is substituted into Eq. (3) to obtain the corresponding coefficient matrix of the conic equation described.
Five coefficients of the conic curve that corresponds to the first set of poses can be obtained by solving the linear system. To further solve the total of 126 combinations, the optimal value of the 126 groups for the error calculation is 0.12 mm. The minimum value of the function corresponds to a set of coordinates P1, P3, P6, P8, and P9.
It should be emphasized that the five points are selected from a group of points P1–P9, whereas points P10–P12 only impact the calculation of the error. Next, the mixed synthesis problem in Table 2 is transformed into a precise synthesis problem.
The coordinates are substituted into Eqs. (8)–(11), which generates the following results:
It can be found that Eqs. (15)–(16) are a quaternary system with two variables, which takes less time to be solved. Equations (8)–(11) are too complicated to show the specific details, so only the equation form is given. Equations (13)–(16) demonstrate the efficiency of equation solving. Finally, the values of a1x, a1y, b1x, and b1y are obtained by solving Eqs. (13)–(16).
The results are provided in Table 3, and the planar tracing results are provided in Fig. 4. Note that these solutions were generated by a personal computer (Intel Core (TM) I7-6700 CPU and 16 GB RAM). The total calculation time is 87 s, where the conic filtering algorithm took 68.30 s to screen 128 groups and 18.30 s to solve the results. This demonstrates the efficiency of the developed method.
This paper proposes a method to solve the mixed synthesis problem of planar four-bar linkages. The mixed synthesis problem is first transformed into the exact motion synthesis problem by a filtering algorithm. Then, the equations of the motion synthesis problem are re-derived, where the more concise equations of motion synthesis are governed. Based on these, the equations of motion synthesis, i.e. , become more elegantly solved by the general equation solvers.
The main contribution of this work bridges the research gap of a class of mixed synthesis problems (, M>5). Besides, compared with the kinematics mapping method proposed in Zimmerman (2018), our developed conic filtering algorithm is easier for realizing the automatic solving. Furthermore, compared with the analytic method based on the Fourier approximation proposed in Sharma et al. (2019), our work supports more concise solution steps as there is no need to consider additional correspondence.
The developed method is suitable for the mixed synthesis problems that study the combination of motion and path generation. In addition, the principle of the developed method which approximates a higher-order curve with a lower-order curve has potential values to solve other nonlinear problems, such as the path synthesis of planar four-bar linkages with N points (N>9), which will be studied in the future studies.
All the research data are provided in the tables.
RW conceived and wrote the manuscript. RW, RL, HL, and FN were involved in writing, reviewing, and editing the manuscript. RL and FN are responsible for project development management. RW and HL process data together.
The authors declare that they have no conflict of interest.
The authors thank the reviewers and topical editor for their constructive comments and Copernicus Publications for their professional language services and earnest typesetting services.
This research has been supported by the Key Research and Development Project of Shanxi Province (grant nos. 201903D421051 and 201803D421027), the Postgraduate Innovation Project of Shanxi Province (grant no. 2020BY090), and the General Program of the Natural Science Foundation of Shanxi Province (grant no. 201801D221235).
This paper was edited by Daniel Condurache and reviewed by two anonymous referees.
Bai, S., Li, Z., and Li, R.: Exact coupler-curve synthesis of four-bar linkages with fully analytical solutions, Mech. Mach. Theory, 143, 1–15, https://doi.org/10.1016/j.mechmachtheory.2019.103625, 2020. a
Bai, S., Wu, R., and Li, R.: Exact Coupler-Curve Synthesis of Four-Bar Linkages with Fully Analytical Solutions, in: Advances in Robot Kinematics 2020, vol. 15, 82–89, Springer International Publishing, Slovenia, https://doi.org/10.1007/978-3-030-50975-0_11, 2021. a
Bai, S. P. and Angeles, J.: Coupler-curve synthesis of four-bar linkages via a novel formulation, Mech. Mach. Theory, 94, 177–187, https://doi.org/10.1016/j.mechmachtheory.2015.08.010, 2015. a
Blechschmidt, J. L. and Uicker, J. J. J.: Linkage synthesis using algebraic curves, J. Mech. Design, 108, 543–548, https://doi.org/10.1115/1.3258767, 1986. a
Brake, D. A., Hauenstein, J. D., Murray, A. P., Myszka, D. H., and Wampler, C. W.: The complete solution of Alt-Burmester synthesis problems for four-bar linkages, J. Mech. Robot., 8, 041018, https://doi.org/10.1115/1.4033251, 2016. a, b
Buskiewicz, J.: Reduced number of design parameters in optimum path synthesis with timing of four-bar linkage, J. Theor. Appl. Mech., 56, 43–55, https://doi.org/10.15632/jtam-pl.56.1.43, 2018. a
Cabrera, J. A., Ortiz, A., Nadal, F., and Castillo, J. J.: An evolutionary algorithm for path synthesis of mechanisms, Mech. Mach. Theory, 46, 127–141, https://doi.org/10.1016/j.mechmachtheory.2010.10.003, 2011. a
Guigue, A. and Hayes, M. J. D.: Continuous approximate synthesis of planar function-generators minimising the design error, Mech. Mach. Theory, 101, 158–167, https://doi.org/10.1016/j.mechmachtheory.2016.03.012, 2016. a
Khan, N., Ullah, I., and Al-Grafi, M.: Dimensional synthesis of mechanical linkages using artificial neural networks and Fourier descriptors, Mech. Sci., 6, 29–34, https://doi.org/10.5194/ms-6-29-2015, 2015. a
Li, X. G., Wei, S. M., Liao, Q. Z., and Zhang, Y.: A novel analytical method for four-bar path generation synthesis based on Fourier series, Mech. Mach. Theor., 144, 103671, https://doi.org/10.1016/j.mechmachtheory.2019.103671, 2020. a
Morgan, A. P. and Wampler, C. W.: Solving a planar four-bar design problem using continuation, J. Mech. Design, 112, 544–550, https://doi.org/10.1115/1.2912644, 1990. a
Nolle, H.: Linkage coupler curve synthesis: A historical review–II. Developments after 1875, Mech. Mach. Theory, 9, 325–348, https://doi.org/10.1016/0094-114X(74)90018-4, 1974. a
Pennestri, E. and Valentini, P. P.: An application of Yaglom's geometric algebra to kinematic synthesis of linkages for prescribed planar motion of oriented lines, J. Mech. Design, 140, 1–17, https://doi.org/10.1115/1.4038924, 2018. a
Sharma, S., Purwar, A., and Ge, Q. J.: A motion synthesis approach to solving Alt-Burmester problem by exploiting Fourier descriptor relationship between path and orientation data, J. Mech. Robot., 11, 011016, https://doi.org/10.1115/1.4042054, 2019. a, b, c, d
Sleesongsom, S. and Bureerat, S.: Optimal synthesis of four-bar linkage path generation through evolutionary computation with a novel constraint handling technique, Comput. Intell. Neurosc., 2018, 1–16, https://doi.org/10.1155/2018/5462563, 2018. a
Tong, Y., Myszka, D. H., and Murray, A. P.: Four-bar linkage synthesis for a combination of motion and path-point generation, in: Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Division, Vol. 6A, 1–10, ASME, Portland, https://doi.org/10.1115/DETC2013-12969, 2013. a, b
Wampler, C. W., Morgan, A. P., and Sommese, A. J.: Complete solution of the nine-point path synthesis problem for four-bar linkages, J. Mech. Design, 114, 153–159, https://doi.org/10.1115/1.2916909, 1992. a
Wen-Tsun, W.: Basic principles of mechanical theorem proving in elementary geometries, J. Autom. Reasoning, 2, 221–252, https://doi.org/10.1007/BF02328447, 1986. a
Wu, R., Li, R., and Bai, S.: A fully analytical method for coupler-curve synthesis of planar four-bar linkages, Mech. Mach. Theory, 155, 1–9, https://doi.org/10.1016/j.mechmachtheory.2020.104070, 2021. a
Zhao, P., Ge, X., Zi, B., and Ge, Q. J.: Planar linkage synthesis for mixed exact and approximated motion realization via kinematic mapping, J. Mech. Robot., 8, 051004, https://doi.org/10.1115/1.4032212, 2016a. a
Zhao, P., Li, X., Zhu, L., Zi, B., and Gee, Q. J.: A novel motion synthesis approach with expandable solution space for planar linkages based on kinematic-mapping, Mech. Mach. Theory, 105, 164–175, https://doi.org/10.1016/j.mechmachtheory.2016.06.021, 2016b. a
Zimmerman, R.: Planar linkage synthesis for mixed motion, path, and function generation using poles and rotation angles, J. Mech. Robot., 10, 025004, https://doi.org/10.1115/1.4039064, 2018. a, b, c