Design and development of a novel monolithic compliant XY stage with centimeter travel range and high payload capacity

This article proposes a novel monolithic compliant spatial parallel XY stage (SPXYS). An important feature of the SPXYS lies in that it can deliver centimeter travel range and sustain large out-of-plane payload while possessing a compact structure, which makes the SPXYS suitable for some special applications such as Ultra-Violet Nanoimprint Lithography and soft-contact lithography. Different from conventional compliant positioning stages, the proposed SPXYS consists of a monolithic spatial parallel linear compliant mechanism (SPLCM) driven by four matching designed voice coil motors (VCMs). The moving platform of the stage is connected to the base by four spatial prismatic-prismatic (PP) joints, which are enveloped from planar PP joint based on the position space reconfiguration (PSR) method to realize desired travel range, payload capacity and compact size. The mechatronic model of the SPXYS is established by integrated using matrix structural analysis (MSA) and the method of images. The design flow chart of the SPXYS is given based on the key parameter sensitivity analysis. Furthermore, a reified SPXYS is designed and manufactured. The analytical design of the stage is confirmed by experiments. The reified stage has a travel range of 20.4 × 20.6 mm², a compact structure with area ratio 1.87 %, and the resonant frequencies of the two working modes at 22.98 and 21.31 Hz. It can track a circular trajectory with the radius of 4.5 mm. The root mean squares (RMS) tracking error is 2 µm. The positioning resolution is 100 nm. The payload capacity test shows that the reified stage can bear 20 kg out-of-plane payload.

1 Introduction

Compliant positioning stages (CPSs) possess many merits, such as reduced number of parts, no friction, no backlash and free of lubrication (Howell, 2001; Smith, 2000), which make them have extensive applications such as micro manufacturing, optical fiber alignment, biological engineering, scanning probe microscopy (SPM) and lithography (Yong et al., 2012; Kenton et al., 2012; Chen et al., 1992; Muthuswamy et al., 2002). But some special applications such as Ultra-Violet Nanoimprint Lithography (UV-NIL) and soft-contact lithography (Teo, 2014; Qu, 2014) expect that the CPS has not only large travel range, but also large out-of-plane payload carrying capacity without any other auxiliary supporting equipment. Moreover, restrained by space limitation, compact mechatronic design of CPS is usually expected. Hence, this article is concentrated on the design and development of a compliant XY position stage which has large travel range, compact structure, high out-of-plane payload capacity and matching design of voice coil motors (VCMs).

Figure 1 Schematic diagram of a 4-PP decoupled parallel mechanism.

Figure 2 Two types of PP joints: (a) planar PP joint and (b) spatial PP joint.

Figure 3 Structure of the proposed (a) SPLCM and (b) SPXYS.

Parallel XY stage (PXYS) is the most common layout of XY stages because of its advantages including identical dynamic features in working axes, low inertia, and low cumulative positioning errors (Teo, 2014). In order to obtain parallel XY stages with large travel and compact size, leaf spring parallelograms are widely used as prismatic (P) joints. Normally, leaf spring parallelograms are used in couples forming a PP joint to realize kinematically decoupling. According to whether the leaf springs are in the plane of motion or normal to the plane of motion, PP joints can be divided into two types: planar and spatial PP joints. Parallel XY stages using planar or spatial PP joints are defined as planar parallel XY stages (PPXYSs) or spatial parallel XY stages (SPXYSs) in this article.

PPXYSs are the most common XY stages because of its easy manufacturability. In order to obtain large travel of PPXYS, much interest has been focused on structural design. A large number of millimeter-scale PPXYSs were proposed by researchers. Awtar (2004), Trease et al. (2004), Tang et al. (2006), Xu (2012) and Yu et al. (2015) have designed and developed millimeter even centimeter scale PPXYSs. However, there are two main defects of these PPXYSs: (a) the structures of the stages are relatively loose. It is challenging to design an XY stage with a large workspace and a compact physical dimension, simultaneously. Using the modified area ratio (Xu, 2012) whose denominators the actuators' dimensions should be added into, the area ratios of the stages proposed in Awtar (2004), Xu (2012) and Yu et al. (2015) are only about 0.067, 0.069 and 0.026 % respectively; (b) the out-of-plane payload capacity is weak. When applied large out-of-plane payload, the load-stiffening phenomenon (Awtar et al., 2007) emerges in PPXYSs, which would induce nonlinearity and cause the loss of travel range.

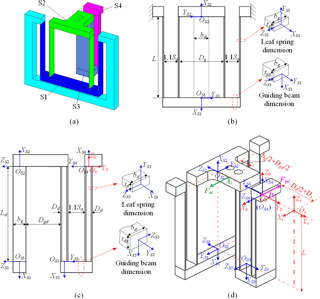
Figure 4 (a) Structural division and dimensions of the leg (b) front view (c) side view and (d) isometric view.

Researchers have been trying to develop a large travel range PXYS with compact size and high out-of-plane payload simultaneously. By stacking two identical planar XY stages, Xu (2014) has tried to use cubical space to obtain large travel and compact size. The area ratio of the stage is significantly improved to 0.13 % and the out-of-plane payload capacity is indeed increased. But the actuation force is also increased by 14 % and the nonlinearity of the stage becomes obvious in the whole travel range. Nevertheless, Xu pointed a possible direction using the cubical space to meet the above conflicting requirements. Since spatial PP joint has the remarkable supporting capacity in the length direction of the leaf spring, Hao (2011), Hao and Kong (2012) and Shang et al. (2015) have figured out using the combination of spatial parallelograms and planar compliant joints to enhance the out-of-plane stiffness. The out-of-plane stiffness is enhanced indeed, but the Shang's stage suffers from relatively short travel range and low area ratio (only 0.002 %) because the spatial parallelogram used in the stage is lumped compliance parallelogram. The stage proposed by Hao and Kong (2012) meets the requirement of large travel range (20 × 20 mm motion range), compact structure (area ratio: 0.14 %) and high out-of-plane payload capacity. But the structural configuration of the stage is too complex to be fabricated monolithically. Therefore, the stage should be an assembly which would induce the assemble error.

Due to the merits of large stroke, no friction and vacuum compatibility, VCM is widely used in CPSs. Therefore, besides the spatial parallel linear compliant mechanism (SPLCM), VCM directly influences the compactness of CPSs. For example, the stage proposed by Xu (2014) actually has a reachable workspace of 20 × 20 mm² with the area ratio of 2.78 %. However, constrained by the commercial VCM, the actual workspace is only about 11.75 × 11.66 mm² and the area ratio drops to only about 0.13 %. Kang et al. (2009) proposed a compact XY scanner with specially designed voice coil motors (VCMs) and leaf springs. The VCMs were embedded in the stage to make the stage compact. However, the supporting structure comprised an assembly of leaf springs, thereby introducing assembly error and deteriorating positioning accuracy. Hence, the matching design VCM is adopted in this paper to achieve the goal of compact size and the VCM and SPLCM should be co-designed in the fully consideration of the coupling relationships between the actuators and the supporting structure.

Inspired by the aforementioned researcher's work, a novel SPXYS is presented in this article. Different from conventional compliant positioning stages, the proposed SPXYS consists of a monolithic SPLCM driven by four matching designed VCMs. The moving platform of the stage is connected to the base by four spatial PP joints, which are enveloped from planar PP joint based on the position space reconfiguration (PSR) method to realize desired centimeter travel range, compact structure, as well as high out-of-plane payload capacity. The matching designed VCMs further ensure the structural compactness. For the sake of realizing the co-design process of the VCM and SPLCM, the design mechatronic model of VCMs matching for the SPXYS, which describes the coupling relationships between the actuators and the supporting structure, is derived by integrated using matrix structural analysis (MSA) and the method of images. The integrated design flow chart including both mechanical and electromagnetic of the whole SPXYS is given based on the key parameter sensitivity analysis. Furthermore, a reified SPXYS is designed and manufactured. The analytical design of the stage is confirmed by experiments. The reified stage has a travel range of 20.4 × 20.6 mm², a compact structure with area ratio 1.87 %, and the resonant frequencies of the two working modes at 22.98 and 21.31 Hz. It can track a circular trajectory with the radius of 4.5 mm. The root mean squares (RMS) tracking error is 2 µm. The positioning resolution is 100 nm. The payload capacity test shows that the reified stage can bear 20 kg out-of-plane payload. The designed SPXYS is suitable for precision positioning applications, such as Ultra-Violet Nanoimprint Lithography (UV-NIL) and soft-contact lithography, which expect a compact compliant positioning stage has not only large travel range, but also large out-of-plane payload carrying capacity without any other auxiliary supporting equipment.

The rest of the article is organized as follows: In Sect. 2, the conceptual design of the SPXYS is introduced based on the kinematic substitution and position spaces method. In Sect. 3, the whole mechatronic model of the proposed SPXYS is derived. In Sect. 4, the integrated design flow chart is established and a reified SPXYS is realized. Performances discussion is conducted by FEA analysis and a series of experiments involving static performance test, dynamic performance test, out-of-plane payload capacity test and tracking performance test in Sect. 5, followed by conclusions in Sect. 6.

2 Conceptual Design of the Novel SPXYS

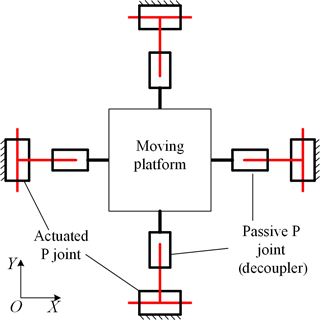
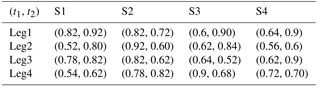
The SPXYS can be obtained based on the kinematic substitution and position spaces method (Hao et al., 2016; Li and Hao, 2016; Li et al., 2016). The conceptual design procedure starts from the design of a rigid body 4-PP decoupled parallel mechanism as shown in Fig. 1. Each PP leg is composed of two P joints in series. The outer P joint connected to the base is actuated and the inner one is passive joint as a decoupler. The motion directions of the two adjacent P joints are perpendicular to each other to achieve kinematical decoupling, which is the necessary condition for two-axis XY parallel mechanisms.

The second step is to replace each traditional P joints in the above rigid body 4-PP decoupled parallel mechanism (Fig. 1) with certain appropriate compliant P joints. In order to increase the motion range, alleviate the cross-axis coupling and geometric stiffening effects, planar double leaf spring parallelograms are selected to construct the basic compliant P joints. Two basic compliant P joints combined together to construct a PP decoupled compliant block.

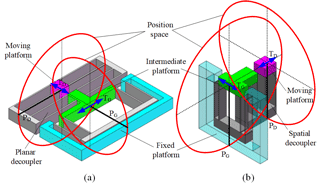
With the goal to produce a compact and monolithic XY compliant stage with the smallest possible size in length and width directions, an improved spatial PP decoupled compliant block (S-PP-DCB) is derived with position spaces concept from the frequently-used planer PP decoupled compliant block (P-PP-DCB). Each P joint in the P-PP-DCB can be simplified to a “black straight line”, one end point of which is fixed while another end point of which has a translation, T_P, represented by a “blue straight line”. The position space of the P joint is designated as a “red circle” about its translation, T_P as shown in Fig. 2. One can identify the most compact PP compliant block with smallest size along its guiding axis and its decoupling axis by arranging P_G parallel to P_D. The compliant block is termed S-PP-DCB due to that P_G, P_D, T_G, T_D are not coplanar.

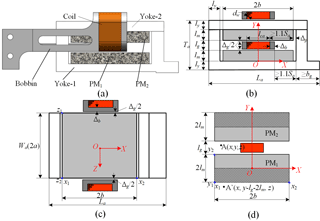
Figure 5 VCM: (a) physical structure, (b) and (c) front and top profile views, and (d) equivalent magnetic structure.

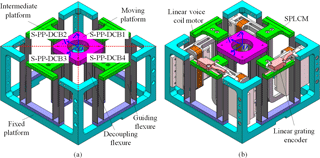
A compact and monolithic fabrication XY positioning stage with large translational travel range and high out-of-plane payload capacity can be produced by combining four S-PP-DCBs, four voice coil motors (VCMs) and two optical linear encoders, as shown in Fig. 3. It can be termed as SPXYS due to the S-PP-DCBs. The mechanical structure of the SPXYS composed of four S-PP-DCBs can be named as spatial parallel linear compliant mechanism (SPLCM). The VCMs are specially designed according to the structure of the SPLCM for compact size, instead of using the existing commercial VCMs to meet the requirements of travel range, peak force and conformity with the inner structure of the SPLCM simultaneously. In order to reduce the number of motor drivers, the two VCMs on the pair of opposite sides of the SPLCM are parallel connected to the same motor driver. Each parallel connected VCM pair provides translational actuating force along guiding axis and some rotational constraint damping along XYZ axes that can suppress the unwanted angular vibration caused by high order rotational modes along XYZ axes without any power consumption. The optical scales of the linear grating encoders are fixed at the intermediate platforms instead of the moving platform and still capable of measuring the position of the moving platform precisely, which is verified in Hao (2017).

3 Mechatronic Model of SPXYS

3.1 SPLCM modeling

The stiffness characteristic of compliant mechanism has direct effects on the workspace, load-carrying capacity, dynamic behavior and positioning accuracy of the entire mechanism (Zhu et al., 2015). The mathematical model of SPLCM is established by Matrix of structural analysis (MSA) (Przemieniecki, 1968). There are four guiding leaf spring flexures and four decoupling leaf spring flexures in each S-PP-DCB. These leaf springs, guiding beams and three platforms form two guiding parallelograms and two basic decoupling parallelograms, denoted as S1–S4, which is shown in Fig. 4a. Details about definitions of the dimensions and coordinate of each parallelogram are shown in Fig. 4b–d.

Each S-PP-DCB can be viewed as four basic parallelograms connected in series. The details of the derivation are already shown in Liu et al. (2017). The relationship of the displacement δ_s at the center of the platform and the external force F_e as well as the actuator forces F_ai is:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left[\sum _{i=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{l}i\mathrm{s}}^T{\left(\sum _{j=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}j}^T\right)}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{l}i\mathrm{s}}\right]{\mathit{\delta }}_{\mathrm{s}}\\ {\displaystyle }& {\displaystyle }={\mathit{F}}_{\mathrm{e}}+\sum _{i=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{l}i\mathrm{s}}^T\left[{\left(\sum _{j=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}j}^T\right)}^{-\mathrm{1}}\right.\\ \text{(1)}& {\displaystyle }& {\displaystyle }\left.\sum _{j=\mathrm{1}}^{\mathrm{2}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{as}j}^T\right]F_{\mathrm{a}i},\end{array}$$

where T_lsj is the transformation matrix from jth basic parallelogram coordinate to the leg coordinate, K_sj is the stiffness of the jth basic parallelogram, T_lis is the transformation matrix from the moving platform to the ith leg, T_asi is the transformation matrix of the ith parallelogram with respect to the location of the actuation force. Actually, the second item on the right-hand side of Eq. (1) is the equivalent external force F_ae generated by actuation force F_ai, which is in form of:

$$\begin{array}{}\text{(2)}& {\mathit{F}}_{\mathrm{ae}}=\sum _{i=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{l}i\mathrm{s}}^T\left[{\left(\sum _{j=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}j}^T\right)}^{-\mathrm{1}}\sum _{j=\mathrm{1}}^{\mathrm{2}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{asj}^T\right]{\mathit{F}}_{\mathrm{a}i}.\end{array}$$

1. When the actuator forces F_ai are equal to zero, the stiffness of the stage related to the displacement δ_s at the center of the platform and the external force F_e is

   $$\begin{array}{}\text{(3)}& {\mathbf{K}}_{\mathrm{s}}={\displaystyle \frac{\partial {\mathit{F}}_{\mathrm{e}}}{\partial {\mathit{\delta }}_{\mathrm{s}}}}=\sum _{i=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{l}i\mathrm{s}}^T{\left(\sum _{j=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}j}^T\right)}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{l}i\mathrm{s}}.\end{array}$$

   According to Liu et al. (2017), the displacement δ_asi of the ith leg at the actuator point caused by the external force F_e is

   $$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\delta }}_{\mathrm{a}i}={\mathit{T}}_{\mathrm{as}\mathrm{2}}\left({\mathit{T}}_{\mathrm{ls}\mathrm{2}}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}\mathrm{1}}{\mathbf{K}}_{\mathrm{s}\mathrm{1}}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}\mathrm{1}}^T+{\mathbf{K}}_{\mathrm{s}\mathrm{2}}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}\mathrm{2}}^T\right)\\ \text{(4)}& {\displaystyle }& {\displaystyle }{\left(\sum _{j=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}j}^T\right)}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{l}i\mathrm{s}}{\mathbf{K}}_{\mathrm{s}}^{-\mathrm{1}}{\mathit{F}}_{\mathrm{e}}.\end{array}$$

   Equation (4) can be utilized to analyze the influences of the external loads applied at the moving platform on the motion of the actuator.

2. When the external forces F_e are equal to zero, the displacement of the stage under actuator forces can be written as:

   $$\begin{array}{}\text{(5)}& {\mathit{\delta }}_{\mathrm{s}}={\mathbf{K}}_{\mathrm{s}}^{-\mathrm{1}}{\mathit{F}}_{\mathrm{ae}}\end{array}$$

   The displacement under actuator forces at one force point is:

   $$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\stackrel{\mathrm{̃}}{\mathit{\delta }}}_{\mathrm{a}i}={\mathit{T}}_{\mathrm{as}\mathrm{2}}\left({\mathit{T}}_{\mathrm{ls}\mathrm{2}}^T{\mathit{T}}_{\mathrm{ls}\mathrm{1}}{\mathbf{K}}_{\mathrm{s}\mathrm{1}}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{s}\mathrm{1}\mathrm{a}i}+{\mathbf{K}}_{\mathrm{s}\mathrm{2}}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{s}\mathrm{2}\mathrm{a}i}\right){\mathit{F}}_{\mathrm{a}i}\\ {\displaystyle }& {\displaystyle }-{\mathit{T}}_{\mathrm{as}\mathrm{2}}\left({\mathit{T}}_{\mathrm{ls}\mathrm{2}}^T{\mathit{T}}_{\mathrm{ls}\mathrm{1}}{\mathbf{K}}_{\mathrm{s}\mathrm{1}}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}\mathrm{1}}+{\mathbf{K}}_{\mathrm{s}\mathrm{2}}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}\mathrm{2}}\right)\\ {\displaystyle }& {\displaystyle }{\left(\sum _{j=\mathrm{1}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{ls}j}^T\right)}^{-\mathrm{1}}\\ \text{(6)}& {\displaystyle }& {\displaystyle }\left(\sum _{j=\mathrm{1}}^{\mathrm{2}}{\mathit{T}}_{\mathrm{ls}j}{\mathbf{K}}_{\mathrm{s}j}^{-\mathrm{1}}{\mathit{T}}_{\mathrm{s}j\mathrm{a}i}{\mathit{F}}_{\mathrm{a}i}-{\mathit{T}}_{\mathrm{l}i\mathrm{s}}{\mathit{\delta }}_{\mathrm{s}}\right)\end{array}$$

   According to Eq. (6), the unexpected displacement of one actuator caused by another actuator, the actuator isolation expressed in form of the input coupling displacement (Jiang et al., 2015), ${\stackrel{\mathrm{̃}}{\mathit{\delta }}}_{\mathrm{a}i-y}$, can be obtained. Based on which, the clearance between the coil and stator of the VCM can be determined.

Meanwhile, the transmission performance from the actuator to the moving platform, named as lost motion, can be obtained by the difference displacement between the actuation point and the moving platform in Eqs. (5) and (6).

According to the Lagrange's equation, the natural resonant frequencies of the stage can be obtained as follows:

$$\begin{array}{}\text{(7)}& f={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}\sqrt{{\displaystyle \frac{{\mathbf{K}}_{\mathrm{s}}}{\mathbf{M}}}},\end{array}$$

where M is the mass matrices in which the mass of the VCMs' movers is also included, M = diag {M_x, M_y, M_z, J_x, J_y, J_z} and M_x=M_y, J_x=J_y because of the symmetric structure of the stage.

Since K_s is the function of structure parameters of the stage, the relationship between structural parameter and resonant frequencies can be revealed similarly by numerical method.

Table 1 The desired key performance indicators of the example case.

Figure 6 Actuator design area.

Figure 7 Relationships of the SPXYS's parameters.

Figure 8 Results of the parameter sensitivity analysis: (a) travel range, (b) area ratio, (c) first resonant frequency, and (d) out-of-plane payload.

3.2 VCM modeling

VCMs are selected as the actuators because of their large travel range, lubrication-free property, and vacuum compatibility. The VCM adopted in this article is designed in a dual permanent magnet (PM) configuration as shown in Fig. 5a. The specific dimensions of the actuator are shown in Fig. 5b and c. In order to reach the full travel range of the SPLCM, the dimensions of the VCM should meet the following constraints:

$$\begin{array}{}\text{(8)}& \left\{\begin{array}{l}{L}_{\mathrm{a}}\ge \mathrm{2}b+\mathrm{2}{\mathrm{\Delta }}_{\mathrm{p}}+l_{\mathrm{y}}+b_{\mathrm{g}}\\ W_{\mathrm{a}}=\mathrm{2}a\\ T_{\mathrm{a}}=\mathrm{2}{l}_{\mathrm{y}}+\mathrm{2}{l}_{\mathrm{m}}+l_{\mathrm{g}}\\ \mathrm{2}b\ge l_{\mathrm{ca}}+\mathrm{2.2}{S}_{\mathrm{a}}+\mathrm{2}{\mathrm{\Delta }}_{\mathrm{b}}-\mathrm{2}{\mathrm{\Delta }}_{\mathrm{p}}\end{array}\right.,\end{array}$$

where L_a, W_a and T_a are the length, width and thickness of the VCM's stator; 2a, 2b and l_m are the length, width and thickness of the PM, respectively; b_g is the width of the guiding leaf spring; l_y and l_g are the thickness of the yoke and the air gap; l_ca is the axial length of the coil; Δ_p is the clearance between the permanent magnet and the yoke; Δ_b is the thickness of the bobbin.

Accordance with the conservation of magnetic flux, the constraint of the yoke's thickness that the yoke's thickness should be larger than the saturated thickness can be expressed as

$$\begin{array}{}\text{(9)}& l_{\mathrm{y}}\ge {\displaystyle \frac{B_{\mathrm{g}}\cdot \mathrm{2}b}{\mathrm{2}{B}_{\mathrm{s}}}}\end{array}$$

Since the permeability of the yoke of the VCM is relatively high and the configuration of the VCM is symmetric, the method of images is used to obtain the analytical model of the gap's field (Furlani, 2001) and the equivalent magnetic structure is shown in Fig. 5d. The vertical component B_gz of the gap magnetic flux density due to equivalent PM₁ with the dimension of 2a × 2b × 2l_m shown in Fig. 5d is provided in Eq. (10).

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{B}_{\mathrm{g}z}\left(x,y,z\right)={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}{M}_{\mathrm{s}}}{\mathrm{4}\mathit{\pi }}}\sum _{k=\mathrm{1}}^{\mathrm{2}}\sum _{n=\mathrm{1}}^{\mathrm{2}}\sum _{m=\mathrm{1}}^{\mathrm{2}}{\left(-\mathrm{1}\right)}^{m+n+k}\arctan \\ \text{(10)}& {\displaystyle }& {\displaystyle }\left[{\displaystyle \frac{\left(x-x_{\mathrm{m}}\right)\left(z-z_n\right)}{\left(y-y_k\right)}}g\left(x,y,z;x_n,y_{\mathrm{m}},z_k\right)\right]\end{array}$$

where M_s represent the magnetization, and μ₀ is the magnetic permeability of air,

$$\begin{array}{}\text{(11)}& \left\{\begin{array}{l}g\left(x,y,z;x_n,y_{\mathrm{m}},z_k\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{{\left(x-x_n\right)}^{\mathrm{2}}+{\left(y-y_{\mathrm{m}}\right)}^{\mathrm{2}}+{\left(z-z_k\right)}^{\mathrm{2}}}}}\\ x_{\mathrm{m}}={\left(-\mathrm{1}\right)}^m\cdot b\begin{array}{ll}& y_k={\left(-\mathrm{1}\right)}^k\cdot l_{\mathrm{m}}\end{array}\begin{array}{ll}& z_n={\left(-\mathrm{1}\right)}^n\cdot a\end{array}\end{array}\right.\end{array}$$

According to the magnetic symmetry of a single PM, the vertical component B_gz of the gap magnetic field at the point A (x, y, z) due to PM₂ is equal to the value of the gap magnetic field at point A^′(x, y, z-l_g-2l_m) due to PM₁. Hence the vertical component B_gzs generated by the two PMs is

$$\begin{array}{}\text{(12)}& B_{\mathrm{g}z\mathrm{s}}=B_{\mathrm{g}z}\left(x,y,z\right)+B_{\mathrm{g}z}\left(x,y-l_{\mathrm{g}}-\mathrm{2}{l}_{\mathrm{m}},z\right)\end{array}$$

The effective coil length, l_ce, is related to the width of PM, W_a, and the number of turns in the coil, n_l × n_c, and is expressed as:

$$\begin{array}{}\text{(13)}& l_{\mathrm{ce}}=n_{\mathrm{l}}\cdot n_{\mathrm{c}}\cdot W_{\mathrm{a}}\end{array}$$

where n_l is the layer number of the coil, and n_c is the number of turns per layer of the coil, given as

$$\begin{array}{}\text{(14)}& \left\{\begin{array}{l}{n}_{\mathrm{l}}=\mathrm{fix}\left({\displaystyle \frac{\mathrm{2}(l_{\mathrm{g}}-{\mathrm{\Delta }}_{\mathrm{g}})+\left(\sqrt{\mathrm{3}-\mathrm{2}}\right)d_{\mathrm{w}}}{\sqrt{\mathrm{3}{d}_{\mathrm{w}}}}}\right)\\ n_{\mathrm{c}}=\mathrm{fix}(l_{\mathrm{ca}}/d_{\mathrm{w}})\end{array}\right.\end{array}$$

In Eq. (14), d_w is the diameter of the wire, Δ_g is the clearance between the coil and the stator which should be carefully designed according to Eq. (5), in case the coil contacts with the stator. l_ca is the axial length of the coil and fix(x) is the rounding function for the numeric value x.

Hence, the Lorentz force f_i generated by the ith VCM is

$$\begin{array}{}\text{(15)}& f_i=B_{\mathrm{g}z\mathrm{s}}\cdot i_i\cdot l_{\mathrm{ce}i}\begin{array}{ll}& \left(i=\mathrm{1},\mathrm{\cdots },\mathrm{4}\right)\end{array}\end{array}$$

where i_i and l_cei is the current and effective length of the ith coil in the gap.

Figure 9 Flow chart of the SPXYS design.

Figure 10 Experiment setups of the SPXYS for (a) stiffness test and (b) motion characteristic test.

Figure 11 Stiffness test result.

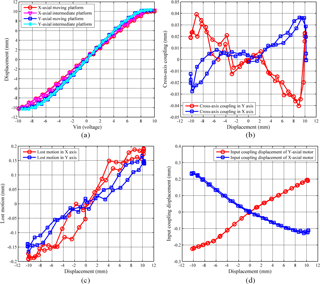
Figure 12 (a) Travel range test and its corresponding (b) cross-axis coupling, (c) lost motion and (d) the actuator isolation.

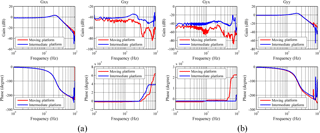
Figure 13 Frequency response of the stage: (a) X-axis frequency response and its Y-axial coupling response and (b) Y-axis frequency response and its X-axial coupling response.

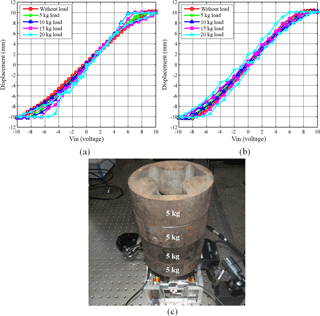
Figure 14 Out-of-plane payload test: (a) X-axial test results, (b) Y-axial test results and (c) 20 Kg payload test photo.

Figure 15 Tracking performance on a radius of 4.5 mm circular trajectory at 0.1 Hz: (a) tracking results and (b) tracking errors.

Figure 16 Resolution test of the stage.

4 Deign Method and Case Study

Section 3 focused on the mechatronic modeling of the SPXYS including both the SPLCM and VCMs, while this section mainly concentrates on illustrating how to design the SPXYS by establishing a design flow chart and an example case study. The desired key performance indicators of the reified example SPXYS are tabulated in Table 1.

4.1 Design constraints

4.1.1 Geometric constraint

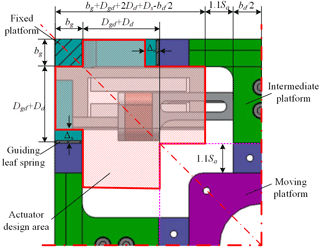
In order to obtain high area ratio, the actuators in the stage are conformal-designed and make the most of the inner space of the SPLCM. The design area of the VCM, namely the geometric coupling relationship, is shown in Fig. 6.

Since the VCM used in the stage is linear motor, the stator has to be in a rectangle shape. Hence, the stator of the VCM should be designed within the following dimensions:

$$\begin{array}{}\text{(16)}& \left\{\begin{array}{l}{L}_{\mathrm{a}}\le b_{\mathrm{g}}+D_{\mathrm{gd}}+\mathrm{2}{D}_{\mathrm{d}}+D_{\mathrm{s}}-b_{\mathrm{d}}/\mathrm{2}\\ W_{\mathrm{a}}\le L_{\mathrm{g}}-\mathrm{2}{\mathrm{\Delta }}_{\mathrm{b}}-\mathrm{2}{l}_{\mathrm{g}}\\ T_{\mathrm{a}}\le D_{\mathrm{gd}}+D_{\mathrm{d}}-{\mathrm{\Delta }}_{\mathrm{s}}\end{array}\right.\end{array}$$

where Δ_s is the clearance between the stator and the outer guiding leaf spring, which is intended to provide enough space for the outer guiding leaf spring's maximum deflection, S_a∕2, and given as

$$\begin{array}{}\text{(17)}& {\mathrm{\Delta }}_{\mathrm{s}}\ge S_{\mathrm{a}}/\mathrm{2}+t_{\mathrm{g}}-l_{\mathrm{y}}+\mathrm{3.5}\end{array}$$

4.1.2 Performance constraint

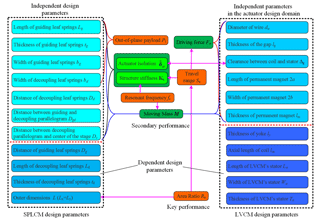
Besides the geometric coupling relationships, there are some coupling relationships associated with the performances of the SPLCM and VCMs including the key performances listed in Table 1 and the secondary performances (e.g., the driving force, stiffness, actuator isolation and moving mass of the stage), which is depicted in Fig. 7. The key performances normally depend on the secondary performances, while the secondary performances are directly related to the design parameters.

Key performances

Since the out-of-plane payload is sustained by the leaf spring in its length direction, the dimensions of guiding and decoupling leaf springs have direct effect on the out-of-plane payload capacity. The out-of-plane payload capacity of the stage depends on the critical buckling load of secondary parallelograms of guiding or decoupling parallelograms, namely S2 or S4 in Fig. 5. There are eight leaf springs of guiding or decoupling parallelograms under compressive load, so the maximum out-of-plane payload P_L max is limited by the minor one, given as

$$\begin{array}{}\text{(18)}& P_{\mathrm{L}\max }\le min\left({\displaystyle \frac{\mathrm{2}{\mathit{\pi }}^{\mathrm{2}}E{I}_{z\left(g\right)}}{n_{\mathrm{st}}{L}_{\mathrm{g}}^{\mathrm{2}}}},{\displaystyle \frac{\mathrm{2}{\mathit{\pi }}^{\mathrm{2}}E{I}_{z\left(\mathrm{d}\right)}}{n_{st}{L}_{\mathrm{d}}^{\mathrm{2}}}}\right)\end{array}$$

where E is the Young's modulus, I_z is the Z-axial area moment of inertia and equal to bt³/12, n_st is the safety factor, normally over 2, L_g and L_d is the lengths of the guiding and decoupling leaf springs.

The length of the stage, according to the specific dimensions in Fig. 4, is

$$\begin{array}{}\text{(19)}& L_x=L_y=\mathrm{2}{b}_{\mathrm{g}}+\mathrm{2}{D}_{\mathrm{gd}}+\mathrm{4}{D}_{\mathrm{d}}+\mathrm{2}{D}_{\mathrm{s}}+\mathrm{2.2}{S}_{\mathrm{a}}\end{array}$$

Hence, the area ratio of the stage is given as:

$$\begin{array}{}\text{(20)}& R_{\mathrm{a}}=\mathrm{4}{S}_{\mathrm{a}}^{\mathrm{2}}/{\left(\mathrm{2}{b}_{\mathrm{g}}+\mathrm{2}{D}_{\mathrm{gd}}+\mathrm{4}{D}_{\mathrm{d}}+\mathrm{2}{D}_{\mathrm{s}}+\mathrm{2.2}{S}_{\mathrm{a}}\right)}^{\mathrm{2}}\end{array}$$

The relationship of the resonant frequency f_r with the stiffness K_s and moving mass M has been clearly illustrated in Eq. (7).

Secondary performance

The travel range S_a depends on the driving force F_a and the stiffness K_s according to Eq. (5). The maximum driving force F_{a_max} needed in the stage should be larger than the sum of elastic force and inertia force. The maximum driving force F_{a_max} provided by the actuator is determined by the gap magnetic flux density B_gz, the effective length l_ce and the maximum current i_max, which associates with all the independent parameters of the actuator.

The stiffness, cross-axis coupling, lost motion and actuator isolation are depended on all of the independent parameters of the SPLCM.

The actuator isolation should be taken into special consideration in designing the actuator. The clearance Δ_g between the coil and stator should be two or three times larger than the input coupling displacement ${\stackrel{\mathrm{̃}}{\mathit{\delta }}}_{\mathrm{a}i-y}$, that is,

$$\begin{array}{}\text{(21)}& {\mathrm{\Delta }}_{\mathrm{g}}\ge (\mathrm{3}\sim \mathrm{4}){\stackrel{\mathrm{̃}}{\mathit{\delta }}}_{\mathrm{a}i-y}\end{array}$$

In the contrast, the clearance Δ_g should be as small as possible during the actuator design according to Eq. (14), so that it can make the coil as long as possible and obtain as large driving force as possible.

4.1.3 Other constraints

In order to ensure the linearity of the stage, the small deflection condition should be satisfied by choosing appropriate length L of the leaf spring as follows

$$\begin{array}{}\text{(22)}& L\ge \mathrm{10}{y}_{max}=\mathrm{5}{S}_{\mathrm{a}}\end{array}$$

where y_max is the maximum deflection of each leaf spring, $y_{\max }=S_{\mathrm{a}}/\mathrm{2}$.

Based on the maximal shear theory, the thickness t of the leaf spring is given by

$$\begin{array}{}\text{(23)}& t\le {\displaystyle \frac{\mathrm{2}{\mathit{\sigma }}_y{L}^{\mathrm{2}}}{\mathrm{3}{S}_{\mathrm{f}}E{y}_{max}}}={\displaystyle \frac{\mathrm{4}{\mathit{\sigma }}_y{L}^{\mathrm{2}}}{\mathrm{3}{S}_{f}E{S}_{\mathrm{a}}}}\end{array}$$

where σ_y is the yeilding stress, S_f is the safe factor.

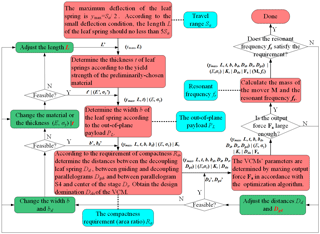
4.2 Sensitivity analysis and design flow chart

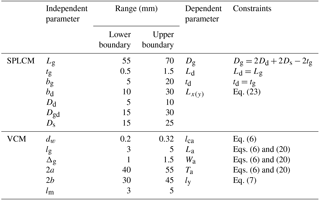
Since the relationships between design parameters and performances are relatively complicated, it is necessary to analyze the sensitivities of the key design parameters. The independent design parameters in the SPLCM are investigated to verify their influences on the primary performances since the independent design parameters of the VCM are constrained within the design domain. The design parameters of the VCM would be determined to maximize the driving force by means of the genetic algorithms. The variation ranges and relationships of the design parameters are presented in Table 2.

Table 2 Variation ranges and relationships of the design parameters of the stage.

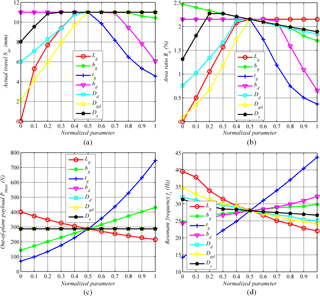
The initial values of the parameters of the stage are the respective medians of their variation ranges. The boundary limits of each parameter are normalized into [0, 1]. The normalized parametric analysis (Xu, 2014) results of SPLCM and VCM are presented in Fig. 8.

As shown in Fig. 8, the change trends of travel range and area ratio are almost identical, whereas the change trends of travel range S_a and resonant frequency f_r are opposite. Therefore, design optimization should maximize one performance indicator on the premise of ensuring the sufficiency of the others. The three most important parameters influencing the travel range, area ratio and resonant frequency of the stage are the length and thickness of the leaf spring and the distance between the guiding and decoupling parallelograms; while the three most important parameters for out-of-plane payload are the length, width and thickness of the leaf springs. Among the parameters, the most sensitive parameters are the length and thickness of the leaf springs; the secondary parameter is the distance between the guiding and decoupling parallelograms; then the width of the leaf springs and lastly the rest of the parameters. Hence, the design of the stage should begin with the parameters, which have the clear relationship with the design goals, and try to meet the design goals as much as possible and adjust the parameters in accordance with the sensitivity descending order until the design goals are all satisfied. The specific design flow chart of the stage is shown in Fig. 9.

4.3 Parameter determination of reified SPXYS

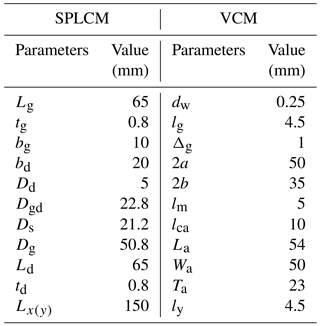
According to the proposed design procedure and manufacturability requirements, the travel range S_a is designed to 10 mm (a total motion range is 20 mm), and the other parameters of the structure are designed as the results in Table 3. The dimensions of the stage are 150 × 150 × 86 mm³. The material of the stage is aluminum alloy (7075-T6) with Young's modulus E=7.2 × 10¹⁰ Pa, yield strength σ_y=5.05 × 10⁸ Pa, density ρ=2810 kg m⁻³. And the PMs are the NdFeB (type: N50M) with the residual magnetic flux density of 1.41 T.

5 FEA Verification and Experimental Test

In order to verify the analytical model and inspect the characteristics of the proposed SPXYS, a series of FEA and experimental studies on four primary performances tests as well as the secondary performances, e.g., the stiffness and actuator isolation, have been carried out.

The prototype of the SPXYS was fabricated by two main working procedures: milling process and wire electrodischarge machine (wire-EDM). The large stress generated by the milling process led to serious deformations of leaf springs during the wire-EDM process. The actual thicknesses of the prototype's leaf springs listed in Table 4 are quite different with the design value.

Hence, in order to verify the correctness of the theoretical model and eliminate the influence of the manufacturing error, the analytical and FEA models adopt the actual thickness in this section. The analytical and FEA performances are in good agreements with each other as tabulated in Table 5, which indicates that the theoretical model is validated.

Figure 10 shows the experimental setups for the stiffness and motion characteristic tests of the SPXYS. In the stiffness test, a contact displacement sensor (Mitutoyo LGF-110L) with resolution 1 µm and a strain pressure transducer (VISTE VS16) with resolution 0.5 N is utilized to measure the displacement and force experienced by the moving platform while the micrometer is used as a loader to generate force and displacement. In the motion characteristics test, two linear grating encoders (MicroE Systems Mercury II 6500) with 50 nm resolution are used as the semi-closed loop sensors measuring the displacement of the intermediate platform. And two types of the external laser displacement sensors (Keyence LB72: 20 mm measuring range with the repeatability 2 µm and LK-G30: 10 mm measuring range with the repeatability 50 nm) are utilized to obtain the lost motion between the moving and intermediate platform and verify the position precision of the stage, respectively. A semi-practical simulation system of dSPACE (ds1103) is utilized as a precise controller, which acquires the feedback data of sensors and outputs control commands.

5.1 Static performance test

In order to verify the correctness of the theoretical modeling, the static performances of the stage, such as stiffness, travel range, lost motion, actuator isolation and area ratio would be tested first.

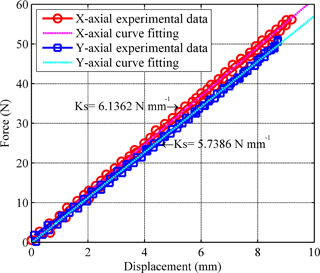
The stiffness test results and the curve fitting results obtained by the method of linear least square (LLS) are shown in Fig. 11. The experimental errors with respect to theoretical stiffness are less than 1.5 %, which further indicates that the stiffness modeling is correct.

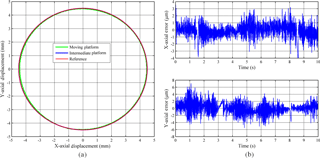
The test results of travel range, lost motion and actuator isolation, as well as area ratio were obtained by applying a triangle-wave signal with amplitude of 10 V to the VCMs. Only one axis is under driven and the other one is set free. As Fig. 12a shown, the non-load travel ranges of the SPXYS in X-axis direction and Y-axis direction are 20.4 and 20.6 mm and the design target of travel range is realized, which further confirm the correctness of theoretical modeling. The stage possesses planar dimensions of 150 × 150 mm². Thus, the area ratio of the stage is 1.87 %, which is the most compact stage among related works.

As shown in Fig. 12b, the maximum cross-axis coupling displacement is about 0.04 mm, which indicates that the stage is well decoupled. Besides, the cross-axis coupling relationship can be depressed by adopting decoupling control. The maximum lost motions shown in Fig. 12c are less than 2 % of the travel range, and X-axial lost motion is a little larger than that of Y-axis, which may be caused by the stiffness difference in the two axes. The maximum input coupling displacement, representative of actuator isolation, in Fig. 12d are 0.266 mm and 0.267 mm and meets the design constraint in Eq. (23).

5.2 Dynamic performance test

To investigate the dynamic performance of the developed stage, a chirp signal with amplitude of 1V and frequency ranging from 0.1 to 200 Hz is applied to the VCM. The inputs are denoted as V_x and V_y (in volts), and the outputs are D_x and D_y (in millimeters). The frequency responses of $G_{xx}=D_x/V_x$, $G_{xy}=D_y/V_x$, $G_{yx}=D_x/V_y$ and $G_{yy}=D_y/V_y$ are shown in Fig. 13. So, G_xy and G_yx represent for the dynamic coupling of the stage.

Table 3 Main design parameters of the stage.

Table 4 The actual thicknesses of the leaf springs.

Table 5 FEA results of the stiffness-equivalent model.

The two working mode resonant frequency of the stage is 22.98 and 21.31 Hz in X-axis and Y-axis respectively, which is close to the theoretical and FEA results with the error about 10 %. The dynamic responses of the moving platform and intermediate platform are almost identical before 60 Hz, which indicates that the decoupling leaf spring has relative large transmission stiffness and paves the way of half-closed loop control. Figure 13 shows that the magnitudes of the coupling terms G_xy and G_yx are about 40 dB less than that of G_xx and G_yy, which are small enough to be neglected and indicate kinematic decoupling of the stage. The close loop bandwidth (−3 dB) of the stage is 60.5 Hz in the two working directions.

5.3 Out-of-plane payload capacity test

In order to determine the out-of-plane payload capacity, a variety of payloads (0–20 kg) were applied on the load clamp and the results are depicted in Fig. 14a and b. Figure 14c is a test photo of 20 Kg out-of-plane payload. As the load increases, the travel ranges of the two working axes slightly change, which sufficiently implies that SPXYS has high out-of-plane payload capacity and could meet the payload requirements of UV-NIL's positioning stage. The flat curves at the ends of the test curves, which are also found in the travel range test shown in Fig. 12a, are caused by the structural limitations of both SPLCM and VCMs. The stiffness of the stage slightly decreases with the increment of the payloads, which makes it easy for the VCMs to drive the moving platform to reach the max travel range and causes the longer flat curves.

5.4 Tracking performance test

To further study the positioning characteristics of the stage, the tracking performance and resolution of the stage are tested by applying a circular trajectory and a consecutive step, respectively. The tracking trajectory is a circle of radius 4.5 mm at the frequency of 0.1 Hz, as shown in Fig. 15. It is noted that the stage can follow the large travel range command with the RMS (root of mean square) tracking errors about 0.98 and 1.6 µm in X-axis and Y-axis, which makes it superiority in large travel precision applications. The trajectory of the moving platform is non-circular inside of the intermediate platform's trajectory, which may be caused by the different lost motions of the two axes and the coordinate misalignment between the measuring block and the stage.

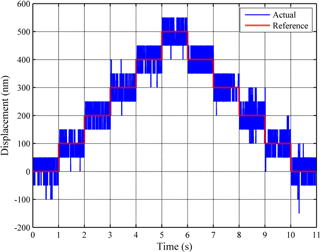
Figure 16 shows the experimental results of the 100 nm consecutive steps positioning, which indicates that the positioning resolution is about 100 nm.

6 Conclusions

A novel monolithic compliant spatial parallel XY stage with centimeter travel range, compact size and high out-of-plane payload capacity has been proposed. The mechatronic model of the whole SPXYS involving both SPLCM and VCMs is derived for mechanism and electromagnetic matching design. The integrated design flow chart is established and a reified SPXYS is realized for case study. It can be concluded from both the analytical and experimental results that, the prototype of the SPXYS has a large range of motion up to 20.4 × 20.6 mm with a relatively compact structure only 150 × 150 mm, which makes the area ratio of the stage about 1.87 %. The stage exhibits a relatively high precision including well-constraint cross-axis decoupling displacement less than 0.04 mm, and acceptable lost motion below 2 % of the primary motion. The stage also shows a good dynamic characteristic with the resonant frequencies about 22.98 and 21.31 Hz along X-axis and Y-axis, and a capability of sustaining about 20 Kg out-of-plane payload without decreasing the travel range, which makes it superiority in space-limited precision applications with high payload capability requirement. The developed stage exhibits a good capability of tracking a circle of radius 4.5 mm with RMS tracking error of 2 µm and possessing a relatively high resolution of 100 nm.