Trajectory planning for manipulator grasping with obstacle avoidance and visual occlusion in a complex environment

Manipulators often face challenges of reliable trajectory planning under limited visibility. This paper proposes an obstacle avoidance grasping path planning method based on monocular vision. A multi-layer neural network model is to recognize target features, enabling rapid environmental perception. The environment topology is segmented using convex hulls, and multi-objective optimization is applied to achieve agile obstacle avoidance for the robot. The main contributions include the following: (1) an improved mask region convolutional neural network architecture is constructed to predict features under limited information, and (2) an innovative path planning strategy that combines Gaussian sampling with Hopfield neural networks is developed to improve the non-dominated sorting genetic algorithm. The algorithm achieves an identification accuracy of 99.50 % in complex scenarios, and the optimized trajectory shows improvements in smoothness and motion efficiency by approximately 60 % and 10 %, respectively. Through simulations and experiments, the significant effects on enhancing the robot's operability in complex environments have been validated.

1 Introduction

Vision servo-based robotic arm grasping systems are widely used in many industrial and agricultural fields, including logistics sorting, object grasping and fruit picking (Konstantinidis et al., 2023). Obstacles in randomly occluded scenes, such as naturally growing branches and leaves, and randomly placed packages bring challenges to the accurate grasping of target objects (Othman et al., 2018).

In visual recognition, Shang et al. (2014) proposed a monocular method for measuring the position of a translationally one-dimensional object containing at least two known feature points only. Zhang et al. (2023) developed a weighted voting integrated regression algorithm for predicting the dimensional deviation of the workpiece imaging. Pan et al. (2020) implemented object height measurement using a depth camera based on the Sobel operator and a low-pass filter, but it requires high hardware cost and computational overhead. The above studies mainly focus on single object geometric feature recognition. To further improve the recognition ability in complex scenes, Li et al. (2024) presented a canopy labeling method for U-Net and lightweight segmentation networks. The method introduces a lightweight backbone network. It greatly reduced the computational complexity required for large-scale canopy segmentation. For this purpose, Yoon and Han (2023) pointed out a box object detection method, which can realize depth information extraction in occluded scenes but with lower accuracy. Zhao et al. (2023) developed a 3D novel end-to-end parcel picking model designed to segment stacked objects hierarchically. Yu et al. (2019) constructed a strawberry fruit auto-detection model based on Mask R-CNN, demonstrating better generality and robustness when handling overlapping and hidden fruits. Ge et al. (2023) designed a visual strategy for grasping occluded objects, fusing color information and recoded depth information to improve accuracy in object segmentation.

Figure 1 Monocular imaging schematic.

In vision servo grasping and planning, Auh et al. (2024) applied a sequence planning method based on A* search algorithm applied to unload randomly stacked different boxes from a logistics container. Fan et al. (2022) established a PF-RRT* algorithm based on target bias strategy for UAV trajectory planning in cluttered environments. In Cong et al. (2020), based on the second generation of the non-dominated genetic algorithm (NSGA-II), the new population obtained from taboo search was added to the elite retention strategy to achieve the optimization of the solution efficiency. As the scenes of robotic applications become increasingly complex and unstructured, the demand for simultaneous optimization of multiple objectives (≥3) is increasing, while algorithms such as A* and RRT* are currently mostly used for single-objective solving, so path planning methods based on optimization strategies such as ant colony (Saenphon et al., 2014), genetic (Elhoseny et al., 2018), or particle swarm (Tavana et al., 2016) have been widely used.

In these methods, the third-generation non-dominated genetic algorithm (NSGA-III) is based on reference point selection by optimizing the selection and update mechanism of the population. The convergence efficiency of the algorithm and the global optimization solution search ability are improved. In the field of agriculture, Li et al. (2023) solved the path optimization problem based on the NSGA-III algorithm to achieve the goal of harvesting kiwi fruit. In the industrial field, Wang et al. (2021) employed the RRT* algorithm to search for collision-free paths and optimized the problem using the NSGA-III algorithm to solve a bi-objective path planning problem for arc welding. Xiao et al. (2020) combined the NSGA-III algorithm with a penalty function to solve a multi-objective optimization problem with constraints.

In conclusion, complex scene grasping under visual occlusion requires the integrated use of image recognition and motion planning. A deep neural network model is constructed for feature prediction with visual occlusion to realize accurate target localization. The Hopfield neural network and Gaussian sampling strategy are designed to optimize and improve the Non-dominated Sorting Genetic Algorithm (NSGA-III), enhancing the efficiency of path planning and the global optimization solving ability, which can realize autonomous target recognition and intelligent grasping in complex scenes.

Figure 2 ECA module structure diagram.

Figure 3 RFP add feature structure diagram.

2 Complex scene perception based on machine vision

Two monocular industrial cameras were used with an Improved Mask R-CNN to identify the geometric features of obstacles. The goal is to enhance machine vision's ability to perceive complex scenes.

Figure 4 Improved Mask R-CNN framework.

Figure 5 Schematic diagram of robotic arm running path.

Figure 6 Collision risk diagram of a robotic arm.

2.1 Recognize and extract geometric features of obstacles

2.1.1 Extracting geometric features of obstacles

Features of obstacles are extracted using the holistically nested edge detection (HED) (Xie and Tu (2015)) instead of the traditional Canny edge detection algorithm due to the better efficiency and accuracy. The contour of a rectangular body consists of scattered discrete points, and Hough transform is also used. The circle on the upper surface of the cylinder is generally elliptical in the image plane of the monocular camera. Ellipse fitting consists of two processes: one is the detection of the ellipse's edge points, and the other is ellipse fitting to the edge points to determine the center of the ellipse.

2.1.2 Monocular imaging principle

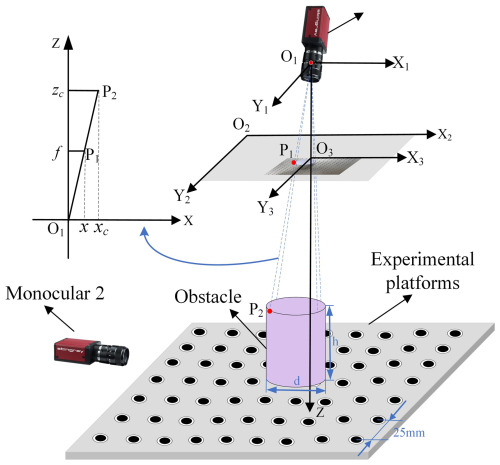
The geometric relationship of monocular industrial camera imaging is shown in Fig. 1, assuming that there exists any P₂ in the space and its projected position in the image is P₁. According to the similarity theorem of the right triangle, the following formula can be obtained:

$$\begin{array}{}\text{(1)}& x={\displaystyle \frac{x_{\mathrm{c}}}{z_{\mathrm{c}}}}f,y={\displaystyle \frac{y_{\mathrm{c}}}{z_{\mathrm{c}}}}f,\end{array}$$

where f is the focal length, x and y are the image coordinates of P₁, and x_c, y_c, and z_c are the coordinates of space P₂ under the coordinate system of the industrial video camera.

According to the camera imaging model, the projection transformation from the world coordinate system to the image coordinate system can be expressed by Eq. (2), where the image coordinates $[u,v,\mathrm{1}{]}^{\mathrm{T}}$ are obtained by linear transformation of the inner reference matrix A and the outer reference matrix [R t]. The input is the $[X,Y,Z,\mathrm{1}{]}^{\mathrm{T}}$ of the world coordinates and  s is the scale factor.

$$\begin{array}{}\text{(2)}& s\left(\begin{array}{c}u\\ v\\ \mathrm{1}\end{array}\right)=\mathbf{A}\left[\mathbf{R}\mathit{t}\right]\left(\begin{array}{c}X\\ Y\\ Z\\ \mathrm{1}\end{array}\right)\end{array}$$

The matrix A is then calibrated according to Zhengyou (1999).

2.2 Recognition of object visual occlusion

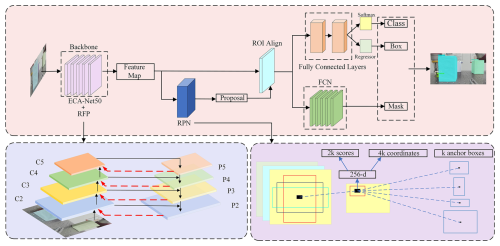
Mask R-CNN (He et al., 2017) is an instance segmentation algorithm. In this study, we proposed an Improved Mask R-CNN based on ECA-Net50 (Wang et al., 2020) and the Recursive Feature Pyramid (RFP) (Qiao et al., 2021), as shown in Fig. 4.

2.2.1 Backbone network ECA-Net50

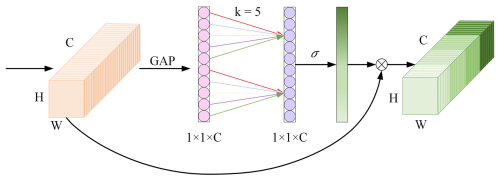
ECA-Net50 uses ResNet50 as the backbone network framework and adds the Efficient Channel Attention (ECA) module after each residual block, as shown in Fig. 2.

Table 1 Geometric information of the cuboid.

Table 2 Geometric information of the cylinder.

Aggregated features are obtained by global average pooling (GAP). Channel weights are generated using a one-dimensional convolution operation with kernel size k, and weights are mapped to 0–1 intervals by the sigmoid function. The calculation can be represented in Eq. (3).

$$\begin{array}{}\text{(3)}& k=|t{|}_{\text{odd}}={\left|{\displaystyle \frac{{\log }_{\mathrm{2}}\left(C\right)}{\mathit{\gamma }}}+{\displaystyle \frac{b}{\mathit{\gamma }}}\right|}_{\text{odd}},\end{array}$$

where $|t{|}_{\text{odd}}$ denotes the closest odd number to t, γ and b are set to 2 and 1, and C represents the number of channels of input features.

2.2.2 Recursive feature pyramid

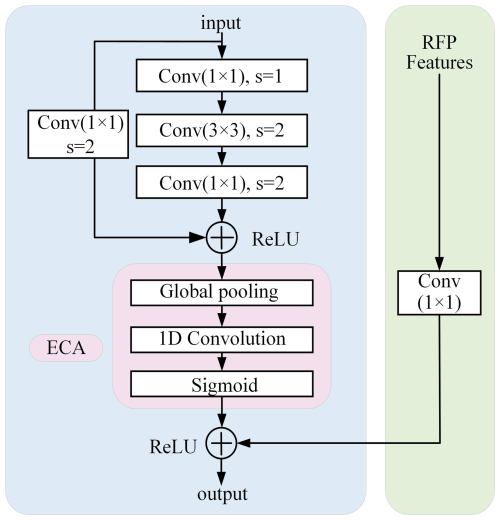
RFP adds feedback connections that can be better adapted to the detection or segmentation tasks. The RFP adds the transformed features to the first block of each stage of ECA-Net50, as shown in Fig. 3.

The calculation process can be formulated as

$$\begin{array}{}\text{(4)}& f_i=F_i(f_{i+\mathrm{1}},x_i)x_i=B_i(x_{i-\mathrm{1}},R_i(f_i\left)\right),\end{array}$$

where f_i is the feature map output from the current stage i, F_i denotes the top-down FPN operation, B_i represents the stage i of the bottom-up backbone network, and R_i(f_i) indicates the feedback processing.

3 NSGA-III algorithm based on Hopfield neural network with Gaussian sampling improvement (HG-NSGAIII)

This paper proposes an improved algorithm, HG-NSGAIII, based on the NSGA-III. The algorithm combines Hopfield neural network and Gaussian sampling to achieve global path planning and multi-objective optimization with more than three objectives, which improves the efficiency and accuracy of manipulator trajectory planning.

3.1 Construction of the optimization objective function

The safe operation of manipulators needs to take into account the mechanical performance, environmental characteristics and application requirements, but the increase of constraints and their mutual conflicts will increase the computational difficulty. For this reason, it is necessary to transform the environmental information and operation goals into executable objective functions to construct the optimization space. In this paper, we focus on three constraints: path length, obstacle threat and path smoothness.

3.1.1 Path length

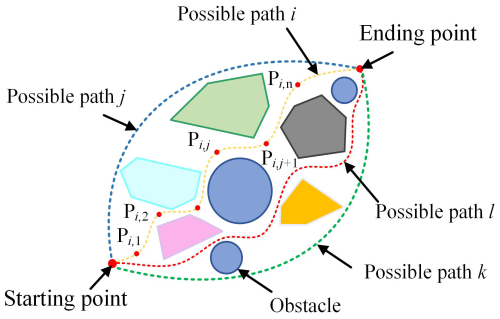
The path length is a key factor that affects the indexes of robotic arm operation efficiency and energy consumption. The jth point on the ith path is denoted as $P_{i,j}=(x_{i,j},y_{i,j},z_{i,j})$, as shown in Fig. 5.

The sum of the lengths of all discrete path points is defined as the path cost function:

$$\begin{array}{}\text{(5)}& f_{\mathrm{1}}=\sum _{j=\mathrm{0}}^{n-\mathrm{1}}\Vert P_{i,j}\to P_{i,j+\mathrm{1}}\Vert ,\end{array}$$

where $\Vert P_{i,j}\to P_{i,j+\mathrm{1}}\Vert$ denotes the Euclidean distance between two neighboring path points P_i,j and $P_{i,j+\mathrm{1}}$, calculated as

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\displaystyle }& {\displaystyle }\Vert P_{ij}\to P_{ij+\mathrm{1}}\Vert =\\ {\displaystyle }& {\displaystyle }\sqrt{\begin{array}{l}(x_{i,j+\mathrm{1}}-x_{i,j}{)}^{\mathrm{2}}+(y_{i,j+\mathrm{1}}-y_{i,j}{)}^{\mathrm{2}}+(z_{i,j+\mathrm{1}}-z_{i,j}{)}^{\mathrm{2}}.\end{array}}\end{array}\end{array}$$

Figure 7 Feature extraction of the cylinder and cuboid.

Table 3 Improved Mask R-CNN, U-Net and YOLOv8 comparison.

Figure 8 Comparison of Improved Mask R-CNN and U-Net.

3.1.2 Threats of obstacles

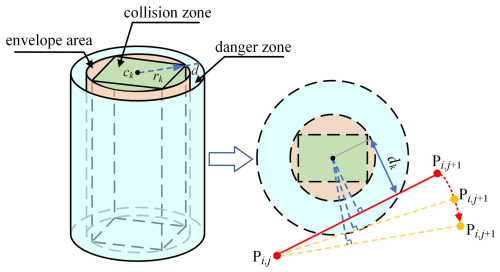
To measure the risk of collision, the obstacle is enclosed in a circle using the envelope method, with the center and radius of the circle denoted as c_k and r_k, as shown in Fig. 6. The region with a radius of r_k+d is defined as the dangerous region. When the trajectory of the manipulator moving from P_i,j to the next path point $P_{i,j+\mathrm{1}}$ traverses through the hazardous region, the manipulator is in possible danger, so obstacle threat cost can be described as

$$\begin{array}{}\text{(7)}& f_{\mathrm{2}}=\sum _{j=\mathrm{0}}^{n-\mathrm{1}}\sum _{k=\mathrm{1}}^m{T}_k(P_{i,j}\to P_{i,j+\mathrm{1}}),\end{array}$$

where k is the number of obstacles and T_k is a segmented function on the distance d_k between the obstacles and local path $P_{i,j}\to P_{i,j+\mathrm{1}}$ with the following expression:

$$\begin{array}{}\text{(8)}& T_k=\left\{\begin{array}{ll}\mathrm{0}& (d_k>d+r_k)\\ {\mathit{\gamma }}_{\mathrm{c}}\left(\right(d+r_k)-d_k)& (r_k<d_k\le d+r_k)\\ +\mathrm{\infty }& (d_k\le r_k),\end{array}\right.\end{array}$$

where γ_c=25 represents the penalty coefficient.

3.1.3 Path smoothness

The degree of smoothing of the robotic arm path affects the operating efficiency of the robotic arm and the stability of the robotic arm. The combined force calculation function is

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }{\mathit{F}}_{a+\mathrm{1},a}={\displaystyle \frac{P_{i,a+\mathrm{1}}-P_{i,a}}{\Vert P_{i,a+\mathrm{1}}-P_{i,a}\Vert }}\text{(10)}& {\displaystyle }& {\displaystyle }{f}_{\mathrm{3}}=\sum _{j=\mathrm{1}}^{n-\mathrm{1}}({\mathit{F}}_{j+\mathrm{1},j}+{\mathit{F}}_{j-\mathrm{1},j}),\end{array}$$

where ${\mathit{F}}_{a+\mathrm{1},a}$ is the result of normalizing the forces at the path point P_i,a to the direction of the path point $P_{i,a+\mathrm{1}}$.

3.2 HG-NSGAIII algorithm

This paper adopts Gaussian sampling strategy to generate initial paths. The sampling points are concentrated near the expansion points to reduce uncertainty and avoid local optimization. This optimizes the initial population of NSGA-III and improves efficiency of the algorithm.

Figure 9 Image prediction with complex occlusion.

Figure 10 3D view of robotic arm trajectory planning in different scenes.

3.2.1 Specific flow of the HG-NSGA-III algorithm

Step 1:

A monocular industrial camera is used to extract geometric features of obstacles to build a map of the working environment of the robotic arm.

Step 2:

Establish the starting position of the robotic arm as the QS and the end as QE.

Step 3:

A path planning algorithm based on Hopfield neural network algorithm is used to obtain a collision-free initial path P_init.

Step 4:

The initial path is equally divided into N path points based on equal step length T and path length L_init.

Step 5:

A Gaussian sampling algorithm is used to generate N×num candidate points near N path points to form a candidate region.

Step 6:

Randomly select the path points from each candidate region to generate an initial population P_t containing dim paths.

Step 7:

The NSGA-III is used to perform multi-objective optimization on the initial population P_t in Step 6.

Figure 11 Top view of robotic arm trajectory planning in different scenes.

Table 4 Solving path length and time and number of nodes.

3.2.2 Nonlinear interpolation based on five-times B-splines

With the advantages of a high degree of freedom and good local modifiability, B-splines are widely used in robot path planning. The initial trajectory P_optimize is interpolated by fifth-order B-splines. Given n+1 control points $C{P}_{\mathrm{0}},C{P}_{\mathrm{1}},\mathrm{\cdots },C{P}_n$ and node sequence $u=\mathit{\{}{u}_{\mathrm{0}},u_{\mathrm{1}},\mathrm{\cdots },u_m\mathit{\}}$, the five-times B-spline function for the ith path can be constructed as follows:

$$\begin{array}{}\text{(11)}& P_{i,j}=\sum _{j=\mathrm{0}}^n{N}_{j,\mathrm{5}}\left(u\right)C{P}_{j}u\in [\mathrm{0},\mathrm{1}],\end{array}$$

where P_i,j is the path point and N_j,5(u) is the B-spline basis function, which can be obtained by the Cox–de Boor recursive method.

At the start and end points, the velocity and acceleration are all 0, $v_{t_{\mathrm{0}}}=\mathrm{0}$ and $v_{t_n}=\mathrm{0}$. The velocity is the first-order derivative of the position, and according to the B-spline theory, the first-order derivatives of the p-times B-spline curves are still p-1-times B-spline curves:

$$\begin{array}{}\text{(12)}& v_{i,j}={\displaystyle \frac{\mathrm{d}{P}_{i,j}}{\mathrm{d}u}}=\sum _{j=\mathrm{0}}^{n-\mathrm{1}}{N}_{j+\mathrm{1},\mathrm{4}}\left(u\right)D_j,\end{array}$$

where D_j denotes the new control point, and the expression can be described as

$$\begin{array}{}\text{(13)}& D_j={\displaystyle \frac{p}{u_{j+\mathrm{6}}-u_{j+\mathrm{1}}}}(C{P}_{j+\mathrm{1}}-C{P}_j).\end{array}$$

Similarly, its acceleration γ_i,j can be further derived.

4 Simulation and experiment

4.1 Gripping simulation and emulation

4.1.1 Extraction of spatial features of obstacles

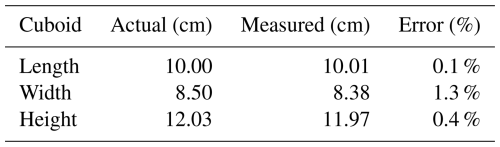
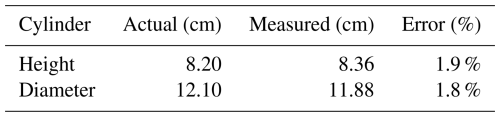
The contour features of the object are extracted, and the results are shown in Fig. 7. The geometric features of the object obtained by monocular measurement and vernier calipers are listed in Tables 1 and 2, respectively.

According to Tables 1 and 2, the error between the actual measurement value and the monocular measurement value is less than 2 %.

Figure 12 Further optimized trajectory.

Figure 13 Trajectory planning experiment platform.

4.1.2 Training and prediction simulation under occlusion

The data in this experiment contain 874 images, divided into training and validation sets according to 8:2. The image extension dataset is expanded by adding noise, increasing or decreasing brightness, rotating the image, etc. We use AutoDL, PyTorch 1.10 and Python 3.7 for training. After 300 rounds, the initial learning rate is 0.008, decreasing to 0.0008 and 0.00008 at the 60th and 200th rounds.

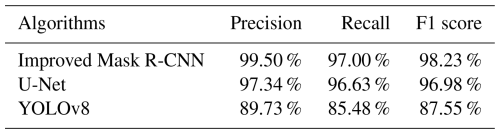
To validate the accuracy of the Improved Mask R-CNN, we compared it with U-Net and YOLOv8. Precision, recall and F1 score were used as evaluation metrics.

$$\begin{array}{}\text{(14)}& {\displaystyle }& {\displaystyle }\text{precision}={\displaystyle \frac{\text{TP}}{\text{TP}+\text{FP}}}\text{(15)}& {\displaystyle }& {\displaystyle }\text{recall}={\displaystyle \frac{\text{TP}}{\text{TP}+\text{FN}}}\text{(16)}& {\displaystyle }& {\displaystyle }\text{F1 score}={\displaystyle \frac{\mathrm{2}\times \text{precision}\times \text{recall}}{\text{precision}+\text{recall}}}\end{array}$$

where TP, FP and FN denote the sample size of true positive, false positive and false negative cases. The F1 score of the Improved Mask R-CNN is 1.25 % higher than U-Net and 10.68 % higher than YOLOv8, as listed in Table 3.

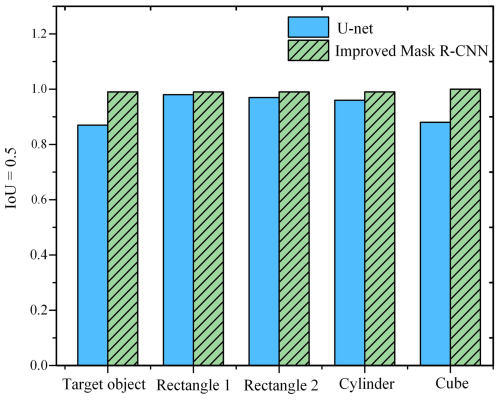
In the area of computer vision, IoU is an important evaluation metric commonly used in the task of image segmentation to measure the degree of overlap between the predicted results and the actual annotations.

$$\begin{array}{}\text{(17)}& \text{IoU}={\displaystyle \frac{\text{area}(U_{\mathrm{p}}\cap U_{\text{gt}})}{\text{area}(U_{\mathrm{p}}\cup U_{\text{gt}})}},\end{array}$$

where area(U_p∩U_gt) denotes the area of the intersection of the predicted mask and the real mask, and area(U_p∪U_gt) denotes the region of intersection. The results are shown in Fig. 8.

Figure 14 Obstacle avoidance trajectory planning.

Three different scenarios are simulated. Taking scene 2 as an example, the predictions are compared using three visual recognition methods, and the results are shown in Fig. 9. Compared with U-Net and YOLOv8, the Improved Mask R-CNN has better adaptation to occlusion and higher accuracy with complete occlusion.

4.1.3 Autonomous generation of obstacle avoidance paths

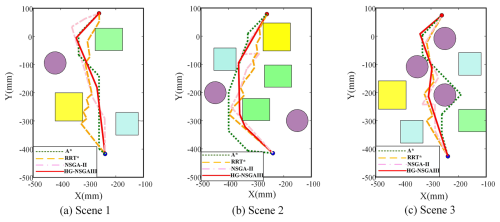
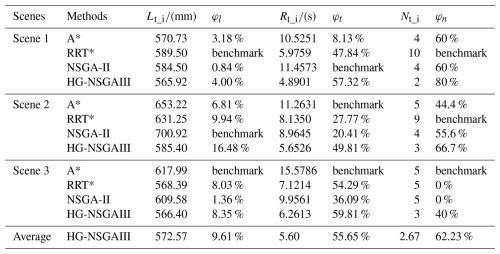
The HG-NSGAIII algorithm is comprehensively compared with the A*, RRT* and NSGA-II to validate the algorithm's convergence efficiency and accuracy. Three different scenes are simulated, as shown in Figs. 10 and 11. In order to further evaluate the performance of each algorithm in terms of computational efficiency and accuracy, the optimization percentages of iteration time, path length and number of nodes are computed, respectively.

$$\begin{array}{}\text{(18)}& \left\{\begin{array}{ll}{\mathit{\phi }}_l={\displaystyle \frac{L_{\text{t\_max}}-L_{t_i}}{L_{\text{t\_max}}}}\times \mathrm{100}\mathit{\%}& \\ {\mathit{\phi }}_t={\displaystyle \frac{R_{\text{t\_max}}-R_{t_i}}{R_{\text{t\_max}}}}\times \mathrm{100}\mathit{\%}& (i=\mathrm{1},\mathrm{2},\mathrm{\dots },\mathrm{4})\\ {\mathit{\phi }}_n={\displaystyle \frac{N_{\text{t\_max}}-N_{t_i}}{N_{\text{t\_max}}}}\times \mathrm{100}\mathit{\%},& \end{array}\right.\end{array}$$

where L_{t_i}, R_{t_i} and N_{t_i} represent path length, iteration time and the number of nodes optimized by the algorithms of this category. L_{t_max}, R_{t_max} and N_{t_max} symbolize the maximum value (benchmark of comparison) in which φ_l, φ_t and φ_n represent the percentage-related comparison data optimized by different algorithms, respectively, as listed in Table 4.

It can be seen that in the process of finding the global optimal solution, the HG-NSGAIII algorithm shortens the path length by 10 % on average compared with other algorithms and improves the computational efficiency by 55.65 %. The minimum number of inflection points is generated, which indicates that the HG-NSGAIII algorithm generates smoother and more continuous paths.

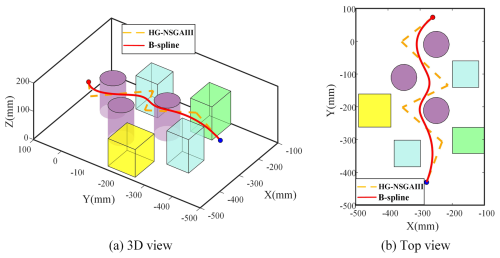
The initial optimal path generated under the constraints is characterized by poor geometric properties, and the trajectory often has sharp points that make it difficult to satisfy the C3 continuity. To improve the smoothness, the initial optimized path based on HG-NSGAIII is nonlinearly fitted with five-times B-splines, and the trajectory through the secondary optimization is shown in Fig. 12.

4.2 Experiment analysis

4.2.1 Construction of the experimental platform

In this paper, experiments were conducted based on a 6 DoF manipulator. The algorithm was programmed and operated on a computer, and the control systems of the manipulator arm and the computer were connected through the Internet. The air pump, AC2010 duplex and solenoid valve are connected to the pneumatic hand gripper. The solenoid valve is controlled by the computer to open and close the pneumatic hand gripper. The information is transmitted between the industrial camera and the computer, and the experimental platform is shown in Fig. 13a and b.

4.2.2 Autonomous capture of complex scenes

The experimental process of autonomous grasping by a robotic arm in a complex scene is shown in Fig. 14. The blue dashed line indicates the path not traveled by the robotic arm, and the yellow solid line indicates the path traveled by the robotic arm.

5 Conclusions

For target grasping scenarios with multiple occlusions, this paper proposes a trajectory planning method that combines the Improved Mask R-CNN and the HG-NSGAIII, and the main conclusions are as follows:

1. The monocular industrial camera extracts features of objects with different shapes. The error in the measured length is within 2 %, meeting the production requirements.

2. With the Improved Mask R-CNN algorithm, the accuracy of recognizing occluded objects in complex scenes is as high as 99.5 %, and the average accuracy of segmentation of various types of objects is 99 % (IoU=0.5), which shows good accuracy and precision.

3. HG-NSGAIII has a strong global optimization solution search capability in complex scenes. Compared with RRT*, A* and NSGA-II, the NSGA-III algorithm based on the Gaussian sampling-improved Hopfield neural network is able to guarantee global convergence and obtain better optimized solutions. The motion efficiency and trajectory smoothness can be improved by about 9.61 % and 62.23 %, respectively.