Adaptive chaos control of a humanoid robot arm: a fault-tolerant scheme

Safety in human–robot physical interaction and cooperation is of paramount interest. In this work, a human–humanoid interaction and cooperation scenario is considered. The robot arm is controlled by a proportional derivative (PD) controller in combination with an inherently fault-tolerant sliding-mode controller. During normal operation, if any of the joints of the robot arm develops a fault, the robot arm end effector may go into chaotic and dangerous motion. If such a scenario occurs, it poses a serious danger to the human in the loop as well as the robot. In this paper, an adaptive chaos sliding-mode controller is proposed to recover the tracking of the end effector when a fault occurs in any of the actuators. This tracking restoration is very important to complete a safety-critical task. The proposed scheme may help in addressing some safety issues arising from a joint failure, allowing it to finish the task at hand and stop it from going into a dangerous situation. The scheme is tested in simulation on the four degrees of freedom (DOF) model of the Bristol Robotics Laboratory (BRL) robot arm. Simulation results show efficient tracking recovery after a joint actuator failure. The controller demonstrated good performance in terms of tracking and stability when dealing with different joint actuator failures.

1 Introduction

Although robots have been around for decades, their integration into social environments and physical interaction with human beings is still relatively new and very challenging. For researchers and robot manufacturers, the main concern with robot–human interaction is ensuring the reliability of the robot and the safety of the human (Khan et al., 2018, 2010b; Li et al., 2023). In human–robot physical interaction tasks, the human is inside the robot's motion space, and any random and uncontrolled move can be catastrophic. Therefore, in the social domain, various layers of safety are required to protect humans in the vicinity of the robot.

In recent years, the subject of safe robot–human interaction has received its share of attention, and a vast amount of literature has been compiled on the subject. Among the main control algorithms and methods are those based on compliance control and cooperative control. However, with all the care being taken, robots are still prone to sudden failures in their actuators and/or sensors, which poses a great challenge, as many safety related issues arise from these faults. For instance, when one of the joint actuators of a robot arm fails completely, the robot arm starts to move haphazardly and chaotically, which could harm the humans with whom the robot interacts.A human–robot cooperative scenario, such as passing a cup of a hot coffee or a sharp object to a human, can make the situation even worse in the face of actuator failure. For these reasons and many other concerns, the research topic of robotic actuator fault detection and isolation has become quite popular among roboticists and researchers around the world. It is of paramount importance to minimize safety issues that arise due to faulty actuators in human–robot cooperation (HRC) and physical human–robot interaction (pHRI). In the event of an actuator failure, it may be vital to safely complete the task at hand or safely degrade without causing any safety hazard (English and Maciejewski, 1996; Paviglianiti et al., 2010; Saleem et al., 2023; Anjum et al., 2022).

Actuators and sensors are essential elements of any robotic system, whether it is meant for social or industrial applications. Any deficiencies in these components may lead to a degradation in the performance of the robot and even its instability (Khan et al., 2017; Van et al., 2023; Islam et al., 2023). Some of the most common of these failures are locked joint faults, free swinging, actuator saturation, and ramp actuator faults (McIntyre et al., 2005; Visinsky et al., 1994; Xiao et al., 2020; Zahaf et al., 2020).

Recently, the work by Wang and Zhang (2018) presented a fuzzy logic-based controller for actuator failures. In this work, active (controller with online actuator adaptive strategies to address unknown actuator faults) and passive techniques (preprogrammed controller) are used to deal with actuator failures. In the work by Chen et al. (2017), a fault control method for networked cooperation systems or robots was proposed. Their control scheme does not require fault detection or isolation, but it effectively deals with partial actuator or communication link faults using an adaptive control strategy for which a detailed stability of the proposed algorithm was provided. In the work by Kashiri et al. (2016), a position control strategy was proposed for a manipulator with a passively compliant actuator, which can be used to deal with unexpected scenarios. For example, a robot may be able to deal with unplanned or unintended physical interactions with the environment or power failures of actuators, or it can demand position discontinuities.

In addition to control schemes developed specifically to be fault-tolerant, some existing control methods are implicitly fault-tolerant including some sliding-mode schemes (Edwards et al., 2000; Yan and Edwards, 2007). According to Mekki et al. (2015), sliding-mode controllers can effectively deal with unmatched uncertainties and structural deficiencies. A direct consequence of this property is that it helps reduce the effect of actuator faults or failures. A fault-tolerant sliding-mode-based controller was proposed in the work by Freddi et al. (2018a) (see also Freddi et al., 2018b) with an application to a dual robot arm system. The developed scheme was shown to have the ability to detect joint torque faults and compensate for them at the kinematic level to improve the tracking performance of the controller. Another important fault-tolerant control scheme was proposed in the work by Ma and Yang (2016). This controller is model based and deals with both actuator and sensor faults simultaneously using an adaptive sliding-mode observer that estimates the parameters related to these faults.

Researchers have also considered dissipative control schemes that deal with the influence of actuator faults. For instance, a controller was proposed in the research work by Tao et al. (2017) aimed at Takagi–Sugeno fuzzy systems with Markov jumping parameters. The theoretical analysis was supported by a robot arm's simulation results dealing with actuator faults.

More recently, many researchers such as Zhang et al. (2023), Sacchi et al. (2023), and Van et al. (2023) have proposed various schemes to deal with faults in actuators. However, most of these techniques are complex, and especially the reinforcement learning and other neural-network-based schemes are not very suitable due to their high degree of complexity and high computational requirements. In many instances, those schemes can only be applied if high computational power is available. In most cases, these techniques have been applied only to one to two degrees of freedom systems.

As mentioned above, sliding-mode control schemes are inherently fault-tolerant and very popular for controlling robot manipulators despite excessive chattering and aggressive behavior. However, alone it cannot fully overcome the actuator fault. The adaptive chaos control element combined in this work with the sliding-mode controller has shown greater efficiency overcoming chaotic behavior and recovering the tracking.

In this paper, a redundant robot arm controlled by a sliding-mode controller to follow a desired trajectory is considered. If for some reason one of the actuators is subjected to a fault during operation and becomes free swinging, then the end effector ends up following a chaotic trajectory as depicted in simulation results shown (for instance, see Fig. 5). In order to overcome this unsafe and unpredictable chaotic behavior, an adaptive chaos controller is proposed in this work to control the chaotic behavior and recover the tracking performance using the remaining joints. The proposed controller employs an energy dissipative element (Tereshko, 2009). This energy dissipative chaos controller is completely model-free and its gain parameters are tuned by means of adaptive laws taking into account the instantaneous position and velocity errors. To the best of the author's knowledge, this adaptive energy dissipative tangent hyperbolic-based function, with auto-tuning of the gains and combined with the sliding-mode controller, is novel and has not been attempted previously in the literature.

If we compare the scheme proposed here with the literature cited above, the scheme here is very simple but very effective for redundant humanoid robot arm joints actuators failure. The assumption of redundancy is very realistic in this case, as the majority of the humanoid robotic arms are multi-redundant anthropomorphic arms. For instance, in our case, the robot arm has seven joints; i.e., shoulder flexion, shoulder abduction, humeral rotation, elbow flexion, wrist rotation, wrist abduction, and wrist pronation. For simplicity, only four joints were employed here in this work. This overall scheme exploits the inherent robustness and fault tolerance of the sliding-mode controller and the simplicity of the energy dissipative element. Hence, the main reasons for proposing this energy altering technique to control the chaotic motion of the robot arm after joint failure are its simplicity, ease of implementation, model-free nature, and excellent tracking and stabilizing performance. This makes it a good contender for dealing with actuator faults.

The remainder of the paper is arranged as follows. In Sect. 2, the problem formulation of the paper is presented in which the general structure of a robot's dynamics is described. In Sect. 3, Cartesian sliding-mode control of the humanoid BERT2 arm is presented. An adaptive energy dissipative element has been combined with the Cartesian sliding-mode controller to form a novel, robust, and fault-tolerant control scheme. In Sect. 4, simulation results are included and discussed. Finally, Sect. 5 concludes the paper with some remarks.

2 Problem formulation

The BERT2 robot arm contains seven degrees of freedom (DOF) (Fig. 3). Of these, only four are employed in this study, namely, the shoulder flexion (joint 1), shoulder abduction (joint 2), humeral rotation (joint 3), and elbow flexion (joint 4). The robot arm dynamic model can be described as

$$\begin{array}{}\text{(1)}& \mathit{\eta }\left(\mathit{\theta }\right)\ddot{\mathit{\theta }}+\mathbf{\Psi }(\mathit{\theta },\dot{\mathit{\theta }})+{\mathit{\mu }}_{\mathit{\theta }}\left(\mathit{\theta }\right)={\mathit{\tau }}_{\mathit{\theta }},\end{array}$$

where $\mathit{\theta }\in {\mathbb{R}}^{\mathrm{4}\times \mathrm{1}}$ is a vector containing the four joint angles, $\mathit{\eta }\in {\mathbb{R}}^{\mathrm{4}\times \mathrm{4}}$ is the arm's positive definite and symmetric inertia matrix, $\mathbf{\Psi }\in {\mathbb{R}}^{\mathrm{4}\times \mathrm{1}}$ is the Coriolis/centripetal vector representing viscous and nonlinear damping forces, ${\mathit{\mu }}_{\mathit{\theta }}\in {\mathbb{R}}^{\mathrm{4}\times \mathrm{1}}$ is the gravity vector, and ${\mathit{\tau }}_{\mathit{\theta }}\in {\mathbb{R}}^{\mathrm{4}\times \mathrm{1}}$ is the input torque vector.

Cartesian space is modeled as​​​​​​​

$$\begin{array}{}\text{(2)}& {\mathit{\eta }}_{\text{cc}}\left(\mathit{\theta }\right){\ddot{X}}_{\text{cc}}+{\mathbf{\Psi }}_{\text{cc}}(\mathit{\theta },\dot{\mathit{\theta }})+{\mathit{g}}_{\text{cc}}\left(\mathit{\theta }\right)=\mathit{\rho },\end{array}$$

where ${\mathit{\eta }}_{\text{cc}}=(J_{\mathit{\theta }}{\mathit{\eta }}^{-\mathrm{1}}{J}_{\mathit{\theta }}^T{)}^{-\mathrm{1}}$ is the Cartesian inertia matrix. The Cartesian centripetal/Coriolis force vector is given by ${\mathbf{\Psi }}_{\text{cc}}={\overline{J}}_{\mathit{\theta }}^T\mathbf{\Psi }-{\mathit{\eta }}_{\text{cc}}{\dot{J}}_{\mathit{\theta }}\dot{\mathit{\theta }}$.

The Cartesian gravity force vector is given by ${\mathit{g}}_{\text{cc}}={\overline{J}}_{\mathit{\theta }}^T{\mathit{\mu }}_{\mathit{\theta }}$. The end-effector Cartesian force is $\mathit{\rho }={\overline{J}}_{\mathit{\theta }}^T{\mathit{\tau }}_{\mathit{\theta }}$. The vector, $X_{\text{cc}}=[x,z{]}^T$, is the Cartesian position in the X–Z plane. The Jacobian matrix, J_θ, is derived from the kinematics X_cc=H(θ), where H is the transformation, i.e., $J_{\mathit{\theta }}=\mathit{\delta }{X}_{\text{cc}}/\mathit{\delta }\mathit{\theta }$.

The Cartesian velocity vector is given by ${\dot{X}}_{\text{cc}}=J_{\mathit{\theta }}\dot{\mathit{\theta }}$. The pseudo-Jacobian inverse (inertia-weighted) matrix, ${\overline{J}}_{\mathit{\theta }}$, is given by ${\overline{J}}_{\mathit{\theta }}={\mathit{\eta }}^{-\mathrm{1}}{J}_{\mathit{\theta }}^T(J_{\mathit{\theta }}{\mathit{\eta }}^{-\mathrm{1}}{J}_{\mathit{\theta }}^T{)}^{-\mathrm{1}}$ (Khatib, 1987; Nemec and Zlajpah, 2000).

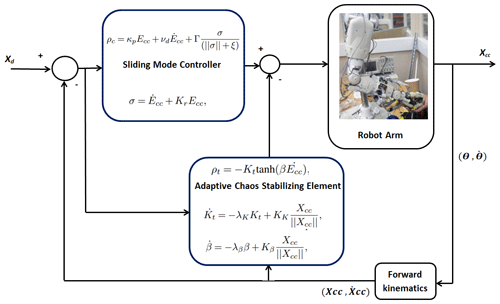
In this work a fault-tolerant sliding-mode controller is proposed which employs an adaptive (self-tuned) energy-dissipating element to deal with an actuator fault in the humanoid robot during a human–robot physical interaction.

3 Controller for the robot arm

In this section, first a sliding-mode scheme for the dynamics of the end effector in Eq. (2) to deal with uncertainty is presented. Then, an adaptive scheme which is based on the sliding-mode controller is constructed to address the chaos control problem.

3.1 Sliding-mode control

In this section, the Cartesian space controller for the BERT2 robot arm to follow a certain desired trajectory is described. The Cartesian proportional derivative (PD) sliding-mode controller (SMC) is employed here due to the robustness and fault-tolerant nature (Ahmad Taher Azar, 2015; Shtessel et al., 2014; Ahmad et al., 2023; Anjum et al., 2022; Saleem et al., 2023). The SMC scheme is considered to be one of the most widely used nonlinear control techniques due to its remarkable characteristics including high accuracy, robustness, and ease of tuning and implementation. As mentioned before, sliding-mode controller has gained a lot of popularity lately for controlling robotic manipulator due to its proven fault tolerance.

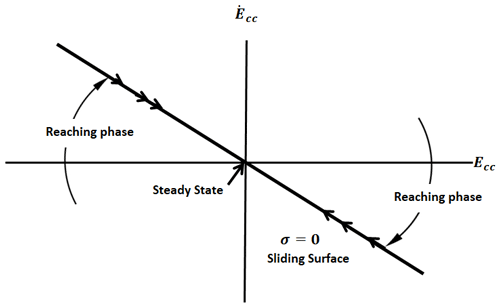
A sliding-mode controller is normally designed in two parts. First, a sliding surface is defined in the system's state space to satisfy certain design specifications as shown in Fig. 1. Then, a suitable control law is selected with the aim of making the system states attracted to this surface.

Figure 1 Sliding surface and sliding variable.

For controlling the BERT2 humanoid robot arm, a simple sliding-mode control is employed (Ahmad Taher Azar, 2015; Shtessel et al., 2014). As mentioned above, four joints of the BERT2 humanoid arm have been employed for simulating this scheme, i.e., elbow flexion, shoulder flexion, humeral rotation, and shoulder abduction joints.

The SMC Cartesian control law is introduced here. In this paper, the SMC variable σ is defined as (Spurgeon, 2014)

$$\begin{array}{}\text{(3)}& \mathit{\sigma }={\dot{E}}_{\text{cc}}+K_r{E}_{\text{cc}},\end{array}$$

where E_cc denotes the Cartesian position error vector given by $E_{\text{cc}}=[X_{\mathrm{d}}-X_{\text{cc}}]$ with $X_{\mathrm{d}}=[x_{\mathrm{d}},z_{\mathrm{d}}{]}^T$. It should be noted that the robot's end effector with the x–z plane is controlled, and thus the vertical y direction is ignored for simplicity. Also note that the matrix-valued parameter K_r is a full rank 2×2 real matrix with positive elements tuned experimentally or heuristically to achieve the best tracking performance. The control law for the SMC is, then, defined as

$$\begin{array}{}\text{(4)}& {\mathit{\rho }}_c={\mathit{\kappa }}_{\mathrm{p}}{E}_{\text{cc}}+{\mathit{\nu }}_{\mathrm{d}}{\dot{E}}_{\text{cc}}+\mathrm{\Gamma }{\displaystyle \frac{\mathit{\sigma }}{(\Vert \mathit{\sigma }\Vert +\mathit{\xi })}}.\end{array}$$

The scalars ${\mathit{\kappa }}_{\mathrm{p}}\in {\mathbb{R}}^{\mathrm{2}\times \mathrm{2}}$ is the proportional gain, and ${\mathit{\nu }}_{\mathrm{d}}\in {\mathbb{R}}^{\mathrm{2}\times \mathrm{2}}$ is the derivative gain. A large positive value of Γ should be selected to minimize the effect of uncertainty and for robust behavior of the controller (Edwards et al., 2000; Bucak, 2020).

Typically, this SMC control method has a high-frequency switching nature, which in mechanical systems such as the one at hand may lead to an oscillatory behavior (chattering). To minimize this chattering problem, the scalar ξ is introduced in the control law (Shtessel et al., 2014). Since the robot end effector is moved in the X–Z plane only, there are two redundant degrees of freedom. This redundancy can be taken advantage of in order to overcome the chaotic and haphazard behavior arising as a result of actuator failures (Edwards et al., 2000; Bucak, 2020).

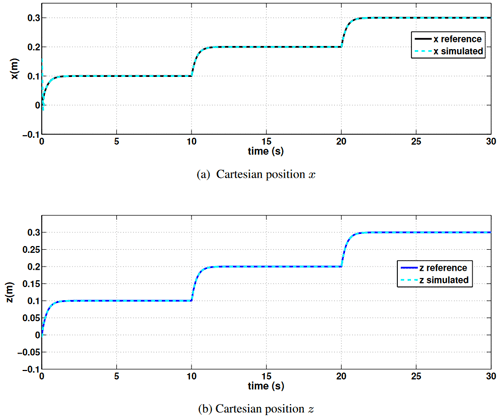
Figure 2 shows the tracking performance of the SM controller (Eq. 4) given a smoothed multi-step desired position X_d(n). The results show a close to perfect tracking of the desired trajectory, which agrees with the well-established results as reported in many studies throughout the related literature.

Figure 2 Cartesian sliding-mode control.

Figure 3 Human–robot physical interaction scenario.

3.2 Adaptive chaos control

Dynamical systems have been used for centuries to model real-life natural phenomena and engineered systems. The stability of these systems has always been a major concern, starting from the works of Lagrange (1736–1813) and Henri Poincaré (1854–1912) on the movement and dynamics of celestial bodies to more cutting-edge and modern complex systems. It was noticed that some dynamical systems exhibited a strange behavior in that they have a bounded solution with a seemingly very unpredictable behavior even if there is a small variation in the initial condition. For this reason, they became known as chaotic systems.

In recent years, chaos has found its way into numerous applications within the robotics field including mobile robots and robotic manipulators (Petavratzis et al., 2023; Yang et al., 2023; Khan et al., 2019). A good summary of some of these applications can be found in the work by Zang et al. (2016).

In this paper, a chaotic motion scenario of the end effector due to the actuator fault is considered. More specifically, the robot arm end effector exhibits a chaotic behavior if one of the four joints under control is subjected to a complete failure. This is easy to observe as will be shown in the next section. In order to overcome this chaotic behavior, a stabilization controller based on the energy altering technique presented in Tereshko (2009) is employed (see also Khan et al., 2019), in conjunction with the SMC control law (Eq. 4).

Khan et al. (2019) have implemented a model reference compliance controller (Khan et al., 2010b, a, 2011a, b, c; Jallani et al., 2011; Herrmann et al., 2016; Khan and Jalani, 2016; Spiers et al., 2016) for master slave robot cooperation to deal with an actuator fault. In contrast to the work by Khan et al. (2019), in this work, the chaos element is adaptive and self-tuned. This makes it more beneficial to deal with the situation more effectively. In addition, this avoids a trial–error process in selection of β and K_t. Moreover, the main control scheme here is sliding-mode-based which is proven to be more fault-tolerant.

It should be noted that a lot of work has been done in the area of chaotic dynamical system stabilization. In fact, the amount of related studies has grown at an exponential rate ever since the late 1980s. Perhaps the most successful and practical of all the proposed controllers are those falling under the energy altering class, which employs experimentally obtained information from the time domain data of the observable variables for guiding the controller. One of the earliest methods is the Ott–Grebogi–Yorke (OGY) method (Ott et al., 1990). For stabilizing an unstable periodic orbit (UPO), the OGY method introduces a little perturbation in the control parameters of the system. The OGY method has been researched extensively and many different forms have been proposed such as the quasi-continuous OGY (Hubinger et al., 1994).

Another controller proposed in the work by Tereshko (2009) employs the principal of energy dissipation, i.e., altering the time-averaged compound kinetic and potential energy of oscillation in order to achieve the desired behavior through a hyperbolic tangent term. This controller is described by the rather simple following formula:

$$\begin{array}{}\text{(5)}& g\left(\dot{X}\right)=K_t\tanh \left(\mathit{\beta }\dot{X}\right),\end{array}$$

with appropriately selected scalars K_t and β>0. The scheme was proposed initially in Tereshko (2009) for typical chaotic oscillatory systems. For instance, Duffing nonlinear oscillators and the Van der pol system were stabilized through this. However, later on, it was demonstrated (Chen et al., 2017) that, in general, other faulty chaotic systems can also be stabilized with the hyperbolic tangent term. The aim here is to add the following feedback term:

$$\begin{array}{}\text{(6)}& {\mathit{\rho }}_t=-K_t\text{tanh}\left(\mathit{\beta }{\dot{E}}_{\text{cc}}\right),\end{array}$$

to the control law (Eq. 4) in order to suppress the chaotic behavior observed when a joint fails.

Figure 4 Block diagram of the scheme.

The main difficulty with the control law (Eq. 6) is the tuning of the parameters K_t and β, as any small change may render the controller useless. The main novelty of this study is the adaptive control of these two parameters in order to ensure the chaotic behavior is minimized. Hence, the overall control law is given by

$$\begin{array}{}\text{(7)}& {\mathit{\rho }}_{\text{acc}}={\mathit{\rho }}_c-K_t\text{tanh}\left[\mathit{\beta }{\dot{E}}_{\text{cc}}\right],\end{array}$$

where the instantaneous parameters K_t and β are calculated based on the adaptive laws

$$\begin{array}{}\text{(8)}& \dot{\mathit{\beta }}=-{\mathit{\lambda }}_{\mathit{\beta }}\mathit{\beta }+K_{\mathit{\beta }}{\displaystyle \frac{X_{\text{cc}}}{\Vert X_{\text{cc}}\Vert }},\end{array}$$

and

$$\begin{array}{}\text{(9)}& {\dot{K}}_t=-{\mathit{\lambda }}_K{K}_t+K_K{\displaystyle \frac{X_{\text{cc}}}{\Vert X_{\text{cc}}\Vert }},\end{array}$$

respectively. Note that the four parameters λ_β, λ_K, K_β, and K_K are appropriately chosen positive scalars. In the next section, simulation results for the adaptive chaos controller given by Eq. (7) are presented and discussed. The block diagram of the overall scheme is shown in Fig. 4.

The main result is stated in the following theorem.

Theorem 1.

The adaptive chaos control law presented in Eq. (7) is capable of recovering the tracking performance of the end effector of the robotic system in Eq. (2) in the presence of a fault.

Proof. The proof follows the standard derivation of sliding-mode control presented in Ahmad Taher Azar (2015) and Shtessel et al. (2014). The convergence of parameters in the adaptive chaos control law in Eq. (7) is derived similarly from Tereshko (2009).

□

The term given by Eq. (6) is inherently stable, as this is an energy dissipative term, while the proportional derivative plus slide mode control's stability has been proved in many publications including the work by Ahmad Taher Azar (2015) and Shtessel et al. (2014).

As mentioned above, sliding-mode control is by nature a fault-tolerant scheme. Adding the energy dissipation term can enhance fault tolerance further. In comparison to the previous work, this is a simple technique to minimize the impact of failure and provide an immediate safeguard against instability which may arise from an actuator fault. Therefore, the aim is to enhance the safety of the human and robot during a human–robot interaction scenario.

4 Results and discussion

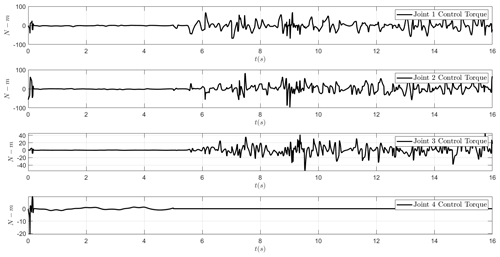
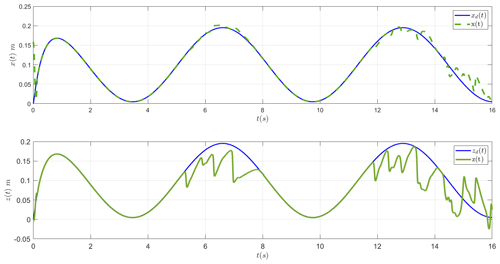
The suggested scheme has been tested in simulation on the Bristol Robotics Laboratory's humanoid BERT robot arm Cartesian control (controlling, x, and z.) employing four joints of the robot arm using the sliding-mode controller only (see Fig. 2). In Fig. 5a, it is shown that if one joint (elbow flexion joint, i.e., joint 4) fails, the robot arm end-effector motion will go into chaos. In most cases, this chaotic motion is bounded. However, it may also become unstable in some cases. Figure 5b shows the phase space which confirms the chaotic nature of the end-effector motion. The control signals (control torques) for all the four joints are shown in Fig. 6. The control torques (for the healthy joints) become very chattery and increase in magnitude after the actuator failure; i.e., the shoulder flexion joint where the control input torque becomes zero.

Figure 5 The Cartesian controller without adaptive chaos scheme for the sinusoidal trajectory case.

Figure 6 Control signal without adaptive chaos control.

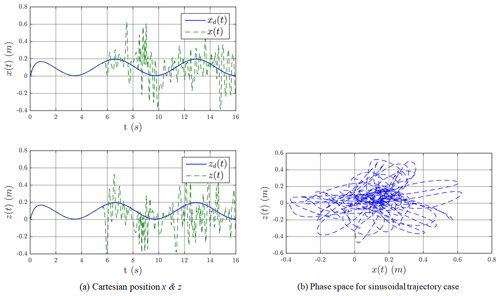
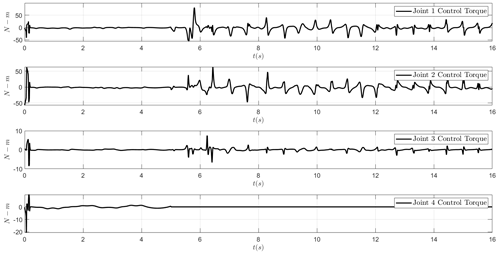
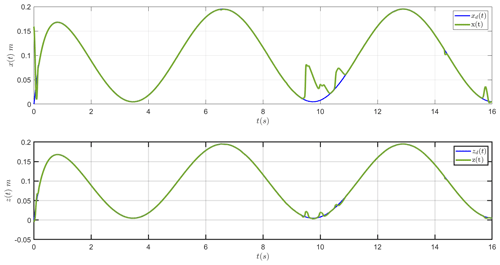
Figure 7a and b show the results when the adaptive chaos controller (sliding mode and energy dissipative element) is in action while a joint fails at t=5 s. It is evident that the adaptive chaos controller recovers the trajectory and the end effector follows the demand trajectory as before in the situation where elbow flexion joint is free swinging due to a fault. The control signals are shown in Fig. 8. It is obvious that the chattering and the magnitude of healthy joints control reduced significantly when adaptive chaos controller elements are combined with the sliding-mode controller. Figure 7c and d shows convergence of the terms β and K_t, respectively.

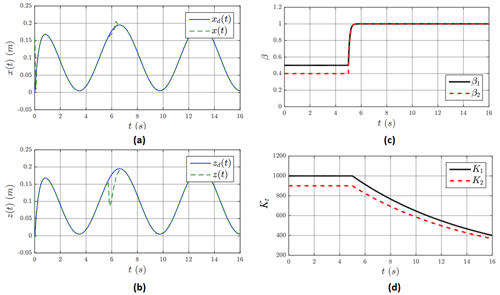
Figure 7 The Cartesian positions x (a) and z (b) for the sinusoidal trajectory case. (c) The evolution of β for the sinusoidal trajectory case. (d) The evolution of K_t for the sinusoidal trajectory case.

Figure 8 Control signal with adaptive chaos control.

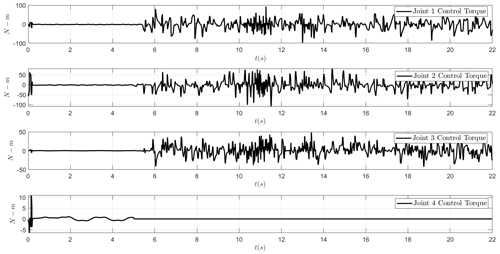
Figure 9a shows the results for a multi-step demand. After an actuator fails, robot arm motion become chaotic (see also Fig. 9b for phase space). Control signals or input torques of the joints are shown in Fig. 10.

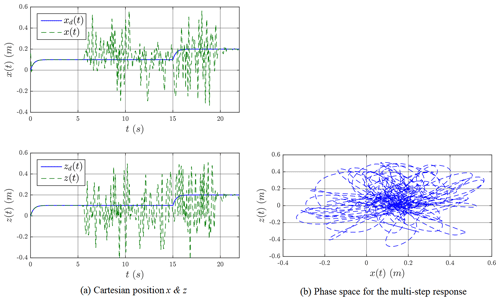
Figure 9 The Cartesian positions x and z without the proposed adaptive chaos control law for the multi-step response.

Figure 10 Control signal without adaptive chaos control.

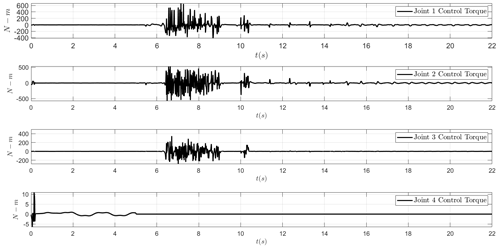
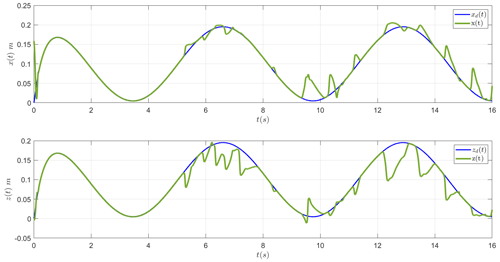
In Fig. 11a and b, results are shown when the adaptive chaos controller is employed after joint failure occurs (See Fig. 9c for β and Fig. 11d for K_t estimates). In this case also, the controllers are capable of recovering the trajectory tracking. The control signals are shown in Fig. 10.

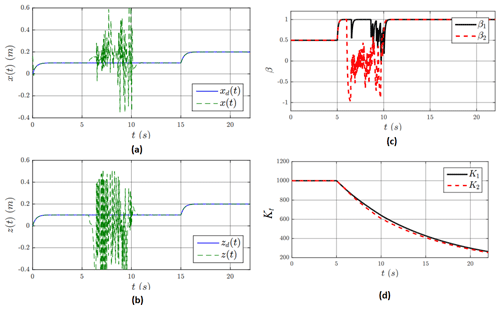
Figure 11 Cartesian position x and z for the multi-step response. (c) The evolution of β for the multi-step case. (d) The evolution of K_t for the multi-step case.

Figure 12 Control signal for the for the multi-step response shown in Fig. 11 above.

Figure 13 Faulty shoulder flexion joint.

Figure 14 Faulty shoulder abduction joint.

Figure 15 Faulty shoulder flexion and shoulder abduction joints.

The results shown in Figs. 5–12 are mainly based on the actuator fault that occurred in joint no. 4, i.e., the elbow flexion joint. However, any joint can fail during the normal operation of the robot arm. The performance of the proposed controller in terms of full restoration of tracking depends on how critical the failed joint is. For instance, if a joint or the link connected to that joint has a greater role to reach a particular location in the Cartesian space, then the failure of the joint may significantly degrade the tracking performance. If there is another healthy joint which can complete the tracking task at hand, then tracking performance and overall behavior will be less affected. As mentioned above, redundant robotic arms in this case will be able to deal with the actuator fault more efficiently using this simple but effective scheme. Figures 13 and 14 show tracking when the shoulder flexion joint and shoulder abduction joint become faulty, respectively, while Fig. 15 shows the tracking when two joints, i.e., shoulder flexion and shoulder abduction joints, become faulty. In these cases, the controller successfully keeps the robot arm stable, and the tracking performance does not degrade significantly.

5 Conclusions

Similar to any other mechanical system, the occurrence of faults in actuators or sensors during the operation of a humanoid robot is not uncommon. However, unlike industrial robots, the occurrence of faults in humanoid robots is more dangerous and may lead to catastrophic outcomes, especially in terms of the safety of the humans interacting with the robot. In this paper, a scenario is presented where a humanoid robot arm is in cooperation with a human when suddenly one of the four joints being used fails completely and the end effector goes into a frenzy. The robot is controlled by a sliding-mode (SMC) Cartesian controller that drives the end effector towards a desired position in the x–z plane by means of four joints: shoulder flexion, shoulder abduction, humeral rotation, and elbow flexion. Once the failure occurs, the controller adds a new term to the SMC term that works to alter the energy of the system by means of a hyperbolic tangent-based function, thereby stabilizing the end effector and recovering the desired trajectory tracking. The proposed controller exploits the redundancy in the number of joints to mitigate the chaotic response. This scheme is effective for containing an adverse situation arising from an actuator failure. However, the tracking recovery will only be possible if robot has redundancy i.e., more actuators are available than what is required to complete a task. Also, different joint failures will have different impacts on performance.