Optimal synthesis of four-bar linkages for path generation using the individual repairing method

Constraints are one of the main factors that hinder the optimal synthesis of linkages to obtain the global optimum. At present, the most commonly used constraint handling method is called the penalty function (PF) method, but this technique has proven to be inefficient and unreliable in path synthesis. In this paper, a novel and effective constraint handling method called the individual repairing (IR) method is developed for the optimization model of four-bar mechanisms for path synthesis. The function of the IR method is to check the conformity of each individual to the Grashof condition, the sequence condition, and the variable range condition after population initialization and each iteration as well as to repair all unreasonable individuals according to the corresponding repairing technique to make them all satisfy the constraint conditions. In other words, the new constraint handling method establishes a transformation method so that each infeasible point in the search space uniquely corresponds to a feasible point. Based on the IR method, the optimization of path synthesis can be effectively carried out. Finally, the validity and reliability of the new constraint handling method are verified using three examples.

1 Introduction

A linkage mechanism is a kind of commonly used mechanism that is employed to realize the motion transformation and power transmission (Sandor and Erdman, 1984; Erdman et al., 1984). Among various linkage mechanisms, the four-bar mechanism is essential and widely used due to its simple structure, stable output, and the fact that it is easy to control and maintain (Buśkiewicz, 2019; Kadarno et al., 2021; Lee et al., 2021; Yildiz, 2021; Zhao et al., 2014).

A class of design tasks for linkage mechanisms is called path synthesis. The purpose of path synthesis is to find the optimal dimensional parameters of a mechanism so that a point on the coupler link can move along a desired curve (Fox and Willmert, 1967; Han, 1966; Li et al., 2020; Khan et al., 2015). In general, the desired curve of path synthesis usually refers to a sequence of precision points. Because of the high nonlinearity of the problem, the path synthesis task is usually treated as an optimization problem (Marín and González, 2003). In order to ensure the rationality of the final linkage solution, three constraints are usually introduced into the optimization model of path synthesis of four-bar mechanisms, including the Grashof condition, the sequence condition, and the variable range condition. However, the introduction of constraints leads to a highly discontinuous search space. In general, constraints are considered to be one of the main factors hindering the optimal synthesis of linkages to obtain the global optimum (Angeles et al., 1988; Acharyya and Mandal, 2009; Lin, 2010; Peñuñuri et al., 2011; Ebrahimi and Payvandy, 2015; Sleesongsom and Bureerat, 2018; Bureerat and Sleesongsom, 2021).

At present, the penalty function (PF) method is the most commonly used method to deal with the constraint conditions in path synthesis. The principle of the PF method is to add a very large value to the objective function of individuals who do not meet the constraint conditions so that these individuals will be eliminated in the optimization. However, this causes the vast majority or even all of the individuals of the initial population to be eliminated by the penalty function, especially when dealing with the sequence condition (Acharyya and Mandal, 2009; Peñuñuri et al., 2011). As a result, the PF method usually requires a very large population, otherwise the optimization will be inefficient or will even fail (Sleesongsom and Bureerat, 2018; Bureerat and Sleesongsom, 2021). However, a large population is accompanied by a sharp increase in the computational cost. In this context, researchers have made some useful explorations. Acharyya and Mandal (2009) first proposed a method to rearrange the randomly generated input angles in the initial population to reduce the probability of individuals being rejected in the next iteration. Additionally, they proposed a refinement scheme to ensure that all individuals in the initial population satisfy the Grashof condition by reassigning link lengths to individuals that do not satisfy the abovementioned condition. Lin (2010) further introduced the method of rearranging input angles during both population initialization and each iteration, so that the sequence condition of input angles could be ignored until the end of the optimization. Ebrahimi and Payvandy (2015) developed an innovative technique to generate the initial population that satisfies the Grashof condition. Sleesongsom and Bureerat (2018) and Bureerat and Sleesongsom (2021) designed two new individual generation techniques for the Grashof condition and the sequence condition, respectively, which can ensure the generation of individuals that satisfy the constraints. However, the individual generation techniques that they designed did not take the parameters of the original individual into account and, instead, generated a completely new individual.

In this paper, a novel and effective constraint handling method called the individual repairing (IR) method is introduced. The principle of the IR method is to develop the corresponding repairing technique for each constraint condition of the optimization model, so as to ensure that all of the individuals in the optimization always meet the constraints. The design of these repairing techniques follows the same criterion, which is to transform the original unreasonable individual into a unique corresponding reasonable individual. In other words, the IR method transforms every infeasible point in the search space into a unique corresponding feasible point. This is the difference between this study and other relevant studies and is also the main innovation described in this work. Based on the new constraint handling method, the optimization of path synthesis can be effectively carried out.

In Sect. 2, the kinematics analysis and the classic optimization model of four-bar mechanisms for path synthesis are described. Section 3 then introduces three repairing techniques corresponding to the three constraint conditions of the classic optimization model of four-bar mechanisms for path synthesis. Following this, Sect. 4 shows the optimization results using the new IR method through three classical path synthesis tasks. Finally, the conclusions of the paper and the plan for future work are presented in Sect. 5.

2 Problem formulation

2.1 Kinematics analysis

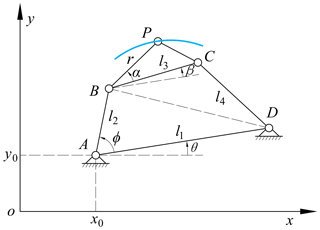
The schematic diagram of a planar four-bar mechanism is shown in Fig. 1. The mechanism is represented by nine independent design variables:

$$\begin{array}{}\text{(1)}& X=[l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}},r,\mathit{\alpha },\mathit{\theta },x_{\mathrm{0}},y_{\mathrm{0}}].\end{array}$$

Here, l₁ is the length of the fixed link AD, l₂ is the length of input link AB, and l₃ and l₄ represent the lengths of coupler link BC and output link CD, respectively. The coupler point P is a point on the coupler link BC which generates a continuous curve, and r and α determine the position of P relative to the coupler link BC. x₀, y₀ and θ determine the offset and rotation angle of the fixed link AD relative to the coordinate system xoy, respectively.

Figure 1 The planar four-bar mechanism and its parameters.

Based on the variable definition shown in Fig. 1, the position of the coupler point P can be formulated as follows:

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{l}{P}_x=l_{\mathrm{2}}\cos (\mathit{\varphi }+\mathit{\theta })+r\cos (\mathit{\alpha }+\mathit{\beta }+\mathit{\theta })+x_{\mathrm{0}}\\ P_y=l_{\mathrm{2}}\sin (\mathit{\varphi }+\mathit{\theta })+r\sin (\mathit{\alpha }+\mathit{\beta }+\mathit{\theta })+y_{\mathrm{0}}\end{array}\right.,\end{array}$$

where the variable β represents the angle between the coupler link BC and the fixed link AD.

Actually, the variable β is a dependent variable, and Freudenstein (1954) provides the relation equation of the variable β, the input angle ϕ, and the dimensional parameters of the mechanism.

$$\begin{array}{}\text{(3)}& K_{\mathrm{1}}+K_{\mathrm{2}}\cos \mathit{\varphi }+K_{\mathrm{3}}\cos \mathit{\beta }=\cos (\mathit{\varphi }-\mathit{\beta }),\end{array}$$

where

$$\begin{array}{}\text{(4)}& \left\{\begin{array}{l}{K}_{\mathrm{1}}=\frac{l_{\mathrm{4}}^{\mathrm{2}}-l_{\mathrm{3}}^{\mathrm{2}}-l_{\mathrm{2}}^{\mathrm{2}}-l_{\mathrm{1}}^{\mathrm{3}}}{\mathrm{2}{l}_{\mathrm{2}}{l}_{\mathrm{3}}}\\ K_{\mathrm{2}}=\frac{l_{\mathrm{1}}}{l_{\mathrm{3}}}\\ K_{\mathrm{3}}=\frac{l_{\mathrm{1}}}{l_{\mathrm{2}}}\end{array}\right..\end{array}$$

The following simplified equation can then be derived:

$$\begin{array}{}\text{(5)}& \mathit{\beta }=\mathrm{2}\arctan {\displaystyle \frac{-B\pm \sqrt{B^{\mathrm{2}}-\mathrm{4}AC}}{\mathrm{2}A}},\end{array}$$

where

$$\begin{array}{}\text{(6)}& \left\{\begin{array}{l}A=(K_{\mathrm{2}}+\mathrm{1})\cos \mathit{\varphi }+K_{\mathrm{1}}-K_{\mathrm{3}}\\ B=-\mathrm{2}\sin \mathit{\varphi }\\ C=(K_{\mathrm{2}}-\mathrm{1})\cos \mathit{\varphi }+K_{\mathrm{1}}+K_{\mathrm{3}}\end{array}\right..\end{array}$$

The two solutions of Eq. (5) represent two respective branches of the four-bar mechanism. In summary, the Eq. (2) can be simplified as follows:

$$\begin{array}{}\text{(7)}& P=f(X,\mathit{\varphi }).\end{array}$$

2.2 Classic optimization model

The path synthesis problem is usually considered to be an optimization problem, and an objective function is specified to minimize the difference between the desired curve and an actual generated curve. The tracking error is the most commonly used objective function to quantify this difference, and it is defined as the sum of the squares of the Euclidian distances between the target points and the same number of comparison points on the generated curve. In order to obtain these comparison points, the classical model introduces N input angles as optimization variables in addition to the nine design variables of the four-bar mechanism, where N is equal to the number of target points. In addition, the Grashof condition, the sequence condition, and the variable range condition are used as constraint functions in the classic optimization model of four-bar mechanisms for path synthesis. Therefore, the optimization variables of the classic model usually include the following:

$$\begin{array}{}\text{(8)}& X_{\mathrm{0}}=[l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}},r,\mathit{\alpha },\mathit{\theta },x_{\mathrm{0}},y_{\mathrm{0}},{\mathit{\varphi }}_{\mathrm{1}},{\mathit{\varphi }}_{\mathrm{2},}\mathrm{\dots },{\mathit{\varphi }}_N].\end{array}$$

As a result, the classic model can be defined as follows:

$$\begin{array}{}\text{(9)}& \begin{array}{l}\min \\ \mathrm{subject}\mathrm{to}\end{array}\begin{array}{l}{f}_{\mathrm{obj}}=\mathit{\left\{}{\sum }_{i=\mathrm{1}}^N\right[(G_i^x-D_i^x{)}^{\mathrm{2}}\\ +(G_i^y-D_i^y{)}^{\mathrm{2}}]\mathit{\}}\\ \left(\mathrm{a}\right)l_{\mathrm{2}}<min\left(l_{\mathrm{1}},l_{\mathrm{3}},l_{\mathrm{4}}\right)\mathit{\&}\mathit{\&}{l}_{\mathrm{2}}\\ +max\left(l_{\mathrm{1}},l_{\mathrm{3}},l_{\mathrm{4}}\right)<\mathrm{sum}\left(l_{\mathrm{1}},l_{\mathrm{3}},l_{\mathrm{4}}\right)\\ -max\left(l_{\mathrm{1}},l_{\mathrm{3}},l_{\mathrm{4}}\right),\\ \left(\mathrm{b}\right){\mathit{\varphi }}_j<{\mathit{\varphi }}_{\mathrm{mod}(j+\mathrm{1},N)}<\mathrm{\dots }\\ <{\mathit{\varphi }}_{\mathrm{mod}(j+N-\mathrm{1},N)},\\ \left(\mathrm{c}\right)x_i\in [L_i,U_i],\forall x_i\in X_{\mathrm{0}},\end{array}\end{array}$$

where ($G_i^x,G_i^y$) is the position of the actual generated precision points for comparison, ($D_i^x,D_i^y$) is the prescribed position of the target point, ${\mathit{\varphi }}_j=min\mathit{\{}{\mathit{\varphi }}_{\mathrm{1}},{\mathit{\varphi }}_{\mathrm{2}},\mathrm{\dots },{\mathit{\varphi }}_N\mathit{\}}$, mod(m,n) is the remainder of the quotient of $m/n\left(\mathrm{set}\mathrm{mod}\right(m,m)=m)$, x_i is the ith parameter in X₀, and L_i and U_i are the lower and upper limits of the variable x_i, respectively.

Constraint conditions (a)–(c) in Eq. (9) represent the Grashof condition, the sequence condition, and the variable range condition, respectively. It should be noted that this paper uses the crank–rocker mechanism as the research object, so the link AB is directly defined as the shortest link in constraint (a). In addition, it should be mentioned that the purpose of the sequence condition is to restrict the rotation direction of the crank so that it cannot be rotated backwards. Currently, some literature forces input angles to be arranged in increasing order, which overdefines the sequence condition and may lead to a reduced potential for the optimization to obtain the optimal solution. As far as we know, a reasonable expression for the sequence condition was first proposed by Cabrera et al. (2002), but they miswrote the comparison symbol in the formula. The correct definition of the sequence condition is represented in constraint (b). Finally, constraint (c) ensures that all optimization variables are within their respective predetermined reasonable ranges.

3 Individual repairing (IR) method

Although it is the most common constraint handling method in path synthesis, the PF method has been proven to be inefficient and to have poor repeatability (Sleesongsom and Bureerat, 2018; Bureerat and Sleesongsom, 2021; Acharyya and Mandal, 2009; Lin, 2010; Peñuñuri et al., 2011; Ebrahimi and Payvandy, 2015). Actually, using PF methods to deal with constraint functions will result in most or all of the individuals in the initial population being eliminated by penalty functions, especially when dealing with the sequence condition.

The probability that a uniform random sequence is already sorted is $\mathrm{1}/n\mathrm{!}$ (Peñuñuri et al., 2011). Therefore, the probability of randomly generated individuals meeting the sequence condition is $\mathrm{1}/(n-\mathrm{1})\mathrm{!}$. A simple example is illustrated here. For the path synthesis task with six target points, 3 000 000 individuals were randomly generated by a uniform distribution to form the initial population. Among them, the proportion of individuals conforming to the Grashof condition is 12.4944 %, the proportion of individuals conforming to the sequence condition is 0.8356 %, and the proportion of individuals conforming to both constraints is 0.1039 %. This means that the vast majority of randomly generated individuals do not satisfy the constraint conditions. In this case, the PF method will lead to the majority or even all of the individuals in the initial population being eliminated, resulting in the inefficiency or even failure of the optimization. In addition, it is easy to understand that even if the optimization is successful, the optimization completed by a few initial individuals conforming to the constraints will not have satisfactory repeatability. This is especially problematic when there are more target points.

Therefore, a new constraint handling method called the IR method is developed in this section. The principle of the IR method is to develop different individual repairing techniques corresponding to each constraint condition, so as to repair the individuals that do not meet the constraint condition after the initial population generation and each iteration. The repairing techniques corresponding to the constraint conditions of the optimization model for path synthesis of four-bar mechanisms are described below.

3.1 Grashof condition repairing technique

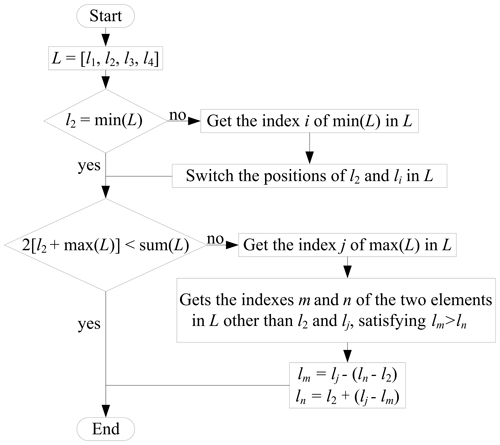
The Grashof condition is a constraint on the link lengths of a four-bar mechanism. Its purpose is to ensure the existence of a crank in the four-bar mechanism. In this work, a linkage repairing technique is proposed to transform all of the non-Grashof linkage solutions into reasonable solutions in the optimization process. The flow of the linkage repairing technique is shown in Fig. 2.

As shown in Fig. 2, the linkage repairing technique is mainly divided into two steps, making the link lengths meet the two respective inequality constraints of the Grashof condition as shown in Eq. (9). The function of the first step is to ensure that link AB becomes the shortest link, which is easy to understand. The function of the second step is to ensure that the sum of the shortest link and longest link is less than the sum of the other two links, which may be difficult to intuitively understand. The principle of the second step is presented in Fig. 3.

Figure 2 The flow of the linkage repairing technique.

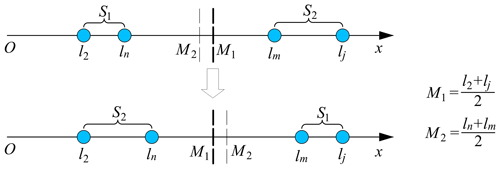
Assuming that the link length values are arranged on a positive line as shown in Fig. 3, the second inequality constraint of the Grashof condition can be transformed into a more graphical representation: the thick dashed line representing the average length M₁ of the longest and shortest links must be to the left of the thin dashed line representing the average length M₂ of the remaining two links. For linkages that do not satisfy this inequality constraint, Fig. 3 shows an ingenious repairing technique that takes x=M₁ as the axis of symmetry and then redefines the values of l_m and l_n.

Figure 3 Schematic diagram of the linkage repairing technique.

In contrast to the work of Ebrahimi and Payvandy (2015), Sleesongsom and Bureerat (2018), and Bureerat and Sleesongsom (2021), the linkage repairing technique developed in this study is based on the parameters of the irrational linkage solution itself, rather than regenerating another completely unrelated linkage solution. Based on this new technique, the repaired linkage solution is more likely to remain competitive in the next iteration.

3.2 Sequence condition repairing technique

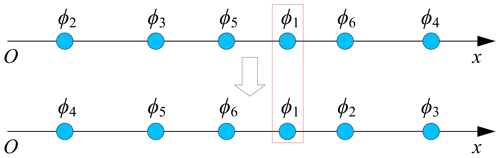
Similar to the studies of Acharyya and Mandal (2009), Lin (2010), and Ebrahimi and Payvandy (2015), this study also adopted the method of rearranging input angles in increasing order to ensure that all individuals meet the sequence condition in the optimization process. However, in contrast to the method of Acharyya and Mandal (2009) and Ebrahimi and Payvandy (2015), who randomly selected an input angle as the first angle, and the method of Lin (2010), who selected the smallest input angle as the first angle, this study keeps the original first input angle unchanged. Figure 4 shows the schematic of the angle repairing technique used in this study.

Figure 4 Schematic diagram of the angle repairing technique.

Assuming that a randomly generated set of input angles is arranged on a positive line, the angles' arrangement is likely to be chaotic, as shown in Fig. 4. The function of the angles repairing technique is to give this set of angles a new order so that the angles are neatly arranged on the positive line according to the sequence condition.

3.3 Variable range condition repairing technique

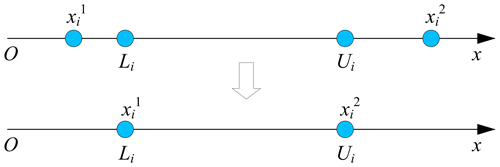
In the iterative process of population, some parameters of some individuals are likely to break through the predetermined range. At present, the commonly used optimization technique is to set the parameter value of the breakthrough range as the boundary value, but there is no relevant research on path synthesis to describe this handling technique of the variable range condition. Figure 5 illustrates the principle of this variable range repairing technique in detail.

Figure 5 Schematic diagram of the variables repairing technique.

Similarly, suppose that a parameter value and its corresponding boundary value of an individual in the population are arranged on a positive line as shown in Fig. 5. The principle of variables repairing technique is to set parameters beyond the upper boundary as the upper boundary and parameters beyond the lower boundary as the lower boundary.

3.4 Application of the IR method in optimization

Based on the three individual repairing techniques shown above, the elitism of population was guaranteed during the whole optimization procedure. Finally, the application method of these repairing techniques in the path synthesis of four-bar mechanism is shown in Fig. 6.

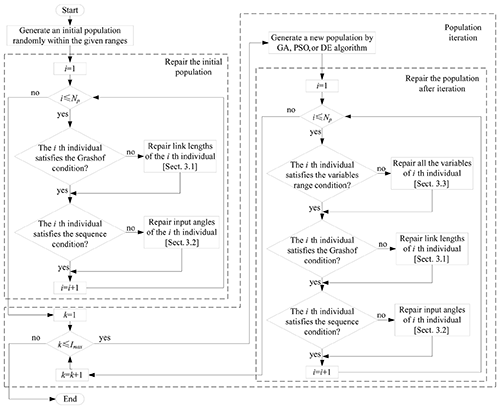
Figure 6 Schematic diagram of the application of the IR method with different optimization algorithms.

In Fig. 6, the variable N_p represents the population number and I_max represents the maximum iteration number.

4 Numerical examples

In order to verify the validity and reliability of the new constraint handling method, three classic path synthesis tasks are discussed in this section, including one path synthesis task without prescribed timing and two path synthesis tasks with prescribed timing. Additionally, three classical optimization algorithms are selected to search for the optimal solution. The parameters of these optimization algorithm are set as follows:

1. for the genetic algorithm (GA), C_p = 0.8 and M_p = 0.2;

2. for the particle swarm optimization (PSO), w=0.7, c₁=1.49, and c₂=1.49;

3. for the differential evolution (DE), F=0.5 and C_p = 0.9.

Here, the parameters C_p, M_p, w, c₁, c₂, and F represent the crossover probability, the mutation probability, the inertia factor, the global learning weight, the local learning weight, and the scaling factor, respectively. Additionally, the population number N_p is set to 100, and the maximum iteration number I_max is set to 1000. Finally, results from other studies using the same optimization algorithms were compared with the results of this study.

4.1 Example 1: six target points and 15 optimization variables

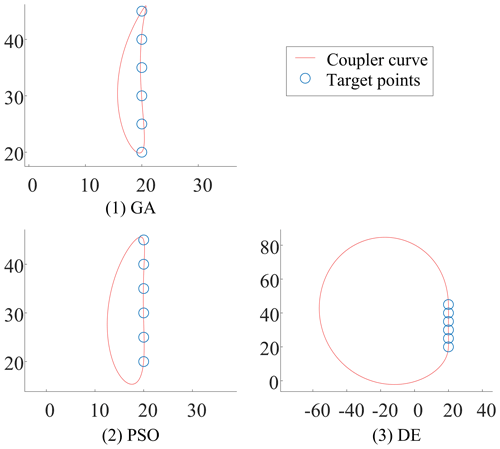
This example is a path synthesis task without prescribed timing for a straight-line path with six target points. The range of the design variables in this example is defined as follows:

$$\begin{array}{rl}& l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}}\in [\mathrm{0},\mathrm{60}];r\in [\mathrm{0},\mathrm{85}];\\ & x_{\mathrm{0}},y_{\mathrm{0}}\in [-\mathrm{60},\mathrm{60}];\mathit{\alpha },\mathit{\theta }\in [\mathrm{0},\mathrm{2}\mathit{\pi }].\end{array}$$

Figure 7 Coupler curves obtained in this study for Example 1.

The target points are

$$\begin{array}{rl}{D}_i=\mathit{\{}& (\mathrm{20},\mathrm{20});(\mathrm{20},\mathrm{25});(\mathrm{20},\mathrm{30});(\mathrm{20},\mathrm{35});\\ & (\mathrm{20},\mathrm{40});(\mathrm{20},\mathrm{45})\mathit{\}}.\end{array}$$

The optimization variables are

$$\begin{array}{rl}{X}_{\mathrm{0}}=[& l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}},r,\mathit{\alpha },\mathit{\theta },x_{\mathrm{0}},y_{\mathrm{0}},{\mathit{\varphi }}_{\mathrm{1}},{\mathit{\varphi }}_{\mathrm{2}},{\mathit{\varphi }}_{\mathrm{3}},\\ & {\mathit{\varphi }}_{\mathrm{4}},{\mathit{\varphi }}_{\mathrm{5}},{\mathit{\varphi }}_{\mathrm{6}}].\end{array}$$

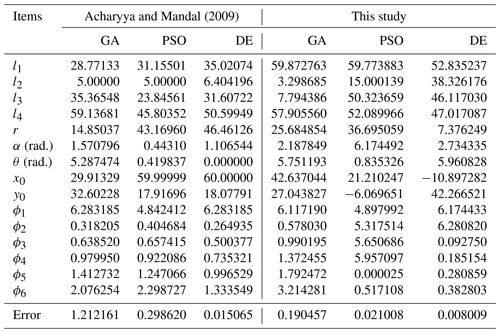
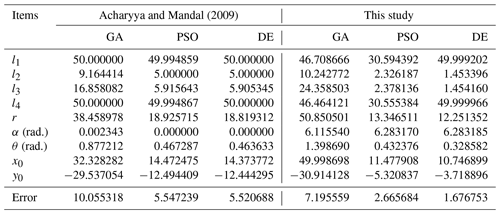
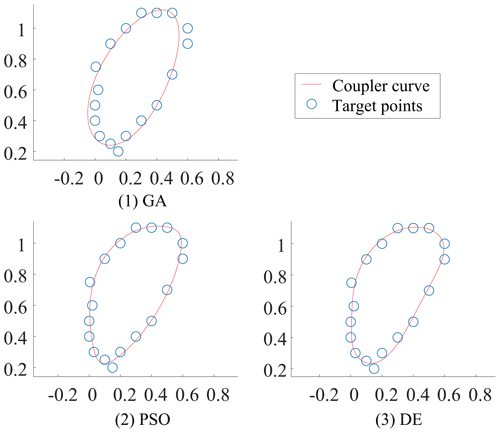
Table 1 shows the optimization results of the new method proposed in this study using the three optimization algorithms for Example 1. In addition, the results from Acharyya and Mandal (2009) using the same optimization algorithms are also shown in Table 1. It is worth noting that the original literature does not show the tracking error; instead, it shows the square root of the tracking error. As can be seen from Table 1, the results obtained by adopting the IR method are better than those obtained using other constraint handling methods in previous work under the same optimization algorithm. Figure 7 shows the coupler curve of the linkage solutions obtained in this study for Example 1.

Table 1 Linkage solutions and structural errors obtained in previous work and in this study for Example 1.

4.2 Example 2: six target points and nine optimization variables

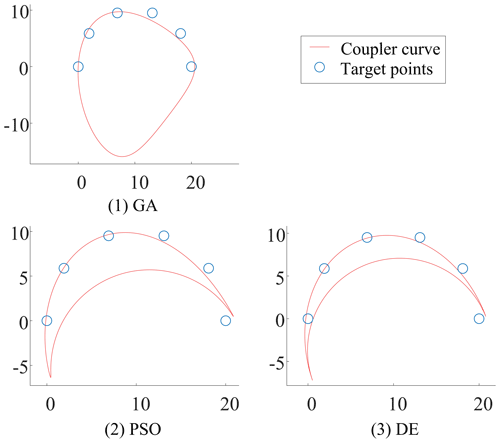
This example is a path synthesis task with prescribed timing for a semicircular arc path with six target points. The range of the design variables in this example is defined as follows:

$$\begin{array}{rl}& l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}}\in [\mathrm{5},\mathrm{50}];r\in [\mathrm{0},\mathrm{70}];\\ & x_{\mathrm{0}},y_{\mathrm{0}}\in [-\mathrm{50},\mathrm{50}];\mathit{\alpha },\mathit{\theta }\in [\mathrm{0},\mathrm{2}\mathit{\pi }];\text{and}\\ & {\mathit{\varphi }}_i=\left[{\displaystyle \frac{\mathit{\pi }}{\mathrm{6}}},{\displaystyle \frac{\mathit{\pi }}{\mathrm{3}}},{\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}},{\displaystyle \frac{\mathrm{2}\mathit{\pi }}{\mathrm{3}}},{\displaystyle \frac{\mathrm{5}\mathit{\pi }}{\mathrm{6}}},\mathit{\pi }\right].\end{array}$$

The target points are

$$\begin{array}{rl}{D}_i=\mathit{\{}& (\mathrm{0},\mathrm{0});(\mathrm{1.9098},\mathrm{5.8779});(\mathrm{6.9098},\mathrm{9.5106});\\ & (\mathrm{13.09},\mathrm{9.5106});(\mathrm{18.09},\mathrm{5.8779});(\mathrm{20},\mathrm{0})\mathit{\}}.\end{array}$$

The optimization variables are

$$X_{\mathrm{0}}=[l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}},r,\mathit{\alpha },\mathit{\theta },x_{\mathrm{0}},y_{\mathrm{0}}].$$

Table 2 shows the optimization results of the new method proposed in this study using the three optimization algorithms for Example 2. Similarly, it can be seen from Table 2 that the error of the linkage solutions obtained by the IR method is smaller than the error of the linkage solutions obtained by previous work (Acharyya and Mandal, 2009) using the same three optimization algorithms. Figure 8 shows the coupler curve of the linkage solutions obtained in this study for Example 2.

Figure 8 Coupler curves obtained in this study for Example 2.

Table 2 Linkage solutions and structural errors obtained in previous work and in this study for Example 2.

4.3 Example 3: 18 target points and 10 optimization variables

This example is a path synthesis task with prescribed timing for a path with 18 target points. The range of the design variables in this example is defined as follows:

$$\begin{array}{rl}& l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}}\in [\mathrm{5},\mathrm{50}];r\in [\mathrm{0},\mathrm{70}];\\ & x_{\mathrm{0}},y_{\mathrm{0}}\in [-\mathrm{50},\mathrm{50}];\mathit{\alpha },\mathit{\theta }\in [\mathrm{0},\mathrm{2}\mathit{\pi }];\text{and}\\ & {\mathit{\varphi }}_i={\mathit{\varphi }}_{\mathrm{1}}+{\displaystyle \frac{\mathit{\pi }}{\mathrm{9}}}\times \left(i-\mathrm{1}\right),i=\mathrm{1},\mathrm{\dots },\mathrm{18}.\end{array}$$

The target points are

$$D_i=\left\{\begin{array}{l}(\mathrm{0.5},\mathrm{1.1});(\mathrm{0.4},\mathrm{1.1});(\mathrm{0.3},\mathrm{1.1});(\mathrm{0.2},\mathrm{1});\\ (\mathrm{0.1},\mathrm{0.9});(\mathrm{0.005},\mathrm{0.75});(\mathrm{0.02},\mathrm{0.6});\\ (\mathrm{0},\mathrm{0.5});(\mathrm{0},\mathrm{0.4});(\mathrm{0.03},\mathrm{0.3});(\mathrm{0.1},\mathrm{0.25});\\ (\mathrm{0.15},\mathrm{0.2});(\mathrm{0.2},\mathrm{0.3});(\mathrm{0.3},\mathrm{0.4});(\mathrm{0.4},\mathrm{0.5});\\ (\mathrm{0.5},\mathrm{0.7});(\mathrm{0.6},\mathrm{0.9});(\mathrm{0.6},\mathrm{1})\end{array}\right\}.$$

The optimization variables are

$$X_{\mathrm{0}}=[l_{\mathrm{1}},l_{\mathrm{2}},l_{\mathrm{3}},l_{\mathrm{4}},r,\mathit{\alpha },\mathit{\theta },x_{\mathrm{0}},y_{\mathrm{0}},{\mathit{\varphi }}_{\mathrm{1}}].$$

Table 3 shows the optimization results of the new method proposed in this study using the three optimization algorithms for Example 3. Additionally, this example has also been studied by Cabrera et al. (2002) and Peñuñuri et al. (2011) using the GA and DE algorithms, respectively.

Table 3 Linkage solutions and structural errors obtained in previous work and in this study for Example 3.

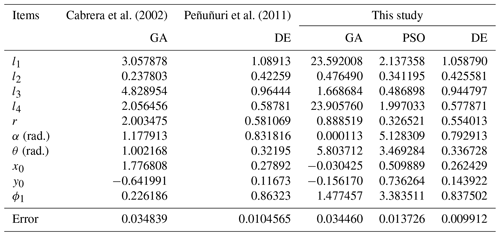
As can be seen from Table 3, the results obtained by adopting the IR method are better using the same optimization algorithms. Figure 9 shows the coupler curve of the linkage solutions obtained in this study for Example 3.

Figure 9 Coupler curves obtained in this study for Example 3.

5 Conclusions

In this paper, different constraint handling methods are discussed in detail, and a new constraint handling method based on the idea of individual repairing is proposed for the path synthesis of four-bar mechanisms. The function of the new method is to transform individuals that do not meet the constraints into the individuals that meet the constraints in time, so as to ensure the success and effectiveness of the optimization. More precisely, the principle of the new constraint processing method is to build a converter based on the constraints of the optimization model, so as to transform any infeasible point in the search space into a unique corresponding feasible point. Experimental results show that, compared with other constraint handling methods, the proposed method can obtain better linkage solutions using the same optimization algorithm for the same path synthesis task. The core innovation of this research is the constraint handling method based on the idea of individual repairing, which is universal in theory and can be matched with different optimization algorithms, so as to be applied to other constrained engineering optimization problems. In the future, it is planned to extend the constraint handling method based on the idea of individual repairing to the kinematics synthesis of six-bar mechanisms, eight-bar mechanisms, and other mechanisms in the field of mechanical design, including not only path synthesis but also motion synthesis and function synthesis.