Type synthesis approach for the 2R1T compliant parallel mechanism with a suitable constrained branch

In the aerospace field, the precision and stiffness for 2R1T (R denotes the rotation and the T denotes the translation) degree of freedom (DOF) space posture adjustment mechanisms are required. Compliant parallel mechanisms (CPMs) with a suitable constrained branch (SCB) have the advantages of high precision and high stiffness. Based on screw theory, a new type synthesis approach for a 2R1T compliant parallel mechanism with a suitable constrained branch is proposed. The proposed approach is an improvement of the freedom and constraint topology approach. It combines with other methods, including the rigid-body-replacement method, the principle of symmetry, etc. In order to obtain CPMs with a suitable constrained branch, the criterion for the type synthesis is presented. Using this proposed type synthesis approach, a series of CPMs is obtained. They include, but are not limited to, the existing typical 2R1T CPMs with a suitable constrained branch. Furthermore, it identifies the correctness and effectiveness of the approach by analyzing the DOF of the synthesized mechanism. This approach is also suitable for the type synthesis of 4, 5, and 6 DOF compliant parallel mechanisms with a suitable constrained branch.

1 Introduction

Compliant mechanisms (CMs) have been used in a variety of applications at micro and macro scales, such as bioengineering (Bhargav et al., 2015), micro electro mechanical systems (MEMSs) (Zhang et al., 2016; Chen and Ma, 2015; Chen et al., 2021), aerospace (S. L. Chen et al., 2018), laser communication (Clark et al., 2016; Cui et al., 2021), and other fields (Yu et al., 2014; Qiu et al., 2018; Y. C. Chen et al., 2018; Qi et al., 2018). They transmit motion/loads by the elastic deformation of materials. This revolutionary change leads to many potential merits, such as reduced part count (up to monolithic configuration), zero backlashes, no need for lubrication, reduced wear, increased reliability, high precision, and compact configuration in comparison with the rigid-body counterparts. However, the applications of CMs are limited because it is hard to make a precision micro-positioning system with both a large workspace and high stiffness at the same time.

Researchers have conducted related studies for parallel mechanisms (PMs) with a suitable constrained branch that have the advantage of high stiffness (Chen et al., 2019; Li et al., 2020; L. T. Wang et al., 2019). A 4 PUS/UP (P denotes a translational pair, U denotes a universal pair, and S denotes a spherical pair) parallel mechanism with a suitable constrained branch is proposed to manufacture complex curved surfaces of large-scale heterogeneous components in the aerospace field (Zhang and Fang, 2018). A 4 SPS/CU (C denotes a cylinder pair) parallel mechanism is proposed. Its kinematics and mechanical are analyzed (Wang et al., 2012). A 5 UPS/PRPU (R denotes a rotational pair) parallel manipulator is proposed. Its performances of kinematics and dynamics are analyzed (Yao et al., 2017). The reference proposes a 3 SPS/RPR parallel mechanism with high stiffness (Hu and Liu, 2020). Compared with their rigid-body counterparts, the compliant parallel mechanisms (CPMs) can provide the merits of both parallel and compliant mechanisms.

The advantages of CPMs compared with their rigid-body counterparts have raised a growing interest in developing the methods for their conceptual synthesis. The three main synthesis approaches in this challenging area are the pseudo-rigid-body model (PRBM) approach (Cannon and Howell, 2005; Moon et al., 2013; Yang et al., 2021), freedom and constraint topology (FACT) approach (Hopkins and Culpepper, 2010a, b; Yu et al., 2011, 2015, 2016), and topology optimization approach (Bowen et al., 2013; Liang et al., 2020; Emmendoerfer et al., 2020). For example, a compliant parallel mechanism with high precision and a wide working area is presented using the new flexure hinges (Kozuka et al., 2012). Based on the FACT approach, a new method for type synthesis of a 2T (where T denotes translation) redundant actuated CPM is proposed (Li et al., 2021). A new 5 DOF (degrees of freedom) grating and splicing CPM is proposed according to the high-precision requirements of large-diameter grating and splicing mechanisms (Shao et al., 2018). Based on the topology optimization approach, a new method considering stress constraints, manufacturing uncertainty, and geometric nonlinearity is proposed (da Silva et al., 2020). A 4 PPR CPM is proposed. Its kinematics and static stiffness are analyzed (Yang et al., 2019).

However, the CPMs with a suitable constrained branch usually are designed by the PRBM approach (Zhang et al., 2011; Yang et al., 2017; Bilancia et al., 2018; Wang and Zhang, 2017). A new 3 SPS/RPR CPM is proposed, and the notch flexible hinges are used (Yun and Li, 2011). Based on the 3 PUS/PU parallel mechanism, a new CPM with a suitable constrained branch is proposed. The 4 DOF hybrid parallel–serial compliant mechanism is presented, and the notch flexure hinges are used (Pinskier et al., 2018). On the one hand, the PRBM approach is based on rigid-parallel mechanisms and is currently unable to solve the problem of topology selection. On the other hand, a plate flexible unit cannot be directly selected to replace a motion pair for the PRBM approach. Compared with the PRBM approach, the new approach has some advantages. The new synthesis approach can obtain new configurations, and the process of the synthesis is easy. As the same time, the plate flexible unit can be directly selected. Compared with the freedom and constraint topology approach, the new approach has also some advantages. The new synthesis approach can obtain the compliant mechanism with high precision and high stiffness by creatively considering the accuracy performance and stiffness performance. Thus, a systematic type synthesis approach for CPM with a suitable constrained branch is proposed. Based on the new synthesis approach, a series of new compliant mechanisms with a large workspace, high precision, and high stiffness are obtained.

The rest of this paper is organized as follows: Sect. 2 provides a survey of the freedom and constraint space and introduces the parasitic displacement and precision. Section 3 addresses the type synthesis conditions and the process for CPMs with a suitable constrained branch. Section 4 obtains the series of the 2R1T (where R denotes the rotation) motion and high-precision and high-stiffness type of CPMs with a suitable constrained branch based on the proposed type synthesis approach. Finally, conclusions are drawn.

2 Theoretic foundation

2.1 Freedom and constraint space

When a rigid body is constrained by several mechanical connections providing n non-redundant constraints, n DOF of the body are removed, correspondingly, while 6–n DOF will remain. In this regard, every constraint wrench in the n system is reciprocal to the twist (6–n) system.

It is clear that the above result complies with Maxwell's principles of constraint. This may be expressed as follows:

$$\begin{array}{}\text{(1)}& M=\mathrm{6}-n,\end{array}$$

where M is the number of DOF.

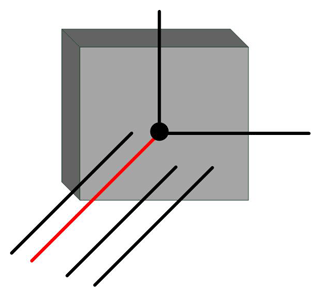
In order to visualize the relationship between freedoms and constraints in a mechanical system, Blanding (1999) introduced both constraint lines and freedom lines, as shown in Fig. 1. At the same time, he addressed the rule of complementary patterns that states that every freedom line intersects all constraint lines, as shown in Fig. 2.

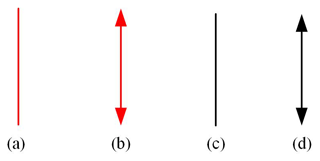
Figure 1 Freedom and constraint line. (a) Rotation freedom. (b) Translation freedom. (c) Force constraint. (d) Moment constraint.

Figure 2 The relationship of the freedom line and all constraint lines.

Based on the visual constraint-based design method proposed by Blanding, Hopkins and Culpepper extended this method and further proposed a FACT approach (Hopkins and Culpepper, 2011) to achieve a visual type synthesis of compliant mechanisms. For this purpose, they denoted a collection of commonly used freedom and constraint screw sets as freedom spaces (FSs) and constraint spaces (CSs), respectively, and established luxuriant patterns representing the unique mapping between FSs and their complementary CSs.

2.2 Parasitic displacement and the precision

In this paper, parasitic displacement is used to characterize the precision of compliant mechanisms (Zhao et al., 2012). The compliant mechanism with a large parasitic displacement is a low-precision compliant mechanism. The compliant mechanism with a small parasitic displacement is a high-precision compliant mechanism. Compared with the asymmetric compliant mechanism, a symmetrical compliant mechanism has a smaller parasitic displacement. Thus, the symmetrical compliant mechanism has higher precision.

Figure 3 Symmetrical compliant mechanism. (a) Schematic diagram. (b) PRBM.

Figure 4 Asymmetrical compliant mechanism. (a) Schematic diagram. (b) PRBM.

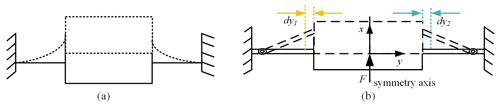
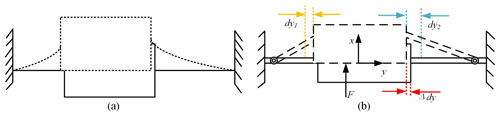
The schematic diagram and a pseudo-rigid-body model of a symmetric CM are shown in Fig. 3. The schematic diagram and a pseudo-rigid-body model of an asymmetric CM are shown in Fig. 4. The reference (Pucheta and Cardona, 2010) can explain the parasitic displacement equation of the flexible beam. Through a superposition operation, the parasitic displacement Δdy of CM is expressed as follows:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }\mathrm{dy}=\mathrm{dy}\mathrm{1}+\mathrm{dy}\mathrm{2},\end{array}$$

where dyi ($i=\mathrm{1},\mathrm{2}$) is the parasitic displacement of a flexible beam.

As shown in Fig. 3b, a symmetric mechanism has two flexible beams, and their parasitic displacements are equal and opposite. Thus, the parasitic displacement relationship for symmetric arrangement of two flexible beams is expressed as follows:

$$\begin{array}{}\text{(3)}& \mathrm{dy}\mathrm{1}=-\mathrm{dy}\mathrm{2}.\end{array}$$

Similarly, for the asymmetric mechanism, the parasitic displacements of two flexible beams are not equal, and they have a different direction, as shown in Fig. 4b. Thus, the parasitic displacement relationship for a symmetric arrangement of two flexible beams is expressed as follows:

$$\begin{array}{}\text{(4)}& \mathrm{dy}\mathrm{1}\ne -\mathrm{dy}\mathrm{2}.\end{array}$$

The above results show that the parasitic displacements of the symmetric mechanism can be offset. However, the parasitic displacements of the asymmetric mechanism cannot be offset. As a result, compared with asymmetric CMs, symmetric CMs can achieve higher precision. Thus, the arrangement of the mechanism determines the precision of the mechanism. In order to obtain high-precision CPMs, a symmetric arrangement for the compliant motion branch will be ensured.

3 Type synthesis approach

3.1 Criterion for type synthesis of the CPM with suitable constrained branch

To ensure that the synthesized mechanism can meet application requirements including motion, precision, and stiffness, a criterion for the type synthesis of the CPM with suitable constrained branch is presented. The following two points should be emphasized for the proposed type synthesis approach.

• a.

  To ensure that the CPM with a suitable constrained branch can achieve the desired motion, the compliant branch need to meet the following conditions:

  $$\begin{array}{}\text{(5)}& {\displaystyle }{M}_{\mathrm{1}}=M,\text{(6)}& {\displaystyle }{M}_{\mathrm{2}}\ge \mathrm{6},\end{array}$$

  where M₁ is the number of DOF of the compliant suitable constrained branch, and M₂ is the number of DOF of the compliant active branch. For a 2R1T space posture adjustment mechanism as the example, M is equal to three. In order to achieve the desired motion, M₁ and M₂ are equal to three and six, respectively. At the same time, in order to reduce errors and simplify the kinematics and dynamics model of the mechanism, the compliant branch needs to be as short as possible.

• b.

  In order to achieve the high precision and high stiffness, the CPM with a suitable constrained branch needs to meet follow conditions:

  $$\begin{array}{}\text{(7)}& {\displaystyle }{n}_{\mathrm{s}}>M+\mathrm{1},\text{(8)}& {\displaystyle }{n}_{\mathrm{1}}=M,\end{array}$$

  where n_s is the number of the compliant branch for a CPM with suitable constrained branch, and n₁ is the number of identical compliant active branches for a CPM with suitable constrained branch.

First, the number of the compliant active branch and compliant suitable constrained branch is determined, respectively. Then, the appropriate arrangement form is obtained according to the principle of symmetry. The key point for the mechanism is the symmetrical arrangement. The parasitic displacement of the mechanism will be lower, and the high-precision configuration will be obtained by symmetrical arrangement.

For a 2R1T space posture adjustment mechanism as the example, the requirement of high stiffness is obtained. In order to ensure that the mechanism can resist shock and vibration in the rocket during launch, the CPMs with a suitable constrained branch are designed. Compared with the usual CPMs, the CPMs with a suitable constrained branch have higher stiffness. When M is equal to three, in order to achieve the high precision, the n_s and n₁ are equal to four and one, respectively. As the same time, in order to reduce the occupied space of the mechanism, the CPMs with a suitable constrained branch need to have as compact a structure and as small a size as possible.

3.2 Type synthesis process of the CPM with suitable constrained branch

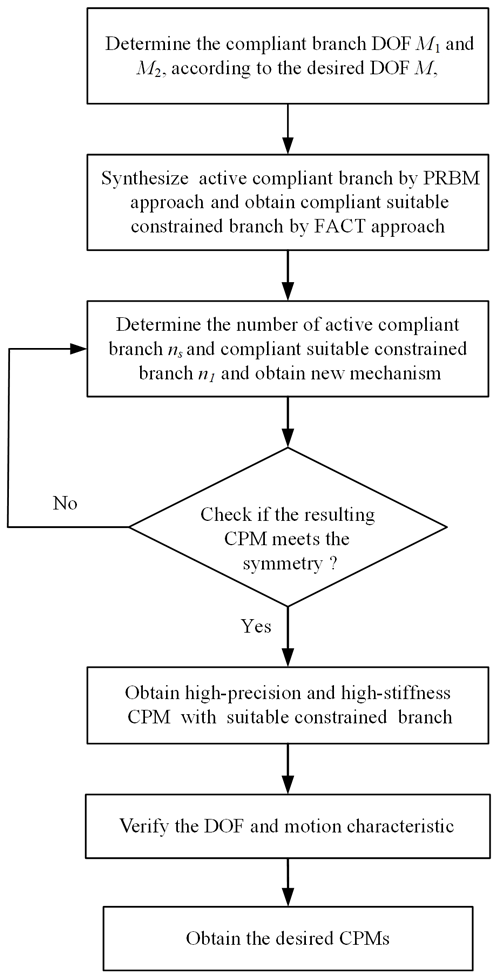
According to the criterion for the type synthesis of the CPM with a suitable constrained branch, a new synthesis approach is proposed for CPMs with a suitable constrained branch based on the PRBM and FACT methods. According to the given DOF, the number of DOF of the compliant suitable constrained branch, M₁, is determined, and the number of DOF of the compliant active branch, M₂, is determined. A compliant branch with a different motion is synthesized based on the PRBM and FACT approaches, respectively. According to the criterion for the type synthesis of the CPM with a suitable constrained branch, the number of compliant active and compliant suitable constrained branches are obtained, respectively. According the principle of symmetry, the new configuration of the symmetrical arrangement mechanism is proposed. The degrees of freedom and motion characteristics of the mechanism are verified by the finite element simulation method. The process for the type synthesis of the CPM with a suitable constrained branch is described in Fig. 5.

Figure 5 Flow chart for the new approach for type synthesis of the CPM.

4 Synthesis of 2R1T compliant parallel mechanism

4.1 Synthesis of compliant active branch

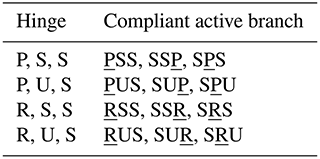
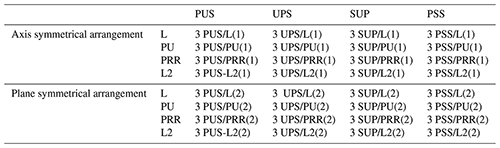
In order to synthesize the 2R1T compliant parallel mechanism, we need to synthesize the compliant active branch based on the proposed synthesis approach. Thus, the motion chain with the 6 DOF need to be synthesized. Besides, according to Sect. 3.1 of the requirements, the short motion chain is selected for the synthesis. Thus, based on the existing 6 DOF serial mechanisms (SMs) in the reference (Lang et al., 2019), these serial mechanisms with only three kinematic pairs are selected as the original branch. This obtains a series of 6 DOF compliant active branches by the rigid-body-replacement method, and some of the branches are illustrated in Table 1. For PUS as the example, the P denotes the flexible hinge with connected to the fixed platform, the S denotes the flexible hinge with connected to the moving platform, and the P denotes the flexible hinge as the actuated hinge.

Table 1 Some types of the compliant active branches.

4.2 Synthesis of the compliant suitable constrained branch

According to the high-stiffness requirement in Sect. 3.1, the CPMs with compliant suitable constrained branches are synthesized to improve the stiffness of the mechanisms. In order to synthesize the 2R1T compliant suitable constrained branch, the DOF of the compliant suitable constrained branch need to be determined based on the proposed type synthesis approach. Thus, a 3 DOF compliant suitable constrained branch needs to be synthesized. The total steps are performed for the synthesis process of the 2R1T compliant suitable constrained branch.

Step 1. Specify the desired freedom space (FS) according to the specifications of a synthesized CM and specify the reciprocal constraint space (CS) by the dual rule. For the 2R1T mechanisms, the freedom space and constraint space are shown in Fig. 6.

Figure 6 Freedom and constraint spaces of the 2R1T motion branch. (a) Freedom space. (b) Constraint space.

Step 2. Determine all possible reciprocal subspaces representing the constraints from step 1 and generate a complete fundamental building block (FBB) library by decomposing all reciprocal constraint subspaces. For the constraints of the 2R1T motion compliant branch, the FBBs and the simple set symbol are illustrated in Fig. 7.

Figure 7 Fundamental building blocks.

Step 3. Obtain all possible subspaces equivalent to the FS based on the set operation for FBBs. Note that, in this paper, the union and intersection of the sets are designated by ∪ and ∩, respectively. For the 2R1T motion compliant branch, the set operation is expressed as follows:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}L\left(N,u\right)& =U\left(N_{\mathrm{1}},n\right)\cup R\left(N_{\mathrm{2}},u\right)\\ & =F\left(N_{\mathrm{1}},u_{\mathrm{1}},n\right)\cup R\left(N_{\mathrm{2}},u_{\mathrm{2}}\right)\\ & =R\left(N_{\mathrm{1}},u_{\mathrm{1}}\right)\cup R\left(N_{\mathrm{2}},u_{\mathrm{1}}\right)\cup R\left(N_{\mathrm{2}},u_{\mathrm{2}}\right)\\ & =R\left(N_{\mathrm{1}},u_{\mathrm{1}}\right)\cup R\left(N_{\mathrm{2}},u_{\mathrm{2}}\right)\cup P\left(n\right)\\ & =R\left(N_{\mathrm{1}},u_{\mathrm{1}}\right)\cup P\left(n\right)\cup R\left(N_{\mathrm{2}},u_{\mathrm{2}}\right)\\ & =U\left(N_{\mathrm{1}},n\right)\cup P\left(n\right).\end{array}\end{array}$$

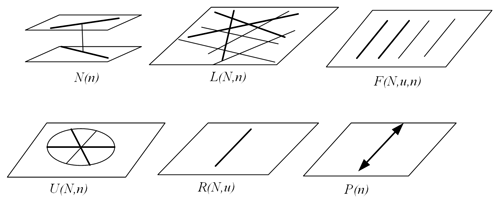
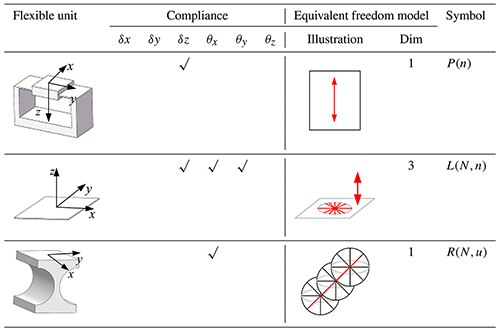
Step 4. Establish the mapping relationship between the FBB and the flexure unit, and select the appropriate flexure unit instead of the FBB. For example, R(N,u) represents a rotational degree of freedom (Yu et al., 2010; Lobontiu, 2002). So, a right circular notched flexible unit (θ_x) can be represented by R(N,u). P(n) represents a translational degree of freedom (Yang et al., 2021). So, a translational flexible unit (δz) can be represented by P(n). L(N,n) represents a plane constraint with 3 DOF. The flexible straight beam unit (θ_x, θ_y, and δz) can be represented by L(N,n) (Jia et al., 2015). Some flexible units are shown in Table 2.

Table 2 Equivalent freedom FBBs of two flexible units.

Table 3 Some types of the suitable constraint compliant branches.

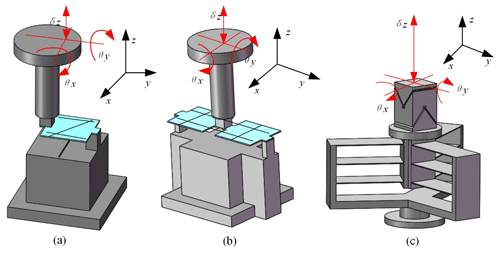
Figure 8 (a) L1 compliant suitable constrained branch. (b) L2 compliant suitable constrained branch. (c) PU compliant suitable constrained branch.

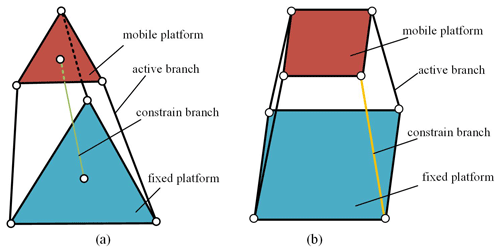
Figure 9 The two different arrangements for the compliant mechanisms. (a) Axis symmetric. (b) Plane symmetric.

Table 4 Some of the new configurations of compliant parallel mechanism.

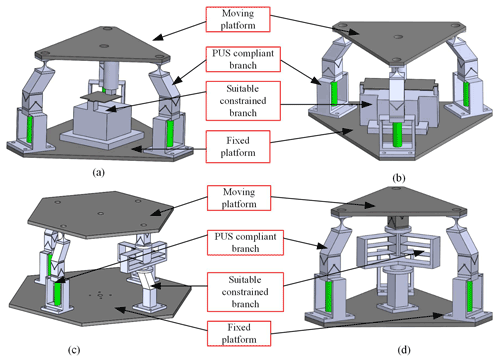
Figure 10 The four new CPMs for the suitable constrained branch. (a) 3 PUS/L(1) CPM. (b) 3 PUS/L2(1) CPM. (c) 3 PUS/PU(2) CPM. (d) 3 PUS/PU(1) CPM.

Step 5. Obtain the compliant suitable constrained branch via the serial layout. Yu et al. (2010) proposed that the DOF of the flexible straight beam is changed when the dimension parameters of the flexible straight beam are changed (Jia et al., 2015). In this paper, the dimension parameters of the flexible straight beam are selected. The narrow flexible straight beam unit has 3 DOF and can achieve two rotational motions and one translational motion, respectively. Thus, the beam can realize a 2R1T motion. For the flexible straight beam, part of the compliant suitable constrained branches are shown in Fig. 8a–b. For the circular notched flexure unit, part of the compliant suitable constrained branches are shown in Fig. 8c.

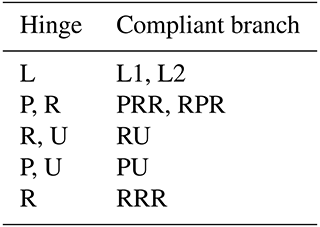
In Fig. 8, three kinds of compliant suitable constrained branches are shown. Among them, each branch has 3 DOF. As shown in Fig. 8a, the L1 compliant suitable constrained branch only has a flexible straight beam. The flexible beam provides three constrained forces, including two parallel constrained forces. The two parallel constrained forces are equivalent to one constrained force and one constrained moment. Thus, this branch can achieve 2R1T motion. Similarly, as shown in Fig. 8b, the L2 compliant suitable constrained branch has two flexible straight beams, and those two flexible straight beams provide two constrained forces and one constrained moment. Thus, the L2 compliant suitable constrained branch can achieve 2R1T motion. As shown in Fig. 8c, the PU compliant suitable constrained beam has a flexible prismatic hinge and a flexible universal joint. The branch can achieve 2R1T motion.

Through steps 1–5, a series of 2R1T compliant suitable constrained branches are synthesized, and some of them are illustrated in Table 3. For L1 as an example, L denotes the flexible straight beam, and 1 denotes the number of the flexible straight beam.

4.3 Synthesis of the high precision CPM

Based on the new type synthesis approach, the number of compliant suitable constrained branches and compliant active branches, respectively, need to been determined. After the synthesis of compliant branches is completed, one compliant suitable constrained branch and two compliant active branches are selected by Eqs. (7) and (8). According to the high-precision requirement in Sect. 3.1, the symmetrical arrangement is selected.

Figure 11 3 PUS/PU(1) compliant parallel mechanism.

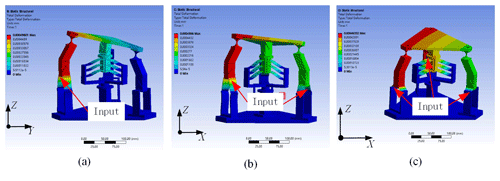
Figure 12 The deformation distribution, with (a) one actuator, (b) two actuators, and (c) three actuators, respectively.

Thus, in order to obtain a 2R1T motion CPM with high precision, this section proposes two special symmetrical arrangements. The first symmetrical arrangement can be called the axis symmetrical arrangement. It is considered as two separated components, where three identical compliant active branches are distributed at 120^∘ around the edge of two platforms, and a compliant suitable constrained branch connects to the center of two platforms. Its structure diagram is shown in Fig. 9a. The second symmetrical arrangement can be called the plane symmetrical arrangement. As shown in Fig. 9b, its structure diagram shows that three identical compliant active branches and one compliant suitable constrained branch are distributed at 90^∘ around the edge of two platforms.

As a result, based on the synthesized compliant active branches and compliant suitable constrained branches, the arrangements are determined. The axis symmetrical (Zhang et al., 2011) and the plane symmetrical arrangements (Pakzad et al., 2019) can achieve high precision when they move in a principal motion direction. As shown in Table 4, a series of the high-precision and high-stiffness CPMs with a suitable constrained branch are proposed through this symmetrical arrangement, and they are illustrated in Fig. 10.

As shown in Table 4, the new 3 PUS/PU(1) compliant parallel mechanism is proposed. For the 3 PUS/PU(1) compliant parallel mechanism as the example, PUS denotes the PUS compliant active branch, PU denotes the PU compliant suitable constrained branch, and (1) denotes the axis symmetrical arrangement.

In Fig. 10, four kinds of CPMs are demonstrated. Among them, each mechanism has four compliant branches, and the 6 DOF compliant active branches are the PUS compliant branch. As shown in Fig. 10a, 3 PUS/L(1) CPM is an axis symmetrical CPM. The suitable constrained branch has only a narrow flexible straight beam and is applies two constraining forces along the x axis and the y axis and one constraining moment around the z axis on the moving platform. Thus, the new 3 PUS/L1(1) CPM can achieve 2R1T motion. As shown in Fig. 10b, 3 PUS/L2(1) CPM is an axis symmetrical CPM. The suitable constrained branch has two narrow flexible straight beams. The two beams ensure the co-planar plane and apply two constraining forces along the x axis and the y axis and one constraining moment around the z axis on the moving platform. Thus, the new 3 PUS/L2(1) CPM can achieve 2R1T motion. As shown in Fig. 10c, 3 PUS/PU(2) CPM is an plane symmetrical CPM. The suitable constrained branch has a flexible prismatic hinge and a flexible universal joint. The branch applies two constraining forces along the x axis and the y axis and one constraining moment around the z axis on the moving platform. Similarly, as shown in Fig. 10d, 3 PUS/PU(1) CPM has a suitable constrained branch. The branch applies two constraining forces along the x axis and the y axis and one constraining moment around the z axis on the moving platform.

4.4 DOF analysis of the CPM

In order to verify the correctness of the proposed synthesis approach, the DOF of the synthesized mechanism is analyzed. In this section, taking the 3 PUS/PU(1) compliant parallel mechanism as the example, a finite element simulation (Zheng et al., 2015; M. Wang et al., 2019) is carried out to validate the DOF and the motion characteristic of 3 PUS/PU(1) compliant parallel mechanism, as shown in Fig. 11.

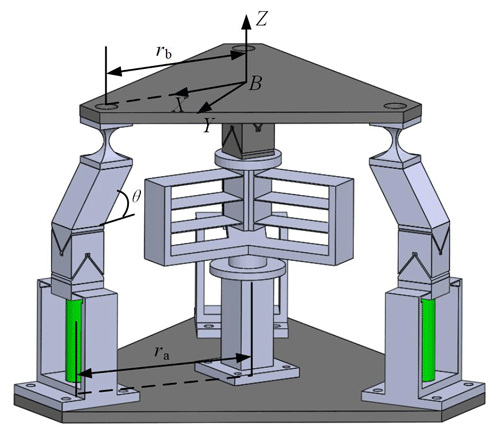
For the finite element model (FEM) of the 3 PUS/PU(1) compliant parallel mechanism, let the circumradius of the moving platform, r_b, be 150 mm, the circumradius of the fixed platform, r_a, be 200 mm, and the intersection angle of the compliant active branch with the fixed platform, θ, be 60^∘. The material is titanium alloy, with a low density and high strength. The material properties are identified, where Young's modulus E is 96 GPa, Poisson's ratio μ is 0.36, and the density ρ is 4620 kg m⁻³.

For the 3 PUS/PU(1) compliant parallel mechanism, the von Mises resultant deformations will be obtained based upon different inputs of the three actuators. One actuator is turned on, two actuators are turned on, and three actuators are turned on, respectively, and the results are shown in Fig. 12.

The deformation results of the 3 PUS/PU(1) compliant parallel mechanism are illustrated in Fig. 12. It can be clearly seen that the moving platform rotates around the x axis, as illustrated in Fig. 12a, the moving platform rotates around the y axis, as illustrated in Fig. 12b, and the moving platform translations along the z axis, as illustrated in Fig. 12c. Thus, the 3 PUS/PU(1) compliant parallel mechanism can achieve 2R1T motion. The results demonstrate the correctness and feasibility of the proposed synthesized approach for CPM with a suitable constrained branch.

5 Conclusion

In this paper, a systematic methodology for a type synthesis of a 2R1T compliant parallel mechanism with a suitable constrained branch is introduced. The whole type synthesis principle is built upon the PRBM approach and the FACT approach, which is also combined with the principle of symmetry. The criteria for the type synthesis of the CPM with a suitable constrained branch is introduced, and the process of the type synthesis is described in detail. A series of 2R1T CPMs with a suitable constraint branch are proposed. Using the finite element simulation, the DOF of the synthesized mechanism is analyzed. The results show that the type synthesis approach is corrected and enables the type synthesis to be simple and effective. These synthesized high-precision and high-stiffness mechanisms have potential applications to space posture adjustments for the space optical load in the aerospace field.

Appendix A: Nomenclature

CM	Compliant mechanism
CPM	Compliant parallel mechanism
CS	Constraint space
DOF	Degree(s) of freedom
FACT	Freedom and constraint topology
FBB	Fundamental building block
FEM	Finite element model
FS	Freedom space
MEMS	Micro electro mechanical system
PM	Parallel mechanism
PRBM	Pseudo-rigid-body model
SCB	Suitable constrained branch
SMs	Serial mechanisms