the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The singular value decomposition method of improved incidence matrix for isomorphism identification of epicyclic gear trains
Mingshuai Zhou
Rongxuan Wu
Wenxu Fu
The epicyclic gear train (EGT) is an advanced gear transmission mechanism, which is widely applied in drive systems. It is of great significance to eliminate the same structure in the type synthesis of EGTs. In this paper, an isomorphism identification method of EGTs based on the singular value decomposition of improved incidence matrix is proposed. Firstly, the improved incidence matrix is used to describe the structure of EGTs. Then, the degree sequence of links and kinematic pairs can be extracted and used as a basic information for preliminary screening. The improved incidence matrix can effectively distinguish multiple joints. Next, the topological connection relationship between the links and the kinematic pairs is extracted by the singular value decomposition of the matrix, which is used as the final value for isomorphism identification of EGTs. Finally, the effectiveness of this method is verified through a lot of examples.
- Article
(476 KB) - Full-text XML
- BibTeX
- EndNote
The epicyclic gear train (EGT) has been commonly used in the transmission of various high-end mechanical equipment due to its advantages of large transmission ratio range, compact structure, large bearing capacity, etc. The configuration synthesis is an effective method to ensure the discovery of potential high-performance EGT structures. The purpose of configuration synthesis is to generate all feasible configurations required by a given number of links and degrees of freedom. In the process of configuration synthesis, it is inevitable to produce numerous EGTs with the same structure, so the isomorphism identification of EGTs shows its important significance. However, due to the large number of configurations generated during the synthesis process, manual screening alone is not practical. Therefore, scholars are committed to developing an algorithm that can automatically distinguish repetitive structures. Since the 1950s and 1960s, the isomorphism identification of kinematic chains has always been a theoretical conundrum in the process of their configuration synthesis, and there is still no completed solution to solve this problem (the EGT is a special kinematic chain with gear pairs). To solve the problem of isomorphism identification of kinematic chains, the proposed methods are mainly divided into the following two categories:
-
The first one is to find the characteristic constant of kinematic chains. Yan and Hall (1982, 1981), Tsai (1987), and Tsai and Lin (1989) utilized methods of the characteristic polynomial based on adjacency matrix for isomorphism identification of kinematic chains, but there are cases of failure. The standard code method (Shin and Krishnamurty, 1992, 1993, 1994) was proposed by Shin et al., but its detection efficiency is not high. The Hamming number (Rao and Rao, 1993a, b; Rao and Raju, 1991) was also used for isomorphism identification of kinematic chains. Its accuracy of the identification is superior, which can effectively differentiate the structural information of the matrix, but there are still some failure cases. Sun et al. (2017) used an improved Hamming number method to solve the problem of isomorphism identification of kinematic chains with multiple joints and have achieved good results, but their method does not have the ability to decode. The eigenvalues and eigenvectors of the adjacency matrix (Cubillo and Wan, 2005; Zhou et al., 2018; Liu and Yu, 2012) were utilized for isomorphism identification, with a certain accuracy, but there are also counterexamples. The loop method (Yang and Ding, 2018; Prasad Raju Pathapati and Rao, 2002) was applied for isomorphism identification of kinematic chains, but the number of loops will increase sharply with the increase of the number of vertices in the topological graph, which will cause a large number of operations. The distance matrix (Yadav et al., 1995; Yadav et al., 1996) was used to describe the connection relationship between the links of the kinematic chain, which represents the shortest distance between the links. However, the structural information contained in the matrix will be destroyed due to some highly symmetrical structures. In recent years, Sun et al. (2020) proposed a set of methods based on the power of the adjacency matrix to extract the feature invariants of kinematic chains, which can be used for the kinematic chain or the EGT, and have achieved good results. Deng et al. (2020) proposed a method for isomorphism identification using topological index, which can also be applied to the EGT. It has achieved good results.
-
The second one is to detect isomorphism from the isomorphic definition of graphs. It is common to start from the topological graph of the kinematic chain and quickly search for the bijective relationship between the vertices and edges of the isomorphic graph through optimization algorithms. Genetic algorithms (Rao, 2003; Feng and Chen, 2001) and an ant algorithm (Yang et al., 2007) were used to identify isomorphism. The advantage of these methods is the fact that they will not easily fall into the local optimal solutions but easily find the global optimal solutions. However, their convergence speed is slow, and they cannot guarantee a high enough correct rate. The neural network algorithm (Rao, 2002) also has similar characteristics.
The research method of pure-rotating-pair kinematic chains is relatively mature, but the problem of EGTs has become more complicated due to the addition of gear pairs in ordinary kinematic chains, which leads to the inapplicability of many existing isomorphism identification methods. Therefore, people have to explore new solutions to expand the scope of application of algorithms.
For the isomorphic identification of the EGT, it is most common to use an adjacent matrix to describe the EGT, but few scholars use the incidence matrix to describe it, mainly because the incidence matrix is not necessarily a square matrix, and the subsequent data processing is difficult. Starting from improving the incidence matrix, the singular value decomposition of the matrix is applied to extract the incidence matrix invariants, which is used as a judgment for the isomorphic identification of the EGT. The method has certain advantages in accuracy and efficiency.
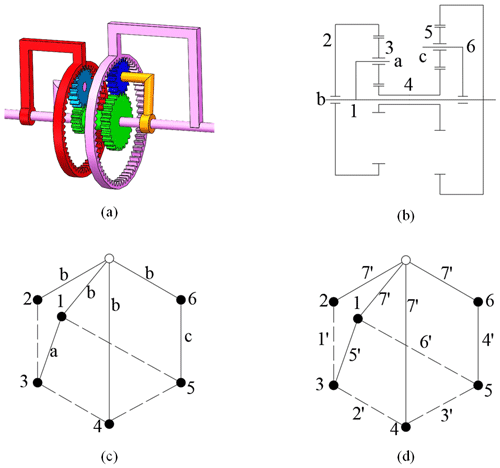
In this paper, the structure of the EGT is described in a topological graph. The topological graph can clearly show its structural characteristics, and it is convenient to convert it into a matrix or array to quantify the structural information of the EGT. Figure 1a shows a three-dimensional model of a Simpson planetary gear train, and Fig. 1b shows its structural graph. This paper utilizes the bicolor topological graph by Yang and Ding (2018) to represent the EGT. As shown in Fig. 1c, the solid vertex represents the link, the hollow vertex represents the multiple joints, the solid line edge represents the rotating pair, and the dotted line edge represents the gear pair. The edges associated with the hollow vertex can be regarded as the same kinematic pair. The serial numbers of links and kinematic pairs are marked as “ i ” and “ i′ ”, respectively, in Fig. 1d.
In order to facilitate analysis and processing, the structural information of the topology can be stored in a digital matrix. Consequently, this paper proposes an improved incidence matrix to describe the topological graph of the EGT.
Definition 1. The definition of the improved incidence matrix A is as follows:
where i (1, 2, …, m) represents the ith vertex (i.e., the ith link), and j (1, 2, …, n) represents the jth edge (i.e., the jth kinematic pair); then,
For example, the following equation (Eq. 3) is the improved incidence matrix corresponding to the EGT topological graph in Fig. 1, in which the second row represents Link 2, which is adjacent to Gear Pair 1 in the first column and Rotating Pair 7 in the seventh column, respectively.
The improved incidence matrix Am×n (i.e., the link–kinematic-pair matrix) can clearly express the information about links and kinematic pairs of the EGT. Therefore, the basic structural constants obtained from the matrix are as follows:
-
The number of rows of the matrix represents the number of links of the EGT, and the number of columns of the matrix represents the number of kinematic pairs of the EGT.
-
Nonzero elements in Row i of the matrix represent kinematic pairs adjacent to Link i, and different numbers represent different types of kinematic pairs.
-
The number of nonzero elements in Column j of the matrix is the number of links adjacent to Kinematic Pair j. When it is more than two, it is with multiple joints, i.e., the compound kinematic pair.
Definition 2. The code of link (CL) is the kinematic pair information connected with the corresponding link; the sequence of the CL from large to small is called the CLS, which is expressed as CL in the paper. It is defined as follows:
where
Here, rpi represents the number of rotating pairs associated with Link i, and gpi represents the number of gear pairs associated with Link i.
Definition 3. The code of kinematic pair (CKP) is the number of links connected with the corresponding kinematic pair; the sequence of the CKP from large to small is called the CKPS, which is expressed as Ckp in the paper. It is defined as follows:
where
Here, nlj indicates the number of links adjacent to Kinematic Pair j.
Definition 4. (Feng and Chen, 2001) Given undirected graphs and and if there is bijection f such that , , then G1 and G2 are isomorphic and denoted as G1≃G2.
According to the definition of isomorphism, the nodes of the topological graph with the same structure have a one-to-one mapping relationship. It is deduced that the topological adjacency relationship between nodes of isomorphic topological graph is also the same. There is then the following definition:
Definition 5. If the number and type of links and kinematic pairs and the topological constraints between links in two EGTs are identical, then these two EGTs could be considered to be isomorphic.
For the above basic structural constants, the CLS and the CKPS can be obtained directly from the improved incidence matrix. However, it is difficult to extract directly the topological constraints between links. Generally, the eigenvalue and eigenvector method is used to extract the characteristic structural constants of matrices, but the precondition for this method is that the matrix must be a square matrix. The numbers of rows and columns of the improved incidence matrix are related to the numbers of links and kinematic pairs, so it is not necessarily a square matrix. The singular value does not change with the exchange of rows and columns of the matrix, so it is a characteristic invariant of the matrix. Therefore, the singular value of the improved incidence matrix can be used as the structural characteristic information of the topological connection between the EGT's links.
For the matrix , where m and n are any positive integers, the following matrix decomposition theorem exists:
Theorem 1. If , where r>0, then there is the orthogonal matrix Um×m, Vn×n, which makes
where Dm×n is a rectangular diagonal matrix, and r is the number of nonzero elements on the diagonal of the matrix.
It has the following definition: if , then the nonnegative square root of the nonzero eigenvalue of the matrix ATA is the singular value of matrix A, and all of them are denoted as σ(A). Equation (9) is called the singular value decomposition (SVD). The calculation formula of SVD is as follows:
where λ is the eigenvalue of the matrix ATA, and x is the eigenvector corresponding to λ.
By solving Eq. (11), we can obtain the eigenvalue set of the matrix ATA. Thus, the singular value set σ(A) of matrix A is
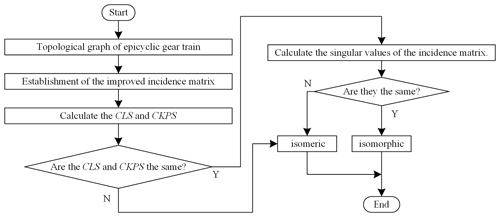
Therefore, the algorithmic steps of isomorphism identification are as follows:
-
Step 1. One should attain the bicolor topological graphs of the two EGTs to be compared and construct the improved incidence matrices of the two EGTs.
-
Step 2. One should compare the basic structure constants of the two matrices, including the sequence of the CL and the sequence of the CKP. If they are the same, then go to Step 3; if not, they are isomeric, so go to Step 4.
-
Step 3. Calculate the singular values of the two incidence matrices. If they are the same, then they are considered to be isomorphic; otherwise, they are isomeric, so go to Step 4.
-
Step 4. The algorithm is over.
The isomorphism identification flowchart is given in Fig. 2.
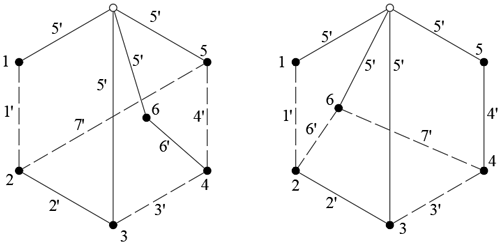
Case 1. Figure 3 shows the bicolor topological graphs of two 6-link EGTs with multiple joints. The method in this paper is utilized in the isomorphism identification of the two EGTs, and the specific process is as follows.
The two improved incidence matrices of the two EGTs are as follows:
That is, the basic structure constants of the two EGTs are the same.
The singular value decompositions of the two matrices are performed:
Here, , which proves that the two EGTs are isomorphic. By changing the positions of vertex 6 and vertex 5 in Fig. 3, right, we can know that they are isomorphic. The result of isomorphism identification is consistent with reality.
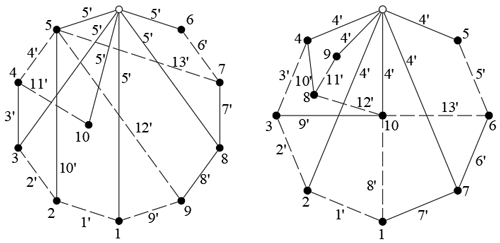
Case 2. Figure 4 shows the topological graphs of two 8-link EGTs. It is observed that the two are isomeric. The method in this paper is used in the isomorphism identification of the two EGTs, and the specific process is as follows.
The two improved incidence matrices of the two EGTs are as follows:
Here, but , which shows that the two EGTs are isomeric. The result of isomorphism identification is consistent with reality. The judgment process is over in advance.
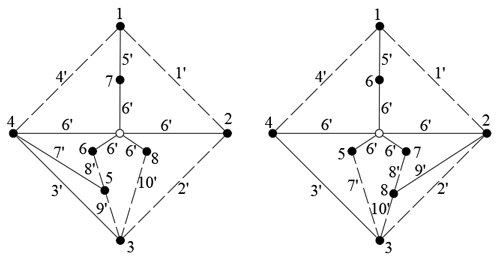
Case 3. Figure 5 shows the topological graphs of two 10-link EGTs. It is carefully observed that the two EGTs are isomorphic. Then the method in this paper is employed in the isomorphism identification of the two EGTs.
These two EGTs are isomorphic, which means that the result of isomorphism identification is consistent with reality.
The three above cases show two different results, namely, isomorphism and isomerism. Since the number of links of the EGTs in the first two cases is small, we can easily observe whether the two EGTs are isomorphic manually. However, in the last case, the EGTs have a large number of links and complex topology, so it will be difficult to manually judge whether they are isomorphic. Moreover, in the process of configuration synthesis, a large number of EGT structures will be generated, and manual comparison will be very time-consuming. Therefore, the automatic algorithm of isomorphism identification shows its main significance.
-
In this paper, the improved incidence matrix is used to describe the EGT structure. The improved incidence matrix is convenient to retain the information of links and kinematic pairs of the EGT. Compared with the adjacency matrix, it can effectively and intuitively determine multiple joints.
-
Compared with some mainstream methods, the SVD method is very simple in implementation and judgment efficiency is high. For example, the loop method needs to find all loops (or loops with given requirements) and then classify and code these. As the number of loops increases, the amount of computation increases exponentially. The adjacency matrix eigenvalue and eigenvector method utilizes the link-to-link adjacency matrix to store structural information. The method is relatively simple, but there are many counterexamples and low reliability. The standard code is used for isomorphism identification, but the power of the matrix needs to be used many times to compare the symmetrical links in the mechanism. It is computationally expensive and has many steps. Relatively speaking, the SVD method only needs to compare CLS and CKPS for preliminary discrimination, and the two can be obtained directly from the improved incidence matrix. Calculating the singular value of the improved incidence matrix, the topological connection relationship between EGTs' links can be obtained. At present, there have been no failure cases.
All data included in this study are available upon request by contacting the corresponding author.
MZ conceived the original ideas and drafted the manuscript. WS supervised the project and reviewed the writing. RW produced the figures in this article. WF helped with the writing and language.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Advances in Service and Industrial Robotics – RAAD2021”. It is a result of the 30th International Conference on Robotics in Alpe-Adria-Danube Region, RAAD 2021, Futuroscope-Poitiers, France, 21–23 June 2021.
This work is supported in part by the National College Students Innovation and Entrepreneurship Training Program (China) (grant no. S202110488043), the National Natural Science Foundation of China (grant no. 51875418), Youth Fund of Hubei Science and Technology Department (grant no. 2021CFB135), Foundation of Hubei Provincial Education Department (grant no. B2020011), and Wuhan University of Science and Technology (WUST) National Defense Pre-research Foundation (grant no. GF202008).
This research has been supported by the Youth Fund of Hubei Science and Technology Department (grant no. 2021CFB135), and the National College Students Innovation and Entrepreneurship Training Program (China) (grant no. S202110488043), National Natural Science Foundation of China (grant no. 51875418), Foundation of Hubei Provincial Education Department (grant no. B2020011), Wuhan University of Science and Technology (WUST) National Defense Pre-research Foundation (grant no. GF202008).
This paper was edited by Mohamed Amine Laribi and reviewed by Joonhong Park and one anonymous referee.
Cubillo, J. P. and Wan, J.: Comments on mechanism kinematic chain isomorphism identification using adjacent matrices, Mech. Mach. Theory, 40, 131–139, https://doi.org/10.1016/j.mechmachtheory.2004.07.004, 2005.
Deng, T., Xu, H., Tang, P., Liu, P., and Yan, L.: A novel algorithm for the isomorphism detection of various kinematic chains using topological index, Mech. Mach. Theory, 146, 103740, https://doi.org/10.1016/j.mechmachtheory.2019.103740, 2020.
Feng, C. and Chen, Y.: Mechanism kinematics chain isomorphism identification based on genetic algorithms, Chin. J. Mech. Eng., 37, 27–30, https://doi.org/10.3901/JME.2001.10.027, 2001.
Liu, J. and Yu, D.: Representations & isomorphism identification of planar kinematic chains with multiple joints based on the converted adjacent matrix, J. Mech. Eng., 48, 15–21, https://doi.org/10.3901/JME.2012.05.015, 2012.
Prasad Raju Pathapati, V. V. N. R. and Rao, A. C.: A new technique based on loops to investigate displacement isomorphism in planetary gear trains, J. Mech. Design, 124, 662–675, https://doi.org/10.1115/1.1503373, 2002.
Rao, A. C.: An artificial neural network approach to mechanism kinematic chain isomorphism identification, Mech. Mach. Theory, 37, 549–551, https://doi.org/10.1016/S0094-114X(02)00004-6, 2002.
Rao, A. C.: A genetic algorithm for epicyclic gear trains, Mech. Mach. Theory, 38, 135–147, https://doi.org/10.1016/S0094-114X(02)00094-0, 2003.
Rao, A. C. and Raju, D. V.: Application of the hamming number technique to detect isomorphism among kinematic chains and inversions, Mech. Mach. Theory, 26, 55–75, https://doi.org/10.1016/0094-114X(91)90022-V, 1991.
Rao, A. C. and Rao, C. N.: Loop based pseudo hamming values–I testing isomorphism and rating kinematic chains, Mech. Mach. Theory, 28, 113–127, https://doi.org/10.1016/0094-114X(93)90051-V, 1993a.
Rao, A. C. and Rao, C. N.: Loop based pseudo hamming values–II inversions, preferred frames and actuators, Mech. Mach. Theory, 28, 129–143, https://doi.org/10.1016/0094-114X(93)90052-W, 1993b.
Shin, J. K. and Krishnamurty, S.: Development of a standard code for colored graphs and its application to kinematic chains, Proceedings of the ASME 1992 Design Technical Conferences, 22nd Biennial Mechanisms Conference: Flexible Mechanisms, Dynamics, and Analysis, Scottsdale, Arizona, USA, 13–16 September 1992, DETC1992-0387, https://doi.org/10.1115/DETC1992-0387, 1992.
Shin, J. K. and Krishnamurty, S.: Standard code technique in the enumeration of epicyclic gear trains, Mech. Mach. Theory, 28, 347–355, https://doi.org/10.1016/0094-114X(93)90075-7, 1993.
Shin, J. K. and Krishnamurty, S.: On identification and canonical numbering of pin-jointed kinematic chains, J. Mech. Design, 116, 182–188, https://doi.org/10.1115/1.2919344, 1994.
Sun, L., Cui, R., Ye, Z., Zhou, Y., Xu, Y., and Wu, C.: Similarity recognition and isomorphism identification of planar kinematic chains, Mech. Mach. Theory, 145, 103678, https://doi.org/10.1016/j.mechmachtheory.2019.103678, 2020.
Sun, W., Kong, J., and Sun, L.: The improved hamming number method to detect isomorphism for kinematic chain with multiple joints, J. Adv. Mech. Des. Syst., 11, JAMDSM0061, https://doi.org/10.1299/jamdsm.2017jamdsm0061, 2017.
Tsai, L. W.: An application of the linkage characteristic polynomial to the topological synthesis of epicyclic gear trains, J. Mech. Trans. and Automation, 109, 329–336, https://doi.org/10.1115/1.3258798, 1987.
Tsai, L. W. and Lin, C. C.: The creation of nonfractionated, two-degree-of-freedom epicyclic gear trains, J. Mech. Trans. and Automation, 111, 524–529, https://doi.org/10.1115/1.3259033, 1989.
Yadav, J. N., Pratap, C. R., and Agrawal, V. P.: Computer aided detection of isomorphism among kinematic chains and mechanisms using the concept of modified distance, Mech. Mach. Theory, 31, 439–444, https://doi.org/10.1016/0094-114X(95)00078-D, 1996.
Yadav, J. N., Pratap, C. R., and Agrawal, V. P.: Detection of isomorphism among kinematic chains using the distance concept, J. Mech. Design, 117, 607–611, https://doi.org/10.1115/1.2826728, 1995.
Yan, H. S. and Hall, A. S.: Linkage characteristic polynomials: definitions, coefficients by inspection, J. Mech. Design, 103, 578–584, https://doi.org/10.1115/1.3254957, 1981.
Yan, H. S. and Hall, A. S.: Linkage characteristic polynomials: assembly theorems, uniqueness, J. Mech. Design, 104, 11–20, https://doi.org/10.1115/1.3256301, 1982.
Yang, P., Pei, Z., Liao, N., and Yang, B.: Isomorphism identification for epicyclic gear mechanism based on mapping property and ant algorithm, Eng. Comput., 23, 49–54, https://doi.org/10.1007/s00366-006-0041-y, 2007.
Yang, W. and Ding, H.: The perimeter loop-based method for the automatic isomorphism detection in planetary gear trains, J. Mech. Design, 140, 123302, https://doi.org/10.1115/1.4041572, 2018.
Zhou, Z., Kong, J., Sun, L., and Xiao, Q.: Representation and isomorphism identification of planar kinematic chains with multiple joints on value-added matrix, Mech. Sci. Tech. Aer. Eng., 37, 657–662, https://doi.org/10.13433/j.cnki.1003-8728.2018.0501, 2018.
- Abstract
- Introduction
- Topological descriptions of the EGT
- The improved incidence matrix
- Isomorphism identification
- Numerical examples
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Topological descriptions of the EGT
- The improved incidence matrix
- Isomorphism identification
- Numerical examples
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References