Multi-objective optimization of a redundantly actuated parallel robot mechanism for special machining

In order to improve the accuracy and efficiency of special machining for a complex surface, a 2RPU-2SPR (where R, P, U, and S stand for revolute, prismatic, universal, and spherical joints, respectively) over-constrained redundantly actuated parallel robot mechanism is proposed. And six performance evaluation indexes are established to ensure the working performance including workspace, motion/force transmission efficiency, stiffness, dexterity, energy efficiency, and the inertia coupling index. Furthermore, a collaborative optimal configuration algorithm is conducted based on an orthogonal experimental design algorithm and a multi-objective particle swarm optimization algorithm. On the basis given above, a simulation analysis of a multi-objective optimization is conducted. Compared with two traditional, intelligent optimization algorithms of a multi-objective particle swarm optimization algorithm and an orthogonal experimental design method, the improved collaborative multi-objective optimization algorithm has a better optimization effect.

1 Introduction

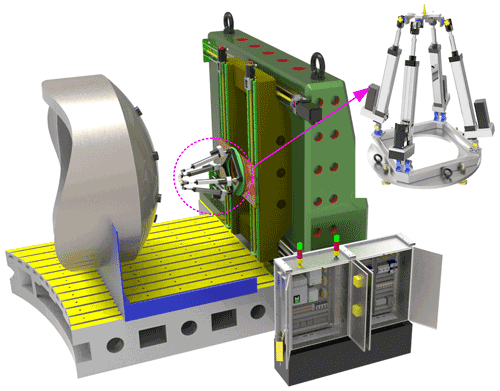
With the continuous development of the manufacturing industry, machine tools play an important role in the processing of large and complex specially shaped work pieces. The requirements of parts that process quality and accuracy are also increasing, and processing equipment is developed in the mode of traditional equipment to advanced equipment and high-level equipment. Zhang et al. (2019a) presented a novel redundantly actuated parallel manipulator that can be employed to form a five-axis hybrid kinematic machine tool for large heterogeneous complex structural component machining in the aerospace field. Yang et al. (2019) invented a new three degrees of freedom (DOF) asymmetric translational parallel manipulator that is adapted to pick-and-place operation under heavy load. Wu et al. (2019) provided formulations of shape singularity and illustrate the application of shape singularity in an adjustable compliance mechanism design. Therefore, the research on redundantly actuated parallel mechanism is great valuable for special machining. Zhang et al. (2018) proposed a novel mobile serial–parallel mechanism with legs for in-pipe use and analyzed the singularities of the parallel mechanism. In addition, the parallel mechanism can achieve a continuous and equivalent rotation.

However, an over-constrained redundantly actuated parallel mechanism is a special parallel mechanism which has the characteristics of multi-variability, strong coupling, and complex nonlinearity. Reveles et al. (2016) presented a method for the joint trajectory planning of kinematically redundant parallel manipulators, and the working modes could be chosen and combined to complete the whole path by applying this approach. Furthermore, an accurate dynamic model of over-constrained redundantly actuated parallel mechanisms is extremely complex because of the coupling relationship between the branches of the parallel mechanism. Zhang et al. (2019c) simplified the dynamics mathematical model of the parallel manipulator by employing D'Alembert's principle and the principle of virtual work. Russo et al. (2018) solved the problems of inverse and forward kinematic for a parallel mechanism with 3-UPR (where R, P, and U, stand for revolute, prismatic, and universal joints, respectively) architecture and computed the Jacobian matrix to evaluate the singular positions of the end-effector. Chen et al. (2012) derived the velocity and the force Jacobian matrix of the parallel mechanism and analyzed the distribution of different dexterity measures in workspace, respectively. Tian et al. (2020) presented a general approach for the error modeling of a lower-mobility parallel mechanism based on screw theory, and then the geometric errors affecting the compensable accuracy of the end-effector were separated using the properties of dual vector space. Zou et al. (2021) proposed a 3 DOF parallel robot without rotation ability and calculated the distributions of maximum joint effect of force and speed. At present, many researchers at home and abroad have carried out abundant related researches on multi-objective performance optimization in different application fields. Enferadi et al. (2017) proposed a kinematics index that is called global workspace conditioning index and adopted a multi-objective evolutionary algorithm to find the optimal solutions and Pareto frontier. Asker et al. (2019) conducted dimensional synthesis based on maximizing the workspace index and the global force transmission and stiffness indices to optimize the device dimensions. Zhang et al. (2017) reflected a competitive mechanism based on multi-objective particle swarm optimization. Zeng et al. (2021) adopted an improved calculation of crowding distance, which substituted a traditional addition operation with multiplication operation. In addition, differential evolution was concatenated to diversify the population, and the key parameters of differential evolution had been assigned different adjusting strategies to further enhance the overall performance. A novel hybrid system was proposed by Xiang et al. (2015) based on an improved gravitational search algorithm which has good performance in solving function optimization problems. In order to accelerate the convergence to the Pareto frontier, Liu et al. (2018) presented a dynamic multiple population particle swarm optimization algorithm based on the decomposition and prediction. Wu et al. (2020) proposed a new algorithm to improve the convergence speed of a dynamic multi-objective optimization algorithm by combining the evolutionary algorithm and the dynamic strategy. Houssein et al. (2022) adopted a multi-objective optimization algorithm, based on the slime mold algorithm, which had the ability to provide better solutions in terms of the Pareto sets proximity and inverted generational distance in decision space indicators compared with the other algorithms.

In short, reasonable structural parameters are the basis of mechanical design. The quality of the mechanism parameters directly determines whether the mechanical performance of the mechanism is excellent or not. However, there are many design variables and solving processes of the objective function when designing the structural parameters of over-constrained redundantly actuated parallel mechanism. The research mechanism parameters cannot be optimized effectively if one simply considers a certain performance index when optimizing the parameters of parallel mechanism. The main contribution of this paper is as follows: a novel, redundantly over-constrained 2PRU-2SPR parallel mechanism is presented, and its structure is introduced in detail. Simultaneously, the kinematics and dynamics analysis of a 2RPU-2SPR parallel mechanism is deduced. What is more, in order to obtain more reasonable design structural parameters and improve the working performance of the 2RPU-2SPR parallel mechanism, six performance evaluation indexes are established to ensure the working performance, including workspace, stiffness, motion/force transmission efficiency, dexterity, energy efficiency, and the inertia coupling index. Furthermore, a multi-objective particle swarm optimization configuration algorithm based on orthogonal experiment response design is proposed in this paper, aiming at special machining complex surfaces. Compared with a traditional multi-objective optimization algorithm, the improved, collaborative multi-objective optimization algorithm has a better optimization effect.

2 2RPU-2SPR over-constrained redundantly actuated parallel mechanism

2.1 Description of each kinematic joint

An over-constrained 2RPU-2SPR redundantly actuated parallel mechanism is proposed in order to meet the machining requirements of complex surfaces and improve the machining quality. As shown in Fig. 1, the mechanism is mainly composed of a fixed platform, moving platform, end-effector, and two joints of actuating branches with the same structure. The fixed platform of the mechanism relates to moving platform through these two joints of actuating branches. One joint of branches is the RPU kinematic branch chain, and the kinematic joints include a revolute (R) joint, a prismatic (P) joint, and a universal (U) joint. The other joint of branches is the SPR kinematic branch, and the kinematic joints include a spherical (S) joint, a prismatic (P) joint, and a revolute (R) joint. It is worth noting that the mechanism has 3 degrees of freedom, namely two rotational degrees of freedom and one translational degree of freedom. However, the number of actuating joints is four, and the number of actuating joints is greater than free degrees. So, the mechanism belongs to a redundant actuated mechanism.

Figure 1 The five-axis linkage processing equipment.

2.2 Establishment of mechanism coordinate system

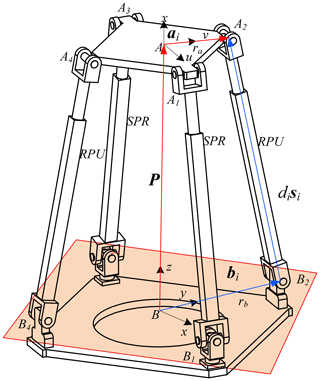
With B as the center, a fixed coordinate system B–xyz is established on the mechanism base B₁B₂B₃B₄, in which the directions of the x axis and y axis are parallel to BB₄ or BB₁, and the direction of the z axis is determined according to the right-hand rule. The coordinate system of the moving platform A₁A₂A₃A₄ is established with the geometric center of A in the mechanism, and the directions of u axis and v axis on the coordinate system are parallel to AA₄ or AA₁. Similarly, the w axis is determined according to the right-hand rule (as shown in Fig. 2).

Figure 2 Structure diagram of a parallel mechanism.

2.3 Kinematics and dynamics analysis of 2RPU-2SPR parallel mechanism

The kinematics problem of a parallel mechanism is to construct the mapping relationship between the actuating component and the output component and to study the regular motion task performed by output components under the action of an actuating force or torque. A kinematics and dynamics analysis of the parallel mechanism is a critical step. It is not only a necessary condition for an integrated performance evaluation, scale synthesis and real-time control research but also a prerequisite for improving the motion accuracy of the mechanism. The introduction of the redundantly actuated structure of the redundantly actuated parallel mechanism means that it can effectively improve the stiffness of the mechanism and workspaces, avoid singularity, and keep the actuating force stable. However, this will make it difficult to analyze the kinematics and dynamics of the parallel mechanism.

As shown in Fig. 2, it can be obtained based on the closed vector method as follows:

$$\begin{array}{}\text{(1)}& {\mathit{b}}_i+d_i{\mathit{s}}_i=\mathit{p}+{\mathit{a}}_i,{\mathit{a}}_i={}^{\mathrm{B}}{R}_{\mathrm{A}}^{\mathrm{A}}{\mathit{a}}_i,\end{array}$$

where d_i represents the linear displacement of the actuator, and b_i is the position vector of the joint hinge point in the fixed coordinate system. p=[xyz]^T represent the position vector of moving platform coordinate system under the fixed coordinate system, and s_i is the unit vector of actuator. ^BR_A represents rotation matrix of moving platform relative to the fixed coordinate system, a_i represents position vector of ^Aa_i in fixed coordinate system, and ^Aa_i represents the position vector of the hinge point of moving platform in dynamic coordinate system, i.e., as follows:

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{ll}{\mathit{b}}_{\mathrm{1}}={\left(\begin{array}{ccc}\mathrm{0}& r_{\mathrm{b}}& \mathrm{0}\end{array}\right)}^{\mathrm{T}},& {\mathit{b}}_{\mathrm{2}}={\left(\begin{array}{ccc}-r_{\mathrm{b}}& \mathrm{0}& \mathrm{0}\end{array}\right)}^{\mathrm{T}},\\ & {\mathit{b}}_{\mathrm{3}}={\left(\begin{array}{ccc}\mathrm{0}& -r_{\mathrm{b}}& \mathrm{0}\end{array}\right)}^{\mathrm{T}},\\ & {\mathit{b}}_{\mathrm{4}}={\left(\begin{array}{ccc}{r}_{\mathrm{b}}& \mathrm{0}& \mathrm{0}\end{array}\right)}^{\mathrm{T}}\\ {}^{\mathrm{A}}{\mathit{a}}_{\mathrm{1}}={\left(\begin{array}{ccc}\mathrm{0}& r_{\mathrm{a}}& \mathrm{0}\end{array}\right)}^{\mathrm{T}},& {}^{\mathrm{A}}{\mathit{a}}_{\mathrm{2}}={\left(\begin{array}{ccc}-r_{\mathrm{a}}& \mathrm{0}& \mathrm{0}\end{array}\right)}^{\mathrm{T}},\\ & {}^{\mathrm{A}}{\mathit{a}}_{\mathrm{3}}={\left(\begin{array}{ccc}\mathrm{0}& -r_{\mathrm{a}}& \mathrm{0}\end{array}\right)}^{\mathrm{T}},\\ & {}^{\mathrm{A}}{\mathit{a}}_{\mathrm{4}}={\left(\begin{array}{ccc}{r}_{\mathrm{a}}& \mathrm{0}& \mathrm{0}\end{array}\right)}^{\mathrm{T}}.\end{array}\right.\end{array}$$

The homogeneous coordinate transformation matrix T can be obtained by three transformations, that is, revolute α around the x axis, moving h along the z axis, and then revolute β around the v axis, and ^BR_A represents the rotation matrix. Then, the homogeneous coordinate transformation matrix can be expressed in Eq. (3) as follows:

$$\begin{array}{}\text{(3)}& \mathbf{T}=\left[\begin{array}{cc}{}^{\mathrm{B}}{R}_{\mathrm{A}}& \mathit{p}\\ \mathrm{0}& \mathrm{1}\end{array}\right]=\left[\begin{array}{cccc}\mathrm{c}\mathit{\beta }& \mathrm{0}& \mathrm{s}\mathit{\beta }& \mathrm{0}\\ \mathrm{s}\mathit{\alpha }\mathrm{s}\mathit{\beta }& \mathrm{c}\mathit{\alpha }& -\mathrm{s}\mathit{\alpha }\mathrm{c}\mathit{\beta }& -h\mathrm{s}\mathit{\alpha }\\ -\mathrm{s}\mathit{\beta }\mathrm{c}\mathit{\alpha }& \mathrm{s}\mathit{\alpha }& \mathrm{c}\mathit{\alpha }\mathrm{c}\mathit{\beta }& h\mathrm{c}\mathit{\alpha }\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\end{array}$$

where sin and cos are abbreviated as s and c, respectively.

As can be seen from Eq. (3), the position vector p=[xyz]^T is a function of independent parameter variable X=[zαβ]^T, and the coupled motion of its pose can be expressed in Eq. (4) as follows:

$$\begin{array}{}\text{(4)}& x=\mathrm{0},y=-h\sin \mathit{\alpha },z=h\cos \mathit{\alpha },y=-z\tan \mathit{\alpha }.\end{array}$$

The inverse position solution of Eq. (1) can be expressed in Eq. (5) as follows:

$$\begin{array}{}\text{(5)}& d_i=\mathrm{|}\mathrm{|}\mathit{p}+{\mathit{a}}_i-{\mathit{b}}_i\mathrm{|}\mathrm{|},{\mathit{s}}_i=(\mathit{p}+{\mathit{a}}_i-{\mathit{b}}_i)/d_i,\end{array}$$

where ||•|| represents the Euclidean norm of actuating vector, and s_i is the unit vector of the actuator.

Equation (5) calculates arithmetic square root, which can be expressed in Eq. (6) as follows:

$$\begin{array}{}\text{(6)}& \left\{\begin{array}{l}{d}_{\mathrm{1}}=\sqrt{{\left(z\tan \mathit{\alpha }-r_{\mathrm{a}}c\mathit{\alpha }+r_{\mathrm{b}}\right)}^{\mathrm{2}}+{\left(z+r_{\mathrm{a}}s\mathit{\alpha }\right)}^{\mathrm{2}}}\\ d_{\mathrm{2}}=\sqrt{{\left(z+r_{\mathrm{a}}c\mathit{\alpha }c\mathit{\beta }\right)}^{\mathrm{2}}+{\left(b-r_{\mathrm{a}}c\mathit{\alpha }\right)}^{\mathrm{2}}+{\left(z\tan \mathit{\alpha }+r_{\mathrm{a}}s\mathit{\alpha }s\mathit{\beta }\right)}^{\mathrm{2}}}\\ d_{\mathrm{3}}=\sqrt{{\left(z\tan \mathit{\alpha }+r_{\mathrm{a}}c\mathit{\alpha }-r_{\mathrm{b}}\right)}^{\mathrm{2}}+{\left(z-r_{\mathrm{a}}s\mathit{\alpha }\right)}^{\mathrm{2}}}\\ d_{\mathrm{4}}=\sqrt{{\left(z-r_{\mathrm{a}}c\mathit{\alpha }c\mathit{\beta }\right)}^{\mathrm{2}}+{\left(b-r_{\mathrm{a}}c\mathit{\alpha }\right)}^{\mathrm{2}}+{\left(z\tan \mathit{\alpha }-r_{\mathrm{a}}s\mathit{\alpha }s\mathit{\beta }\right)}^{\mathrm{2}}}.\end{array}\right.\end{array}$$

Given the position of the moving platform, the actuating joint of 2RPU-2SPR over-constrained redundantly actuated parallel mechanism can be obtained from the inverse solution equation of pose, as shown in Eq. (6).

Then, we find the first derivative of time from Eq. (6) as follows:

$$\begin{array}{}\text{(7)}& \dot{q}={\mathbf{J}}_{\mathrm{0}}\dot{X},\end{array}$$

where $\dot{q}=[{\dot{d}}_{\mathrm{1}},{\dot{d}}_{\mathrm{2}},{\dot{d}}_{\mathrm{3}},{\dot{d}}_{\mathrm{4}}{]}^{\mathrm{T}}$ and J₀ are the Jacobian matrix of the parallel mechanism. For the derivation process of the Jacobian matrix, i.e., J₀, has been explained by Zhang et al. (2020) in detail. The acceleration of the actuating joint can be obtained by deriving the time on both sides of Eq. (7), as follows:

$$\begin{array}{}\text{(8)}& \ddot{q}={\dot{\mathbf{J}}}_{\mathrm{0}}\dot{X}+{\mathbf{J}}_{\mathrm{0}}\ddot{X},\end{array}$$

where ${\dot{\mathbf{J}}}_{\mathrm{0}}$ is the derivative of Jacobian matrix.

Due to the coupling relationship between branches of the parallel mechanism, its accurate dynamic model is extremely complex. Therefore, it is necessary to establish an accurate dynamic model as much as possible and build a mapping relationship between the output of the mechanism's moving platform and the force of actuating joint. According to the virtual work principle and D'Alembert's principle, the forces acting on mass center of each system component include gravity, inertial force, and inertial moment. When considering the whole system and ignoring influence of friction in components, the general expression of generalized coordinate dynamic model, based on workspace, can be expressed in Eq. (9) as follows:

$$\begin{array}{}\text{(9)}& \mathbf{M}\left(X\right)\ddot{X}+\mathbf{C}(\dot{X},X)\dot{X}+\mathbf{N}\left(X\right)={\mathbf{J}}_{\mathrm{0}}^{\mathrm{T}}{\mathit{\tau }}_{\mathrm{a}},\end{array}$$

where M(X) is a positive definite inertia matrix of the parallel robot mechanism, $\mathbf{C}(\dot{X},X)$ is a centripetal and Coriolis force coefficient matrix, N(X) is the sum of gravity term matrix and external load, and τ_a is the actuating branch chain control force vector.

3 Establishment of mechanism performance evaluation index

3.1 Workspace evaluation index

Workspace refers to working area that can be reached by the end-effector on the moving platform, which is the direct embodiment of working performance to mechanism. It is also a crucial performance index to measure the comprehensive performance of a mechanism for a redundantly actuated parallel mechanism introduced in this paper. Wang et al. (2020) proposed a variable human–robot workspace based on the user and introduced two kinds of trajectory planning methods. Generally, the analysis methods for the workspace of parallel mechanism mainly include an analytical and numerical method. The method used in this paper is limit boundary search method, which divides the parallel mechanism into four motion branches and then determines the motion range of a single branch chain according to mechanism parameters and motion joint constraints. The envelope surface of the parallel mechanism motion space is obtained, and the workspace range of the mechanism is determined.

The size of a global workspace can be measured by the volume ratio of an effective workspace to search space, namely Eq. (10), as follows:

$$\begin{array}{}\text{(10)}& \text{WSI}={\displaystyle \frac{\int N_{\text{feasible}}\mathrm{d}z\mathrm{d}\mathit{\alpha }\mathrm{d}\mathit{\beta }}{\int N_{\text{total}}\mathrm{d}z\mathrm{d}\mathit{\alpha }\mathrm{d}\mathit{\beta }}}.\end{array}$$

In the formula, α, β is the attitude angle, N_feasible indicates the reachable work area, and N_total represents entire work area.

WSI is a measurement index of a mechanism workspace. Its value indicates the effective workspace range of a mechanism. According to index definition, the value range of WSI should be between 0 and 1. In a search space, the value of 0 indicates that the end-effector has no pose points that can meet the motion conditions, and the value of 1 indicates that the end-effector can reach all points.

3.2 Motion/force transmission performance index

In order to optimize motion/force transfer of a parallel mechanism, Zhao et al. (2017) proposed the constant power transfer and motion/force transfer criteria of a parallel mechanism under a different position based on the screw theory, establishing a motion/force transfer characteristic index to easily unify the dimension based on the unit index in a calculation process. It is usually used as a main performance evaluation index of the redundantly actuated parallel mechanism, especially for the motion joint of a revolute and prismatic coupling mechanism.

The minimum value of the input and output transmission power is expressed as λ₁ and λ₂, respectively. The local motion/force transfer performance index can be expressed as the minimum value of the input and output indexes, i.e., χ. Considering that the configuration value changes with the change in position, the average value of the task space is used as global evaluation index to evaluate performance of mechanism which can be expressed in Eq. (11) as follows:

$$\begin{array}{}\text{(11)}& \stackrel{\mathrm{‾}}{\mathit{\chi }}={\displaystyle \frac{{\int }_{W_t}\mathit{\chi }\mathrm{d}{W}_t}{{\int }_{W_t}\mathrm{d}{W}_t}}.\end{array}$$

3.3 Stiffness evaluation index

The stiffness value of an over-constrained redundantly actuated parallel mechanism will directly affect the motion accuracy and stability when performing surface machining tasks. The greater the stiffness value of the mechanism, the stronger the ability of the mechanism to resist deformation. Sufficient stiffness can ensure that the mechanism maintains high motion accuracy and stability, even when it is disturbed by outside world. In order to optimize the dimension and structure parameters of parallel robotic manipulators, Wang et al. (2017) introduced a new type of stiffness performance evaluation index based on kineto-elastic statics analysis. The stiffness model of a manipulator was expressed as a set of two sets of matrix equations based on a unified mathematical formula, and the elasticity of the connection between the independent connecting rod and connecting rod was described in the form of constraints. Klimchik et al. (2018) proposed a unified and systematic method, which saved the calculation time of stiffness modeling.

The characteristic formula of stiffness matrix can be expressed in Eq. (11) as follows:

$$\begin{array}{}\text{(12)}& \mathit{\tau }={\mathbf{J}}_{\mathrm{0}}^{\mathrm{T}}{K}_{\mathrm{0}}{\mathbf{J}}_{\mathrm{v}}\mathrm{\Delta }X,K={\mathbf{J}}_{\mathrm{0}}^{\mathrm{T}}{K}_{\mathrm{0}}{\mathbf{J}}_{\mathrm{v}},\end{array}$$

where, in the following:

$$\begin{array}{}\text{(13)}& {\displaystyle }\begin{array}{rl}& K_{\mathrm{0}}=\left[\begin{array}{ccc}{K}_{\mathrm{a}}& {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}& {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}\\ {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}& K_{\mathrm{c}}& {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}}\\ {\mathrm{0}}_{\mathrm{2}\times \mathrm{4}}& {\mathrm{0}}_{\mathrm{2}\times \mathrm{4}}& K_{\mathit{\tau }}\end{array}\right],\\ & K_{\mathrm{a}}=\text{diag}\left[\begin{array}{cccc}{k}_{\mathrm{a}\mathrm{1}}& k_{\mathrm{a}\mathrm{2}}& k_{\mathrm{a}\mathrm{3}}& k_{\mathrm{a}\mathrm{4}}\end{array}\right],\\ & K_{\mathrm{c}}=\text{diag}\left[\begin{array}{cccc}{k}_{\mathrm{r}\mathrm{1}}& k_{\mathrm{r}\mathrm{2}}& k_{\mathrm{r}\mathrm{3}}& k_{\mathrm{r}\mathrm{4}}\end{array}\right]\\ & K_{\mathit{\tau }}=\left[\begin{array}{cc}\frac{k}{\mathit{\tau }{l}_{\mathrm{10}}+\mathit{\tau }(e_{\mathrm{1}}\times l_{\mathrm{10}})}\frac{k}{\mathit{\tau }{l}_{\mathrm{10}}+\mathit{\tau }(e_{\mathrm{1}}\times l_{\mathrm{10}})}& {\mathrm{0}}_{\mathrm{1}\times \mathrm{2}}\\ & \\ {\mathrm{0}}_{\mathrm{1}\times \mathrm{2}}& \frac{k}{\mathit{\tau }{l}_{\mathrm{30}}+\mathit{\tau }(e_{\mathrm{1}}\times l_{\mathrm{30}})}\frac{k}{\mathit{\tau }{l}_{\mathrm{30}}+\mathit{\tau }(e_{\mathrm{1}}\times l_{\mathrm{30}})}\end{array}\right]\end{array}\text{(14)}& {\displaystyle }\begin{array}{rl}{\mathbf{J}}_{\mathrm{v}}& =\left[\begin{array}{c}{\mathbf{J}}_{\mathrm{a}}\\ {\mathbf{J}}_{\mathrm{rc}}\\ {\mathbf{J}}_{\mathit{\tau }\mathrm{c}}\end{array}\right],{\mathbf{J}}_{\mathrm{rc}}={\mathbf{J}}_{\mathrm{c}}(\mathrm{1}:\mathrm{4},\mathrm{1}:\mathrm{6}),\\ {\mathbf{J}}_{\mathit{\tau }\mathrm{c}}& =\left[\begin{array}{cc}{\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^{\mathrm{T}}& l_{\mathrm{10}}^{\mathrm{T}}\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^{\mathrm{T}}& (e_{\mathrm{1}}\times l_{\mathrm{10}}{)}^{\mathrm{T}}\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^{\mathrm{T}}& l_{\mathrm{30}}^T\\ {\mathrm{0}}_{\mathrm{3}\times \mathrm{1}}^{\mathrm{T}}& (e_{\mathrm{1}}\times l_{\mathrm{30}}{)}^{\mathrm{T}}\end{array}\right]\mathbb{F}\end{array}\text{(15)}& {\displaystyle }{\mathit{\tau }}_i=e_{\mathrm{1}}\times e_{\mathrm{2}},e_{\mathrm{1}}={\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\end{array}\right)}^{\mathrm{T}},e_{\mathrm{2}}=R{\left(\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\end{array}\right)}^{\mathrm{T}}.\end{array}$$

k_ai is tension compression stiffness coefficient of a branch rod, and k_ri is bending stiffness coefficient.

In order to evaluate the stiffness distribution of a mechanism in the workspace, the maximum and minimum eigenvalues of K are usually calculated with Eq. (16) to measure stiffness performance of parallel mechanism, i.e., as follows:

$$\begin{array}{}\text{(16)}& K_{\mathrm{1}}=max\mathit{\left\{}\text{eig}\right(K\left)\mathit{\right\}}.\end{array}$$

In order to evaluate the overall stiffness performance of mechanism, the global stiffness index is defined in Eq. (17) as follows:

$$\begin{array}{}\text{(17)}& k_{\mathrm{s}}={\displaystyle \frac{{\int }_W{K}_{\mathrm{1}}\mathrm{d}W}{{\int }_W\mathrm{d}W}}.\end{array}$$

The larger the value of k_s, the stronger the resistance to deformation of mechanism, and the better its stiffness performance, and the higher its motion accuracy when performing work tasks.

3.4 Dexterity index

Dexterity refers to how much posture the end-effector can obtain in a workspace. The better the dexterity of the mechanism, the more posture the end-effector can achieve in the workspace. However, its physical meaning is difficult to express clearly because of the inconsistency of dimensions for a parallel mechanism. Therefore, the characteristic length is used to normalize the Jacobian matrix so that the Jacobian matrix has no dimension. Wei et al. (2018) found the inverse of a robot forward-kinematics Jacobian matrix, which can be used in a singularity analysis, designed for isotropy and optimal control, based on a dexterity index.

Similarly, in order to accurately evaluate the motion flexibility of the mechanism in the workspace, the global condition number index is defined in Eq. (18) as follows:

$$\begin{array}{}\text{(18)}& k_{\mathrm{g}j}={\displaystyle \frac{{\int }_W{k}_{\mathrm{J}}\mathrm{d}W}{{\int }_W\mathrm{d}W}},\end{array}$$

where, in the following:

$$\begin{array}{}\text{(19)}& {\displaystyle }{k}_J=\mathrm{1}/\text{cond}\left({\mathbf{J}}_{\mathrm{0}}^{\prime }\right)={\mathit{\lambda }}_{min}\left({\mathbf{J}}_{\mathrm{0}}^{\prime }\right)/{\mathit{\lambda }}_{max}\left({\mathbf{J}}_{\mathrm{0}}^{\prime }\right)\text{(20)}& {\displaystyle }{\mathbf{J}}_{\mathrm{0}}^{\prime }=\left[\begin{array}{cc}{\mathbf{J}}_{\mathrm{0}}(:,\mathrm{1})& \frac{\mathrm{1}}{L}{\mathbf{J}}_{\mathrm{0}}(:,\mathrm{2}:\mathrm{3})\end{array}\right]\text{(21)}& {\displaystyle }{\mathbf{J}}_{\mathrm{0}}=\left[\begin{array}{cc}{\mathbf{J}}_{\mathrm{0}}(:,\mathrm{1})& {\mathbf{J}}_{\mathrm{0}}(:,\mathrm{2}:\mathrm{3})\end{array}\right]\text{(22)}& {\displaystyle }L=\sqrt{{\displaystyle \frac{n_{\mathrm{1}}\text{Trace}\left[{\mathbf{J}}_{\mathrm{0}}\right(:,\mathrm{2}:\mathrm{3}{)}^{\mathrm{T}}{\mathbf{J}}_{\mathrm{0}}(:,\mathrm{2}:\mathrm{3})]}{n_{\mathrm{2}}\text{Trace}\left[{\mathbf{J}}_{\mathrm{0}}\right(:,\mathrm{1}{)}^{\mathrm{T}}{\mathbf{J}}_{\mathrm{0}}(:,\mathrm{1})]}}}.\end{array}$$

λ_max and λ_min represent the maximum and minimum singular values of matrix, and n₁ and n₂ represent the number of movement and rotation, where n₁=1 and n₂=2. “Trace” represents the sum of the main diagonal elements of the matrix. The range of k_J is [0,1], and its value changes with the change in the mechanism pose. Its value is closer to 1, which means that the flexibility of the mechanism is better. The closer the value is to 0, the worse the flexibility of the mechanism is, and the closer it is to a singular position, the harder mechanism is to control.

3.5 Energy efficiency index

The energy efficiency is one of the key indicators to evaluate the feasibility of a mechanism. It is a macro embodiment to measure the size parameters of a mechanism and the rationality of structural design. Zhang et al. (2019b) proposed a simple method to quickly solve the maximum virtual power coefficient, which greatly simplifies establishment process of motion force transmission performance evaluation index. At the level of dynamic characteristic analysis, a dimensionless mechanism performance evaluation index independent of coordinate system is established to evaluate the energy conversion efficiency of mechanism, which has important guiding significance for reasonably optimizing mechanical structure and improving dynamic performance of mechanism.

The output energy on the end-effector of the moving platform of a mechanism is regarded as the effective energy, and its proportion in all energy input by parallel mechanism is defined as the energy efficiency, which can be expressed in Eq. (23) as follows:

$$\begin{array}{}\text{(23)}& \mathit{\eta }=E_{\mathrm{p}}/E_{\text{all}},\end{array}$$

where E_p is the energy of the moving platform, and E_all is the energy of a parallel mechanism system.

In order to evaluate the energy transfer efficiency of an organization more accurately, the global energy efficiency index is defined in Eq. (24) as follows:

$$\begin{array}{}\text{(24)}& k_{\text{ge}}={\displaystyle \frac{{\int }_W{\mathit{\eta }}_{\mathrm{2}}\mathrm{d}W}{{\int }_W\mathrm{d}W}}.\end{array}$$

3.6 Inertia coupling index

One of the main factors affecting the dynamic response characteristics of parallel mechanisms is the inertial coupling index, and the coupling generally exists in redundant actuated parallel mechanisms. In fact, the coupling characteristics of inertial force/torque will affect the output accuracy of the mechanism. Li et al. (2019) established a dynamic model considering the joint friction effect and gave inertia coupling a characteristic evaluation index. Then, the variation law in the coupling evaluation index with the motion of the mechanism was studied in a workspace of the parallel mechanism. Therefore, in order to improve the control accuracy of mechanism and reduce the error caused by inertial coupling, it is of great significance to design a reasonable method to evaluate the inertial coupling characteristics of a parallel robot mechanism.

Similarly, in order to evaluate the inertial coupling characteristics of a mechanism more reasonably, the global inertial coupling characteristic index is defined in Eq. (25) as follows:

$$\begin{array}{}\text{(25)}& k_{\text{gc}}={\displaystyle \frac{{\int }_W{k}_{\mathrm{c}}\mathrm{d}W}{{\int }_W\mathrm{d}W}},\end{array}$$

where, in the following:

$$\begin{array}{}\text{(26)}& {\displaystyle }{k}_{\mathrm{c}}={\displaystyle \frac{\mathrm{|}{M}_{x\mathrm{12}}\mathrm{|}+\mathrm{|}{M}_{x\mathrm{13}}\mathrm{|}+\mathrm{|}{M}_{x\mathrm{21}}\mathrm{|}+\mathrm{|}{M}_{x\mathrm{23}}\mathrm{|}+\mathrm{|}{M}_{x\mathrm{31}}\mathrm{|}+\mathrm{|}{M}_{x\mathrm{32}}\mathrm{|}}{\mathrm{|}{M}_{\mathrm{11}}\mathrm{|}+\mathrm{|}{M}_{\mathrm{22}}\mathrm{|}+\mathrm{|}{M}_{\mathrm{33}}\mathrm{|}}}\text{(27)}& {\displaystyle }\mathbf{M}\left(X\right)=(M_{xij}{)}_{\mathrm{3}\times \mathrm{3}}.\end{array}$$

The meaning of the global inertial coupling characteristic index k_gc is that the smaller k_gc and the weaker coupling characteristic of mechanism leads to a higher control accuracy of the mechanism.

4 Research on multi-objective optimization

4.1 Design of initial parameters for multi-objective optimization

First, the initial structural parameters of a parallel mechanism are set on the premise of ensuring the machining of complex surfaces, and then the constraints are determined according to the engineering requirements and geometric relations. The crucial problems of an over-constrained redundantly actuated parallel mechanism are selecting reasonable structural parameters under known constraints for multi-objective optimization, which requires the comprehensive consideration of performance evaluation indexes to make the mechanism achieve a more balanced and excellent performance.

Therefore, according to the above design ideas and purposes, the mathematical model of a multi-objective optimization design of a redundantly actuated parallel mechanism can be described in Eq. (28) as follows:

$$\begin{array}{}\text{(28)}& \left\{\begin{array}{l}\text{maximize}/\text{minimize }F\left(X\right)=\left[\begin{array}{cccc}{k}_{\mathrm{1}}\left(X\right)& k_{\mathrm{2}}\left(X\right)& \mathrm{\cdots }& k_m\left(X\right)\end{array}\right]\\ \text{subject to }\left\{\begin{array}{c}{g}_i\left(X\right)\le \mathrm{0}\\ h_i\left(X\right)=\mathrm{0}\end{array}\right.\end{array}\right.,\end{array}$$

where $\mathbf{X}=\left[\begin{array}{cccc}{x}_{\mathrm{1}}& x_{\mathrm{2}}& \mathrm{\cdots }& x_n\end{array}\right]$, matrix X represents the parameter design variables, the element x_i represents the structural parameters to be designed, and k_m(X) represents the objective function that is the performance evaluation index. g_i(X) represents the inequality constraint equation, namely the design parameter range of the over-constrained parallel mechanism according to the engineering requirements. Simultaneously, h_i(X) represents the equality constraint equation, namely the Jacobin matrix of the dynamic platform and actuating joint of the mechanism, the relationship between the branch chain and the dynamic platform, and the position inverse solution equation.

The above six global performance evaluation indexes are taken as the objective function of the 2RPU-2SPR over-constrained redundantly actuated parallel mechanism, namely workspace, stiffness, motion/force transmission efficiency, dexterity, energy efficiency, and the inertia coupling index. In order to facilitate the representation and description, the optimization objective can be expressed as k_i(X).

This is where $maxF\left(X\right)=\left[k_{\mathrm{1}}\left(X\right)k_{\mathrm{2}}\left(X\right)k_{\mathrm{3}}\left(X\right)k_{\mathrm{4}}\left(X\right)k_{\mathrm{5}}\left(X\right)\right.$ −k₆(X)], k₁, k₂, k₃, k₄, k₅, k₆ represent the global index of workspace, motion/force transmission efficiency, stiffness, dexterity, energy efficiency, and the inertia coupling respectively.

Therefore, the main optimization design variables of the 2RPU-2SPR over-constrained redundantly actuated parallel mechanism can be summarized in Eq. (29) as follows:

$$\begin{array}{}\text{(29)}& X=\left[\begin{array}{ccccccc}{r}_{\mathrm{a}}& r_{\mathrm{b}}& h_{\mathrm{a}}& h_{\mathrm{1}}& h_{\mathrm{2}}& R_{\mathrm{1}}& R_{\mathrm{2}}\end{array}\right],\end{array}$$

where r_a, r_b, h_a, h₁, h₂, R₁, and R₂ represents the radius of the moving platform, fixed platform radius, thickness of moving platform, length of actuating lower branch chain, length of actuating upper branch chain, outer circle radius of actuating lower branch chain, and outer circle radius of actuating upper branch chain, respectively.

4.2 Multi-objective particle swarm optimization algorithm and orthogonal experimental design method

The multi-objective particle swarm optimization algorithm is a biological evolutionary computer technology. Its basic principle is to randomly select the population within the range of design parameter variables, and then the initialized population corrects its own parameters through learning. The correction process depends on the previous population, and the population constantly updates to search for local optimization. There is no crossover and mutation, and the setting parameters are simple compared with the genetic algorithm. It does not need a frequent adjustment and is easy to implement. However, it is not conducive to find the global best if the initial population deviates from the Pareto solution set and the search process will be long. In other words, the selection of the initial population will have a great impact on the search ability of the particle swarm optimization algorithm and will directly affect the speed and efficiency of the multi-objective optimization.

Trial design is a crucial step in mechanism parameter design. An appropriate test method can not only reduce the cost and experiment time but also help to obtain more accurate and actual orthogonal experiment results. There are many experimental design methods, including the factor experiment, response surface model, and Taguchi experimental design method. The test method used in this paper is the orthogonal experiment method, which is an efficient method for finding the objective solution of multiple design parameters. It can analyze various changes in input and output parameters under the conditions of a short test cycle and little test data.

4.3 Multi-objective particle swarm optimization based on orthogonal experimental design

Through the above analysis, a multi-objective optimization of the structural parameters of a 2RPU-2SPR over-constrained redundantly actuated parallel mechanism needs to comprehensively measure seven design variables and six objective functions, which makes it difficult to establish a dynamic and kinematic model. Therefore, this paper aims to find a simple and effective multi-objective optimization design method.

An improved multi-objective particle swarm optimization configuration algorithm, based on orthogonal experimental response surface fitting design, is proposed. This method combines the advantages of an orthogonal experimental design method and multi-objective particle swarm optimization algorithm to effectively analyze the influence of the initial population on a multi-objective optimization algorithm. In the process of an optimization calculation, a fuzzy experimental value is generated in advance through the orthogonal experimental design. The experimental value is taken as the initial population in a feasible region, and then the multi-objective particle swarm optimization algorithm is used to search uniformly and carefully in the whole feasible region. The basic steps of the multi-objective particle swarm optimization algorithm, based on an orthogonal experimental design, are as follows:

1. Establishing the multi-objective optimization design mathematical model of a redundantly actuated 2RPU-2SPR over-constrained redundantly actuated parallel mechanism, involving the design variables, constraints, and objective functions.

2. Determining the factor of the design parameters and selecting an appropriate orthogonal table to obtain the data of the experiment.

3. Analyzing the correlation between parameter variables and the objective function and calculating the fitting accuracy of the output results.

4. Allowing, on this basis, for the population to search in the whole feasible region and, finally, obtaining the optimal Pareto solution and Pareto frontier with dominant indexes.

Table 1 Experiment design objective function value.

5 Simulation analysis of multi-objective optimization

5.1 Initial optimal Pareto solution and Pareto frontier

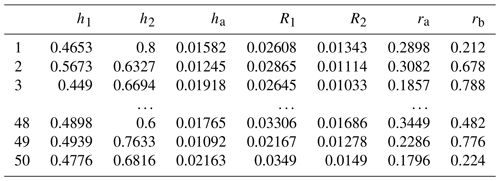
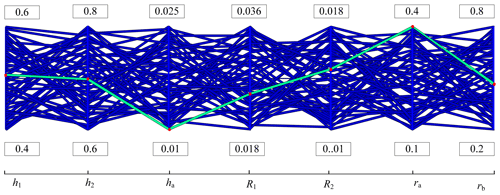
In the multi-objective particle swarm optimization design, the population size is 10, maximum number of iterations is 50, inertia weight is 0.9, global increment is 0.9, particle increment is 0.9, maximum speed is 0.1, penalty value for the running failure is 1.0 × 10³⁰, and target value for the running failure is 1.0 × 10³⁰. The parameter range of the design variable factors is shown in Table 1.

Table 2 Parameter variable design matrix in the experimental design.

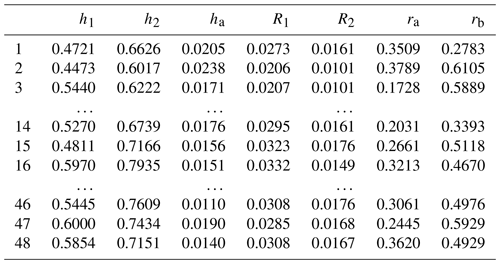
According to the parameter range of the design variable factors in Table 1, a 50 × 7 experiment design matrix can be generated, and some data are shown in Table 2.

Table 3 Experiment design objective function value.

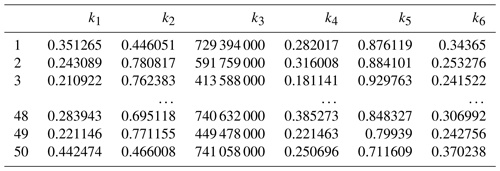
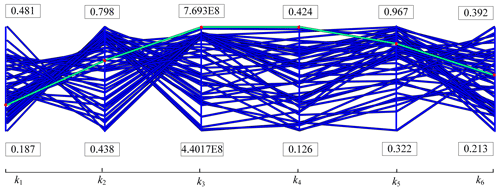
The data points of the experiment in the design matrix will be programmed and calculated to obtain the corresponding objective function values. Some results are shown in Table 3.

Figure 3 Parametric design variable combination matching.

Figure 4 Multi-objective optimization design Pareto front target response value.

After the simulation analysis of the experimental design, the ideal Pareto solution and Pareto front of the mechanism can be obtained. The value process of the design parameters h₁, h₂, h_a, r₁, r₂, r_a, and r_b is shown in Fig. 3. The blue line represents the best design variable matching combination in a feasible region, and the red dot represents the ideal initial optimal Pareto solution, with values of 0.5061, 0.698, 0.01, 0.02424, 0.1473, 0.4, and 0.469, respectively. The response values of the objective functions k₁, k₂, k₃, k₄, k₅, and k₆ are shown in Fig. 4. The blue line represents function response value corresponding to the combination of design variables in feasible area, and the red dot represents Pareto front, with values of 0.260417, 0.682066, 7.63×10⁸, 0.423911, 0.862877, and 0.30866, respectively.

Figure 5 Main effect diagram of the different objective functions.

5.2 Mapping relationship between design variables and multi-performance indicators

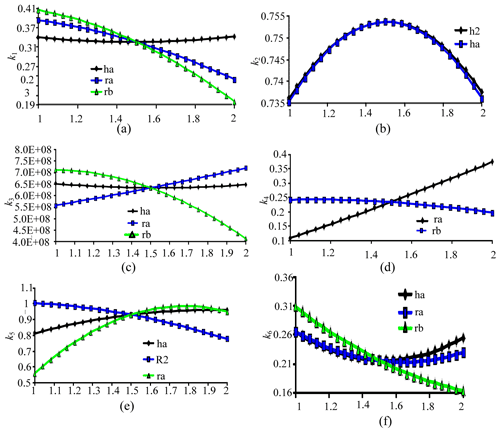
The corresponding target performance change trend can be obtained according to different levels of design variables. It can be seen from Fig. 5a that the workspace performance k of a parallel mechanism is affected by the thickness h_a of moving platform r_a and fixed platform r_b. According to curve change trend, the larger the values of design variables r_a and r_b, the lower the average value of performance evaluation index k₁. It can be seen from Fig. 5b that the rod length h₂ and thickness h_a of the moving platform have an impact on the performance evaluation index k₂, and the impact needs to be considered in sections. The first half shows that the rod length h₂ and the thickness h_a of the moving platform have a positive correlation with the flexibility of the mechanism, and the latter part of the conclusions is just the opposite. It also shows that two design variables have a nonlinear relationship with evaluation index k₂. Figure 5c shows that, the larger the design variable r_a is, the higher the mean value of performance evaluation index k₃, while the larger the design variable r_b, the lower the mean value of performance evaluation index k₃. As shown in Fig. 5d, the performance evaluation index k₄ is affected by the design variables r_a and r_b, which is similar to the performance evaluation index k₃. The extreme points of the design variable r_a in Fig. 5e and f on performance evaluation indexes k₅ and k₆ are not uniformly monotonous. In short, the existence of a main effect relationship depends on the trend of the change curve. If the slope of the curve is larger, then it indicates that the design variable has a greater impact on the target performance.

5.3 Correlation analysis of input parameter variables to output targets

Correlation analysis is a linear analysis method based on Pearson correlation coefficient, Spearman correlation coefficient, and Kendall correlation coefficient. For the Pearson correlation coefficient, a calculation formula can be expressed in Eq. (30) as follows:

$$\begin{array}{}\text{(30)}& {\displaystyle }\begin{array}{rl}{r}_{XY}& ={\displaystyle \frac{\sum (X-\stackrel{\mathrm{‾}}{X})(Y-\stackrel{\mathrm{‾}}{Y})}{\sqrt{\sum (X-\stackrel{\mathrm{‾}}{X}{)}^{\mathrm{2}}}\sqrt{\sum (Y-\stackrel{\mathrm{‾}}{Y}{)}^{\mathrm{2}}}}}={\displaystyle \frac{\sum xy}{\sqrt{\sum x^{\mathrm{2}}}\sqrt{\sum y^{\mathrm{2}}}}}\\ & ={\displaystyle \frac{S_{XY}}{S_X{S}_Y}}\end{array}\text{(31)}& {\displaystyle }x=X-\stackrel{\mathrm{‾}}{X},y=(Y-\stackrel{\mathrm{‾}}{Y})\text{(32)}& {\displaystyle }{S}_{XY}={\displaystyle \frac{\sum xy}{n-\mathrm{1}}},S_X=\sqrt{{\displaystyle \frac{\sum x^{\mathrm{2}}}{n-\mathrm{1}}}},S_Y=\sqrt{{\displaystyle \frac{\sum y^{\mathrm{2}}}{n-\mathrm{1}}}},\end{array}$$

where S_XY represents the total variance of the sample, S_X represents the sample standard deviation of X, and S_Y represents the sample standard deviation of Y.

Figure 6 Correlation matrix of the design variables and objective functions.

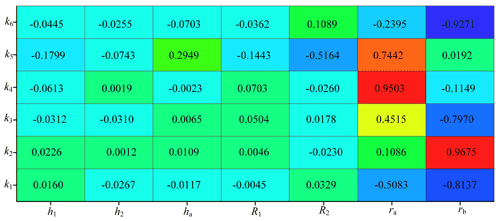
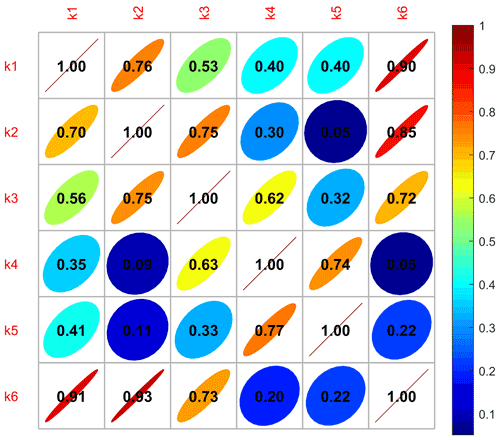
The characterization of the correlation can be measured by a positive correlation and negative correlation. If $\mathrm{0}<r<\mathrm{1}$, it means that the dependent variable is positively correlated with independent variable. At this time, the dependent variable will increase with the increase in the independent variable; if $-\mathrm{1}<r<\mathrm{0}$, it means that the dependent variable is negatively correlated with the independent variable. At this time, the dependent variable will decrease with the increase in the independent variable. The closer the absolute value of r is to 1, the higher correlation between the independent variables and dependent variables and the stronger the dependence between them will be. On the contrary, the closer the absolute value of r is to 0, the weaker the correlation between independent variable and dependent variable will be. The numerical relationships of the correlation matrix between the design variables and objective function of the 2RPU-2SPR over-constrained parallel mechanism are shown in Fig. 6.

The prediction algorithm of the regression model usually adopts the mean square error, root mean square error, mean absolute error, R², adjusted R², etc. In this paper, the determination coefficient method is used to predict the regression model, and its mathematical can be expressed in Eq. (33) as follows:

$$\begin{array}{}\text{(33)}& R^{\mathrm{2}}=\mathrm{1}-{\displaystyle \frac{{\sum }_i({\widehat{y}}_i-y_i{)}^{\mathrm{2}}}{{\sum }_i({\stackrel{\mathrm{‾}}{y}}_i-y_i{)}^{\mathrm{2}}}},\end{array}$$

where ${\sum }_i({\widehat{y}}_i-y_i{)}^{\mathrm{2}}$ represents the sum of the square differences between real value and predicted value, and ${\sum }_i({\stackrel{\mathrm{‾}}{y}}_i-y_i{)}^{\mathrm{2}}$ represents the sum of the square differences between real value and mean value.

The numerical range of the fitting accuracy is (0,1). The quality of the regression model can be judged according to the value of the fitting accuracy. When the fitting accuracy of the experiment sample is higher, the value is closer to 1, and when the fitting accuracy is lower, the value is closer to 0. The fitting accuracy between the target functions in experiment design is shown in Fig. 7.

Figure 7 Fitting accuracy between the objective functions.

Table 4 Optimal Pareto solution set for a multi-objective optimization.

Because the data samples of the experiment are relatively discrete, the full factor experiment design is not adopted, and there is coupling and competition among the objective functions, making the distribution law not obvious, so it is difficult to achieve a high degree of response surface linear fitting. Through multi-objective particle swarm optimization, 48 sets of Pareto non-inferior solution sets can be obtained because of the orthogonal experimental design, and the response value of the corresponding objective function is the Pareto front, as shown in Table 4.

Table 5 Design values of the main parameters of 2RPU-2SPR over a constrained parallel mechanism.

Table 6 Comparison of objective function values after an improved collaborative multi-objective optimization algorithm.

Table 7 Comparison of three traditional optimization algorithms.

5.4 Comparative analysis of optimization results

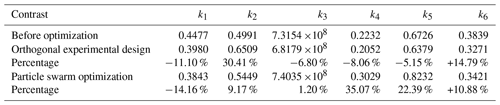
After the optimization, there are 48 groups of optimal Pareto solutions. But these objective functions are basically contradictory and conflicting. The increase in one performance index will inevitably damage the other. The Pareto solution cannot continue to improve the performance of the mechanism without weakening other performance indexes. Finally, the optimization system selects the design matching value of the 14th group of parameters as the optimal Pareto solution, according to the minimum distance method. The values of the design parameters before and after optimization are shown in Table 5, and the response values of performance evaluation indexes before and after optimization are shown in Table 6.

It can be seen from Table 6 that the workspace index k₁ has been reduced by 27.27 % after optimization, while, for the global motion/force transmission efficiency k₂, global stiffness index k₃, global dexterity index k₄, and global energy efficiency index k₅, it can be seen from the numerical value that the improvement rates after optimization are 21.80 %, 16.69 %, 72.98 %, and 38.83 %, respectively. The smaller the value of the global inertia coupling index k₆, the better. Its performance index is improved by 14.59 % after optimization, indicating that the improvement of other performance evaluation indexes must be at expense of the workspace, and the optimization design result is feasible.

Table 7 compares the three intelligent optimization algorithms. The comparison results show that the traditional orthogonal experimental design is not very ideal. The global stiffness, global flexibility and global energy transfer efficiency index have decreased. The particle swarm optimization algorithm shows better results compared with the orthogonal experimental design. However, the stiffness performance index is more of a concern for mechanism designers for complex surface machining tasks. So, the results obtained by particle swarm optimization algorithm are also not very ideal. Using the particle swarm optimization algorithm based on the orthogonal experimental design proposed in this paper, the stiffness performance of the mechanism is greatly improved, and there are some improvements in other performance indexes, which are more in line with the application needs of practical machining.

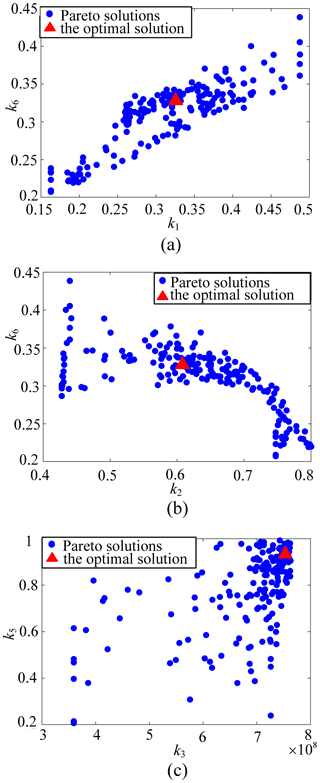
The optimization comparison results show that multi-objective optimization design problem is complex, and the relationship between the performance indexes of the mechanism are influenced and restricted by each other. The improvement in some performance indexes must be based on sacrifice of other indexes. The parameter design should be considered selectively and comprehensively, according to needs of actual processing tasks. The over-constrained redundantly actuated parallel mechanism 2RPU-2SPR is mainly for specific complex surface machining tasks. Figure 8 shows the optimal design combination of parameters obtained by multi-objective particle swarm optimization, which can be selected and decided on for designers.

Figure 8 Pareto solutions and the optimal solution.

As shown in Fig. 8, the competitive relationship between the performance evaluation indexes k₁ and k₆ is relatively obvious. The increase in the k₁ value will, correspondingly, lead to the increase in the k₆ value. However, the performance evaluation indexes of k₂ and k₆ maintain a negative growth relationship in local areas. Therefore, we should consider the value of each objective function and compromise on the parameter design variables in the multi-objective parameter design, so as to obtain the best mechanism performance and the best design parameter combination as far as possible.

6 Conclusions

In order to complete the machining task of a complex curved surface accurately and efficiently, this paper proposes an over-constrained redundantly actuated parallel mechanism and introduces and analyses six performance evaluation indexes. However, because of difficulties in establishing kinematic and dynamic models, it is laborious to balance the optimization of multi-performance indexes. Therefore, a multi-objective particle swarm optimization configuration algorithm, based on an orthogonal experimental design, is proposed. The orthogonal experimental design is used to obtain the initial population through polynomial function fitting, and then the multi-objective particle swarm optimization algorithm is used to search uniformly and carefully in the whole feasible region space, so as to obtain optimal scale parameters. It is of great significance to improve the potential working space, kinematics, stiffness, and dynamic performance of the parallel mechanism and to meet the requirements of surface processing tasks. Simultaneously, the research results of this paper have an important theoretical basis and engineering application value to guide the development of hybrid configuration processing equipment.

The following conclusions are drawn from the experimental results:

1. The kinematics and dynamics analysis are the basis of an integrated performance evaluation, scale synthesis, and real-time control researches for an over-constrained redundantly actuated parallel mechanism. This paper analyses the pose inverse solution of the 2RPU-2SPR parallel mechanism, based on the closed vector method, and briefly introduces the kinematics and dynamics of the mechanism.

2. For the performance requirements of special machining, this paper proposes a performance evaluation system for the 2RPU-2SPR over-constrained redundantly actuated parallel mechanism, which integrates the global index of workspace, motion/force transmission efficiency, stiffness, dexterity, energy efficiency, and inertia coupling. It is conducive to the subsequent comprehensive optimization design of the 2RPU-2SPR over-constrained redundantly actuated parallel mechanism, based on an orthogonal experimental design algorithm and multi-objective particle swarm optimization algorithm.

3. Compared with the two traditional intelligent optimization algorithms, the results show that particle swarm optimization configuration algorithm, based on an improved orthogonal experiment design, has a better optimization effect in which the workspace, motion/force transmission efficiency, stiffness, dexterity, energy efficiency, and inertia coupling index of optimized 2RPU-2SPR over-constrained redundantly actuated parallel mechanism are improved to a certain extent.

4. An over-constrained redundantly actuated parallel mechanism is a special kind of parallel mechanism which has the characteristics of multi-variability, strong coupling, and complex nonlinearity. The evaluation indexes of a multi-objective optimization design are often contradictory, and the designer needs to compromise and select an appropriate parameter design value.