Study on dynamic load-sharing characteristics of face gear dual-power split transmission system with backlash, support and spline clearance

The dynamic load-sharing characteristics of aircraft face gear dual-power split transmission system (FGDPSTS) are taken as the research object. Considering the factors of time-varying meshing stiffness, comprehensive error, backlash, support clearance, spline clearance, torsional stiffness, and support stiffness, the dynamic load-sharing model was constructed based on the lumped-parameter method. The loaded tooth contact analysis (LTCA) simulation method was used to calculate the time-varying meshing stiffness. The dynamic load-sharing coefficient (DLSC) is obtained by using Runge–Kutta method. The influences of errors, backlash, support clearance, spline clearance, torsional stiffness and support stiffness on DLSC were analyzed, and the biggest factors affecting dynamic load-sharing performance were found out. The results show that the influence of the backlash of the two-stage herringbone gear pair on the DLSC is more sensitive. The influence of support clearance on the DLSC is less. The load-sharing coefficient increases with the increase of the installation error and eccentricity error, and the influence of the error of the two-stage gears on the system load-sharing performance is the most sensitive. The torsional stiffness has little effect on the load-sharing coefficient of one stage but has great effect on the two-stage load-sharing coefficient. The influence of support stiffness on the DLSC of two-stage is stronger. It provided a theoretical basis for the dynamic stability optimization design of the system.

1 Introduction

The face gear transmission system (Heath and Bossler, 1993; Handschuh et al., 1996) replaces the original bevel gear transmission on the third-generation Apache armed helicopter. Compared with the bevel gear transmission, the face gear is used in the one-stage transmission, which has a good power-splitting effect, and can realize the reversing and splitting at the same time. The number of transmission stages is reduced from four to three stages, the weight of the transmission system is reduced by 40 %, and the bearing capacity is increased by 35 %. The support structure of spiral bevel gear is complex, and the pinion driven by face gear is not subject to axial force, which is conducive to reducing weight and noise, improving reliability and service life.

Many researchers at home and abroad have done a lot of research on gear-related theory and load-sharing technology. Krantz (1996a, b) has done further research on the load sharing of the two branches of the cylindrical gear. By defining the synchronous angle, the influence on the load-sharing performance of the power split transmission is studied, and the mathematical relationship between the same step angle and load-sharing coefficient is tested and verified. Robert and James (2006) proposed applying the face gear to a configuration similar to the planetary gear transmission. Using two face gears with the same axis, the face gear on the input shaft and the small gear mesh, the small gear on the other end of the coaxial gear and a fixed rotating face gear mesh, the small gear shaft is installed on the output shaft. Stevens et al. (2009) put forward the variable speed configuration of the fixed axis star gear and face gear. The face gear is used to replace the fixed axis star gear on the transmission chain. The face gear is designed as an idler gear to achieve the same high- and low-speed output steering of the transmission system. Because the input and output shafts of the face gear are installed in the same axis, the structure is tight and the commutation is more stable. Peng et al. (2016) take the coaxial face gear transmission system as the research object, establish the geometric model and kinematic model of the face gear transmission, study the parameter instability of the face gear transmission, and analyze the load distribution characteristics of the coaxial face gear transmission system under different working speeds. Jin et al. (2019a, b) considered the backlash, the time-varying meshing stiffness between the gear pairs, the gear eccentricity error, the shaft torsion and the support stiffness and constructed the dynamic model of the face gear cylindrical gear two power split transmissions, focusing on the influence of the torsional stiffness of each transmission shaft on the load-sharing coefficient of the system. Mo et al. (2020) established the bending torsional coupling dynamic load-sharing model of multi-power input face gear branch transmission system and studied the influence of meshing phase and error on the load-sharing coefficient. Dong et al. (2019) analyzed the assembly, power flow and load sharing of the coaxial face gear split torsional transmission system, deduced the assembly and installation conditions suitable for the coaxial face gear split torsional transmission system, and studied the power distribution direction of the system through the finite element method, and analyzed the influence of load conditions, distribution angle and installation angle. Wang et al. (2013) studied the influence of the dynamic load-sharing characteristics of the face gear split torsional transmission system. Bao et al. (2019) studied the load-sharing and dynamic characteristics of the variable speed helicopter transmission system and analyzed the influence of input power, input speed and friction factor on the load-sharing and dynamic characteristics of the system. Wang et al. (2019) studied the load-sharing performance of the two-branching cylindrical gear split torsional transmission system and analyzed the influence of working conditions, torsional stiffness, support stiffness, meshing phase difference and other factors on the load-sharing performance of the system. Zhang and Zhu (2018) studied the static load-sharing characteristics of a herringbone planetary gear system with floating combined inner gear ring and qualitatively analyzed the influence of the eccentricity error of each component, the floating mode and floating amount of the central component, the torsional rigidity of the flexible inner gear ring and other parameters on the static load-sharing characteristics of the system.

In previous studies, the influence of backlash and support clearance on the load-sharing characteristics of face gear drive is seldom considered, and the average mesh stiffness is mostly used in the establishment and calculation of the model, which cannot fully reflect the influence of the meshing process of tooth surface on the dynamic load-sharing characteristics of the system. According to the structure layout and transmission characteristics of the helicopter main reducer, and the advantages of two branch power split transmission of face gear, a face gear dual-power split transmission system configuration with dual-power split characteristics is proposed. Based on the lumped-parameter method, the dynamic model of the system is constructed, the dynamic differential equation is derived, the dynamic load-sharing coefficient (DLSC) is obtained, and the influence of parameters on the DLSC is analyzed. It provides the theoretical basis for the dynamic vibration stability optimization design of the face gear dual-power split transmission system.

2 Transmission system configuration and dynamic model establishment

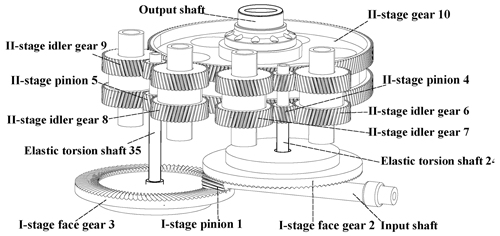
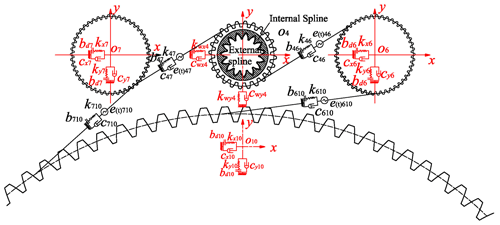
Figure 1 is the configuration diagram of the face gear dual-power split transmission system (FGDPSTS), with the technical characteristics of one-stage face gear pair power split, two-stage pinion secondary power split, two-stage idler gear convergence, two-stage gear output. Compared with the face gear two-branch transmission system implemented by an art program of the United States (Handschuh et al., 1996), this configuration adopts a two-stage split twist layout to meet the requirements of a large transmission ratio, high power density ratio and large thrust weight ratio. The transmission power of the gear is divided by multiple channels, and the torque transmitted by the gears in each branch is reduced, so that the bearing capacity of the gear is improved, and the service life and reliability of the system are further improved.

Figure 1 Schematic diagram of the FGDPSTS.

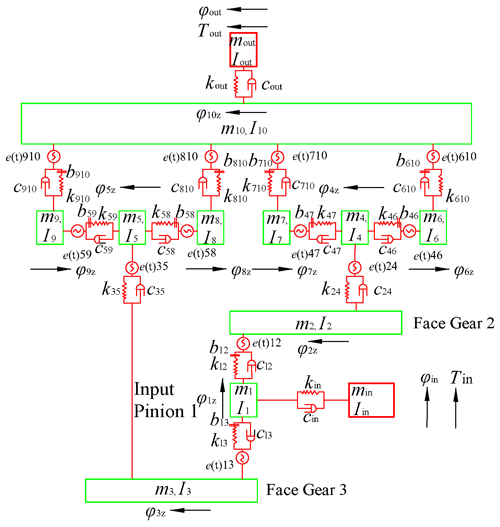
Figure 2 shows the torsional dynamic model of this system.

Figure 2 Torsional dynamic model of the system.

Here, T_in and T_out, k_in and k_out, and c_in and c_out are the input torque and output torque, torsional stiffness and torsional damping of input and output shafts, respectively. φ_in and φ_out, m_in and m_out, and I_in and I_out are the torsion angle, equivalent lumped mass and moment of inertia of prime mover and loaded, respectively. k_ij, c_ij, e_(t)ij and b_ij are the time-varying meshing stiffness, meshing damping, comprehensive error and backlash of each gear pair ij, respectively. φ_iz is the torsional vibration micro-displacement of each gear i. m_i is the equivalent concentrated lumped-mass gear i. I_i is the moment of inertia of component i. k₂₄ and k₃₅ and c₂₄ and c₃₅ are the torsional stiffness and torsional damping of connecting shaft 24 and connecting shaft 35.

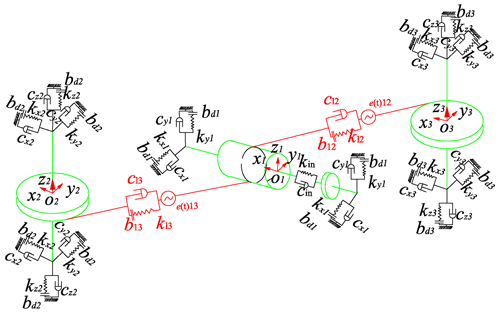
The dynamic model of one-stage face gear is established as shown in Fig. 3. k_xi and k_yi are the support stiffness in x direction and y direction of gear i, respectively. c_xi and c_yi are the support damping in x direction and y direction of gear i, respectively. b_ij is the average meshing backlash. b_di is the average elastic clearance. The input spur gear coordinate system is O₁x₁y₁z₁. The face gear coordinate system is O₂x₂y₂z₂ and O₃x₃y₃z₃, respectively. The z axis is the vertical upward axial direction of the face gear. The input gear shaft is perpendicular to the x direction, y direction and xz plane.

Figure 3 Dynamic model of the one-stage face gear.

The generalized vibration displacement vector δ with 32 degrees of freedom can be expressed as Eq. (1). Here, x_i, y_i and z_i are the transverse bending deformation of each gear in the x direction, y direction and z direction, respectively. φ_iz, φ_in and φ_out are the torsional angular displacement of gear i, prime mover and load components.

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\mathit{\delta }=& \mathit{\{}{z}_{\mathrm{1}},z_{\mathrm{2}},z_{\mathrm{3}},x_{\mathrm{4}},\mathrm{\dots },x_{\mathrm{10}},y_{\mathrm{1}},y_{\mathrm{2}},\mathrm{\dots },y_{\mathrm{10}},{\mathit{\phi }}_{\mathrm{in}},\\ & {\mathit{\phi }}_{\mathrm{1}y},{\mathit{\phi }}_{\mathrm{2}z},{\mathit{\phi }}_{\mathrm{3}z},\mathrm{\dots },{\mathit{\phi }}_{\mathrm{10}z},{\mathit{\phi }}_{\mathrm{out}}\mathit{\}}\end{array}\end{array}$$

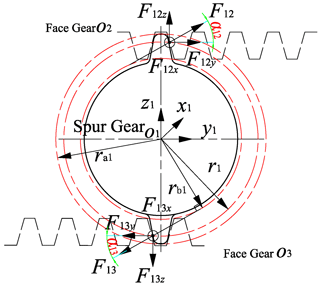
Force analysis of the one-stage face gear pair is shown in Fig. 4.

Figure 4 Schematic diagram of the force distribution of the face gear pair.

Here, r₁ is the pitch radius. r_a1 is the top circle radius. The vibration displacement of pinion O₁ is y₁ and z₁ along y direction and z direction, respectively. The vibration displacement of face gear O₂ and O₃ along y direction and z direction is y₂, y₃ and z₂, z₃, respectively.

The meshing forces of F₁₂ and F₁₃ can be expressed as follows:

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{l}{F}_{\mathrm{12}x}=\mathrm{0},F_{\mathrm{12}y}=F_{\mathrm{12}}\cos {\mathit{\alpha }}_{\mathrm{12}},F_{\mathrm{12}z}=F_{\mathrm{12}}\sin {\mathit{\alpha }}_{\mathrm{12}},\\ F_{\mathrm{13}x}=\mathrm{0},F_{\mathrm{13}y}=F_{\mathrm{13}}\cos {\mathit{\alpha }}_{\mathrm{13}},F_{\mathrm{13}z}=F_{\mathrm{13}}\sin {\mathit{\alpha }}_{\mathrm{13}}\end{array}\right..\end{array}$$

3 Establishment of differential equations of system dynamics

Based on the lumped-parameter method, the torsional vibration dynamic equation of the system is established as follows:

$$\begin{array}{}\text{(3)}& \left\{\begin{array}{l}{I}_{\mathrm{in}}{\ddot{\mathit{\phi }}}_{\mathrm{in}}+c_{\mathrm{in}}\left({\dot{\mathit{\phi }}}_{\mathrm{in}}-{\dot{\mathit{\phi }}}_{\mathrm{1}y}\right)+k_{\mathrm{in}}\left({\mathit{\phi }}_{\mathrm{in}}-{\mathit{\phi }}_{\mathrm{1}y}\right)=T_{\mathrm{in}}\\ I_{\mathrm{1}z}{\ddot{\mathit{\phi }}}_{\mathrm{1}y}-c_{\mathrm{in}}\left({\dot{\mathit{\phi }}}_{\mathrm{in}}-{\dot{\mathit{\phi }}}_{\mathrm{1}y}\right)-k_{\mathrm{in}}\left({\mathit{\phi }}_{\mathrm{in}}-{\mathit{\phi }}_{\mathrm{1}y}\right)+F_{\mathrm{12}}{r}_{b\mathrm{1}}\cos {\mathit{\alpha }}_n\\ +F_{\mathrm{13}}{r}_{b\mathrm{1}}\cos {\mathit{\alpha }}_n=\mathrm{0}\\ I_{\mathrm{2}z}{\ddot{\mathit{\phi }}}_{\mathrm{2}z}-F_{\mathrm{12}}{r}_{b\mathrm{2}}\cos {\mathit{\alpha }}_n+c_{\mathrm{24}}\left({\dot{\mathit{\phi }}}_{\mathrm{2}z}-{\dot{\mathit{\phi }}}_{\mathrm{4}z}\right)+k_{\mathrm{24}}\left({\mathit{\phi }}_{\mathrm{2}z}-{\mathit{\phi }}_{\mathrm{4}z}\right)=\mathrm{0}\\ I_{\mathrm{3}z}{\ddot{\mathit{\phi }}}_{\mathrm{3}z}-F_{\mathrm{13}}{r}_{b\mathrm{3}}\cos {\mathit{\alpha }}_n+c_{\mathrm{35}}\left({\dot{\mathit{\phi }}}_{\mathrm{3}z}-{\dot{\mathit{\phi }}}_{\mathrm{5}z}\right)+k_{\mathrm{35}}\left({\mathit{\phi }}_{\mathrm{3}z}-{\mathit{\phi }}_{\mathrm{5}z}\right)=\mathrm{0}\\ I_{\mathrm{4}z}{\ddot{\mathit{\phi }}}_{\mathrm{4}z}+F_{\mathrm{46}}{r}_{b\mathrm{4}}\cos {\mathit{\alpha }}_n\cos {\mathit{\beta }}_{\mathrm{4}}+F_{\mathrm{47}}{r}_{b\mathrm{4}}\cos {\mathit{\alpha }}_n\cos {\mathit{\beta }}_{\mathrm{4}}\\ -c_{\mathrm{24}}\left({\dot{\mathit{\phi }}}_{\mathrm{2}z}-{\dot{\mathit{\phi }}}_{\mathrm{4}z}\right)-k_{\mathrm{24}}\left({\mathit{\phi }}_{\mathrm{2}z}-{\mathit{\phi }}_{\mathrm{4}z}\right)=\mathrm{0}\\ I_{\mathrm{5}z}{\ddot{\mathit{\phi }}}_{\mathrm{5}z}+F_{\mathrm{58}}{r}_{b\mathrm{5}}\cos {\mathit{\alpha }}_n\cos {\mathit{\beta }}_{\mathrm{5}}+F_{\mathrm{59}}{r}_{b\mathrm{5}}\cos {\mathit{\alpha }}_n\cos {\mathit{\beta }}_{\mathrm{5}}\\ -c_{\mathrm{35}}\left({\dot{\mathit{\phi }}}_{\mathrm{3}z}-{\dot{\mathit{\phi }}}_{\mathrm{5}z}\right)-k_{\mathrm{35}}\left({\mathit{\phi }}_{\mathrm{3}z}-{\mathit{\phi }}_{\mathrm{5}z}\right)=\mathrm{0}\\ I_{iz}{\ddot{\mathit{\phi }}}_{iz}-F_{ij(ij=\mathrm{46},\mathrm{47},\mathrm{58},\mathrm{59})}{r}_{bi(i=\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9})}\cos {\mathit{\alpha }}_n\cos {\mathit{\beta }}_i\\ +F_{i\mathrm{10}}{r}_{bi}\cos {\mathit{\alpha }}_n\cos \mathit{\beta }=\mathrm{0}\\ I_{\mathrm{10}z}{\ddot{\mathit{\phi }}}_{\mathrm{10}z}-\sum F_{i\mathrm{10}}{r}_{\mathrm{10}}\cos {\mathit{\alpha }}_n\cos {\mathit{\beta }}_{i(i=\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9})}-c_{\mathrm{out}}\left({\dot{\mathit{\phi }}}_{\mathrm{out}}-{\dot{\mathit{\phi }}}_{\mathrm{10}z}\right)\\ -k_{\mathrm{out}}\left({\mathit{\phi }}_{\mathrm{out}}-{\mathit{\phi }}_{\mathrm{10}z}\right)=\mathrm{0}\\ I_{\mathrm{out}}{\ddot{\mathit{\phi }}}_{\mathrm{out}}+c_{\mathrm{out}}\left({\dot{\mathit{\phi }}}_{\mathrm{out}}-{\dot{\mathit{\phi }}}_{\mathrm{10}z}\right)+k_{\mathrm{out}}\left({\mathit{\phi }}_{\mathrm{out}}-{\mathit{\phi }}_{\mathrm{10}z}\right)=-T_{\mathrm{out}}\end{array}\right..\end{array}$$

Here, ${\ddot{\mathit{\phi }}}_{iz}$, ${\ddot{\mathit{\phi }}}_{\mathrm{in}}$ and ${\ddot{\mathit{\phi }}}_{\mathrm{out}}$ are the angular acceleration of torsional vibration corresponding to gear i, prime mover and load component. ${\dot{\mathit{\phi }}}_{iz}$, ${\dot{\mathit{\phi }}}_{\mathrm{in}}$ and ${\dot{\mathit{\phi }}}_{\mathrm{out}}$ are the angular velocity of torsional vibration corresponding to gear i, prime mover and load component. r_bi represents the radius of base circle of gear i, where r_b2 and r_b3 represent the radius of base circle of face gear, $r_{b\mathrm{2}}=r_{b\mathrm{3}}=$ (r_L1+r_L2), and r_L1 is the inner radius of the face gear determined by the undercutting condition, and r_L2 is the outer radius of the face gear determined by the tip sharpening condition. I_i(i=1, 2, …, 10) is the moment of inertia of each component. α_n is the normal meshing pressure angle of gear pair meshing.

The angular displacement form is transformed into the linear displacement form, which can be expressed as ${\ddot{u}}_i=r_{bi}{\ddot{\mathit{\phi }}}_{iz},{\dot{u}}_i=r_{bi}{\dot{\mathit{\phi }}}_{iz},u_i=r_{bi}{\mathit{\phi }}_{iz}$. The mass m_eq,i can be expressed as $m_{\mathrm{eq},i}=I_i/r_{bi}^{\mathrm{2}}$.

The expressions of torsional damping c₂₄ and c₃₅ are as follows:

$$\begin{array}{}\text{(4)}& \left\{\begin{array}{l}{c}_{\mathrm{24}}=\mathrm{2}{\mathit{\zeta }}_{\mathrm{24}}\sqrt{k_{\mathrm{24}}/\left(\mathrm{1}/I_{\mathrm{2}}+\mathrm{1}/I_{\mathrm{4}}\right)}\\ c_{\mathrm{35}}=\mathrm{2}{\mathit{\zeta }}_{\mathrm{35}}\sqrt{k_{\mathrm{35}}/\left(\mathrm{1}/I_{\mathrm{3}}+\mathrm{1}/I_{\mathrm{5}}\right)}\end{array}\right..\end{array}$$

Here, ζ₂₄ and ζ₃₅ are the damping coefficients.

Based on Newton's second law, the lateral vibration equation of the system is established as follows:

$$\begin{array}{}\text{(5a)}& {\displaystyle }\left\{\begin{array}{l}{m}_{\mathrm{1}}{\ddot{z}}_{\mathrm{1}}+c_{z\mathrm{1}}{\dot{z}}_{\mathrm{1}}+k_{z\mathrm{1}}{f}_{z\mathrm{1}}\left(z_{\mathrm{1}},b_{d\mathrm{1}}\right)+F_{\mathrm{12}z}+F_{\mathrm{13}z}=\mathrm{0}\\ m_{\mathrm{1}}{\ddot{y}}_{\mathrm{1}}+c_{y\mathrm{1}}{\dot{y}}_{\mathrm{1}}+k_{y\mathrm{1}}{f}_{y\mathrm{1}}\left(y_{\mathrm{1}},b_{d\mathrm{1}}\right)+F_{\mathrm{12}y}+F_{\mathrm{13}y}=\mathrm{0}\\ m_{\mathrm{2}}{\ddot{z}}_{\mathrm{2}}+c_{z\mathrm{2}}{\dot{z}}_{\mathrm{2}}+k_{z\mathrm{2}}{f}_{z\mathrm{2}}\left(z_{\mathrm{2}},b_{d\mathrm{2}}\right)+F_{\mathrm{12}z}=\mathrm{0}\\ m_{\mathrm{2}}{\ddot{y}}_{\mathrm{2}}+c_{y\mathrm{2}}{\dot{y}}_{\mathrm{2}}+k_{y\mathrm{2}}{f}_{y\mathrm{2}}\left(y_{\mathrm{2}},b_{d\mathrm{2}}\right)+F_{\mathrm{12}y}=\mathrm{0}\\ m_{\mathrm{3}}{\ddot{z}}_{\mathrm{3}}+c_{z\mathrm{3}}{\dot{z}}_{\mathrm{3}}+k_{z\mathrm{3}}{f}_{z\mathrm{3}}\left(z_{\mathrm{3}},b_{d\mathrm{3}}\right)+F_{\mathrm{13}z}=\mathrm{0}\\ m_{\mathrm{3}}{\ddot{y}}_{\mathrm{3}}+c_{y\mathrm{3}}{\dot{y}}_{\mathrm{3}}+k_{y\mathrm{3}}{f}_{y\mathrm{3}}\left(y_{\mathrm{3}},b_{d\mathrm{3}}\right)+F_{\mathrm{13}y}=\mathrm{0}\end{array}\right.\text{(5b)}& {\displaystyle }\left\{\begin{array}{l}{m}_{\mathrm{4}}{\ddot{x}}_{\mathrm{4}}+F_{Wx\mathrm{4}}+F_{\mathrm{46}}\sin {\mathit{\alpha }}_{\mathrm{46}}+F_{\mathrm{47}}\sin {\mathit{\alpha }}_{\mathrm{47}}=\mathrm{0}\\ m_{\mathrm{4}}{\ddot{y}}_{\mathrm{4}}+F_{Wy\mathrm{4}}+F_{\mathrm{46}}\cos {\mathit{\alpha }}_{\mathrm{46}}+F_{\mathrm{47}}\cos {\mathit{\alpha }}_{\mathrm{47}}=\mathrm{0}\\ m_{\mathrm{5}}{\ddot{x}}_{\mathrm{5}}+F_{Wx\mathrm{5}}+F_{\mathrm{58}}\sin {\mathit{\alpha }}_{\mathrm{58}}+F_{\mathrm{59}}\sin {\mathit{\alpha }}_{\mathrm{59}}=\mathrm{0}\\ m_{\mathrm{5}}{\ddot{y}}_{\mathrm{5}}+F_{Wy\mathrm{5}}+F_{\mathrm{58}}\cos {\mathit{\alpha }}_{\mathrm{58}}+F_{\mathrm{59}}\cos {\mathit{\alpha }}_{\mathrm{59}}=\mathrm{0}\\ \left.\begin{array}{l}{m}_i{\ddot{x}}_i+c_{xi}{\dot{x}}_i+k_{xi}{f}_{xi}\left(x_i,b_{di}\right)-F_{ij}\cdot \sin {\mathit{\alpha }}_{ij}\\ +F_{i\mathrm{10}}\cdot \sin {\mathit{\alpha }}_{i\mathrm{10}}=\mathrm{0}\\ m_i{\ddot{y}}_i+c_{yi}{\dot{y}}_i+k_{yi}{f}_{yi}\left(y_i,b_{di}\right)-F_{ij}\cdot \cos {\mathit{\alpha }}_{ij}\\ +F_{i\mathrm{10}}\cdot \sin {\mathit{\alpha }}_{i\mathrm{10}}=\mathrm{0}\\ m_{\mathrm{10}}{\ddot{x}}_{\mathrm{10}}+c_{x\mathrm{10}}{\dot{x}}_{\mathrm{10}}+k_{x\mathrm{10}}{f}_{x\mathrm{10}}\left(x_{\mathrm{10}},b_{d\mathrm{10}}\right)\\ -\sum F_{i\mathrm{10}}\sin {\mathit{\alpha }}_{i\mathrm{10}}=\mathrm{0}\\ m_{\mathrm{10}}{\ddot{y}}_{\mathrm{10}}+c_{y\mathrm{10}}{\dot{y}}_{\mathrm{10}}+k_{y\mathrm{10}}{f}_{y\mathrm{10}}\left(y_{\mathrm{10}},b_{d\mathrm{10}}\right)\\ -\sum F_{i\mathrm{10}}\cos {\mathit{\alpha }}_{i\mathrm{10}}=\mathrm{0}\end{array}\right\}(i=\mathrm{6},\mathrm{\dots },\mathrm{9})\end{array}\right..\end{array}$$

Here, ${\ddot{x}}_i$, ${\dot{x}}_i$ and x_i are the lateral x-direction vibration acceleration, velocity and displacement, respectively. ${\ddot{y}}_i$, ${\dot{y}}_i$ and y_i are the lateral y-direction vibration acceleration, velocity and displacement, respectively. ${\ddot{\mathrm{z}}}_i$, ${\dot{z}}_i$ and z_i are the lateral z-direction vibration acceleration, velocity and displacement, respectively.

F_Wxi and F_Wyi of gear i(i=4, 5) are the component of the supporting force of the spline shaft in x and y directions. Taking pinion O₄ as an example, the dynamic mechanical analysis model is shown in Fig. 5.

Figure 5 Dynamics model of the two-stage pinion O₄ under the supporting action of spline shaft.

k_wxi and k_wyi as well as c_wxi and c_wyi are bending stiffness and bending damping of spline shaft in x and y directions. F_m=τF_N is the friction force between the internal and external splines in the process of transmitting torque. F_N represents the normal positive pressure between the internal and external splines. τ is the coefficient of friction. $\mathit{\tau }={\mathit{\tau }}_{\mathrm{0}}\cdot sgn\left(v_{\mathrm{s}}\right)$, τ₀ is the amplitude of friction coefficient, v_s is the relative sliding speed, and sgn(v_s) is the symbol function of v_s. Here, τ₀=0.1, sgn(v_s>0)=1, τ=0.1.

Comprehensive displacement of gear i (i=4, 5) in x direction and y direction can be expressed as $R_i=\sqrt{x_i^{\mathrm{2}}+y_i^{\mathrm{2}}}$. R_i is the total displacement and also represents the value of spline.

The lateral bending supporting forces F_Wxi and F_Wyi can be described as follows:

$$\begin{array}{}\text{(6)}& \begin{array}{l}{F}_{Wxi}=\left\{\begin{array}{l}-c_{wxi}{\dot{R}}_i\cos \left({\mathit{\xi }}_i\right)-k_{wxi}{R}_i\cos \left({\mathit{\xi }}_i\right)\mathrm{0}\le R_i<{\mathrm{S}}_{\mathrm{1}}\\ -c_m\cos \left({\mathit{\xi }}_i\right)-F_m\cos \left({\mathit{\xi }}_i\right)S_{\mathrm{1}}\le R_i\le {\mathrm{S}}_{\mathrm{2}}\\ -\left(c_m+c_{wxi}{\dot{R}}_i\right)\cdot \cos \left({\mathit{\xi }}_i\right)\\ -\left(F_m+k_{wxi}\left(R_i-{\mathrm{S}}_{\mathrm{2}}\right)\right)\cos \left({\mathit{\xi }}_i\right)R_i>{\mathrm{S}}_{\mathrm{2}}\end{array}\right.\\ F_{Wyi}=\left\{\begin{array}{l}-c_{wyi}{\dot{R}}_i\sin \left({\mathit{\xi }}_i\right)-k_{wyi}{R}_i\sin \left({\mathit{\xi }}_i\right)\mathrm{0}\le R_i<{\mathrm{S}}_{\mathrm{1}}\\ -c_m\sin \left({\mathit{\xi }}_i\right)-F_m\sin \left({\mathit{\xi }}_i\right)S_{\mathrm{1}}\le R_i\le {\mathrm{S}}_{\mathrm{2}}\\ -\left(c_m+c_{wyi}{\dot{R}}_i\right)\sin \left({\mathit{\xi }}_i\right)\\ -\left(F_m+k_{wyi}\left(R_i-{\mathrm{S}}_{\mathrm{2}}\right)\right)\sin \left({\mathit{\xi }}_i\right)R_i>{\mathrm{S}}_{\mathrm{2}}\end{array}\right..\end{array}\end{array}$$

Here, c_m is friction damping. S₁ and S₂ are the radial clearance of internal and external splines. ξ_i is direction angle of vector (x_i, y_i). By combining the differential equations of dynamic torsion and transverse vibration mentioned above, the bending–torsion coupled non-linear dynamic differential equations can be obtained.

4 DLSC calculation

The backlash f_ij(x_ij, b_ij) and support clearance f_xi(x_i, b_di), f_yi(y_i, b_di) and fz_i (z_i, b_di) are expressed as follows:

$$\begin{array}{}\text{(7)}& \begin{array}{l}{f}_{ij}(x_{ij},b_{ij})=\left\{\begin{array}{ll}{x}_{ij}-b_{ij}& x_{ij}>b_{ij}\\ \mathrm{0}& -b_{ij}\le x_{ij}\le b_{ij}\\ x_{ij}+b_{ij}& x_{ij}<-b_{ij}\end{array}\right.\\ f_{xi}(x_i,b_{di})=\left\{\begin{array}{ll}{x}_i-b_{di}& x_i>b_{di}\\ \mathrm{0}& -b_{di}\le x_i\le b_{di}\\ x_i+b_{di}& x_i<-b_{di}\end{array}\right.\\ f_{yi}(y_i,b_{di})=\left\{\begin{array}{ll}{y}_i-b_{di}& y_i>b_{di}\\ \mathrm{0}& -b_{di}\le y_i\le b_{di}\\ y_i+b_{di}& y_i<-b_{di}\end{array}\right.\\ f_{zi}(z_i,b_{di})=\left\{\begin{array}{ll}{z}_i-b_{di}& z_i>b_{di}\\ \mathrm{0}& -b_{di}\le z_{\mathrm{1}}\le b_{di}\\ z_i+b_{di}& z_i<-b_{di}\end{array}\right.,\end{array}\end{array}$$

where x_ij is the relative vibration displacement.

Dynamic meshing force F_Lij (L= I, II) can be expressed as follows:

$$\begin{array}{}\text{(8)}& F_{Lij}=P_{Lij}+D_{Lij}=k_{ij}{f}_{ij}\left(x_{ij},b_{ij}\right)+c_{ij}{\dot{x}}_{ij}.\end{array}$$

The meshing damping c_ij is calculated according to the following empirical formula (Dong et al., 2018):

$$\begin{array}{}\text{(9)}& c_{ij}=\mathrm{2}{\mathit{\zeta }}_{gij}\sqrt{{\displaystyle \frac{k_{mij}\left(I_i{r}_{bi}^{\mathrm{2}}\cdot I_j{r}_{bj}^{\mathrm{2}}\right)}{\left(I_i{r}_{bi}^{\mathrm{2}}+I_j{r}_{bj}^{\mathrm{2}}\right)}}},\end{array}$$

where k_mij is the average meshing stiffness. ζ_gij is the damping coefficient.

Elastic force P_Iij and P_IIij as well as meshing damping force D_Iij and D_IIij can be expressed as follows:

$$\begin{array}{}\text{(10)}& \left\{\begin{array}{l}{P}_{\mathrm{I}ij}=k_{ij}{f}_{ij}\left(x_{ij},b_{ij}\right)=k_{ij}(r_{bi}{\mathit{\phi }}_i-r_{bj}{\mathit{\phi }}_j\\ +\left(z_i-z_j\right)\cos {\mathit{\alpha }}_{\mathrm{I}ij}+\left(y_i-y_j\right)\sin {\mathit{\alpha }}_{\mathrm{I}ij}\\ -e(t{)}_{ij},b_{ij})\\ P_{\mathrm{II}ij}=k_{ij}{f}_{ij}\left(x_{ij},b_{ij}\right)=k_{ij}(r_{bi}{\mathit{\phi }}_i-r_{bj}{\mathit{\phi }}_j\\ +\left(x_i-x_j\right)\cos {\mathit{\alpha }}_{\mathrm{II}ij}+\left(y_i-y_j\right)\sin {\mathit{\alpha }}_{\mathrm{II}ij}\\ -e(t{)}_{ij},b_{ij})\\ D_{\mathrm{I}ij}=c_{ij}{\dot{x}}_{ij}=c_{ij}(r_{bi}{\dot{\mathit{\phi }}}_i-r_{bj}{\dot{\mathit{\phi }}}_j\\ +\left({\dot{z}}_i-{\dot{z}}_j\right)\cos {\mathit{\alpha }}_{\mathrm{I}ij}+\left({\dot{y}}_i-{\dot{y}}_j\right)\sin {\mathit{\alpha }}_{\mathrm{I}ij}\\ -\dot{e}\left(t{)}_{ij}\right)\\ D_{\mathrm{II}ij}=c_{ij}{\dot{x}}_{ij}=c_{ij}(r_{bi}{\dot{\mathit{\phi }}}_i-r_{bj}{\dot{\mathit{\phi }}}_j\\ +\left({\dot{x}}_i-{\dot{x}}_j\right)\cos {\mathit{\alpha }}_{\mathrm{II}ij}+\left({\dot{y}}_i-{\dot{y}}_j\right)\sin {\mathit{\alpha }}_{\mathrm{II}ij}\\ -\dot{e}\left(t{)}_{ij}\right)\end{array}\right..\end{array}$$

Here, α_Iij is the positive angle between the meshing line and the center line of the one-stage face gear pair and the z axis, α_Iij(i=1, j=2, 3) $=-\mathit{\pi }/\mathrm{2}+{\mathit{\alpha }}_n+{\mathit{\gamma }}_{\mathrm{I}ij}$, and γ_Iij is the positive angle between the center line of the one-stage face gear pair and the z axis. α_IIij is the positive angle between the meshing line and the center line of the two-stage cylindrical gear pair and the x axis, α_IIij(i=4, 5, j=6, 7, 8, 9) $=\mathit{\pi }/\mathrm{2}-{\mathit{\alpha }}_n+{\mathit{\gamma }}_{\mathrm{I}ij}$, α_IIij (i=6, 7, 8, 9, j=10) $=-\mathit{\pi }/\mathrm{2}+{\mathit{\alpha }}_n+{\mathit{\gamma }}_{ij}$, and γ_IIij is the positive angle between the center line of the two-stage cylindrical gear pair and the x axis. r_bi and r_bj are the radius of base circle of gear i and j.

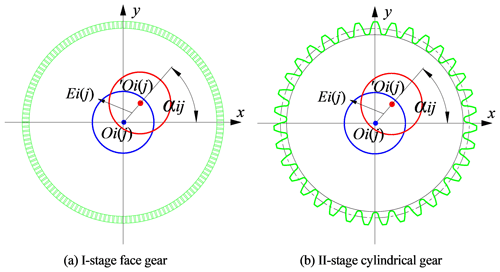
The eccentricity errors of one-stage face gear and two-stage cylindrical gear are shown in Fig. 6

Figure 6 Diagram of the eccentricity error.

Figure 7 LTCA model of the one-stage face gear pair and two-stage gear pair.

Here, O_i(j) is theoretical center position. ^′O_i(j) is actual center position. α_ij is the angle between installation error and eccentricity error and x axis.

Table 1 Gear parameters.

Table 2 Parameters of equivalent stiffness.

The equivalent meshing error e(t)_ij can be expressed as follows:

$$\begin{array}{}\text{(11)}& \left\{\begin{array}{l}e(t{)}_{ij(ij=\mathrm{12},\mathrm{46},\mathrm{58},\mathrm{610},\mathrm{810})}=E_i\sin \left(-{\mathit{\omega }}_{i}t+{\mathit{\eta }}_i+{\mathit{\alpha }}_{ij}\right)\\ -E_j\sin \left(-{\mathit{\omega }}_{j}t+{\mathit{\eta }}_j+{\mathit{\alpha }}_{ij}\right)+A_i\sin \left({\mathit{\delta }}_i+{\mathit{\alpha }}_{ij}\right)\\ -A_j\sin \left({\mathit{\delta }}_j+{\mathit{\alpha }}_{ij}\right)\\ e(t{)}_{ij(ij=\mathrm{13},\mathrm{4}\mathrm{7},\mathrm{5}\mathrm{9},\mathrm{7}\mathrm{10},\mathrm{9}\mathrm{10})}=-E_i\sin \left(-{\mathit{\omega }}_{i}t+{\mathit{\eta }}_i+{\mathit{\alpha }}_{ij}\right)\\ +E_j\sin \left(-{\mathit{\omega }}_{j}t+{\mathit{\eta }}_j+{\mathit{\alpha }}_{ij}\right)-A_i\sin \left({\mathit{\delta }}_i+{\mathit{\alpha }}_{ij}\right)\\ +A_j\sin \left({\mathit{\delta }}_j+{\mathit{\alpha }}_{ij}\right)\end{array}\right..\end{array}$$

Here, E_i and E_j are eccentricity error. A_i and A_j are installation error. η_i and η_j are eccentricity error phase angle. δ_i and δ_j are installation error phase angle. ω_i and ω_j are excitation frequency.

The dimensionless time is defined as τ_n=ω_nt. Here, τ is the time variable of equations before dimensionless treatment. ${\mathit{\omega }}_n=\sqrt{{\stackrel{\mathrm{‾}}{k}}_{\mathrm{12}}\left(I_{\mathrm{1}}{r}_{\mathrm{2}}^{\mathrm{2}}+I_{\mathrm{2}}{r}_{\mathrm{1}}^{\mathrm{2}}\right)/\left(I_{\mathrm{1}}{I}_{\mathrm{2}}\right)}$. ${\stackrel{\mathrm{‾}}{k}}_{\mathrm{12}}$ is the average meshing stiffness of one-stage gear pair. The displacement nominal scale b_c is given. The dimensionless displacement, dimensionless velocity and dimensionless acceleration are expressed as $x_i={\stackrel{\mathrm{‾}}{x}}_i{b}_c$, ${\dot{x}}_i={\dot{\stackrel{\mathrm{‾}}{x}}}_i{b}_c{\mathit{\omega }}_n$ and ${\ddot{x}}_i={\ddot{\stackrel{\mathrm{‾}}{x}}}_i{b}_c{\mathit{\omega }}_n^{\mathrm{2}}$, respectively. The backlash and support clearance are expressed as $b_{ij}={\stackrel{\mathrm{‾}}{b}}_{ij}{b}_c$ and $b_{di}={\stackrel{\mathrm{‾}}{b}}_{di}{b}_c$, respectively. Spline clearance is expressed as $R_i={\stackrel{\mathrm{‾}}{R}}_i{b}_c$. The dimensionless forms of excitation frequency are ${\mathrm{\Omega }}_i={\mathit{\omega }}_i/{\mathit{\omega }}_n$, ${\mathrm{\Omega }}_j={\mathit{\omega }}_j/{\mathit{\omega }}_n$, ${\mathrm{\Omega }}_{bi}={\mathit{\omega }}_{bi}/{\mathit{\omega }}_n$ and ${\mathrm{\Omega }}_{bj}={\mathit{\omega }}_{bj}/{\mathit{\omega }}_n$, respectively. The dimensionless damping variable is $\stackrel{\mathrm{‾}}{C}=c/\mathrm{2}m{w}_n$, the dimensionless stiffness variable is $\stackrel{\mathrm{‾}}{K}=k/m{w}_n^{\mathrm{2}}$, and the dimensionless excitation force is $\stackrel{\mathrm{‾}}{F}=F/m{b}_c{w}_n^{\mathrm{2}}$.

The above-mentioned differential equations are normalized in dimension and solved by the Runge–Kutta method. The DLSCs of Ω_I and Ω_II are obtained as follows:

$$\begin{array}{}\text{(12)}& \left\{\begin{array}{ll}{\mathrm{\Omega }}_{\mathrm{I}}& =max\left[{\mathrm{\Omega }}_{\mathrm{12}},{\mathrm{\Omega }}_{\mathrm{13}}\right]=max\left(\frac{{\left({\stackrel{\mathrm{‾}}{P}}_{\mathrm{I}\mathrm{12}},{\stackrel{\mathrm{‾}}{P}}_{\mathrm{I}\mathrm{13}}\right)}^T}{\frac{T_{\mathrm{in}}/\mathrm{2}}{r_{\mathrm{1}}\cos a_n}}\right)\\ {\mathrm{\Omega }}_{\mathrm{II}}& =max\left[{\mathrm{\Omega }}_{\mathrm{610}},{\mathrm{\Omega }}_{\mathrm{710}},{\mathrm{\Omega }}_{\mathrm{810}},{\mathrm{\Omega }}_{\mathrm{910}}\right]\\ & =max\left(\frac{{\left({\stackrel{\mathrm{‾}}{P}}_{\mathrm{I}\mathrm{610}},{\stackrel{\mathrm{‾}}{P}}_{\mathrm{I}\mathrm{710}},{\stackrel{\mathrm{‾}}{P}}_{\mathrm{I}\mathrm{810}},{\stackrel{\mathrm{‾}}{P}}_{\mathrm{I}\mathrm{910}}\right)}^T}{\left(\frac{T_{\mathrm{in}}/\mathrm{2}}{r_{\mathrm{1}}\cos a_n\cos \mathit{\beta }}{I}_{\mathrm{12}}{I}_{\mathrm{46}}\right)/\mathrm{2}}\right)\end{array}\right..\end{array}$$

Here, Ω_I is the one-stage DLSC. Ω_II is the two-stage DLSC. Ω_ij(ij=12, 13, 610, …, 910) is the one-stage and two-stage DLSC of each branch. ${\stackrel{\mathrm{‾}}{P}}_{\mathrm{I}ij}$ and ${\stackrel{\mathrm{‾}}{P}}_{\mathrm{II}ij}$ are the average dynamic meshing force of each gear pair at one-stage and two-stage DLSC. I₁₂ and I₄₆ are the transmission ratio of gear pairs 12 and 46. The DLSC represents the load distribution of the system under the dynamic vibration response. The smaller the DLSC, the better the load-sharing performance of the system.

5 Time-varying meshing stiffness calculation based on LTCA

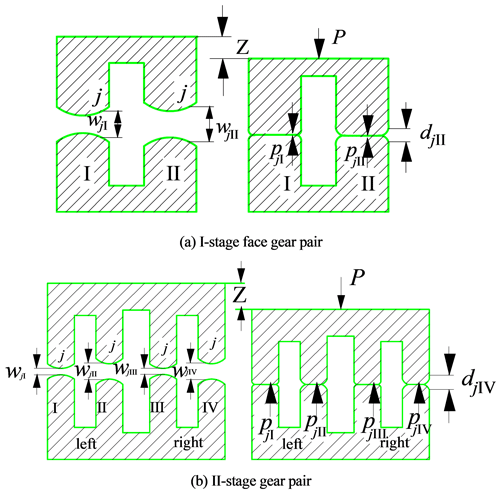
The loaded tooth contact analysis (LTCA) model of one-stage face gear pair (Li and Zhu, 2010) and two-stage gear pair (Wang et al., 2010) is shown in Fig. 7. j_k is a point along the relative principal direction, k= 1, 2 for one-stage face gear, k= 1, 2, 3, 4 for two-stage gear pair. Here, the tooth surface initial clearance w is $[w{]}_k=[\mathit{\delta }{]}_k+[b{]}_k$. $[w{]}_k=[w_{\mathrm{1}k},w_{\mathrm{2}k}$, …, w_ik, …, w_jk,w_nk]^T, $[b{]}_k=[b_{\mathrm{1}},b_{\mathrm{2}}$, …, $b_i,\mathrm{\dots },b_n{]}^T$, n is the number of discrete points. δ is the geometric transmission error, $[\mathit{\delta }{]}_k=[\mathrm{1},\mathrm{1},\mathrm{\dots },\mathrm{1},\mathrm{\dots },\mathrm{1}{]}^T$. b_j is tooth surface normal clearance ($j=\mathrm{1},\mathrm{\dots },n$). Z is the displacement direction.

Figure 8 Time-varying meshing stiffness curve of each gear pair.

Figure 9 DLSC changed with dimensionless time.

Under the action of load P, the deformation coordination condition of the elastic deformation is as follows:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& {\left(\mathbf{F}\right)}_k{\left(p\right)}_k+{\left(w\right)}_k={\left(Z\right)}_k+{\left(d\right)}_k(k=\mathrm{I},\mathrm{II})\\ & \stackrel{\text{function}}{⟶}\left(\begin{array}{l}{\left(p\right)}_k={\left(p_{\mathrm{1}k},p_{\mathrm{2}k},\mathrm{\dots },p_{ik},\mathrm{\dots },p_{jk},p_{nk}\right)}^T\\ {\left(Z\right)}_k={\left(\mathrm{1},\mathrm{1},\mathrm{\dots },\mathrm{1},\mathrm{\dots },\mathrm{1}\right)}^T\\ {\left(d\right)}_k={\left(d_{\mathrm{1}k},d_{\mathrm{2}k},\mathrm{\dots },d_{ik},\mathrm{\dots },d_{jk},d_{nk}\right)}^T\end{array}\right).\end{array}\end{array}$$

(F)_k is the normal flexibility coefficient matrix of the gear pair. p_j($j=\mathrm{1},\mathrm{2},\mathrm{\dots },nk$) is the contact loaded at the point j of the tooth k. Apparently, the contact force p_j($j=\mathrm{1},\mathrm{2},\mathrm{\dots },nk$) satisfies the following Eqs. (17)–(18):

$$\begin{array}{}\text{(14)}& \left\{\begin{array}{l}\sum _{j=\mathrm{1}}^n{p}_{j\mathrm{I}}+\sum _{j=\mathrm{1}}^n{p}_{j\mathrm{II}}\\ =p(\mathrm{I}-\mathrm{stage}\mathrm{face}-\mathrm{gear}\mathrm{pair})\\ \sum _{j=\mathrm{1}}^n{p}_{j\mathrm{I}}+\sum _{j=\mathrm{1}}^n{p}_{j\mathrm{II}}+\sum _{j=\mathrm{1}}^n{p}_{j\mathrm{III}}+\sum _{j=\mathrm{1}}^n{p}_{j\mathrm{IV}}\\ =p(\mathrm{II}-\mathrm{stage}\mathrm{gear}\mathrm{pair})\end{array}\right.\left(p_j\left(j=\mathrm{1},\mathrm{2},\mathrm{\dots },n\right)\right).\end{array}$$

If p_jk>0, [d]_jk=0. If [p]_jk=0, [d]_jk>0. f, P and w are known conditions. The contact forces [p]_jk, final backlash [d]_jk and tooth approach [Z] are unknown. The known parameters (f, P, w) and unknown parameters (p, d, Z) constitute a non-linear program model. According to the tooth approach Z_k, the objective function is established as follows:

$$\begin{array}{}\text{(15)}& \text{minimize}\left(p{)}^T\mathit{\right\{}\left(F\right)\left(p\right)+\left(w\right)-\left(Z\right)\mathit{\}}.\end{array}$$

The objective function equation can be expressed as follows:

$$\begin{array}{}\text{(16)}& \left\{\begin{array}{l}\begin{array}{ll}\mathrm{Min}& \sum _{j=\mathrm{1}}^{\mathrm{2}n+\mathrm{1}}{X}_j\end{array}\\ -\left(F\right)\left(p\right)+\left(Z\right)+\left(d\right)+\left(X\right)=\left(w\right)\\ S\cdot t\cdot {\left(e\right)}^T\left(p\right)+X_{\mathrm{2}n+\mathrm{1}}=P\\ p_j\ge \mathrm{0},d_j\ge \mathrm{0},Z\ge \mathrm{0},X_j\ge \mathrm{0};p_j=\mathrm{0}\text{or}{d}_j=\mathrm{0};\end{array}\right.\end{array}$$

X_j (j=1, 2, …, 2n+1) is the artificial variables, (X) = (X₁, …, X_2n)^T, (e) = 1.

The transmission error of the gear bearing in meshing is mainly composed of three parts of the geometric transmission error δ₁, the bending deformation δ₂ and the contact deformation δ₃. The geometric transmission errors δ₁ can be expressed as δ₁(T(k))=a. The bending deformation errors δ₂ can be expressed as δ₂(T(k))=bT (k). The function relationship between the contact deformation δ₃(T(k)) and the loaded T(k) can be expressed as ${\mathit{\delta }}_{\mathrm{3}}\left(T\right(k\left)\right)=cT(k{)}^{\mathrm{2}/\mathrm{3}}$.

Table 3 Parameters of equivalent damping.

Figure 10 DLSC changed with dimensionless time.

The relational expression of the integrated angular deformation Δφ_ij(T_ij(k)) and torque T_ij(k) of the gear pairs of the system can be expressed as follows:

$$\begin{array}{}\text{(17)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\phi }}_{ij}\left(T_{ij}\left(k\right)\right)& ={\mathit{\delta }}_{\mathrm{1}}\left(T\right(k\left)\right)+{\mathit{\delta }}_{\mathrm{2}}\left(T\right(k\left)\right)+{\mathit{\delta }}_{\mathrm{3}}\left(T\right(k\left)\right)\\ & ={\displaystyle \frac{T_{ij}\left(k\right)}{\left|T_{ij}\left(k\right)\right|}}\left(a+b{T}_{ij}\left(k\right)+c{T}_{ij}{\left(k\right)}^{\mathrm{2}/\mathrm{3}}\right).\end{array}\end{array}$$

Here, a, b and c are the constant terms in the formula. T_ij(k) is the torque of the kth meshing position.

By solving the LTCA equations, the load transmission error Δφ_ij[0.1T_ij[k]], Δφ_ij[0.5T_ij[k]] and Δφ_ij[0.9T_ij[k]] can be obtained. The coefficient a, b and c can be obtained by taking the obtained transmission error into Eq. (17).

The time-varying meshing stiffness k_ij(k) can be obtained as follows:

$$\begin{array}{}\text{(18)}& k_{ij}\left(k\right)={\displaystyle \frac{T_{ij}\left(k\right)}{r_{bi}^{\mathrm{2}}\cos a_n\cos {\mathit{\beta }}_i}}\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }{\mathit{\phi }}_{ij}\left(T_{ij}\left(k\right)\right)}}.\end{array}$$

Figure 11 DLSC changed with dimensionless time.

6 Example analysis

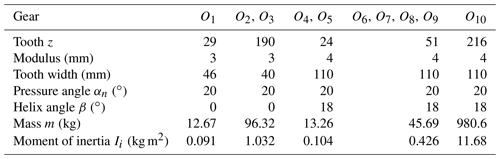
Input power P=2000 kW, input speed n=8780 r min⁻¹, installation error A_i=50 µm, eccentricity error E_i=50 µm, and one-stage face gear backlash $b_{\mathrm{12}}=b_{\mathrm{13}}=\mathrm{10}$ µm. Two-stage gear pair backlash $b_{\mathrm{610}}=b_{\mathrm{710}}=b_{\mathrm{810}}=b_{\mathrm{910}}=\mathrm{17}$ µm. Spline clearance S₂=50 µm. Support clearance b_di=10 µm. The gear parameters are shown in Table 1.

The parameters of equivalent support stiffness, torsional stiffness and meshing stiffness are shown in Table 2. The support stiffness is calculated according to GB/T 3073-1996.

Figure 12 DLSC changed with installation and eccentricity error.

The parameters of equivalent supporting damping, torsional damping, and meshing damping are shown in Table 3.

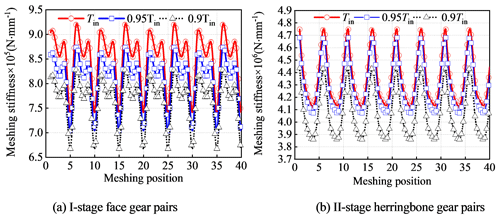
The calculated time-varying meshing stiffness curve is shown in Fig. 8. The meshing stiffness fluctuation range of one-stage face gear pairs is (7.46 × 10⁵–9.27 × 10⁵) N mm⁻¹. The meshing stiffness fluctuation range of two-stage idler gear pairs is (3.77 × 10⁶–4.78 × 10⁶) N mm⁻¹. The meshing stiffness fluctuation range of two-stage big gear pair is (6.17 × 10⁶–6.68 × 10⁶) N mm⁻¹. Due to the different meshing stiffness of each meshing position of the tooth surface, the DLSC of different meshing positions will be changed slightly.

Figure 13 Influence of backlash on the DLSC.

Figure 14 Influence of support clearance on the DLSC.

6.1 Effect of installation and eccentricity errors on the DLSC

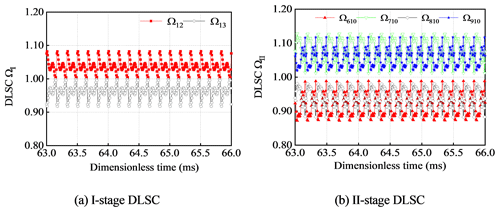
Under the combined action of installation error and eccentricity error, the DLSC presents periodic changes with time, as shown in Fig. 9. The one-stage DLSC is Ω₁₂=1.0383 and Ω₁₃=0.9617. Torque T₁₂ and T₁₃ are fluctuated around in 1129.33 N m and 1046.0 N m. Torque distribution is 51.92 % and 48.09 %. The two-stage DLSC is Ω₆₁₀=0.914, Ω₇₁₀=1.086, Ω₈₁₀=0.948 and Ω₉₁₀=1.052. Torque T₆₁₀, T₇₁₀, T₈₁₀ and T₉₁₀ are fluctuated around in 6920.5, 8222.9, 7178.1 and 7965.4 N m, respectively. The influence of one-stage gear pair 12 and two-stage gear pair 710 on the load-sharing characteristics is maximum impact. The overall DLSC is Ω_Z=1.086. The DLSCs of the system are Ω_I=1.0383 and Ω_II=1.0860, respectively. The DLSC changed periodically with time.

Figure 15 Load-sharing coefficient changed with the spline clearance.

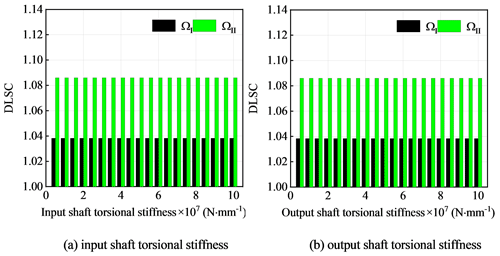
Figure 16 Influence of input and output shaft torsional stiffness on dynamic load-sharing coefficient.

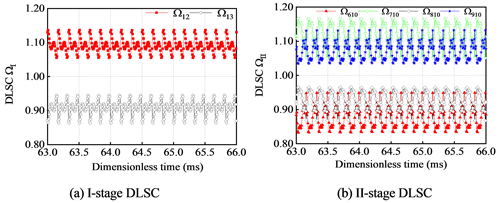
Other parameters remain unchanged, when given $b_{\mathrm{12}}=b_{\mathrm{13}}=\mathrm{0}$ µm. The DLSC under the combined action of errors is shown in Fig.10. The one-stage DLSCs of Ω_I change from 1.0383 to 1.0921. The two-stage DLSCs of Ω_II change from 1.0860 to 1.1220. The one-stage face gear backlash has a great influence on the one-stage DLSC and a little influence on the two-stage DLSC.

Other parameters remain unchanged, when given one-stage backlash $b_{\mathrm{12}}=b_{\mathrm{13}}=\mathrm{0}$ µm, two-stage backlash $b_{\mathrm{610}}=b_{\mathrm{710}}=b_{\mathrm{810}}=b_{\mathrm{910}}=\mathrm{0}$ µm. The DLSC under the combined action of errors is shown in Fig. 11. The one-stage DLSCs of Ω_I change from 1.0383 to 1.131. The two-stage DLSCs of Ω_II change from 1.0860 to 1.3507. Under the combined action of the errors, the load-sharing performance becomes worse with the decrease of the backlash.

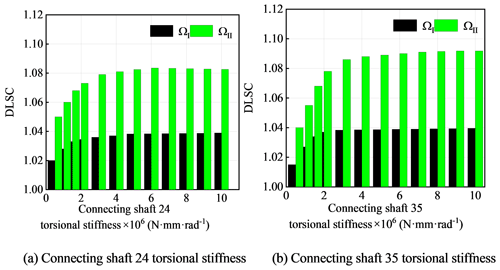
Figure 17 Influence of torsional stiffness of connecting shaft on the dynamic load-sharing coefficient.

Figure 18 Influence of support stiffness on the dynamic load-sharing coefficient.

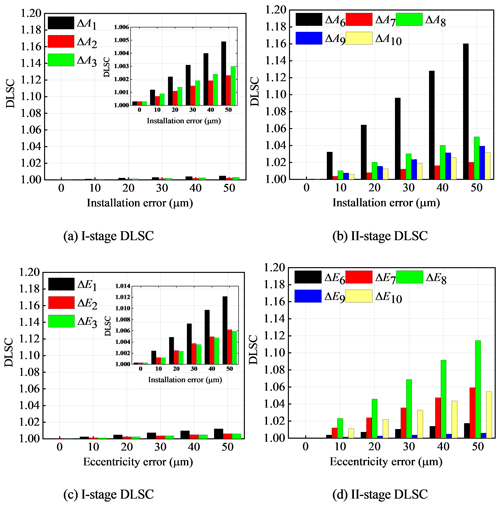
The DLSC changes with the errors as shown in Fig. 12. Figure 12a and b show the influence of installation errors on the DLSC, and Fig. 12c and d show the influence of eccentricity errors on the DLSC. When the given error range is from 0–50 µm, the influence range of installation error on one-stage DLSC is 1.0003–1.0049, the influence range of installation error on two-stage DLSC is 1.0001–1.1605, the influence range of manufacturing error on one-stage DLSC is 1.0005–1.0125, and the influence range of manufacturing error on two-stage DLSC is 1.0005–1.1160. The installation errors and eccentricity errors have less influence on the one-stage DLSC and more influence on the two-stage DLSC. The eccentricity errors are more sensitive than the installation errors on the one-stage DLSC.

6.2 Effect of backlash, support clearance and spline clearance on the DLSC

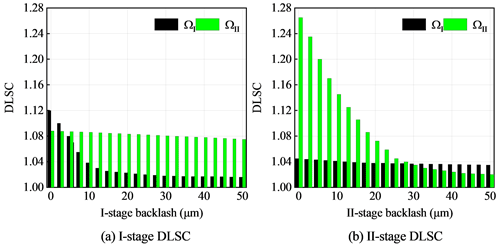
The change of the DLSC Ω_I and Ω_II with the backlash is shown in Fig. 13. The one-stage DLSC Ω_I changed strongly with the increase of one-stage backlash, which changed from 1.121–1.016. The influence of one-stage backlash on the two-stage DLSC Ω_II changes little, which changed from 1.088–1.075. The influence of two-stage backlash on two-stage DLSC is more sensitive. With the increase of backlash, the DLSC gradually decreases from 1.268–1.021. The influence of two-stage backlash on one-stage DLSC is less, which changed from 1.045–1.035. In a certain range, the one-stage DLSC and two-stage DLSC decrease with the increase of the backlash. The backlash can compensate the deformation caused by the errors and improve the load-sharing performance to a certain extent.

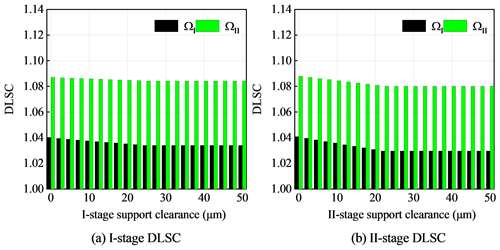
When other parameters remain unchanged, the changes with the one-stage and two-stage DLSC support clearance and are shown in Fig. 14. With the increase of one-stage support clearance, the DLSC decreases gradually. Ω_I changed from 1.0402–1.0341 and Ω_II changed from 1.0870–1.0842. With the increase of two-stage support clearance, the DLSC Ω_I decreased from 1.0408–1.0297, and Ω_II decreased from 1.0879–1.0801. The influence of the support clearance on the DLSC is small.

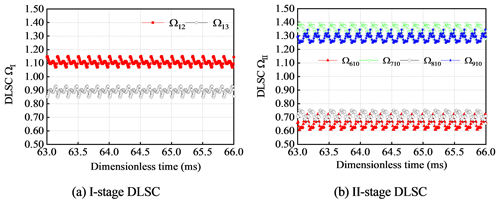
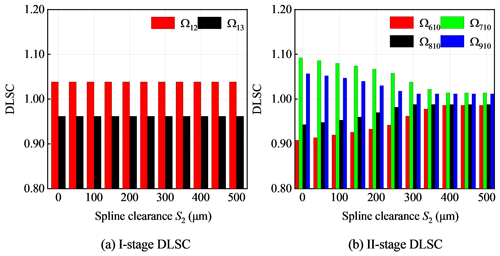
Figure 15 shows the curves of one-stage and two-stage DLSC with the spline clearance from 0–450 µm. With the change of spline clearance, one-stage DLSC does not change at 1.0383, while two-stage DLSC changes from 1.0921–1.012. The influence of spline clearance on the one-stage DLSC is almost unchanged and has a great impact on the two-stage DLSC. When the spline clearance is 0 mm, it is equivalent to the bending stiffness of the spline shaft to provide support. The DLSC is Ω₆₁₀=0.9079, Ω₇₁₀=1.0921, Ω₈₁₀=0.9432 and Ω₉₁₀=1.0568. When the spline clearance is greater than the total displacement R₅ (0.271 mm), the two-stage pinion O₅ is in a fully floating state. When the spline clearance is greater than the total displacement R₄ (0.382 mm), the two-stage pinion O₄ and O₅ enter a full floating state at the same time, and the load-sharing characteristic is improved, and the DLSC is stable at Ω_II=1.012. Among them, the DLSCs of two-stage gear pairs are Ω₆₁₀=0.9861, Ω₇₁₀=1.0139, Ω₈₁₀=0.988 and Ω₉₁₀=1.012. Two-stage pinion O₄ and pinion O₄ are independent in floating behavior.

6.3 Effect of torsional stiffness and support stiffness on the DLSC

The influence curve of DLSC of input shaft and output shaft is shown in Fig. 16 when the torsional stiffness changed from (0.5–10.0) × 10⁷ N mm rad⁻¹. Input shaft and output shaft have almost no influence on the dynamic load-sharing coefficient of the system. This conclusion is consistent with the conclusion of the influence of torsional stiffness on the load-sharing coefficient of power split transmission system analyzed in Jin et al. (2019a, b).

Other parameters remain unchanged, and the DLSC changes with the torsional stiffness of connecting shaft 24 and connecting shaft 35 at (0.5–10.0) × 10⁶ N mm rad⁻¹, as shown in Fig. 17. With the increase of the torsional stiffness of connecting shaft 24 and connecting shaft 35, the DLSC gradually becomes larger, the average load characteristics become worse, and the influence trend is the same. The influence of torsional stiffness on the two-stage DLSC is more obvious than that of the one-stage DLSC. Although the geometry of the system is symmetrical, but because of the different direction of meshing force and the geometry of the connecting axis, the force situation is not consistent, resulting in a certain difference in the dynamic load-sharing characteristics.

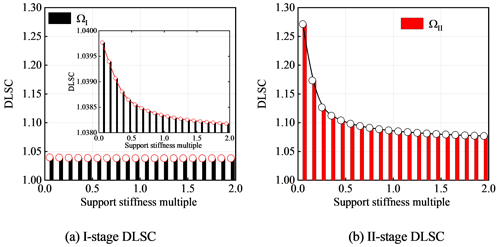
With other parameters unchanged, the overall support stiffness of each gear shown in Table 2 is (2–0.05) times that of the change, and the influence curve of the overall support stiffness on the DLSC of the system is shown in Fig. 18.

With the decrease of the support stiffness multiple, the DLSC becomes larger, and the dynamic performance becomes worse. Especially when the overall support stiffness multiple is (0.5–0.05), the influence of the dynamic load-sharing coefficient of two-stage DLSC is stronger, and the change of Ω_II is from 1.0763–1.2714, but it has little influence on the dynamic load-sharing coefficient of one-stage DLSC, and the change of Ω_I is from 1.0381–1.0397.

7 Conclusions

In this paper, a new configuration of face gear dual-power split transmission system is proposed, and the effects of backlash, support clearance, error, torsional stiffness and support stiffness on dynamic load-sharing characteristics are analyzed, which provides the theoretical basis for further optimization design of vibration stability. The conclusions are as follows:

1. With the increase of backlash, the DLSCs gradually decrease and tend to be stable. The two-stage DLSC has a great influence with the change of backlash. Increasing the backlash of each two-stage gear pair properly is conducive to improving the load-sharing characteristics. With the increase of the support clearance, the DLSC decreases, but the change value is small. The increase of the support clearance has little effect on the improvement of the dynamic load-sharing characteristics. The increase of spline clearance is beneficial to the improvement of even load characteristics.

2. With the increase of installation error and eccentricity error, the DLSC is larger and the system load-sharing performance is worse. The installation error and eccentricity error of each gear in level 2 have the greatest influence on the dynamic load-sharing coefficient. The installation and manufacture of each gear in level 2 should be considered in the design.

3. With the increase of torsional stiffness, the DLSC increases, and the load-sharing characteristics become worse. The change trend of the dynamic load-sharing coefficient is relatively consistent between the connecting shaft 24 and the connecting shaft 35. In the optimal design of the load-sharing structure, the flexible connecting shaft meeting the strength should be selected to improve the load-sharing performance. With the decrease of support stiffness, the change two-stage DLSC is more intense. Choosing a reasonable rigid support in the optimal design is conducive to ensuring a better load-sharing performance.