the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel algorithm by combining nonlinear workspace partition with neural networks for solving the inverse kinematics problem of redundant manipulators
Hui Dong
Chen Li
Wentao Wu
Ligang Yao
Hao Sun
Redundant manipulators (RMs) have been gaining more attention thanks to their excellent merits of operating flexibility and precision. Inverse kinematics (IK) study is critical to the design, trajectory planning, and control of RMs, while it is usually more complicated to solve IK problems which may inherently have innumerable solutions. In this work, a novel approach for solving the IK problems for RMs while retaining the redundancy characteristics has been proposed. By employing a constraint function, the method delicately reduces the infinite IK solutions of a RM to a finite set. Furthermore, the workspace of RMs is divided into nonlinear partitions through diverse joint angle intervals, which have further simplified the mapping correlations between the desired point and manipulators' joint angles. For each partition, a pre-trained neural network (NN) model is established to acquire its IK solutions with high efficiency and precision. After combing all nonlinear partitions, multiple reasonable IK solutions are available. The presented method offers a possible selection of the most appropriate solution for trajectory planning and energy consumption and therefore has the potential for facilitating novel robot development.
- Article
(1379 KB) - Full-text XML
- BibTeX
- EndNote
Redundant manipulators (RMs) have been widely used in many fields, such as industrial and agricultural production, equipment manufacturing, and surgical operation. RMs can move freely in joint space without affecting the position and pose of the end effector. Once the pose of an end effector is defined, the secondary target can be satisfied by changing joints' positions. Thus, dynamic performance of the whole robot can be significantly improved. In general, control of a manipulator requires computationally efficient solutions of the inverse kinematics (IK) problem, while for a desired position and orientation, combinations of joint variables of a RM may be infinite. This issue is caused by two things: (a) deficient definition for joint angles; (b) symmetry of trigonometric functions. Correspondingly, the IK issues of RMs are often too complicated to be solved, especially for the complex systems meeting real time and high precision.
In the past years, IK problems of RMs have been studied widely. Closed-form and numerical methods have been mainly employed. The closed-form method can be further divided into two categories: the geometric and algebraic. The algebraic method, which is able to obtain analytical solutions, has been dominantly utilized rather than the geometric one in engineering typically. Of these, by simplifying a RM into a non-redundant manipulator, IK issues were solved (Zaplana and Basanez, 2018). Similarly, analytical solutions for RMs (Ananthanarayanan and Ordóñez, 2015) and RMs with joint limits (Shimizu and Kakuya, 2008) and wrist offset were obtained. Also, by dividing a manipulator into several parts, analytical solutions of IK problems were solved (Mu et al., 2018; Kofinas et al., 2015). The main limitations of the closed-form method are that the solution can be merely acquired when the number of variables of the joint's DOF (degree-of-freedom) and forward kinematics equations are equal. The numerical iteration method of the Jacobian matrix is a standard method for finding the inverse solution. For instance, algorithms for obtaining IK solutions of serial manipulators have been presented (Dulęba et al., 2013; Shi et al., 2006). Also, a weighted minimum norm method (Wan et al., 2018) for obtaining IK solutions of serial manipulators has also been proven to be effective. In particular, for the manipulator with specific connection types, many valid numerical approaches were available (Parikh et al., 2005; Tanev et al., 2000). For the inverse kinematics of a novel parallel platform with offset, RR (rotating–rotating) joints were mathematically modeled and numerical iterative computation was performed (Han et al., 2019). Although the utility of this conventional method has been confirmed, it cannot be used for all mechanisms. There is still a need to develop algorithms for solving IK issues of RMs.
With the development of computer science, numerical methods are becoming more popular. Workspace density resulting from Fourier transforms and convolution theorems was used to solve the IK problem of planar serial revolute manipulators (Dong et al., 2013). Similarly, an approach for calculating collision-free paths in complex environments with multiple obstacles has been successfully used for planar RMs (Dong and Du, 2015). Meanwhile, a workspace density function was also used to select the optimal geometric parameters for the manipulator for optimizing design (Du and Dong, 2015). Approaches based on recursive (Baerlocher and Boulic, 2004), bionic (Artemiadis et al., 2010), adaptive critical (Patchaikani et al., 2011), and path sampling (Rolf et al., 2010) algorithms have been leveraged for solving the IK issues. Of these, the bionic method has an advanced calculating efficiency. Derived from the bionic method, many algorithms have been proposed to solve IK problems, such as particle swarm optimization and the natural-CCD (cyclic-coordinate-descent) algorithm (Lin et al., 2016; Martin et al., 2018). Two different methods combined with a genetic algorithm were applied to solve the IK problem of a spatial binary hyper-redundant manipulator (Bayram et al., 2013). Also, the genetic algorithm was successfully used for searching the optimal solutions of path planning (Carbone et al., 2008). In addition, a neural network algorithm (Kóker et al., 2014) combined with a genetic algorithm (Kóker, 2013a) or a simulated annealing algorithm (Kóker, 2013b) was verified to be capable of solving the IK problem of a planar three-link manipulator. Also, composite neural network algorithms were utilized to obtain an IK solution of non-redundant manipulators (Duka, 2014; Kóker et al., 2004). A reinforcement learning algorithm (Duguleana et al., 2012), a quantum particle swarm optimization algorithm (Ayyılldılz and Çetinkaya, 2016), a radial basis neural network (RBF) algorithm, a neural network (NN) algorithm (Sari, 2014; Toshani and Farrokhi, 2014), and a recursive neural network algorithm (Xiao and Zhang, 2014) were proven to be effective in solving IK problems. In particular, for an IK study of series-parallel manipulators and a soft manipulator IK study, a wavelet neural network algorithm (Rahmani et al., 2015) and supervised learning methods (Giorelli et al., 2015) were verified to be efficient, respectively. In practice, the neural network method relies on the acquisition of training data, and thus it is essential to build IK mapping formats between the end effector and the joint space for RMs.
In this work, we proposed a new approach based on multiple neural network models to solve IK issues of RMs. In particular, a constraint function was used to transform RM to a non-redundant manipulator. Also, the number of IK solutions of the manipulator is decreased by reducing the range motion of each joint, and therefore the quantity of the IK solution can be limited. Then, the nonlinear workspace of a RM was divided into several parts which were correspondingly fitted by a neural network model. Finally, by combining all of the workspace with mapping formats, the complete workspace of the RM was acquired, and the global optimal solutions for specific working conditions can be directly obtained as well. In particular, the approach merely requires Denavit and Hartenberg (D–H) parameters for the model establishment. Therefore, the implementation of this work can be potentially extended to solve IK problems in the scenario of hyper-redundant robots. We used Robai Cyton Gamma 300, a 7-DOF robot arm installed in the International Space Station, as the test manipulator. In the Ubuntu system, a GTX1060 graphics card and an i7-CPU processor were employed for calculation. The programming language was Python, and simulations were carried out using the MATLAB software. Results showed that the method was accurate and effective while retaining redundancy characteristics of the RM. Multiple feasible solutions are available for users according to various working conditions. Thanks to the pre-trained NN models, the method is suitable for real-time redundant manipulator control and has the potential to prompt RM development.
The method we proposed is combined from a constraint function and neural networks: the constraint function is used to eliminate the redundancy, while neural networks are applied to calculate IK solutions for part workspaces. Finally, the global optimal IK solutions could be acquired by combining all results of all neural networks.
2.1 Constraint function
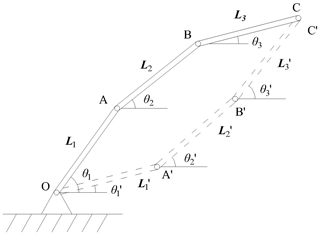
For a 3-DOF manipulator, the workspace is two-dimensional, and thus the redundancy equals 1 and the IK solution for the end effector in position C (Fig. 1) should not be unique.
Here, L1, L2, and L3 are the lengths of each arm in Fig. 1; θ1, θ2, and θ3 are the joint rotation angles; x and y are the position coordinates of the end effector. The existence of an undefined angle may lead to infinite solutions of the entire workspace. We propose a constraint function as shown in Eq. (2) which is constructed by using the projection method and scaling method. The constraint function should be continuous in order to avoid a sudden change in the constrained angular motion.
Here, θi is one of the angles of the joints; x and y are the known position; is the upper/lower limit of the angle's restricted range. The range of the first angle is set between −180 and 180∘ and substituted into Eq. (2). Then, the solutions of Eq. (1) can be obtained as presented in Eqs. (3) and (4). Although θ1 can be fixed, θ2 and θ3 are not unique due to the symmetry of the trigonometric functions.
To solve the above issues, a novel IK algorithm by dividing a nonlinear workspace by constraint functions was presented. For each divided workspace, the data were fitted using a neural network. After the trained models of each workspace were acquired, a whole workspace can be obtained. However, the relationship of the constraint function with IK solutions of the manipulator is not monotonous. By limiting the range of the angles, mapping relationships can be effectively simplified, and the noise that occurs in the data training for neural networks will be reduced.
Furthermore, we find that different joint angle combinations may result in various IK solutions. If P denotes the number of constraint functions that are used to constrain variables and m is the group number of divided joint angles of the manipulator, the total number of mapping relations should be Pm. For multiple solutions, users can choose the most appropriate one according to the working conditions.
2.2 Neural network
We divided the whole nonlinear workspace into several partitions by a specific range of joints, and a specially designed neural network was employed for calculation of the IK for each partition.
2.2.1 Frame of the neural network
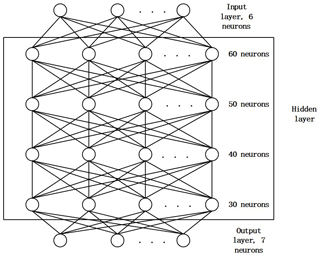
The overall structure of the neural network (Fig. 2), including six layers determined by multiple simulation tests: in detail, six neurons and seven neurons were contained in the input and output layers, respectively. For the middle-hidden layer, 60, 50, 40, and 30 neurons were utilized. The six neurons of the input layer represent the position (x, y, z) and posture (α, β, γ); the seven neurons of the output layer are the inverse kinematics solutions (θ1, θ2… θ7).
2.2.2 Data acquisition
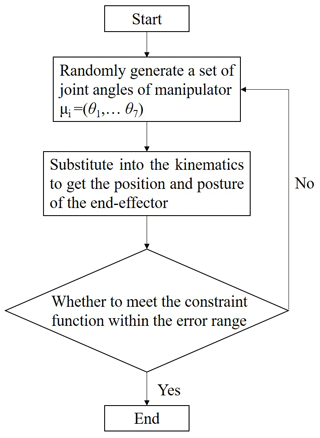
Neural networks require data for training, validation, and test; therefore, data acquisition is an important process. Here, data are randomly generated and substituted into the forward kinematics, and we just retain the results satisfying the constraint function within an error of ±0.01 mm. Those data are finally used to train neural networks and test. The whole process of data acquisition is illustrated as Fig. 3.
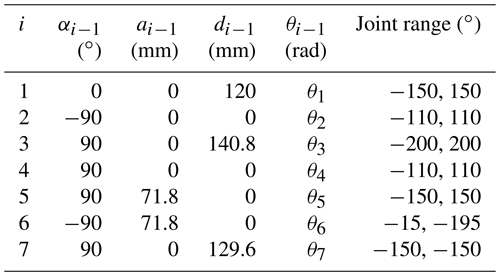
Robai Cyton Gamma 300 with 7 DOFs shown in Fig. 4 was used as a typical model for a simulation study. The manipulator has a maximum payload of 300.0 g with a total length of 53.4 cm and a weight of 1.2 kg. D–H parameters of the manipulator have been shown in Table 1.
ai−1 is the distance moved from zi−1 to zi along the xi−1 axis, di is marked as the distance moved from xi−1 to xi along the zi axis, and the angle revolving from angle zi−1 to zi around the xi−1 axis is αi−1. The Cartesian coordinate system set by the D–H method is shown in Fig. 4a, and the rotational direction of the joint's axes is described in Fig. 4b.
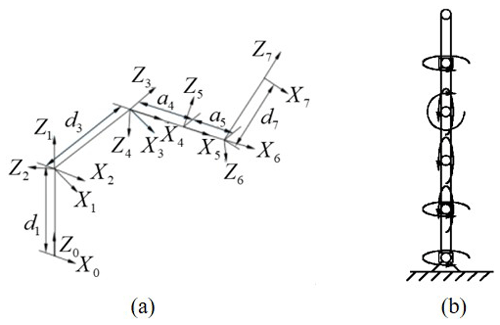
Figure 4(a) Cartesian coordinate system of Cyton Gamma 300. (b) Joint rotation direction of Cyton Gamma 300.
3.1 Forward kinematics
, the transformation matrix of , was calculated by Eq. (5); here, cθi and sθi mean cos θi and sin θi, respectively.
Then, the forward kinematics matrix of a 7-DOF manipulator can be obtained, as shown in Eq. (6):
, , and were denoted by n, o, and a for, respectively, the posture of the end effector to simplify the calculation. We used α, β, and γ as shown in Eq. (7) to describe the posture; indicates the position information in which r14, r24, and r34 were the position directions of the x, y, and z coordinate axes.
r31, r32, r33, r23, and r13 are the parameters of matrix T, and sβ stands for sin (β).
3.2 Inverse kinematics
3.2.1 Constrain function and joint angle division
A constraint function is introduced to eliminate the redundancy of the equations. We set the first joint angle within a range of [−150, 150∘], and the constraint function can be constructed as Eq. (8) according to Eq. (2):
Provided that we alternated the values of θup and θdown, the constraint function and the mapping relationships should be modified as described by Eq. (9):
In order to eliminate the noise in the training data caused by the symmetry of the joint angles, we set the range of joint angles in a range of 0 to 45∘ which were divided into several intervals according to different step values.
3.2.2 Setup of the neural network
We employed the neural network (NN) algorithm for data fitting. The overall structure of the NN (Fig. 2): the whole workspace was divided into seven parts corresponding to the joint angles which were defined in Table 2; 200 000 groups of data were used, among which 199 000 groups of data were used as training data and 900 sets of data were used for validation, and the remaining 100 sets of data were used for tests. Those data were randomly generated and substituted into the forward kinematics. The results satisfying the constraint function within an error of 0.01 mm (radian system) were retained. Finally, trained neural networks would be able to calculate the IK solutions of target points.
4.1 Effect of joint angle range on calculation performance
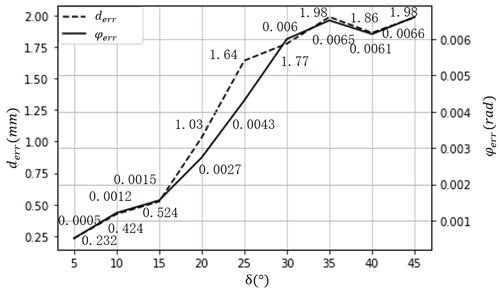
In order to study the effect of joint rotation range on the performance of NN models, the interval of the joint angle of each model is defined as parameter δ from 15 to 45∘, which is shown in Table 2. The position and pose error, namely derr and φerr, can be calculated following Eqs. (10) and (11):
Here, xerr of Eq. (12) represents the variation between the target value x′ and the predicted value x of the x-axis position; yerr and zerr are expressed following a similar way. αerr of Eq. (13) represents the variation between the target value α′ and the predicted value α of the α-axis position; βerr and γerr are expressed following a similar way.
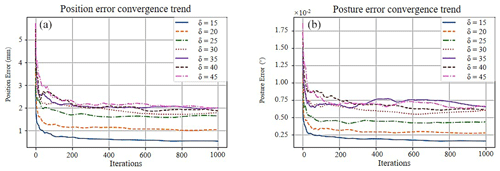
We performed the experiment using diverse intervals and obtained the results as plotted in Fig. 5 (position and posture error) and Fig. 6 (convergence). It can be concluded that the position and posture error were apparently improved when the interval of the joint angles decreased. The position and posture errors were close to 8.5 and 13.2 times for the intervals of 5 and 45∘. In parallel, as shown in Fig. 6, although all curves have a descending trend, the static convergence value of the smaller joint angle interval was lower. For the random update of network calculation weights, when the new weights are not suitable or better than the formal weights, the errors would be diverse to the old ones; therefore, there would be some fluctuation in curves. However, in a general trend, the errors tend to be convergent to a minimal value. In general, it can be found that the joint angle division has a significant influence on the precision of the IK problem.
We recorded the running time cost using different models with various ranges of joint angles. A convergence plot describing the trend of the position (posture) error against the number of iterations is shown in Fig. 6a (Fig. 6b). Obviously, the errors of position and posture were both decreased with a smaller angle interval, which was consistent with the above discussion. Furthermore, for these two plots, it can be found that the variation of iteration steps or time cost of convergence was almost undetectable with different joint angles (from 15 to 45∘).
4.2 Study of multiple solutions
4.2.1 Test of the constraint function
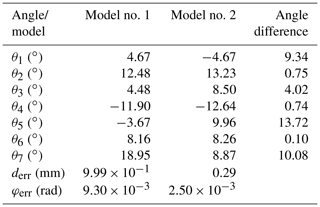
For an identical joint angle range, the correlation of different constraint functions and IK solution quantities was studied. The range of the joint angles was set following Table 2. When the angle δ was defined as 15∘ and for a random position and posture of the end effector (192.833 mm, 18.945 mm, 384.467 mm, 0.138∘, 0.436∘, 0.0593∘), joint angles of a reductant arm can be obtained as in Table 3 following Eq. (7) (function no. 1) and Eq. (8) (function no. 2). From these data, we can find that the solutions for different constraint functions were various for the same position, posture, and joint angle range.
4.2.2 Test of joint angle range
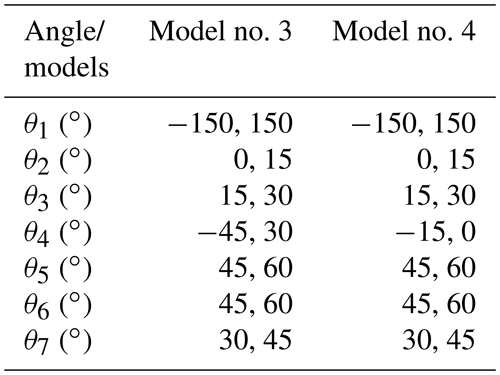
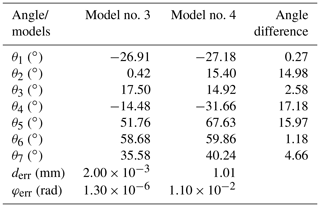
Similarly, we also investigated the effect of joint angle range on multiple IK solutions caused by the symmetry of the joint angles by performing a comparison between two models. The models can be distinguished by the interval of θ4, while the position, posture, and constraint function were consistent. Joint angle intervals of models are summarized as shown in Table 4. For a random position and posture of end effector (183.678 mm, 115.800 mm, 371.048 mm, 0.804∘, 1.561∘, 0.610∘), we acquired the corresponding solutions of the two different models as shown in Table 5. It can be observed that the position and pose errors were acceptable for an IK solution.
From the above simulation tests, we can conclude that more than one group of joint angles were available, while the position and posture of the end effector and constraint function were consistent. In particular, the angle groups were all reasonable for controlling the joint motion, indicating that the IK problem was solved effectively.
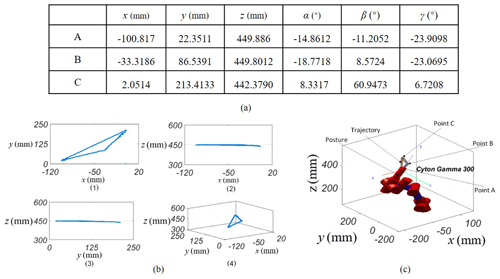
Figure 7(a) Position information of points A, B, and C and values of alpha, beta, and gamma describing the posture of the end effector. (b) Projected trajectory of a defined curve. (c) Simulation configuration using MATLAB.
4.3 Simulation test of predefined trajectory
A standard trajectory was used to further evaluate the motion accuracy of a 7-DOF manipulator obtained by the algorithm. The trajectory can be seen as a triangular curve with three vertex points A, B, and C (spatial information in Fig. 7a). According to the interpolation process of trajectory planning, each side of the curve was partitioned by 100 points. By substituting the position data of each point into the model, multiple solutions of joint angles were obtained. The number of solutions was affected by the quantity of models. On the other hand, the pre-trained neural network models can output multiple sets of feasible solutions during the solution-searching process for a planned trajectory. Criteria for choosing the global optimal solution are often determined according to practical requirements. For this case, the actual trajectory of the manipulator projected onto the standard planes was continuous (Fig. 7b). The whole trajectory of the end effector of the redundant manipulator was shown in Fig. 7c. All the simulation results verified that the algorithm based on neural network models by this work performed well.
4.4 Calculation efficiency
Similarly, data (x, y, z, α, β, γ) including the information of position and posture were randomly generated. Using a GTX1060 graphics card and the i7-CPU processor, different amounts of the data were input into the pre-trained model for analysis of test time cost. Detailed information of time consumptions is listed in Table 6. From this information, we can observe that the data amount can affect time cost of calculation using a CPU. There was a monotone increasing trend of time cost with data amount climbing. In this case, time for calculating one group and 1.00 million groups cost about and 1.70 s, respectively, while for a GPU which was capable of parallel calculation, it took and s for one group and 1.00 million groups, respectively. The time costs of two separated calculations were on the same scale. Therefore, the presented method has a good ability of parallel calculation and provides a practical tool for dealing with a large-amount data set.
4.5 Comparative study
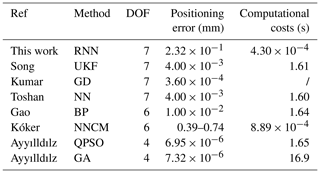
We also performed a comparative study focused on performance using various methods; the results are illustrated in Table 7.
Of these, for 7-DOF manipulators, the numerical sequence processing method combing with a closed-loop framework was utilized to solve IK problem (Song et al., 2020). Gradient descent (Kumar et al., 2010) and radial basis function (RBF) neural networks (Toshani and Farrokhi, 2014) were also employed. For the manipulators with fewer DOFs, 1.65 s and 16.9 s were consumed using QPSO and GA methods with an error of 10−6 (Ayyılldılz and Çetinkaya, 2016). In addition, BP (Gao, 2020) and NNCM (Ayyılldılz and Çetinkaya, 2016) were utilized to obtain IK solutions. From the different results by these methods (Table 7) and previously reported literature (Hassan et al., 2020), we can find that the computational costs by the approach are best. More specifically, we employed a parameter evaluating the effects of position error and computational time costs together, namely Pec = position error × computational costs. Then, for a 7-DOF issue, Pec reaches the minimum value () by our approach which is 2 orders of magnitude less than relative methods. Therefore, it further indicates the presented approach is well suitable to study IK issues for redundant manipulators.
In this work, we proposed a novel approach which utilizes multiple neural network models to delicately solve IK issues of RMs. A constraint function was used to transform RMs to non-RMs. The number of IK solutions of the manipulator was decreased by reducing the range motion of each joint. The number of IK solutions was reduced to finite. Then, the nonlinear workspace of a RM was divided into several parts, followed by a fitting process via a neural network. By combining all of the workspace with mapping formats, the complete workspace of the RM was acquired, and the global optimal solutions were readily obtained. The approach provided less time computation and custom-defined calculating precision: the calculation time of a single point is only s, and for 1.00 million points the time is 1.70 s. Further, calculation error was only 0.23 mm. A 7-DOF robot arm was employed for simulation test. Results of simulation showed that the method was accurate and effective while retaining redundancy characteristics of the RM. Finally, multiple feasible solutions were available for users according to specific working conditions. The strategy and algorithm by this work can be universally utilized to solve IK problems of hyper-redundant robots and thus have the potential to improve the research and development of RMs.
All the code used in this paper can be obtained upon request from the corresponding author.
All the data used in this paper can be obtained upon request from the corresponding author.
HD, CL and WW contributed to establishing the IK solving method and performed the related experiments. LY and HS helped data processing and paper review.
The authors declare that they have no conflict of interest.
The authors are grateful to the National Natural Science Foundation of China and the Natural Science Foundation of Fujian Province.
This research has been supported by the National Natural Science Foundation of China (grant no. 51605092) and the Natural Science Foundation of Fujian Province (grant no. 2017J01691).
This paper was edited by Giuseppe Carbone and reviewed by three anonymous referees.
Ananthanarayanan, H. and Ordóñez, R.: Real-time Inverse Kinematics of (2n+1) DOF hyper-redundant manipulator arm via a combined numerical and analytical approach, Mech. Mach. Theory, 91, 209–226, 2015.
Artemiadis, P. K., Katsiaris, P. T., and Kyriakopoulos, K. J.: A biomimetic approach to inverse kinematics for a redundant robot arm, Auton. Robot, 29, 293–308, 2010.
Ayyılldılz, M. and Çetinkaya, K.: Comparison of four different heuristic optimization algorithms for the inverse kinematics solution of a real 4-DOF serial robot manipulator, Neural Comput. Appl., 27, 825–836, 2016.
Baerlocher, P. and Boulic, R.: An inverse kinematics architecture enforcing an arbitrary number of strict priority levels, Visual Comput., 20, 402–417, 2004.
Bayram, A. and ózgóren, M. K.: The position control of a spatial binary hyper redundant manipulator through its inverse kinematics, P. I. Mech. Eng. C.-J. Mec., 227, 359–372, 2013.
Carbone, G., Ceccarelli, M., and Oliveira, P. J.: An optimum path planning for Cassino parallel manipulator by using inverse dynamics, Robotica, 26, 229–239, 2008.
Dong, H., Du, Z., and Chirikjian, G. S.: Workspace density and inverse kinematics for planar serial revolute manipulators, Mech. Mach. Theory, 70, 508–522, 2013.
Dong, H. and Du, Z.: Obstacle avoidance path planning of planar redundant manipulators using workspace density, Int. J. Adv. Rob. Syst, 12, 9, https://doi.org/10.5772/59973, 2015.
Du, Z. and Dong, H.: Optimal dimension of redundant manipulator using the workspace density function, P. Inst. Mech. Eng. C, 230, 1787–1794, 2015.
Duguleana, M., Barbuceanu, F. G., and Teirelbar, A.: Obstacle avoidance of redundant manipulators using neural networks based reinforcement learning, Rob. Comput. Integr. Manuf, 28, 132–146, 2012.
Duka, A. V.: Neural network based inverse kinematics solution for trajectory tracking of a robotic arm, Proc. Tech., 12, 20–27, 2014.
Dulęba, I. and Opałlka, M.: A comparison of Jacobian-based methods of inverse kinematics for serial robot manipulators, Int. J. Appl. Math. Comput. Sci., 23, 373–382, 2013.
Gao, R.: Inverse kinematics solution of Robotics based on neural network algorithms, J. Amb. Intel. Hum. Comp., 11, 6199–6209, 2020.
Giorelli, M., Renda, F., and Calisti, M.: Neural network and jacobian method for solving the inverse statics of a cable-driven soft arm with nonconstant curvature, IEEE T. Robot., 31, 823–834, 2015.
Han, H., Han, C. Y., and Xu, Z. B.: Kinematics analysis and testing of novel 6-P-RR-R-RR parallel platform with offset RR-joints, P. Inst. Mech. Eng. C, 233, 3512–3530, 2019.
Hassan, A. A., El-Habrouk, M., and Deghedie, S.: Inverse Kinematics of Redundant Manipulators Formulated as Quadratic Programming Optimization Problem Solved Using Recurrent Neural Networks: A Review, Robotica, 38, 1495–1512, 2020.
Kofinas, N., Orfanoudakis, E., and Lagoudakis, M. G.: Complete analytical forward and inverse kinematics for the NAO humanoid robot, J. Intell. Rob. Syst., 77, 251–264, 2015.
Kóker, R.: A genetic algorithm approach to a neural-network-based inverse kinematics solution of robotic manipulators based on error minimization, Inf. Sci., 222, 528–543, 2013a.
Kóker, R.: A neuro-simulated annealing approach to the inverse kinematics solution of redundant robotic manipulators, Eng. Comput., 29, 507–515, 2013b.
Kóker, R., Óz, C., and Çakar, T.: A study of neural network based inverse kinematics solution for a three-joint robot, Auton. Syst., 49, 227–234, 2004.
Kóker, R., Çakar, T., and Sari, Y.: A neural-network committee machine approach to the inverse kinematics problem solution of robotic manipulators, Eng. Comput., 30, 641–649, 2014.
Kumar, S., Sukavanam, N., and Balasubramanian, R.: An optimization approach to solve the inverse kinematics of redundant manipulator, International Journal of Information and System Sciences, 6, 414–423, 2010.
Lin, C. J., Li, T. H. S., and Kuo, P. H.: Integrated particle swarm optimization algorithm based obstacle avoidance control design for home service robot, Electr. Eng, 56, 748–762, 2016.
Martin, A., Barrientos, A., and del Cerro, J.: The natural-CCD algorithm, a novel method to solve the inverse kinematics of hyper-redundant and soft robots, Soft Robot., 5, 242–257, 2018.
Mu, Z., Yuan, H., and Xu, W.: A segmented geometry method for kinematics and configuration planning of spatial hyper-redundant manipulators, IEEE Trans. Syst. Man. Cy. A, 50, 1746–1756, https://doi.org/10.1109/TSMC.2017.2784828, 2018.
Parikh, P. J. and Lam, S. S. Y.: A hybrid strategy to solve the forward kinematics problem in parallel manipulators, IEEE T. Rob., 21, 18–25, 2005.
Patchaikani, P. K., Behera, L., and Prasad, G.: A single network adaptive critic-based redundancy resolution scheme for robot manipulators, IEEE T. Ind. Electron, 59, 3241–3253, 2011.
Rahmani, A., Ghanbari, A., and Mahboubkhah, M.: Kinematics analysis and numerical simulation of hybrid serial-parallel manipulator based on neural network, Neural Netw. World, 25, 427–442, 2015.
Rolf, M., Steil, J. J., and Gienger, M.: Goal babbling permits direct learning of inverse kinematics, IEEE T. Auton. Ment. Dev, 2, 216–229, 2010.
Sari, Y.: Performance evaluation of the various training algorithms and network topologies in a neural-network-based inverse kinematics solution for robots, Int. J. Adv. Robot. Syst., 11, 64, https://doi.org/10.5772/58562, 2014.
Shi, Z. X., Luo, Y. F., and Hang, L. B.: A simple method for inverse kinematic analysis of the general 6R serial robot, International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, Pennsylvania, USA, 10015013 September 2006, DETC2006-99088, https://doi.org/10.1115/DETC2006-99088, 2006.
Shimizu, M., Kakuya, H., and Yoon, W. K.: Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution, IEEE T. Robot., 24, 1131–1142, 2008.
Song, G., Su, S., Li, Y., Zhao, X., and Zhao, Y.: A Closed-Loop Framework for the Inverse Kinematics of the 7 Degrees of Freedom Manipulator, Robotica, https://doi.org/10.1017/S0263574720000582, online first, 2020.
Tanev, T. K.: Kinematics of a hybrid (parallel-serial) robot manipulator, Mech. Mach. Theory., 35, 1183–1196, 2000.
Toshani, H. and Farrokhi, M.: Real-time inverse kinematics of redundant manipulators using neural networks and quadratic programming: a Lyapunov-based approach, Robot. Auton. Syst., 62, 766–781, 2014.
Wan, J., Wu, H. T., and Ma, R.: A study on avoiding joint limits for inverse kinematics of redundant manipulators using improved clamping weighted least-norm method, J. Mech. Sci. Technol, 32, 1367–1378, 2018.
Xiao, L. and Zhang, Y.: Solving time-varying inverse kinematics problem of wheeled mobile manipulators using Zhang neural network with exponential convergence, Nonlinear Dyn., 76, 1543–1559, 2014.
Zaplana, I. and Basanez, L.: A novel closed-form solution for the inverse kinematics of redundant manipulators through workspace analysis, J. Mech. Mach. Theory, 121, 829–843, 2018.