Dynamic analysis of the flexible protection system for electricity transmission engineering

Due to the low cost and short erection period, the flexible protection system is gradually replacing the traditional cross-frame design based on a large steel structure and becoming the main means of protection in power construction. The accurate dynamic analysis of the process of wire falling into a nylon rope net after tension failure is the key to the design and optimization of the flexible protection system. Efficient modeling and analysis of rope network are the core problems. In this investigation, the absolute nodal coordinate formulation cable element is used to model the transmission wire and the nylon rope net. The form finding of the net is performed based on the iterative force density method. The static condensation method is introduced to perform the dynamic analysis of the net to ensure the simulation efficiency. An experiment is carried out to verify the proposed modeling and analysis method. Configurations are compared between the simulation and experimental results so that the feasibility of the proposed method can be demonstrated.

1 Introduction

In the high-voltage transmission line construction process, if the tension failure of the wire occurs, it will cause serious damage to the existing facilities below. For this reason, it is necessary to set up a shelter device called a cross frame, which directly carries the impact away from the wire. The traditional cross frame is a kind of large-scale steel structure with many degrees of freedom, long assembly and disassembly cycles, and high technical risk. In recent years, a new design of the cross frame with nylon rope nets is being increasingly applied in electrical construction engineering. This new type of cross frame design has the advantages of low cost, short erection time, high level of safety, and high maintainability. Two types of cross frames are shown in Fig. 1. In order to ensure safety, the accurate prediction of the drastic dynamic behavior of the wire and the impact to the cross frame is important.

The dynamic analysis of the wire impacting the net is a typical geometric nonlinear dynamic problem, involving large rotation, large deformation, and complex contact search. It is a huge challenge to simulate the movement of wires. Zhang et al. (2021) proposed a systematical simulation procedure based on the vector-form intrinsic finite-element method to analyze the whole process of large deformation and internal force distribution of the non-prestressed cable net structure or similar structures, which provides an important method reference for the numerical analysis of such large deformations and strongly nonlinear engineering problems. Shehata et al. (2005) proposed a detailed numerical model that can be used to predict the structural performance of a transmission tower as part of a transmission line system under downburst loading. In the field of aerospace engineering, the deployable antenna composed of rope mesh and structural parts has the same technical difficulties and processing methods because of its similar structure (Maddio et al., 2024). Nie et al. (2017) presented a parameterized deployment analysis method for space cable net structures considering geometric nonlinearity and topological diversity, and the cable's sag is presented. The stiffness of the cable was determined by its slack or tensional state, and the coupling between the deployment of trusses and the deformation of cable nets is considered by updating the coordinate values of boundary nodes in each time step (Nie et al., 2017). In the research reported on by Du et al. (2018), an analysis method of the deployment of antennas consisting of cable net and flexible truss was proposed. Using the principle of minimum potential energy, the equilibrium state of the quasi-static configuration at an instance of the deployment is computed. In the field of civil engineering, the impact dynamics analysis of steel wire rope mesh used for rockfall protection also has a strong reference value for this research. Guo et al. (2024) developed an enhanced model to predict the performance degradation and failure of steel wire ring nets under such an impact. The authors coupled ductile and shear damage criteria with the material's constitutive equation to consider stress-state-dependent damage behavior. New techniques and modeling methods had also been applied. In the literature published by Cecot et al. (2017), both the finite-element method (FEM) with the higher-order shape functions and the meshless finite-difference method (MFDM) were used to address numerical modeling of overhead power-line cables subjected to static loads. The cable extensibility, their large 3D displacements, and an interaction with strings of insulators and elastic towers are considered (Cecot et al., 2017). Details about the meshless method are also found in the literature (Ahmadi et al., 2023, 2024).

Figure 1 Two different forms of cross frames: (a) double-gauge propulsive and (b) flexible protecting system.

On the other hand, the absolute nodal coordinate formulation (ANCF) provides an elegant solution for the highly nonlinear dynamic problems. Differently from the traditional FEM, ANCF uses global position and gradient vectors as node coordinates, so no transformation is required. As a result, the mass matrix of the element is constant, and the equation of motion of the system is simple. Because it is easy to apply, ANCF has been successfully applied in many engineering scenes after it was conceptualized (Shabana, 2023). The ANCF cable element has been proven to be suitable for modeling the electricity wire, rope, strand, and other such flexible slender components. The planar and spatial ANCF cable elements were developed by Berzeri and Shabana (2000) and Sugiyama et al. (2003), respectively. Afterwards, Gerstmayr and Irschik (2008) modified the definition of bending and axial deformation and gave more accurate formulation of the cable elastic model. Since the definition of element strain energy contains curvature of the centerline, resulting in complex formulation of the generalized elastic force. Zhang et al. (2022) used the curvature constrained interpolation method and decoupling elastic line approach, obtaining a simple expression of the element elastic model. Ding and Ouyang (2022) proposed a variable-length arbitrary Lagrange–Euler rational ANCF cable element. The new element employed rational polynomials as an element shape function so it would be able to accurately describe conic and circular curves (Ding and Ouyang, 2022). Westin and Irani (2023) compared four types of semi-implicit integrators for real-time cable simulations through three benchmark studies. Yang and Gong (2023) refined the section of nodal coordinates and configuration description of the element, forming an enhanced ANCF to greatly reduce the number of required modeling degrees of freedom (DOFs). Unlike the traditional ANCFs, the absolute position vector of an arbitrary point of the element was calculated by evaluating an integral of the element gradient over the element length with the position vector of the starting node of the element added. This led to considerable DOF saving.

In engineering applications, the ANCF cable element has been widely used in the wire and steel rope modeling (Fotland and Haugen, 2022). Li et al. (2022) built a tower crane model in which an arbitrary Lagrange–Euler (ALE) ANCF cable element was used to describe the varying of string length in the hoisting system. A swing control algorithm based on the phase plan method was given (K. Li et al., 2022). In the ocean engineering field, Fan et al. (2024) presented a dynamic analysis model for a catenary anchor leg mooring (CALM) system based on the ANCF cable element. A comparative analysis of the ANCF mooring cable model with OpenFAST and MoorDyn accentuated the program's practical value in real engineering applications. In the study proposed by Yang et al. (2024), the ALE-ANCF cable element was employed to model variable-length flexible towing cables. Detailed investigation into the impact of cable deployment/retrieval on towing depth was conducted. Wang et al. (2024) applied the ALE-ANCF cable element in the investigation of the nonlinear dynamics of variable-length underwater tethered systems going over obstacles. The adaptive element techniques were adopted to efficiently simulate the moving contact. Fine meshes were generated autonomously to capture the detailed contact behaviors in contact areas, while coarse meshes emerge in non-contact areas, thus significantly reducing DOFs and contact pairs. In space engineering, the ANCF cable element was used to build the net model to capture space debris objects (Shan et al., 2020). In the space elevator system, the use of the ANCF cable element was capable of better reflecting the local flexible deformation of the space elevator rope and had better calculation stability than FEM (Luo et al., 2021). Hu et al. (2024) proposed a novel analysis method based on energy flow to reveal the dynamic deployment characteristics of the cable–membrane system. The accuracy of the dynamic model of the cable–membrane system was verified by experimental validation of the deployment process (Hu et al., 2024). In the pipe dynamics field, due to the lack of advanced models and analytical methods, the study of pipes conveying fluid usually only considers the in-plane vibration of straight pipes. In the research reported by Yuan and Ding (2023), a 3D finite-element model for the curved pipe was developed based on ANCF. The nonlinear dynamic equations of the pipe system were derived using extended Lagrange equations. The natural frequencies and modes were calculated by linearizing the equations (Yuan and Ding, 2023). Zhou et al. (2022) investigated the dynamical problem of straight and curved fluid-conveying pipes consisting of both flexible and rigid pipe segments. To obtain the universal nonlinear governing equations of the considered pipe system, the two-node planar initially curved ANCF cable elements are utilized to discretize the pipe, and the extended Lagrange equations written for systems containing non-material volumes are employed (Zhou et al., 2022).

In the power transmission wire modeling aspect, Escalona et al. (2013) used ANCF cable elements to model the sliding contact using sliding joint constraints, obtaining an efficient and accurate strip-catenary model. Pappalardo et al. (2019) proposed a series of research works in which the ANCF cable element was used to build the catenary model and applied in the contact force control. For transmission wire modeling, Zhang et al. (2021b) considered the nonlinear mechanical properties inside the wire. A strain-decoupled ANCF cable element was derived. By analyzing the geometry of the stranded flexible cable as well as the relative sliding and friction between the wires in the cable, the axial stiffness and bending stiffness calculation formulae were obtained, and the decoupled-stranded model was established (Zhang et al., 2021). Gu et al. (2021) proposed a systematical algorithm to simulate the nonlinear constraint with the iron tower, the efficient contact to the cross frame and the co-simulation solving strategy. A simple experiment was also proposed by the authors (Gu et al., 2021). In the research reported by Peng et al. (2022), as catenary cables have large initial displacements and can exhibit strong vibration and undergo large deformations in train operation, a new method based on the ANCF cable element with an adaptive variable length was proposed to accurately compute the initial equilibrium configuration of the catenary.

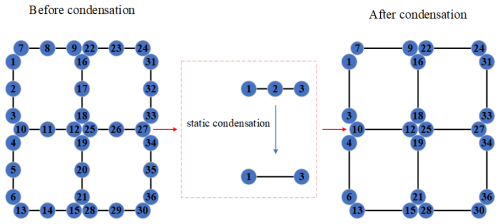
In this investigation, the ANCF cable element is used to build the transmission wire and nylon rope net model. The nylon rope net has a large number of degrees of freedom, and the dynamic simulation is time-consuming. Model order reduction algorithms are needed. In order to reduce memory requirements, Benatia et al. (2023) performed element-level static condensation of internal degrees of freedom. Ji et al. (2023) constructed a super element by the static condensation method, and the stiffness and mass matrices of the super element are parameterized. Zhou et al. (2020) minimized the computational cost by the static condensation of Lagrange multipliers and the elimination of displacement unknowns at the subdomain interface. In order to accurately simulate concrete cracking in large-scale structures, Mezher developed an adaptive static condensation (ASC) method (Mezher et al., 2024). Laskowski et al. (2020) compared classic implicit strategies for the full Jacobian system to the recently developed static condensation technique for discontinuous Galerkin spectral element method on Gauss–Lobatto nodes (GL-DGSEM). Rueda-Ramírez et al. (2021) presented a statically condensed GL-DGSEM for compressible Navier–Stokes equations. Cheng et al. (2023) used the hybrid mimetic mixed (HMM) scheme, which can be efficiently implemented by the static condensation method. In order to reduce the complexity of the model, Liu et al. (2020) perform static condensation substructure construction on the sampled lattice substructures. Nicolaidou demonstrated how the error associated with static condensation can be efficiently approximated during model reduction (Nicolaidou et al., 2021). For solid mechanics, the machine learning surrogate model proposed by Parish performs static condensation on the degrees of freedom in the inner domain (Parish et al., 2024). X. Li et al. (2022) used the static condensation method to transform the stiffness matrix and the mass matrix to obtain the natural vibration frequency of the variable curvature beam. Lee et al. (2024) combined the substructure with the static condensation method to further improve the computational efficiency of the reanalysis without losing accuracy. Arun et al. (2024) transformed the Euler–Poisson (EP) system into a differential-algebraic equation (DAE) system by static condensation. In order to reduce the order of the near-field dynamic model, Galadima et al. (2020) proposed a model reduction algorithm based on the static condensation method. Waseem et al. (2019) used the static condensation method to obtain the global basis of the steady-state response and solved the eigenvalue problem to obtain the global basis of the transient response. Bayat et al. (2021) used the static condensation method to solve the coupled nonlinear ordinary differential equations obtained by the Galerkin method. Sheng et al. (2021) obtained a simplified nonlinear ordinary differential equation based on the static condensation method and the Galerkin method. Sheng and Wang (2020) used the Galerkin method and the static condensation method to derive the reduced-order nonlinear differential equation. In order to reduce the number of ordinary differential equations, Amiri and Talebitooti (2022) adopted the static condensation method. Botti and Di Pietro (2021) studied how the combination of p coarsening and static condensation affects the V-cycle iteration. Based on the polynomial chaos expansion (PCE) form, Kumar et al. (2021) extended the static condensation method to the random case to obtain a reduced-order stochastic finite-element model. Based on the static condensation method, Galadima et al. (2022) proposed a model reduction method to reduce the order of the transient thermal model of near-field dynamics.

The rest of this paper is organized as follows: in Sect. 2, the ANCF cable element, which is used in wire and nylon rope net modeling, is briefly introduced. The method of applying initial tension to the wire is given. In Sect. 3, the form-finding method of the nylon rope net is presented. Section 4 introduces the strategy for the model order reduction for the nylon rope net. The contact-detecting algorithm is discussed in Sect. 5. Section 6 presents the simulation results. Section 7 gives the concluding remarks.

2 Modeling of the transmission wire

The ANCF cable element is used to describe the dynamic behavior of the wire that will undergo large rotation and deformation. The kinematic description, the definition of the elastic force, and the application of initial tension in the wire are briefly introduced in this section.

2.1 Kinematic description

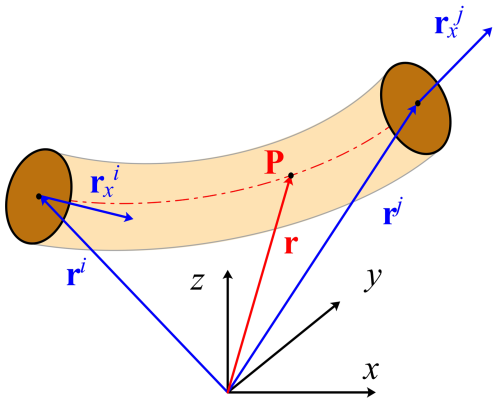
As shown in Fig. 2, The ANCF cable element is developed based on the Euler–Bernoulli beam model (Berzeri and Shabana, 2000). The cross section of the element is assumed to be undeformed and perpendicular to the centerline. Only the axial material coordinate of the centerline is included in the element shape function. The global position and gradient vectors at both ends are taken as nodal coordinates, so the total number of DOFs is 12 for the cable element. The global position of an arbitrary point on the element is defined as r=Se. e is the element nodal coordinate vector:

$$\begin{array}{}\text{(1)}& \mathit{e}={\left[{\mathit{r}}^{i^T},{\mathit{r}}_x^{i^T},{\mathit{r}}^{j^T},{\mathit{r}}_x^{j^T}\right]}^{\mathrm{T}}.\end{array}$$

The shape function is defined as follows:

$$\begin{array}{}\text{(2)}& \mathit{S}=\left[S_{\mathrm{1}}{\mathit{I}}_{\mathrm{3}\times \mathrm{3}},S_{\mathrm{2}}{\mathit{I}}_{\mathrm{3}\times \mathrm{3}},S_{\mathrm{3}}{\mathit{I}}_{\mathrm{3}\times \mathrm{3}},S_{\mathrm{4}}{\mathit{I}}_{\mathrm{3}\times \mathrm{3}}\right],\end{array}$$

where the element shape functions are

$$\begin{array}{}\text{(3)}& \left\{\begin{array}{l}{S}_{\mathrm{1}}=\mathrm{1}-\mathrm{3}{\mathit{\xi }}^{\mathrm{2}}+\mathrm{2}{\mathit{\xi }}^{\mathrm{3}},\\ S_{\mathrm{2}}=l\left(\mathit{\xi }-\mathrm{2}{\mathit{\xi }}^{\mathrm{2}}+{\mathit{\xi }}^{\mathrm{3}}\right),\\ S_{\mathrm{3}}=\mathrm{3}{\mathit{\xi }}^{\mathrm{2}}+\mathrm{2}{\mathit{\xi }}^{\mathrm{3}},\\ S_{\mathrm{4}}=l\left(-{\mathit{\xi }}^{\mathrm{2}}+{\mathit{\xi }}^{\mathrm{3}}\right).\end{array}\right.\end{array}$$

In the equations above, $\mathit{\xi }=x/l$ is the dimensionless material coordinate and l is the element length. The mass matrix is defined by the following expression:

$$\begin{array}{}\text{(4)}& \mathit{M}={\int }_V\mathit{\rho }{\mathit{S}}^T\mathit{S}\mathrm{d}V,\end{array}$$

From the formulation above, one can find that the mass matrix of the element is constant. This feature makes it possible to perform the decomposition to the mass matrix to improve the efficiency of the simulation (Yakoub and Shabana, 1999).

Figure 2 ANCF cable element.

2.2 Element elastic force

Due to the lack of a gradient vector in the cable elements used in this study, the general expressions of continuum mechanics are not applicable to the cable elements. The strain energy of the cable element can be divided into two parts. One relates to axial stretching or compression of the centerline and the other to bending:

$$\begin{array}{}\text{(5)}& U={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\int }_{\mathrm{0}}^{l}EA({\mathit{\epsilon }}_{xx}{)}^{\mathrm{2}}\mathrm{d}x+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\int }_{\mathrm{0}}^{l}EI(\mathit{\kappa }{)}^{\mathrm{2}}\mathrm{d}x,\end{array}$$

where E is Young's modulus, A is the cross-section area, and I is the moment inertial of the cross section. In this investigation, the elastic model developed by Gerstmayr and Irschik (2008) is used. The axial strain is defined as ${\mathit{\epsilon }}_{xx}=\left|{\mathit{r}}_x\right|-\mathrm{1}$, and the curvature of the element centerline is $\mathit{\kappa }=\left|{\mathit{r}}_x\times {\mathit{r}}_{xx}\right|/{\left|{\mathit{r}}_x\right|}^{\mathrm{2}}$. r_x and r_xx are the first and second gradient vectors of the element. According to the virtual work principle, the generalized elastic force can be obtained through the partial derivative of the strain energy with respect to the generalized coordinate:

$$\begin{array}{}\text{(6)}& {\mathit{Q}}_{\mathrm{e}}={\displaystyle \frac{\partial U}{\partial \mathit{e}}}={\mathit{Q}}_{\mathrm{s}}+{\mathit{Q}}_{\mathit{\kappa }}.\end{array}$$

In this equation, Q_s and Q_κ are the generalized elastic force associated with stretch and bending, respectively. When the implicit integrator is used, the Jacobian of the generalized elastic force with respect to element nodal coordinates should also be calculated. The specific formulation of the elastic force and its Jacobian can be found in a literature previously published by the authors (Lan et al., 2019).

2.3 Initial tension of the wire

In the electricity construction process, tension is applied to the transmission wire is by a tensioning machine. In other words, the steel wire reaches a state of equilibrium with its own elasticity, tension, and gravity. According to industry standards, the tensile force can reach 12 %–18 % of the breaking force of the steel wire. This means that the tension force should be included in the initial configuration of the wire. In this section, a scenario which contains two steps is given. First, the static solving is performed to obtain the equilibrium configuration of the wire. Afterwards, it is used as the initial value of the system nodal coordinates in the dynamic analysis stage. In this manner, the initial strain can be introduced into the wire model. The statical equilibrium equation is given as follows:

$$\begin{array}{}\text{(7)}& {\mathit{Q}}_{\mathrm{ela}}\left(\mathit{e}\right)-{\mathit{Q}}_{\mathrm{ext}}=\mathrm{0}.\end{array}$$

In the equation above, Q_ela is the generalized elastic force which is the nonlinear function of system nodal coordinates. Q_ext is the external force including gravity and tension force. This is a typical nonlinear algebraic equation which can be solved by Newton–Raphson iteration. The iterative formula is as follows:

$$\begin{array}{}\text{(8)}& {\mathit{e}}^{k+\mathrm{1}}={\mathit{e}}^k-{\left.{\mathbf{J}}^{-\mathrm{1}}\right|}_{{\mathit{e}}^k}\left[{\left.{\mathit{Q}}_{\mathrm{ela}}\right|}_{{\mathit{e}}^k}-{\mathit{Q}}_{\mathrm{ext}}\right].\end{array}$$

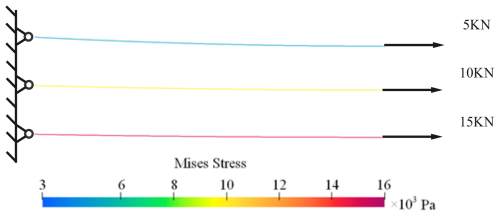
In this equation, e^k is the system nodal coordinate vector at the kth iteration step. J is the Jacobian matrix of the elastic force, and it is evaluated at the current iteration step along with the elastic force. Figure 3 gives the equilibrium configuration of a wire 19 m in length under different values of tension force. It can be seen that the larger the initial tension, the straighter the wire configuration and the larger the initial deformation energy stored.

Figure 3 Equilibrium configuration under different tension force.

3 Form finding of the nylon rope net

Nylon rope net will have a certain natural droop after hanging, which is the result of its gravity, tension, and elastic force balance. In the modeling process, it is difficult to describe the initial configuration directly, but the equilibrium configuration with initial deformation can be obtained by some iterative solving algorithm. In this paper, the force density method (FDM) given by Linkwitz and Schek is used (Li et al., 2024). The basic principle is to linearize the internal force balance equations at the cable–net connection points.

Figure 4 Force density principle.

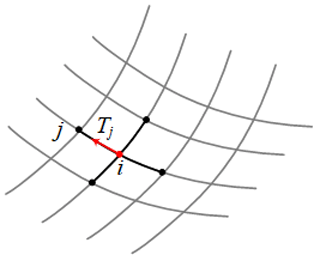
Figure 4 illustrates a local vision of the net. Assuming that the cable segment connected at the connection point i has s roots, the force density coefficient of the jth cable segment is expressed as follows:

$$\begin{array}{}\text{(9)}& q_j={\displaystyle \frac{T_j}{l_j}},\end{array}$$

where T_j and l_j represent the tension and length of the jth cable, respectively. In the coordinate system $\left(X,Y,Z\right)$, the position of point i is marked as $\left(x_i,y_i,z_i\right)$. According to the force density method, the linear equilibrium equations of the force density at the connection point i can be expressed as

$$\begin{array}{}\text{(10)}& \left\{\begin{array}{l}\sum _{j=\mathrm{1}}^s{q}_j\left(x_j-x_i\right)=\mathrm{0},\\ \sum _{j=\mathrm{1}}^s{q}_j\left(y_j-y_i\right)=\mathrm{0},\end{array}\right.\end{array}$$

where x_j and y_j are the x and y coordinates of the other endpoints of the jth cable except the i point. Similarly, the linear equilibrium equations at all cable segment connection points in the system can be obtained, and the x and y coordinates of all connection points can be obtained by solving these simultaneous linear equilibrium equations.

For the traditional force density method, the force density coefficient, q_j, of each cable segment is assumed to be a constant, so the tension of the cable segment can be expressed as

$$\begin{array}{}\text{(11)}& T_j^{\prime }=q_j{l}_j^{\prime },\end{array}$$

where $l_j^{\prime }$ is the new length of the jth cable segment, which can be solved by the spatial coordinates of the obtained connection points. When the length of the cable section changes, the tension of the cable section will also change, so the traditional force density method will make the tension of the cable section no longer uniform. In order to address this issue, Morterolle et al. (2012) proposed an iterative force density method. The main idea is to update the force density coefficient in each iteration step so that the tension of each cable segment in the final form-finding result is equal to the uniform tension, T_d. According to this method, the updated force density coefficient of the jth cable segment in each iteration step can be expressed as follows:

$$\begin{array}{}\text{(12)}& q_j^{(p+\mathrm{1})}=q_j^{\left(p\right)}{T}_d/T_j^{\left(p\right)},\end{array}$$

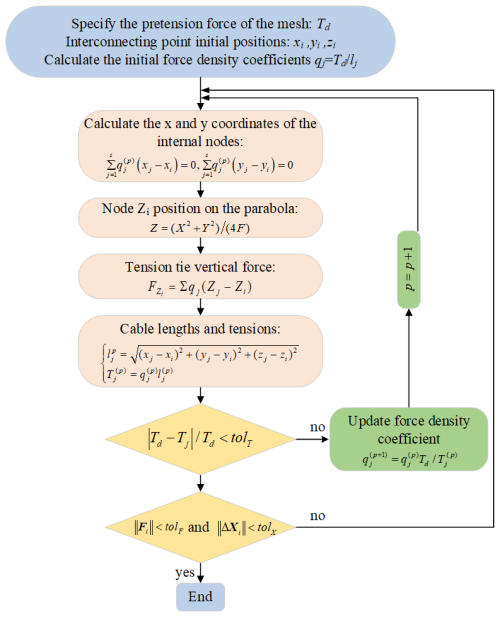
where p represents the current iteration step and T_d is the initial uniform tension value of the cable segment. The iterative convergence condition is $\left|T_d-T_j^{\left(p\right)}\right|/T_d<{\mathrm{tol}}_T$, where tol_T is the specified tension convergence error, which is set to 10⁻³. Moreover, a node is considered to be in equilibrium if the norm of its total outbalanced force, F_i, is inferior to tol_F, which is set to 10⁻⁵ and considered stable in position if between two consecutive iterations, and if its coordinate variation, ΔX_i, is inferior to tol_X, which is set to 10⁻⁶. The whole process of the form-finding algorithm is illustrated in Fig. 5. With the iterative update of the force density coefficient, the tension value of the cable section will be closer to the preset uniform tension value, T_d, of the cable section. Therefore, after using the iterative force density method for form finding, the maximum tension ratio of the pre-tension of each cable section in the cable net is almost equal to one, which meets the requirements of the tension uniformity of the cable section. The results of the form finding are shown in Fig. 6.

It is worth to be pointed out that in this research, the cable net has a relatively average mesh size and material properties. In other applications, when dealing with the net which has highly irregular or uneven mesh, including rapidly changed curvature, cross-section area, and material properties, the iterative force density method may fail on estimation of the tension force, resulting in unmatched simulation results compared with the actual form (Morterolle et al., 2012).

Figure 5 Form-finding algorithm.

Figure 6 The von Mises stress distribution of the mesh surface.

4 Model order reduction

4.1 Schur complement method

In order to accurately describe the nonlinear dynamic behavior of cable network, such as large rotation and large deformation, it is necessary to use a dense finite-element mesh to model it. With the increase in the number of elements, the dimension of the dynamic equation increases, which makes the computational efficiency drop sharply. On the premise of not affecting the calculation accuracy of the cable network system, the substructure method – that is, the Schur complement method – is used to solve the dynamic equation efficiently. In the static analysis of structural finite element, the static equilibrium equation is solved as follows:

$$\begin{array}{}\text{(13)}& \mathbf{K}\mathit{U}=\mathit{R},\end{array}$$

where K is the stiffness matrix, U is the displacement vector, and R is the load vector. The basic idea of the Schur complement method is to divide the system into several substructures, then condense the internal degrees of freedom to the boundary, and finally reduce the scale of Eq. (13). The linear equilibrium equations similar to Eq. (13) need to be solved for each numerical iteration step in the dynamics calculation of multi-body systems. Therefore, the method of solving the equations can be extended to the process of solving the dynamics of multi-body systems. In the Schur complement method, the static equilibrium equation of the substructure is similar to Eq. (13) and can be written as follows:

$$\begin{array}{}\text{(14)}& \left[\begin{array}{cc}{\mathbf{K}}^{\mathrm{ii}}& {\mathbf{K}}^{\mathrm{ib}}\\ {\mathbf{K}}^{\mathrm{bi}}& {\mathbf{K}}^{\mathrm{bb}}\end{array}\right]\left[\begin{array}{c}{\mathit{U}}^{\mathrm{i}}\\ {\mathit{U}}^{\mathrm{b}}\end{array}\right]=\left[\begin{array}{c}{\mathit{R}}^{\mathrm{i}}\\ {\mathit{R}}^{\mathrm{b}}\end{array}\right],\end{array}$$

where Uⁱ and U^b are the displacement vectors of the inner node and the boundary node of the substructure, respectively. Kⁱⁱ, K^ib, K^bi, and K^bb are the submatrices corresponding to the substructure stiffness matrix K, and Rⁱ and R^b are the internal and boundary components of the load vector, respectively. Because the internal nodes of the substructure are independent of other substructures, the degrees of freedom of the internal nodes can be condensed. The Uⁱ expression can be obtained from Eq. (14) as follows:

$$\begin{array}{}\text{(15)}& {\mathit{U}}^{\mathrm{i}}={\left({\mathbf{K}}^{\mathrm{ii}}\right)}^{-\mathrm{1}}\left({\mathit{R}}^{\mathrm{i}}-{\mathbf{K}}^{\mathrm{ib}}{\mathit{U}}^{\mathrm{b}}\right).\end{array}$$

By substituting Eq. (15) into Eq. (14), the static equilibrium equation of the substructure after complementation is obtained:

$$\begin{array}{}\text{(16)}& \stackrel{\mathrm{‾}}{\mathbf{K}}{\mathit{U}}^{\mathrm{b}}=\stackrel{\mathrm{‾}}{\mathit{F}},\end{array}$$

where

$$\begin{array}{}\text{(17)}& \left\{\begin{array}{l}\stackrel{\mathrm{‾}}{\mathbf{K}}={\mathbf{K}}^{\mathrm{bb}}-{\mathbf{K}}^{\mathrm{bi}}{\left({\mathbf{K}}^{\mathrm{ii}}\right)}^{-\mathrm{1}}{\mathbf{K}}^{\mathrm{ib}},\\ \stackrel{\mathrm{‾}}{\mathit{F}}={\mathit{R}}^{\mathrm{b}}-{\mathbf{K}}^{\mathrm{bi}}{\left({\mathbf{K}}^{\mathrm{ii}}\right)}^{-\mathrm{1}}{\mathit{R}}^{\mathrm{i}}.\end{array}\right.\end{array}$$

Since the dimension of Eq. (16) is much lower than that of Eq. (13), the displacement of the boundary node can be obtained by efficiently solving Eq. (16). By substituting the calculation results into Eq. (15), the displacement of internal nodes can be obtained.

4.2 Static condensation of the net

In order to improve the computational efficiency, the flexible multi-body system is divided into n independent subsystems. The degrees of freedom of each subsystem are divided into internal degrees of freedom and boundary degrees of freedom. The boundary degrees of freedom of the Lagrange multiplier connecting adjacent subsystems are defined to ensure the continuity of the displacement field between subsystems. After solving the interface equation, the degrees of freedom of all subsystems are solved by back substitution. The internal degrees of freedom and Lagrange multipliers of each subsystem are condensed using the Schur complement method introduced in Sect. 4.1, as illustrated in Fig. 7.

Figure 7 Static condensation of the net.

Taking the kth subsystem as an example, the following linear algebraic equations need to be solved in the Newton–Raphson iteration process:

$$\begin{array}{}\text{(18)}& \begin{array}{rl}& \left.\left(\left[\begin{array}{ll}{\mathbf{K}}_k& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\end{array}\right]\right.+\left[\begin{array}{ll}{\mathbf{\Phi }}_k^T{\mathbf{\Phi }}_k& {\mathbf{\Phi }}_k^T\\ {\mathbf{\Phi }}_k& \mathrm{0}\end{array}\right]\right)\left[\begin{array}{c}\mathrm{\Delta }{\mathit{q}}_k\\ \mathrm{\Delta }{\mathit{\lambda }}_k\end{array}\right]\\ & =-\left[\begin{array}{l}{\mathit{F}}_k^r\\ {\mathit{F}}_k^c\end{array}\right],\end{array}\end{array}$$

where

$$\begin{array}{}\text{(19)}& \left\{\begin{array}{l}{\mathbf{K}}_k=\widehat{\mathit{\beta }}{\mathbf{M}}_k+{\mathbf{JQ}}_k,\\ {\mathit{F}}_k^r={\mathbf{M}}_k{\ddot{\mathit{q}}}_k+\mathit{Q}{k}_k+{\mathbf{\Phi }}_k^T{\mathit{\lambda }}_k-\mathit{Q}{e}_k-\mathit{Q}{c}_k,\\ {\mathit{F}}_k^c={\mathit{C}}_k.\end{array}\right.\end{array}$$

M_k, JQ_k, Qk_k, Φ_k, Qe_k, Qc_k, and C_k are the mass matrix of the kth subsystem, the Jacobian matrix of the elastic force vector, the elastic force vector, the Jacobian matrix of the constraint equation, the gravity and contact force vectors, and the constraint equation, respectively. Δq_k and Δλ_k are the generalized coordinate increment and Lagrange's multiplier increment of the kth subsystem, respectively. According to Eq. (14), Eq. (18) can be expressed as follows:

$$\begin{array}{}\text{(20)}& \left[\begin{array}{ll}{\mathbf{\Gamma }}_k^{\mathrm{ii}}& {\mathbf{\Gamma }}_k^{\mathrm{ib}}\\ {\mathbf{\Gamma }}_k^{\mathrm{bi}}& {\mathbf{\Gamma }}_k^{\mathrm{bb}}\end{array}\right]\left[\begin{array}{l}\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{q}}}_k^{\mathrm{i}}\\ \mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{q}}}_k^{\mathrm{b}}\end{array}\right]=-\left[\begin{array}{l}{\mathit{F}}_k^{\mathrm{i}}\\ {\mathit{F}}_k^{\mathrm{b}}\end{array}\right],\end{array}$$

where

$$\begin{array}{}\text{(21)}& \begin{array}{l}{\mathbf{\Gamma }}_k^{\mathrm{ii}}=\left[\begin{array}{ll}{\mathbf{K}}_k^{\mathrm{ii}}+{\mathbf{\Phi }}_k^{\mathrm{i}T}{\mathbf{\Phi }}_k^{\mathrm{i}}& {\mathbf{\Phi }}_k^{\mathrm{i}T}\\ {\mathbf{\Phi }}_k^{\mathrm{i}}& \mathrm{0}\end{array}\right],\\ {\mathbf{\Gamma }}_k^{\mathrm{ib}}=\left[\begin{array}{ll}{\mathbf{K}}_k^{\mathrm{ib}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\end{array}\right],{\mathbf{\Gamma }}_k^{\mathrm{bi}}=\left[\begin{array}{ll}{\mathbf{K}}_k^{\mathrm{bi}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\end{array}\right],\\ {\mathbf{\Gamma }}_k^{\mathrm{bb}}=\left[\begin{array}{ll}{\mathbf{K}}_k^{\mathrm{bb}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\end{array}\right]+\left[\begin{array}{ll}{\mathbf{\Phi }}_{k\mathrm{b}T}{\mathbf{\Phi }}_k^{\mathrm{b}}& {\mathbf{\Phi }}_k^{\mathrm{b}T}\\ {\mathbf{\Phi }}_k^{\mathrm{b}}& \mathrm{0}\end{array}\right],\end{array}\end{array}$$

and

$$\begin{array}{}\text{(22)}& \begin{array}{rl}\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{q}}}_k^{\mathrm{i}}& =-\left[\begin{array}{l}\mathrm{\Delta }{\mathit{q}}_k^{\mathrm{i}}\\ \mathrm{\Delta }{\mathit{\lambda }}_k^{\mathrm{i}}\end{array}\right],\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{q}}}_k^{\mathrm{b}}=-\left[\begin{array}{l}\mathrm{\Delta }{\mathit{q}}_k^{\mathrm{b}}\\ \mathrm{\Delta }{\mathit{\lambda }}_k^{\mathrm{b}}\end{array}\right],\\ {\mathit{F}}_k^{\mathrm{i}}& =\left[\begin{array}{l}{\mathit{F}}_k^{\mathrm{ri}}\\ {\mathit{F}}_k^{c\mathrm{i}}\end{array}\right],{\mathit{F}}_k^{\mathrm{b}}=\left[\begin{array}{l}{\mathit{F}}_k^{\mathrm{rb}}\\ {\mathit{F}}_k^{c\mathrm{b}}\end{array}\right].\end{array}\end{array}$$

According to Eq. (20), the increment of the internal variable of the kth subsystem can be expressed as follows:

$$\begin{array}{}\text{(23)}& \mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{q}}}_k^{\mathrm{i}}=-{\left({\mathbf{\Gamma }}_k^{\mathrm{ii}}\right)}^{-\mathrm{1}}\left({\mathbf{\Gamma }}_k^{\mathrm{ib}}\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{q}}}_k^{\mathrm{b}}+{\mathit{F}}_k^{\mathrm{i}}\right).\end{array}$$

By substituting Eq. (23) into Eq. (20), the boundary variable increment can be obtained by solving the following equation:

$$\begin{array}{}\text{(24)}& \begin{array}{rl}& \left(\left[\begin{array}{ll}{\stackrel{\mathrm{‾}}{\mathbf{K}}}_k& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\end{array}\right]+\left[\begin{array}{ll}{\mathbf{\Phi }}_k^{\mathrm{b}T}{\mathbf{\Phi }}_k^{\mathrm{b}}& {\mathbf{\Phi }}_k^{\mathrm{b}T}\\ {\mathbf{\Phi }}_k^{\mathrm{b}}& \mathrm{0}\end{array}\right]\right)\left[\begin{array}{l}\mathrm{\Delta }{\mathit{q}}_k^{\mathrm{b}}\\ \mathrm{\Delta }{\mathit{\lambda }}_k^{\mathrm{b}}\end{array}\right]\\ & =-\left[\begin{array}{l}{\stackrel{\mathrm{‾}}{\mathit{F}}}_k^r\\ {\stackrel{\mathrm{‾}}{\mathit{F}}}_k^c\end{array}\right],\end{array}\end{array}$$

where

$$\begin{array}{}\text{(25)}& \left\{\begin{array}{l}{\stackrel{\mathrm{‾}}{\mathbf{K}}}_k={\mathbf{K}}_k^{\mathrm{bb}}-{\mathbf{K}}_k^{\mathrm{bi}}{\mathbf{R}}_k^{rr}{\mathbf{K}}_k^{\mathrm{ib}},\\ {\stackrel{\mathrm{‾}}{\mathit{F}}}_k^r={\mathit{F}}_k^{\mathrm{rb}}-{\mathbf{K}}_k^{\mathrm{bi}}{\mathbf{R}}_k^{rr}{\mathit{F}}_k^{\mathrm{ri}}-{\mathbf{K}}_k^{\mathrm{bi}}{\mathbf{R}}_k^{rc}{\mathit{F}}_k^{c\mathrm{i}},\\ {\mathit{F}}_k^c={\mathit{F}}_k^{c\mathrm{b}},\\ {\mathbf{R}}_k={\left({\mathbf{\Gamma }}_k^{\mathrm{ii}}\right)}^{-\mathrm{1}}=\left[\begin{array}{ll}{\mathbf{R}}_k^{rr}& {\mathbf{R}}_k^{rc}\\ {\mathbf{R}}_k^{cr}& {\mathbf{R}}_k^{cc}\end{array}\right].\end{array}\right.\end{array}$$

Finally, the equilibrium after the condensation of each subsystem is assembled to obtain the equilibrium equations of the interface problem as follows:

$$\begin{array}{}\text{(26)}& \begin{array}{r}\left(\left[\begin{array}{ll}{\mathbf{A}}_{j=\mathrm{1}}^n{\stackrel{\mathrm{‾}}{\mathbf{K}}}_j& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\end{array}\right]+\left[\begin{array}{ll}{\mathbf{\Phi }}^{\mathrm{b}T}{\mathbf{\Phi }}^{\mathrm{b}}& {\mathbf{\Phi }}^{\mathrm{b}T}\\ {\mathbf{\Phi }}^{\mathrm{b}}& \mathrm{0}\end{array}\right]\right)\\ \left[\begin{array}{l}{\mathbf{A}}_{j=\mathrm{1}}^n\mathrm{\Delta }{\mathit{q}}_j^{\mathrm{b}}\\ \mathrm{\Delta }{\mathit{\lambda }}^{\mathrm{b}}\end{array}\right]=-\left[\begin{array}{l}{\mathbf{A}}_{j=\mathrm{1}}^n{\stackrel{\mathrm{‾}}{\mathit{F}}}_j^r\\ {\stackrel{\mathrm{‾}}{\mathit{F}}}^c\end{array}\right].\end{array}\end{array}$$

It needs to be noted that researchers and engineers should pay attention to the displacement coupling between the boundary and inner nodes in the substructure when using the static condensation method, especially in the highly nonlinear and large-strain dynamic response analysis; otherwise, potential inaccuracy could be introduced. Besides, the energy balance is another important issue when applying the Schur complement method since it could affect the accuracy of the frequency and transient analysis (Gkritzalis and Papadrakakis, 2023).

5 Results and discussion

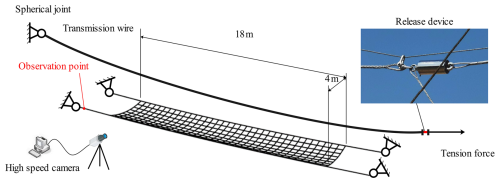
In this investigation, a transmission wire and flexible protecting system model is set up as shown in Fig. 8. The simulation results are tested by the experiment. A wire is fixed at its one end by a spherical joint, while on the other end, tension is applied by the tension machine. Three values of the tension force are used, which are 5, 10, and 15 kN. Two wire lengths, of 19 and 21 m, were used in the experiment. A release device is mounted in a series in the wire and controlled by a wireless signal. When the wire is released, the timer starts, and the high-speed camera begins to capture the configurations of the wire. They will be compared with the numerical simulation results. The high-speed camera used in this experiment is from Mindvision, and the model is MV-XG170GC/M-T. The resolution is 1600×1100 px, and the frame rate is 662 fps. The experiment was conducted outdoors. The day of the experiment was clear and windless. The temperature is 25 °C.

Figure 8 Simulation and experiment setup.

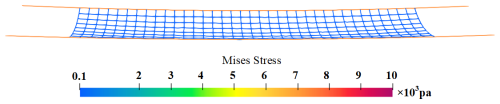
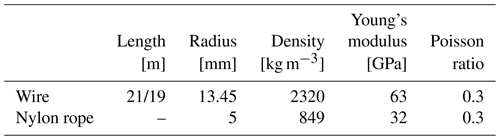
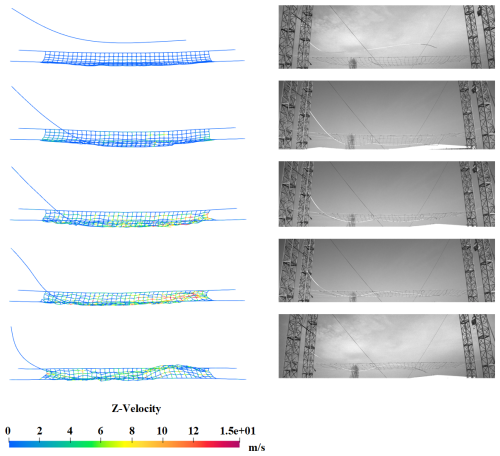
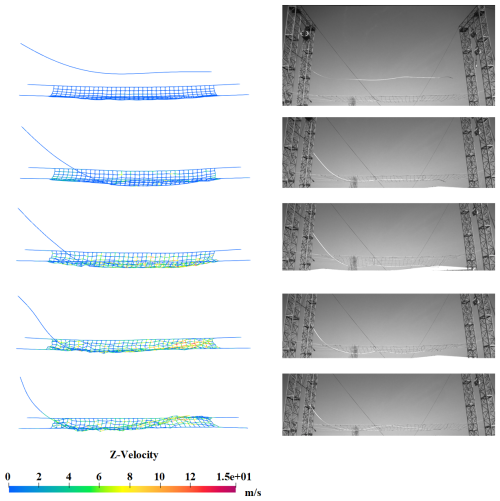
The nylon rope net has 644 elements and 7608 DOFs. After condensation, the number of DOFs is reduced to 1167. The cable element used to discretize the wire has the length of 0.5 m for its reference configuration. The nylon rope net is hung by four spherical joints, and the mesh size is 0.4 m ×0.4 m. Other parameters of the wire and nylon rope can be found in Table 1. The contact between the wire and the nylon rope net is detected by the primary–replica algorithm, and the contact forces are calculated based on the penalty method. Details about the contact model can be found in the literature (Wang et al., 2014, 2015) and a previous publication of one of the authors (Gu et al., 2021). The obtained system dynamic equation is a set of index-3 differential-algebraic equations. The integrator selected in this investigation is the generalized alpha method since it shows good convergence and robustness in solving the contact dynamics problem of large flexible bodies. The program is written and run in a C$++$ environment. The simulation is performed on a Dell PowerEdge T5820 desktop with an Intel Xeon W-2245 central processing unit and 32 GB memory. The visualization of the results is implemented in an open-source data visualization software called ParaView. Figure 9 presents the vertical velocity of the wire free tip, while Fig. 10 gives the change in the axial stress of the detection point on the rope. Figures 11 and 12 show the snapshots of the wire and rope net and compared with the experiments.

Table 1 Parameters of the wire and nylon rope.

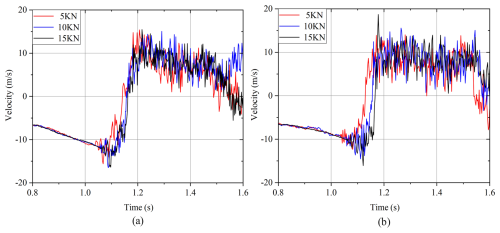
Figure 9 Comparison of the vertical velocity of the free tip for different wire length: (a) 19 m and (b) 21 m.

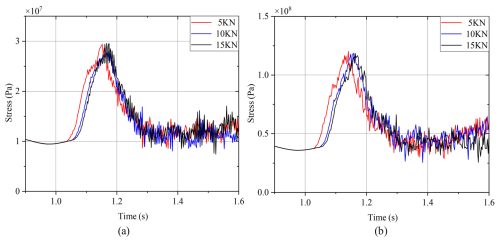
Figure 10 Comparison of the stress of the detection point for different wire lengths: (a) 19 m and (b) 21 m.

Figure 11 Comparison of the configuration between the simulation and the experiment (19 m, 5 kN).

From the results shown in Figs. 9 and 10, an interesting phenomenon can be observed: the impact time corresponding to the smaller initial tension happens slightly earlier than the larger initial tension condition is achieved. This is because the wires in the experiment were fixed to the steel structure truss rather than a perfect rigid body. With the increase in the initial tension, the deformation of the truss structure tends to be obvious. After the tension is released, the stress release of the structure will drive the wire to produce a more obvious swing, resulting in a relative lag in the impact time. Configurations captured by the camera clearly show the whole process of the wire falling and impact on the cable net. The net vibrated dramatically after the impact happened and successfully managed to catch the falling wire at last. The numerical simulation results also show the dynamic process observed in the experiment completely. The experimental results verify the correctness of the simulation method proposed in this paper. The results of the program can help engineers find weak points in protective structures and strengthen them. The calculation method proposed in this paper can greatly shorten the design and development period of the flexible protection system, save the development cost, and provide theoretical and technical support for the safe construction of the power system.

Figure 12 Comparison of the configuration between the simulation and the experiment (21 m, 15 kN).

6 Conclusions

The dynamic analysis of the transmission wire impact nylon rope net is the core problem for the design and optimization for the flexible protecting system, which is increasingly used in electricity construction engineering. In this investigation, a systematical modeling and analysis method is proposed based on the absolute nodal coordinate formulation cable element. The pre-tension of the wire is achieved by statically solving the equilibrium configuration of the wire under the effect of the tension, elastic, and gravity force. In order to obtain an accurate description of the initial configuration of the nylon rope net, the iterative force density method is modified and adopted. Only the axial stretch of the rope is considered. An even distribution of the initial stress can be obtained. Furthermore, a condensation method is developed for the nylon rope net. The division and connection of sub-systems of the net is realized using Schur's complement method. The total number of DOFs of the net can be effectively reduced. Finally, an experiment is performed as verification. A pre-tension wire is released and falls on the nylon rope net. The snapshots of the wire and net are recorded by a high-speed camera and compared with the simulation results. It can be summarized from the comparison that the modeling and dynamic analysis method proposed in this investigation is capable of providing theoretical and technical assistant for the design and safe use of the flexible protection system.