Research on 3D information collection path planning for hyper-redundant space robots (HSRs)

This paper proposes a path-planning method for 3D information collection on the space station surface via the hyper-redundant space robot (HSR). Firstly, to efficiently acquire information on the space station surface, the space station is reduced to a cylindrical model for modelling, and the initial mapping of the temperature field is carried out by a popular Gaussian process. Based on the active information collection method, the collision-free viewpoint trajectory of the space station surface can be planned to improve the efficiency of surface information collection. Then, the path planning of the space station surface information collection can be realized by importing the space station model and temperature field data and performing weight initialization, stochastic search, and continuous optimization. Finally, simulation experiments show that the root-mean-square errors in the surface information collection process are lower than 1 mm relative to the true value. It proves the effectiveness of the online information collection path-planning (IP) method.

1 Introduction

Micro-meteorite flows, other particles and satellite debris in space runs the risk of impacting the space stations (Kirchner et al., 2013). Once the space station module, solar sail panels, etc. suffer object impact, cracks, holes, and other problems, this may bring about catastrophic consequences (Reinhardt and Peck, 2016). Using the space robot for timely and effective detection of surface cracks or holes can eliminate hidden problems and reduce the risk of astronaut spacewalk maintenance (Flores-Abad et al., 2014). The application of robots in routine structural inspection and damage detection has become very popular in civil aviation and industrial fields (Gomes et al., 2019; Zhang et al., 2021). Most international space stations use multi-joint tandem rigid robots for maintenance tasks. The movement is performed through multiple target interfaces outside the space station module. However, in multi-target environments and non-cooperative structural spaces, such as truss structures outside space stations or solar sail areas, the rigid robots are larger, have fewer degrees of freedom, and are less flexible and operable (Ma et al., 2023; Jiang et al., 2022). In comparison, the hyper-redundant space robot (HSR) has a wider working space, better flexibility, and longer range of motion and can assist astronauts with damage assessment outside the space station, screw detection on the module surface, thermal analysis of pipelines, etc. (Duan et al., 2022; Mu et al., 2022). The European Space Agency has developed a three-armed HSR that provides more flexibility in the workspace to accomplish scientific tasks. Each arm is equipped with a camera at the end to obtain environmental information. The Harbin Institute of Technology designed a multi-joint flexible robotic arm based on a microgravity environment and rope drive characteristics, which can complete space station inspection tasks through vision tools (Peng et al., 2021; Yan et al., 2019). NASA has designed the flying robotic arm based on HSR and space vehicles. Through collaborative movements, the space station structure inspection task can be accomplished with high mobility and can meet the need for operational flexibility in complex space (Rybus, 2018). The dynamic control of HSR is very complicated due to the hyper-redundant degrees of freedom and the strongly coupled dynamic characteristics of the HSR (Peng et al., 2020; Ivanescu et al., 2010). For HSR motion control problems, scholars have studied different methods using classical control theory (proportional differential control) and intelligent control theory (​​​​​​​fuzzy control, Xu and Ordóñez, 2016, and neural network control, Dong et al., 2021). Marchese et al. (2016) developed a soft-body HSR dynamic control strategy to achieve an accurate grasping task through a locally optimized open-loop control strategy. Peng et al. (2019)​​​​​​​ proposed a trajectory tracking control method for HSR based on differential algebraic equations (DAEs). Benzaoui et al. (2016) used a fuzzy adaptive control approach for the obstacle avoidance task in the case of model uncertainty. Braganza et al. (2007) proposed an HSR control method using a neural network feed-forward component to compensate for dynamic uncertainty. Li et al. (2021) proposed the symplectic instantaneous optimal control (IOC) method to realize the dynamic control of rope-driven HSR obstacle avoidance. Ménager et al. (2024) proposed a method based on continuum medium mechanics for trajectory optimization of continuum robots. For path-planning and information collection problems, Jasour and Farrokhi (2014) designed a nonlinear model neural network predictive control method to track the expected path while avoiding static or moving obstacles in the robot workspace. Bircher et al. (2016) proposed a new 3D coverage path-planning (CP) method for autonomous inspection path planning of space stations. Marcucci et al. (2023) proposed a trajectory planning method to efficiently and reliably plan HSRs around obstacles through convex optimization. Wang et al. (2023) proposed a sample search optimization framework for motion planning method for unoccupied aerial vehicles (UAVs) and robots. Neininger and Szpanowski (2011) proposed an incremental-sampling-based inspection planning method – namely, the fast search random tree method. With a given model of structural parameters, onboard sensors, etc., initializing the robot configuration and constraints can obtain a full-coverage inspection path (Faghihi et al., 2022). Del Castillo et al. (2015) propose a Gaussian process for the parametric reconstruction of free-form surfaces. Surface coordinates are calculated using manifold learning and parametric algorithms to simulate space station surface data. Obstacle modelling is one of the key problems of obstacle avoidance algorithms. To reduce computational effort and improve obstacle avoidance efficiency, simple geometric models and their assemblies are usually used to characterize the robot and its working environment (Wu et al., 2016). Guo and Zhang (2012) optimized the joint trajectory by defining a distance objective function to achieve zero-space obstacle avoidance of the robotic arm. Tsardoulias et al. (2016) used raster graphics and polygons to construct the HSR workspace and obtained collision-free paths. For HSR, how to perform trajectory optimization for the 3D surface information collection process is a challenging and rarely studied problem.

This paper presents a hyper-redundant space robot (HSR) path-planning method for space station surface inspection and 3D information acquisition tasks. The space station surface information field is mapped using a manifold Gaussian method. Based on the active information collection method, the objective function is designed to plan the collision-free viewpoint trajectory of HSR in 3D space. The efficiency of surface information collection can then be improved by successive optimization of viewpoints and collision avoidance. This paper is divided into five sections. Section 2 presents an overview of the structural features and kinematic modelling of the HSR. Section 3 introduces the 3D surface information collection path-planning (IP) method. Section 4 compares the experiments to prove the effectiveness of the path-planning method, and, finally, Sect. 5 gives the conclusion of this paper.

2 HSR modelling

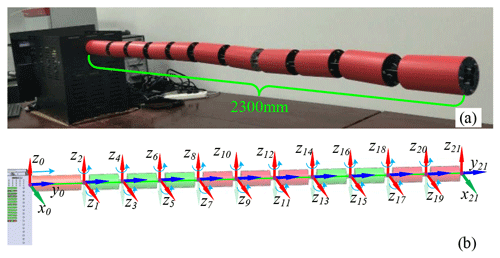
To further explore the space station surface defect detection technology as well as to carry out application testing of inspection algorithms, performing kinematic modelling and accurate dynamic control of the HSR, which is an important part of HSR surface information collection, is required. The HSR designed for the task of space station surface information collection is shown in Fig. 1, which mainly includes a multi-joint arm, a feeding platform, a drive box, and a vision tool. The multi-joint arm consists of several joint units connected in a series by universal joints, and the motion is controlled by screw modules in the drive box that pull the cables. Each joint unit is equipped with cable tension sensors so that all the drive cables of the HSR are always in a tension state to provide power for the movement of each joint unit and complete the information collection tasks of the space station surface. According to the structure of the HSR, modified Denavit–Hartenberg (DH) parameters are used to establish the kinematic model of the HSR, as shown in Table 1, where δ_i+1 is the rotation angle around the z_2i+1 axis, d_i+1 is the displacement along the z_2i+1 axis, γ_i+1 is the rotation angle around the z_2i+2 axis and the displacement of a_i+1 along the y_2i axis, and l_i is the total length of the universal joint and joint unit. If the HSR has n joint units, it has 2n rotational degrees of freedom and 1 feed degree of freedom.

Figure 1 Multi-joint HSR design. (a) HSR prototype. (b) HSR coordinate system.

Table 1 HSR kinematic parameters.

For the ith joint unit of the HSR, the homogeneous transformation matrix is as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{D}_i^{i+\mathrm{1}}=& \mathrm{tr}(\mathrm{0},l_i,\mathrm{0})\cdot R\left(y_{\mathrm{2}i+\mathrm{1}},{\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}\right)\cdot R(z_{\mathrm{2}i+\mathrm{1}},{\mathit{\delta }}_{i+\mathrm{1}})\\ & \cdot R\left(y_{\mathrm{2}i+\mathrm{2}},-{\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}\right)\cdot R(z_{\mathrm{2}i+\mathrm{2}},{\mathit{\gamma }}_{i+\mathrm{1}})\\ =& \left[\begin{array}{cccc}c{\mathit{\gamma }}_{i+\mathrm{1}}& -s{\mathit{\gamma }}_{i+\mathrm{1}}& \mathrm{0}& \mathrm{0}\\ c{\mathit{\delta }}_{i+\mathrm{1}}s{\mathit{\gamma }}_{i+\mathrm{1}}& c{\mathit{\delta }}_{i+\mathrm{1}}c{\mathit{\gamma }}_{i+\mathrm{1}}& -s{\mathit{\delta }}_{i+\mathrm{1}}& l_i\\ s{\mathit{\delta }}_{i+\mathrm{1}}s{\mathit{\gamma }}_{i+\mathrm{1}}& s{\mathit{\delta }}_{i+\mathrm{1}}c{\mathit{\gamma }}_{i+\mathrm{1}}& c{\mathit{\delta }}_{i+\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right].\end{array}\end{array}$$

Therefore, the coordinates of the endpoint of the ith joint unit in the base coordinate system can be obtained as follows:

$$\begin{array}{}\text{(2)}& \left[\begin{array}{c}{x}_{\mathrm{0}}\\ y_{\mathrm{0}}\\ z_{\mathrm{0}}\\ \mathrm{1}\end{array}\right]=\mathrm{tr}(\mathrm{0},l_{\mathrm{0}})\cdot D_{\mathrm{1}}^{\mathrm{2}}\cdot D_{\mathrm{2}}^{\mathrm{3}}\cdot \mathrm{\dots }{D}_{i-\mathrm{1}}^i\cdot \left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \mathrm{0}\\ \mathrm{1}\end{array}\right],\end{array}$$

where l_i denotes the joint unit length, c denotes cos, and s denotes sin. From the kinematic model, it is obtained that a single joint unit has 2 degrees of freedom for rotation about the z_i and x_i axes. With the increase in the number of joint units, the HSR degree of freedom gradually increases as well and the flexibility improves, so the task of collecting information on the surface of the space station in any complex path can be accomplished using encircling and so on.

3 Surface information collection path planning

3.1 Surface information mapping

To verify the correctness of the method of collecting information on the surface of the space station, it is first necessary to perform the construction mapping of the surface information of the space station. We assume that the information field of the space station surface is a continuous function defined on the Riemannian manifold, f, and such that $x\in \mathit{\psi }\subset {\mathbb{R}}^{\mathrm{3}}$ is a location on the space station surface. The information field, f∼GP(μk), is mapped using a manifold-constrained Gaussian process. This information field contains the mean function, μ(x), and the covariance function, $k(x,x^{\prime }$), and the following covariance function is used to model the relevance of this space:

$$\begin{array}{}\text{(3)}& k\left(x,x^{\prime }\right)={\mathit{\sigma }}_f^{\mathrm{2}}\left(\mathrm{1}+{\displaystyle \frac{\sqrt{\mathrm{3}}{d}_g(x,x^{\prime })}{l}}\right)\exp \left({\displaystyle \frac{-\sqrt{\mathrm{3}}{d}_g(x,x^{\prime })}{l}}\right),\end{array}$$

where $d_g(x,x^{\prime }$) is the distance between x and x^′ on a continuous function ψ. We assume that the space station surface is discrete and consists of a mesh of n triangular faces. We define a set of noise measurements at position ${\mathit{\psi }}^{\ast }=[x_{\mathrm{1}},\mathrm{\dots },x_m{]}^m$ as $y=[y_{\mathrm{1}},\mathrm{\dots },y_m{]}^T$ and use Gaussian regression to calculate the posterior distribution of the field:

$$\begin{array}{}\text{(4)}& {\displaystyle }\mathit{\mu }=\mathit{\mu }\left({\mathit{\psi }}^{\ast }\right)+K_{{\mathit{\psi }}^{\ast }\mathit{\psi }}{\left[K_{\mathit{\psi }}+{\mathit{\sigma }}^{\mathrm{2}}{I}_n\right]}^{-\mathrm{1}}\left(y-\mathit{\mu }\left(\mathit{\psi }\right)\right),\text{(5)}& {\displaystyle }P=K_{{\mathit{\psi }}^{\ast }}-K_{{\mathit{\psi }}^{\ast }\mathit{\psi }}{\left[K_{\mathit{\psi }}+{\mathit{\sigma }}^{\mathrm{2}}{I}_n\right]}^{-\mathrm{1}}{K}_{{\mathit{\psi }}^{\ast }\mathit{\psi }},\end{array}$$

where σ² is the noise parameter.

$$\begin{array}{}\text{(6)}& {\displaystyle }{K}_{{\mathit{\psi }}^{\ast }\mathit{\psi }}=k(x,x^{\prime })\left\{\begin{array}{l}{x}^{\prime }\in \mathit{\psi }\\ x\in {\mathit{\psi }}^{\ast }\end{array}\right.\text{(7)}& {\displaystyle }{K}_{{\mathit{\psi }}^{\ast }}=k(x,x^{\prime })\left\{\begin{array}{l}{x}^{\prime }\in {\mathit{\psi }}^{\ast }\\ x\in {\mathit{\psi }}^{\ast }\end{array}\right.\text{(8)}& {\displaystyle }{K}_{\mathit{\psi }}=k(x,x^{\prime })\left\{\begin{array}{l}{x}^{\prime }\in \mathit{\psi }\\ x\in \mathit{\psi }\end{array}\right.\end{array}$$

As the HSR continuously collects measurement data, the collected data need to be fused into a field map of the manifold-constrained Gaussian process. The regression calculation of Eqs. (4) and (5) is very resource-intensive for the system in the face of such a large space field on the space station in the process of computing. To address the above problems and the needs of special application environments, the map update using Bayesian data fusion technology is proposed:

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathit{\mu }}^{+}={\mathit{\mu }}^{-}+P^{-}{\mathbf{H}}^T{\left(\mathbf{H}{P}^{-}{\mathbf{H}}^T+R\right)}^{-\mathrm{1}}\left(y-\mathbf{H}{\mathit{\mu }}^{-}\right),\text{(10)}& {\displaystyle }{P}^{+}=P^{-}+P^{-}{\mathbf{H}}^T{\left(\mathbf{H}{P}^{-}{\mathbf{H}}^T+R\right)}^{-\mathrm{1}}\mathbf{H}{P}^{-},\end{array}$$

where + and − denote the variables before and after data fusion, respectively, and $\mathbf{H}\in {\mathbb{R}}^{m\times n}$ is the observation matrix, which is essentially a selection of the partial positions $x_{\mathrm{1}},\mathrm{\dots },x_m$ of all the triangular faces observed through the visual tool.

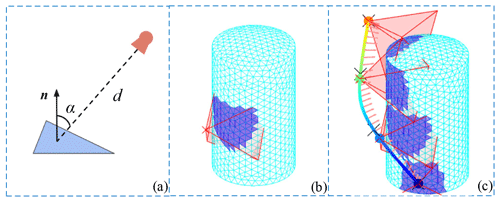
Since the field of view of the HSR vision tool is relatively fixed, the following conditions must be satisfied for the surface information to be collected: (1) the centre of the triangular surface must be located within the field of view of the vision tool. (2) The distance, d, from the centre of this triangular surface to the visual tool must be within the effective range, i.e. $d\in [d_{min},d_{max}]$. (3) The incident angle, α, of this triangular face relative to the visual tool should be smaller than the maximum effective angle, i.e. $\mathit{\alpha }\le {\mathit{\alpha }}_{max}$. (4) This triangular face is not obscured by other surface parts of the space station surface. Ignoring the measurement uncertainty, the triangular surface of the space station surface visible to the visual tool is shown as the dark blue area in Fig. 2.

Figure 2 Space station surface information collection. (a) Range and incidence angle of a single surface. (b) Triangular surface visible to the camera. (c) Planned path of the camera.

3.2 Information collection path planning

In this section, an online information collection path-planning method is proposed to plan a continuous feasible motion trajectory for the HSR of the space station surface, which has the advantage of being able to use the already acquired rough space station surface information distribution for path optimization. The target is to carry out as much of the collection of information from the space station surface as possible during HSR movement. The objective function for online information collection path planning is​​​​​​​

$$\begin{array}{}\text{(11)}& \left\{\begin{array}{l}{\mathcal{M}}^{\ast }=\underset{\mathcal{M}\in \mathbb{Q}}{\mathrm{argmax}}\frac{I\left(\mathrm{measure}\left(\mathcal{M}\right)\right)}{\mathrm{time}\left(\mathcal{M}\right)},\mathrm{time}\left(\mathcal{M}\right)\le B,\\ \mathrm{collision}\left(\mathcal{M}\right)=\mathrm{\Phi },\end{array}\right.\end{array}$$

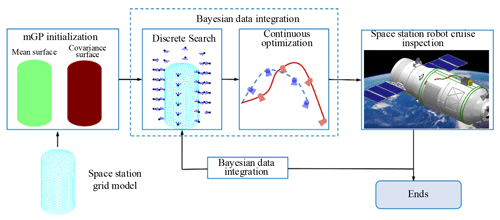
where ℳ^∗ is the optimization path of the HSR end-effector, ℚ is the set of all continuous feasible trajectories of the HSR end-effector, B is the time budget of the HSR end for structural inspection at the space station surface, I denotes the quantized measurement information, and measure(ℳ) contains a finite sequence of optimized trajectories and measurement information. The functions time(ℳ) and collision(ℳ) return the running time of the HSR and the collision part of the trajectory, respectively. HSR online information collection path planning designed in this paper is specifically divided into the following four steps: trajectory parameterization, discrete path-point searching, continuous optimization, and obstacle avoidance, as shown in Fig. 3.

Figure 3 HSR path-planning method.

Firstly, the continuous trajectory, M, at the end of the HSR is represented in polynomial form while parameterizing the N sequences of control path points to be visited, $C=\mathit{\{}{c}_{\mathrm{1}},\mathrm{\dots },c_N\mathit{\}}$. The Kth-order spline curves are used to connect the path control points and are used to calculate the reference velocity and acceleration of the vision tool at the end of the HSR. The HSR vision tool then performs information collection at a constant frequency.

Secondly, the sequential greedy search is performed in the predefined viewpoint library, ℚ. Multiple input parameters are added by the sequential greedy search method, including the current space station surface map, L; the viewpoint, c₁, of the current HSR vision tool; the path point, N; and the viewpoint library, ℚ. The output is a series of path points, $C=\mathit{\{}{c}_{\mathrm{1}},\mathrm{\dots },c_N\mathit{\}}$. After giving the current viewpoint, c_prev, the next best viewpoint, c^∗, is calculated using the viewpoint library to make it the most efficient information collection.

$$\begin{array}{}\text{(12)}& c^{\ast }=\underset{c\in \mathbb{Q}}{\mathrm{argmax}}{\displaystyle \frac{I\left(c\right)}{\mathrm{time}(c_{\mathrm{prev}},c)}}\end{array}$$

We define information gain as follows:

$$\begin{array}{}\text{(13)}& I\left(c\right)=\mathrm{tr}\left(P^{-}\right)-\mathrm{tr}\left(P^{+}\right),\end{array}$$

where tr is the trace of the covariance matrix and P⁻ and P⁺ denote the covariance of the space station surface map before and after the measurement at viewpoint position c. The process of updating the space station surface map, ($L^{\ast },c^{\ast }$), and the covariance, P⁺, does not require the actual measurements, but it does require the perspective of the visual tool as shown in Eq. (12). The HSR can successfully simulate the covariance evolution process of the space station surface map through the iterative calculation of the collecting viewpoints.

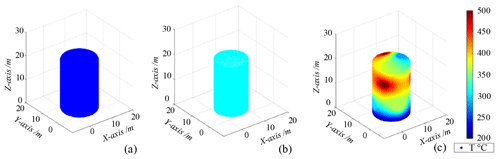
Figure 4 Space station temperature field distribution. (a) Minimum temperature. (b) Surface interpolation results. (c) Temperature data visualization.

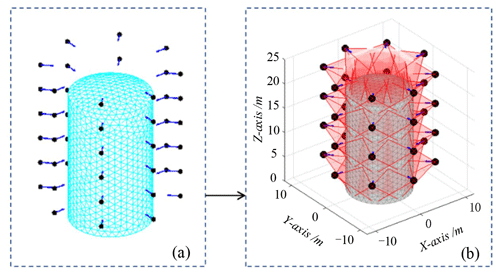
Figure 5 The calculation process of the space station surface viewpoints. (a) Grid viewpoints. (b) Coverage viewpoints.

Thirdly, the objective function is calculated by connecting the set of path points, C, at the end of the HSR using polynomial interpolation. The continuous optimization is performed by searching for the collection viewpoints along the objective function to update the map covariance of the space station surface. The objective to be maximized is defined as the average time information gain:

$$\begin{array}{}\text{(14)}& U_{\inf }={\displaystyle \frac{I\left(\mathrm{measure}\left(\mathcal{M}\right)\right)}{\mathrm{time}\left(\mathcal{M}\right)}},\end{array}$$

where the gain function, I, is the same as the covariance of the space station surface map defined in Eq. (13). Finally, a 3D distance field is created based on the given grid structure. In the improved space station surface greedy search phase, a new constraint is added which requires the next viewpoint, c^∗, to be consistent with the current viewpoint, c_prev. The current viewpoint can provide the initial phase of obstacle avoidance requirements for subsequent continuous optimization. We add an objective function to penalize collisions in the continuous optimization phase:

$$\begin{array}{}\text{(15)}& U_{\mathrm{coll}}=w_{\mathrm{coll}}\sum _{p\in T}g\left(p\right),\end{array}$$

where p is the sampling position of the polynomial trajectory and w_coll is the weight coefficient of the penalized collision objective function.

$$\begin{array}{}\text{(16)}& g\left(p\right)=\left\{\begin{array}{ll}\mathrm{0}& \mathrm{if}D\left(p\right)\ge r,\\ -\mathrm{1}& \mathrm{otherwise},\end{array}\right.\end{array}$$

where D(p) denotes the Euclidean distance of the current sampling point and r denotes the radius of the robot's workspace. Therefore, the final objective function to be maximized is

$$\begin{array}{}\text{(17)}& U=U_{\inf }+U_{\mathrm{coll}}.\end{array}$$

Figure 6 Online information collection path-planning simulation. (a) True value. (b) Mean value. (c) Illustration of the difference between variance and covariance matrix traces of 164. (d) Information path planning.

4 Simulation validation

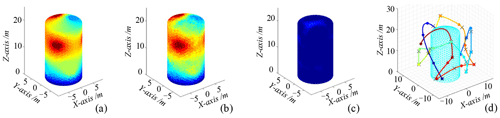
The space station module is set to be a cylindrical tank with a height of 20 m and a diameter of 12 m. Before the information collection path planning, the map of the space station surface needs to be constructed and the input parameters mainly include x, y, and z coordinates and the corresponding temperature values. The input values are mapped to the space of the space station surface to complete the modelling of the manifold-constrained Gaussian process. By reading the simulated temperature field data from the surface of the space station for visualization data processing, the temperature distribution of the space station surface can be constructed as shown in Fig. 4. In the grid viewpoint calculation, a set of predefined viewpoints is created as shown in Fig. 5. The viewpoint of the space station surface is then calculated based on the prior model. Based on the prior model and the grids for parameterization, the position of each adjacent grid region is calculated to complete the calculation of the final grid viewpoints.

The grids of the space station surface are triangulated to obtain 1097 nodes and 2190 triangular surfaces. By grid division, different heat sources are added at the centre of each node, and the temperature distribution of the space station surface is simulated by the thermal simulation tool as shown in Fig. 6a. The HSR vision tool camera noise parameters are set to a=0.04 and b=0.15, respectively, and the data are fused by simulating Gaussian measurement noise. The number of controlling HSR trajectory points is N=5, and the running time of the whole trajectory is set to 130 s. The manifold-constrained Gaussian process is used for online information collection path planning on the space station surface, and the results are shown in Fig. 6b–d. The results show that the final mean map based on the information collection path-planning method is very close to the real map. The difference in trace between the variance and covariance matrix is 164. The colour of the whole map shows a dark-blue colour, which proves that the information collection path-planning method is more effective.

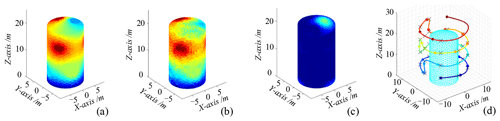
Figure 7 Coverage path-planning simulation. (a) True value. (b) Mean value. (c) Illustration of the difference between variance and covariance matrix traces of 926. (d) Coverage path planning.

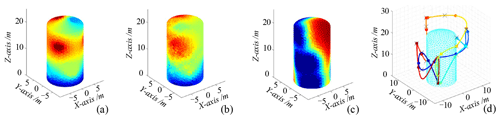
Figure 8 Random path-planning simulation. (a) True value. (b) Mean value. (c) Illustration of the difference between variance and covariance matrix traces of 1694. (d) Random path planning.

To verify the effectiveness of the online information collection path planning designed in this paper, it is compared with the traditional coverage path-planning and random path-planning (RP) techniques for experiments. One of the coverage path-planning techniques focuses on providing a complete coverage path of the space station surface through a set of viewpoints, presenting a spiral scanning inspection route. The random path planning mainly selects random viewpoints from the viewpoint library and generates polynomial routes for information collection, as shown in Figs. 7–8. It can be obtained that the final mean maps of both path-planning methods are different compared to the real maps on the surface of the space station, but the coverage path planning is relatively better. Figures 7c and 8c show that the difference in trace between the final mean map and the real map variance and the covariance matrix is 926 and 1694, respectively, and that the calculated variance value of the coverage path is smaller and the path planning is better. Comparing this with the information collection path planning results in Fig. 9; the difference in the trace between the variance and covariance matrices is 164, and the final mean map is also closer to the space station surface map in the real situation, which proves the effectiveness of the information collection path-planning method.

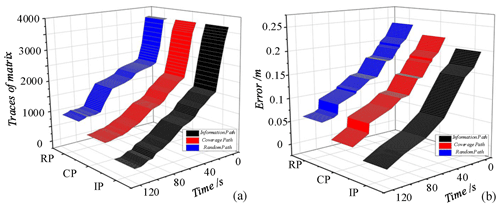
Figure 9 Information collection path-planning error analysis. (a) Difference between variance and covariance matrix traces. (b) The root-mean-square error.​​​​​​​

The online information collection path-planning results are compared with the results of coverage path planning and random path planning. The difference between the traces of the matrix and the root-mean-square error in the collective results relative to the true value is calculated, respectively, and the results achieved after multiple averaging are shown in Fig. 9. It can be obtained that random path planning (RP) can achieve reasonable space station surface information collection in the initial stage, but the performance gradually deteriorates with time, and the final error is 7.5 mm. The coverage path planning (CP) is performed in a uniform way to reduce the uncertainty and error in the map, with a final error of 3.4 mm. In comparison, the online information collection path planning (IP) can quickly reduce the uncertainty and error, with a final error of 0.95 mm, further proving the effectiveness of the information collection path-planning method.

5 Conclusions

Space robots are playing an increasingly important role in the exploration of space resources, daily structural inspection of space stations, and damage detection. This paper proposes a hyper-redundant space robot (HSR) online information collection path-planning method for the space station surface information collection task. Firstly, a multi-joint HSR is designed, and a kinematic model is established. For the engineering task of space station surface information collection, an HSR online information collection path-planning method is proposed. The space station is simplified to a cylindrical model and modelled with a randomly simulated temperature field. The information field is mapped using the manifold-constrained Gaussian process. The active information collection method is used to plan collision-free viewpoint trajectories on the space station surface to improve information collection efficiency. By importing the space station model and simulated temperature field data and starting the initialization of weight information, stochastic search, and continuous optimization, in that order, the 3D path planning of the HSR can be realized. Finally, the effectiveness of different path-planning methods is compared and calculated by simulation experiments. The information collection results show that online information collection path planning can quickly reduce uncertainty and error and improve information collection efficiency compared with coverage path planning and random path planning.

In the future, we will continue to develop the HSR and the vision tools for prototype testing. More space station surface information (temperature, stress, light, different surfaces, etc.) will be integrated for online information collection path planning to further improve the efficiency of surface information collection.