Time-varying reliability models for parallel systems consisting of beam structures with crack flaws

Time-varying reliability assessment of parallel systems of beam structures with crack defects is of great importance for structural safety evaluation. In this paper, time-varying reliability models for parallel systems with cracked beams are proposed. In the modeling process, the statistical correlation between crack depth, random working load, random strength degradation, and random stress response as well as the complex failure correlation jointly caused by these factors are considered. Based on the finite element analysis of the cracked beams, the reliability models are constructed by combining the neural network and the response surface agent model. The validity of the model is verified by the Monte Carlo simulation method. The results show that crack depth and working load dispersion have important effects on reliability and failure correlation.

1 Introduction

With the increase in the demand for work tasks, performance diversification, and safety of industrial products, engineering systems have become more and more complex (Hao and Kong, 2012; Liang et al., 2021; Yavuz and Öztürk, 2021). Considering system composition and working mechanism, complex mechanical systems need to be expressed as a more complex system logic block diagram for system reliability evaluation (Huang et al., 2019). The complex logic block diagram of mechanical systems, such as a series–parallel system, parallel–series system, or bridge system, can be decomposed into the typical series systems and parallel systems by using the methods such as minimal cut set method, minimal path set method, etc. (Lv et al., 2017; Huang et al., 2009). However, the reliability calculation of mechanical parallel systems is usually difficult, because the components in a mechanical parallel system are subjected to homologous loads, which affect each others performance. Moreover, the components in the parallel system may contain certain defects, such as cracks or holes. These defects can cause mutual influence on the performance degradation of each component (Hsu and Shu, 2010; van Noortwijk, 2009; Arama et al., 2020). Therefore, the time-varying reliability evaluation of mechanical parallel systems with performance degradation of components becomes extremely complicated due to the complex failure dependence among components. Hence, it is necessary to propose time-varying reliability models of parallel systems with defective components, which can be used to quantitatively analyze the time-varying effects of system and component performance on system reliability and to provide a theoretical basis for the fault diagnosis and maintenance strategy development of mechanical systems.

Figure 1 Parallel systems in practical engineering.

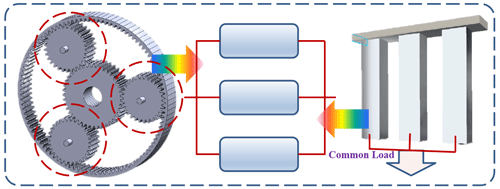
Parallel systems are one of the most important types of systems in the reliability analysis of structural systems. Engineering systems such as planetary gears and cantilever beams that share a common load can usually be simplified as parallel systems as shown in Fig. 1. In practice, from the stress analysis point of view, many engineering structures can be simplified as cantilever beam structures for qualitative or quantitative reliability analysis. At present, a great deal of research has been carried out on the dynamics of beams with flawed construction. Chondros et al. (1998) developed a continuous cracked beam vibration model for solving the lateral vibration problem of cracked beams. The Hu–Washizu–Barr variational formulation is used, and the cracked beam is considered a one-dimensional continuum. Besides, the vibration characteristics of beams with localized crack flexibility are investigated in this paper and compared with the continuous model (Chondros et al., 1998). The authors also proposed a vibration model of beams with breathing cracks, which can be used to predict the dynamic response of cracked beams in transverse vibration. In the model, the beam with a breathing crack was assumed to be a piecewise linear system (Chondros et al., 2001). Saavedra and Cuitino presented an approach for investigating crack detection and vibration behavior in different multi-beam systems. The additional flexibility caused by a crack was evaluated by means of linear fracture mechanics theory, and a new crack finite element stiffness matrix was further derived. The method avoided the limitations of traditional direct inspection methods, such as ultrasonic and X-rays, which require frequent periodic inspections (Saavedra and Cuitino, 2001). Zheng and Kessissoglou proposed a free vibration analysis method for cracked beams based on the finite element method. The total flexibility matrix and the stiffness matrix were obtained by adding an overall additional flexibility matrix. Then a shape function was constructed which can satisfy the local flexibility condition at the crack location to give more accurate vibration modes (Zheng and Kessissoglou, 2004). Orhan investigated the application of free and forced vibration in identifying cracks in beam-type structures. Free and forced vibration analyses of beams with unilateral and bilateral cracks were carried out by a finite element program. The results show that free vibration analysis can identify single and two-edge cracks, while forced vibration can only identify single unilateral cracks (Orhan, 2007). Wei and Shang analyzed the nonlinear vibration behavior of a breathing cracked beam. A vibration model was proposed by using the finite difference method and the transfer matrix method. Numerical simulations verify the validity of the proposed model and the accuracy of the calculation method (Wei and Shang, 2019). Wang et al. developed a crack detection method for beams based on Bayesian inference and an analytical solution of vibration modes. The expression of vibration modes was obtained by analytical solution, and Bayesian inference was used to obtain the probability density function of the crack parameters and to evaluate the uncertainty of the modes (Wang et al., 2021). These models provide useful tools for vibration analysis of cracked structures.

In addition, creative work has been done in the area of reliability calculations for systems with parallel structures. Coit and Zio described system reliability optimization problems in the field of reliability engineering and system safety. The redundancy assignment problem, the reliability assignment problem, and the reliability–redundancy assignment problem involved in parallel systems were introduced (Coit and Zio, 2019). Li et al. (2020) presented a serial and parallel reliability model for robot arm reliability analysis. The structure and system types of robot arms were introduced. Then a serial system reliability model based on the total probability theorem was proposed, which takes into account the statistical dependence between load strength, number of load actions, component strength, and component failures (Li et al., 2020). Ashok et al. studied the reliability of multi-component systems. The cases of stresses and strengths obeying the Fréchet distribution, the mixed Fréchet distribution, etc., were analyzed, and the law of change of system reliability was derived by calculating the reliability at different parameter values (Ashok et al., 2019). Kumar et al. developed a complex system reliability assessment method based on universal generating function (UGF) and the fuzzy set theory by using the weighted average operator (Kumar et al., 2019). Fang et al. proposed a bivariate degradation model for a coherent system whose performance characteristics are positively correlated by the degradation processes. The effects of environmental stress variables were considered in the model, and dependence between the two degradation processes was addressed via a copula function (Fang et al., 2020). These models offer a solid foundation for evaluating the reliability of parallel systems.

Despite the fact that many studies have been conducted on the dynamic analysis of beam structures and reliability modeling of parallel systems, the quantitative calculation of the reliability of parallel systems for mechanical structures still faces the following challenges.

The failure dependence mechanism of the parallel systems with cracked beams is complex. The stresses on the beams in a system are statistically correlated, because the beams jointly share a common load. The crack extension in each component is mutually dependent due to the correlated stresses on each beam. Moreover, crack propagation correlations again affect the change and dependence of stresses on each beam and correlate the change in residual strength. These complex correlations interact with each other and affect the entire system failure process. Thus, these mechanisms need to be explored and considered in the modeling process.

Empirical parameters for characterizing failure dependence between components cannot be used to express the complex system failure dependence stated above in system reliability modeling. The failure rate of mechanical structures is often not constant, and the empirical parameters cannot be explained mechanistically. Consequently, a parallel system reliability model that has a distinct physical meaning is required.

When some components in a parallel system fail, load redistribution will occur, and the redistribution time is stochastic due to the stochastic nature of the performance degradation. The problem of stochastic load redistribution in parallel systems will greatly increase the modeling difficulty and computational burden.

In order to solve the problems above, a time-varying reliability model for the parallel systems with cracked beams is proposed in this paper. The method for calculation of the stochastic dynamic response of the system is presented in Sects. 2 and 3, which are used for the stress solution of the system components. Then, the complex failure dependence mechanism in the parallel system is elaborated on in Sect. 4, and the time-varying reliability models of the parallel systems considering the complex mechanism is further established in Sect. 5. In Sect. 6, the validity and correctness of the model is illustrated by numerical examples. Finally, the conclusion is given in Sect. 7.

2 Stochastic response for cracked beams

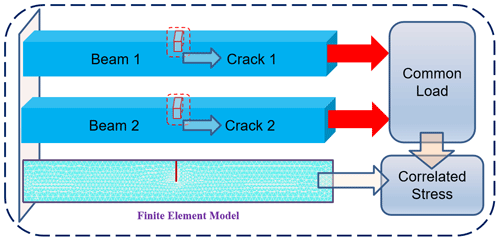
The finite element method is an important method for structural response analysis (Ozakpolor et al., 2021). The cracks affect the stiffness and strength of the beams shown in Fig. 2. When the beams are subjected to dynamic loading, the cracks show the “breathing effect”. The cracks open and close periodically, and the crack surface is periodically subjected to compressive stress or no contact state, resulting in periodic changes in the stiffness of the beams. The finite element model of a cracked beam structure can be expressed as follows (Saavedra and Cuitino, 2001):

$$\begin{array}{}\text{(1)}& {\mathbf{M}}_{\mathrm{s}}\ddot{X}+{\mathbf{C}}_{\mathrm{s}}\dot{X}+{\mathbf{K}}_{\mathrm{s}}\mathbf{X}={\mathbf{F}}_{\mathrm{s}},\end{array}$$

where M_s is the overall mass matrix of the cracked beam, K_s is the overall stiffness matrix of the cracked beam, C_s is the damping matrix of the cracked beam, X is the displacement matrix in the overall coordinate system, and F_s is the external force matrix. The stiffness of the cracked element can be calculated as follows if only the effect of the stiffness change on the force and motion state of the system is considered:

$$\begin{array}{}\text{(2)}& K_{\mathrm{c}}=\mathbf{T}{C}^{-\mathrm{1}}{\mathbf{T}}^{\mathrm{T}},\end{array}$$

where $\mathbf{T}=\left[\begin{array}{cccccc}\mathrm{0}& \mathrm{0}& -\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{1}\\ \mathrm{0}& -\mathrm{1}& -l& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\end{array}\right]$ is the length of the beam element, $C=C^{\mathrm{0}}+C^{\mathrm{1}}$, C⁰ is the matrix consisting of the flexibility coefficients of the uncracked beam element, and C¹ is the matrix consisting of the flexibility coefficients caused by the crack.

Figure 2 Stochastic response analysis of cracked beams.

If the effect of stresses generated by cracks on the strength of the system as well as crack extension is further considered, finite element models based on two-dimensional planar elements used to simulate cracked beams are currently gaining wide acceptance. The use of contact elements to simulate the breathing effect of cracks in finite element calculations solves the problems of the traditional finite element model that requires real-time identification of crack opening and closing states and real-time stiffness calculations. In the finite element calculation of the system, the contact force at the crack surface can be expressed as

$$\begin{array}{}\text{(3)}& F_n=\left\{\begin{array}{ll}\mathrm{0}& \mathit{\epsilon }>\mathrm{0},\\ K_{\mathrm{n}}{\mathit{\epsilon }}^q+\mathit{\delta }\dot{\mathit{\epsilon }}& \mathit{\epsilon }\le \mathrm{0},\end{array}\right.\end{array}$$

where K_n is the contact normal stiffness, ε is the penetration distance between contact nodes, and δ is the damping coefficient. Meanwhile, the singularity of the crack tip is simulated by using a $\mathrm{1}/\mathrm{4}$ node element, and the approximate stress value near the crack is obtained.

The method above is used for solving the system response under deterministic working load. When the system is subjected to a random working load, the discrete distribution vector F_t representing the random external load of the system at moment t is expressed as follows:

$$\begin{array}{}\text{(4)}& {\mathit{F}}_t=[f_{\mathrm{1}t},f_{\mathrm{2}t},\mathrm{\dots }{f}_{\text{nt}}],\end{array}$$

where nt is the total number of discretely distributed values of random external loads on the system. Suppose a parallel system consists of n beams, each with a crack in it, and the crack length at moment t is a_jt ($jt=\mathrm{1},\mathrm{2},\mathrm{\dots },n$). For f_it ($i=\mathrm{1},\mathrm{2},\mathrm{\dots },n$) at moment t, the stresses generated by the load at each beam crack can be expressed as

$$\begin{array}{}\text{(5)}& S_{\text{it}}=\left[s_{\text{it}\mathrm{1}}\right(a_{\mathrm{1}t}),s_{\text{it}\mathrm{2}}(a_{\mathrm{2}t}),\mathrm{\dots },s_{\text{it}n}(a_{\text{nt}}\left)\right].\end{array}$$

Thus, the discrete distribution of individual beam stresses under random load F_t at time t can be obtained as follows:

$$\begin{array}{}\text{(6)}& S_t=\left[\begin{array}{c}{s}_{\mathrm{1}t\mathrm{1}}\left(a_{\mathrm{1}t}\right),s_{\mathrm{1}t\mathrm{2}}\left(a_{\mathrm{2}t}\right),\mathrm{\dots },s_{\mathrm{1}tn}\left(a_{\text{nt}}\right)\\ s_{\mathrm{2}t\mathrm{1}}\left(a_{\mathrm{1}t}\right),s_{\mathrm{2}t\mathrm{2}}\left(a_{\mathrm{2}t}\right),\mathrm{\dots },s_{\mathrm{2}tn}\left(a_{\text{nt}}\right)\\ \mathrm{\cdots }\\ s_{\text{nt}\mathrm{1}}\left(a_{\mathrm{1}t}\right),s_{\text{nt}\mathrm{2}}\left(a_{\mathrm{2}t}\right),\mathrm{\dots },s_{\text{nt}n}\left(a_{\text{nt}}\right)\end{array}\right].\end{array}$$

3 Time-varying response of systems with variable crack parameters based on neural network and response surface model

Although the finite element computational models provide an effective method for the calculation of stresses and displacements of beams, with the increase in the number of cracks, the number of constituent parts of the parallel system and the number of load actions, as well as the continuous expansion of the cracks under repeated actions of the loads, the stress data that need to be calculated for the system will be huge. Thus, the combination of back-propagation (BP) neural network fitting technique and a crack extension response surface model will be used in this paper to solve the problem of stochastic response calculation of parallel systems with cracked beams. This method can reduce the number of samples and improve the computational efficiency.

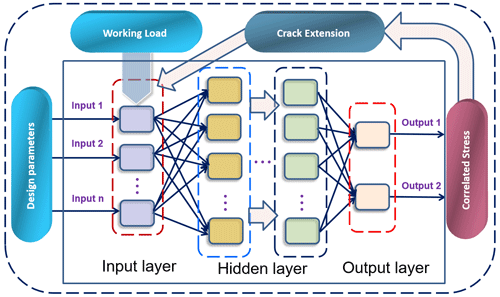
Neural networks have advantages in data prediction and fitting (Shah and Karabulut, 2022). The traditional BP neural network is a multi-layer feed-forward neural network that performs error correction through an error back-propagation algorithm. Its working principle is that the input information reaches the output layer through the input layer and a specified number of hidden layers. If the fitting result has a large error with the actual result, the error is returned in the reverse direction and the weights of the layers are modified to realize the back-propagation process. Therefore, in practice, the input data of the neural network are forward propagated, while the fitting error is backward propagated.

In this paper, the BP neural network is used to analyze the process by taking a finite number of working loads and the length of each crack as inputs, and the stresses of each beam obtained by finite element calculation as outputs, as shown in Fig. 3. The input and output are expressed as $X_{\text{in}}=[x_{\text{in}\mathrm{1}},x_{\text{in}\mathrm{1}},\mathrm{\cdots },x_{\text{in}j}]$ and $Y_{\mathrm{o}}=[y_{\mathrm{o}\mathrm{1}},y_{\mathrm{o}\mathrm{1}},\mathrm{\cdots },y_{\mathrm{o}j}]$, respectively, and the output can be obtained as follows (Li et al., 2019).

$$\begin{array}{}\text{(7)}& y_{\mathrm{o}j\mathrm{1}}=\mathit{\tau }\left(\sum _{h=\mathrm{1}}^H\left[W_{\mathrm{h}}\cdot \mathit{ϵ}\left(\sum _{j=\mathrm{1}}^{\text{in}j}{w}_j{x}_j+{\mathit{\gamma }}_{\mathrm{1}}\right)\right]+{\mathrm{\Gamma }}_{\mathrm{2}}\right),\end{array}$$

where H is the number of hidden layers, W_h and w_j are the transfer weights, γ₁ and γ₂ are the neuron transfer thresholds, and τ(∗) and ϵ(∗) are information transfer functions. As a result, the fitted value between input and output can be obtained, which reduces the number of samples and improves the computational efficiency.

Figure 3 Time-varying response calculation considering crack extension.

The above model is capable of obtaining the stress response of each component with a constant crack depth. However, cracks can expand under conditions such as cyclic action of stresses and corrosion, which changes the response of each component within the system. Besides, crack expansion is a slow-change process relative to the change in system response, and the amount of change is quite small during each operating cycle. In addition, the crack expansion increment is generally related to the stress and the current crack depth. Therefore, relative to the Ith working cycle, the response surface relationship equation of crack extension $\widehat{\mathrm{\Delta }a}$ with stress s and crack depth a at the end of the Ith cycle during the I + 1 working cycle is expressed as follows:

$$\begin{array}{}\text{(8)}& \widehat{\mathrm{\Delta }a}=y(s,\mathit{\eta },a)\widehat{\mathit{\beta }},\end{array}$$

where η is the material parameter vector, $y(s,\mathit{\eta },a)$ is the input parameter matrix, and $\widehat{\mathit{\beta }}$ is the fitting coefficient matrix. With the experimental samples in different crack states, the response surface model fitting coefficient matrix can be obtained, and the crack extension can be obtained with less sample size. The method is also capable of timely calculations of crack extensions based on new acting stresses and existing crack depth. If only the effects of the I + 1th working cycle stress and the Ith working cycle crack depth on the crack extension amount are considered, the polynomial response surface model in Eq. (8) for crack extension can be approximated as

$$\begin{array}{}\text{(9)}& \begin{array}{rl}Y(I+\mathrm{1})=& b_{\mathrm{0}}(I+\mathrm{1})+b_{\mathrm{1}}(I+\mathrm{1})s_{I+\mathrm{1}}+b_{\mathrm{2}}(I+\mathrm{1})a_I\\ & +b_{\mathrm{3}}(I+\mathrm{1})s_{I+\mathrm{1}}^{\mathrm{2}}+b_{\mathrm{4}}{s}_{I+\mathrm{1}}{a}_I+b_{\mathrm{5}}{a}_I^{\mathrm{2}}.\end{array}\end{array}$$

Then the crack length at the jth working cycle can be expressed as

$$\begin{array}{}\text{(10)}& a_j=\left\{\begin{array}{ll}{a}_{\mathrm{1}}& j=\mathrm{1},\\ a_{\mathrm{1}}+{\sum }_{j\mathrm{1}=\mathrm{1}}^{j-\mathrm{1}}{b}_{\mathrm{0}}(j\mathrm{1}+\mathrm{1})+b_{\mathrm{1}}(j\mathrm{1}+\mathrm{1})s_{j\mathrm{1}+\mathrm{1}}\\ +b_{\mathrm{2}}(j\mathrm{1}+\mathrm{1})a_{j\mathrm{1}}+b_{\mathrm{3}}(j\mathrm{1}+\mathrm{1})s_{j\mathrm{1}+\mathrm{1}}^{\mathrm{2}}\\ +b_{\mathrm{4}}{s}_{j\mathrm{1}+\mathrm{1}}{a}_{j\mathrm{1}}+b_{\mathrm{5}}{a}_{j\mathrm{1}}^{\mathrm{2}}& j\ge \mathrm{2}.\end{array}\right.\end{array}$$

Hence, the crack extension trajectory can be obtained by synthesizing the depth of the crack at different working cycles. Then, the stochastic response of the cracked beams in the parallel system considering crack extension can be obtained with the results from the neural network brought into Eq. (10) and iterated continuously as shown in Fig. 3. The proposed method lays the foundation for the time-varying reliability modeling.

4 Failure dependence analysis of parallel systems containing cracked beams

In this paper, we will analyze the complex failure dependence mechanism and reliability evaluation methods of parallel systems in the failure mode of fatigue. The stiffness degradation and strength degradation phenomena caused by crack extension are considered in the failure dependence mechanism analysis and reliability modeling process. The classical parallel system reliability models are developed via the system structure function and the reliability of each component. However, the dependence between components is always ignored. If considering the statistical correlation of components, a system reliability model has to be establish based on the failure rate of components, and then the system failure rate has to be corrected by empirical parameters. However, this approach is unrealistic for the parallel systems with cracked beams, because the failure rate of beams is greatly affected by structural parameters, material parameters, system loads, etc., and presents a very obvious non-constant state. Thus it is impossible to obtain such a huge sample size to calculate the failure rate directly through actual testing. Furthermore, this model cannot directly reflects the working mechanism and failure mechanism of cracked beams and the physical sense of the empirical parameters is not well explained. In this section, the complex failure dependence mechanism existing in the parallel system containing cracked beams will be explained.

In order to consider the effects of stress and strength during the working process of a system, the well-known stress–strength interference (SSI) model and its extension are widely used in mechanical reliability calculations. The stress on the jth component in a parallel system during the Ith operating cycle is denoted by s_j(I) with its probability density function (PDF) denoted by $f_{s_j}\left(s_j\right(I\left)\right)$. Denote the residual strength of the jth component in the system during the Ith operating cycle by r_j(I) with its PDF denoted by $f_{r_j}\left(r_j\right(I\left)\right)$. According to the SSI model, the reliability of the jth component in the system can be expressed as

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{R}_j\left(I\right)=& P\left(s_j\right(I)<r_j(I\left)\right)\\ =& \underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{s_j}\left(s_j\right(I\left)\right)\underset{s_j\left(I\right)}{\overset{\mathrm{\infty }}{\int }}{f}_{r_j}\left(r_j\right(I\left)\right)\mathrm{d}{r}_j\left(I\right)\mathrm{d}{s}_j\left(I\right)\end{array}\end{array}$$

For a parallel system with n statistically independent components, the reliability of the parallel system during the Ith operating cycle can be expressed as

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{R}_{\mathrm{1}}\left(I\right)=& \mathrm{1}-\prod _{j\mathrm{2}=\mathrm{1}}^n[\mathrm{1}-\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{s_{j\mathrm{2}}}(s_{j\mathrm{2}}\left(I\right))\\ & \times \underset{s_{j\mathrm{2}}\left(I\right)}{\overset{\mathrm{\infty }}{\int }}{f}_{r_{j\mathrm{2}}}\left(r_{j\mathrm{2}}\right(I\left)\right)\mathrm{d}{r}_{j\mathrm{2}}\left(I\right)\mathrm{d}{s}_{j\mathrm{2}}\left(I\right)]\end{array}\end{array}$$

The reliability of the system after N working cycles without failure can be expressed as

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{R}_{\text{sys}\mathrm{1}}\left(N\right)=& \prod _{j\mathrm{3}=\mathrm{1}}^N\mathit{\{}\mathrm{1}-\prod _{j\mathrm{2}=\mathrm{1}}^n[\mathrm{1}-\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{s_{j\mathrm{2}}}\left(s_{j\mathrm{2}}\right(j\mathrm{3}\left)\right)\\ & \times \underset{s_{j\mathrm{2}}\left(j\mathrm{3}\right)}{\overset{\mathrm{\infty }}{\int }}{f}_{r_{j\mathrm{2}}}\left(r_{j\mathrm{2}}\right(j\mathrm{3}\left)\right)\mathrm{d}{r}_{j\mathrm{2}}\left(j\mathrm{3}\right)\mathrm{d}{s}_{j\mathrm{2}}\left(j\mathrm{3}\right)\left]\mathit{\right\}}\end{array}\end{array}$$

In the above classical reliability model based on the assumption of independence, the respective loads are considered to be independent. Nevertheless, when a common load is applied, the stresses applied to the individual components are not statistically independent from each other. Assuming that the working load of the system in the Ith working cycle is F(I), and the load shared by the jth component is F_j(I), then if the statistical characteristics of F(I) are known, the statistical characteristics of F_j(I) and s_j(I)c an be obtained. Then, the failure of each component in the system is correlated due to sharing the system working load.

Figure 4 Failure dependence in reliability evaluation.

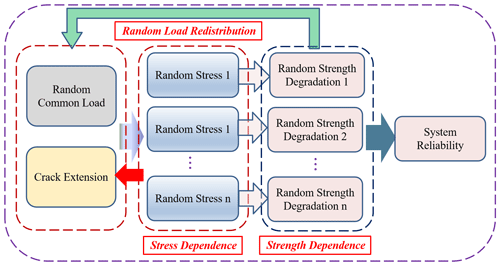
As stated above, crack expansion determined by stress. Therefore, not only the stresses on each component in the system are statistically correlated, but also the crack expansion behavior in the components is statistically correlated. The statistical correlation of crack extension will also have an effect on the statistical correlation between component stresses again in conjunction with the external loads of the system. In addition, the strength degradation of individual components within the system is the function of stress. As a result, there is a very complex statistical correlation between system operating loads, crack propagation, component stresses, and component residual strength, as shown in Fig. 4. This complex correlation leads to the complex failure dependence between the beams in the system, which will have a large impact on the accurate quantitative reliability evaluation of the system, and this failure dependence mechanism must be taken into account in the time-varying reliability modeling process.

5 System reliability modeling

In this paper, stiffness degradation caused by crack extension is considered. The failure criterion of the system is that the failure of all the components of the system causes the system failure. The failure criterion of components is that the residual strength is less than the working stress. In this section, a time-varying system reliability model considering the above complex failure dependence will be developed. The residual strength of cracked beams is continuously decreasing due to the presence of failure modes such as corrosion and fatigue. Failure of the system arises not only from cyclic stress effects, but also from stresses generated by larger assigned transient loads (e.g., shock loads). In parallel systems, some beams may fail, and then the remaining beams of the system that have not failed will bear the system working load. The load redistribution phenomenon occurs at this time. According to the definition of parallel system reliability, the system undergoes N operating cycles without failure, which requires at least one component to be able to work normally within this specified time. Random failure of part of the beams in the parallel system and the corresponding random load redistribution could occur during the N operating cycles. Load redistribution is currently a difficult problem in time-varying reliability modeling of parallel systems, especially in the case of complex failure dependence among components in the systems.

During these N operating cycles, all of the n beams that make up the system may not fail or n1 $(\mathrm{1}\le n\mathrm{1}<n)$ beams may fail. The failure of any of the n1 beams may occur in any one of the N operating cycles. Hence, define the system working cycle vector as follows.

$$\begin{array}{}\text{(14)}& W=[i\mathrm{1},i\mathrm{2},i\mathrm{3},\mathrm{\dots },in],\end{array}$$

where ij $(j=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{\dots },n)$ indicates the number of operating cycles in which the jth beam can operate normally. For example, i5=3 means that the fifth part of the system can operate normally for three operating cycles and fails at the fourth cycle. In particular, ij=N means that the jth component does not fail in all N operating cycles. ij=0 means that the first component fails after the first operating cycle. Thus, the probability that the parallel system will not fail for a period of N operating cycles, i.e., the reliability of the system, can be expressed as follows

$$\begin{array}{}\text{(15)}& R_{\text{sys}\mathrm{2}}\left(N\right)=\sum _{i\mathrm{1}=\mathrm{0}}^N\sum _{i\mathrm{2}=\mathrm{0}}^N\mathrm{\cdots }\sum _{in=\mathrm{0}}^{N}P\left(W\right),\end{array}$$

where P(W) denotes the probability of failure of beam j at cycle ij+1, which can be expressed as

$$\begin{array}{}\text{(16)}& P\left(W\right)=\prod _{j=\mathrm{1}}^n{P}_j\left(ij\right).\end{array}$$

It should be noted that when $max\left(ij\right)<N$, R_sys2(N)=0. Moreover, when the stresses applied to the components in the system are independent, the probability of failure of the jth component at the (ij+1)th cycle, denoted by P_j(ij), can be expressed as

$$\begin{array}{}\text{(17)}& \begin{array}{rl}{P}_j\left(ij\right)=& \left(\prod _{j\mathrm{4}=\mathrm{1}}^{ij}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{s_j}\right(s_j\left(j\mathrm{4}\right))\\ & \times \underset{s_j\left(j\mathrm{4}\right)}{\overset{\mathrm{\infty }}{\int }}{f}_{r_j}\left(r_j\right(j\mathrm{4}\left)\right)\mathrm{d}{r}_j\left(j\mathrm{4}\right)\mathrm{d}{s}_j\left(j\mathrm{4}\right))\\ & \times \left[\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{s_j}\right(s_j(j\mathrm{4}+\mathrm{1}))\\ & \times \underset{-\mathrm{\infty }}{\overset{s_j(j\mathrm{4}+\mathrm{1})}{\int }}{f}_{r_j}\left(r_j\right(j\mathrm{4}+\mathrm{1}\left)\right)\\ & \times \mathrm{d}{r}_j(j\mathrm{4}+\mathrm{1})\mathrm{d}{s}_j(j\mathrm{4}+\mathrm{1})].\end{array}\end{array}$$

However, from the failure dependence mechanism analysis in Sect. 4, it can be seen that the stresses of each component are statistically correlated to each other and are affected by the system working load F(j4) and crack depth at the same time, which are obtained by the method in Sect. 3. Consequently, when the statistical correlation between the stresses is taken into account, the above equation becomes

$$\begin{array}{}\text{(18)}& \begin{array}{rl}{P}_j\left(ij\right)=& \left[\prod _{j\mathrm{4}=\mathrm{1}}^{ij}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{s_j}\right(s_j(j\mathrm{4},F(j\mathrm{4}),a_j(j\mathrm{4}\left)\right))\\ & \times \underset{s_j(j\mathrm{4},F(j\mathrm{4}),a_j(j\mathrm{4}\left)\right)}{\overset{\mathrm{\infty }}{\int }}{f}_{r_j}\left(r_j\right(j\mathrm{4}\left)\right)\\ & \times \mathrm{d}{r}_j\left(j\mathrm{4}\right)\mathrm{d}{s}_j(j\mathrm{4},F(j\mathrm{4}),a_j(j\mathrm{4}\left)\right)]\\ & \times \left[\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{s_j}\right(s_j(j\mathrm{4}+\mathrm{1},F(j\mathrm{4}),a_j(j\mathrm{4}\left)\right))\\ & \times \underset{-\mathrm{\infty }}{\overset{s_j(j\mathrm{4}+\mathrm{1},F(j\mathrm{4}),a_j(j\mathrm{4}\left)\right)}{\int }}{f}_{r_j}\left(r_j\right(j\mathrm{4}+\mathrm{1}\left)\right)\\ & \times \mathrm{d}{r}_j(j\mathrm{4}+\mathrm{1})\mathrm{d}{s}_j\left(s_j\right(j\mathrm{4}+\mathrm{1},F\left(j\mathrm{4}\right),a_j\left(j\mathrm{4}\right)\left)\right)]\end{array}.\end{array}$$

If the stochastic properties of F(∗) is considered, such that its PDF is expressed as f_F(F(∗)), then P(W) can be expressed as

$$\begin{array}{}\text{(19)}& P\left(W\right)=\prod _{j\mathrm{5}=\mathrm{1}}^N\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{f}_F\left(F\right(j\mathrm{5}\left)\right)\left(\prod _{j=\mathrm{1}}^n{P}_j\left(j\mathrm{5}\right)\right)\mathrm{d}{f}_F\left(F\right(j\mathrm{5}\left)\right),\end{array}$$

where

$$\begin{array}{}\text{(20)}& P_j\left(j\mathrm{5}\right)=\left\{\begin{array}{l}{\int }_{s_j(j\mathrm{5},F(j\mathrm{5}),a_j(j\mathrm{5}\left)\right)}^{\mathrm{\infty }}{f}_{r_j}\left(r_j\right(j\mathrm{5}\left)\right)\mathrm{d}{r}_j(j\mathrm{5},F(j\mathrm{5}\left)\right),\\ \text{ beam }j\text{ works at the }j\mathrm{5}\text{th cycle};\\ {\int }_{-\mathrm{\infty }}^{s_j(j\mathrm{5},F(j\mathrm{5}),a_j(j\mathrm{5}\left)\right)}{f}_{r_j}\left(r_j\right(j\mathrm{5}\left)\right)\mathrm{d}{r}_j\left(j\mathrm{5}\right),\\ \text{ beam }j\text{ fails at the }j\mathrm{5}\text{th cycle}.\end{array}\right.\end{array}$$

It should be noted that when the jth beam has failed before the j5th cycle, P_j(j5)=1. Furthermore, the load redistribution due to the failure of the jth component is taken into account in the stress solution process of other components, and the stresses of each component after the load redistribution are obtained using the method proposed in Sect. 3.

6 Numerical examples

Consider a parallel system consisting of two cantilever beams with the same structural dimensions and material parameters as shown in Fig. 2, which are listed in Table 1. Each beam has a straight crack, which is at the mid-point position of the beam and may have different depths. The two beams are jointly subjected to the same random working load F. The random statistical characteristics of the working loads are shown in Table 1. μ(∗) represents the mean value of a random variable, and σ(∗) represents the standard deviation (SD) of a variable. The residual strengths of the two beams under the action of the loads continuously degrade, and the degradation law can be expressed as follows (Gao and Yan, 2013):

$$\begin{array}{}\text{(21)}& r\left(n\right)=r_{\mathrm{0}}{\left(\mathrm{1}-{\displaystyle \frac{n{\int }_{\mathrm{0}}^{\mathrm{\infty }}{s}^m{f}_{\mathrm{s}}\left(s\right)\mathrm{d}s}{C}}\right)}^{\mathit{\vartheta }},\end{array}$$

where r₀ is the initial strength; a and C are material parameters.

Table 1 Load parameters, geometric parameters and material parameters.

Figure 5 MCS flowchart for system reliability assessment.

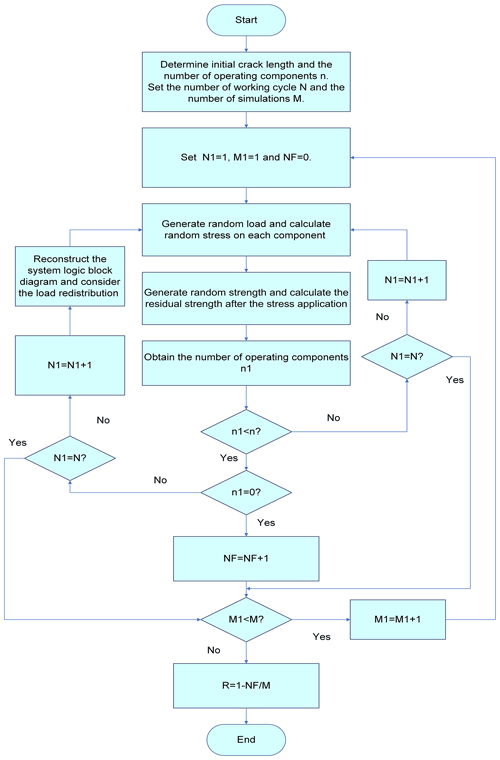
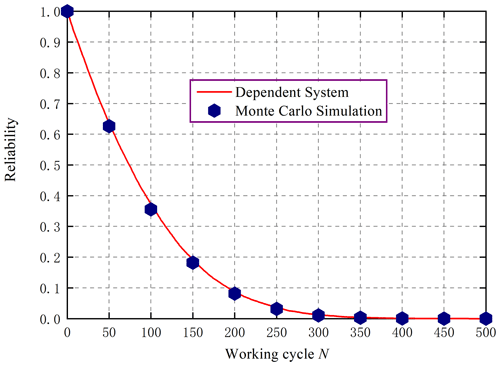
In order to verify the validity and correctness of the proposed system reliability model, when the crack depths of the two beams are 0.025 mm, the Monte Carlo simulation (MCS) method shown in Fig. 5 is used to compare with the time-varying system reliability proposed in this paper. The MCS method does not rely on a specific reliability model and is used to simulate the working process of the beams, which is fundamentally different from the proposed analytical reliability model. The results from the two methods are shown in Fig. 6.

Figure 6 System reliability in the case of crack depth of 0.025 mm.

As can be seen from Fig. 6, the MCS method has a good agreement with the reliability model proposed in this paper. Besides, it can be known from Fig. 6 that the system reliability has the characteristic of decreasing with the working time. When the crack depths are both 0.025 mm, the reliability decreasing rate decreases continuously, and the reliability decreases the fastest at the beginning of the working stage. Due to the large crack depth, the stresses on the system are significantly high, leading to a rapid decrease in residual strength. As a result, the service life of the system is lower and the reliability decreases rapidly. As a result of the significant reduction in system service life, the initial smooth decline time of the system as a proportion of the full life cycle undergoes a significant shrinkage, demonstrated by the rapid decline in reliability shown in Fig. 6. The results from the proposed models are validated using the MCS in this numerical example. The MCS verification process is presented in Fig. 5. When the structural, load, and material parameters of the system are obtained, the MCS validation can be carried out according to the flow shown in Fig. 5. The proposed validation method is not limited to the specific parameters provided in this numerical example.

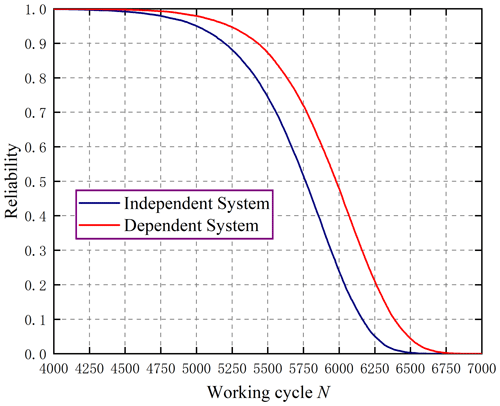
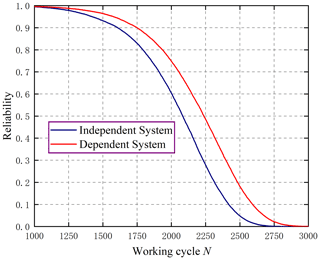
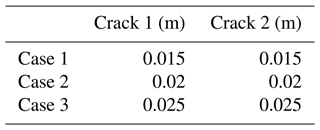
In order to analyze the effect of crack depth on reliability and failure correlation, the system reliability was calculated for the two beams with different values of crack depth. The three different crack depth parameters are shown in Table 2. The system reliability when stress dependence due to load-sharing and random load redistribution are considered, and the system reliability results in the case that stresses on both beams are independent are shown in Figs. 7 to 9.

Figure 7 Comparison of system reliability in the case of crack depth of 0.015 mm.

Figure 8 Comparison of system reliability in the case of crack depth of 0.02 mm.

Figure 9 Comparison of system reliability in the case of crack depth of 0.025 mm.

Table 2 Crack depth parameters

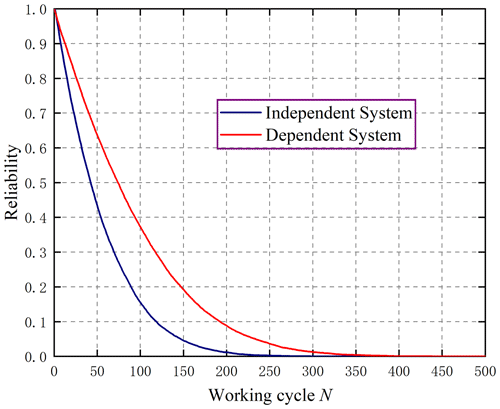
As shown in Figs. 7–9, crack depth has a pronounced effect on both time-varying system reliability and failure correlation. As the crack deepens, the time-varying reliability of the system decreases significantly. When the crack depth is small, the time-varying reliability of the system decreases at a rate that first increases and then decreases. When the crack depth is large, the time-varying reliability of the system shows an obvious characteristic of decreasing more and more slowly. Moreover, the crack depth has a greater effect on the failure correlation of the two beams in the system and the system reliability under the independent assumption is significantly lower than that under the failure dependence assumption. The time-varying system reliability under the independent assumption has a similar trend to the time-varying system reliability with failure dependence caused by stress correlation. This demonstrates that the conventional system reliability model for the independent assumption is not applicable to the load-sharing parallel system composed of cracked beams. In addition, the difference between the reliability of the independent system and that of the dependent system first increases and then decreases with time. The failure dependence becomes more obvious with the increase of crack depth and the error between the system reliability calculated under the independent assumption and the actual becomes larger due to the increase of crack depth.

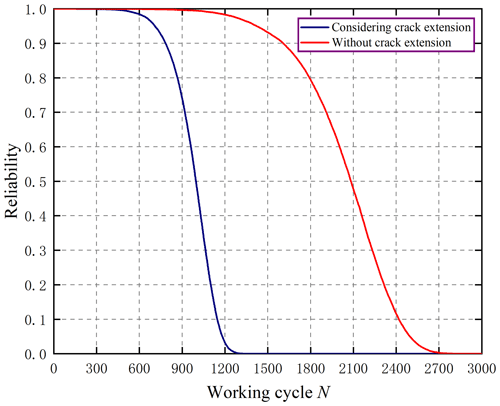
In order to analyze the effect of crack extension on the system reliability, it is assumed that the crack expands with stress at different operating cycles and can be expressed as

$$\begin{array}{}\text{(22)}& a_{j+\mathrm{1}}=a_j+(s/\mathrm{100})\times \mathrm{0.00003}.\end{array}$$

Then the time-varying system reliability considering the two cases of crack extension and crack non-extension with the initial depth of cracks of both beams being 0.02 m is shown in Fig. 10. From Fig. 10, it can be seen that the crack extension will cause the time-varying system reliability to decrease rapidly. Therefore, in engineering practice, the serious destructiveness of the crack on the system reliability is in concern.

Figure 10 Effects of crack extension on system reliability.

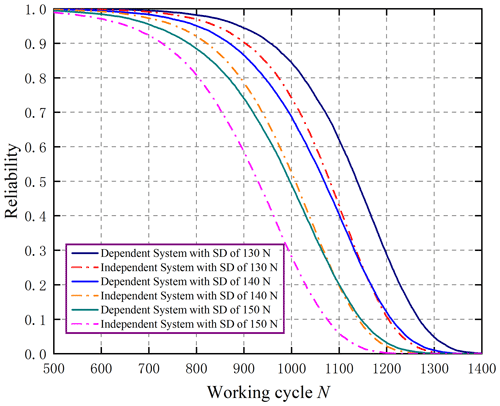
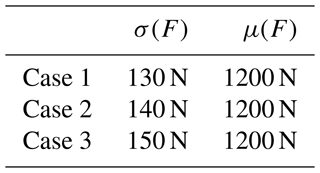
In addition, in order to analyze the effect of work load dispersion on the time-varying system reliability, the system reliability in the case where the working load has different SD, which is listed in Table 3, is shown in Fig. 11.

Figure 11 Effects of load dispersion on system reliability.

Table 3 Working load parameters.

From Fig. 11, it can be known that the working load dispersion has a large effect on the time-varying reliability and failure correlation of the system. As the working load dispersion increases, the system reliability decreases. The reliability trends of the dependent and independent systems are similar. However, with the increase of working load dispersion, the calculation error caused by the independent assumption increases, which will have a greater impact on the accurate assessment of system safety.

7 Conclusions

A time-varying reliability model of load-sharing parallel systems composed of beams with cracks is presented in this paper. By finite element analysis of cracked beams, a stochastic response statistics method based on a neural network and a response surface model is proposed. The statistical correlation between crack depth, random working load, random strength degradation, and random stress response as well as the complex failure correlation caused by the combination of these factors are considered in the time-varying reliability model of the parallel system with cracked beams. The validity and correctness of the model are verified by the MCS method. It is shown that crack depth has a quite important effect on the time-varying reliability and failure dependence of the system. An increase in crack depth leads to a rapid decrease in system reliability, while exacerbating the error in the assessment of system reliability under the assumption of independence. In addition, the work load dispersion also has a large impact on the time-varying reliability of the cracked beam system. An increase in working load dispersion will reduce the time-varying reliability of the system and also aggravate the failure dependence effect. Overall, crack depth, system stress, and other factors that contribute to the complex failure dependence of a system have a large impact on both reliability and the rate of reliability degradation, causing the reliability curves to exhibit different patterns. These analytical conclusions provide a theoretical basis for mechanical system failure diagnosis.