the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Type synthesis of non-overconstrained and overconstrained two rotation and three translation (2R3T) parallel mechanisms with three branched chains
Yu Rong
Xingchao Zhang
Tianci Dou
Hongbo Wang
In this paper, a new synthesis method of 2R3T (R denotes rotation and T denotes translation) overconstrained and non-overconstrained parallel mechanisms (PMs) with three branched chains based on the displacement sub-manifold method is presented. Firstly, the displacement sub-manifolds of mechanisms were determined based on 2R3T motions. Subsequently, the displacement sub-manifolds of the branched chains were derived using the displacement sub-manifold theory, and their corresponding motion diagrams were provided. Additionally, a comprehensive analysis of non-overconstrained 2R3T PMs with a single-constraint branched chain was conducted, and the type synthesis of overconstrained 2R3T PMs with two or three identical constraints was also performed, accompanied by the presentation of partial mechanism diagrams. Finally, the number of DOF (degrees of freedom) of the mechanism was calculated using the modified Kutzbach–Grübler equation for a new PMs,and the screw theory was used to verify the kinematic characteristics, proving this new method's correctness.
- Article
(5160 KB) - Full-text XML
- BibTeX
- EndNote
The parallel mechanisms (PMs) have the advantages of high rigidity, high bearing capacity, and small cumulative error and are widely used in aerospace, machining, medical rehabilitation, bionics, and other fields (Li et al., 2021; Zhou et al., 2022; L. Wang et al., 2022; Niu et al., 2023). According to the constraints of branched chains in relation to the moving platform, PMs can be divided into overconstrained and non-overconstrained PMs. The overconstrained PMs have two or more identical constraints, such as redundant constraints that can improve the stiffness of the mechanism, which has attracted extensive research by scholars on overconstrained PMs in recent years. Chen et al. (2021) proposed a new overconstrained PM without parasitic motion, clarified the reasons for the non-parasitic motion characteristics of the mechanism, and studied its kinematics and dynamics. Ibrahim et al. (2015) designed a 4-DOF, endoscopic, dexterous PM for minimally invasive surgery, deduced the mechanism's forward and inverse kinematic solutions, and studied the singularity using the screw theory (Sun et al., 2018). As an example, a 2-DOF overconstrained PM was applied to an assembly line, and the kinematic calibration problem of an overconstrained PM was studied. Du et al. (2022) established the geometric error model of the 2UPR–RPU (where U, P, R, C, and S represent universal, prismatic, revolute, cylindrical, and spherical joints, respectively) overconstrained PM and performed a sensitivity analysis on the error source.
Although the overconstrained PMs have excellent stiffness and load-carrying capacity, they are often required to meet special geometric conditions and are very sensitive to part-manufacturing and assembly errors. If these conditions cannot be met, the mechanism will not only be challenged to ensure motion accuracy but will also be unable to maintain the designed motion characteristics. Therefore, it is equally important to study non-overconstrained PMs. Huang et al. (2011) proposed a systematic synthesis method of symmetric non-overconstrained 3-DOF translational PMs using the screw theory. Ye et al. (2022) presented a type synthesis method of 4-DOF non-overconstrained parallel mechanisms (PMs) with symmetrical structures using screw theory. Ye and Hu (2021) proposed a novel 3-DOF RPU+UPU+SPU PM, and its complete kinematics and stiffness are studied. Kuo et al. (2014) proposed a non-overconstrained 3-DOF parallel-positioning mechanism. The inverse and forward kinematic solutions of the mechanism are provided.
Type synthesis is the essential factor that determines the function and performance of mechanical equipment, and it is also the first step in the exploration of the development of new processing equipment and is worthy of in-depth study. Type synthesis seeks the specific topology structure of the mechanism under the constraint of the number and characteristics of the desired DOF, and its core is to describe mechanism motion patterns. Therefore, based on the different description methods, the existing type synthesis methods can be divided into two categories: instantaneous motion-based methods and finite motion-based methods. Among them, the instantaneous motion-based methods include the constrained screw synthesis method (S. Wang et al., 2022; X. Li et al., 2022), the map method (Lu and Ye, 2017), and the differential geometry synthesis method (Meng et al., 2007; Li et al., 2011). These methods can only describe the motion of mechanisms in instantaneous states and cannot express the motion characteristics of mechanisms in continuous motion processes. The finite motion-based methods include the displacement sub-group and/or sub-manifold synthesis method (Hervé, 1999), the GF (generalized function) synthesis method (Zhang et al., 2018), the linear transformation method (Gogu, 2009), the POC (position and orientation characteristic) set method (Jin and Yang, 2004), and the finite screw method (Yang et al., 2016). These methods can describe the continuous motion of mechanisms, avoiding the synthesis result being an instantaneous mechanism, and do not require checks regarding full-cycle mobility.
In 1978, Hervé (1978) introduced Lie group theory into mechanism analysis, laying the theoretical foundation for using Lie group theory to analyze the DOF of mechanisms. In 2004, Li et al. (2004) systematically expounded the method's general theory and process. Based on this theory, Li et al. (2017) studied the equivalent mechanism of 3-DOF RPR branched-chain motion. L. Li et al. (2022) synthesized a 3-DOF parallel mechanical branch with double branches. Wei and Dai (2019) studied a reconfigurable parallel mechanism and the configuration transformation problem. Note that, among the numerous studies on type synthesis, there are relatively few works that are focused on 2R3T PMs. Most of the existing 2R3T PMs are composed of a single constrained branched chain and multiple unconstrained branched chains, and there are many joints in 2R3T PMs, such as the 2UPS+UPU PM (Rong et al., 2018), the 5PSS+UPU PM (Li et al., 2019), and the 4UCU+UCR PM (Luo et al., 2021). The joint is the weak part of the mechanism, which is the main reason for the deformation and clearance of the mechanism; thus, a mechanism with a small number of joints theoretically has better accuracy and stiffness. Therefore, an effective way to reduce the number of joints and to improve the accuracy and stiffness of the mechanism is to replace unconstrained branch chains with constrained branched chains and make the mechanisms become overconstrained PMs. Unfortunately, there are few reports on the configuration of overconstrained 2R3T PMs.
This paper studies various combinations of constrained branched chains and proposes a type synthesis method for non-overconstrained and overconstrained 2R3T PMs. The rest of this article is organized as follows. In Sect. 2, based on the displacement sub-manifold method, the synthesis steps of 2R3T PMs are proposed, as are branched-chain bonds {X(u)}{R(N,u)} and {G(v)}{G(u)}. Type synthesis of non-overconstrained and overconstrained 2R3T PMs with a branched chain of {X(u)}{R(N,u)} has been conducted in Sect. 3. Type synthesis of non-overconstrained 2R3T PMs with a branched chain of {G(v)}{G(u)} has been conducted in Sect. 4. In Sect. 5, a representative configuration is selected for DOF analysis to verify the correctness of the new configuration. Section 6 discusses an optimal type for practical application, and a physical prototype is given.
In 1978, Hervé (1978) enumerated all 12 kinds of displacement sub-groups, as shown in Table 1. It also can be readily proven that the displacement sub-manifold {Me} of the end effector is the intersection of the sub-groups or sub-manifolds {MLi} produced by all branched chains, both of which must satisfy the following equation (Lin et al., 2022):
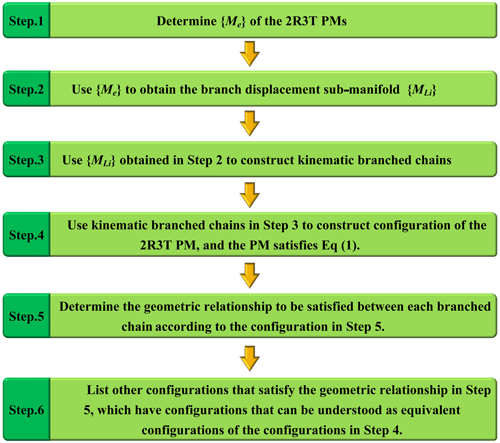
where {MLi} is the product of the kinematic joint displacement sub-manifold that makes up the branched chain i, and the displacement sub-manifold synthesis method for the 2R3T PMs in this paper is summarized in the following six steps, see Fig. 1.
According to the representation method of the displacement sub-manifold, the displacement sub-manifold of rigid-body motion with a 2R3T property is
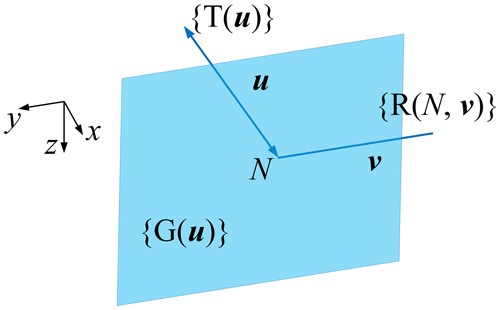
In Eq. (2), there are two cases where the first displacement sub-group of {T} is {T(x)}, {T(x)}{T(y)}{T(z)}, and {T(x)}{T(z)}{T(y)}. If x∥u and u⊥v (∥ and ⊥ represent the parallel and vertical geometric relationship, respectively), then , and combined with Table 1's {X(u)}, we can get
Figure 2 shows the motion diagram of the displacement sub-manifold {X(u)}{R(N,u)} corresponding to the kinematic branch uPuGvR (G represents planar pair, and the superscripts represent the axis direction of the prismatic or revolute joint), in which the line with double arrows indicates translational, the planar area indicates plane motion, and the straight line indicates rotational.
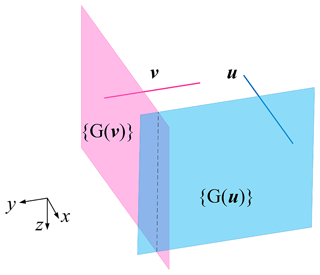
The 3-D displacement sub-group G(u) represents the two translationals in a plane and the rotational about the plane normal. Table 2 lists the branched chains constituting the plane pair and the corresponding displacement sub-group.
From Table 2, we can get the displacement sub-manifolds and the corresponding branched chains xPuRzPuRvR, xPuRuRuRvR, xPzPuRuRvR, xPuRuRzPvR, xPzPuRyPvR, xPuRzPyPvR, and xPzPyPuRvR.
Based on the displacement sub-manifold method, the corresponding rigid-body motion is also 2R3T. According to the product closure of the displacement sub-manifold, there will be , which can get
where {G(v)}{G(u)} is the displacement sub-manifold of the vGuG, and Fig. 3 is a schematic diagram of the displacement sub-manifold {G(v)}{G(u)}. It can be seen from Table 2 that the number of {G(u)} is 7 so the number of {G(v)}{G(u)} is 7 × 7 = 49.
From the above analysis, we can see that there are two types of {X(u)}{R(N,u)} and {G(v)}{G(u)} in the {MLi} of 2R3T PMs.
3.1 Type synthesis of non-overconstrained 2R3T PMs
For conciseness, this paper defines the UPS, URS, PRPS, and PRRS branched chains as 6i (i=1, 2, 3, 4) and defines xPuRzPuRvR, xPuRuRuRvR, xPzPuRuRvR, xPuRuRzPvR, xPzPuRyPvR, xPuRzPyPvR, and xPzPyPuRvR branched chains as 5j, j=1, 2, …, 7.
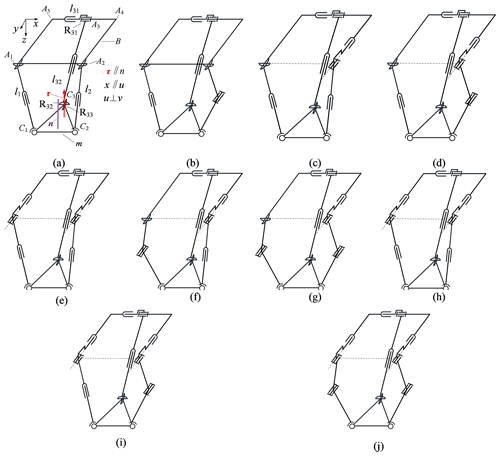
Figure 4Category 6–6–51 PMs. (a) 2UPS–uPuRPuRvR. (b) UPS–URS–uPuRPuRvR. (c) UPS–yPyRPS–xPuRPuRvR. (d) UPS–yPyRyRS–uPuRPuRvR. (e) 2URS–uPuRPuRvR. (f) URS–yPyRPS–uPuRPuRvR. (g) URS–yPyRyRS–uPuRPuRvR. (h) 2yPyRPS–uPuRPuRvR. (i) yPyRPS–yPyRyRS–uPuRPuRvR. (j) 2yPyRyRS–uPuR-PuRvR.
By combining a single constrained branch chain 51 with unconstrained branch chains, 10 configurations can be obtained, as shown in Fig. 4. The 2UPS–PRPU PM in Fig. 4a includes a moving platform (m); a base platform (B); two UPS branched chains (l1 and l2); and one PRPU branched chain (l3), where l3 is further divided into l31 and l32. Here, m is an isosceles triangle with three vertices Ci (i=1, 2, 3) and the normal of the plane, in which m is located in n. B is a rectangle with four vertices Ai (i=1, 2, 4, 5), and A3 is the center of the R joint in the branch chain l3. Considering the fact that there are seven types of single constrained branch chains, combined with Fig. 4, it can be concluded that there are 70 types of category 6–6–5 PMs.
According to the characteristic of the constrained force and/or torque of the branches of the PMs with limited DOF, Ye and Hu (2021) proposed a rule for judging the constrained force and/or torque:
- a.
In each leg, the constrained forces should be perpendicular to all P joints and coplanar with all R joints.
- b.
The constrained torques should be perpendicular to all R joints in each leg.
Let Rij be the jth R joint from B to m in the branched chain li. According to rules (a) and (b), it can be seen that, in the constraint branched chain l3 of the PMs shown in Fig. 4, one constrained torque τ is perpendicular to R12, R12, and R13. It can be seen that the mechanisms synthesized in this section are non-overconstrained PMs.
3.2 Type synthesis of overconstrained 2R3T PMs with two identical constraints
This section selects the unconstrained branched chain 63 and the same constrained branched chains 5i–5i as specific types for analysis. The 2PRPU–PRPS PM in Fig. 5a includes a moving platform (m), a base platform (B), two PRPU branched chains (l1 and l2), and one PRPS branched chain (l3). Here, A1, A2, and A3 are the centers of the R joints, C1 and C2 are the centers of the U joints, C3 is the center of the S joint, and m is an isosceles triangle with three vertices Ci (i=1, 2, 3), and the normal of the plane in which m is located is n. N is the midpoint of C1 and C2, and Rij denotes the jth R joint in branched chain li. As shown in Fig. 5, the kinematic bond of branched chain li in Fig. 5a is
where {T(u)} represents the translation along u, {R(A1,u)} represents the rotation through point A1, and the axis of rotation is u; u and v represent the related joints' unit direction vector. Vector wi is collinear with AiCi. In Eq. (5), {R(A1,u)}, {T(w1)}, and {R(C1,u)} can form {G(u)} so {L1} can also be expressed as
Similarly, {L2} can also be expressed as
Because C1C2 passes through point N and is parallel to axis v, . The displacement set of the moving platform is as follows:
According to Eq. (8), the DOF of 2uPuRPuRvR–yPyRPS PM is 2R3T, and the DOF of the other mechanisms in Fig. 5 is also 2R3T, which is not verified here. At the same time, according to Fig. 5, it can be known that the geometric conditions for realizing two constrained branched chains uPuGvR to maintain 2R3T are as follows: the normals of the two plane pairs are parallel to each other, and the axes of the revolute pairs are collinear.
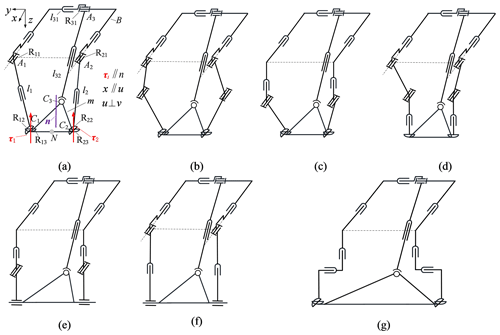
Figure 5Category 5i–5i–63 PMs. (a) 2uPuRPuRvR–yPyRPS. (b) 2uPuRuRuRvR–yPyRPS. (c) 2uPzPuRuRvR–yPyRPS. (d) 2uPuRuRPvR–yPyRPS. (e) 2uPzPuRvPvR–yPyRPS. (f) 2uPuRPvPvR–yPyRPS. (g) 2uPzPyPuRvR–yPyRPS.
In Sect. 3.1, four kinds of unconstrained branched chains are listed so, in this section, there are 7 × 4 = 28 kinds of PMs with the same configuration of constrained branched chains and 21 × 4 = 84 kinds of PMs with different configurations of constrained branched chains. It can be seen that there are (28 + 84) = 112 kinds of three-branched-chain PMs composed of double-constraint branched chains. Table 3 lists PMs of category 5–5–63.
According to the constrained force and/or torque judgment rules (a) and (b), in Fig. 5, there exists a constrained torque τ1, which is perpendicular to R1j (j=1, 2, 3) in branched chain l1, and a constrained torque τ2, which is perpendicular to R2j (j=1, 2, 3) in branched chain l2. Also, because of R11 ∥ R21 ∥ x, the direction vectors of constrained torques τ1 and τ2 are parallel to each other, and the branch chains l1 and l2 impose identical constraints on the moving platform. Similarly, the other configurations in Fig. 5 have such constraint relationships.
3.3 Type synthesis of overconstrained 2R3T PMs with three identical constraints
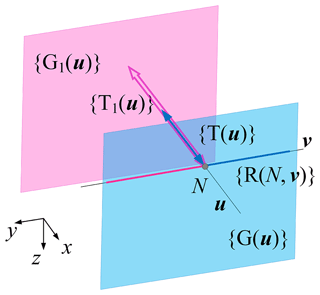
The multi-constraint branched-chain {X(u)}{R(N,u)} PMs studied in this subsection are used to replace the unconstrained branched chain in the double-constraint branched-chain mechanism with a constrained branched chain so that all three branched chains are constrained branched chains.
In Sect. 3.2, the kinematic bond of branched chains 1 and 2 is . According to the definition of {X(u)} in Table 1, there is . Let the kinematic bond of branched chain 3 be {G(u)}{T(u)}{R(N,v)}. Figure 6 is a schematic diagram of the displacement sub-manifold 2-{X(u)}{R(N,u)}.
Equation (9) shows that the motion of the mechanism composed of the kinematic branched chains uGuPvR and 2uPuGvR is still 2R3T.
In Sect. 3.2, it is obtained that the {X(u)}{R(N,u)}-type mechanism has 7 single-constraint branched chains and 28 double-constraint branched chains. Therefore, there are 7 × 28 = 196 kinds of three-constrained PMs. Figure 7 shows part of the mechanism schematic diagram of type 51–51–uGuPvR. The 2PRPU–RPRPR PM in Fig. 5a includes a moving platform (m), a base platform (B), two PRPU branched chains (l1 and l2), and one RPRPR branched chain l3. Here, A1, A2, and A3 are the centers of the R joints, C1 and C2 are the centers of the U joints, C31 and C32 are the centers of the R joints in branched chain l3, and m is an isosceles triangle with three vertices (C1, C2, and C32), and the normal of the plane in which m is located is n. N is the midpoint of C1 and C2, and Rij denotes the jth R joint in branched chain li. In Fig. 7a, the kinematic bond of branched chain 3 can be written as
where wi is the unit vector of branched chain i; combined with Eqs. (6) and (7), this can get
According to Eq. (11), the property of the DOF of the mechanism 2uPuRPuRvR–uRPuRuPvR is 2R3T. We can also verify other PMs in Fig. 6, which will not be repeated here.
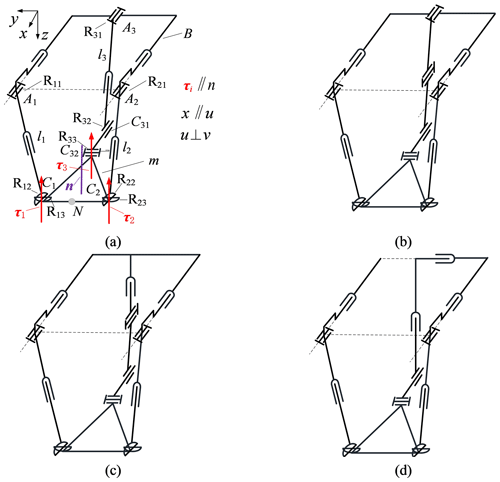
Figure 7Category 51–51–uGuPvR PMs. (a) 2uPuRPuRvR–uRPuRuPvR. (b) 2uPuRPuRvR–uRuRuRuPvR. (c) 2uPuRPuRvR–zPuRuRuPvR. (d) 2uPuRPuRvR–yPzPuRuPvR.
According to the constrained force and/or torque judgment rules (a) and (b), in Fig. 7, a constrained torque τi is perpendicular to Rij (j=1, 2, 3) in branched chain li (i=1, 2, 3). Because of R11 ∥ R21 ∥ R31∥x, the direction vectors of constrained torques τ1, τ2, and τ3 are parallel, and the branch chains l1, l2, and l3 impose identical constraints on the moving platform. Similarly, the other configurations in Fig. 7 have such constraint relationships.
According to Sect. 2, the 5-D displacement sub-group {G(v)}{G(u)} can be obtained by combing {G(v)}, {G(u)}, and v⊥u. In this section, a PM of type {G(v)}{G(u)} can be obtained by combining planar pair G(v), planar pair G(u), and the unconstrained branched chain. From Table 2, it can be seen that the G(u) has seven configurations so there are 49 kinds of {G(v)}{G(u)} constraint branched chains, as shown in Table 4. Figure 3 in Sect. 3.1 shows 10 types of double unrestrained branched chains (6–6). Therefore, the PMs composed of {G(v)}{G(u)} branched chains and unconstrained branched chains (6–6) have a total of 49 × 10 = 490 kinds. Figure 8 shows part of the mechanism schematic diagram of category 63–63–vRPvRuG.
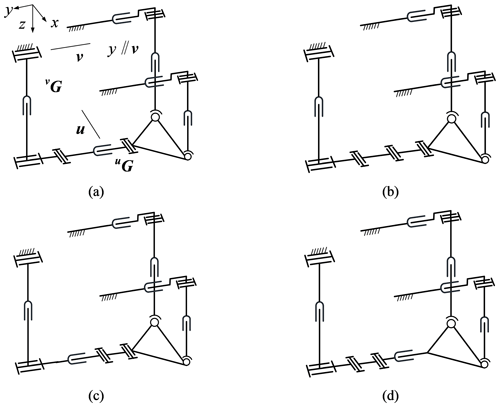
Figure 8Category 63–63–vRPvRuG PMs. (a) 2yPvRPS–vRPvRuRPuR. (b) 2yPvRPS–vRPvRuRuRuR. (c) 2yPvRPS–vRPvRvPuRuR. (d) 2yPvRPS–vRPvRuRuRP.
Combined with the previous content, a total of 868 new types are synthesized in this paper, of which there are 378 PMs of {X(u)}{R(N,u)} class (70 PMs with single-constraint branched chains, 112 PMs with double-constraint branched chains, and 196 PMs with multi-constraint branched chains) and 490 PMs of {G(v)}{G(u)} class, enriching the types of 2R3T PMs.
In order to verify the correctness of the type synthesis method, this section adopts the modified Kutzbach–Grübler equation to calculate the number of DOF and uses the screw theory to verify the property of DOF. Taking 2uPuRPuRvR–uRPuRuPvR as an example in Fig. 6a, point A3 is selected as the origin of the static coordinate system, and the screw system of branched chains l1 and l2 is
Based on the screw theory, the constraint wrench of branched chains 1 and 2 can be expressed as
The twist system of branched chain uRPuRxPvR is
The constraint wrench of branched chain uRPuRxPvR can be expressed as
From Eqs. (13) and (15), the overall restraint wrench of the 2xPuRPuRvR–uRPuRxPvR PM can be expressed as
where $ represents the constrained torque perpendicular to the plane of the two rotational pairs uR and vR. Therefore, the constraint torques of the three branched chains are parallel to each other, forming a common constraint. There is only one constraint torque in the 2uPuRPuRvR–uRPuRuPvR PM, and the mechanism can generate 2R3T motion.
The number of DOF of the 2xPuRPuRvR–uRPuRxPvR is calculated using the Kutzbach–Grübler equation:
where M is the number of DOF of the mechanism, v is the total number of overconstrained PMs, g is the number of joints, n represents the number of rigid bodies in the PM, fi represents the DOF number of the ith joint, and η is the number of redundancy DOF. For the 2xPuPuRvR/uRPuRxPvR PM, the number of DOF is
In practical engineering applications, it is vital to consider the feasibility of fabrication and assembly and the requirements of the task's degrees of freedom. The PMs with two constraint branched chains shown in Fig. 5 have three advantages:
-
The PMs have fewer joints (16 kinematic joints), which reduces errors due to joint gaps.
-
Fewer kinematic joints reduce the manufacturing costs and assembly difficulties of the PMs, which is more convenient for manufacturing and practical application.
-
The double-drive PMs contain two double-drive branch chains (i.e., there are two drivers on one branch chain), and this type of PM reduces the number of branch chains while maintaining the DOF, resulting in a high degree of dexterity.
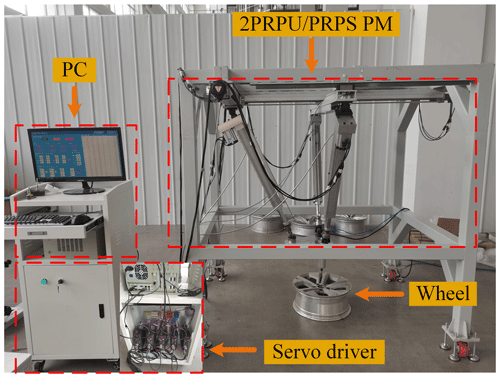
Based on the 2uPuRPuRvR–yPyRPS shown in Fig. 5, we established its 3-D model and physical prototype, as shown in Figs. 9 and 10. Motion experiments were conducted on the prototype to demonstrate the feasibility of the PMs with double-constraint branched chains; as shown in Fig. 11, the end effector moves to eight points on the upper end of the hub in sequence. Through this experiment, we demonstrated the feasibility of the 2uPuRPuRvR–yPyRPS PM prototype and validated its workspace's effectiveness. It provides an essential foundation for further research.
In order to obtain 5-DOF PMs with fewer joints, a three-branch 2R3T PM type synthesis method is proposed, and the validity of the method is verified with a new 2R3T PM with three branched chains, as an example.
-
The displacement sub-groups {X(u)}{R(N,u)} and {G(u)}{G(v)} of the constraint branch of the 2R3T PMs are derived in detail, and the motion diagrams of the corresponding displacement sub-groups are presented, providing an intuitive and concise representation method for chain kinematic bonds in the configuration synthesis process.
-
The PMs synthesized in this paper can be categorized into three types: non-overconstrained PMs, overconstrained PMs with two constrained branched chains, and overconstrained PMs with three constrained branched chains. The analysis shows that the constraints of the three types of PMs are the same. Specifically, the direction of constrained torque is mutually perpendicular to all revolute joints in the constrained branched chains.
-
A class of three branched-chain 2R3T PMs with the fewest kinematic joints (15 kinematic joints) is synthesized based on the type synthesis method proposed in this paper. The number and property of the DOF of the typical PM are verified using the screw theory and the modified Kutzbach–Grübler equation.
-
Future research will focus on the stiffness analysis, dynamics analysis, and control algorithms of the 2uPuRPuRvR–yPyRPS mechanism prototype, aiming to enable the 2uPuRPuRvR–yPyRPS mechanism prototype to be applied in actual production tasks.
The data that support the findings of this study are available from the corresponding author upon reasonable request.
YR and XZ conceptualized the study, wrote the original draft of the paper, and reviewed and edited the paper. TD and HW assisted with the theory. All the authors read and approved the final paper.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We would like to thank the Hebei Natural Science Foundation (grant no. E2021203018) for the financial support.
This research has been supported by the Natural Science Foundation of Hebei Province (grant no. E2021203018).
This paper was edited by Haiyang Li and reviewed by three anonymous referees.
Chen, M., Zhang, Q., Qin, X., and Sun, Y.: Kinematic, dynamic, and performance analysis of a new 3-DOF over-constrained parallel mechanism without parasitic motion, Mech. Mach. Theory, 162, 104365, https://doi.org/10.1016/j.mechmachtheory.2021.104365, 2021.
Du, X., Wang, B., and Zheng, J.: Geometric Error Analysis of a 2UPR-RPU Over-Constrained Parallel Manipulator, Machines, 10, 990, https://doi.org/10.3390/machines10110990, 2022.
Gogu, G.: Structural synthesis of maximally regular T3R2-type parallel robots via theory of linear transformations and evolutionary morphology, Robotica, 27, 79–101, https://doi.org/10.1017/S0263574708004542, 2009.
Hervé, J. M.: Analyse structurelle des mécanismes par groupe des déplacements, Mech. Mach. Theory, 13, 437–450, https://doi.org/10.1016/0094-114X(78)90017-4, 1978.
Hervé, J. M.: The Lie group of rigid body displacements, a fundamental tool for mechanism design, Mech. Mach. Theory, 34, 719–730, https://doi.org/10.1016/S0094-114X(98)00051-2, 1999.
Huang, Y. G., Du, L., Chen, Y. H., and Feng, J.: Type Synthesis of Symmertrical Non-overconstrained 3-DOF Translational Parallel Manipulators Based on Srew Theory, Adv. Mat. Res., 2135–2138, https://doi.org/10.4028/www.scientific.net/AMR.308-310.2135, 2011.
Ibrahim, K., Ramadan, A., Fanni, M., Kobayashi, Y., Abo-Ismail, A., and Fujie, M. G.: Development of a new 4-DOF endoscopic parallel manipulator based on screw theory for laparoscopic surgery, Mechatronics, 28, 4–17, https://doi.org/10.1016/j.mechatronics.2015.02.006, 2015.
Jin, Q. and Yang, T. L.: Theory for topology synthesis of parallel manipulators and its application to three-dimension-translation parallel manipulators, J. Mech. Des., 126, 625–639, https://doi.org/10.1115/1.1758253, 2004.
Kuo, C.-H., Dai, J. S., and Legnani, G.: A non-overconstrained variant of the Agile Eye with a special decoupled kinematics, Robotica, 32, 889–905, https://doi.org/10.1017/S0263574713001100, 2014.
Li, L., Fang, Y., Yao, J., and Wang, L.: Type synthesis of a family of novel parallel leg mechanisms driven by a 3-DOF drive system, Mech. Mach. Theory, 167, 104572, https://doi.org/10.1016/j.mechmachtheory.2021.104572, 2022.
Li, Q., Huang, Z., and Hervé, J. M.: Type synthesis of 3R2T 5-DOF parallel mechanisms using the Lie group of displacements, IEEE T. Robot. Autom., 20, 173–180, https://doi.org/10.1109/TRA.2004.824650, 2004.
Li, Q., Xu, L., Chen, Q., and Ye, W.: New family of RPR-equivalent parallel mechanisms: Design and application, Chin. J. Mech. Eng. 30, 217–221, https://doi.org/10.1007/s10033-017-0045-0, 2017.
Li, S., Zhou, Y., Shan, Y., Chen, S., and Han, J.: Synthesis method of two translational compliant mechanisms with redundant actuation, Mech. Sci., 12, 983–995, https://doi.org/10.5194/ms-12-983-2021, 2021.
Li, X., Zhang, Q., Zhang, Z., Yang, X., Wu, H., Li, Y., and Qu, H.: Type Synthesis Based on Modular Combination with Virtual Rotation Center and Application, Int. J. Rotating Mach., 2022, 5216327, https://doi.org/10.1155/2022/5216327, 2022.
Li, Y. B., Zheng, P., Sun, P., Xu, T. T., Wang, Z. S., and Qin, S. Y.: Dynamic modeling with joint friction and research on the inertia coupling property of a 5-PSS/UPU parallel manipulator, J. Mech. Eng.-En., 55, 43–52, https://doi.org/10.3901/JME.2019.03.043, 2019.
Li, Z., Lou, Y., and Li, Z.: Type synthesis and kinematic analysis of a new class Schönflies motion parallel manipulator, in: 2011 IEEE International Conference on Information and Automation, Shenzhen, China, 6–8 June 2011, IEEE, 267–272, https://doi.org/10.1109/ICINFA.2011.5949000, 2011.
Lin, R., Guo, W., and Cheng, S. S.: Type synthesis of 2R1T remote center of motion parallel mechanisms with a passive limb for minimally invasive surgical robot, Mech. Mach. Theory, 172, 104766, https://doi.org/10.1016/j.mechmachtheory.2022.104766, 2022.
Lu, Y. and Ye, N.: Type synthesis of parallel mechanisms by utilizing sub-mechanisms and digital topological graphs, Mech. Mach. Theory, 109, 39–50, https://doi.org/10.1016/j.mechmachtheory.2016.11.008, 2017.
Luo, X., Xie, F. G., Liu, X. J., and Xie, Z. H.: Kinematic calibration of a 5-axis parallel machining robot based on dimensionless error mapping matrix, Robot. Cim.-Int. Manuf., 70, 102115, https://doi.org/10.1016/j.rcim.2021.102115, 2021.
Meng, J., Liu, G., and Li, Z.: A geometric theory for analysis and synthesis of sub-6 DoF parallel manipulators, IEEE T. Robot., 23, 625–649, https://doi.org/10.1109/TRO.2007.898995, 2007.
Niu, B., Yang, D., Wang, P., Yang, H., Zhang, L., Gu, Y., and Jiang, L.: Virtual‐force‐guided intraoperative ultra-sound scanning with online lesion location prediction: A phantom study, Int. J. Med. Robot, 19, e2491, https://doi.org/10.1002/rcs.2491, 2023.
Rong, Y., Liu, S. Y., Wang, H. B., and Han, Y.: Dynamics modeling and drive parameter prediction of a 5-DOF wheel grinding manipulator arm, Chin. J. Mech. Eng.-En., 29, 449–456, http://www.cmemo.org.cn/CN/Y2018/V29/I04/449 (last access: 16 December 2023), 2018.
Sun, T., Lian, B., Zhang, J., and Song, Y.: Kinematic calibration of a 2-DoF over-constrained parallel mechanism using real inverse kinematics, IEEE Access, 6, 67752–67761, https://doi.org/10.1109/ACCESS.2018.2878976, 2018.
Wang, L., Tian, J., Du, J., Zheng, S., Niu, J., Zhang, Z., and Wu, J.: A Hybrid Mechanism-Based Robot for End-Traction Lower Branched chain Rehabilitation: Design, Analysis and Experimental Evaluation, Machines, 10, 99, https://doi.org/10.3390/machines10020099, 2022.
Wang, S., Li, S., Li, H., Zhou, Y., Wang, Y., and Wang, X.: Type synthesis of 3T2R decoupled hybrid mechanisms with large bearing capacity, J. Mech. Sci. Technol., 36, 2053–2067, https://doi.org/10.1007/s12206-022-0340-2, 2022.
Wei, J. and Dai, J. S.: Reconfiguration-aimed and manifold-operation based type synthesis of metamorphic parallel mechanisms with motion between 1R2T and 2R1T, Mech. Mach. Theory, 139, 66–80, https://doi.org/10.1016/j.mechmachtheory.2019.04.001, 2019.
Yang, S. F., Sun, T., Huang T., Li, Q. C., and Gu, D. B.: A finite screw approach to type synthesis of three-DOF translational parallel mechanisms, Mech. Mach. Theory, 104, 405–419, https://doi.org/10.1016/j.mechmachtheory.2016.02.018, 2016.
Ye, N. and Hu, B.: Kinematic and Stiffness Modeling of a Novel 3-DOF RPU+UPU+SPU Parallel Manipulator, IEEE Access, 10, 6304–6318, https://doi.org/10.1109/ACCESS.2021.3139089, 2021.
Ye, W., Li, Q., and Chai, X.: Type Synthesis of 4-DOF Non-Overconstrained Parallel Mechanisms with Symmetrical Structures, Machines, 10, 1123, https://doi.org/10.3390/machines10121123, 2022.
Zhang, J., Jin, Z., and Feng, H.: Type synthesis of a 3-mixed-DOF protectable leg mechanism of a firefighting multi-legged robot based on GF set theory, Mech. Mach. Theory, 130, 567–584, https://doi.org/10.1016/j.mechmachtheory.2018.08.026, 2018.
Zhou, Y., Li, S., Sun, J., and Yi, L.: Type synthesis approach for the 2R1T compliant parallel mechanism with a suitable constrained branch, Mech. Sci., 13, 67–78, https://doi.org/10.5194/ms-13-67-2022, 2022.
- Abstract
- Introduction
- A synthesis method of 2R3T PMs
- Type synthesis of 2R3T PMs with {X(u)}{R(N,u)}
- Type synthesis of 2R3T PMs with {G(u)}{G(v)}
- Case analysis
- Engineering applications
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- A synthesis method of 2R3T PMs
- Type synthesis of 2R3T PMs with {X(u)}{R(N,u)}
- Type synthesis of 2R3T PMs with {G(u)}{G(v)}
- Case analysis
- Engineering applications
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References