Type synthesis of non-overconstrained and overconstrained two rotation and three translation (2R3T) parallel mechanisms with three branched chains

In this paper, a new synthesis method of 2R3T (R denotes rotation and T denotes translation) overconstrained and non-overconstrained parallel mechanisms (PMs) with three branched chains based on the displacement sub-manifold method is presented. Firstly, the displacement sub-manifolds of mechanisms were determined based on 2R3T motions. Subsequently, the displacement sub-manifolds of the branched chains were derived using the displacement sub-manifold theory, and their corresponding motion diagrams were provided. Additionally, a comprehensive analysis of non-overconstrained 2R3T PMs with a single-constraint branched chain was conducted, and the type synthesis of overconstrained 2R3T PMs with two or three identical constraints was also performed, accompanied by the presentation of partial mechanism diagrams. Finally, the number of DOF (degrees of freedom) of the mechanism was calculated using the modified Kutzbach–Grübler equation for a new PMs,and the screw theory was used to verify the kinematic characteristics, proving this new method's correctness.

1 Introduction

The parallel mechanisms (PMs) have the advantages of high rigidity, high bearing capacity, and small cumulative error and are widely used in aerospace, machining, medical rehabilitation, bionics, and other fields (Li et al., 2021; Zhou et al., 2022; L. Wang et al., 2022; Niu et al., 2023). According to the constraints of branched chains in relation to the moving platform, PMs can be divided into overconstrained and non-overconstrained PMs. The overconstrained PMs have two or more identical constraints, such as redundant constraints that can improve the stiffness of the mechanism, which has attracted extensive research by scholars on overconstrained PMs in recent years. Chen et al. (2021) proposed a new overconstrained PM without parasitic motion, clarified the reasons for the non-parasitic motion characteristics of the mechanism, and studied its kinematics and dynamics. Ibrahim et al. (2015) designed a 4-DOF, endoscopic, dexterous PM for minimally invasive surgery, deduced the mechanism's forward and inverse kinematic solutions, and studied the singularity using the screw theory (Sun et al., 2018). As an example, a 2-DOF overconstrained PM was applied to an assembly line, and the kinematic calibration problem of an overconstrained PM was studied. Du et al. (2022) established the geometric error model of the 2UPR–RPU (where U, P, R, C, and S represent universal, prismatic, revolute, cylindrical, and spherical joints, respectively) overconstrained PM and performed a sensitivity analysis on the error source.

Although the overconstrained PMs have excellent stiffness and load-carrying capacity, they are often required to meet special geometric conditions and are very sensitive to part-manufacturing and assembly errors. If these conditions cannot be met, the mechanism will not only be challenged to ensure motion accuracy but will also be unable to maintain the designed motion characteristics. Therefore, it is equally important to study non-overconstrained PMs. Huang et al. (2011) proposed a systematic synthesis method of symmetric non-overconstrained 3-DOF translational PMs using the screw theory. Ye et al. (2022) presented a type synthesis method of 4-DOF non-overconstrained parallel mechanisms (PMs) with symmetrical structures using screw theory. Ye and Hu (2021) proposed a novel 3-DOF RPU+UPU+SPU PM, and its complete kinematics and stiffness are studied. Kuo et al. (2014) proposed a non-overconstrained 3-DOF parallel-positioning mechanism. The inverse and forward kinematic solutions of the mechanism are provided.

Type synthesis is the essential factor that determines the function and performance of mechanical equipment, and it is also the first step in the exploration of the development of new processing equipment and is worthy of in-depth study. Type synthesis seeks the specific topology structure of the mechanism under the constraint of the number and characteristics of the desired DOF, and its core is to describe mechanism motion patterns. Therefore, based on the different description methods, the existing type synthesis methods can be divided into two categories: instantaneous motion-based methods and finite motion-based methods. Among them, the instantaneous motion-based methods include the constrained screw synthesis method (S. Wang et al., 2022; X. Li et al.,  2022), the map method (Lu and Ye, 2017), and the differential geometry synthesis method (Meng et al., 2007; Li et al., 2011). These methods can only describe the motion of mechanisms in instantaneous states and cannot express the motion characteristics of mechanisms in continuous motion processes. The finite motion-based methods include the displacement sub-group and/or sub-manifold synthesis method (Hervé, 1999), the GF (generalized function) synthesis method (Zhang et al., 2018), the linear transformation method (Gogu, 2009), the POC (position and orientation characteristic) set method (Jin and Yang, 2004), and the finite screw method (Yang et al., 2016). These methods can describe the continuous motion of mechanisms, avoiding the synthesis result being an instantaneous mechanism, and do not require checks regarding full-cycle mobility.

In 1978, Hervé (1978) introduced Lie group theory into mechanism analysis, laying the theoretical foundation for using Lie group theory to analyze the DOF of mechanisms. In 2004, Li et al. (2004) systematically expounded the method's general theory and process. Based on this theory, Li et al. (2017) studied the equivalent mechanism of 3-DOF RPR branched-chain motion. L. Li et al. (2022) synthesized a 3-DOF parallel mechanical branch with double branches. Wei and Dai (2019) studied a reconfigurable parallel mechanism and the configuration transformation problem. Note that, among the numerous studies on type synthesis, there are relatively few works that are focused on 2R3T PMs. Most of the existing 2R3T PMs are composed of a single constrained branched chain and multiple unconstrained branched chains, and there are many joints in 2R3T PMs, such as the 2UPS+UPU PM (Rong et al., 2018), the 5PSS+UPU PM (Li et al., 2019), and the 4UCU+UCR PM (Luo et al., 2021). The joint is the weak part of the mechanism, which is the main reason for the deformation and clearance of the mechanism; thus, a mechanism with a small number of joints theoretically has better accuracy and stiffness. Therefore, an effective way to reduce the number of joints and to improve the accuracy and stiffness of the mechanism is to replace unconstrained branch chains with constrained branched chains and make the mechanisms become overconstrained PMs. Unfortunately, there are few reports on the configuration of overconstrained 2R3T PMs.

This paper studies various combinations of constrained branched chains and proposes a type synthesis method for non-overconstrained and overconstrained 2R3T PMs. The rest of this article is organized as follows. In Sect. 2, based on the displacement sub-manifold method, the synthesis steps of 2R3T PMs are proposed, as are branched-chain bonds {X(u)}{R(N,u)} and {G(v)}{G(u)}. Type synthesis of non-overconstrained and overconstrained 2R3T PMs with a branched chain of {X(u)}{R(N,u)} has been conducted in Sect. 3. Type synthesis of non-overconstrained 2R3T PMs with a branched chain of {G(v)}{G(u)} has been conducted in Sect. 4. In Sect. 5, a representative configuration is selected for DOF analysis to verify the correctness of the new configuration. Section 6 discusses an optimal type for practical application, and a physical prototype is given.

2 A synthesis method of 2R3T PMs

In 1978, Hervé (1978) enumerated all 12 kinds of displacement sub-groups, as shown in Table 1. It also can be readily proven that the displacement sub-manifold {M_e} of the end effector is the intersection of the sub-groups or sub-manifolds {M_Li} produced by all branched chains, both of which must satisfy the following equation (Lin et al., 2022):

$$\begin{array}{}\text{(1)}& \left\{M_{\mathrm{e}}\right\}=\sum _{i=\mathrm{1}}^n\left\{M_{\mathrm{Li}}\right\},i=\mathrm{1},\mathrm{\dots },n,\end{array}$$

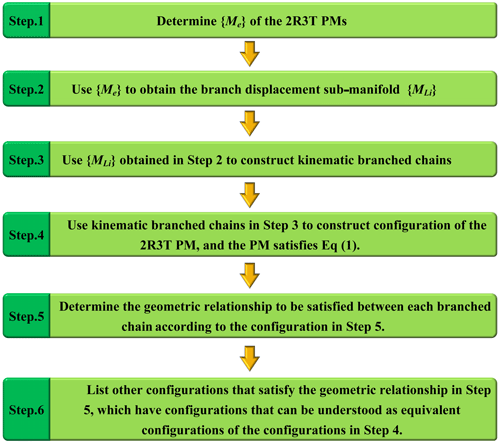
where {M_Li} is the product of the kinematic joint displacement sub-manifold that makes up the branched chain i, and the displacement sub-manifold synthesis method for the 2R3T PMs in this paper is summarized in the following six steps, see Fig. 1.

Table 1 Displacement sub-groups.

Figure 1 Synthesis flow chart of a 2R3T PM based on the displacement sub-manifold method.

According to the representation method of the displacement sub-manifold, the displacement sub-manifold of rigid-body motion with a 2R3T property is

$$\begin{array}{}\text{(2)}& \left\{\mathrm{T}\right\}\left\{\mathrm{R}\left(N,\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\},\left\{\mathrm{T}\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{u}\right)\right\}.\end{array}$$

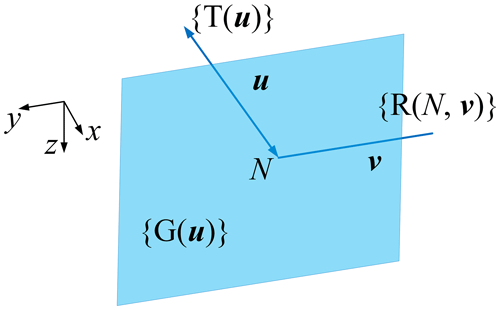
In Eq. (2), there are two cases where the first displacement sub-group of {T} is {T(x)}, {T(x)}{T(y)}{T(z)}, and {T(x)}{T(z)}{T(y)}. If x∥u and u⊥v (∥ and ⊥ represent the parallel and vertical geometric relationship, respectively), then $\mathit{\left\{}\mathrm{T}\right(\mathit{z}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{T}\right(\mathit{y}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N,\mathit{u}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{G}\right(\mathit{u}\left)\mathit{\right\}}$, and combined with Table 1's {X(u)}​​​​​​​, we can get

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& \left\{\mathrm{T}\left(\mathit{x}\right)\right\}\left\{\mathrm{T}\left(\mathit{z}\right)\right\}\left\{\mathrm{T}\left(\mathit{y}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\\ & =\left\{\mathrm{T}\left(\mathit{x}\right)\right\}\left\{\mathrm{G}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}.\end{array}\end{array}$$

Figure 2 shows the motion diagram of the displacement sub-manifold {X(u)}{R(N,u)} corresponding to the kinematic branch ^uP^uG^vR (G represents planar pair, and the superscripts represent the axis direction of the prismatic or revolute joint), in which the line with double arrows indicates translational, the planar area indicates plane motion, and the straight line indicates rotational.

Figure 2 Motion diagram of {X(u)}{R(N,u)}.

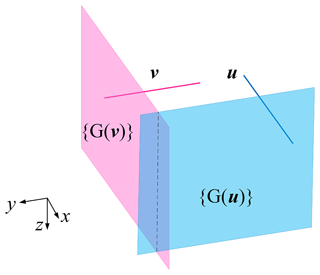
The 3-D displacement sub-group G(u) represents the two translationals in a plane and the rotational about the plane normal. Table 2 lists the branched chains constituting the plane pair and the corresponding displacement sub-group.

Table 2 Generators of {G(u)}.

From Table 2, we can get the displacement sub-manifolds $\mathit{\left\{}\mathrm{X}\right(u\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N,\mathit{v}\left)\mathit{\right\}}\left(\mathit{\right\{}\mathrm{T}\left(\mathit{x}\right)\mathit{\left\}}\mathrm{G}\right(\mathit{u}\left)\mathit{\right\{}\mathrm{R}(N,\mathit{v})\mathit{\left\}}\right)$ and the corresponding branched chains ^xP^uR^zP^uR^vR, ^xP^uR^uR^uR^vR, ^xP^zP^uR^uR^vR, ^xP^uR^uR^zP^vR, ^xP^zP^uR^yP^vR, ^xP^uR^zP^yP^vR, and ^xP^zP^yP^uR^vR.

Based on the displacement sub-manifold method, the $\mathit{\left\{}\mathrm{T}\right(\mathit{x}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{T}\right(\mathit{z}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{T}\right(\mathit{y}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N,\mathit{v}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N,\mathit{u}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N_{\mathrm{1}},\mathit{u}\left)\mathit{\right\}}$ corresponding rigid-body motion is also 2R3T. According to the product closure of the displacement sub-manifold, there will be $\mathit{\left\{}\mathrm{C}\right(N,\mathit{u}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{T}\right(\mathit{y}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N,\mathit{u}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{R}\right(N,\mathit{u}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{T}\right(\mathit{y}\left)\mathit{\right\}}$, which can get

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& \left\{\mathrm{T}\left(\mathit{x}\right)\right\}\left\{\mathrm{T}\left(\mathit{z}\right)\right\}\left\{\mathrm{T}\left(\mathit{y}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{u}\right)\right\}\\ & =\left\{\mathrm{T}\left(\mathit{x}\right)\right\}\left\{\mathrm{T}\left(\mathit{z}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\left\{\mathrm{T}\left(\mathit{y}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N_{\mathrm{1}},\mathit{u}\right)\right\}\\ & =\left\{\mathrm{G}\left(\mathit{v}\right)\right\}\left\{\mathrm{G}\left(\mathit{u}\right)\right\},\end{array}\end{array}$$

where {G(v)}{G(u)} is the displacement sub-manifold of the ^vG^uG, and Fig. 3 is a schematic diagram of the displacement sub-manifold {G(v)}{G(u)}. It can be seen from Table 2 that the number of {G(u)} is 7 so the number of {G(v)}{G(u)} is 7 × 7 = 49.

Figure 3 Motion diagram of {G(v)}{G(u)}.

From the above analysis, we can see that there are two types of {X(u)}{R(N,u)} and {G(v)}{G(u)} in the {M_Li} of 2R3T PMs.

3 Type synthesis of 2R3T PMs with {X(u)}{R(N,u)}

3.1 Type synthesis of non-overconstrained 2R3T PMs

For conciseness, this paper defines the UPS, URS, PRPS, and PRRS branched chains as 6_i (i=1, 2, 3, 4) and defines ^xP^uR^zP^uR^vR, ^xP^uR^uR^uR^vR, ^xP^zP^uR^uR^vR, ^xP^uR^uR^zP^vR, ^xP^zP^uR^yP^vR, ^xP^uR^zP^yP^vR, and ^xP^zP^yP^uR^vR branched chains as 5_j, j=1, 2, …, 7.

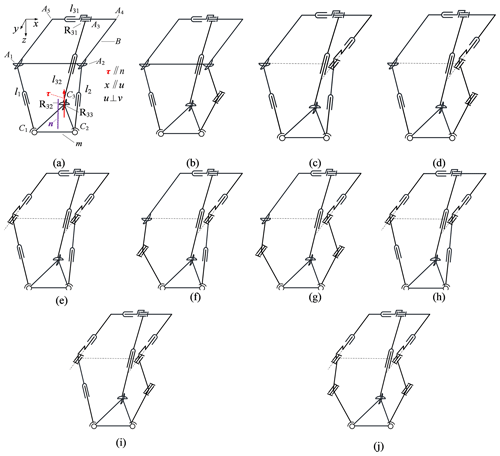
Figure 4 Category 6–6–5₁ PMs. (a) 2UPS–^uP^uRP^uR^vR. (b) UPS–URS–^uP^uRP^uR^vR. (c) UPS–^yP^yRPS–^xP^uRP^uR^vR. (d) UPS–^yP^yR^yRS–^uP^uRP^uR^vR. (e) 2URS–^uP^uRP^uR^vR. (f) URS–^yP^yRPS–^uP^uRP^uR^vR. (g) URS–^yP^yR^yRS–^uP^uRP^uR^vR. (h) 2^yP^yRPS–^uP^uRP^uR^vR. (i) ^yP^yRPS–^yP^yR^yRS–^uP^uRP^uR^vR. (j) 2^yP^yR^yRS–^uP^uR-P^uR^vR.

By combining a single constrained branch chain 5₁ with unconstrained branch chains, 10 configurations can be obtained, as shown in Fig. 4. The 2UPS–PRPU PM in Fig. 4a includes a moving platform (m); a base platform (B); two UPS branched chains (l₁ and l₂); and one PRPU branched chain (l₃), where l₃ is further divided into l₃₁ and l₃₂. Here, m is an isosceles triangle with three vertices C_i (i=1, 2, 3) and the normal of the plane, in which m is located in n. B is a rectangle with four vertices A_i (i=1, 2, 4, 5), and A₃ is the center of the R joint in the branch chain l₃. Considering the fact that there are seven types of single constrained branch chains, combined with Fig. 4, it can be concluded that there are 70 types of category 6–6–5 PMs.

According to the characteristic of the constrained force and/or torque of the branches of the PMs with limited DOF, Ye and Hu (2021) proposed a rule for judging the constrained force and/or torque:

• a.

  In each leg, the constrained forces should be perpendicular to all P joints and coplanar with all R joints.

• b.

  The constrained torques should be perpendicular to all R joints in each leg.

Let R_ij be the jth R joint from B to m in the branched chain l_i. According to rules (a) and (b), it can be seen that, in the constraint branched chain l₃ of the PMs shown in Fig. 4, one constrained torque τ is perpendicular to R₁₂, R₁₂, and R₁₃. It can be seen that the mechanisms synthesized in this section are non-overconstrained PMs.

3.2 Type synthesis of overconstrained 2R3T PMs with two identical constraints

This section selects the unconstrained branched chain 63 and the same constrained branched chains 5_i–5_i as specific types for analysis. The 2PRPU–PRPS PM in Fig. 5a includes a moving platform (m), a base platform (B), two PRPU branched chains (l₁ and l₂), and one PRPS branched chain (l₃). Here, A₁, A₂, and A₃ are the centers of the R joints, C₁ and C₂ are the centers of the U joints, C₃ is the center of the S joint, and m is an isosceles triangle with three vertices C_i (i=1, 2, 3), and the normal of the plane in which m is located is n. N is the midpoint of C₁ and C₂, and R_ij denotes the jth R joint in branched chain l_i. As shown in Fig. 5, the kinematic bond of branched chain l_i in Fig. 5a is

$$\begin{array}{}\text{(5)}& \left\{L_{\mathrm{1}}\right\}=\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(A_{\mathrm{1}},u\right)\right\}\left\{\mathrm{T}\left({\mathit{w}}_{\mathrm{1}}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},u\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{v}\right)\right\},\end{array}$$

where {T(u)} represents the translation along u, {R(A₁,u)} represents the rotation through point A₁, and the axis of rotation is u; u and v represent the related joints' unit direction vector. Vector w_i is collinear with A_iC_i. In Eq. (5), {R(A₁,u)}, {T(w₁)}, and {R(C₁,u)} can form {G(u)} so {L₁} can also be expressed as

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\left\{L_{\mathrm{1}}\right\}& =\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(A_{\mathrm{1}},\mathit{u}\right)\right\}\left\{\mathrm{T}\left({\mathit{w}}_{\mathrm{1}}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{v}\right)\right\}\\ & =\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{G}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{v}\right)\right\}\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{v}\right)\right\}.\end{array}\end{array}$$

Similarly, {L₂} can also be expressed as

$$\begin{array}{}\text{(7)}& \left\{L_{\mathrm{2}}\right\}=\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{2}},\mathit{v}\right)\right\}.\end{array}$$

Because C₁C₂ passes through point N and is parallel to axis v, $\mathit{\left\{}\mathrm{R}\right(C_{\mathrm{1}},\mathit{v}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{R}\right(C_{\mathrm{2}},\mathit{v}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{R}\right(N,\mathit{v}\left)\mathit{\right\}}$. The displacement set of the moving platform is as follows:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{v}\right)\right\}\cap \left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{2}},\mathit{v}\right)\right\}\cap \left\{\mathrm{D}\right\},\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(o,\mathit{v}\right)\right\}\cap \left\{\mathrm{D}\right\},\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(o,\mathit{v}\right)\right\}.\end{array}\end{array}$$

According to Eq. (8), the DOF of 2^uP^uRP^uR^vR–^yP^yRPS PM is 2R3T, and the DOF of the other mechanisms in Fig. 5 is also 2R3T, which is not verified here. At the same time, according to Fig. 5, it can be known that the geometric conditions for realizing two constrained branched chains ^uP^uG^vR to maintain 2R3T are as follows: the normals of the two plane pairs are parallel to each other, and the axes of the revolute pairs are collinear.

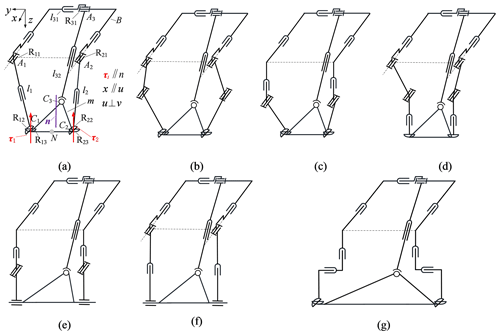
Figure 5 Category 5_i–5_i–6₃ PMs. (a) 2^uP^uRP^uR^vR–^yP^yRPS. (b) 2^uP^uR^uR^uR^vR–^yP^yRPS. (c) 2^uP^zP^uR^uR^vR–^yP^yRPS. (d) 2^uP^uR^uRP^vR–^yP^yRPS. (e) 2^uP^zP^uR^vP^vR–^yP^yRPS. (f) 2^uP^uRP^vP^vR–^yP^yRPS. (g) 2^uP^zP^yP^uR^vR–^yP^yRPS.

Table 3 Category 5_i–5_j–6₁ PMs.

In Sect. 3.1, four kinds of unconstrained branched chains are listed so, in this section, there are 7 × 4 = 28 kinds of PMs with the same configuration of constrained branched chains and 21 × 4 = 84 kinds of PMs with different configurations of constrained branched chains. It can be seen that there are (28 + 84) = 112 kinds of three-branched-chain PMs composed of double-constraint branched chains. Table 3 lists PMs of category 5–5–6₃.

According to the constrained force and/or torque judgment rules (a) and (b), in Fig. 5, there exists a constrained torque τ₁, which is perpendicular to R_1j (j=1, 2, 3) in branched chain l₁, and a constrained torque τ₂, which is perpendicular to R_2j (j=1, 2, 3) in branched chain l₂. Also, because of R₁₁ ∥ R₂₁ ∥ x, the direction vectors of constrained torques τ₁ and τ₂ are parallel to each other, and the branch chains l₁ and l₂ impose identical constraints on the moving platform. Similarly, the other configurations in Fig. 5 have such constraint relationships.

3.3 Type synthesis of overconstrained 2R3T PMs with three identical constraints

The multi-constraint branched-chain {X(u)}{R(N,u)} PMs studied in this subsection are used to replace the unconstrained branched chain in the double-constraint branched-chain mechanism with a constrained branched chain so that all three branched chains are constrained branched chains.

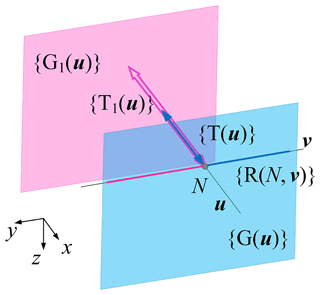
In Sect. 3.2, the kinematic bond of branched chains 1 and 2 is $\mathit{\left\{}\mathrm{X}\right(\mathit{u}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N,\mathit{u}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{T}\right(\mathit{u}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{G}\right(\mathit{u}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{R}\right(N,\mathit{u}\left)\mathit{\right\}}$. According to the definition of {X(u)} in Table 1, there is $\mathit{\left\{}\mathrm{X}\right(\mathit{u}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{T}\right(\mathit{u}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{G}\right(\mathit{u}\left)\mathit{\right\}}=\mathit{\left\{}\mathrm{G}\right(\mathit{u}\left)\mathit{\right\}}\mathit{\left\{}\mathrm{T}\right(\mathit{u}\left)\mathit{\right\}}$. Let the kinematic bond of branched chain 3 be {G(u)}{T(u)}{R(N,v)}. Figure 6 is a schematic diagram of the displacement sub-manifold 2-{X(u)}{R(N,u)}.

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& \left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{G}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\cap \left\{\mathrm{G}\left(\mathit{u}\right)\right\}\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\cap \left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\end{array}\end{array}$$

Equation (9) shows that the motion of the mechanism composed of the kinematic branched chains ^uG^uP^vR and 2^uP^uG^vR is still 2R3T.

Figure 6 Motion diagram of 2-{X(u)}{R(N,u)}.

In Sect. 3.2, it is obtained that the {X(u)}{R(N,u)}-type mechanism has 7 single-constraint branched chains and 28 double-constraint branched chains. Therefore, there are 7 × 28 = 196 kinds of three-constrained PMs. Figure 7 shows part of the mechanism schematic diagram of type 5₁–5₁–^uG^uP^vR. The 2PRPU–RPRPR PM in Fig. 5a includes a moving platform (m), a base platform (B), two PRPU branched chains (l₁ and l₂), and one RPRPR branched chain l₃. Here, A₁, A₂, and A₃ are the centers of the R joints, C₁ and C₂ are the centers of the U joints, C₃₁ and C₃₂ are the centers of the R joints in branched chain l₃, and m is an isosceles triangle with three vertices (C₁, C₂, and C₃₂), and the normal of the plane in which m is located is n. N is the midpoint of C₁ and C₂, and R_ij denotes the jth R joint in branched chain l_i. In Fig. 7a, the kinematic bond of branched chain 3 can be written as

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& \left\{\mathrm{R}\left(A_{\mathrm{3}},\mathit{u}\right)\right\}\left\{\mathrm{T}\left({\mathit{w}}_i\right)\right\}\left\{C\left(D_{\mathrm{3}},\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{v}\right)\right\}\\ & =\left\{\mathrm{R}\left(A_{\mathrm{3}},\mathit{u}\right)\right\}\left\{\mathrm{T}\left({\mathit{w}}_i\right)\right\}\left\{\mathrm{R}\left(D_{\mathrm{3}},\mathit{u}\right)\right\}\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{1}},\mathit{v}\right)\right\}\\ & =\left\{\mathrm{G}\left(\mathit{u}\right)\right\}\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{3}},\mathit{v}\right)\right\},\end{array}\end{array}$$

where w_i is the unit vector of branched chain i; combined with Eqs. (6) and (7), this can get

$$\begin{array}{}\text{(11)}& \begin{array}{rl}& \left\{L_{\mathrm{1}}\right\}\cap \left\{L_{\mathrm{2}}\right\}\cap \left\{L_{\mathrm{3}}\right\}\\ & =\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{G}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\cap \left\{\mathrm{G}\left(\mathit{u}\right)\right\}\left\{\mathrm{T}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{3}},\mathit{v}\right)\right\}\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}\cap \left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(C_{\mathrm{3}},\mathit{v}\right)\right\}\\ & =\left\{\mathrm{X}\left(\mathit{u}\right)\right\}\left\{\mathrm{R}\left(N,\mathit{v}\right)\right\}.\end{array}\end{array}$$

According to Eq. (11), the property of the DOF of the mechanism 2^uP^uRP^uR^vR–^uRP^uR^uP^vR is 2R3T. We can also verify other PMs in Fig. 6, which will not be repeated here.

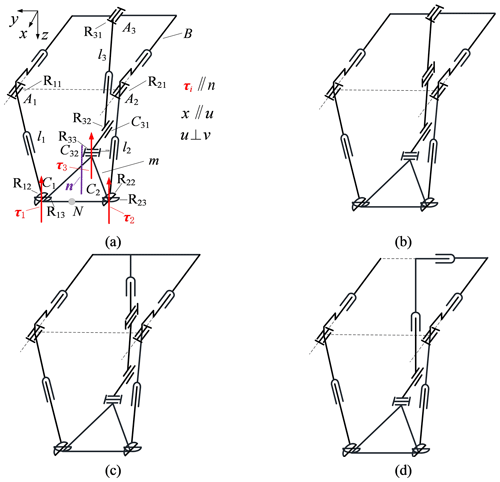
Figure 7 Category 5₁–5₁–^uG^uP^vR PMs. (a) 2^uP^uRP^uR^vR–^uRP^uR^uP^vR. (b) 2^uP^uRP^uR^vR–^uR^uR^uR^uP^vR. (c) 2^uP^uRP^uR^vR–^zP^uR^uR^uP^vR. (d) 2^uP^uRP^uR^vR–^yP^zP^uR^uP^vR.

According to the constrained force and/or torque judgment rules (a) and (b), in Fig. 7, a constrained torque τ_i is perpendicular to R_ij (j=1, 2, 3) in branched chain l_i (i=1, 2, 3). Because of R₁₁ ∥ R₂₁ ∥ R₃₁∥x, the direction vectors of constrained torques τ₁, τ₂, and τ₃ are parallel, and the branch chains l₁, l₂, and l₃ impose identical constraints on the moving platform. Similarly, the other configurations in Fig. 7 have such constraint relationships.

4 Type synthesis of 2R3T PMs with {G(u)}{G(v)}

According to Sect. 2, the 5-D displacement sub-group {G(v)}{G(u)} can be obtained by combing {G(v)}, {G(u)}, and v⊥u. In this section, a PM of type {G(v)}{G(u)} can be obtained by combining planar pair G(v), planar pair G(u), and the unconstrained branched chain. From Table 2, it can be seen that the G(u) has seven configurations so there are 49 kinds of {G(v)}{G(u)} constraint branched chains, as shown in Table 4. Figure 3 in Sect. 3.1 shows 10 types of double unrestrained branched chains (6–6). Therefore, the PMs composed of {G(v)}{G(u)} branched chains and unconstrained branched chains (6–6) have a total of 49 × 10 = 490 kinds. Figure 8 shows part of the mechanism schematic diagram of category 6₃–6₃–^vRP^vR^uG.

Table 4 Category G_k–G_j constraint branched chain.

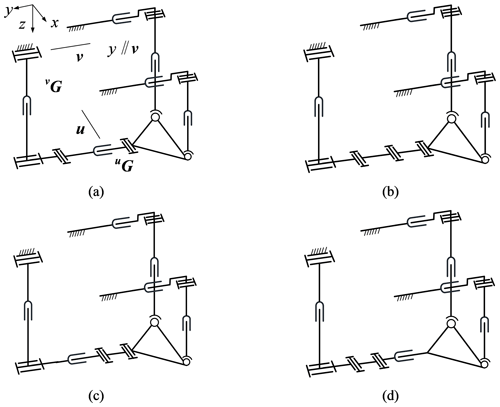
Figure 8 Category 6₃–6₃–^vRP^vR^uG PMs. (a) 2^yP^vRPS–^vRP^vR^uRP^uR. (b) 2^yP^vRPS–^vRP^vR^uR^uR^uR. (c) 2^yP^vRPS–^vRP^vR^vP^uR^uR. (d) 2^yP^vRPS–^vRP^vR^uR^uRP.​​​​​​​

Combined with the previous content, a total of 868 new types are synthesized in this paper, of which there are 378 PMs of {X(u)}{R(N,u)} class (70 PMs with single-constraint branched chains, 112 PMs with double-constraint branched chains, and 196 PMs with multi-constraint branched chains) and 490 PMs of {G(v)}{G(u)} class, enriching the types of 2R3T PMs.

5 Case analysis

In order to verify the correctness of the type synthesis method, this section adopts the modified Kutzbach–Grübler equation to calculate the number of DOF and uses the screw theory to verify the property of DOF. Taking 2^uP^uRP^uR^vR–^uRP^uR^uP^vR as an example in Fig. 6a, point A₃ is selected as the origin of the static coordinate system, and the screw system of branched chains l₁ and l₂ is

$$\begin{array}{}\text{(12)}& \begin{array}{rl}& {\mathit{\$}}_{i\mathrm{1}}=\left(\mathrm{0},\mathrm{0},\mathrm{0};\mathrm{1},\mathrm{0},\mathrm{0}\right),\\ & {\mathit{\$}}_{i\mathrm{2}}=\left(\mathrm{1},\mathrm{0},\mathrm{0};\mathrm{0},\mathrm{0},\mathrm{0}\right),\\ & {\mathit{\$}}_{i\mathrm{3}}=\left(\mathrm{0},\mathrm{0},\mathrm{0};l_{i\mathrm{3}},m_{i\mathrm{3}},n_{i\mathrm{3}}\right),\\ & {\mathit{\$}}_{i\mathrm{4}}=\left(\mathrm{1},\mathrm{0},\mathrm{0};\mathrm{0},q_{i\mathrm{4}},r_{i\mathrm{4}}\right),\\ & {\mathit{\$}}_{i\mathrm{5}}=\left(\mathrm{0},m_{i\mathrm{5}},n_{i\mathrm{5}};p_{i\mathrm{5}},q_{i\mathrm{5}},r_{i\mathrm{5}}\right).\end{array}\end{array}$$

Based on the screw theory, the constraint wrench of branched chains 1 and 2 can be expressed as

$$\begin{array}{}\text{(13)}& {\mathit{\$}}_i^{\mathrm{r}}=\left(\mathrm{0},\mathrm{0},\mathrm{0};\mathrm{0},-n_{i\mathrm{5}},m_{i\mathrm{5}}\right).\end{array}$$

The twist system of branched chain ^uRP^uR^xP^vR is

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{31}}=\left(\mathrm{1},\mathrm{0},\mathrm{0};\mathrm{0},\mathrm{0},\mathrm{0}\right),\\ & {\mathit{\$}}_{\mathrm{32}}=\left(\mathrm{0},\mathrm{0},\mathrm{0};\mathrm{0},m_{\mathrm{32}},n_{\mathrm{32}}\right),\\ & {\mathit{\$}}_{\mathrm{33}}=\left(\mathrm{1},\mathrm{0},\mathrm{0};\mathrm{0},q_{\mathrm{33}},r_{\mathrm{33}}\right),\\ & {\mathit{\$}}_{\mathrm{34}}=\left(\mathrm{0},\mathrm{0},\mathrm{0};\mathrm{1},\mathrm{0},\mathrm{0}\right),\\ & {\mathit{\$}}_{\mathrm{35}}=\left(\mathrm{0},m_{\mathrm{35}},n_{\mathrm{35}};p_{\mathrm{35}},q_{\mathrm{35}},r_{\mathrm{35}}\right).\end{array}\end{array}$$

The constraint wrench of branched chain ^uRP^uR^xP^vR can be expressed as

$$\begin{array}{}\text{(15)}& {\mathit{\$}}_{\mathrm{3}}^{\mathrm{r}}=\left(\mathrm{0},\mathrm{0},\mathrm{0};\mathrm{0},-n_{\mathrm{35}},m_{\mathrm{35}}\right).\end{array}$$

From Eqs. (13) and (15), the overall restraint wrench of the 2^xP^uRP^uR^vR–^uRP^uR^xP^vR PM can be expressed as

$$\begin{array}{}\text{(16)}& {\mathit{\$}}_m^{\mathrm{r}}=\left(\mathrm{0},\mathrm{0},\mathrm{0};\mathrm{0},-n_{i\mathrm{5}},m_{i\mathrm{5}}\right),i=\mathrm{1},\mathrm{2},\mathrm{3},\end{array}$$

where $${}_m^{\mathrm{r}}$ represents the constrained torque perpendicular to the plane of the two rotational pairs ^uR and ^vR. Therefore, the constraint torques of the three branched chains are parallel to each other, forming a common constraint. There is only one constraint torque in the 2^uP^uRP^uR^vR–^uRP^uR^uP^vR PM, and the mechanism can generate 2R3T motion.

Figure 9 CAD model of 2^uP^uRP^uR^vR–^yP^yRPS PM.

Figure 10 The physical prototype of the 2^uP^uRP^uR^vR–^yP^yRPS PM.

Figure 11 Motion tests of physical prototypes.

The number of DOF of the 2^xP^uRP^uR^vR–^uRP^uR^xP^vR is calculated using the Kutzbach–Grübler equation:

$$\begin{array}{}\text{(17)}& M=\mathrm{6}\left(n-g-\mathrm{1}\right)+\sum _{i=\mathrm{1}}^g{f}_i+v-\mathit{\eta },\end{array}$$

where M is the number of DOF of the mechanism, v is the total number of overconstrained PMs, g is the number of joints, n represents the number of rigid bodies in the PM, f_i represents the DOF number of the ith joint, and η is the number of redundancy DOF. For the 2^xP^uP^uR^vR/^uRP^uR^xP^vR PM, the number of DOF is

$$\begin{array}{}\text{(18)}& M=\mathrm{5}\left(\mathrm{11}-\mathrm{12}-\mathrm{1}\right)+\mathrm{15}=\mathrm{5}.\end{array}$$

6 Engineering applications

In practical engineering applications, it is vital to consider the feasibility of fabrication and assembly and the requirements of the task's degrees of freedom. The PMs with two constraint branched chains shown in Fig. 5 have three advantages:

1. The PMs have fewer joints (16 kinematic joints), which reduces errors due to joint gaps.

2. Fewer kinematic joints reduce the manufacturing costs and assembly difficulties of the PMs, which is more convenient for manufacturing and practical application.

3. The double-drive PMs contain two double-drive branch chains (i.e., there are two drivers on one branch chain), and this type of PM reduces the number of branch chains while maintaining the DOF, resulting in a high degree of dexterity.

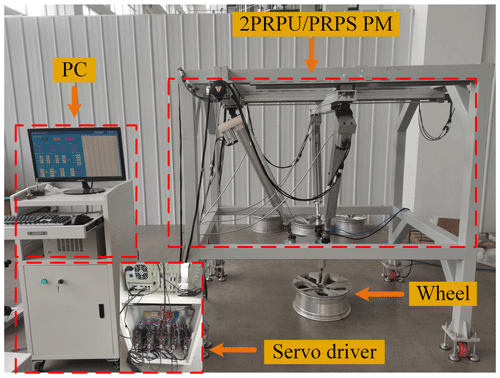
Based on the 2^uP^uRP^uR^vR–^yP^yRPS shown in Fig. 5, we established its 3-D model and physical prototype, as shown in Figs. 9 and 10. Motion experiments were conducted on the prototype to demonstrate the feasibility of the PMs with double-constraint branched chains; as shown in Fig. 11, the end effector moves to eight points on the upper end of the hub in sequence. Through this experiment, we demonstrated the feasibility of the 2^uP^uRP^uR^vR–^yP^yRPS PM prototype and validated its workspace's effectiveness. It provides an essential foundation for further research.

7 Conclusions

In order to obtain 5-DOF PMs with fewer joints, a three-branch 2R3T PM type synthesis method is proposed, and the validity of the method is verified with a new 2R3T PM with three branched chains, as an example.

1. The displacement sub-groups {X(u)}{R(N,u)} and {G(u)}{G(v)} of the constraint branch of the 2R3T PMs are derived in detail, and the motion diagrams of the corresponding displacement sub-groups are presented, providing an intuitive and concise representation method for chain kinematic bonds in the configuration synthesis process.

2. The PMs synthesized in this paper can be categorized into three types: non-overconstrained PMs, overconstrained PMs with two constrained branched chains, and overconstrained PMs with three constrained branched chains. The analysis shows that the constraints of the three types of PMs are the same. Specifically, the direction of constrained torque is mutually perpendicular to all revolute joints in the constrained branched chains.

3. A class of three branched-chain 2R3T PMs with the fewest kinematic joints (15 kinematic joints) is synthesized based on the type synthesis method proposed in this paper. The number and property of the DOF of the typical PM are verified using the screw theory and the modified Kutzbach–Grübler equation.

4. Future research will focus on the stiffness analysis, dynamics analysis, and control algorithms of the 2^uP^uRP^uR^vR–^yP^yRPS mechanism prototype, aiming to enable the 2^uP^uRP^uR^vR–^yP^yRPS mechanism prototype to be applied in actual production tasks.