Gear injury equilibrium-oriented self-adjusted shifting strategy and advanced servo control

The application of a self-adjusted strategy has received increasing attention in current transmission design. This paper proposes a gear injury equilibrium oriented self-adjusted shifting strategy (EASS), which can make injury of different gears consistent. First, the injury value of different gears was judged in real time, and the working time of the gear with the largest injury value was reduced by adjusting the shift curve. Second, by considering key points as constraints, an optimal displacement trajectory for a synchronizer was proposed, and then a compound control method using adaptive nonsingular global fast-terminal sliding-mode control (AN-GFTSMC) was developed, which enables a high tracking performance and a better parameter perturbation rejection ability. Finally, both the simulation and real-vehicle experimental results showed that, compared with conventional control, the designed control strategy had good performance: response time was decreased, gear injury tended to be consistent, and transmission reliability was improved.

1 Introduction

Fuel economy and emissions are the first two most important targets of power-train design, and reliability optimization has been the third core part (Wu, 2010) as gearbox reliability directly affects the vehicle-driving experience as well as the overall reliability and safety. Currently, more research studies about fuel economy and emission optimization that aim at reliability are being proposed. There is still space for traditional methods towards lightweight design and improving the fuel economy. So, this paper tries to propose a new form of health monitoring system named the equilibrium oriented self-adjusted shifting strategy (EASS) alongside a high-performance tracking control algorithm for reliability optimization.

Related studies have presented lots of methods for gear injury monitoring (Wu et al., 2023; Xia et al., 2020; Wang et al., 2015). Basoalto and Papaelias (2020) presented a finite-element gear pair model, based on a physics-based dislocation slip model, to quantify and predict gearbox injury. Jiang et al. (2018) performed a lifecycle assessment that aimed to evaluate the environmental impact of a wind turbine gearbox based on its calculated reliability, while another reliability prediction method was applied stepwise to estimate the total failure rate of an offshore wind turbine gearbox (Bhardwaj et al., 2019). In Dhiman's research (Dhiman et al., 2023), a feature selection-based methodology that essentially works on regression models was used to identify faulty scenarios. Reducing gear working time according to the EASS is a feasible way of optimizing gear reliability, and it can be realized by adjustment of the shift curve (Wu and Si, 2013) through synchronizer control. Barathiraja et al. (2021) used a regression analysis to study the critical factors and levels for synchronizer wear reduction and thereby proposed various means of improving the life of the synchronizer. A detailed multibody dynamic model (Walker and Zhang, 2014; Walker et al., 2017) is proposed and widely used. In the Shen et al. (2014) paper, a model of a shifting actuator is established and a nonlinear system sliding-mode controller of the gearshift motor is constructed based on the control principle of a variable structure sliding mode (Yang et al., 2008). An advanced synchronizer control algorithm with good tracking performance and robustness can improve the overall performance of the whole system, and the nonsingular terminal sliding-mode control (NTSMC) with optimization towards “adaptive” is the current preferred option (Mustafa et al., 2020; Anh et al., 2019; Duc et al., 2018; Hashtarkhani and Khosrowjerdi, 2019). An adaptive sliding-mode control was presented for use in cases where explicit knowledge of the system dynamics is not available (Li and Yurkovich, 2000). A fault-tolerant attitude controller based on adaptive control and fast-terminal sliding-control theory was designed to handle actuator uncertainties (Qi et al., 2019). Adaptive sliding-mode control is also widely adopted for trajectory tracking and disturbance observation (Li et al., 2019; Yi and Zhai, 2019; Yan et al., 2021; Sun et al., 2021; Rabiee et al., 2019). An adaptive nonsingular fast-terminal sliding mode (ANTSMC) has a great ability to handle system uncertainty and external disturbance (Boukattaya et al., 2018; Labbadi and Cherkaoui, 2020; Rodriguez et al., 2022). In Wang and Hao (2021), a robust nonsingular fast-terminal sliding-mode control scheme with adaptive neural networks was presented for a class of nonlinear systems with unknown bounds of uncertainties. In addition, a novel fast nonsingular terminal sliding-mode surface was designed using an adaptive methodology, with adaptive update laws employed to estimate the boundaries of various uncertainties (Miao et al., 2019). Wang and Hao (2021) utilized an adaptive sliding-mode control issue for switched nonlinear systems with both matched and mismatched uncertainties. An adaptive sliding-mode control law was also designed by means of a back-stepping method to compensate for the unknown and uncertain parts of aircraft systems (Zhuang et al., 2021). Adaptive sliding-mode control has thus been widely studied in recent years, particularly because of its obvious advantages in nonlinear systems with uncertainties (Ghorbani et al., 2021; Liu et al., 2019; Nguyen et al., 2019).

Considering that previous reliability-relevant research studies rarely mention self-adjusted strategy, this paper proposed an EASS alongside an adaptive nonsingular global fast-terminal sliding-mode control (AN-GFTSMC) for reliability optimization as gear injury is one of the main issues with transmission reliability. Due to the different environments and driving styles with which different drivers use vehicles, the working strengths and working times of different gears are different. Therefore, the overall strength of the transmission gears needs to be increased during the design process. However, this process can lead to excessive redundancy in the strength of the transmission gears, which not only reduces the economy of the vehicle, contrary to lightweight design but also increases manufacturing costs. The method designed in this article starts by predicting the injury values of transmission gears, comparing the injury values of different gears in real time, and adjusting the gears in time, making the injury values of each gear in the transmission tend to be consistent and solving the above problems.

This paper is organized as follows. First, the real-time value of the gear injury is calculated by cooperating with the Technische Universität Darmstadt in Germany (Esser et al., 2020); this is used as the input of the EASS. The second section designs the EASS specifically, which can intelligently adjust the shift curve of the transmission by comparing the injury value of each gear in real time in order to make each gear's injury tend to be consistent. As a means of realizing the EASS, Sect. 3 proposes a novel AN-GFTSMC for a synchronizer based on building an actuation hydraulic and mechanical model. Furthermore, an optimal trajectory for the synchronizer is deployed considering the nonlinear force of its operating process, enabling a high tracking performance. Finally, both the simulation and real-vehicle experimental results show that each gear's injury tends to be consistent by adopting the EASS, and the AN-GFTSMC possesses a good ability to improve the response performance of the synchronizer system, which improves transmission reliability and prolongs its lifespan. This could also be good guidance for industrial design of transmissions, which has positive significance for durability and light weight.

2 Gear injury equilibrium oriented self-adjusted shifting strategy

2.1 Gear injury equilibrium oriented self-adjusted strategy

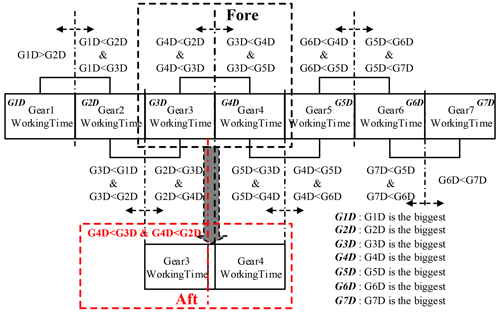
Based on real-time monitoring of the injury to each gear, the identity of the gear with the largest injury at a certain moment can be obtained. Its adjacent gear with the minimum injury can then be assessed and a corresponding gear adjustment carried out so that the gear with the larger injury value is given a shorter working time and the gear with the smaller injury value has a longer working time.

Specific workflows and principles reflecting this are shown in Fig. 1, where GiD represents the injury value of the ith gear (gear i).

Figure 1 Gear injury equilibrium oriented self-adjusted strategy.

Taking a seven-gear transmission as an example and real-time monitoring, the injury values of the seven gears are as follows.

1. The gear with the maximum injury value was identified, in this case as gear 3.

2. The injury values of the two gears adjacent to gear 3, i.e., gear 2 and gear 4, were assessed, and the gear with the smaller injury value was identified.

3. If the injury to gear 4 is less, then the EASS is applied to this gear, increasing the working time of gear 4 by upshifting from gear 3 to gear 4 in advance and delaying downshifting from gear 4 to gear 3. If the injury of gear 2 is less, upshifting to gear 3 will be delayed and downshifting from gear 3 to gear 2 advanced.

4. After the relevant gear adjustment, the injury value of gear 3 should eventually regress from the maximum. This is assessed by judging the injury to all seven gears in real time. After the vehicle runs for a period and if the injury value of gear 4 (or gear 2, as relevant) becomes the maximum, steps (2) to (3) are repeated for the gears adjacent to the new maximum.

5. The injury values of the two gears adjacent to gear 4, i.e., gear 3 and gear 5, were assessed and the gear with the smaller injury value was identified.

6. If the injury to gear 3 is less, then the EASS is applied to this gear, increasing the working time of gear 3 by downshifting from gear 4 to gear 3 in advance and then upshifting from gear 3 to gear 4. If the injury to gear 5 is less, upshifting to gear 5 will be in advance and downshifting from gear 5 to gear 4 thus delayed.

Continuous loops of this strategy will eventually lead to the injury values of all gears reaching equilibrium, making the transmission life longer overall.

2.2 Gear-shifting strategy

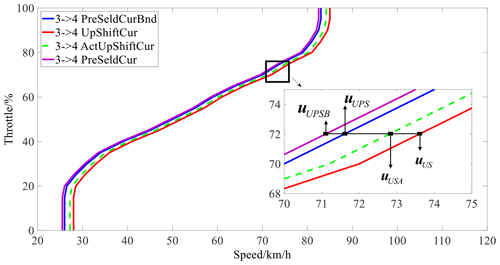
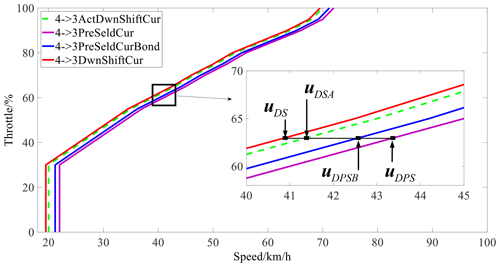
Continue to discuss example (3) in Sect. 2.1. As shown in Fig. 2, the upshift from gear 3 to gear 4 is prioritized on the premise that the pre-select curve remains unchanged, the working time of gear 3 is reduced, and the working time of gear 4 is increased by moving the upshift curve left. Continue to discuss example (6) in Sect. 2.1. On the condition of downshift from gear 4 to gear 3, as shown in Fig. 3, and on the premise that the pre-select curve remains unchanged, moving the downshift curve left reduces the working time of gear 3 and increases the working time of gear 4. Other situations are similar.

Figure 2 Upshift curve adjustment of the EASS.

$$\begin{array}{}\text{(1)}& {\displaystyle }{u}_{\mathrm{USA}}=u_{\mathrm{US}}-(u_{\mathrm{US}}-u_{\mathrm{UPSB}})\cdot {\mathit{\lambda }}_{\mathrm{iGearDamg}}\text{(2)}& {\displaystyle }{u}_{\mathrm{UPSB}}=u_{\mathrm{UPS}}-{\mathrm{\Delta }}_{\mathrm{Up}}\end{array}$$

u_USA is the actual adjusted upshift curve, u_US is the original upshift curve, u_UPSB is the boundary of the upshift curve, λ_iGearDamg is the injury normalization value of the ith gear calculated from the injury, u_UPSB is the pre-select upshift curve, and Δ_Up is the speed change value corresponding to the difference between the boundary of the upshift curve and the pre-select curve that is constrained by the current vehicle speed and the response time of the synchronizer control system. In order to ensure a smooth shift, the pre-select action must be completed before responding to the shift request command, so the following inequality must be satisfied.

$$\begin{array}{}\text{(3)}& {\mathrm{\Delta }}_{\mathrm{Up}}>\underset{\mathrm{0}}{\overset{t_{\mathrm{S}}}{\int }}{\dot{u}}_{\mathrm{veh}}\left(t\right)\mathrm{d}t\end{array}$$

${\dot{u}}_{\mathrm{Veh}}$ is the current driving acceleration of the vehicle, and t_S is the response time of the synchronizer control system.

Figure 3 Downshift curve adjustment of the EASS.

$$\begin{array}{}\text{(4)}& {\displaystyle }{u}_{\mathrm{DSA}}=-\left[(u_{\mathrm{DS}}-u_{\mathrm{DPSB}})\cdot {\mathit{\lambda }}_{\mathrm{iGearDamg}}-u_{\mathrm{DS}}\right]\text{(5)}& {\displaystyle }{u}_{\mathrm{DPSB}}=u_{\mathrm{DPS}}-{\mathrm{\Delta }}_{\mathrm{Dwn}}\end{array}$$

u_DSA is the actual adjusted downshift curve, u_DS is the original downshift curve, u_DPSB is the boundary of the downshift curve, λ_iGearDamg is the injury normalization value of the ith gear, and u_DPS is the pre-select downshift curve. Δ_Dwn is the speed change value corresponding to the difference between the boundary of the downshift curve and the pre-select curve, which is constrained by the current vehicle speed and the response time of the synchronizer control system. In order to ensure a smooth shift, the pre-select action must be completed before responding to the shift request, so the following inequality must be met.

$$\begin{array}{}\text{(6)}& {\mathrm{\Delta }}_{\mathrm{Dwn}}>\underset{\mathrm{0}}{\overset{t_{\mathrm{S}}}{\int }}{\dot{u}}_{\mathrm{veh}}\left(t\right)\mathrm{d}t\end{array}$$

${\dot{u}}_{\mathrm{Veh}}$ is the current driving deceleration of the vehicle, and t_S is the response time of the synchronizer control system.

According to Eqs. (3) and (6), by minimizing the response time t_S of the synchronizer control system, Δ_Up and Δ_Dwn can be minimized, and this should also maximize the effect of the EASS.

3 Synchronizer modeling

In order to optimize the control effect of the EASS, a synchronizer control algorithm is proposed to minimize the response time t_S.

3.1 Modeling of the hydraulic actuation system

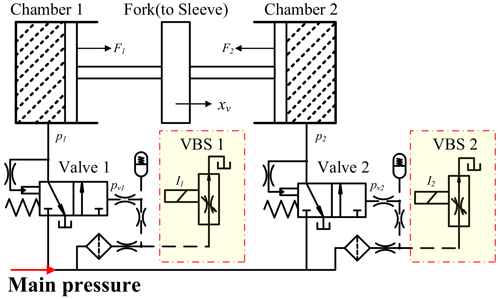
The hydraulic actuation system (HAS) consists of two independent valve systems. Each of these systems consists of one variable-bleed solenoid (VBS) and one two-position four-way valve.

As shown in Fig. 4, the VBS is marked in yellow and is the core of the HAS.

Figure 4 Schematic diagram of the HAS.

VBS suppliers such as BorgWarner guarantee that the output pressure, p_vi of a VBS, is stably linearized with the input current I_i, and p_vi controls the opening area of valve i, which determines the pressure p_i of chamber i. The equation of motion can then be expressed according to Newton's second law as follows.

$$\begin{array}{}\text{(7)}& m{\ddot{x}}_{\mathrm{v}}+\mathit{\varsigma }{\dot{x}}_{\mathrm{v}}+F_{\mathrm{sync}}=F_{\mathrm{1}}-F_{\mathrm{2}}\end{array}$$

x_v is the displacement of the fork. m is the mass of the motion part of the synchronizer, which varies with the different operating stages but is specifically bounded. ς is the hydraulic viscosity coefficient. F_sync is the resistance of the synchronizer in the operating process, and F₁ and F₂ are the hydraulic actuations of the two independent valve systems, respectively.

When the hydraulic system is actuated, its cavity must be filled to allow the output of pressure. Based on the viscosity characteristics of hydraulic oil, when establishing the oil pressure equation for the HAS, the system has certain time-delay characteristics like those shown in Eq. (8).

$$\begin{array}{}\text{(8)}& {\dot{F}}_i+{\mathit{\eta }}_{\mathrm{v}}{F}_i=s_i{p}_i\left(I_{\mathrm{vi}}\right)\end{array}$$

I_vi is the input current of VBSim, and s_i is the hydraulic actuation area of the valve. i is the number of valves. The term p_i(⋅) in Eqs. (8) and (9) denotes the gain function of valve i, while the coefficients of the gain function can be identified by large amounts of experimental data as shown in Fig. 5.

Figure 5 Experiment data used for parameter identification.

$$\begin{array}{}\text{(9)}& p_i\left(I_{\mathrm{v}i}\right)=\sum _{n=\mathrm{0}}^{\mathrm{3}}{a}_{\mathrm{vin}}{I}_{\mathrm{v}i}^n\end{array}$$

$a_{\mathrm{v}i\mathrm{3}}=-\mathrm{3.14}\times {\mathrm{10}}^{-\mathrm{8}}$, $a_{\mathrm{v}i\mathrm{2}}=\mathrm{5.63}\times {\mathrm{10}}^{-\mathrm{5}}$, $a_{\mathrm{v}i\mathrm{1}}=-\mathrm{0.0062}$, and $a_{\mathrm{v}i\mathrm{0}}=-\mathrm{1.89}$.

η_v in Eq. (8) is the nominal value of the time-delay characteristic parameter, which cannot however be accurately solved for. Only the range of η_v can be acquired based on large quantities of experimental data as shown in Fig. 5, and this can be expressed as follows.

$$\begin{array}{}\text{(10)}& {}_{\mathit{\eta }}\le {\mathit{\eta }}_{\mathrm{v}}\le {\stackrel{\mathrm{‾}}{\mathrm{\Delta }}}_{\mathit{\eta }}\end{array}$$

${\stackrel{\mathrm{‾}}{\mathrm{\Delta }}}_{\mathit{\eta }}=\mathrm{1}/\mathrm{0.04}$ and ${\mathrm{\Delta }}_{\mathit{\eta }}=\mathrm{1}/\mathrm{0.06}$ are the upper and lower bounds of η_v, respectively.

3.2 Modeling of the synchronizer mechanical system

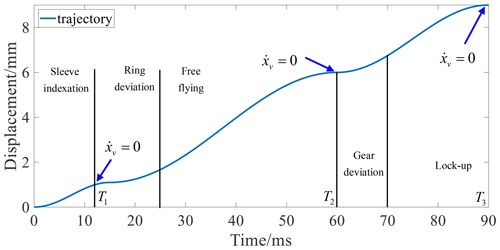
The synchronizer's operating process can be divided into six stages: sleeve indexation, synchronization, ring deviation, free flying, gear deviation, and lock-up.

(1) Sleeve indexation

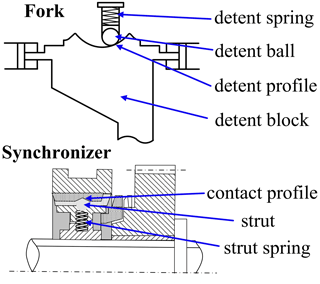
The external force at this stage comes mainly from the deformation of the strut spring of the self-locking device and the deformation of the detent spring of the gear-locking device, which both have positive correlations with displacement, as shown in Fig. 6.

Figure 6 Diagram of the fork and the synchronizer.

An analysis of the force on the synchronizer at this stage shows that it is subject to self-locking resistance F_slc and gear-locking resistance F_B.

$$\begin{array}{}\text{(11)}& {\displaystyle }{F}_{\mathrm{slc}}=n_{\mathrm{sd}}{k}_{\mathrm{slc}}{x}_{\mathrm{v}}\left(\sin {\mathit{\chi }}_{\mathrm{slc}}\cos {\mathit{\chi }}_{\mathrm{slc}}+{\mathit{\mu }}_{\mathrm{slc}}{\cos }^{\mathrm{2}}{\mathit{\chi }}_{\mathrm{slc}}\right)\text{(12)}& {\displaystyle }{F}_{\mathrm{B}}=k_{\mathrm{B}}{x}_{\mathrm{v}}\left(\sin {\mathit{\chi }}_{\mathrm{B}}\cos {\mathit{\chi }}_{\mathrm{B}}+{\mathit{\mu }}_{\mathrm{B}}{\cos }^{\mathrm{2}}{\mathit{\chi }}_{\mathrm{B}}\right)\end{array}$$

k_slc is the elastic coefficient of the strut spring, n_sd is the number of synchronizer sliders, χ_slc is the slope angle of the contact profile between the sleeve and the strut, μ_slc is the friction coefficient of the contact profile between the sleeve and the strut, k_B is the elastic coefficient of the detent spring of the gear-locking device, χ_B is the slope angle of the detent profile, and μ_B is the friction coefficient of the contact surface between the detent ball and the detent block.

(2) Synchronization

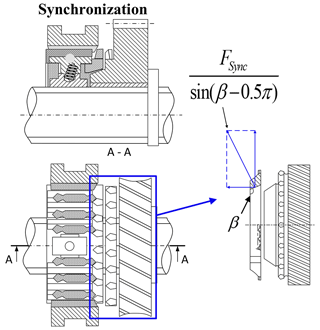
Analysis of the synchronization stage shows that, during this period, the fork does not move, and the force on the fork is used for the synchronization of the ring and the gear ring as shown in Fig. 7.

Figure 7 Synchronization.

This means the following.

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{F}_{\mathrm{Sync}}& =F_{\mathrm{1}}+F_{\mathrm{2}}=a{\displaystyle \frac{\left(J_{\mathrm{Gear}}+J_{\mathrm{Ring}}\right){\ddot{\mathit{\theta }}}_{\mathrm{Gear}}+{\mathit{\mu }}_{\mathrm{Fric}}{\dot{\mathit{\theta }}}_{\mathrm{Gear}}}{{\mathit{\mu }}_{\mathrm{Ring}}{r}_{\mathrm{sync}}}}\\ & \sin \left(\mathit{\beta }-\mathrm{0.5}\mathit{\pi }\right)\end{array}\end{array}$$

μ_ring is the friction coefficient between the ring cone and the gear ring cone, θ_Gear is the rotation angle of the gear, β is the cone angle of the ring, and F_Sync is the axial force at the synchronization stage.

(3) Ring deviation

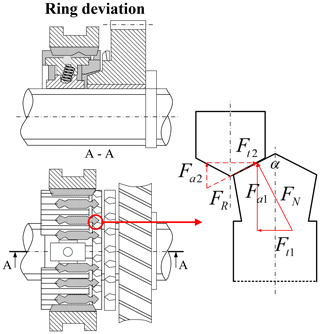
As shown in Fig. 8, the external force at this stage mainly arises from the torque exerted on the ring.

Figure 8 Ring deviation.

The force analysis is therefore as follows.

$$\begin{array}{}\text{(14)}& \begin{array}{rl}{F}_{\mathrm{RD}}& =\mathrm{2}{\displaystyle \frac{(J_{\mathrm{Gear}}+J_{\mathrm{Ring}}){\ddot{\mathit{\theta }}}_{\mathrm{Gear}}+{\mathit{\mu }}_{\mathrm{Fric}}{\dot{\mathit{\theta }}}_{\mathrm{Gear}}}{r_{\mathrm{sync}}}}\\ & \cdot {\displaystyle \frac{\sin \frac{\mathit{\alpha }}{\mathrm{2}}+{\mathit{\mu }}_{\mathrm{RD}}\cos \frac{\mathit{\alpha }}{\mathrm{2}}}{\cos \frac{\mathit{\alpha }}{\mathrm{2}}-{\mathit{\mu }}_{\mathrm{RD}}\sin \frac{\mathit{\alpha }}{\mathrm{2}}}}\end{array}\end{array}$$

F_RD is the axial force at the ring deviation stage, α is the chamfer angle of the sleeve dog, r_sync is the radius of the ring, J_Gear is the rotational inertia coefficient of those parts connected to the gear, J_Ring is the rotational inertia coefficient of the ring, μ_Fric is the equivalent friction coefficient of the parts connected with the gear, and μ_RD is the friction coefficient of the dog.

(4) Free flying

Analysis of the free-flying stage shows that the external force is mainly derived from the motion of the moving components.

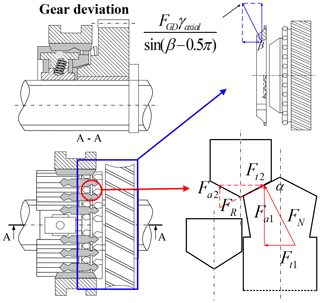
(5) Gear deviation

As shown in Fig. 9, the external force at this stage mainly arises from the torque applied to the gear ring and the friction between the ring and the gear ring.

Figure 9 Gear deviation.

The force analysis is as follows.

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{F}_{\mathrm{GD}}& =\mathrm{2}{\displaystyle \frac{J_{\mathrm{Gear}}{\ddot{\mathit{\theta }}}_{\mathrm{Gear}}+{\mathit{\mu }}_{\mathrm{Fric}}{\dot{\mathit{\theta }}}_{\mathrm{Gear}}}{r_{\mathrm{sync}}}}\\ & \cdot \left[{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{1}}}{(\mathrm{1}-{\mathit{\gamma }}_{\mathrm{axial}}){\mathit{\rho }}_{\mathrm{2}}-{\mathit{\rho }}_{\mathrm{1}}{\mathit{\gamma }}_{\mathrm{axial}}{\mathit{\rho }}_{\mathrm{3}}}}\right]\end{array}\end{array}$$

${\mathit{\rho }}_{\mathrm{1}}=\sin \frac{\mathit{\alpha }}{\mathrm{2}}+{\mathit{\mu }}_{\mathrm{GD}}\cos \frac{\mathit{\alpha }}{\mathrm{2}}$, ${\mathit{\rho }}_{\mathrm{2}}=\cos \frac{\mathit{\alpha }}{\mathrm{2}}-{\mathit{\mu }}_{\mathrm{GD}}\sin \frac{\mathit{\alpha }}{\mathrm{2}}$, and ${\mathit{\rho }}_{\mathrm{3}}=\frac{{\mathit{\mu }}_{\mathrm{ring}}}{\sin (\mathit{\beta }-\mathrm{0.5}\mathit{\pi })}$. F_GD is the axial force at the gear deviation stage, and μ_GD is the friction coefficient of the dog. γ_axial is the axial force coefficient, which is generally very small.

Figure 10 Displacement target trajectory of the synchronizer.

Table 1 List of all the parameter values in this article.

(6) Lock-up

Analysis of the lock-up stage shows that the external force is mainly derived from the motion of the moving components.

Thus, the overall process resistance suffered by the synchronizer during operation can be described in the following forms.

$$\begin{array}{}\text{(16)}& \begin{array}{rl}& F_{\mathrm{sync}}=\\ & \left\{\begin{array}{lll}{F}_{\mathrm{slc}}+F_{\mathrm{B}}& \mathrm{0}\le x_{\mathrm{v}}<\mathrm{1.1}& \mathrm{Sleeve}\mathrm{indexation}\\ F_{\mathrm{Sync}}& x_{\mathrm{v}}=\mathrm{1.1}& \mathrm{Synchronization}\\ F_{\mathrm{RD}}+F_{\mathrm{slc}}+F_{\mathrm{B}}& \mathrm{1.1}<x_{\mathrm{v}}<\mathrm{2.5}& \mathrm{Ring}\mathrm{deviation}\\ \mathrm{0}& \mathrm{2.5}\le x_{\mathrm{v}}<\mathrm{6.0}& \mathrm{Free}\mathrm{flying}\\ F_{\mathrm{GD}}& \mathrm{6.0}\le x_{\mathrm{v}}<\mathrm{7.0}& \mathrm{Gear}\mathrm{deviation}\\ \mathrm{0}& \mathrm{7.0}\le x_{\mathrm{v}}\le \mathrm{9.0}& \text{Lock-up}\end{array}\right.\end{array}\end{array}$$

The critical points at 1.1, 2.5, 6, 7, and 9 mm are obtained by measuring the real synchronizer.

3.3 Synchronizer model

Combining Eq. (7) with Eqs. (10) and (16), the state-space model of the synchronizer system can be obtained as follows.

$$\begin{array}{}\text{(17)}& \begin{array}{rl}\dot{X}=& \left[\begin{array}{ccc}\mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\\ \mathrm{0}& A_{\mathrm{32}}& A_{\mathrm{33}}\end{array}\right]X+\left[\begin{array}{cc}\mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\\ B_{\mathrm{31}}& B_{\mathrm{32}}\end{array}\right]\\ & \left[\begin{array}{l}\sum _{n=\mathrm{0}}^{\mathrm{3}}{a}_{v\mathrm{1}n}{I}_{v\mathrm{1}}^n\\ \sum _{n=\mathrm{0}}^{\mathrm{3}}{a}_{v\mathrm{2}n}{I}_{v\mathrm{2}}^n\end{array}\right]+\left[\begin{array}{l}\mathrm{0}\\ \mathrm{0}\\ -\mathrm{1}\end{array}\right]F_{\mathrm{sync}}\end{array}\end{array}$$

$X=[\begin{array}{ccc}{x}_{\mathrm{v}}& {\dot{x}}_{\mathrm{v}}& {\ddot{x}}_{\mathrm{v}}\end{array}{]}^{\mathrm{T}}$, $A_{\mathrm{32}}=-\frac{\mathit{\varsigma }{\mathit{\eta }}_{\mathrm{v}}+m}{m{\mathit{\eta }}_{\mathrm{v}}}$, $A_{\mathrm{33}}=-\frac{\mathit{\varsigma }}{m{\mathit{\eta }}_{\mathrm{v}}}$, $B_{\mathrm{31}}=\frac{S_{\mathrm{1}}}{m{\mathit{\eta }}_{\mathrm{v}}}$, and $B_{\mathrm{32}}=-\frac{s_{\mathrm{2}}}{m{\mathit{\eta }}_{\mathrm{v}}}$.

The uncertainty part in Eq. (17) can be described as follows.

$$\begin{array}{}\text{(18)}& B_{\min }\le B_{\mathrm{31}}^{-\mathrm{1}}=B_{\mathrm{32}}^{-\mathrm{1}}\le B_{\max }\end{array}$$

$$\begin{array}{}\text{(19)}& A_{\min }\le B_{\mathrm{31}}^{-\mathrm{1}}{A}_{\mathrm{32}}=B_{\mathrm{32}}^{-\mathrm{1}}{A}_{\mathrm{32}}\le A_{\max }\end{array}$$

$$\begin{array}{}\text{(20)}& F_{\mathrm{sync}}<F\end{array}$$

Figure 11 The displacement of the synchronizer.

Figure 12 The velocity of the synchronizer.

Figure 13 Simulation results of the NEDC cycle – speed.

Figure 14 Simulation results of the NEDC cycle – gear.

Table 2 Data sheet of each gear during the test.

Table 3 Improvement of each gear.

4 AN-GFTSMC design

4.1 Controller design based on AN-GFTSMC

The error between actual and target displacement is defined as follows.

$$\begin{array}{}\text{(21)}& e=x_{\mathrm{v}}-x_{\mathrm{d}}\end{array}$$

x_d is the target displacement.

Some model parameters (as in Eq. 17), e.g., the synchronizer motion part mass, m, and the hydraulic system time-delay characteristic parameter, η_v, cannot be obtained accurately. Thus, in order to guarantee rapid and high-precision tracking performance under the parameter perturbations with constraint input, a novel AN-GFTSMC for an uncertain system is proposed. Its sliding-mode surface is defined as follows.

$$\begin{array}{}\text{(22)}& s=e+{\mathit{\sigma }}_{\mathrm{2}}{\left|\ddot{e}\right|}^{o_{\mathrm{2}}}\mathrm{sgn}\left(\ddot{e}\right)+{\mathit{\sigma }}_{\mathrm{1}}{\left|\dot{e}\right|}^{o_{\mathrm{1}}}\mathrm{sgn}\left(\dot{e}\right)+{\mathit{\sigma }}_{\mathrm{0}}{\left|e\right|}^{o_{\mathrm{0}}}\mathrm{sgn}\left(e\right)\end{array}$$

σ₀, σ₁, and σ₂, respectively, are positive parameters. $o_{\mathrm{0}}>o_{\mathrm{1}}>o_{\mathrm{2}}$, $o_{\mathrm{2}}\in (\mathrm{1},\mathrm{2})$, and $o_{\mathrm{1}}\in (\mathrm{1},\mathrm{2})$. o₁ and o₂ are chosen such that $o_i=p_i/q_i(i=\mathrm{1},\mathrm{2})$, where q_i and p_i are positive odd numbers and p_i>q_i. Based on this, the variables e, $\dot{e}$, and $\ddot{e}$ will converge to zero in a finite period of time.

The control input is defined as follows.

$$\begin{array}{}\text{(23)}& u=u_{\mathrm{1}}+u_{\mathrm{2}}\end{array}$$

Equation (23) has the following.

$$\begin{array}{}\text{(24)}& \begin{array}{rl}& u_{\mathrm{1}}=-B_{\mathrm{mean}}\left(A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right)\\ & +A_{\mathrm{mean}}{\ddot{x}}_{\mathrm{v}}-B_{\mathrm{mean}}L-\left\{B_{\mathrm{devia}}\left|A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}\right.\right.\\ & \left.A_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right|\left.+A_{\mathrm{devia}}\left|{\ddot{x}}_{\mathrm{v}}\right|+F+B_{\mathrm{devia}}\left|L\right|\right\}\mathrm{sgn}\left(s\right)\end{array}\end{array}$$

$$\begin{array}{}\text{(25)}& u_{\mathrm{2}}=-k_{\mathrm{31}}s-k_{\mathrm{32}}{\left|s\right|}^{o_{\mathrm{3}}}\mathrm{sgn}\left(s\right)\end{array}$$

$$\begin{array}{}\text{(26)}& A_i={\mathit{\sigma }}_i{o}_i{\left|e^{(i-\mathrm{1})}\right|}^{o_i-\mathrm{1}}\end{array}$$

$$\begin{array}{}\text{(27)}& L=x_{v}d+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{d}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{d}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{d}}\end{array}$$

$$\begin{array}{}\text{(28)}& A_{\mathrm{mean}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(A_{\max }+A_{\min })\end{array}$$

$$\begin{array}{}\text{(29)}& A_{\mathrm{devia}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(A_{\max }-A_{\min })\end{array}$$

$$\begin{array}{}\text{(30)}& B_{\mathrm{mean}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(B_{\max }+B_{\min })\end{array}$$

$$\begin{array}{}\text{(31)}& B_{\mathrm{devia}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(B_{\max }-B_{\min })\end{array}$$

k₃₁ and k₃₂ are positive integers, o₃ is such that $o_{\mathrm{3}}=p_{\mathrm{3}}/q_{\mathrm{3}}$, and q₃ and p₃ are positive odd numbers.

Figure 15 Framework of the real-vehicle test.

Figure 16 Vehicle speed and throttle opening value.

Figure 17 Control current of the VBS.

4.2 Stability proof

Take valve 1 as an example and define a Lyapunov candidate as follows.

$$\begin{array}{}\text{(32)}& V={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{s}^{\mathrm{2}}\end{array}$$

This leads to the following.

$$\begin{array}{}\text{(33)}& \begin{array}{rl}& \dot{V}=s\dot{s}=\\ & B_{\mathrm{31}}{A}_{\mathrm{2}}s\left[-B_{\mathrm{31}}^{-\mathrm{1}}{A}_{\mathrm{32}}{\ddot{x}}_{\mathrm{v}}+u+F_{\mathrm{sync}}+B_{\mathrm{31}}^{-\mathrm{1}}\right.\\ & \left.\left(A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right)-B_{\mathrm{31}}^{-\mathrm{1}}L\right]\end{array}\end{array}$$

Bring Eqs. (24) and (31) into Eq. (33).

$$\begin{array}{}\text{(34)}& \begin{array}{rl}& \dot{V}=s\dot{s}=-k_{\mathrm{31}}{s}^{\mathrm{2}}-k_{\mathrm{32}}{\left|s\right|}^{o_{\mathrm{3}}+\mathrm{1}}+\\ & B_{\mathrm{31}}{A}_{\mathrm{2}}s\left[-B_{\mathrm{31}}^{-\mathrm{1}}{A}_{\mathrm{32}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{mean}}{\ddot{x}}_{\mathrm{v}}+B_{\mathrm{31}}^{-\mathrm{1}}\right.\\ & \left(A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right)\\ & -B_{\mathrm{mean}}\left(A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right)\\ & +B_{\mathrm{31}}^{-\mathrm{1}}L-B_{\mathrm{mean}}L+F_{\mathrm{sync}}\\ & -\left\{B_{\mathrm{devia}}\left|A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right|\right.\\ & \left.\left.+A_{\mathrm{devia}}\left|{\ddot{x}}_{\mathrm{v}}\right|+F+B_{\mathrm{devia}}\left|L\right|\right\}\mathrm{sgn}\left(s\right)\right]\end{array}\end{array}$$

The simplified Eq. (34) is as follows.

$$\begin{array}{}\text{(35)}& \begin{array}{rl}& \dot{V}=B_{\mathrm{31}}{A}_{\mathrm{2}}\left[(B_{\mathrm{31}}^{-\mathrm{1}}-B_{\mathrm{mean}})\left(A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}\right.\right.\\ & \left.+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right)s-B_{\mathrm{devia}}\left|A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right|\\ & \left|s\right|+\left(A_{\mathrm{mean}}-B_{\mathrm{31}}^{-\mathrm{1}}{A}_{\mathrm{32}}\right){\ddot{x}}_{\mathrm{v}}s-A_{\mathrm{devia}}\left|{\ddot{x}}_{\mathrm{v}}\right|\left|s\right|\\ & \left.+F_{\mathrm{sync}}-F+(B_{\mathrm{31}}^{-\mathrm{1}}-B_{\mathrm{mean}})Ls-B_{\mathrm{devia}}\left|L\right|\left|s\right|\right]\\ & -k_{\mathrm{31}}{s}^{\mathrm{2}}-k_{\mathrm{32}}{\left|s\right|}^{o_{\mathrm{3}}+\mathrm{1}}\end{array}\end{array}$$

The simplified Eq. (35) is as follows.

$$\begin{array}{}\text{(36)}& \dot{V}=B_{\mathrm{31}}{A}_{\mathrm{2}}[X_{\mathrm{1}}+X_{\mathrm{2}}+X_{\mathrm{3}}+X_{\mathrm{4}}]-k_{\mathrm{31}}{s}^{\mathrm{2}}-k_{\mathrm{32}}{\left|s\right|}^{o_{\mathrm{3}}+\mathrm{1}}\end{array}$$

This formula has the following.

$$\begin{array}{}\text{(37)}& \begin{array}{rl}& X_{\mathrm{1}}=(B_{\mathrm{31}}^{-\mathrm{1}}-B_{\mathrm{mean}})\left(A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}\right.\\ & \left.{\dot{x}}_{\mathrm{v}}\right)s-B_{\mathrm{devia}}\left|A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{1}}{\ddot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{A}_{\mathrm{0}}{\dot{x}}_{\mathrm{v}}+A_{\mathrm{2}}^{-\mathrm{1}}{\dot{x}}_{\mathrm{v}}\right|\left|s\right|\end{array}\end{array}$$

Equations (29) and (30) show that

$$\begin{array}{}\text{(38)}& B_{\mathrm{31}}^{-\mathrm{1}}-B_{\mathrm{mean}}<B_{\mathrm{devia}}\Rightarrow X_{\mathrm{1}}\le \mathrm{0}\end{array}$$

and

$$\begin{array}{}\text{(39)}& X_{\mathrm{2}}=(A_{\mathrm{mean}}-B_{\mathrm{31}}^{-\mathrm{1}}{A}_{\mathrm{32}}){\ddot{x}}_{\mathrm{v}}s-A_{\mathrm{devia}}\left|{\ddot{x}}_{\mathrm{v}}\right|\left|s\right|.\end{array}$$

Equations (27) and (38) show that

$$\begin{array}{}\text{(40)}& A_{\mathrm{mean}}-B_{\mathrm{31}}^{-\mathrm{1}}{A}_{\mathrm{32}}<A_{\mathrm{devia}}\Rightarrow X_{\mathrm{2}}\le \mathrm{0},\end{array}$$

$$\begin{array}{}\text{(41)}& F_{\mathrm{sync}}\le F\Rightarrow X_{\mathrm{3}}\le \mathrm{0},\end{array}$$

and

$$\begin{array}{}\text{(42)}& B_{\mathrm{31}}^{-\mathrm{1}}-B_{\mathrm{mean}}\le B_{\mathrm{devia}}\Rightarrow X_{\mathrm{4}}\le \mathrm{0}.\end{array}$$

Since k₃₁ and k₃₂ are selected as positive integers,

$$\begin{array}{}\text{(43)}& -k_{\mathrm{31}}{s}^{\mathrm{2}}-k_{\mathrm{32}}{\left|s\right|}^{o_{\mathrm{3}}+\mathrm{1}}\le \mathrm{0}.\end{array}$$

According to Eq. (26),

$$\begin{array}{}\text{(44)}& {\mathit{\sigma }}_i{o}_i{\left|e^{(i-\mathrm{1})}\right|}^{o_i-\mathrm{1}}\ge \mathrm{0}.\end{array}$$

Overall,

$$\begin{array}{}\text{(45)}& \dot{V}\le \mathrm{0}.\end{array}$$

When s=0, $\dot{V}=\mathrm{0}$, the system is asymptotically stable on a large scale.

Figure 18 Gear logic diagram.

5 Verification and analysis

5.1 Parameter settings

All the parameters used in this paper are shown in Table 1.

According to the analysis of Sect. 3.2, the fork moves to the set points at 1.5, 6, and 9 mm with zero velocity. As shown in Fig. 10, to reduce the synchronizer's impact, the fork's motion trajectory must meet the following conditions.

• Condition1: ${\dot{x}}_{\mathrm{v}}\left(t\right)\le \mathit{\nu }$

• Condition2: ${\dot{x}}_{\mathrm{v}}\left(\mathrm{1.1}\right)=\mathrm{0}$

• Condition3: ${\dot{x}}_{\mathrm{v}}\left(\mathrm{6}\right)=\mathrm{0}$

• Condition4: ${\dot{x}}_{\mathrm{v}}\left(\mathrm{9}\right)=\mathrm{0}$

The designed displacement trajectory in this paper is shown in Eqs. (46) and (47), as illustrated in Fig. 10. The velocity trajectory must satisfy the Lipschitz condition as Condition 1, where ν is a positive integer. T_i is also shown in Fig. 10.

$$\begin{array}{}\text{(46)}& \left\{\begin{array}{cc}{x}_{\mathrm{dv}\mathrm{1}}=\frac{T_{\mathrm{1}}}{\mathrm{2}}\left[\mathrm{1}-\cos \left(\mathit{\pi }t\frac{\mathrm{1}}{T_{\mathrm{1}}}\right)\right]& \mathrm{0}\le t<T_{\mathrm{1}}\\ x_{\mathrm{dv}\mathrm{2}}=\frac{T_{\mathrm{2}}-T_{\mathrm{1}}}{\mathrm{2}}\left[\mathrm{1}-\cos \frac{\mathit{\pi }(t-T_{\mathrm{1}})}{T_{\mathrm{2}}-T_{\mathrm{1}}}\right]+\mathrm{1.1}& T_{\mathrm{1}}\le t<T_{\mathrm{2}}\\ x_{\mathrm{dv}\mathrm{3}}=\frac{T_{\mathrm{3}}-T_{\mathrm{2}}}{\mathrm{2}}\left[\mathrm{1}-\cos \frac{\mathit{\pi }(t-T_{\mathrm{2}})}{T_{\mathrm{3}}-T_{\mathrm{2}}}\right]+\mathrm{6}& T_{\mathrm{2}}\le t<T_{\mathrm{3}}\end{array}\right.\end{array}$$

The target displacement trajectory can be obtained as follows.

$$\begin{array}{}\text{(47)}& x_{\mathrm{dv}}=x_{\mathrm{dv}\mathrm{1}}+x_{\mathrm{dv}\mathrm{2}}+x_{\mathrm{dv}\mathrm{3}}\end{array}$$

Parameter perturbations are defined as follows.

$$\begin{array}{}\text{(48)}& m=\mathrm{0.5}\left({\stackrel{\mathrm{‾}}{\mathrm{\Delta }}}_m{-}_m\right)\sin \left(\mathrm{2}\mathit{\pi }t\right)+\mathrm{0.5}{(}_m+{\stackrel{\mathrm{‾}}{\mathrm{\Delta }}}_m)\end{array}$$

$$\begin{array}{}\text{(49)}& {\mathit{\eta }}_{\mathrm{v}}=\mathrm{0.5}\left({\stackrel{\mathrm{‾}}{\mathrm{\Delta }}}_{\mathit{\eta }}{-}_{\mathit{\eta }}\right)\sin \left(\mathrm{2}\mathit{\pi }t\right)+\mathrm{0.5}(\mathit{\eta }+{\stackrel{\mathrm{‾}}{\mathrm{\Delta }}}_{\mathit{\eta }})\end{array}$$

${\stackrel{\mathrm{‾}}{\mathrm{\Delta }}}_m$ and Δ_m are the upper and lower bounds of m.

In Eqs. (46) to (49), t is time, and T_i is as shown in Fig. 10. By setting T_i, the synchronizer performance can be adjusted. This section's design is T₃=90 ms.

Figure 19 The clutch oil pressure.

5.2 AN-GFTSMC analysis

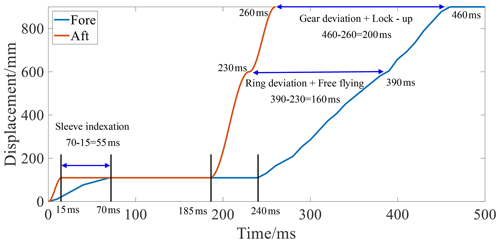
The control algorithm was verified by using the Application SoftWare (ASW) for the dual-clutch transmission (DCT) developed by the researchers' laboratory. Figure 11 shows the result of synchronizer displacement as compared with the conventional control. Using the AN-GFTSMC in the sleeve indexation stage reduced the action time from 70 to 15 ms, a 78.6 % improvement. At the ring deviation + free-flying stage, the action time was reduced from 150 to 45 ms, a 70 % improvement. At the gear deviation + lock-up stage, the action time was reduced from 70 to 30 ms, giving a 57.1 % improvement. The overall actuation time was thus improved by 43.3 %.

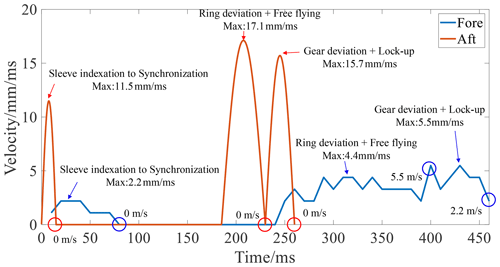
Figure 12 demonstrates the velocity results for the synchronizer. Under conventional control, its peak velocities marked in the blue box were 2.2 m s⁻¹ in the sleeve indexation to synchronization stage, 4.4 m s⁻¹ in the ring deviation + free-flying stage, and 5.5 m s⁻¹ in the gear deviation + lock-up stage. Its instantaneous velocities marked in the blue circle in the free-flying to gear deviation stage were 5.5 and 2.2 m s⁻¹ at the end of the process. There should be an instantaneous zeroing of velocity in the sleeve indexation to synchronization stage, the free-flying to gear deviation stage, and at the end of the process, which is the root cause of the impact. However, the results show in the red box that the maximum velocities under AN-GFTSMC were 11.5 m s⁻¹ in the sleeve indexation to synchronization stage, 17.1 m s⁻¹ in the ring deviation + free-flying stage, and 15.7 m s⁻¹ in the gear deviation + lock-up stage. As marked in the red circle in the free-flying to gear deviation stage at 230 ms and the end of the process at 260 ms, the velocity reached 0 m s⁻¹, satisfying Eq. (47) and achieving the target trajectory shown in Fig. 10. As compared with conventional control, the peak velocity under AN-GFTSMC was thus optimized by 5.2 times in the sleeve indexation to synchronization stage, by 3.8 times during the ring deviation + free-flying stage, and by 2.9 times during the gear deviation + lock-up stage. There was no impact during the whole process.

5.3 EASS experiment

5.3.1 Simulation test

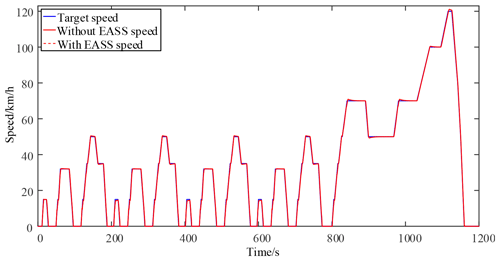
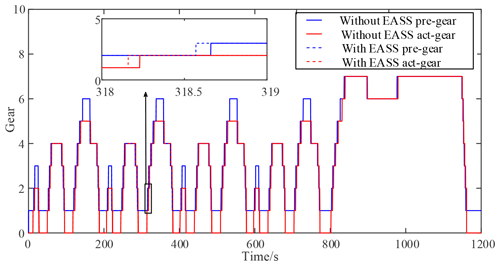
The initial condition was that gear 1 took maximum injury. The EASS was then verified in the New European Driving Cycle (NEDC) condition. Figures 13 and 14 show the speed and gear results, respectively, of the NEDC cycle. Figure 13 showed that the blue line, red line, and red-dot line represent the target speed, the speed without the EASS, and the speed with the EASS, respectively. As shown in Fig. 14, the proposed strategy also reduced the usage time of gear 1 by means of upshifting to gear 2 in advance, thus reducing the injury to gear 1. In this figure, the blue line and blue-dot line show the pre-select gear and the actual gear without the EASS, respectively, while the red line and red-dot line are the pre-select gear and the actual gear with the EASS, respectively.

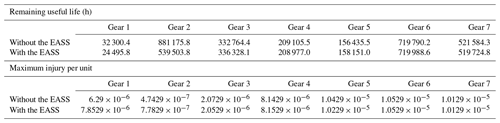
Table 2 shows the maximum injury taken by each gear as assessed after the cycle. The “remaining useful life” was then calculated from these data. Table 3 shows that the peak injury to each gear was reduced by 2.2 %, with the standard deviation reduced by 2.8 %. The injury tended to be consistent, and the performance and reliability of the transmission are improved.

5.3.2 Real-vehicle test

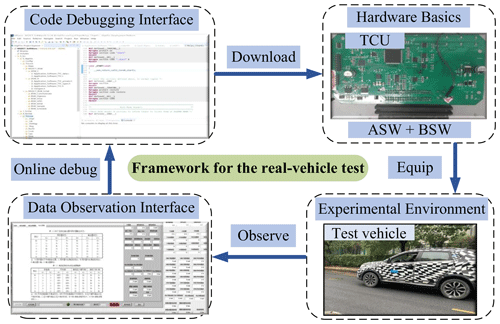
In the real-vehicle verification, the ASW, the Basic SoftWare (BSW), and the hardware developed by the researchers' laboratory for DCT were used as controller carriers. An experimental vehicle equipped with DCT was then used for verification. Figure 15 shows the experimental vehicle and the controller developed for it, with the initial condition of maximum injury for gear 3.

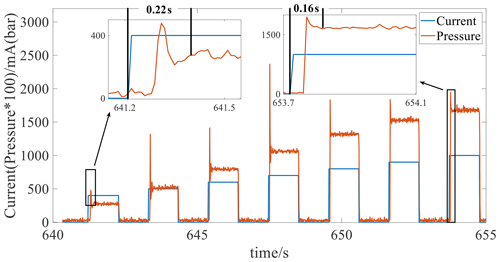
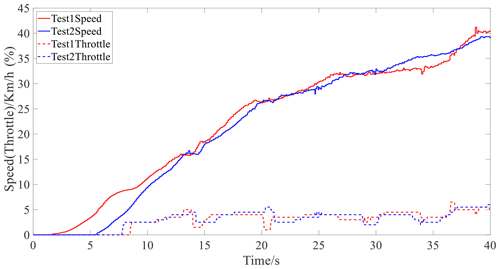
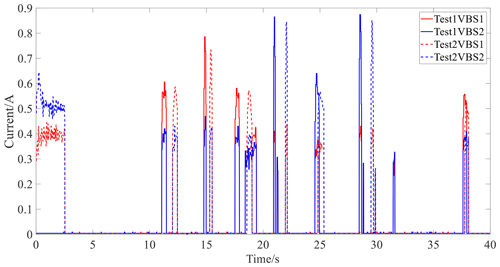
Figure 16 shows the speed and throttle opening results for the real-vehicle experiment. Figure 17 illustrates the control current of the VBS.

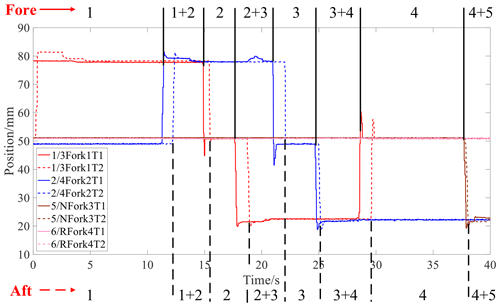
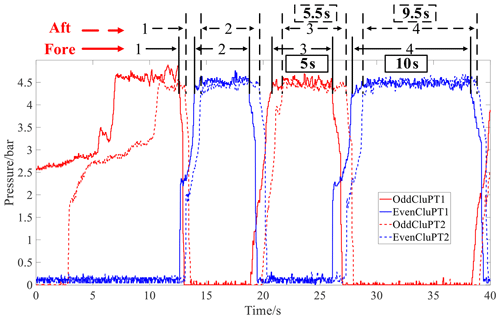
Figures 18 and 19 represent the gear logic diagram and the clutch oil pressure, respectively.

The results show that the proposed strategy intelligently determined that the minimum injury value was gear 4 adjacent to gear 3, and it thus reduced the usage time of gear 3 by upshifting to gear 4 in advance. Therefore, the injury of gear 3 was reduced. As shown in Fig. 19, the working time of gear 4 was thus increased by 5.3 % from 9.5 to 10 s, while the working time of gear 3 was reduced by 9 % from 5.5 to 5 s. This avoided the problem of unbalanced injury across gears that affects the remaining useful life of the transmission overall, thus improving the reliability of the transmission.

6 Conclusions

This paper proposed a gear injury equilibrium oriented self-adjusted shifting strategy (EASS) to equalize the injury values across gears to ensure consistency alongside a novel control algorithm for synchronizer systems based on an adaptive nonsingular global fast-terminal sliding-mode control (AN-GFTSMC), with the latter designed to improve the response performance of the synchronizer.

The EASS judges the gear with the largest injury value in real time and, by adjusting the shift curve, ensures that the gear is then subject to shorter working times, while those adjacent gears with less injury are assigned longer working times. The EASS thus prolongs the overall service life of the transmission and provides the basis for directional lightweight design in such transmission. By considering various key points as constraints, an optimal displacement trajectory for the synchronizer was then proposed, and an AN-GFTSMC algorithm, which reduces the response time of the synchronizer hydraulic system, was presented. The AN-GFTSMC reduced the working time and enlarged the peak velocity during the synchronizer working process, offering improved response performance and ride comfort. Both the simulated and real-vehicle experimental results showed that, as compared with conventional control, the overall improvement in the synchronizer operation time was 43.3 %, while the peak velocity improvement in the sleeve indexation to synchronization stage increased 5.23 times, in the ring deviation + free-flying stage this was 3.88 times, and in the gear deviation + lock-up stage it was 2.9 times. There was no impact during the whole process. The peak value of gear injury decreased by 2.2 %, with the standard deviation also decreasing by 2.8 %. The working time of the gear with the maximum injury value decreased by 9 %, while the working time of the adjacent gear with a smaller injury value increased by 5.3 %.

By applying the proposed EASS strategy, the ongoing injury of gears was more consistent, effectively avoiding focused injury on a single gear in the transmission while allowing other gears to take relatively small amounts of injury, thus affecting the transmission lifecycle. This method designs the EASS to compare the injury values of different gears in real time, adjust the gear in a timely manner, and make the injury values of each gear consistent. Design the optimal trajectory of the synchronizer, design the AN-GFTSMC algorithm to enable the synchronizer to accurately track the optimal trajectory, effectively reduce the impact during the shifting process, improve the shifting speed, and effectively guide the lightweight design of the transmission. The experimental results verified the effectiveness of the proposed strategy. In particular, the results indicated that the proposed method offers better performance with respect to synchronizer control than traditional methods. The application range and limitation of the method are that it is only suitable for mechanisms with gearboxes such as vehicle transmissions and wind turbine gearboxes.

Appendix A: Symbols and abbreviations used in this paper

Symbols and abbreviations	Full name
EASS	Gear injury equilibrium oriented
	self-adjusted shifting strategy
AN-GFTSMC	Adaptive nonsingular global
	fast-terminal sliding-mode
	control
Gear i	GiD represents the injury value
	of the ith gear
HAS	Hydraulic actuation system
VBS	Variable-bleed solenoid
ASW	Application SoftWare
BSW	Basic SoftWare
NEDC	New European Driving Cycle
SD	Standard deviation
DCT	Dual-clutch transmission