Adaptive sliding-mode control for improved vibration mitigation in civil engineering structures

Seismic vibration control using a magneto-rheological damper is a technique that interests several researchers around the world. This technique offers suitable structural building protection, ensuring human safety against earthquake excitation damages. The robustness of these devices depended in many cases on the designed law of control. Over the years, research focused on the development and modelling of various controllers to enhance the structural vibration elimination of buildings. The emphasis of this paper is on the evaluation of semi-active control robustness to reduce the displacements of a three-storey tested structure. The semi-active control device is a magneto-rheological fluid damper installed on the ground floor of the earthquake's excited structure and is controlled by an adaptive non-linear controller coupled to a clipped optimal algorithm to drive the current. The proposed controller is a sliding-mode controller reinforced by an adaptive technique to perform the control gain choice and overcome the chattering problem. The present law of adaptation is a switching conditional law between two laws offering the required gain depending on the system state. The numerical simulation results prove the effectiveness of the proposed semi-active control strategy in attenuating the displacements of the tested structure.

1 Introduction

Earthquake excitations cause building structure damage, city destruction, and human deaths. They directly affect buildings or their structural components through the brutal motion of the ground-propagating vibration. During the last century, earthquakes caused deaths and homelessness of millions of people and destroyed several cities. Algerian towns were affected by strong earthquakes during this period: Algiers in 1916, El Asnam in 1980, Constantine in 1985, Tipasa in 1989, Mascara in 1994, Algiers in 1996, and Boumerdès in 2003 (Gates and Ritchie, 2007). The two strongest earthquakes in Algeria were the El Asnam earthquake of 10 October 1980 with a magnitude of 7.2 that killed about 2500 people (Ambraseys, 1981) and the Boumerdès earthquake of 21 May 2003 with a magnitude of 6.8 that killed 2278 people (Bounif et al., 2004). The need for a developed technology that can easily and in real time minimize structural vibrations caused by earthquake excitation became an extreme obligation. During the last decade, the control of structures has emerged as a possible technological solution for structural vibration reduction, in which a control device is introduced to the main structure to modify and decrease the damping. The control can be an active, semi-active, or passive one according to the used devices.

The passive control system is based principally on isolation or energy dissipation devices designed to develop an opposite control force to the motion of the structure induced by earthquake excitation. The greatest advantages of these devices are that they are simple, economic, and do not need energy to operate, but they have limited robustness against strong dynamical loads, which limits their utilization. The passive control technologies have been widely employed for a large number of buildings in the world. In Kubo et al. (2014) a seismic isolation with a lead rubber bearing isolator of nuclear Japanese reactor buildings is evaluated. The isolated reactor was exposed to a series of seismic responses to discuss the feasibility of the proposed passive isolation system. Wang et al. (2018) proposed and analysed a seismic base isolation with a bearing isolation exposed to an earthquake excitation. The active control system is more expansive than the passive one: it consists of sensors to measure structural responses, a process to treat responses and to compute the required control force with an adequate control law, and actuators to produce the control force and energy source to power the actuators. These systems use in real time a high external energy to modify the undesirable dynamic behaviour of the structure. The measured responses of the excited structures by sensors are sent to the unit treatment in which the required control force is calculated using a control strategy. From the calculated control force, the applied force is determined, and the actuator receives information from unit treatment and provides this force to the structure.

Recently, major attention has been paid to active structural control research. Shahi et al. (2018) investigated the structural vibration reduction of a 40-storey structure subjected to earthquake excitation with a soil–structure interaction effect. The active control of the structure is ensured by an active tuned mass damper controlled with two linear controllers. The first proposed controller was the proportional integral derivative controller (PID), while the second proposed controller was a linear quadratic regulator (LQR) and the parameters of the damper were optimized using a particle swarm optimization (Shahi et al., 2018). Semi-active control is considered to be the system combining the best features of passive and active systems. It offers the adaptability characteristics of an active control system without requiring large power sources and the stability characteristics of passive control systems. This system can modify mechanical properties using only a computer and a small electronic device with a low power source to operate as a battery, which is critical during excitation events. Numerous studies have been performed on the investigation of the application of semi-active control in structure protection against earthquakes or wind excitation. A semi-active control is designed to improve the seismic behavior of a three-storey excited structure in Bozorgvar and Zahrai (2019) using a magneto-rheological damper controlled by an adaptive neuro-fuzzy where a genetic algorithm adjusts premise and subsequent parameters. The results of the proposed algorithm are compared to the results of the neural network predictive control algorithm and linear quadratic Gaussian and clipped optimal control applied to the same case. The evaluation criteria show the effectiveness of the proposed control in reducing structural vibrations subjected to earthquake excitation.

The hybrid control system can also be considered one of the structural control systems which are a combination of the aforementioned systems. Generally, the hybrid system is composed of an active system combined with a passive system. Thereby, the hybrid system offers the advantages of both coupled systems. Remarkable searches have been made over the last decade. An eight-storey structure is controlled using a hybrid control composed of viscous liquid dampers as a passive control and an active tuned mass damper. The active tuned mass damper is installed on the top floor, and on each one of the other floors a viscous liquid damper is placed. To prove the effectiveness of the proposed hybrid control system in eliminating structural vibrations, this structure was subjected to the Kobe, El Centro, Hachinohe, and Northridge earthquakes (Mitchell et al., 2013).

However, in order to tune the control force of the active or semi-active control device in real time, the design of a robust controller is considered an essential step. In the existing literature, several control techniques and algorithms are quoted. Many papers have investigated the use of non-linear controllers in vibration control. In Zapateiro et al. (2008), an adaptive back-stepping control is proposed to control a 10-storey building using a magneto-rheological damper coupled with passive base isolation. Moreover, a sliding-mode controller was designed to control a multi-freedom structure using a magneto-rheological damper in an experimental and simulated study (Neelakantan and Washington, 2008). From a theoretical point of view, linear controllers are the most preferred one in structural vibration control. These controllers are simple, easy to implement, and converge quickly. Despite this, these controllers do not operate in the presence of non-linearities or uncertainties in the controlled model, which is the practical case. Zizouni et al. (2017) proposed a linear quadratic regulator to control a scaled three-storey structure subjected to the 1940 El Centro earthquake records. The numerical simulation results show the robustness of the linear proposed controller coupled with a clipped optimal algorithm to adjust the magneto-rheological damper tension (Zizouni et al., 2017). Another class of non-linear controllers is called the intelligent controllers, in which the designs do not need any mathematical model. A neural network algorithm is proposed in Zizouni et al. (2019) based on an LQR control trainer to suppress the vibration of civil engineering excited structures using a magneto-rheological damper. The intelligent controller is composed of four layers and three neurons in each hidden layer. The performed neural network controller used only two inputs, in contrast to the original controller needing six inputs for a three-storey scaled structure, reducing the number of sensors to about 77 %. The proposed controller robustness is proven by the numerical simulation responses of a three-storey scaled structure exposed to both the 2011 Tohoku and 2003 Boumerdès earthquakes.

In the civil engineering structural semi-active control, the principal key of reliability and efficiency is the suitable choice of the adopted controller. However, the sliding-mode controller is one of the most used controllers in this field because of its several promises, especially in a complex presence. Otherwise, in the presence of a switching part, this controller exposed an obvious stability phenomenon called chattering caused by an infinite oscillation frequency. Furthermore, the adaptation is the widely adopted solution to suppress the chattering and offer more stability to the sliding-mode controller. Ideally, the desired law of adaptation must offer perfect adjustment of the control gain depending on the system state using low computational energy (Haddad et al., 2001). Recently, the sliding-mode adaptation interested several researchers and has been the investigation subject of various works and studies, especially for suppressing structural vibrations using a magneto-rheological damper for civil engineering structures subjected to earthquake loads. Therefore, an exponential law adaptation of the switching gain of sliding-mode control is investigated. This technique keeps the gain value nearby the optimal value using the exponential estrangement. Thereby, it offers more stability to the system and keeps it around the sliding surface. The adaptive sliding-mode controller is proposed to control the required force of control delivered using a magneto-rheological damper to reduce the vibration of a three-storey tested structure. The effectiveness of the proposed control is proven by numerical simulation of both the 1940 El Centro and 2003 Boumerdès earthquakes (Fali et al., 2019). However, adaptive control in the presence of uncertainties is proposed in Saidi et al. (2019). The upper bound of the sliding surface unknowingly causes overestimation of the control gain to compensate for it. The proposed adaptive law offers high adjustment to the gain depending on the trajectory of the system to overcome remoteness to the sliding surface. In addition, the adaptive control proves the robustness in the control of undesired vibration caused by earthquakes using a magneto-rheological damper.

In this paper, an adaptive non-linear controller is proposed to reduce undesirable vibrations of a scaled structure caused by seismic excitation. The controller is designed to control a semi-active magneto-rheological damper coupled to a clipped algorithm current driver. The sliding-mode controller is reinforced by a switching adaptive law to ensure stability and to suppress the chattering phenomenon. The suggested law offers adaptation of the boundary layer thickness in the sliding surface of the controller. Therefore, the switching jump length is adapted to maintain the desired stability of the system, although the proposed adaptation law switches between two laws which calculated the gain of control depending on the system position compared to the sliding surface. Under the 1940 El Centro earthquake record, the effectiveness of the proposed semi-active control strategy is evaluated. In order to prove the robustness of the control, the numerical simulation results of the controlled and uncontrolled structures are compared and discussed. The rest of the paper is organized as follows: Sect. 2 is reserved for the system presentation in which the magneto-rheological damper and the test scaled structure modelling are illustrated, where the mathematical model of the controlled system is explained. Next, in Sect. 3 the controller and the adaptive law are formulated, ensuring the Lyapunov stability criterion. The numerical example of the 1940 El Centro earthquake is presented and the comparison of the results of the two cited cases is shown in Sect. 4. Finally, this paper is concluded by the drawn conclusion in the last section.

2 The system presentation

2.1 The magneto-rheological damper model

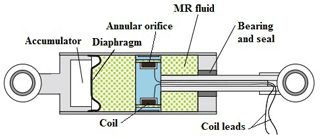
The magneto-rheological device is considered one of the interesting semi-active control devices. The properties offered by the magneto-rheological fluid attracted several numerical and experimental studies and investigations. The main investigations focused on the mathematical modellization of the high non-linear behaviour of the controllable fluid. Nonetheless, in the presence of the current field, this fluid can change its physical properties in milliseconds only. In addition, the device offered simplicity, reliability, and suitable stability in temperature variation (Makris et al., 1996). Recently, magneto-rheological dampers have been used to attenuate structural vibrations caused by earthquake excitation in several buildings. The semi-active control device is presented in Fig. 1.

Figure 1 Cross section of the MR damper body.

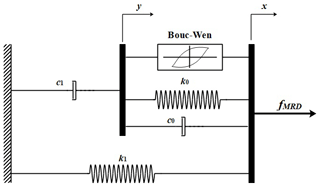
Therefore, from the invention of the magneto-rheological fluid, several studies presented mathematical modelling for the non-linear behaviour of this fluid (Ashtiani et al., 2015; Wang and Liao, 2011). The literature cited different proposed mathematical models, such as the Bingham model (Bingham, 1917), the augmented Bingham model (Gamota and Filisko, 1991), the Herschel–Bulkley model (Herschel and Bulkley, 1926), the Bouc model (Bouc, 1971), and the Bouc–Wen model (Wen, 1976), although the most recently used model is the one established by Spencer et al. (1997) called the generalized Bouc–Wen model presented in Fig. 2.

Figure 2 Generalized Bouc–Wen model of the magneto-rheological damper.

The mathematical generalized Bouc–Wen model is described by the following equations:

$$\begin{array}{}\text{(1)}& {\displaystyle }{c}_{\mathrm{1}}\dot{y}=c_{\mathrm{0}}(\dot{x}-\dot{y})+k_{\mathrm{0}}(x-y)+\mathit{\alpha }z,\text{(2)}& {\displaystyle }\dot{z}=-\mathit{\gamma }|\dot{x}-\dot{y}|z|z{|}^{n-\mathrm{1}}-\mathit{\beta }(\dot{x}-\dot{y}\left)\right|z{|}^n+A(\dot{x}-\dot{y}),\text{(3)}& {\displaystyle }{f}_{\mathrm{MRD}}=c_{\mathrm{0}}(\dot{x}-\dot{y})+k_{\mathrm{0}}(x-y)+k_{\mathrm{1}}(x-x_{\mathrm{0}})+\mathit{\alpha }z,\text{(4)}& {\displaystyle }\mathit{\alpha }={\mathit{\alpha }}_a+{\mathit{\alpha }}_{b}u,\text{(5)}& {\displaystyle }{c}_{\mathrm{1}}=c_{\mathrm{1}a}+c_{\mathrm{1}b}u,\text{(6)}& {\displaystyle }{c}_{\mathrm{0}}=c_{\mathrm{0}a}+c_{\mathrm{0}b}u,\text{(7)}& {\displaystyle }\dot{u}=-\mathit{\eta }(u-v),\end{array}$$

where x and $\dot{x}$ are the damper's rod displacement and velocity, k₀ and c₀ and k₁ and c₁ are, respectively, the accumulator stiffness and viscous damping at low velocity and the accumulator stiffness and viscous damping at high velocity, z is the hysteresis behaviour variable, f_MRD is the damper-generated force, A, α, β, n, and γ are the parameters of the model shape, x₀ is the initial deflection of the spring, y is the damper displacement, u, v, and η are the dynamic phenomenological variable, the applied voltage, and the time response factor, and c_1a, c_1b, c_0a, c_0b, α_a, and α_b are the magneto-rheological damper parameters depending on the applied voltage.

The parameter values of the augmented Bouc–Wen model are shown in Table 1 (Spencer et al., 1997).

Table 1 Parameter values of the augmented Bouc–Wen model.

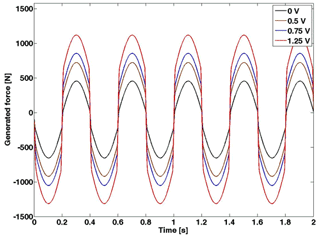
To show the typical hysteresis behaviour of the MR damper, a sinusoidal displacement is applied to the device with a frequency of 2.5 Hz and 1.5 cm amplitude. By contrast, a different constant voltage level is associated with this sinusoidal displacement. The chosen voltage levels are 0, 0.5, 0.75, and 1 V, respectively.

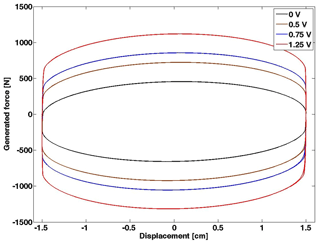
The generated force of the MR damper function of time is illustrated in Fig. 3. Thus, the hysteresis behaviour of the device is depicted in Figs. 4 and 5.

Figure 3 Generated force of the simulated Bouc–Wen model under sinusoidal excitation.

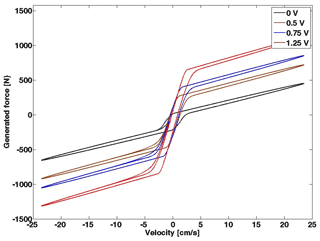
Figure 4 Force–displacement hysteresis loop of the simulated Bouc–Wen model under sinusoidal excitation.

Figure 5 Force–velocity hysteresis loop of the simulated Bouc–Wen model under sinusoidal excitation.

2.2 The tested scaled structure model

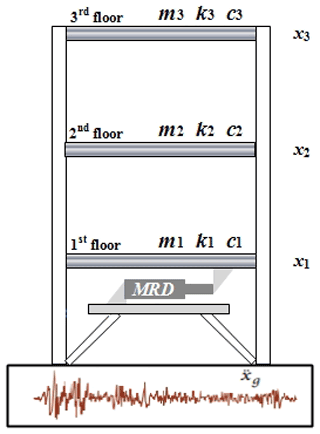
The proposed semi-active control is evaluated using a three-storey scaled structure subjected to a ground motion excitation ${\ddot{x}}_{\mathrm{g}}$. The semi-active control device is a magneto-rheological damper installed on the first floor of the tested structure presented in Fig. 6.

Figure 6 Tested scaled structure model.

The dynamic equation of motion of the system in Fig. 6 is written as

$$\begin{array}{}\text{(8)}& M\ddot{x}+C\dot{x}+Kx=M\mathrm{\Lambda }{\ddot{x}}_{\mathrm{g}}+\mathrm{\Gamma }{f}_{\mathrm{c}},\end{array}$$

where x, $\dot{x}$, and $\ddot{x}$ are the displacement, velocity, and acceleration vectors of the structure, and M, C, and K are the mass, damping, and stiffness matrices of the structure defined as follows.

$$\begin{array}{}\text{(9)}& {\displaystyle }M=\left[\begin{array}{ccc}{m}_{\mathrm{1}}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& m_{\mathrm{2}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& m_{\mathrm{3}}\end{array}\right]=\left[\begin{array}{ccc}\mathrm{98.3}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{98.3}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{98.3}\end{array}\right]\left(\mathrm{kg}\right)\text{(10)}& {\displaystyle }\begin{array}{rl}C& =\left[\begin{array}{ccc}{c}_{\mathrm{1}}+c_{\mathrm{2}}& -c_{\mathrm{2}}& \mathrm{0}\\ -c_{\mathrm{2}}& c_{\mathrm{2}}+c_{\mathrm{3}}& -c_{\mathrm{3}}\\ \mathrm{0}& -c_{\mathrm{3}}& c_{\mathrm{3}}\end{array}\right]\\ & =\left[\begin{array}{ccc}\mathrm{175}& -\mathrm{50}& \mathrm{0}\\ -\mathrm{50}& \mathrm{100}& -\mathrm{50}\\ \mathrm{0}& -\mathrm{50}& \mathrm{50}\end{array}\right]\left(\mathrm{N}\mathrm{s}{\mathrm{m}}^{-\mathrm{1}}\right)\end{array}\end{array}$$

$$\begin{array}{}\text{(11)}& \begin{array}{rl}K& =\left[\begin{array}{ccc}{k}_{\mathrm{1}}+k_{\mathrm{2}}& -k_{\mathrm{2}}& \mathrm{0}\\ -k_{\mathrm{2}}& k_{\mathrm{2}}+k_{\mathrm{3}}& -k_{\mathrm{3}}\\ \mathrm{0}& -k_{\mathrm{3}}& k_{\mathrm{3}}\end{array}\right]\\ & ={\mathrm{10}}^{\mathrm{5}}\left[\begin{array}{ccc}\mathrm{12}& -\mathrm{6.84}& \mathrm{0}\\ -\mathrm{6.84}& \mathrm{13.7}& -\mathrm{6.84}\\ \mathrm{0}& -\mathrm{6.84}& \mathrm{6.84}\end{array}\right]\left(\mathrm{N}{\mathrm{m}}^{-\mathrm{1}}\right)\end{array}\end{array}$$

f_c is the control force, Λ and Γ are the earthquake effect vectors, and the damper position vector is defined as follows.

$$\begin{array}{}\text{(12)}& {\displaystyle }\mathrm{\Lambda }={\left[\begin{array}{ccc}\mathrm{1}& \mathrm{1}& \mathrm{1}\end{array}\right]}^T\text{(13)}& {\displaystyle }\mathrm{\Gamma }={\left[\begin{array}{ccc}-\mathrm{1}& \mathrm{0}& \mathrm{0}\end{array}\right]}^T\end{array}$$

3 Semi-active control algorithm

Since its appearance in the 1950s the sliding-mode controller has been considered one of the most interesting non-linear controllers. The robustness of this controller, especially in the presence of the uncertainties or the system condition variations, makes it one of the most used controllers. However, several investigations and studies are interested in structural vibration control using a sliding-mode controller, whereas the high-frequency oscillation of the switch controller part caused the chattering problem which can affect the system stability and precision (Youn and Özgüner, 1999).

Therefore, various solutions were investigated to suppress the undesirable chattering effect and to perform the sliding-mode controller. Furthermore, several tested techniques proved their efficiency as the boundary layer technique using the saturation function (Utkin and Chang, 2009), the high-order sliding mode (Plestan et al., 2008), the fuzzy sliding mode (Alli and Yakut, 2005), the neural network sliding mode, the adaptive sliding mode (Fali et al., 2019), and others (Chen et al., 2016).

Consider the non-linear system

$$\begin{array}{}\text{(14)}& \dot{x}=f(x,t)+g(x,t)u.\end{array}$$

x and u are, respectively, the state vector and the control input, and f(x) and g(x) are smooth functions.

The sliding-mode controller (SMC) is composed of two components as follows:

$$\begin{array}{}\text{(15)}& u_{\mathrm{SMC}}=u_{\mathrm{eq}}+u_{\mathrm{s}}.\end{array}$$

u_eq is the equivalent part of the controller and u_s is the controller switching part given as

$$\begin{array}{}\text{(16)}& {\displaystyle }{u}_{\mathrm{eq}}(x,t)=-\left(s\right(x,t\left)g\right(x,t\left){)}^{-\mathrm{1}}s\right(x\left)f\right(x,t),\text{(17)}& {\displaystyle }{u}_{\mathrm{s}}=G\cdot \mathrm{sgn}\left(s\right(x,t\left)\right),\end{array}$$

where G is the control switch gain, sgn is the signum function, and s is the sliding surface given by

$$\begin{array}{}\text{(18)}& s(x,t)=Se.\end{array}$$

S is the defined positive switching matrix of the sliding surface and e is the tracking error of the state vector.

In this stage, the switching part of the sliding-mode controller in Eq. (17) caused finite frequency in the dynamic sliding motion called chattering. In this paper, a switching law adaptation is proposed to overcome the chattering problem and perform the switching part of the sliding-mode controller. The main goal of adaptive control is to design the system to maintain the same properties under uncertain conditions. Thereby, the controller modifies its law to manage the new situation based on the currently collected information. Thus, Eq. (17) becomes

$$\begin{array}{}\text{(19)}& u_{\mathrm{as}}=\stackrel{\mathrm{̃}}{G}\cdot \mathrm{sgn}\left(s\right(x,t\left)\right).\end{array}$$

u_as is the adaptive controller switching part and $\stackrel{\mathrm{̃}}{G}$ is the adapting gain depending on the following switching law (Bandyopadhyay et al., 2013):

$$\begin{array}{}\text{(20)}& {\displaystyle }\begin{array}{rl}& \mathrm{If}\left|s\right(x,t\left)\right|>\mathrm{0}⟹\dot{\stackrel{\mathrm{̃}}{G}}=\stackrel{\mathrm{‾}}{G_{\mathrm{1}}}\cdot \left|\right(s(x,t)|\\ & \mathrm{with}\stackrel{\mathrm{‾}}{G_{\mathrm{1}}}>\mathrm{0}\mathrm{and}\stackrel{\mathrm{̃}}{G}\left(\mathrm{0}\right)=\mathrm{0},\end{array}\text{(21)}& {\displaystyle }\mathrm{else}\stackrel{\mathrm{̃}}{G}=\stackrel{\mathrm{‾}}{G_{\mathrm{2}}}\cdot \left|\mathit{\rho }\right|+\stackrel{\mathrm{‾}}{G_{\mathrm{3}}}\mathrm{with}\mathit{\tau }\cdot \dot{\mathit{\rho }}+\mathit{\rho }=\mathrm{sgn}\left(s\right(x,t\left)\right).\end{array}$$

where τ is a positive time constant, ρ is the average value of the low-pass filter; $\stackrel{\mathrm{‾}}{G_{\mathrm{1}}}$ and $\stackrel{\mathrm{‾}}{G_{\mathrm{2}}}$ are positive gains. The Lyapunov stability is satisfied if the following condition is satisfied:

$$\begin{array}{}\text{(22)}& \dot{s}(x,t)\cdot s(x,t)\le \mathrm{0}.\end{array}$$

For this reason, the first Lyapunov candidate function of Eq. (20) is proposed as (Lee and Utkin, 2007)

$$\begin{array}{}\text{(23)}& {\displaystyle }{V}_{\mathrm{1}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{s}^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\gamma }}}(G-G^{*}{)}^{\mathrm{2}},\text{(24)}& {\displaystyle }\begin{array}{rl}{\dot{V}}_{\mathrm{1}}& =s\cdot \mathit{\chi }(x,t)-s\cdot \mathit{\varphi }(x,t)\cdot G\cdot \mathrm{sgn}\left(s\right)\\ & +{\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }}}(G-G^{*}){\stackrel{\mathrm{‾}}{G}}_{\mathrm{1}}\cdot \left|s\right|,\end{array}\end{array}$$

where G^* is the limit value of G, and $\mathit{\chi }(x,t)=\frac{\partial s}{\partial t}\frac{\partial s}{\partial x}f(x,t)$ and $\mathit{\varphi }(x,t)=\frac{\partial s}{\partial x}g(x,t)$ are unknown functions limited by the values χ_m, ϕ_m, and ϕ_M as $\left|\mathit{\chi }\right(x,t\left)\right|\le {\mathit{\chi }}_m$ and ${\mathit{\varphi }}_m\le \mathit{\varphi }(x,t)\le {\mathit{\varphi }}_M$, where ϕ(x,t) is assumed to be positive.

$$\begin{array}{}\text{(25)}& {\displaystyle }{\dot{V}}_{\mathrm{1}}\le \left|s\right|\cdot {\mathit{\chi }}_m-{\mathit{\varphi }}_m\cdot G\left|s\right|+{\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }}}(G-G^{*}){\stackrel{\mathrm{‾}}{G}}_{\mathrm{1}}\cdot \left|s\right|,\text{(26)}& {\displaystyle }\begin{array}{rl}{\dot{V}}_{\mathrm{1}}& \le \left|s\right|\cdot {\mathit{\chi }}_m-{\mathit{\varphi }}_m\cdot G\left|s\right|+{\mathit{\varphi }}_m\cdot G^{*}\left|s\right|-{\mathit{\varphi }}_m\cdot G^{*}\left|s\right|\\ & +{\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }}}(G-G^{*}){\stackrel{\mathrm{‾}}{G}}_{\mathrm{1}}\cdot \left|s\right|,\end{array}\text{(27)}& {\displaystyle }\begin{array}{rl}{\dot{V}}_{\mathrm{1}}& \le ({\mathit{\chi }}_m-{\mathit{\varphi }}_m\cdot G^{*})\left|s\right|+\left(-{\mathit{\varphi }}_m\left|s\right|+{\displaystyle \frac{{\stackrel{\mathrm{‾}}{G}}_{\mathrm{1}}}{\mathit{\gamma }}}\left|s\right|\right)\\ & \cdot (G-G^{*}),\end{array}\end{array}$$

where ${\dot{V}}_{\mathrm{1}}\cdot V_{\mathrm{1}}\le \mathrm{0}$ if $G^{*}>\frac{{\mathit{\chi }}_m}{{\mathit{\varphi }}_m}$ and $\mathit{\gamma }<\frac{{\stackrel{\mathrm{‾}}{G}}_{\mathrm{1}}}{{\mathit{\varphi }}_m}$ are satisfied.

The second Lyapunov candidate function of Eq. (21) is proposed as

$$\begin{array}{}\text{(28)}& {\displaystyle }{V}_{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{s}^{\mathrm{2}}-\left(G_{\mathrm{0}}\right|\mathit{\rho }|+\mathit{\delta }),\text{(29)}& {\displaystyle }{\dot{V}}_{\mathrm{2}}=s\cdot \mathit{\chi }(x,t)-\left(G_{\mathrm{0}}\right|\mathit{\rho }|+\mathit{\delta }),\end{array}$$

where G₀ is the positive gain, ρ is the average sgn(s) value, and the Laplace transformation of the first-order filter $\mathit{\tau }\cdot \dot{\mathit{\rho }}+\mathit{\rho }=\mathrm{sgn}\left(s\right)$ is $\frac{\mathrm{1}}{\mathit{\rho }p+\mathrm{1}}$.

$$\begin{array}{}\text{(30)}& {\dot{V}}_{\mathrm{2}}=\mathit{\chi }(x,t)-\mathit{\rho }\cdot \left(G_{\mathrm{0}}\right|\mathit{\rho }|+\mathit{\delta })\end{array}$$

${\dot{V}}_{\mathrm{2}}\cdot V_{\mathrm{2}}\le \mathrm{0}$ is satisfied if $\mathit{\rho }=(\mathit{\delta }\pm \frac{\sqrt{{\mathit{\delta }}^{\mathrm{2}}\pm \mathrm{4}{G}_{\mathrm{0}}\cdot \mathit{\chi }(x,t)}}{\mathrm{2}{G}_{\mathrm{0}}})$.

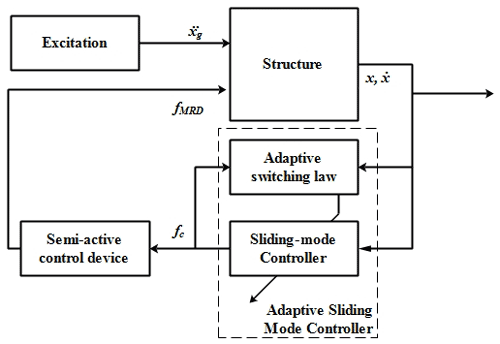
Therefore, the schematic block of the proposed semi-active adaptive control is illustrated in Fig. 7.

Figure 7 The schematic block of the semi-active adaptive control.

When x, $\dot{x}$ are the structural responses, f_MRD, f_c are the magneto-rheological damper-generated force and the controller-calculated force. However, the magneto-rheological damper cannot activate the calculated force directly because the device operates based on the applied current voltage, and thus an algorithm is designed to control the current driver proportionately to the controller's calculated force. Hence, an off–on switching algorithm based on the Heaviside step function is proposed.

$$\begin{array}{}\text{(31)}& v=v_{max}\cdot H\left(\right(f_{\mathrm{c}}-f_{\mathrm{MRD}}\left)f_{\mathrm{MRD}}\right)\end{array}$$

v is the required voltage, v_max is the maximum voltage of the current driver, and H(.) is the Heaviside step function.

4 Numerical example

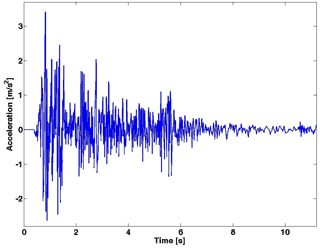
To prove the robustness of the proposed semi-active control strategy using the magneto-rheological damper controlled by an adaptive sliding-mode controller, a numerical test is proposed. Based on the Matlab/Simulink software, the results were carried out and plotted. The tested scaled structure of Fig. 6 is subjected to a time-scaled earthquake record of the 1940 El Centro earthquake presented in Fig. 8.

Figure 8 The NS (north–south) time-scaled component of the 1940 El Centro earthquake.

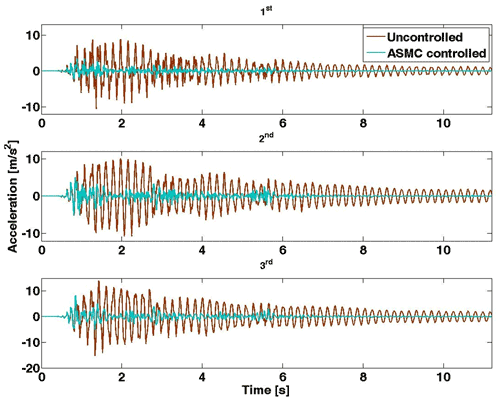
The numerical displacement results of the compared two cases of controlled and uncontrolled structures under the 1940 El Centro excitation are clearly shown for the three floors in Fig. 9. However, the acceleration-compared responses of the structure floors of the uncontrolled and controlled structures are depicted in Fig. 10.

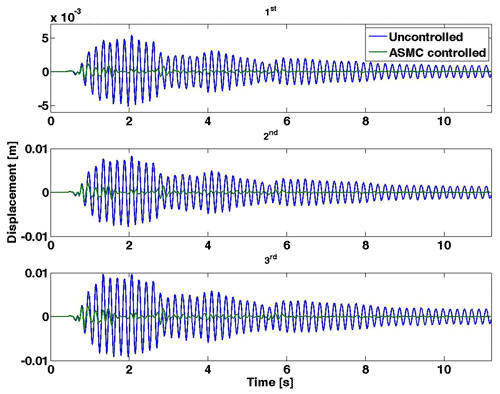
Figure 9 Displacement responses of the first, second, and third floors to the 1940 El Centro earthquake.

Figure 10 Structure floor acceleration responses to the 1940 El Centro earthquake.

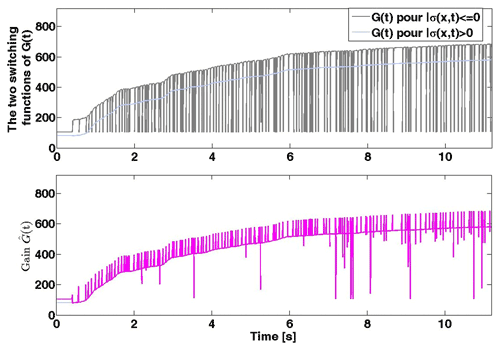
Nevertheless, the time adjustment of the adaptive gain of Eqs. (20) and (21) under the 1940 El Centro earthquake is presented in Fig. 11. In addition, the response of the generated voltage to the magneto-rheological damper function of time during the 1940 El Centro earthquake is presented in Fig. 12.

Figure 11 Time response of adaptive control gain under the 1940 El Centro earthquake.

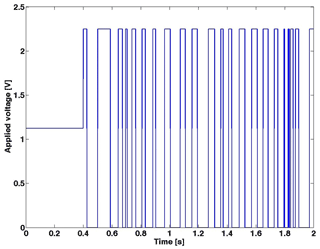
Figure 12 Zoomed time response voltages applied to the MR damper during the 1940 El Centro earthquake.

The effectiveness of the proposed adaptive semi-active control strategy is proven using the displacement floor reduction ratio given by

$$\begin{array}{}\text{(32)}& {\mathrm{Rd}}_{\mathrm{r}}={\displaystyle \frac{\left|x_i^{max}\right|-max\left|x_i\right|}{\left|x_i^{max}\right|}}.\end{array}$$

Table 2 The peak displacement reduction ratio of the SMC and ASMC during the 1940 El Centro earthquake.

Table 3 Values of performance indices of the SMC and ASMC during the 1940 El Centro earthquake.

In addition, two groups of evaluation indices are calculated to confirm the robustness of the semi-active adaptive sliding-mode controller in suppressing structural vibrations. The first group of the index (J₁–J₆) is meant to appraise the structure responses under the proposed control and the second (J₇–J₉) to evaluate the semi-active device performance under the adaptive controller. Hence, the performance indices are calculated as follows.

$$\begin{array}{}\text{(33)}& {\displaystyle }{J}_{\mathrm{1}}={\displaystyle \frac{max\left|d_{\mathrm{i}}\right|}{d_{\mathrm{i}}^{max}}}\text{(34)}& {\displaystyle }{J}_{\mathrm{2}}={\displaystyle \frac{max\left|{\ddot{x}}_{ai}\right|}{{\ddot{x}}_{ai}^{max}}}\text{(35)}& {\displaystyle }{J}_{\mathrm{3}}={\displaystyle \frac{max|\sum m_i{\ddot{x}}_{ai}|}{F_{\mathrm{b}}^{max}}}\text{(36)}& {\displaystyle }{J}_{\mathrm{4}}={\displaystyle \frac{max\left|\right|d_{\mathrm{i}}\left|\right|}{\left|\right|d_{\mathrm{i}}^{max}\left|\right|}}\text{(37)}& {\displaystyle }{J}_{\mathrm{5}}={\displaystyle \frac{max{\ddot{x}}_{ai}}{{\ddot{x}}_{ai}^{max}}}\text{(38)}& {\displaystyle }{J}_{\mathrm{6}}={\displaystyle \frac{max\sum m_i{\ddot{x}}_{ai}}{F_{\mathrm{b}}^{max}}}\text{(39)}& {\displaystyle }{J}_{\mathrm{7}}={\displaystyle \frac{max\left|f_{\mathrm{MRD}}\right|}{W}}\text{(40)}& {\displaystyle }{J}_{\mathrm{8}}={\displaystyle \frac{max\left|y_l^a\right|}{x^{max}}}\text{(41)}& {\displaystyle }{J}_{\mathrm{9}}={\displaystyle \frac{max|\sum v_l|}{x^{max}W}}\end{array}$$

Rd_r is the displacement reduction ratio, x_i is the peak floor displacement, $x_i^{max}$ is the uncontrolled floor peak displacement, ${\ddot{x}}_{ai}$ is the floor peak acceleration, d_i is the drift inter-storey, m_i is the floor's mass, ${\ddot{x}}_i^{max}$ is the uncontrolled floor peak acceleration, f_MRD is the damper-generated force, $F_{\mathrm{b}}^{max}$ is the base shear force, W is the structure weight, $d_{\mathrm{i}}^{max}$ is the uncontrolled floor drift ratio, v_l and $y_l^a$ are the maximum power generated to the damper and the maximum across the damper displacement, and the subscription i is the designed floor number.

The displacement floor reduction ratio results are given in Table 2. However, the results of the calculated performance indices are listed in Table 3.

Using an earthquake record as input excitation to investigate the performance of the adaptive control approach, the responses of the tested structure are examined. The displacement responses of the structure are reduced reasonably compared to the responses of the uncontrolled structure under the selected excitation, as observed from the comparison of the plotted responses of the uncontrolled structure with those of the controlled structure, using the magneto-rheological damper with an adaptive sliding-mode controller in which the semi-active adaptive strategy provides adequate vibration reduction. In addition, through system computation, the stability of the system is observed and the chatter effect is completely reduced. The switching law offers more stability to the controlled system than the previously tested laws (Fali et al., 2019; Saidi et al., 2019) but needed more power of control in computation. The numerical results are used to calculate the evaluation indices to evaluate the adaptive control strategy performance. Offering more stability by the switch adaptation of the sliding-mode controller to the adaptive controller maintains the robustness of the classical controller. In fact, the performance indices are calculated using the two controllers, both classical and adaptive, under the seismic excitation of El Centro in 1940. From the calculated indices it is obvious that the performance of the adaptive sliding-mode controller in reducing the structural vibration using the magneto-rheological damper is proven. In contrast, future amelioration is the perfection of the current law by a precipitation condition for the gain adjustment before reaching the sliding surface to minimize the required control power and reduce the time response of the system.

5 Conclusions

A semi-active adaptive control has been proposed for the vibration response reduction of seismically excited structures. The proposed non-linear sliding-mode controller is designed to calculate the desired control force. In fact, the classical sliding-mode controller provides chatters in numerical simulations. The adaptive proposed law is stability reinforcement to the classical sliding-mode controller. Through numerical simulation investigation of a tested scaled structure, it is noted that the proposed adaptive sliding-mode control approach performs very well with the stability of the system output. The compared numerical simulation results of the displacement responses of the tested structure of the controlled and uncontrolled cases have shown clearly the robustness of the proposed strategy. The effectiveness of the adaptive sliding control using a semi-active magneto-rheological damper to suppress structural vibrations is verified by nine performance indices under the 1940 El Centro earthquake excitation. In addition, the comparison of the sliding-mode controller and the adaptive sliding-mode controller results using the peak displacement reduction ratio and the performance indices proves the reliability of the adaptive approach.