Automatic adjustment of laparoscopic pose using deep reinforcement learning

Laparoscopic arm and instrument arm control tasks are usually accomplished by an operative doctor. Because of intensive workload and long operative time, this method not only causes the operation not to be flow, but also increases operation risk. In this paper, we propose a method for automatic adjustment of laparoscopic pose based on vision and deep reinforcement learning. Firstly, based on the Deep Q Network framework, the raw laparoscopic image is taken as the only input to estimate the Q values corresponding to joint actions. Then, the surgical instrument pose information used to formulate reward functions is obtained through object-tracking and image-processing technology. Finally, a deep neural network adopted in the Q-value estimation consists of convolutional neural networks for feature extraction and fully connected layers for policy learning. The proposed method is validated in simulation. In different test scenarios, the laparoscopic arm can be well automatically adjusted so that surgical instruments with different postures are in the proper position of the field of view. Simulation results demonstrate the effectiveness of the method in learning the highly non-linear mapping between laparoscopic images and the optimal action policy of a laparoscopic arm.

1 Introduction

In recent years, minimally invasive surgery (MIS) has become more and more important. MIS has been applied in various surgeries, including brain, heart, and liver (Chang and Rattner, 2019). This is due to its many benefits in medical practice. In addition to obvious less invasiveness, there are many advantages such as much less postoperative pain and blood loss. MIS also brings advantages of shorter recovery time and less infective rate, which make them beneficial to both inpatients and clinicians (Davies, 1995).

In a typical celiac minimally invasive robot-assisted surgery procedure, the surgeon is needed to control two or three instrument arms (Pandya et al., 2014). A laparoscopic arm is usually controlled by the doctor themselves or by an assistant. When the surgeon controls both instrument arm and laparoscopic arm, the surgeon must frequently stop to change the laparoscopic viewpoint, which causes the operation to be unstable and not smooth. While directing an assistant to control the laparoscopic arm leads to increased operation time, with a laparoscopic pose automatic adjustment system, the surgeon will not have to manually move the laparoscopic arm in a robot-assisted surgery, and the expert assistant can be eliminated.

At present, many researchers have studied that in the method of laparoscopic pose adjustment, which can be classified as follows.

1. The eye-tracking-based method captures human eye movements through the eyeball positioning device, controls camera movement, and adjusts the camera's post and field of vision. Ali et al. (2008) developed an autonomous eye-gaze-based laparoscopic positioning system, which can keep the user's gaze point region at the centre of the laparoscope viewpoint. Cao et al. (2016) developed a laparoscopic post-adjustment system based on pupil variation using a support vector machine classifier (SVM) and a probabilistic neural network classifier (PNN).

2. The kinematics-based method acquires pose information and vector information such as velocity and acceleration of surgical instrument through a sensor and then adjusts the laparoscopic pose using the kinematic model relationship. Sandoval et al. (2021) made the laparoscopic posture able to be automatically adjusted based on the kinematics model and motion data of the surgical instruments. Yu et al. (2017) proposed a method for automatically adjusting the position of the laparoscopic window based on the kinematics model of the laparoscopic arm and surgical field parameters.

3. The vision-based method obtains post and trajectory information of the surgical instrument from laparoscopic imaging through image-processing and visual-tracking technology and then deduces the moving image relationship between the laparoscope and the laparoscopic arm. Shin et al. (2014) proposed a 3D instrument-tracking method using a single camera, which can obtain the 3D positions, roll angle, and grasper angle of the laparoscopic instrument with markers. Zhao et al. (2017) proposed a 2D/3D tracking-by-detection framework, which uses line features to describe the shaft via the RANSAC scheme and uses special image features to depict the end-effector based on deep learning.

4. Other methods: Franz et al. (2014) describe the basic working principles of electromagnetic (EM) tracking systems and summarize the future potential and limitations of EM tracking for medical use. Zinchenko et al. (2015) proposed using combined motion of surgical instruments to suggest robotics arm movements so that the camera can be repositioned, which is called “flag language”.

We present a novel method for laparoscopic pose automatic adjustment based on machine vision and deep reinforcement learning (Kober et al., 2013; Sekkat et al., 2021; Bohez et al., 2017; Zhang et al., 2016) in this paper. The laparoscopic arm will be automatically adjusted according to the condition of the surgical instrument to ensure that the surgical instruments maintain the proper position and size in the operation field.

2 Preliminaries

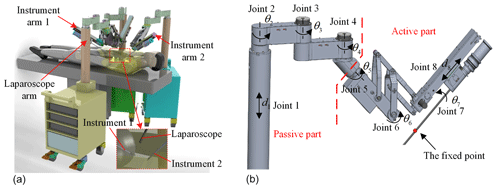
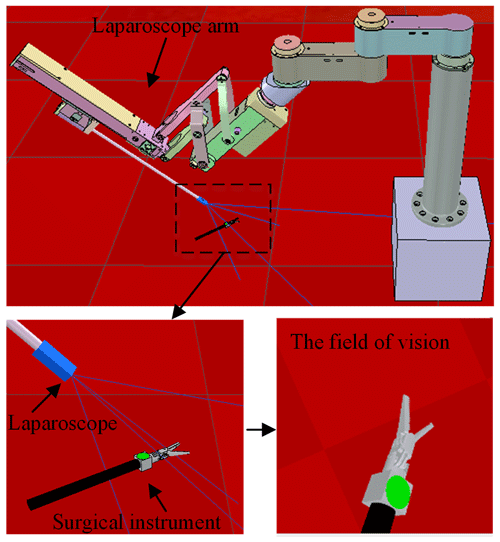
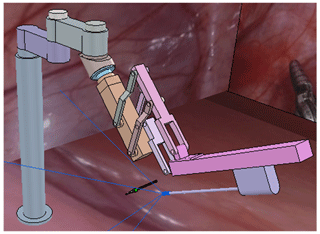
A celiac minimally invasive robot-assisted surgery system generally consists of a robotic arm (laparoscopic arm) with a laparoscope and two or three robotic arms (instrument arm) with a surgical instrument at the end, as shown in Fig. 1a.

The structure of the surgical robotic arm used in this paper is shown in Fig. 1b. The first four joints form the passive parts that are used for robotic arm pre-operative placement. The last four joints are active parts. During the operation, the doctor controls the active part through a master manipulator to adjust the posture of the end surgical instrument or laparoscope.

Figure 1 The MIS robotic system and its robotic arm structure. (a) Celiac minimally invasive robot-assisted surgery system. (b) The structure of the surgical robotic arm.

3 Laparoscopic pose automatic adjustment method

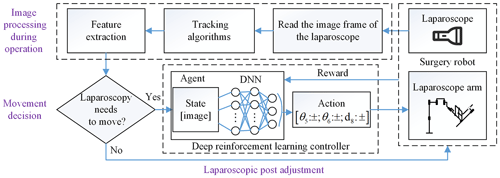
In this section, we give a total introduction of our method frame for laparoscopic pose automatic adjustment. The method is composed of two parts: the image processing and laparoscopic pose adjustment, as shown in Fig. 2. The former is divided into object detection before operation and tracking to obtain the position and size of the surgical instrument as pose parameters and then determine whether the laparoscopic pose needs to be adjusted through movement decision. Finally, we train a motion controller which is composed of a deep neural network (DNN) and reinforcement learning, taking the laparoscopic image as input and the outputting laparoscopic arm action. It controls the adaptive motion of the laparoscopic arm so that the surgical instrument is in the proper position of laparoscopic vision.

Figure 2 Laparoscopic pose automatic adjustment method.

4 Movement decision

In this section, we first describe how to extract features of surgical instruments before operation, and then we use a scale-adaptive algorithm to track surgical instruments. Finally, we describe the movement decision module to determine whether the laparoscope requires movement regulation.

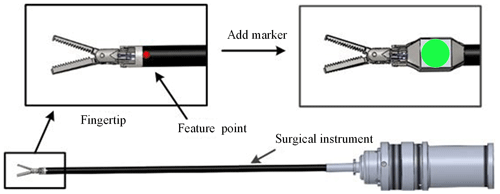
As shown in Fig. 3, we add a simple and specific marker in the surgical instrument. We can indirectly obtain the pose of the surgical instrument by detecting the pose characteristics of the marker, which can avoid the disadvantages of more time and workload for identifying the whole surgical instrument. The design of the marker takes advantage of the rotation invariance of the circular feature. According to the mapping relationship, the circle becomes an ellipse during the rotation, and its long axis size remains unchanged. So, the position information of the surgical instruments is replaced with the coordinates of the circle centre, and the size of the surgical instruments is replaced with the long axis of the circular markers.

Figure 3 Surgical instrument marker setting.

Through the relevant image-processing technology, the pose parameters of the surgical instruments can be obtained. First, we obtain the greyscale probability density map of the image by back projection. Then, we can calculate the elliptic equation using the method of ellipse fitting by image inertia moment and obtain centre coordinates and the elliptic long axis value.

To quickly extract the post parameters of the surgical instrument, we need to quickly track the surgical instruments to obtain the adaptive size region of interest. The continuously adaptive mean shift (CAMShift) (Comaniciu and Meer, 2002) algorithm through OpenCV implementation for tracking was used in this paper. The CAMShift algorithm skilfully exploits the mean-shift algorithm by the adaptive region size adjustment step.

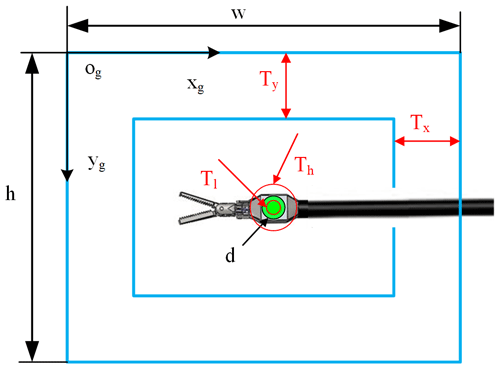
Before controlling the laparoscopic arm movement, it is judged based on the visual field state of the surgical instrument and the set motion decision conditions for whether exercise is required. Specific parameters are as shown in Fig. 4. In this paper, in order to simplify the simulation environment, it is assumed that there is only one surgical instrument in the laparoscopic field of view.

Where the elliptic long-axis value d is used to indicate the relative size of the surgical instrument, the centre coordinate (x,y) shows the position of the surgical instrument in the field of view. T_l and T_h are the lower threshold and upper threshold of the surgical instrument size. T_x and T_y are thresholds of the surgical instrument position. When any one of these thresholds is exceeded, the laparoscopic arm moves. Setting these thresholds can effectively avoid laparoscopic sensitivity to surgical instrument movement.

5 Laparoscopic motion control based on deep reinforcement learning

In this work, we use deep reinforcement learning to map the laparoscopic image end to end to the joint motion of the laparoscopic arm. In Sect. 5.1 the Markov model of laparoscopic visual field adjustment is introduced, in Sect. 5.2 the network structure of the Deep Q Network (DQN) (Mnih et al., 2015) is introduced, and in Sect. 5.3 the reward function and network training algorithm are introduced.

5.1 Markov model of laparoscopic visual field adjustment

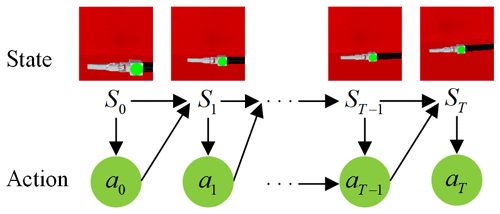
The laparoscopic arm control system makes action decisions based only on the laparoscopic field of view at the current moment, making the active joints of the laparoscopic arm move and obtaining a new laparoscopic field of view for the next step of motion control until the automatic adjustment task of the laparoscopic field of view is completed, as shown in Fig. 5. Therefore, the problem of automatic adjustment of laparoscopic posture can be expressed as the Markov decision process (MDP), a common model of reinforcement learning (RL) (Mnih et al., 2013; Silver et al., 2014; Gu et al., 2016; Mnih et al., 2016). An MDP comprises a five-tuple $\mathit{\{}S,A,R,P,\mathit{\gamma }\mathit{\}}$. Here S is a finite set of states, A is a finite set of actions, P is the transition probability of states, $R:S\times A\times S\to R$ is the reward function, and γ is a discount factor. The goal of an RL agent is to learn the strategy π=p(a|s) to maximize the total discounted reward $G\left(t\right)={\sum }_{k=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\gamma }}^k{R}_{t+k+\mathrm{1}}$. The action-value function predicts all future rewards when performing the action a at the state s according to the strategy $\mathit{\pi }:Q_{\mathit{\pi }}(s,a)=E_{\mathit{\pi }}[G_t\mathrm{|}{S}_t=s,A_t=a]$. The optimal strategy can be obtained by solving the optimal action-value function: $Q_{\ast }(s,a)=R_s^a+\mathit{\gamma }{\sum }_{s^{\prime }\in S}{P}_{s{s}^{\prime }}^{a}max{Q}_{\ast }(s^{\prime },a^{\prime })$.

Figure 4 Threshold setting.

Figure 5 Markov model of laparoscopic visual field adjustment.

5.2 Deep Q Network

In this work, we use a deep neural network to calculate the $Q(s,a;{\mathit{\theta }}_i)$ value for performing action a in a specific state s, and the optimal $Q_{\ast }(s,a;{\mathit{\theta }}_i)$ value is obtained by optimizing the neural network parameter θ. This algorithm that combines deep learning and reinforcement learning to achieve end-to-end learning from state to action is the DQN, which can be described as a pioneering work in deep reinforcement learning. When the state s^′ and $R_s^a$ value obtained by performing action a in state s are unique, the target Q value output by the neural network in the current iteration i can be expressed as $y_i=r+\mathit{\gamma }maxQ(s^{\prime },a^{\prime },{\mathit{\theta }}_i)$. DeepMind released an article (Mnih et al., 2015) in Nature, introducing the concept of a target network to further break the association of the target Q value and the current Q value. The concept of a target network with weight θ⁻ uses the old deep neural network to get the target Q value. Here are the optimization goals for the DQN with a loss function $L_i\left({\mathit{\theta }}_i\right)=E\left[\right(r+\mathit{\gamma }{max}_{a^{\prime }}Q(s^{\prime },a^{\prime };{\mathit{\theta }}_i^{-})-Q(s,a;{\mathit{\theta }}_i){)}^{\mathrm{2}}]$.

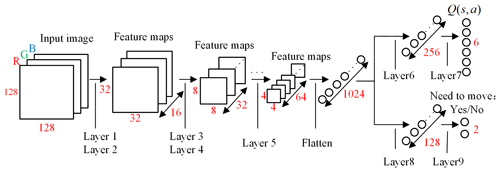
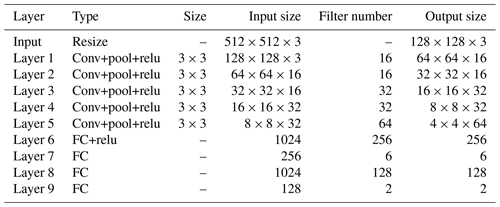
The DQN uses the evaluation network to calculate the $Q(s,a;{\mathit{\theta }}_i)$ and the target network to calculate the $Q(s^{\prime },a^{\prime };{\mathit{\theta }}_i^{-})$. The two networks have the same structure, as shown in Fig. 6. The network uses images obtained from laparoscopy as input, uses convolutional neural networks (CNNs) (Long et al., 2015) to extract features, and uses fully connected (FC) layers for strategy learning. To reduce the size of the feature map and increase the non-linearity, each convolutional layer is connected with a maximum pooling layer and a Relu layer. The image is resized to 128×128 before being forwarded into the network, and it finally obtains a $\mathrm{4}\times \mathrm{4}\times \mathrm{64}$ visual feature map through a series of convolution and pooling operations.

Then the flattened visual features are fed into policy learning networks on the upper side which consist of two fully connected layers of 256 neurons and 6 neurons respectively. The six neurons in the output layer are the Q values of the six actions of the laparoscopic arm. The six actions are the joint variables of rotary joints 5 and 6 and prismatic joint 8 increasing and decreasing. The rotary joint angle increasing/decreasing step is constant at 2^∘, and the prismatic joint displacement is 10 mm. The policy learning network on the lower side determines whether the laparoscopic arm needs to be moved during the testing. The specific network configuration is shown in Table 1.

Figure 6 The network structure for the actor estimation.

Table 1 Network architecture configuration.

5.3 Design of the reward function and the network training algorithm

The reward of each action is determined according to the coordinates (x,y) and relative size of the surgical instrument (z), as shown in Eqs. (1) and (2):

$$\begin{array}{c}\text{(1)}& {\displaystyle }\mathrm{\text{reward}}=\left\{\begin{array}{ll}\mathrm{3}& \text{if }|x-x_{\mathrm{0}}|\le \frac{t_x}{\mathrm{2}}\text{ and }|y-y_{\mathrm{0}}|\le \frac{t_y}{\mathrm{2}}\\ & \text{and }|z-z_{\mathrm{0}}|\le \frac{t_z}{\mathrm{2}},\\ -\mathrm{3}& \text{if }|x-x_{\mathrm{0}}|\le \frac{m_x}{\mathrm{2}}\text{ or }|y-y_{\mathrm{0}}|\le \frac{m_y}{\mathrm{2}},\\ & \text{or }|z-z_{\mathrm{0}}|\le \frac{m_z}{\mathrm{2}}\\ {\text{reward}}_{\text{buff}}& \text{others},\end{array}\right.{\displaystyle }{\text{reward}}_{\text{buff}}=\\ \text{(2)}& {\displaystyle }\sum _{i=x,y,z}{\mathit{\lambda }}_i\left({\displaystyle \frac{\mathrm{2}}{m_i-t_i}}\times max\left(\text{abs}\right(i-i_{\mathrm{0}}),{\displaystyle \frac{t_i}{\mathrm{2}}})+{\displaystyle \frac{t_i}{(m_i-t_i)}}\right),\end{array}$$

where x₀ and y₀ are the coordinates of the centre point of the image, and t₀ is the set standard size of the surgical instrument. $t_x,t_y,t_z$ represents the tolerable error. When $x,y,z$ is within the tolerable error range, the surgical instrument is in the correct position. $m_x,m_y,m_z$ represents the maximum error. When $x,y,z$ is outside the maximum error range, the surgical instrument is in the wrong position. If the surgical instrument is in the correct position and the wrong position, the task is terminated.

We train the DQN model in a simulation environment to obtain the best network parameters. The training process is shown in Algorithm 1. At the beginning of each epoch, we get the initial state. According to the state, we can calculate the reward and judge whether the task is terminated. When the task continues to execute, the model will give a specific action based on the current state: $\mathit{\text{action}}=\arg {max}_{a}Q(s,a,{\mathit{\theta }}_i)$. The simulated environment has 1−e-greedy probability of executing this specific action and e-greedy probability of randomly choosing an action to execute to explore more states. The simulation environment gets a new state after completing an action.

The current state, action, new state, and reward corresponding to the new state are stored in the memory pool as a set of data. When the simulation environment performs several actions, we will train the model, and when the model performs training several times, the parameters of the target network are replaced with the parameters of the evaluation network.

6 Simulation results and discussion

To verify the feasibility of the DQN-based method in learning laparoscopic pose automatic adjustment, we performed some experiments in simulation scenarios. The simulation settings are described in Sect. 6.1, and the simulation results are reported in Sect. 6.2.

Figure 7 V-REP scene.

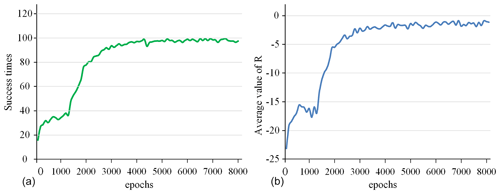
Figure 8 The success rate and the average value of R for all 100 epochs. (a) Success times per 100 epochs. (b) Average value of R per 100 epochs.

6.1 Simulation settings

In the paper, we used the crossed-platform robotics simulator V-REP (Rohmer et al., 2013) to set up the simulation and test scenarios to validate our method. As shown in Fig. 7, the scene consists of a laparoscopic arm and a surgical instrument. A visual sensor is attached to the laparoscopic arm manipulator and can capture RGB images. The laparoscopic arm structure is shown in Sect. 2, in which the active joints 5, 6, and 8 are in the position control mode. We turn the background colour to red in the software to simulate a real surgical environment. The laparoscopic arm is initialized to the same pose and the surgical instrument is also initialized to the centre of the laparoscopic vision at the beginning of each training round. The surgical instrument moves randomly in the three-dimensional space, and the laparoscopic arm performs a series of actions to make the surgical instrument return to the correct position in the field of view.

V-REP offers a remote application programming interface (API) allowing us to control a simulation from an external application. The remote API on the client side is available for many different programming languages. We implement our method in Python using the TensorFlow library.

Table 2 Success rate in different test scenarios (%).

The network weight parameters are trained using RMSprop optimization with the initial learning rate of 0.002. The reward discount factor γ is set to 0.9, e-greedy is set to 0.9 and the batch size is set to 64. The experience replay memory size is set to 20 000. In the training process, the memory pool first collects the experience of the first 200 steps, and then evaluated network parameters are updated every 5 steps. Whenever the evaluation network is updated 200 times, the parameter value of the evaluated network is assigned to the target network. The agent is trained for 8000 epochs.

Figure 9 The real surgical image as the background.

Figure 10 Laparoscopic field of view in different scenarios.

6.2 Simulation results

In this section, first, we give some parameter curves in the training phases. Secondly, we tested the model in different states to verify the robustness of the model. Finally, we analysed some failure cases.

The success rate in every 100 epochs and the average value of R (total reward per epoch) for every 100 epochs are used as indicators to detect the training situation of the model, as shown in Fig. 8. This curve is drawn based on the average value of five experiments. After 5000 epochs of training, the success rate is close to 100 %, and the average value of R converges to around −2. This shows that the model parameters have converged, and the task of tracking surgical instruments and adjusting the visual field has been completed. After the model training is completed, the model parameters are fine-tuned in a simulation environment with different backgrounds and the marker removed to adapt to the complex surgical environment.

Figure 11 The adjustment process of the laparoscopic visual field.

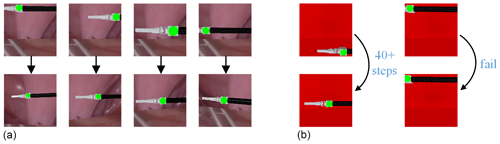
Figure 12 Visualization of test results. (a) Different pose testings of the surgical instrument. (b) Results of mission failure.

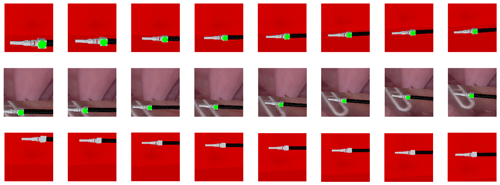
To simulate the complex surgical environment, three different test scenarios are set up. Scenario A uses the training scene as the test scene. Scenario B uses the real surgical image as the background, as shown in Fig. 9. Scenario C uses the training scene but removes the marker on the surgical instruments. Figure 10 shows the laparoscopic field of view in different scenarios. We conducted 5000 experiments in each scenario. In each experiment, the position and size of surgical instruments in the laparoscopic field of view were random. Scenarios A, B, and C achieved 99.88 %, 99.78 %, and 100 % success rates respectively. Figure 11 shows the change process of the laparoscopic field of view in the three scenarios. The experimental results show that the method is less affected by the experimental environment, and when the marker is blocked, it can also achieve the expected goal well. Therefore, our model can be well adapted to the complicated surgical environment during the surgery.

It can be seen from Fig. 12a that the method can adjust the pose of the laparoscopic arm so that the surgical instruments in different postures are in the appropriate field of vision for the doctor. The successful pose adjustment results from various random movements of the surgical instrument demonstrate the performance of the learning method and its generalization capability. We also analysed some failed cases in Scenario A: when the initial surgical instrument position is set to the extreme condition of the visual field, the automatic adjustment task of the laparoscopic visual field will fail, as shown in Fig. 12b. In the initial posture of the surgical instrument shown on the left-hand side of Fig. 12b, the laparoscopic arm needs more than 40 steps to make the surgical instrument return to the correct position in the field of view. On the right-hand side of Fig. 12b, the laparoscope is moved directly to the failure state to avoid the total reward value being too small.

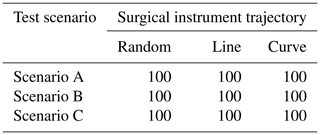
To simulate the actions of doctors in real surgery, we set up three different trajectories of surgical instruments: random motion, line motion, and curve motion. We conducted 500 experiments on each trajectory in each test scenario. In each experiment, if the surgical instrument is always in the correct position in the laparoscopic view, the experiment is considered successful. Table 2 shows the success rate of the task. In these scenarios, the laparoscopic arm can move the surgical instrument into a suitable field of view. It proves that the method is widely effective and can meet the needs of doctors during surgery.

7 Conclusions

In this paper, the effectiveness of the proposed methods is demonstrated by the simulation results. This method based on machine vision and deep reinforcement learning uses convolutional neural networks to extract visual features. Then the related reward function is set up to train a policy learning network to complete the non-linear mapping of a laparoscopic image to the optimal action of a laparoscopic arm. The proposed pose adjustment system does not require camera calibration because it does not need a robot and camera mathematical model.

In addition, there are many aspects to be developed in the future. (1) This article did not experiment in the actual environment because of the expensive cost of a real experiment, so the next step is to develop a model-based data-efficient robot-tracking system to use in the actual surgical procedure. (2) The best view of laparoscopy is simple in this paper. During the operation, the surgeon must not only pay attention to surgical instruments, but also focus on the human body. So, the related reward function needs further design. (3) This article examines the issue of single surgical instrument tracking, but multiple surgical instruments may be required during surgery. The next step is to study the issue of laparoscopic pose automatic adjustment for multiple surgical instruments.