the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel compound topological invariant for isomorphism detection of planar kinematic chains
Yingxian Wang
Rongjiang Cui
Jinxi Chen
The isomorphism identification of the kinematic chain (KC) based on graph theory definition has no advantage in efficiency, especially when the number of links in the KCs is large. The topological characteristic constants for isomorphism identification, such as the power value sequence (PVS), least distance matrix sequence (LDMS), and loop number (LN), are proposed. The fourth PVS, the LDMS, and the LN are compared and arranged in descending order, to form a strong complementary chain, which can identify KCs of at least 15 links with 4 degrees of freedom (DOF). The method is applied to the complete atlas of the following: 8-link 1 DOF, 9-link 2 DOF, 10-link 1 DOF, 12-link 1 DOF, 13-link 2 DOF, and 15-link 4 DOF planar single-joint KCs, 6-link 1 DOF and 7-link 1 DOF planetary gear trains, 8-link 1 DOF planar multiple joint KCs, and contracted graphs with up to six independent loops. All results are in agreement with the reported ones in the literature. Thus, the proposed method possesses good versatility and has been verified as being reliable and efficient.
- Article
(1583 KB) - Full-text XML
-
Supplement
(105 KB) - BibTeX
- EndNote
Isomorphism identification is a key factor affecting the efficiency and accuracy of the comprehensive configuration of the kinematic chain (KC; Yan, 1992). Although the isomorphism identification is accurate by using the definition of graph theory, a large number of computations will be generated, especially when the number of links exceeds 10 (Sun et al., 2020). Scholars have conducted various investigations on isomorphism identification by using the topological characteristic constants of KCs to improve the identification efficiency.
If one-to-one mapping f is available for the two graphs G1=(V1E1) and G2=(V2E2), and the expression is satisfied, then the graphs G1 and G2 are isomorphic. Ding and Huang (2009) proposed the specified matrix-based method with a lower computational complexity than that of McKay for isomorphism identification. However, the judging efficiency of their method decreases with the increase in the number of links (Zeng et al., 2014). Sun et al. (2020) proposed a set of isomorphism identification methods based on graph theory definitions of isomorphism, which has remarkable advantages in the rapid identification of the isomorphism of multilink KCs. However, the judgment will become complicated when both graphs have a large number of similarities.
In addition to the definition method, there are also many characteristic constants methods; for example, Uicker and Raicu (1975) proposed an isomorphism identification method based on the characteristic polynomials of adjacent matrices and emphasized the effectiveness of this method to 1–2 DOF PSKCs (planar simple joint kinematic chains) within the 10 links. Sunkari and Schmidt (2006) provided the correct isomorphism identification method based on the eigenvalue and eigenvector of the adjacency matrix. Although this method was reliable for 14-link KCs within 3 DOF, the reliability could not be ensured when the number of KCs is higher than 14 links. Rao and Raju (1991) first introduced the concept of the Hamming distance in the field of information and communication to the mechanism. Sun et al. (2017) improved the Hamming matrix to identify the isomorphism of KCs. However, the Hamming method is an unnecessary and insufficient condition for isomorphism. Moreover, the method is still far from being considered a candidate for computerized synthesis (Mruthyunjaya, 2003). Ambekar and Agrawal (1986) proposed a coding-based isomorphism identification method. Considering the simplicity of the method, scholars have conducted extensive research on code-based methods (Shin and Krishnamurty, 1993; Tang and Liu, 1993; Rajneesh and Sunil, 2018, 2019). Theoretically, coding-based isomorphic identification methods have coding uniqueness and decodability. Nevertheless, most of the proposed methods can only effectively identify KCs within 10 bars or fewer (Mruthyunjaya, 2003). Yadav et al. (1996) proposed a method based on the link multiplicity distance matrix for isomorphism. Vinjamuri et al. (2017) detected the isomorphism of the linkage and geared KCs using the concept of net distance in graph theory. Although the reliability of this method was reported for 15-link KCs with 4 DOF, the counterexamples have been found at 10-link KCs.
Overall, most of the isomorphism identification methods in the literature require complex computations, and some methods are unreliable when applied to KCs with a large number of links. Moreover, most existing methods have poor versatility; hence, different algorithms are needed for different kinds of KCs. Thus, the topological characteristic constants for isomorphism identification are also proposed to help identify KCs with at least 15 links with 4 DOF.
The rest of this paper is organized as follows. Section 2 proposes the concept of the power value sequence (PVS), least distance matrix sequence (LDMS), and loop numbers (LNs), which is applied for isomorphism identification. Section 3 presents examples to verify the computational complexity and effectiveness of the methods. Section 4 applies the methods to common KCs. Section 5 identifies the result analysis. Section 6 concludes the paper.
2.1 Extraction of topological characteristic constants
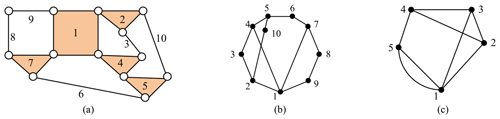
The number of paths taking k steps from one vertex to other vertices in loops, the shortest distance from one vertex to other vertices, and the number of loops starting at one vertex can all be extracted from the topological graph. Figure 1b shows the following: the number of paths taking four steps from vertex 4 to vertex 5 is 4, that is, 4-2-3-1-5, 4-2-3-1-5, 4-3-2-1-5, and 4-3-2-1-5 (the similarity of the paths is due to edge 15, which is a parallel edge), the least distance from vertex 4 to reach vertex 5 is 1 (edge 45 is assigned 1), and the number of loops starting at four vertices is 12, that is, 4-2-1-3-4, 4-2-1-5-4, 4-2-3-1-5-4, 4-2-3-4, 4-3-1-2-4, 4-3-1-5-4, 4-3-2-1-5-4, 4-3-2-4, 4-5-1-2-3-4, 4-5-1-2-4, 4-5-1-3-2-4, and 4-5-1-3-4. There are three characteristic constants of KC extracted by the aforementioned phenomena.
2.1.1 Power of the adjacency matrix
In graph theory, the kth power of the adjacency matrix An×n is the multiplication of the general matrix , where represents the number of paths for vertices vi and vj to reach each other through the k edges.
Definition 1. The row elements of the power of the adjacency matrix are sorted in descending order (i.e., the power value sequence of the adjacency matrix (PVS) ).
Definition 2. The values of each row of PVS are compared and arranged in descending order (i.e., PVSD ).
For example, the fourth power of the adjacency matrix A4, the fourth PVS , and the fourth PVSD of the KC (Fig. 1c) are, respectively, presented as follows:
2.1.2 Least distance matrix
The least distance matrix, in which two points on the graph must take at least a few steps to reach each other through one path, is often used in transportation network analysis. The connected weighting graph is G(V,E), the vertices set is , the edges set is , and the weight on the edge vivj is f(vivj), where . The weight matrix , that is,
Definition 3. The row elements of the least distance matrix are sorted in descending order (i.e., LDMS ).
Definition 4. The values of each row of are compared and arranged in descending order (i.e., LDMSD ).
For example, the least distance matrix D, the LDMS , and the LDMSD of the KC (Fig. 1c) are, respectively, presented as follows:
2.1.3 Loop number matrix
The loop search method is used to obtain the loop number (LN) of each vertex and given in matrix form (i.e., LN).
Definition 5. The row elements of the loop number matrix are sorted in descending order (i.e., LND LNd).
For example, the loop number LN and LNd of the KC (Fig. 1c) are presented as follows:
2.2 Isomorphism identification algorithm
The core idea of the isomorphism identification algorithm is to combine the four PVSD , LDMSD , and LND LNd to form a composite characteristic constant (CCC, and written as 3C). The 3C is denoted as follows:
For example, the 3C of Fig. 1c is shown in Eq. (6).
If the 3C of the two graphs is the same, then the two graphs are judged to be isomorphic; otherwise, they are judged to be non-isomorphic. The main steps of the detection algorithm are illustrated as follows.
Step 1. Calculate the fourth power of the adjacency matrix An×n and determine the . If the parameters of the two graphs are different, then they are non-isomorphic, and the next graph is considered. Otherwise, the next step is performed.
Step 2. Determine the . If the parameters of the two graphs are different, then they are non-isomorphic; otherwise, the next step is performed.
Step 3. Determine the LNt. If the LNt parameters of the two graphs are different, then they are non-isomorphic; otherwise, they are isomorphic. The next graph is then considered until all candidate graphs are identified.
The proposed method is tested on different kinds of KCs, including PSKCs, PMKCs (planar multiple joint kinematic chains), PGTs (planetary gear trains), and contracted graphs of KCs, to prove its versatility. The illustrative examples are provided as follows.
3.1 Examples of PSKCs
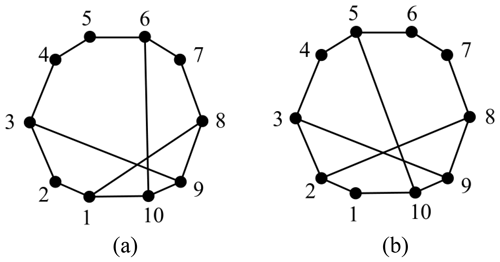
Example 1. There are two 10-link PSKCs considered in Figs. 2a and 4b.
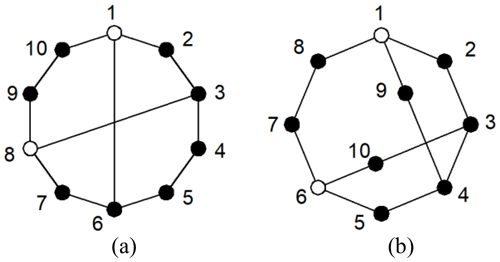
Figure 4(a) An 8-link KC with two multiple joints (1) and an (b) 8-link KC with two multiple joints (2).
The adjacency matrices of Fig. 2a and b are respectively entered into the isomorphism identification programs. The of the two graphs are different, as shown in Eq. (7). Thus, the two graphs are considered non-isomorphic.
The methods of Yadav et al. (1996) and Vinjamuri et al. (2017) are applied to Example 1. Figure 4a and b have the same string, that is, 178-2(20)-2(19)-4(17)-2(16). There two graphs identified as being isomorphic, according to the rule. This result is contradictory to that presented in this paper. The least distance matrix is not a global characteristic constant.
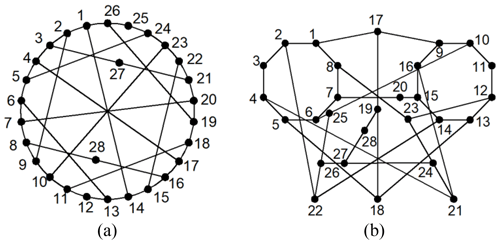
Example 2. There are two 28-link PSKCs considered in Fig. 5a and b, as discussed in Ding and Huang (2009).
The adjacency matrices of Fig. 3a and b are, respectively, entered into the isomorphism identification programs. The 3C of the two graphs is the same. Thus, the two graphs are considered isomorphic.
3.2 Examples of PMKCs
The distinction of multiple joint KCs lies in the existence of the multiple joints, which can be distinguished by setting a hollow vertex (multiple joints) connected edge value of 2. The isomorphism identification method is consistent with the single-hinged KC. For example, two 8-link KCs with two multiple joints are considered in Fig. 4a and b.
The adjacency matrices of Fig. 4a and b are, respectively, entered into the isomorphism identification programs. The of the two graphs are different, as shown in Eq. (8). Thus, the two graphs are considered non-isomorphic.
3.3 Examples of PGTs
Yang and Ding (2019) proposed a new graph model to represent the structure of PGTs (Yang et al., 2018). The new graph representation can completely avoid the generation of pseudo-isomorphic graphs, and the rotation and displacement graphs of PGTs have the same graph model. The distinction of PGTs lies in the existence of the hollow vertex and dashed edges, which can be distinguished by setting a dashed edge value of 3 and a hollow vertex-connected edge value of 2. For example, the adjacency matrix of Fig. 5a is Fig. 5b and that of Fig. 5c is Fig. 5d.
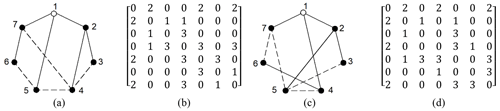
Figure 5(a) A 6-link PGT (1) and (c) 6-link PGT (2). Panels (b) and (d) show the adjacency matrices of panels (a) and (c), respectively.
The adjacency matrices of Fig. 5b and d are, respectively, entered into the isomorphism identification programs. The 3C of the two graphs are the same, as shown in Eq. (9). Thus, the two graphs are considered isomorphic.
3.4 Examples of contracted graphs
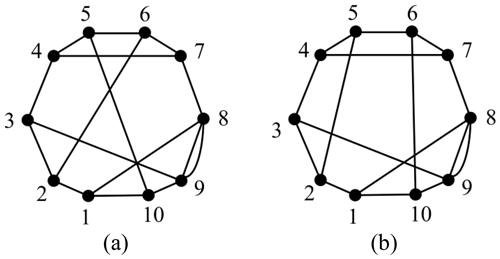
The distinction of contracted graphs lies in the existence of the parallel edges, which can be distinguished by setting the parallel edge value equal to the number of parallel edges. The isomorphism identification method is consistent with the single-hinged KC. For example, two 10-link contracted graphs are considered in Fig. 6a and b.
The adjacency matrices of Fig. 6a and b are entered into the isomorphism identification programs. The of the two graphs are different, as shown in Eq. (10). Thus, the two graphs are considered non-isomorphic.
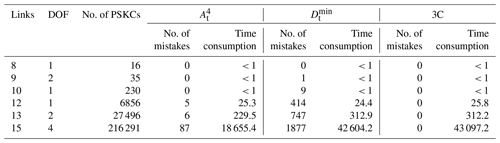
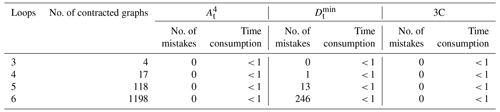
The proposed isomorphism identification algorithm has been fully automated using MATLAB2018a software on a personal computer with a 1.60 GHz Intel® Core™ i5-8250 PC with 8 GB RAM. The isomorphism identification algorithm is applied to the complete atlas of the following: 8 links with 1 DOF, 9 links with 2 DOF, 10 links with 1 DOF, 12 links with 1 DOF, 13 links with 2 DOF, and 15 links with 4 DOF PSKCs, 6 links with 1 DOF and 7 links with 1 DOF PGTs, 8 links with 1 DOF PMKCs, and contracted graphs with up to six independent loops. All the isomorphism identification results are in agreement with those of Yang et al. (2018) and Ding et al. (2011, 2016a, b). The detailed detection results are shown in Tables 1–4.
Many algorithms for graph isomorphism identification are available, but the problems encountered in their applications are due to their computational complexity and effectiveness (Ding and Huang, 2009).
5.1 Computational complexity
Compared with the graph theory definition method to identify the isomorphism, 3C methods are simple. Only the application of can solve most isomorphic problems of KCs. Table 1 shows that cannot identify only six KCs from 27 496 13 links with 2 DOF PSKCs. The time consumption of the computer program is also listed in Tables 1–4. Compared with a single characteristic constant, 3C does not significantly increase the time. For example, the time consumption of 12-link PSKCs when only using , , and 3C is 25.3, 24.4, and 25.8 s, respectively.
5.2 Effectiveness
Compared with other characteristic constant methods, such as eigenvalue, eigenvector, characteristic polynomial, code-based, and distance- or path-based methods, the 3C method in this paper possesses good versatility, as shown in Tables 1–4.
The isomorphism identification of KCs are crucial in the process of mechanism innovation design. This paper presents an identification method based on how the fourth PVSD, the LDMSD, and the LND form a strong complementary chain to identify KCs at least 15 links with 4 DOF. The method is suitable for planar single and multiple joint KCs, PGTs, contracted graphs, and multicolored graphs. The comparison with the literature shows that the proposed method in this study is effective and accurate and can be automatically realized by the computer. Our method is simple, reliable, and efficient and possesses good versatility. The present research is helpful for improving the efficiency of mechanism design.
The code is available in the Supplement.
The data are available upon request from the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/ms-13-585-2022-supplement.
YW is the lead author for the article and was responsible for collecting the research literature, organizing the paper structure, and writing the paper. RC co-wrote the paper with YW and JC. JC is the corresponding author for the paper, presented the idea of this research, and was responsible for the whole process of writing and revising this paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors are grateful to the Launching Project of High-level Talents of Hangzhou Vocational & Technical College (grant no. HZYGCC202103).
This research has been supported by the High-level Talents of Hangzhou Vocational & Technical College (grant no. HZYGCC202103).
This paper was edited by Daniel Condurache and reviewed by three anonymous referees.
Ambekar, A. G. and Agrawal, V. P.: Canonical numbeloop of kinematic chains and isomorphism problem: min code, Mech. Mach. Theory, 22, 453–461, https://doi.org/10.1016/0094-114X(87)90062-0, 1987.
Ding, H. and Huang, Z.: Isomorphism identification of graphs: Especially for the graphs of kinematic chains, Mech. Mach. Theory, 44, 122–139, https://doi.org/10.1016/j.mechmachtheory.2008.02.008, 2009.
Ding, H., Hou, F., Andrés, K., and Huang, Z.: Synthesis of a complete set of contracted graphs for planar non-fractionated simple-jointed kinematic chains with all possible DOFs, Mech. Mach. Theory, 46, 1588–1600, https://doi.org/10.1016/j.mechmachtheory.2011.07.012, 2011.
Ding, H., Huang, P., Yang, W., and Andrés, K.: Automatic generation of the complete set of planar kinematic chains with up to six independent loops and up to 19 links, Mech. Mach. Theory, 96, 75–93, https://doi.org/10.1016/j.mechmachtheory.2015.09.006, 2016a.
Ding, H., Yang, W., Zi, B., and Andrés, K.: The family of planar kinematic chains with two multiple joints, Mech. Mach. Theory, 99, 103–116, https://doi.org/10.1016/j.mechmachtheory.2016.01.003, 2016b.
Mruthyunjaya, T.: Kinematic structure of mechanisms revisited, Mech. Mach. Theory, 38, 279–320, https://doi.org/10.1016/S0094-114X(02)00120-9, 2003.
Rajneesh, K. and Sunil, P.: Kinematic chains isomorphism identification using link connectivity number and entropy neglecting tolerance and clearance, Mech. Mach. Theory, 123, 40–65, https://doi.org/10.1016/j.mechmachtheory.2018.01.013, 2018.
Rajneesh, K. and Sunil, P.: A new algorithm of links labelling for the isomorphism detection of various kinematic chains using binary code, Mech. Mach. Theory, 131, 1–32, https://doi.org/10.1016/j.mechmachtheory.2018.09.010, 2019.
Rao, A. C. and Raju, D. V.: Application of the hamming number technique to detect isomorphism among kinematic chains and inversions, Mech. Mach. Theory, 26, 55–75, https://doi.org/10.1016/0094-114X(91)90022-V, 1991.
Shin, J. K. and Krishnamurty, S.: Standard code technique in the enumeration of epicyclic gear trains, Mech. Mach. Theory, 28, 347–355, https://doi.org/10.1016/0094-114X(93)90075-7, 1993.
Sun, L., Cui, R., Ye, Z., Zhou, Y., Xu, Y., and Wu, C.: Similarity recognition and isomorphism identification of planar kinematic chains, Mech. Mach. Theory, 145, 103678, https://doi.org/10.1016/j.mechmachtheory.2019.103678, 2020.
Sun, W., Kong, J., and Sun, L.: The improved hamming number method to detect isomorphism for kinematic chain with multiple joints, J. Adv. Mech. Des. Syst., 11, JAMDSM0061, https://doi.org/10.1299/jamdsm.2017jamdsm0061, 2017.
Sunkari, R. P. and Schmidt, L. C.: Structural synthesis of planar kinematic chains by adapting a Mckay-type algorithm, Mech. Mach. Theory, 41, 1021–1030, https://doi.org/10.1016/j.mechmachtheory.2005.11.007, 2006.
Tang, C. and Liu, T.: The degree code-a new mechanism identifier, J. Mech. Design, 115, 627–627, https://doi.org/10.1115/1.2919236, 1993.
Uicker, J. J. and Raicu, A.: A method for the identification and recognition of equivalence of kinematic chains, Mech. Mach. Theory, 10, 375–383, https://doi.org/10.1016/0094-114X(75)90037-3, 1975.
Vinjamuri, V., Kuchibhotla, M., and Annambhotla, B.: An Innovative Approach to Detect Isomorphism in Planar and Geared Kinematic Chains Using Graph Theory, J. Mech. Design., 139, 122301, https://doi.org/10.1115/1.4037628, 2017.
Yadav, J., Pratap, C., and Agrawal, V.: Computer aided detection of isomorphism among binary chains using the link-link multiplicity distance concept, Mech. Mach. Theory, 31, 873–877, https://doi.org/10.1016/0094-114X(96)00002-X, 1996.
Yan, H. S.: A methodology for creative mechanism design, Mech. Mach. Theory, 27, 235–242, https://doi.org/10.1016/0094-114X(92)90013-8, 1992.
Yang, W. and Ding, H.: The complete set of one-degree-of-freedom planetary gear trains with up to nine links, J. Mech. Design, 141, 043301, https://doi.org/10.1115/1.4041482, 2019.
Yang, W., Ding, H., Zi, B., and Zhang, D.: New graph representation for planetary gear trains, J. Mech. Design, 140, 012303, https://doi.org/10.1115/1.4038303, 2018.
Zeng, K., Fan, X., Dong, M., and Yang, P.: A fast algorithm for kinematic chain isomorphism identification based on dividing and matching vertices, Mech. Mach. Theory, 72, 25–38, https://doi.org/10.1016/j.mechmachtheory.2013.09.011, 2014.
- Abstract
- Introduction
- Isomorphism identification
- Illustrative examples
- Application of the algorithm
- Identification result analysis
- Conclusions
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Isomorphism identification
- Illustrative examples
- Application of the algorithm
- Identification result analysis
- Conclusions
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement