the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Adaptive multiswarm particle swarm optimization for tuning the parameter optimization of a three-element dynamic vibration absorber
Qing Hui Song
Lin Jing Xiao
Qing Jun Song
Xiu Jie Liu
A reliable optimization of dynamic vibration absorber (DVA) parameters is extremely important to analyze its dynamic damping characteristics and improve its vibration suppression performance. In this paper, we will discuss a parameter optimization method of the Voigt and three-element DVA models according to the H∞ optimization criterion. The particle swarm optimization method is an effective heuristic optimization algorithm; however, it is easy to lose diversity and fall into local extremum. To solve this problem, the adaptive multiswarm particle swarm optimization (AM-PSO) is used to search the solution of the DVA models. Particles in AM-PSO are adaptively divided into multiple swarms, and the variable substitution learning strategy is utilized to reduce their computational complexity and improve the algorithm's global search capability. In addition, the AM-PSO method is employed to optimize the parameters of DVA models and compared with the genetic algorithm and PSO. The simulation results show that the AM-PSO algorithm has superior performance. Also, the adaptive multiswarm numerical design method discussed herein will push the field towards practical applications, including traditional DVA and related complex three-element DVA.
- Article
(1489 KB) - Full-text XML
- BibTeX
- EndNote
Dynamic vibration absorbers (DVAs) have been utilized to suppress the vibration of a primary system for more than 110 years. One of the most common DVAs is the Voigt type, in which the spring is set in parallel with the viscous damper, thereby connecting the primary system to the secondary mass. The main parameters of Voigt DVA model are the tuning frequency ratio and damping ratio. Here, we will discuss a parameters optimization method for the three-element type of DVAs.
There are a few previous studies on the three-element type of DVA (TEDVA). Snowdon developed the TEDVA model in 1974, where the amplitude magnification factor across a simple spring mass system at resonance was investigated (Snowdon, 1974). The TEDVA consists of a viscous damper absorber and two spring elements, where one connects in series with the viscous damper absorber, and the other connects in parallel with the viscous damper absorber. Asami and Nishihara (1999) conducted the optimization design of the TEDVA based on the H∞ optimization criterion and indicated that the it had better vibration control performance than a traditional DVA under the same mass ratio. Later, Asami and Nishihara (2002) discussed the optimization problem of TEDVA in the light of H2 optimization criterion (Asami and Nishihara, 2002) and derived the exact solution for undamped main system. The previous optimization study of TEDVA is based on the fixed-point theory; however, there are significant differences in the optimum solutions obtained by employing the fixed-point theory (Nishihara, 2019).
Anh et al. (2013, 2014) proposed a design method for nontraditional DVAs, in terms of the equivalent linearization method, and gave a weighted dual criterion to approximately replace the damped primary structure with an equivalent undamped structure. However, these results are unavoidably affected by the fixed-point theory of the undamped primary system. Beyond that, Javidialesaadi and Wierschem (2018) introduced, formulated, optimized, and discussed a TEDVA based on the inverter which took full advantage of the potentially high inertial mass of a relatively small mass in the rotation. Chen et al. (2020) applied the TEDVA theory to reduce the car body resonance and obtained the optimal suspension parameters of the underframe equipment under a vertical harmonic excitation, and the research shows that the vehicle with three-element DVA can have a better driving quality.
In order to obtain more efficient solutions, optimization techniques such as the genetic algorithm (GA), Newton–Raphson algorithm, and particle swarm optimization have been applied to vibration absorber optimization. Esen and Koc (2015) studied the dynamic behavior of an anti-aircraft barrel with a passive absorber and acquired the optimization parameters of the vibration absorbers combined with the genetic algorithm. In 2019, Nishihara (2019) gave the optimal parameter value of the three-element DVA by the Newton–Raphson algorithm and indicated that there is no closed solution to the design problem for three-dimensional DVA, even in the case of undamped primary system. The controlling equations of a planar vibration system were described, and the particle swarm optimization (PSO) algorithm was employed to optimize the main parameters of electromagnetic shunt damping absorber (Xie et al., 2014). According to the typical conditions of electric wheels with an in-wheel motor, the PSO algorithm was used to optimize the parameters of the DVA system to obtain acceptable vibration performance (Liu et al., 2017). In the noise control solutions of transportation industry, Jagodzinski et al. (2020) established the objective function of root mean square (RMS) surface velocity and employed the PSO algorithm to optimize the objective function. Thus, the optimal parameter combination of the shock absorber was obtained (Jagodzinski, et al., 2020). In recent years, PSO has been a widely used optimization algorithm inspired by swarm intelligence because of its effectiveness in theory and practice (Gao et al., 2019; Wang et al., 2021).
Besides, even in an undamped primary system, it is impossible to have a closed solution for the three-element DVA. For this reason, a more accurate and easy method is necessary to optimize TEDVA for reducing the vibrations of a damped system. In this paper, an adaptive multiswarm particle swarm optimization is discovered to minimize the maximum amplitude magnification factor of the three-element DVA. The rest of this paper is organized as follows: the traditional Voigt DVA and three-element DVA models are established and explained in Sect. 2. Details of the adaptive multiswarm particle swarm optimization (AM-PSO) are described in Sect. 3. In Sect. 4, the performance of the AM-PSO algorithm is validated based on a variety of experiments. In Sect. 5, the comparisons of the vibration reduction in the performance of DVAs are studied, and the conclusion is provided in Sect. 6.
2.1 Establishment of models
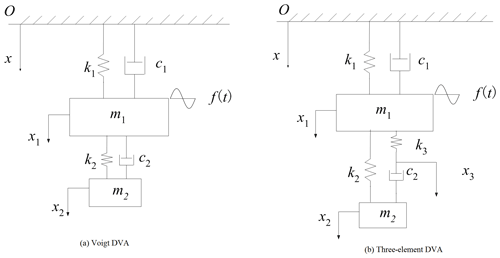
Figure 1 shows the traditional DVA and three-element DVA models attached to a primary system with damping. The primary system consists of a mass (m1), a spring with a spring constant (k1), and a damper with a viscous damping coefficient (c1), and it is excited by a harmonic force excitation f(t)=F0 sin ωt. The traditional DVA is composed of a mass (m2), a spring (k2), and a damper (c2). The three-element DVA is composed of a mass (m2), two springs (k2 and k3), and a damper (c2).
The dynamic equation of the system with two kinds of dynamic vibration absorbers can be established as the Voigt DVA, as follows:
The three-element DVA is as follows:
2.2 Theoretical analysis
When the main system is excited by a harmonic frequency of ω, the nonhomogeneous term F0 sin ωt in Eq. (1) can be transformed into F0ejωt. Here, j is the imaginary unit. So the steady-state solutions are given by the following:
By substituting Eq. (2) into Eq. (1), the steady-state frequency response of the main system is obtained in the following form:
where E1, F1, G1, and H1 are real polynomials in ω, and they are expressed for Voigt DVA as follows:
and for three-element DVA, as follows:
Let the natural frequencies of the main system and the DVA be and , respectively. Then, the following ratios and dimensionless parameters are considered:
The amplitude magnification factor of the base displacement to that of the primary system is represented by a dimensionless frequency response function. Here, the parameter is introduced to represent the static displacement of the main system under the static action, and the amplitude amplification factor of the primary system (A) is expressed by a dimensionless function. The expression of A then becomes the following:
where, for the Voigt DVA model, E2, F2, G2, and H2 in Eq. (6) are, respectively, expressed as follows:
For the three-element DVA, E2, F2, G2, and H2 in Eq. (6) are, respectively, expressed as follows:
We may see that the dimensionless treatment can more directly reflect the connection between the main system and the vibration absorption system and give the general form of the results.
2.3 Parameter optimization formulation
Upon examination of Eq. (6), it can be found that the amplitude amplification factor is a function of the following six variables: λ, μ, v, α, ζ1, and ζ2. The input frequency ratio λ is an unknown input parameter to the system, and the damping ratio ζ1 and mass ratio μ are constant parameters selected by the system and do not need to be optimized in general. The remaining three parameters (v, α, and ζ2) can be selected by the designer to minimize the vibration of the primary system.
At present, there are three typical optimization criteria for selecting the optimum design parameters of DVAs. The object of H∞ optimization is to minimize the maximum amplitude magnification factor (A) of the primary system (Tigli, 2012). The object of the H2 optimization is to minimize the area under the frequency response function to reduce the total vibration energy of the system (Asami and Nishihara, 2002b; Asami et al., 2002). The objective of the stability maximization criterion is to improve the transient vibration of the system (Asami et al., 2002). The design objective of the dynamic vibration absorber in this work is to minimize the maximum vibration amplitude of the main system under harmonic excitation, which is equivalent to the H∞ optimization norm.
The optimization problem proposed in this paper can be expressed as follows:
where λS and λB are the minimum and maximum boundary conditions of λ, respectively.
The constraint conditions of the objective function described in Eq. (8) are as follows:
The optimal solution of Eq. (8) will be α and ζ2, which will minimize the maximum over the distribution region of λ. In this paper, the adaptive multiswarm particle swarm optimization method is employed to obtain the optimal solution of the vibration absorber in order to achieve the minimization of the maximum amplitude magnification factor.
If the DVAs are attached a damped primary system, the closed form algebraic solution of the system based on the H∞ norm cannot be obtained (Nishihara, 2019; Asami et al., 2002). As described above, a number of optimization algorithms, such as the Newton–Raphson method, steepest descent algorithm, and so on, were developed based on gradient-based methods for parameter estimation and solution. Although the gradient-based method is a robust process to update the parameters along the descending direction of the gradient, it tends to a local minimum rather than global minimum (Yin et al., 2020). As an alternative method, the heuristic algorithm, especially the particle swarm optimization algorithm, is more effective in solving the parameter identification problem of DVA models. Heuristic algorithms no longer require any gradient information and do not require the continuity/convexity of the specific search domain information and the objective function, so they have the advantages of robustness, simplicity, and easy implementation (Xiong et al., 2020).
The original idea of a PSO algorithm is to simulate the process of birds foraging to find the optimal solution. Because each particle of the algorithm uses the same iterative formula, the particles are easy to gather at local extremum positions and fall into the local optimization, which makes the particle swarm optimization algorithm lose diversity (Bi et al., 2019). Based on the original particle swarm optimization algorithm, many PSO algorithms have been developed in order to improve the diversity of the population (Chen and Zhao, 2009; Li et al., 2012; Qin et al., 2015; Zhang et al., 2019, 2020; Lai et al., 2020).
3.1 Canonical particle swarm optimization
In a D dimensional search space, the velocity vector and position vector of each particle i (i=1, 2, …, N) are defined as ), and ), respectively. Assuming that the current number of iterations is k, the updating formulas of particle velocity and position are as follows:
where c1 and c2 are learning factors, r1 and r2 are random numbers between 0 and 1, w is an inertia damping term that influences the momentum vector, pi represents the optimal position of the ith particle searched so far, which is called the individual optimal value and recorded as , and pg represent the global optimal position of the whole particle swarm, which is recorded as .
The position of each particle is updated using Eq. (11), and the particle velocity is updated depending on Eq. (10) at each iteration. Due to the existence of numerous parameters, optimizing the parameters of DVA models is a complex optimization problem, which is challenging. As a result, the accuracy and the convergence rate of the standard PSO may not be satisfactory. To strengthen global search ability in PSO, the adaptive learning approach is applied to the standard PSO in this paper.
3.2 Adaptive multiswarm particle swarm optimization
Maintaining population diversity is an important aspect of the complex parameter optimization problem, and it is also the key to preventing particles from falling into a local optimal solution. The multiple swarm PSO technique is an effective adaptive way to maintain diversity through information sharing among different subswarms (Qin et al., 2015). In this paper, the particle swarm is adaptively divided into several subgroups based on the distribution density and cutoff distance of particles.
In order to explore different regions of DVA model search space at the same time and maintain the population diversity and interaction among multiple individual groups, the particles are adaptively divided into several subgroups by the clustering method. Here we define the local density and the minimum distance between particles.
In the process of subgroup division, Euclidean distance is used to calculate the distance (dij) between particles. And the cutoff distance (dc) is used as the evaluation basis for subswarms division of particles, which can be written as below as follows:
The method of subswarm division considers the overall distribution of data from the perspective of density, and the local density ρi represents the number of particles at a certain distance and is given by an equation of the following the form:
We may see that the smaller the Euclidean distance, the larger the local density, and the stronger the ability to find the local optimal solution. At the same time, in order to divide the particle swarm into several subswarms with the highest density, another quantity δi is introduced to represent the minimum distance between particles, which is expressed as follows:
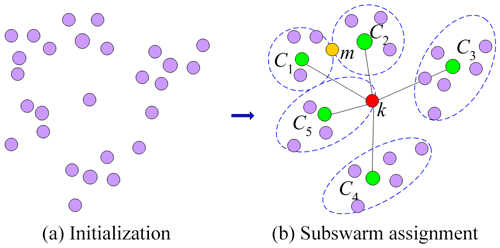
The AM-PSO has a population with several subswarms, where the center particle of each subswarm has higher local density and minimum distance. Each remaining particle is arranged to the nearest subswarm, which has a higher density. Figure 2 illustrates how to divide subswarms by a local density and minimum distance towards the search for the global best solution.
Suppose that the Euclidean distance between the ith particle and the kth particle is the smallest when j=k. Then, δi is equal to dik, which means that kth particle is the central particle of the subswarm. It is assumed that multiple particles have the same minimum distance δi, and the particle with a relatively large local density ρ is taken as the center of the subswarm. Figure 2a is the initialization of the particle, and the green particles (C1, …, C5) in Fig. 2b are the center of each subswarm found by Eqs. (12)–(14).
After determining the center particles of all subswarms, the remaining particles are assigned to different subswarms according to the principle of Euclidean distance dij and form multiple swarms autonomously. When other particles are assigned to the subswarm, there are the following two cases: (1) if the Euclidean distance between the particle and the center of all subswarms is not equal, then the particle belongs to the subswarm with the smallest Euclidean distance, and (2) the Euclidean distance from the particle to the center particle of subswarms is equal. For example, in Fig. 2b, the red particle k belongs to the first case, which has the smallest Euclidean distance from C5 and is assigned to the C5 subswarms. The yellow particle m belongs to the second case, which has the equal Euclidean distance to the central particles C1 and C2, and then the mth particle belongs to the C1 subswarm with higher density.
For the constrained optimization problem of three-element DVA system, many constraint items make the search more difficult, and the particles are easy to mature prematurely, leading to the stagnation of the algorithm. In order to maintain the ability of continuous searching for the optimal solution of the population, the velocity update of particles is characterized by the population diversity. The velocity update formula of the AM-PSO method is as follows:
where S is the number of subswarms, and is a particle diversity function, which increases the guidance of the population information sharing to the particle search process.
It is interesting to note that the local optimal particles in Eq. (15) not only guide the learning of the particles in this subswarm but also explore the information from other subswarms. The best global solution is the average information of S subswarms of pg, which can be used to guide the update of local optimal particles to further improve the population diversity and accelerate the convergence speed.
In addition, for the sake of reducing the computational complexity of the optimization process, the variable substitution learning idea is utilized to simplify problems, and it can improve the algorithm's global search capability. According to the idea of variable substitution, Eq. (10) can be written in the following form:
where δ is found by a linear combination applied to the function and , φ1=r1c1, φ2=r2c2, φ1=r1c1.
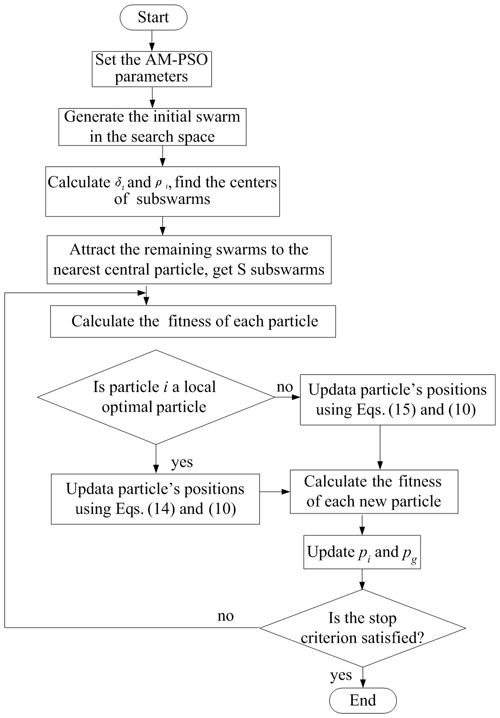
The simplified method of variable substitution can not only improve the diversity of the population but also improve the slow convergence speed caused by too frequent subswarm operations. The flowchart of the AM-PSO strategy is described in Fig. 3.
In order to present the effectiveness of the AM-PSO method employed in this paper, its performance is compared with canonical PSO and GA (genetic algorithm). The basic parameters of AM-PSO and PSO are the same in the following ways: the particle dimension m=3 in the Voigt DVA model or m=4 in the three-element DVA model, the population size N=80, the number of iterations is 100, and the learning factor c1=2 and c2=2. The key parameters of the dynamic vibration absorber are optimized by the canonical PSO, GA, and AM-PSO, respectively, and the optimization process was made by self-developed programs which are conducted in the 64 bit MATLAB version (2017b).
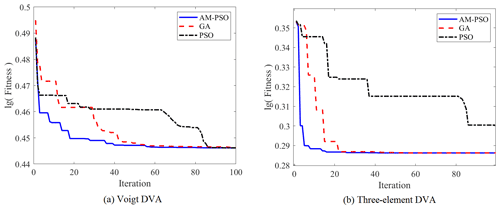
After many experiments, the convergence curves of the fitness function for three algorithms of PSO, AM-PSO, and GA under the optimal case are described in Fig. 4. As can be seen from the figures, the optimization result requires at least 64 (GA), 86 (PSO), and 58 (AM-PSO) iterations to stabilize in the Voigt DVA model. However, the optimization result requires at least 24 (GA), 84 (PSO), and 17 (AM-PSO) iterations to stabilize in the Voigt DVA model. Therefore, the convergence rate of AM-PSO is better in comparison with other algorithms, and the fitness value of the three-element DVA is smaller with the AM-PSO algorithm than the other two algorithms. This also proves that the AM-PSO algorithm is reliable.
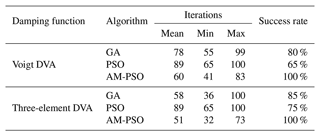
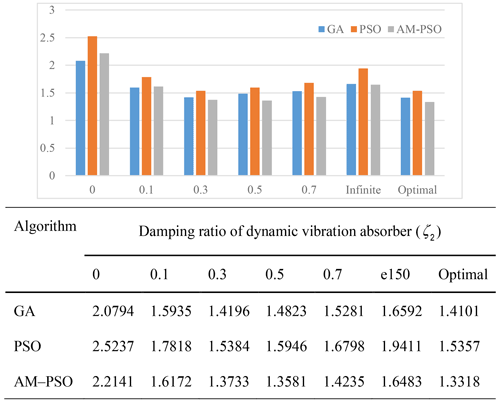
For the evaluation of stability of AM-PSO method in DVA models, it is necessary to estimate the number of iterations required to achieve a certain accuracy. The maximum number of iterations is 100, and the stability analysis results of three algorithms are given in Table 1. The three algorithms run independently 40 times, and the proportion of successful reaching of the given threshold is calculated. Here, the thresholds of the Voigt DVA and the three element DVA are 1.58 and 1.355, respectively.
Table 1 displays that the comprehensive vibration reduction capability and stability of DVAs have improved by using the AM-PSO. For the Voigt and three-element DVA model, the AM-PSO algorithm can reach the given threshold with 100 % success rate, while the success rate of canonical PSO is the lowest. Therefore, compared with PSO and GA algorithm, the AM-PSO algorithm runs stably. Whether the AM-PSO algorithm is applied to the Voigt DVA or the three-element DVA, the maximum, minimum, and average iteration times are all the minimum. The results show that AM -PSO algorithm is superior to the other two algorithms and can obtain a more effective vibration reduction effect in the three-element DVA model.
When damping is present in the primary system, the objective function which is given in Eq. (8) is too complex to obtain an exact solution. Here we obtain the optimal parameters by numerical method based on H∞ optimization criterion.
5.1 Optimizing simulation of DVA parameters
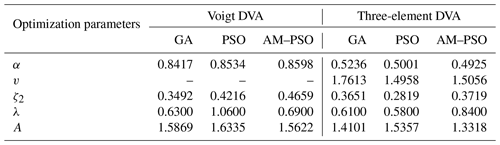
Consider the transformed system in Eq. (1) and select the mass ratio μ=0.1 and the damping ratio of the main system ζ1=0.3. Then, the optimal parameters of the DVAs could be obtained based on the numerical methods of GA, PSO, and AM–PSO. Table 2 presents the result comparisons after optimization by the canonical PSO, GA, and AM–PSO parameters.
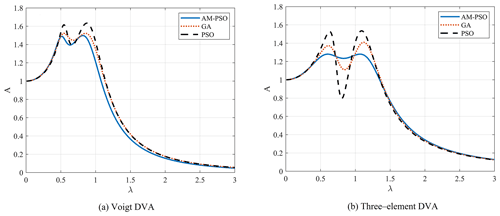
The comparison of the optimal solutions of different optimization algorithms is given in Fig. 5.
The results in Fig. 5 and Table 2 show that the three-element DVA provides a smaller maximum amplitude magnification factor than the standard DVA based on the equivalent mass ratios and damping ratios of the main system. We can see that the peaks obtained by AM–PSO optimization are significantly lower than those of the other two optimization methods. Therefore, the vibration reduction performance is improved by the implementation of the optimal design.
From the comparison, it could be concluded that the three-element DVA is better than Voigt DVA in reducing the vibration of damped main system. In addition, the parameters obtained by the AM–PSO numerical optimization algorithm can not only significantly reduce the amplitude of the resonance region of the main system but also expand the effective frequency range of vibration absorption.
In addition, Fig. 6 shows a comparison of the theory of Den Hartog and the optimization algorithms for the mass ratio μ=0.1 with a damped primary system (ζ1=0.3). The definition of the optimal parameters was proposed in Asami and Nishihara (1999) and Nishihara (2019) as follows:
where , and the parameters in Eq. (19) are expressed as , , and .
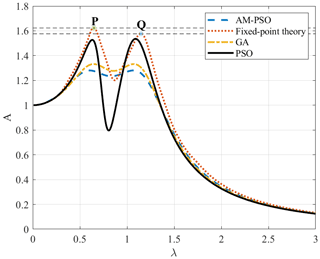
Figure 6Comparison of the theory of Den Hartog and optimization algorithms through the frequency response curve.
As shown in Fig. 6, the maximum amplitude magnification factor obtained by using the fixed-point theory is slightly larger than that obtained by the optimization algorithms, and the output values corresponding to P and Q are 1.577 and 1.623, respectively. That is, the condition that P and Q are unequal in height so that they are in the maximum position on the curve cannot be used as the optimal design condition. Therefore, for a three-element DVA with reference to a damped system, the equal adjustment of the height of P and Q should be determined by the numerical optimization method.
5.2 Analysis of the effectiveness of vibration control
Parameter sensitivity analysis is a measure to study the degree of distribution or quantification of model output changes under different input parameter changes. A different formulation of sensitivity was provided in (Richiedei, et al., 2021) for an undamped system. The inherent assumption in calculating the parameter sensitivity using differential equations is that there is no correlation between input parameters. However, the sensitivity of the parameters does not only depend on the influence of a parameter on the output of the model but also on the changes of the output of the system model due to the interaction of parameters. Considering the coupling relationship between parameters, the parameter sensitivity is calculated by a discrete method as follows:
where Ai represents the maximum amplitude magnification factor of the ith data point obtained by substituting the original optimization parameters into the DVA model. represents the corresponding maximum amplitude magnification factor obtained by substituting the changed parameters into the DVA model, x is a parameter to be analyzed (e.g., μ or ζ1), , and N is the total number of data points. S is the sensitivity of the parameter, and the larger value indicates the higher sensitivity of the parameter.
The procedure of the parameter sensitivity analysis is as follows:
-
Sept1: within the range of variable parameters, select the optimized parameter combination as the reference basis point.
-
Sept2: determine the parameters to be analyzed and increase or decrease the value with its base point value as the center point.
-
Sept3: calculate the outputs and other parameters, except for the analyzed parameter, using the AM–PSO algorithm.
-
Sept4: calculate the parameter sensitivity using Eq. (20) and then sort the parameter sensitivity measure to the influence of each parameter on the model output.
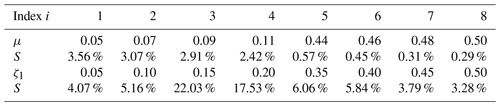
Generally, the mass ratio depends on the specific engineering requirement, and in the previous numerical solution, the mass ratio μ is specified in advance. This subsection gives the results when the mass ratio is also a design variable. The results of mini-max optimization (Eq. 8) will obtain the information about the effects of the change in mass ratio on the amplitude magnification factor. The optimal parameters of the three-element DVA model obtained using the AM–PSO algorithm in Table 4 were selected as the reference basis, and then the sensitivity analysis of the parameters was performed, as described above. The results of some examples are shown in Table 3.
When the mass ratio μ changes from the left side to the right side of the interval, the sensitivity decreases gradually, with an average sensitivity of 1.57 %. The damping ratio of the main system ζ1 tended to the right side of the interval, and the sensitivity changed less, with an average sensitivity of 7.51 % in the entire interval. Therefore, selecting the appropriate μ and ζ1 can improve the robustness of the system.
5.3 Impact of tuning parameters on the three-element DVA
Let the mass ratio μ=0.1 and the damping ratio of the main system ζ1=0.3. Then, we analyzed the influence of input frequency ratio (λ) and damping ratio of dynamic vibration absorber (ζ2) on the vibration reduction of the main system. Some typical normalized amplitude–frequency curves for different damping ratios are shown in Figs. 7 and 8.
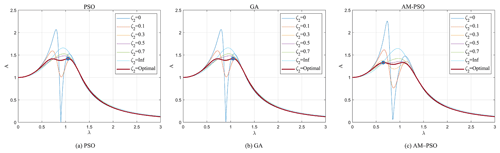
Figure 7Influence of tuning parameter ζ2 on the three-element DVA under different optimization algorithms.
It can be clearly seen that, when λ takes the upper limit of the interval, all amplitude–frequency curves pass through a fixed point, which always causes the normalized A to remain unchanged. When ζ2 takes [0, optimal], then the maximum amplitude magnification factor decreases gradually as the damping ratio of dynamic vibration absorber increases. When ζ2 exceeds the optimal damping ratio, the maximum amplitude magnification factor increases gradually. When ζ2 takes the optimal parameters, the maximum amplitude magnification factor obtained using the AM–PSO optimization algorithm was 1.3318, which is 5.55 % less than GA and 13.28 % less than PSO. It can be seen that the appropriate numerical calculation method is helpful for obtaining a better combination of tuning parameters so as to better suppress the vibration of the main system. In addition, it is not difficult to find that the influence of the tuning parameter ζ2 is consistent for the GA, PSO, and AM-PSO numerical optimization algorithms.
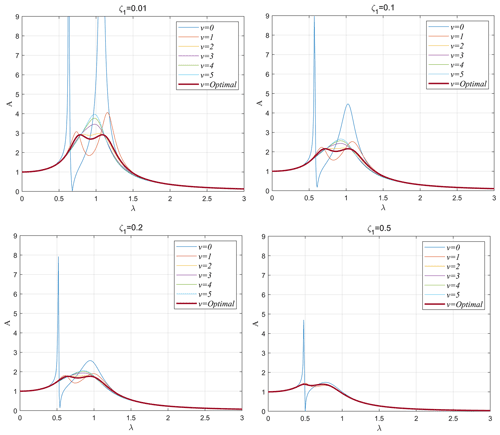
Figure 9 shows the effect of spring ratio (v) on the maximum amplitude magnification factor under the different optimization algorithms. Although the influence of the change in the spring ratio on the model is different, their change law is the same. When the spring ratio takes two boundaries, then the maximum amplitude magnification factor is also at the output of the boundary. When v takes the minimum value, then the value of A takes the maximum value. As v gradually increases from the minimum value to the optimal value or decreases from the maximum value to the optimal value, the value of A gradually decreases from point D and point F to point E (position of the minimum value), respectively.
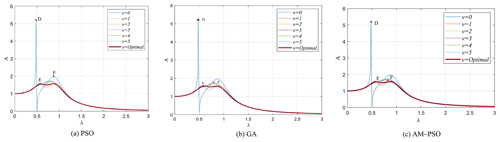
Figure 9Influence of spring ratio (v) on the three-element DVA under different optimization algorithms.
Figure 10 shows the influence of the law of the change in the spring ratio on the three-element DVA model under different damping ratios of the main system based on the AM–PSO optimization algorithm. Obviously, with the increase in the damping ratio of the main system, the maximum amplitude magnification factor decreases gradually. At that time, when ζ1=0.01, then the A value is 2.9152 under the optimal parameter combination, while when ζ1=0.5, then the A value is 1.3302 under the optimal parameter combination. Moreover, when ζ1 takes a smaller value, the change in v has a significant impact on the model output. On the contrary, when ζ1 takes a larger value, the change in v (except for the smaller value of v) has no significant impact on the model output.
An analytical solution for designing the optimal parameters of dynamic vibration absorbers attached to the damped main system is found to be difficult and complicated. In this paper, the adaptive multiswarm particle swarm optimization is applied to parameter optimization, and the numerical solutions of the system are given for the damped main system under sinusoidal force excitation. In the AM-PSO algorithm, the particles are adaptively grouped into several subswarms in accordance with the distributed density of the particles and the minimum distance between particles. In addition, the variable substitution learning strategy of velocity was utilized to improve the algorithm's population diversity.
Comprehensive experiments have been carried out to compare the AM-PSO algorithm with the canonical PSO and GA on the DVA models. The simulation results demonstrate that the comprehensive optimization is better in the AM-PSO than in the canonical PSO and GA. In addition, the main parameters of the DVA models are modified in light of the optimized results of the GA, canonical PSO, and AM-PSO to further verify the effectiveness of the AM-PSO method for optimizing parameters of the DVAs, and the three-element DVA has better robustness.
The optimal results obtained from this study have implications for numerical studies at the parameter optimization and performance evaluation of dynamic vibration absorbers. Moreover, the AM–PSO optimization algorithm proposed in this paper is not affected by the damping of the primary system.
The data used to support the findings of this study are available from the corresponding author upon request.
QHS led the investigation, developed the methodology with HYJ, and curated the data. LJX and QJS acquired the funding, and LJX supervised. QJS reviewed and edited the paper. HYJ validated the paper and wrote the original draft. XJL developed the software and provided the analysis.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors gratefully thank anonymous reviewers, for their valuable comments that improved the paper's quality. This work has been supported by the National Natural Science Foundation of China (grant nos. 51774193 and 52174145), Natural Science Foundation of Shan-dong Provincial China (grant no. ZR2020MF101), University Planning Projects of Science and Technology of Shandong Province (grant nos. J18KB011 and J18KA319), and SDUST Research Fund (grant no. 2018TDJH101).
This research has been supported by the National Natural Science Foundation of China (grant nos. 51774193 and 52174145), Natural Science Foundation of Shandong Province, China (grant no. ZR2020MF101), University Planning Projects of Science and Technology of Shandong Province (grant nos. J18KB011 and J18KA319), and Shandong University of Science and Technology (SDUST) Research Fund (grant no. 2018TDJH101).
This paper was edited by Dario Richiedei and reviewed by two anonymous referees.
Anh, N. D., Nguyen, N. X., and Hoa, L. T.: Design of three-element dynamic vibration absorber for damped linear structures, J. Sound Vib., 332, 4482–4495, 2013.
Anh, N. D., Nguyen, N. X., and Quan, N. H.: Global-local approach to the design of dynamic vibration absorber for damped structures, J. Vib. Control, 22, 3182–3201, 2014.
Asami, T. and Nishihara, O.: Analytical and experimental evaluation of an air damped dynamic vibration absorber: design optimizations of the three-element type model, J. Vib. Acoust., 121, 334–342, 1999.
Asami, T. and Nishihara, O.: H2 optimization of the three-element type dynamic vibration absorbers, J. Vib. Acoust., 124, 583–592, https://doi.org/10.1115/1.1501286, 2002.
Asami, T., Nishihara, O., and Baz, A. M.: Analytical solutions to H∞ and H2 optimization of dynamic vibration absorbers attached to damped linear systems, J. Vib. Acoust, 124, 284–295, 2002.
Bi, Y., Xiang, M., Schäfer, F., Lebwohl, A., and Wang, C. F.: A simplified and efficient particle swarm optimization algorithm considering particle diversity, Cluster Comput., 22, 13273–13282, 2019.
Chen, D. B. and Zhao, C. X.: Particle swarm optimization with adaptive population size and its application, Appl. Soft Comput., 9, 39–48, 2009.
Chen, J., Wu, Y., He, X., Zhang, L., and Dong, S.: Suspension parameter design of underframe equipment considering series stiffness of shock absorber, Adv. Mech. Eng., 12, 1–16, 2020.
Esen, I. and Koc, M. A. .: Optimization of a passive vibration absorber for a barrel using the genetic algorithm, Expert Syst. Appl., 42, 894–905, 2015.
Gao, Q., Feng, J., and Zheng, S.: Optimization design of the key parameters of McPherson suspension systems using generalized multi-dimension adaptive learning particle swarm optimization, P. I. Mech. Eng. D.-J. Aut., 233, 1–22, 2019.
Jagodzinski, D. J., Miksch, M., Aumann, Q., and Müller, G.: Modeling and optimizing an acoustic metamaterial to minimize low-frequency structure-borne sound, Mech. Based Des. Struct., 2020, 1–15, 2020.
Javidialesaadi, A. and Wierschem, N. E.: Three-element vibration absorber-inerter for passive control of single-degree-of- freedom structures, J. Vib. Acoust., 140, 061007, https://doi.org/10.1115/1.4040045, 2018.
Lai, X., Hao, J. K., Fu, Z. H., and Yue, D.: Diversity-preserving quantum particle swarm optimization for the multidimensional knapsack problem, Expert Syst. Appl., 149, 113310, https://doi.org/10.1016/j.eswa.2020.113310, 2020.
Li, C., Yang, S. X., and Nguyen, T. T.: A self-learning particle swarm optimizer for global optimization problems, IEEE T. Syst. Man Cyb., 42, 627–646, 2012.
Liu, M., Gu, F., Huang, J., Wang, C., and Cao, M.: Integration design and optimization control of a dynamic vibration absorber for electric wheels with in-wheel motor, Energies, 10, 2069, https://doi.org/10.3390/en10122069, 2017.
Nishihara, O.: Exact Optimization of a Three-Element Dynamic Vibration Absorber: Minimization of the Maximum Amplitude Magnification Factor, J. Vib. Acoust., 141, 011001.1–7, https://doi.org/10.1115/1.4040575, 2019.
Qin, Q., Shi, C., Zhang, Q., Li, L., and Shi, Y.: Particle swarm optimization with interswarm interactive learning strategy, IEEE T. Cybernetics, 46, 2238–2251, 2015.
Richiedei, D., Tamellin, I., and Trevisani, A.: Beyond the tuned mass damper: a comparative study of passive approaches to vibration absorption through antiresonance assignment, Arch. Comput. Method. E., 29, 519–544, 2021.
Snowdon, J. C.: Dynamic Vibration Absorbers That Have Increased Effectiveness, J. Eng. Ind., 96, 940–944, 1974.
Tigli, O. F.: Optimum vibration absorber (tuned mass damper) design for linear damped systems subjected to random loads, J. Sound Vib., 331, 3035–3049, 2012.
Wang, F., Zhang, H., and Zhou, A.: A Particle Swarm Optimization Algorithm for Mixed-Variable Optimization Problems, Lect. Notes Comput. Sci., 60, 100808.1–12, https://doi.org/10.1016/j.swevo.2020.100808, 2021.
Xie, S., Li, P., Zhang, X., and Bo, Y.: Vibration suppression of structure with electromagnetic shunt damping absorber, Int. J. Appl. Electrom., 45, 395–402, 2014.
Xiong, G. J., Zhang, J., Shi, D. Y., and Yuan, X. F.: A simplified competitive swarm optimizer for parameter identification of solid oxide fuel cells, Energ. Convers. Manage., 203, 112204, https://doi.org/10.1016/j.enconman.2019.112204, 2020.
Yin, Z. Y., Zhang, S. Y., Koh, S., and Linga, P.: Estimation of the thermal conductivity of a heterogeneous CH4-hydrate bearing sample based on particle swarm optimization, Appl. Energ., 271, 115229.1–16, https://doi.org/10.1016/j.apenergy.2020.115229, 2020.
Zhang, X. W., Liu, H., Zhang, T., Wang, Q. W., and Tu, L. P.: Terminal crossover and steering-based particle swarm optimization algorithm with disturbance, Appl. Soft Comp., 85, 105841, https://doi.org/10.1016/j.asoc.2019.105841, 2019.
Zhang, Y., Liu, X., Bao, F., Chi, J., and Liu, P.: Particle swarm optimization with adaptive learning strategy, Knowl.-Based Syst., 96, 105789, https://doi.org/10.1016/j.knosys.2020.105789, 2020.
- Abstract
- Introduction
- Defining the problem
- Numerical optimization
- Performance evaluation of the AM-PSO algorithm
- Comparisons of the vibration reduction performance
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Defining the problem
- Numerical optimization
- Performance evaluation of the AM-PSO algorithm
- Comparisons of the vibration reduction performance
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References