Novel loop tree for the similarity recognition of kinematic chains

The similarity recognition of kinematic chains (KCs) is helpful for improving the efficiency of configuration synthesis, which has been paid more and more attention in recent years. The existing recognition methods are divided into the definition method and feature constant method. Among them, the definition method is difficult to adopt in practice because of its long operation time, especially when the number of similar vertices in KCs is large. In this paper, the new concepts of a loop tree (LT) and a loop tree matrix (LTM) have been proposed, which improve the efficiency of similarity recognition. This method is applied on the complete structure of the following: 8-link with 1 DOF (degree of freedom), 9-link with 2 DOF, 10-link with 1 DOF, 12-link with 1 DOF, 13-link with 2 DOF, 14-link with 3 DOF, 15-link with 4 DOF planar single-joint KCs, and contracted graphs with up to six independent loops. All results are verified by the definition method to prove the good applicability, reliability, and efficiency of the proposed method. Simultaneously, the application case of the similarity recognition in a mechanism creation is given to provide a reference for an innovative design.

1 Introduction

The similarity recognition of kinematic chains (KCs) is an important part of the mechanism of innovation design, which can avoid isomorphism in the synthesis process and reduce the generation of redundant design schemes (Yan, 1992; Tsai, 2000; Sun et al., 2022). At present, relatively little research has been done on similarity recognition, including the definition method and the characteristic constant method. Among them, similarity recognition is accurate when using the definition method of graph theory, but numerous computations will be generated, especially when the number of links exceeds 10 (Sun et al., 2020). And for the characteristic constant method, most of them are not dedicated to similarity recognition but are more often applied to isomorphism recognition. Similarity recognition and isomorphism detection are essentially the same. The difference lies in that one is a recognition within graphs and the other is a recognition between graphs. Therefore, the characteristic constant method applied to isomorphism detection can also be used for similarity recognition.

Vertices in graph theory represent KC components, and a similarity analysis of the KC components can be transformed into a similarity recognition problem of vertices in topological graphs. Harary and Palmar (1966) discussed graph similarity, where it is noted that, if vertices u and v of graph G are similar, then $G-u\cong G-v$ and vice versa. Freudenstein (1967) provided the condition for similarity from the perspective of the permutation cycle of the automorphism group. However, the calculation amount is substantially larger, and a KC with n links requires n! cycle times. Lv (1989) verified the necessary conditions for similar vertices. Wang and Yan (2002) classified the similarity between components into symmetrical, parallel, transferred, and irregular states. This method only uses the vertex degree of the KC and does not reflect the specific connection between the components and misjudgments in several special cases. Sun et al. (2020) proposed similarity recognition methods based on the definition of similarity. However, the judgment is complicated when the number of similar vertices in the KCs are large.

There are many methods for isomorphism discrimination, which can also be used for similarity recognition, such as the eigenvalue, eigenvector, characteristic polynomial (Uicker and Raicu, 1975; Mruthyunjaya, 1984; Mruthyunjaya and Balasubramanian, 1987; Yan and Hall, 1982; He et al., 2005; Cubillo and Wan, 2005; Sunkari and Schmidt, 2006), Hamming number-based (Rao and Varada Raju, 1991; Rao and Rao, 1993, 2008; Dharanipragada and Chintada, 2016; Sun et al., 2017), code-based (Ambekar and Agrawal, 1987; Shin and Krishnamurty, 1992; Tang and Liu, 1993; Rai and Punjabi, 2018, 2019), and distance-based or path-based (Yadav et al., 1996; Venkata Kamesh et al., 2017) methods. For example, Uicker and Raicu (1975) applied characteristic polynomials of adjacent matrices to isomorphism identification. Ambekar and Agrawal (1987) proposed a coding-based isomorphism identification method. Rao and Varada Raju (1991) first introduced the concept of the Hamming distance in the field of information and communication to the mechanism. Sunkari and Schmidt (2006) introduced the eigenvalue and eigenvector of the adjacency matrix as the criterion into the isomorphism identification method. Moreover, Venkata Kamesh et al. (2017) detected the isomorphism of linkage and geared KCs using the concept of net distance in graph theory; counterexamples have been found for 10-link KCs in this paper. By considering the simplicity of the method, scholars, such as Shin and Krishnamurty (1992), Tang and Liu (1993), and Rai and Punjabi (2018, 2019), have conducted extensive research on code-based methods. Overall, the similarity recognition of the KC, based on the graph theory definition has no advantage in efficiency, especially when the number of similar vertices in the KCs are large. Existing characteristic constant methods cannot fully express the vertices and the graph's information, and their reliability will become poor with the large number of links. And many other methods have not been applied to similarity recognition. Therefore, in this paper, an idea with high efficiency and reliability of similarity recognition is proposed using a loop tree (LT) and a loop tree matrix (LTM) method.

The rest of this paper is organized as follows. Section 2 proposes the concept of the LT and LTM. Section 3 applies the LT and LTM to similarity recognition and gives some examples. Section 4 introduces the similarity algorithm application. Section 5 analyzes the recognition results. Finally, Sect. 6 concludes the paper.

2 Concepts of LT and LTM

2.1 LT

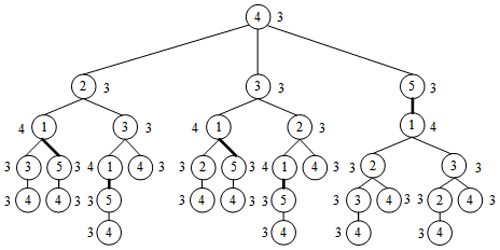
Set A is a vertex of graph G. All loops with A as the starting vertex are searched and given in the form of a tree (where vertex A is the root of the tree). For example, in Fig. 1c, the LT with vertex 4 is as shown in Fig. 2 (thick, solid lines in LT represent parallel edges 1–5).

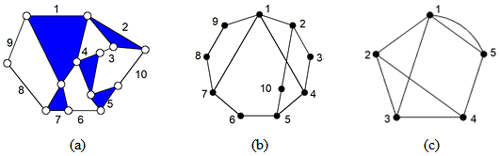
Figure 1 (a) A 10-link with 1 DOF (degree of freedom) KC, (b) a topological graph, and (c) a contracted graph.

Figure 2 The LT with vertex 4 as the root of Fig. 1c.

Figure 3 The LT with vertex 1 as the root of Fig. 1c.

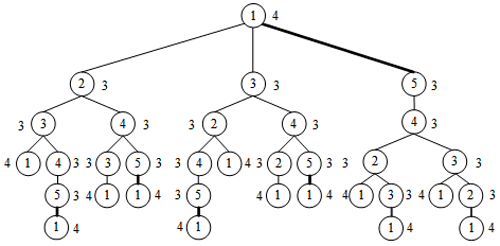
The LT represents all the information of vertices in the graph, such as the vertex degree information, assignment information of connecting edges, and loop information. If the LTs of two vertices are the same, then the statuses of the two vertices in the graph are equivalent. For example, in Fig. 1c, the LT has vertex 1 as the root, as shown in Fig. 3. Although the tree structure is the same as that in Fig. 2, the vertex degree and the assignment information of connection edges are inconsistent; thus, vertices 4 and 1 are non-similar.

2.2 LTM

For the convenience of computer implementation, a matrix expression of LT is proposed, as shown in Table 1. Each number in a loop contains three messages. The first message is the degree of the root, the second message specifies the number of branch edges, and the third message is the value assigned for branch edges (fine and thick solid lines are assigned 1 and 2, respectively). But when a cycle is completed, there is a last number containing only one piece of information (i.e., the degree of the root). For example, the loop 4-2-1-3-4 in Fig. 2 can be expressed as 331, 321, 421, 311, and 3. Other loops can then be expressed, and the sequence of the numbers is converted into a matrix form. The number of digits is insufficient to fill 0. The LTM of Fig. 2 is shown in Eq. (1).

Table 1 Elements of LT.

Definition 1. The row elements of the LTM are sorted in descending order (i.e., L_d). For example, L_d of Fig. 2 is presented as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& \mathrm{LTM}=\left[\begin{array}{rrrrrr}\mathrm{331}& \mathrm{321}& \mathrm{421}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{422}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{412}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{421}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{422}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{412}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{3}& \mathrm{0}\end{array}\right],\\ & L_{\mathrm{d}}=\left[\begin{array}{rrrrrr}\mathrm{331}& \mathrm{321}& \mathrm{422}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{422}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{421}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{421}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{412}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{412}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{312}& \mathrm{421}& \mathrm{321}& \mathrm{3}& \mathrm{0}\end{array}\right].\end{array}\end{array}$$

3 Similarity recognition

3.1 Similarity recognition algorithm

If L_d of two vertices are the same, then the two vertices are judged to be similar; otherwise, they are non-similar. The steps of the similarity recognition algorithm are as follows.

First calculate L_d of each vertex and compare the L_d parameters of two vertices. If L_d parameters of two vertices are different, then these vertices are non-similar, and the next vertices would be considered. Otherwise, these vertices are similar. The next vertices are then considered until all candidate vertices are identified. For example, vertices 2 and 3 in Fig. 1c have the same L_d as shown in Eq. (2); thus, vertices 2 and 3 are similar.

$$\begin{array}{}\text{(2)}& L_{\mathrm{d}\mathrm{2}}=L_{\mathrm{d}\mathrm{3}}=\left[\begin{array}{rrrrrr}\mathrm{331}& \mathrm{422}& \mathrm{311}& \mathrm{321}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{422}& \mathrm{311}& \mathrm{321}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{421}& \mathrm{321}& \mathrm{311}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{421}& \mathrm{321}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{422}& \mathrm{311}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{321}& \mathrm{421}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{411}& \mathrm{3}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{312}& \mathrm{411}& \mathrm{3}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{321}& \mathrm{3}& \mathrm{0}& \mathrm{0}\\ \mathrm{331}& \mathrm{321}& \mathrm{312}& \mathrm{421}& \mathrm{311}& \mathrm{3}\\ \mathrm{331}& \mathrm{321}& \mathrm{312}& \mathrm{421}& \mathrm{3}& \mathrm{0}\end{array}\right].\end{array}$$

3.2 Illustrative examples of similarity recognition

The proposed method is tested on planar single-joint KCs (PSKCs) and contracted graphs of KCs to prove its versatility. Illustrative examples are provided as follows.

3.2.1 Examples of PSKCs

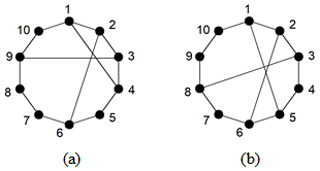
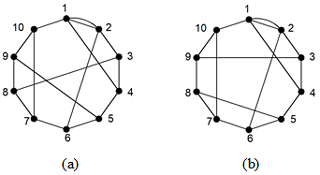
Example 1. In total, two 10-link PSKCs are considered in Fig. 4a and b.

Figure 4 (a) A 10-link PSKC-1 and (b) a 10-link PSKC-2.

The adjacency matrices of two 10-link PSKCs in Fig. 4 are entered into the similarity recognition programs. The L_d of each vertex is solved and compared with other vertices of same graph. Similar information to that in Fig. 4 is shown in Table 2. To some extent, solving the similarity of the graphs can also identify whether they are isomorphic. Because the similar information in Fig. 4a and b is different, it can be judged that they are not isomorphic.

Table 2 Similar information to that in Fig. 4.

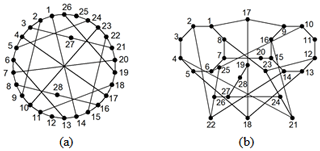
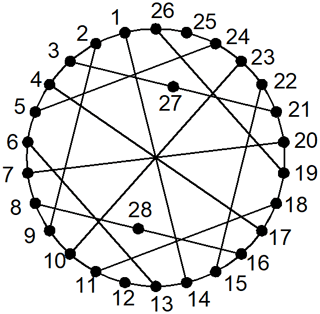
Example 2. In total, two 28-link PSKCs are considered in Fig. 5a and b, as discussed in Uicker and Raicu (1975).

Figure 5 (a) A 28-link PSKC-1 and (b) a 28-link PSKC-2.

The adjacency matrices of two 28-link PSKCs in Fig. 5 are entered into the similarity recognition programs. Similar information to that in Fig. 5 is shown in Table 3. Because the similar information of Fig. 5a and b is the same, there is the possibility of isomorphism between two graphs.

Table 3 Similar information to that in Fig. 5.

3.2.2 Examples of contracted graphs

The distinction of contracted graphs lies in the existence of parallel edges, which can be distinguished by setting up the parallel edge value equal to the number of parallel edges. The similarity recognition method is same as the single-hinged KC. As shown in Fig. 8, two 10-link contracted graphs are considered.

The adjacency matrices of two 10-link contracted graphs in Fig. 6 are entered into the similarity recognition programs. Similar information to that in Fig. 6 is shown in Table 4. Because the similar information of Fig. 6a and b is different, it can be judged that they are not isomorphic.

Figure 6 (a) A 10-link contracted graph (1) and (b) a 10-link contracted graph (2).

Table 4 Similar information to that in Fig. 6.

4 Similarity algorithm application

4.1 KC similarity recognition application

In addition to the examples in Sect. 3, the similarity recognition algorithm is applied to the complete atlas of 10-link with 1 DOF PSKCs. The recognition results are consistent with the definition method of the graph theory, as shown in Appendix A (only the upper triangular elements of the adjacency matrix are given in the Appendix A).

4.2 Innovative mechanism design

Yan (1992) proposed a regenerated KC method for innovative mechanism design, which represents logical reasoning for the KC regeneration process. In logical reasoning, the similarity of the KC components should be analyzed first to reduce redundant design schemes and improve the innovative design efficiency. Vertices in the graph theory represent KC components, and a similar analysis of the KC components can be transformed into a similarity recognition problem of vertices in topological graphs.

The working device of a loader is the main part for realizing the shoveling operation and material loading. Its structure directly affects the working size and comprehensive performance of the loader. Taking the mechanism's innovative design of a 6-link loader as an example, as shown in Fig. 7, the application of similarity recognition in mechanism innovative design is illustrated.

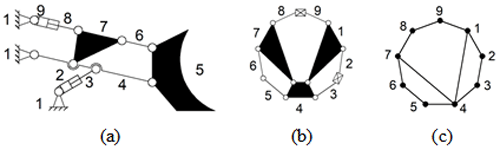
Figure 7 (a) Loader functional schematic, (b) structural representation, and (c) topological graph representation with the (1) rack, (2, 3) rotary bucket oil cylinder, (4) moving arm, (5) bucket, (6) connecting rod, (7) rocker, and (8, 9) lifting oil cylinder.

Step 1. Retrieve the existing design by task and enumerate all the KCs.

Figure 7c shows the original mechanism of the loader's innovative design. According to Tsai (2000), 35 9-link with 2 DOF topological graphs are obtained.

Step 2. Analyze the structural and functional constraints of the original mechanism and conducting topological graphs screening. For example, see the structural and functional constraints of Fig. 7a.

1. There must be a ternary link as a rack.

2. There must be two oil cylinders as the original moving parts, with one as the rotating oil cylinder and one as the lifting oil cylinder, where one end of the lifting oil cylinder is connected to the rack, and the other one is connected to the moving arm. It shows that the topology graph has at least two binary chains of length 2.

3. There must be a binary link as the output bucket, where one end is connected with the moving arm but cannot be directly connected with the rack.

4. There must be a moving arm, for which the one end is connected to the rack, and the other end is connected to the output bucket. One end of the lifting cylinder and the rocker should be connected with the moving arm by considering the coordination and stiffness of the mechanism.

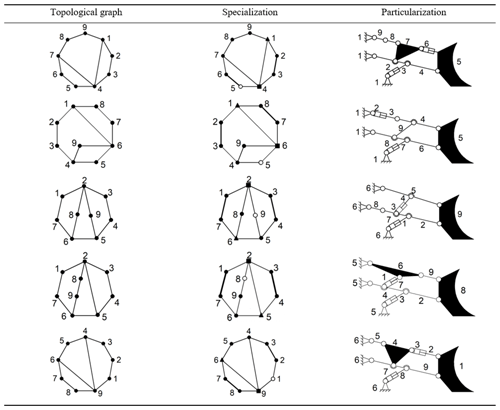
The direct connection between the binary link and hydraulic cylinder should be avoided to overcome the excessive forces on the local components of the transmission. These excessive forces can create the imbalance. The topology graphs that fulfill the above constraint criteria are shown in the first column of Table 5.

Step 3. Specify the topology graphs that meet the structural and functional requirements of the mechanism. For example, see the specialization of Fig. 7c.

First, determine the rack. Both vertex 1 and vertex 7 are three degree vertices and can be used as racks. Vertices 1 and 7 are similar, according to the loop tree matrix, and choosing vertex 1 or vertex 7 as racks is equivalent. In this paper, vertex 1 is chosen as a rack.

Second, the original moving parts are determined. The original moving parts are binary chains of length 2 in topology graph. The edges are assigned to the two that attached to the rack. Binary chain 23 and 56 are no longer similar, according to the loop tree matrix. The binary chains 89 and 23, 89 and 56, and 56 and 23 can be chosen as the original moving parts.

When binary chains 89 and 23 are chosen as the original moving parts, only vertex 5 can be chosen as the output bucket. The final functional schematic is shown in Table 5.

When binary chains 56 and 23 are chosen as the original moving parts, only vertex 5 can be chosen as the output bucket. The final functional schematic is shown in Fig. 7a.

When binary chains 56 and 89 are chosen as the original moving parts, it does not satisfy the structural constraint (4).

According to the above specialization process, other topology graphs are given specifically, as shown in the second column of Table 5. In specialized topological graph, ▴ represents the rack, ∘ represents output the bucket, ▪ represents the moving arm, and the solid lines represent prismatic pair.

Step 4. Draw the schematic graph and delete the existing design as the rest forms the new designs, as shown in the third column of Table 5.

Table 5 The new designs of 6-link loader.

5 Recognition result analysis

At present, there are relatively few studies on the similarity, and the recognition methods are difficult when attempting to meet the requirements in reliability and efficiency. In this paper, a similarity recognition method based on the tree loop was proposed, which aims to provide some theoretical support for configuration synthesis and innovation.

5.1 Computational complexity

Compared with the graph theory definition method for recognizing similar vertices, the application of the LT method can reduce the computer computation considerably. Figure 8 shows the available methods for identifying similar vertices, including the definition method needs a calculation of 28! cycle times. The method of Dharanipragada and Chintada (2016) requires a calculation of $\mathrm{16}\mathrm{!}\times \mathrm{8}\mathrm{!}\times \mathrm{4}\mathrm{!}$ cycle times, and the LT method only needs $\sum _{\mathrm{1}}^{\mathrm{16}}\mathrm{1}+\sum _{\mathrm{1}}^{\mathrm{8}}\mathrm{1}+\sum _{\mathrm{1}}^{\mathrm{4}}\mathrm{1}$ cycle times.

Figure 8 A 28-link PSKC.

5.2 Computational complexity

LTM contains almost all information of the LT, such as the vertex degree information, assignment information of connecting edges, and loop information. Therefore, the LT method used to recognize the similar vertices is effective, as proven by numerous recognition examples.

6 Conclusions

In this paper, the concept of a loop tree containing multidimensional topological information is proposed, and the loop tree matrix is established for similarity recognition. This method is applied to planar single-joint KCs and contracted graphs to reflect its applicability, and its accuracy is verified by the definition method. At the same time, the efficiency of the method is proved by qualitatively comparing the calculation cycle times of various similarity recognition methods. Finally, through the application of the similarity recognition in mechanism creation, the practical significance of this method is shown, which provides a reference for mechanical equipment design.

Appendix A

Table A1 Similarity of the 10-link with 1 DOF PSKCs.

Appendix B

Table B1 L_d of a 10-link with 1 DOF PSKCs.