Short communication: A case study of stress monitoring with non-destructive stress measurement and deep learning algorithms

Non-destructive stress measurement is necessary to provide safety maintenance in some extreme machining environments. This paper reports a case study that reveals the potential application of automatic metal stress monitoring with the aid of the magnetic Barkhausen noise (MBN) signal and deep learning algorithms (convolutional neural network, CNN, and long short-term memory, LSTM). Specifically, we applied the experimental magnetic signals from steel samples to validate the feasibility and efficiency of two deep learning models for stress prediction. The results indicate that the CNN model possesses a faster training speed and a better test accuracy (91.4 %), which confirms the feasibility of automatic stress monitoring applications.

1 Introduction

During manufacturing, machine failure leads to fatal damage to both people and the environment, inducing a high cost and low productivity (Liao et al., 2012). Consequently, the timely diagnosis of the serving status, deformation, and failure possibilities of steel materials has become a necessity. Stress/strain can be used to describe the internal deformation status of a steel material/structure (Rasmussen, 2003), to predict the serving time of components (Zhang et al., 2020), and to prevent material/structure failures (Pejkowski et al., 2018). However, traditional measurements require well-prepared samples and laboratory environments (Motra et al., 2014), which are not suitable for on-site measurement under extreme conditions such as failure monitoring of supporting bearings, high-speed rolling and moving components, and large steel structures. For example, the most widely used strain gauge methods need to stick the strain gauge onto the sample surface and to link to the train bridge box, which is not suitable for moving samples. Stress/strain measured by crosshead motion is not accurate. Moreover, the optical strain measurement method is only suitable transparent materials with photoelasticity.

The magnetic properties of steel materials and their magnetic responses towards applied magnetic stimuli could be influenced by external forces. The magnetic signals include magnetic flux leakage (MFL) (Wu et al., 2021), magnetic acoustic emission (MAE) (Watson et al., 2005), magnetic Barkhausen noise (MBN) (Rocío et al., 2015), and metal magnetic memory (MMM) (Yang et al., 2013). Corresponding methods have been developed for measuring the stress of steel and other ferromagnetic materials. However, magical signals can be influenced by many internal and external factors, such as the material components, defects, the material processing history, the temperature, and the surface quality. All of these factors cause significant uncertainty in stress measurements. Therefore, an analytical model has been developed to study the effect of applied stress on magnetic Barkhausen noise (MBN) in force-exerted steel materials (Rocío et al., 2015). Moreover, Jiles (1993) established a coupled magnetoelastic theory to compute changes in magnetic hysteresis; Alessandro et al. (1990) proposed a Langevin description to build up the computational basis of statistical properties of Barkhausen noise; and Sablik (1993) further extended this model to confirm the equivalent linear increase of the Barkhausen amplitude. Nevertheless, the material-dependent and hard-measured parameters in the model lead to issues with model application.

With the application of artificial intelligence, convolutional neural network (CNN) models can easily detect objects from an image that would be impossible to detect using analytical methods (Lee et al., 2019). Recurrent neural networks (RNN) can accurately convert a sequential voice to text (Graves and Jaitly, 2014). In addition, a fully CNN can segment surface defects by supervised learning without pre- or post-processing (Huang et al., 2020). Using a deep RNN, the spatial frequency–sequential relationships for motor imagery classification can even be explored (Luo et al., 2018). Furthermore, the microstructural/mechanical properties and thickness variations in API X65 steel can be determined in a non-destructive way with magnetic hysteresis loop and artificial neural networks (Mirzaee et al., 2020). However, there have been few attempts to intelligently monitor metal materials using Barkhausen noise signals. One of the few such existing studies is that of Wang et al. (2013), who extracted the multiscale features of Barkhausen noise using wavelet decomposition and used these features as the input for a back-propagation neural network to predict the temperature effect (Wang et al., 2013). Hence, this paper focuses on the feasibility and capacity of deep learning algorithms (CNN and long short-term memory recurrent neural networks, LSTM-RNN) in stress prediction using Barkhausen noise signals, obtained from a series of uniaxial compressive tests on a typical steel material.

2 Methods

2.1 Experiments and results

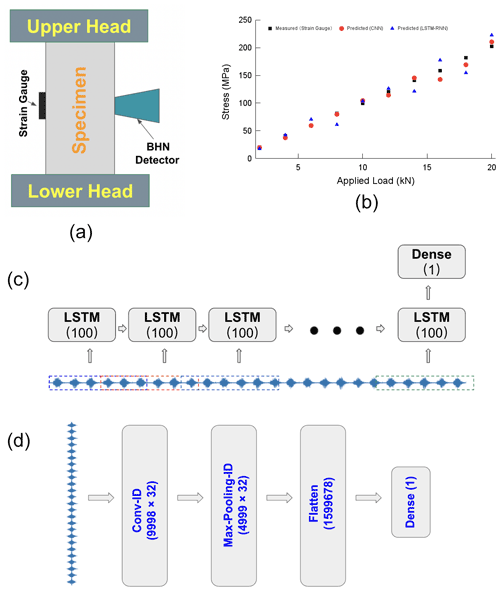
The steel material to be tested was typical low-carbon steel (ASTM A36). For conducting uniaxial compressive testing, we prepared 10 bar-shaped samples with a square 1 cm × 1 cm cross section and a length of 5 cm. A universal testing machine (CMT 5105) was used to apply uniaxial compressive force (Fig. 1a). The applied forces increased from 0 to 20 kN with a step of 2 kN. Strain gauges were used to measure the train of the deformed sample and, thus, to calculate the corresponding stress (Fig. 1b). During the test, periodically alternating magnetic fields (10 Hz) were applied to the samples using a Rollscan 350 analyser. When the external magnetic field changes, the internal domain walls are forced to move, generating Barkhausen noise pulses. The Barkhausen noise of the sample was measured using a Rollscan 350 analyser, as shown in Fig. 1a. For each step force of each sample, 100 Barkhausen noise pulses were taken. Considering that we had 10 samples and an 11-step force action for each sample, we acquired 11 000 data items for neural network training and testing.

Figure 1 (a) A sketch of the experimental set-up; (b) a sample set of measured stresses under different loads; and the neural network structure of the (c) LSTM-RNN and (d) CNN models.

2.2 Deep learning models

There are two types of widely used deep learning models: convolutional neural network (CNN) and recurrent neural network (RNN). To eliminate the issues of gradient vanishing in RNN (Hochreiter and Schmidhuber, 1997), additional modifications have been made on the traditional RNN. LSTM (long short-term memory) is one of the most promising modifications and can effectively solve the vanishing gradient problem in the traditional RNN. Both CNN and LSTM-RNN can be used to predict stress via the measured Barkhausen noise (BHN) signals; in this study, we will examine the performance of both models.

We used Keras to build the models and conduct the training process. Figure 1c shows the neural network structure of the LSTM-RNN model used in this study. It consists of two layers: the LSTM layer with 100 neural units and a dense layer for outputting the prediction. The number of total trainable parameters in this model is 40 901. Figure 1d shows the neural network structure of the CNN model used in this study. It consists of four layers: the “Conv-1D” layer with 32 filters, the “Max-Pooling-1D” layer, the “Flatten” layer, and the “Dense” layer. The overall number of trainable parameters is 160 097. As we are interested in predicting the value of stress, the activation function of the output layer in both models is “linear”, and the loss function is the mean square error. In data processing, 65 % of data items were used for model training, 15 % of data items were used for validation, and the remaining 20 % of data items were used for testing. The respective epoch and batch size were set to 1000.

3 Results

3.1 Experimental results

Figure 1b lists a sample set of the measured stress values under different loads. The stresses of other samples are more or less similar. All of the measured stress values will be used as output for training the two deep learning models. Considering that 100 Barkhausen noise pulses will be taken in each step force of each sample, these 100 items of signal will have the same output stress.

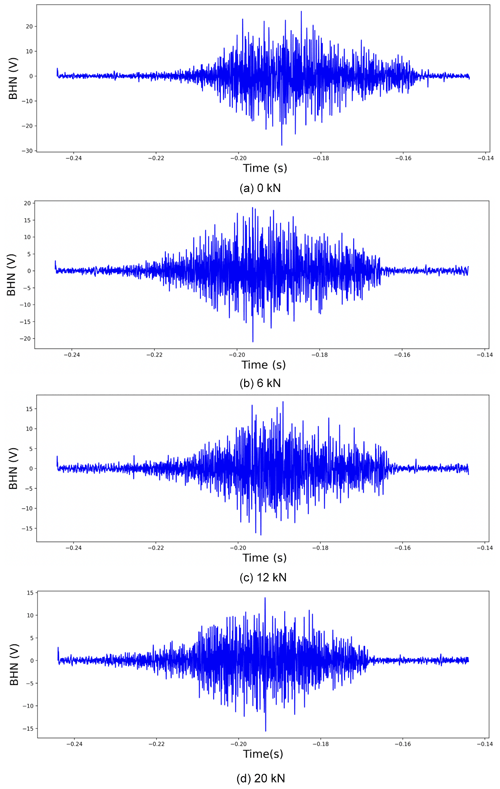
Figure 2 shows the typical Barkhausen noise pulse for a steel sample measured under different stress levels. It conveys that the maximum amplitude of the signal decreases as stress increases. This is because the movement of DWs (domain walls) under compressive stress can be significantly constrained, and the activation energy barrier of Barkhausen noise will increase: the higher the stress, the higher the energy barrier. Therefore, it is more difficult to activate Barkhausen noise.

Figure 2 The Barkhausen noise (BHN) of steel samples under different loads: (a) 0 kN, (b) 6 kN, (c) 12 kN, and (d) 20 kN.

3.2 Model training behaviours

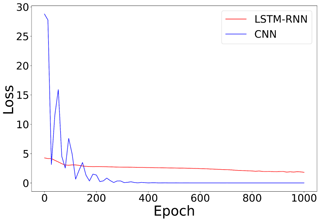
Figure 3 shows the changes in the loss function during the training process of both models. It is clear that the loss in the CNN model is much higher than that in the LSTM-RNN model at the beginning of the training process. However, the performance of the CNN model improved very rapidly and finally achieved a very small loss value. On the contrary, the improvement of the LSTM-RNN model during the training was slow, and the final loss value was also high. This finding is supported by the final training accuracies of two models: 95 % for the CNN model and 86 % for the LSTM-RNN model. Furthermore, the prediction accuracy of the CNN model in the validation and test datasets was 92.5 % and 91.4 % respectively. The prediction accuracy of the LSTM-RNN model in the validation and test datasets was 83.3 % and 78.9 % respectively. It was also noticed that the training speed of the CNN model was much faster than that of the LSTM-RNN model, although the latter model had less trainable parameters. The mean stress prediction values from the CNN and LSTM-RNN models are compared in Fig. 1b, and the CNN datasets are closer to the experimental data.

Figure 3 The loss curves of the LSTM-RNN and CNN models.

The good performance of the CNN model can be explained as follows: although BHN is a time-series data type, the applied stress mainly affects the envelope profile of the BHN rather than the individual magnetic activation event. Many studies have tried to establish a quantitative relationship between the envelope profile features of the BHN pulse, including factors such as its amplitude and width. The CNN model is good at abstracting general features of a signal/image using convolutional filters. Therefore, in this model, it can effectively learn the relationship between the profile features and the applied stress. On the contrary, the LSTM-RNN model is good at learning the local features of sequential data/a signal, and its capacity to detect the long-scale profile features is limited by its long-term memory (LSTM modification has also been applied).

The fast training speed of the CNN model can be explained as follows: although the CNN model used in this work has more trainable parameters (40 901) than that of the LSTM-RNN model (160 097), its real neural network is much deeper than that of the LSTM-RNN model. This is due to the nature of the RNN model. In every RNN model, the input data at each step share the same neural network. However, as the neural network is recurrent in each time step, and we have 10 000 time steps in one sample, the exact number of layers in the LSTM-RNN model used in this study is 10 000 rather than 1. This makes the training speed of the LSTM-RNN model slower than that of the CNN model.

3.3 Comparison of the machine learning model and analytical model

The above results have proven that deep learning models can predict stress via Barkhausen noise with reasonable accuracy. This provides an alternative way to mathematically describe the functional relation in a complex system. In contrast to traditional analytical models, deep learning models do not need complex mathematical formula derivation, strong assumptions, or simplifications, and they only rely on high-quality experimental data. Therefore, they are very suitable for solving various prediction problems in a wide engineering field. However, as the functions described by deep learning algorithms (both CNN and LSTM-RNN) are very complex, the underlying physical meanings of parameters are not explained. This causes difficulty in further exploring the underlying mechanism of a physical phenomenon with insight. Moreover, the prediction capacity of deep learning models is normally limited to specific tasks. If one wants to change a material, experiments should be carried out from the beginning, and the model should be retrained as well. On the contrary, once a physical model is developed for a phenomenon, it can be easily generalised and extended to other cases. Therefore, deep learning can solve the prediction problem, and traditional analytical models should also be studied to explore the underlying mechanism and generalisation.

4 Conclusions

This paper reported a case study on stress prediction using both magnetic Barkhausen noise signal data and two deep learning algorithms (CNN and LSTM-RNN). A total of 11 000 Barkhausen noise data points were obtained in a series of uniaxial compressive tests, and 65 % of the data items were used for model training, 15 % of the model data items were used for validation, and the remaining 20 % of the data items were used for further testing. The results of this work indicated the following:

• the CNN model provides better training accuracy (95 %) and test accuracy (91.4 %) and should be more suitable for learning and predicting the relationship between the Barkhausen noise data and the targeted stress;

• the CNN model possesses a faster training speed and is appropriate for designing intelligent real-time detecting systems using cloud computing;

• the potential for future research regarding industrial applications.

Although CNN possesses better accuracy with respect to training and testing for the uniaxial compressive tests, on-site test results suffer from various environmental factors, such as temperature and humidity. Therefore, future research will focus on the confirmation of CNN feasibility and efficiency in tests for a specific industry.