Dynamic behaviour of a planetary reducer with double planet gears

Planetary reducers have a wide and significant application in modern machine industry. They are extremely compact and reliable, and they can achieve a wide range of gear ratios as well as high efficiency. Since they often operate in extremely changeable working conditions, such as often starting and stoping, it is both interesting and desirable to study their dynamic behaviour. This paper presents a dynamic model of a planetary reducer with double planet gears created by applying Lagrange's equations of the second kind. After a planetary gear reducer has been designed and a CAD model created, the dynamic model was made. Most of characteristic values needed for solution of the equations are taken from the CAD model. Due to their complexity, the equations are solved in math simulation software. A lot of interesting results concerning the dynamic behaviour of the model are obtained, which can be helpful in understanding the dynamic occurrences in the inside of a planetary gearbox. At the end of the paper, conclusions are drawn, and further research directions in this area are given.

1 Introduction

Planetary reducers are widely used in mobile machine drive systems due to their compact design. Operating conditions for power transmissions with planetary reducers are variable within wide application limits. The research area of planetary reducer dynamics is of great importance. Examining the dynamics of those reducer types leads to conclusions that could greatly assist the development of planetary reducers with regard to increasing their compact design, increasing reliability, increasing the lifetime of reducer, reducing vibration and noise in working conditions, etc. Classical types of planetary gears have been well studied in the literature, but for some special types like planetary reducers with double planet gears and movable output ring gear, there are not a lot of published papers.

The interesting field of planetary reducers research before dynamics is kinematic analysis. Kinematic analysis is interesting from many aspects, but the main one is planetary reducer application in multiple transmission ratios usage. This application of the common planetary reducer concept used in multiple transmissions is described in papers which deal with the design and kinematic analysis of compound planetary gears (Troha et al., 2012; Karaivanov et al., 2012). That research is extended in order to show all shifting possibilities of the previously presented concept (Troha et al., 2014). Since in mobile machines gear trains operate in highly changeable working conditions, the analysis of the gear train dynamic behaviour is very significant. Studies of dynamic behaviour of planetary gear trains yield very important conclusions that contribute to the advancement of planetary gear trains by increasing design compactness, operation reliability, service life and efficiency or by reducing noise levels, gear train vibrations, etc. A dynamic model of a double-helical planetary gear train and its theoretical analysis is shown in the paper by Sondkar and Kahraman (2013). The experimental analysis of the double-helical planetary gear, with certain simplifications due to experimental constraints, is presented in Kang and Kahraman (2015). In the available literature, there are a lot of detailed studies on how dynamic stability of planetary gear reducers is affected by manufacturing error of the planetary reducer elements, tooth profile modifications, stiffness of the gear reducer elements, etc. Inalpolat and Kahraman presented a dynamic model to predict modulation sidebands of a planetary gear set having manufacturing errors (Inalpolat and Kahraman, 2010). Bahk and Parker performed an analytical investigation of tooth profile modification effects on planetary gear dynamics (Bahk and Parker, 2013). Luo and Di conducted a dynamics modelling of a planetary gear set considering meshing stiffness based on bond graph (Luo and Di, 2011). Batinic performed extensive research in order to determinate gear mesh stiffness for various parametric excitation (Batinic, 2008; Batinic, 2013). One of the interesting research publications is about eccentricity error in planetary gears (which occurs during the manufacturing) and its impact on the planetary gear dynamics (Gu and Velex, 2013). Chen and Shao performed a dynamic simulation of a planetary gear with tooth root crack in a ring gear (Chen and Shao, 2013). In the paper by Zhang et al. (2016), the dynamic modelling and vibration characteristics of a two-stage closed-form planetary gear train is shown (Zhang et al., 2016). Shakeri Aski et al. (2014) studied the vibration behaviour optimization, while a modal analysis of a planetary gear train with journal bearings was done in the paper by Bu et al. (2012).

Since noise and vibrations have negative effects on operation of planetary gear trains, dynamic analysis of these gear trains is very common in modern investigations (Blagojevic et al., 2009; Blagojevic, et al., 2020). The papers (Sondkar and Kahraman, 2013; Kang and Kahraman, 2015) give a detailed dynamical analysis of planetary gear sets with both central gears stationary. Some newer papers in this field such as Bao et al. (2020) and Chen et al. (2021) are focused on the single meshing points of the gearbox.

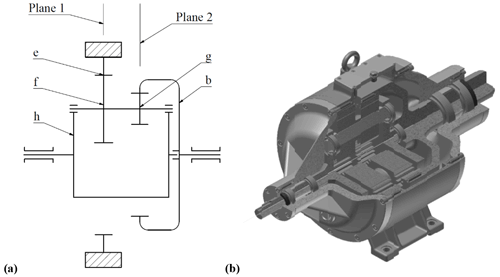
Figure 1 Planetary reducer with double planet gears; (a) kinematic scheme (h – planet gear carrier; e – stationary ring gear; f, g – planet gears; b – movable ring gear); (b) 3D model.

Only two papers from all discussed papers deal with planetary reducers with double planet gears, so the lack of data in that field is evident. This paper presents a dynamic model of a planetary reducer with double planet gears, in which the first ring gear is stationary while the second one revolves around its own axis. This paper should help in better understanding the dynamic occurrences in the planetary reducers which have the double planet gears. The presented dynamic model is based on the previously designed CAD model. The paper concludes with direct points which can be used as a general rule for this type of planet gears and shows the future direction of the research. The presented papers can be used as guidelines for further investigation of aspects of this reducer type, as well as in the design process, considering the vibration in start–stop reducer mode.

2 Basic assumptions of the dynamic model

Before dynamic analysis is conducted, the basic assumptions have to be made. Figure 1 shows the planetary reducer studied in this paper. It is a two-stage planetary reducer with double planet gears, where the first ring gear is stationary (ring gear e), while the second ring gear is movable (ring gear b). The chosen reducer has three planet gears.

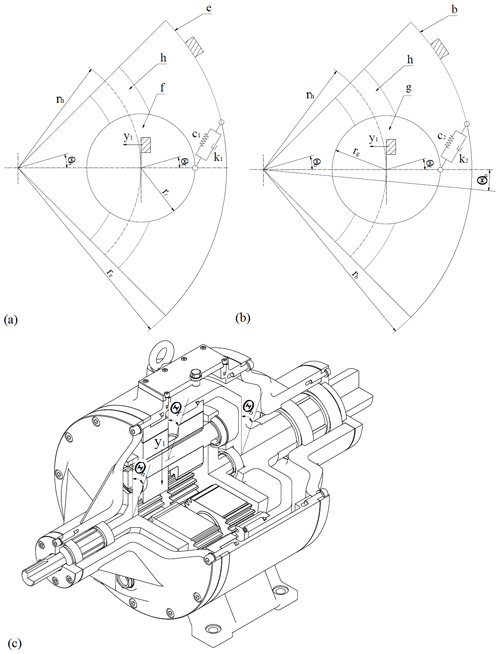
Figure 2 Dynamic model of the planetary reducer with double planet gears: (a) plane 1; (b) plane 2; (c) three-dimensional dynamic model.

The dynamic model of the planetary gear train is defined after the gear train has been observed in two planes (Fig. 1a). Based on the degrees of freedom of the gear reducer, the displacement directions of the dynamical model are determined. Each displacement is presented by the real direction and orientation that occur during the operation of the gear reducer. The pulsating input torque is transferred from the planet gear carrier to the planet gears and then from the planet gears to the movable and the stationary ring gears. The model has 4 degrees of displacement freedom: y₁ – displacement of the satellite and the double planet gears in the radial direction, θ_h – angular displacement of the planet carrier around its own axis, θ_f – angular displacement of the planet gears f–g around its own axis, and θ_b – angular displacement of the movable ring gear round its own axis.

The following contacts between the mashed gear teeth are modelled using the suitable springs and dampers: the contact between the gear e and the gear f (the spring stiffness c₁ and the damper with the damping coefficient k₁) and the contact between the gear g and the gear b (the spring stiffness c₂ and the damper with the damping coefficient k₂). The degrees of displacement freedom and the defined meshes are presented in Fig. 2.

Figure 3 Input torque.

In order to obtain as many accurate results as possible, the total masses of the system elements are taken into account (not the reduced ones). The total masses of the parts and the moments of inertia are obtained from the CAD model, which makes the solution to these equations even more correct.

The dynamical model is defined using Lagrange's equations of the second kind, assuming the displacement y₁ to be collinear with the angular displacements but in the opposite direction. Lagrange's equations of the second kind have the following general form as given in Eq. (1):

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{d}{\mathrm{d}t}}{\displaystyle \frac{\partial E_{\text{k}}}{\partial \dot{q_i}}}-{\displaystyle \frac{\partial E_{\text{k}}}{\partial q_i}}=-{\displaystyle \frac{\partial E_{\text{p}}}{\partial q_i}}-{\displaystyle \frac{\partial \mathit{\varphi }}{\partial \dot{q_i}}}+Q_i,\end{array}$$

where E_k is kinetic energy, E_p is potential energy, Φ is the dissipation function, q_i represents the generalized coordinates, and Q_i represents the conservative forces.

In matrix form, Lagrange's equations of the second kind are as given in Eq. (2):

$$\begin{array}{}\text{(2)}& \mathit{\left\{}M\mathit{\right\}}\mathit{\left\{}\ddot{q}\mathit{\right\}}+B\mathit{\left\{}\dot{q}\mathit{\right\}}+C\mathit{\left\{}q\mathit{\right\}}=D,\end{array}$$

where M is the mass matrix, B is the damping matrix, C is the stiffness matrix, {D} is the generalized forces vector, $\mathit{\left\{}\ddot{q}\mathit{\right\}}$ is the generalized accelerations vector, $\mathit{\left\{}\dot{q}\mathit{\right\}}$ is the generalized velocities vector, and {q} is the generalized displacements vector.

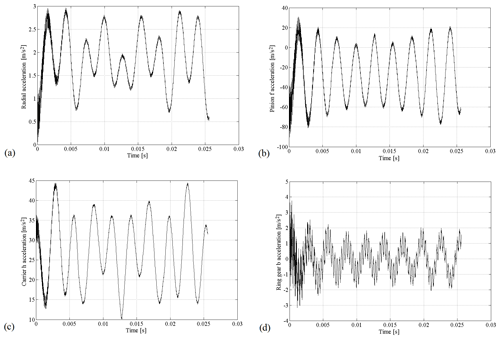
Figure 4 Acceleration diagrams for $c_{\mathrm{1}}=\mathrm{1.67}\times {\mathrm{10}}^{\mathrm{10}}$ N m⁻¹, $c_{\mathrm{2}}=\mathrm{1.56}\times {\mathrm{10}}^{\mathrm{10}}$ N m⁻¹, k₁=3200 N s m⁻¹, and k₂=2400 N s m⁻¹: (a) y₁ direction, (b) θ_h direction, (c) θ_f direction, and (d) θ_b direction.

Figure 5 Velocity diagrams for $c_{\mathrm{1}}=\mathrm{1.67}\times {\mathrm{10}}^{\mathrm{10}}$ N m⁻¹, $c_{\mathrm{2}}=\mathrm{1.56}\times {\mathrm{10}}^{\mathrm{10}}$ N m⁻¹, k₁=3200 N s m⁻¹, and k₂=2400 N s m⁻¹: (a) y₁ direction, (b) θ_h direction, (c) θ_f direction, and (d) θ_b direction.

3 Dynamic model of the planetary reducer with double planet gears

The kinetic energy of the gear reducer is calculated as the sum of kinetic energies of the gear reducer elements. The total kinetic energy is given with Eq. (3):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& E_{\text{k}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[m_{\text{h}}\left(\dot{y_{\mathrm{1}}^{\mathrm{2}}}+r_{\text{h}}^{\mathrm{2}}\dot{{\mathit{\theta }}_{\text{h}}^{\mathrm{2}}}\right)+J_{\text{ch}}\dot{{\mathit{\theta }}_{\text{h}}^{\mathrm{2}}}\right]+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[m_{\text{f}}\left(\dot{y_{\mathrm{1}}^{\mathrm{2}}}+r_{\text{h}}^{\mathrm{2}}\dot{{\mathit{\theta }}_{\text{h}}^{\mathrm{2}}}\right)\right.\\ & \left.+J_{\text{cf}}{\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)}^{\mathrm{2}}\right]+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[m_{\text{g}}\left(\dot{y_{\mathrm{1}}^{\mathrm{2}}}+r_{\text{h}}^{\mathrm{2}}\dot{{\mathit{\theta }}_{\text{h}}^{\mathrm{2}}}\right)+J_{\text{cg}}{\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)}^{\mathrm{2}}\right]\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{J}_{\text{cb}}\dot{{\mathit{\theta }}_{\text{b}}^{\mathrm{2}}}.\end{array}\end{array}$$

The potential energy of the gear reducer is given in Eq. (4):

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& E_{\text{p}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{c}_{\mathrm{1}}\left\{y_{\mathrm{1}}^{\mathrm{2}}+{\left[r_{\text{f}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}\right]}^{\mathrm{2}}\right\}-c_{\mathrm{1}}{y}_{\mathrm{1}}\left[r_{\text{f}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)\right.\\ & \left.+r_{\text{h}}{\mathit{\theta }}_{\text{h}}\right]+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{c}_{\mathrm{2}}\left\{y_{\mathrm{1}}^{\mathrm{2}}+{\left[r_{\text{g}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}-r_{\text{b}}{\mathit{\theta }}_{\text{b}}\right]}^{\mathrm{2}}\right\}\\ & -c_{\mathrm{2}}{y}_{\mathrm{1}}\left[r_{\text{g}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}-r_{\text{b}}{\mathit{\theta }}_{\text{b}}\right].\end{array}\end{array}$$

The dissipation function is given in Eq. (5):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}& \mathit{\varphi }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{k}_{\mathrm{1}}\left\{\dot{y_{\mathrm{1}}^{\mathrm{2}}}+{\left[r_{\text{f}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}\right]}^{\mathrm{2}}\right\}-k_{\mathrm{1}}\dot{y_{\mathrm{1}}}\left[r_{\text{f}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)\right.\\ & +\left.r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}\right]+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{k}_{\mathrm{2}}\left\{\dot{y_{\mathrm{1}}^{\mathrm{2}}}+{\left[r_{\text{g}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}-r_{\text{b}}\dot{{\mathit{\theta }}_{\text{b}}}\right]}^{\mathrm{2}}\right\}\\ & -k_{\mathrm{2}}\dot{y_{\mathrm{1}}}\left[r_{\text{g}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}-r_{\text{b}}\dot{{\mathit{\theta }}_{\text{b}}}\right].\end{array}\end{array}$$

Substituting the corresponding expressions, we get the motion equations of the system in Eqs. (6–9):

$$\begin{array}{}\text{(6)}& {\displaystyle }\begin{array}{rl}& \ddot{y_{\mathrm{1}}}\left(m_{\text{h}}+m_{\text{f}}+m_{\text{g}}\right)+y_{\mathrm{1}}\left(c_{\mathrm{1}}+c_{\mathrm{2}}\right)-c_{\mathrm{1}}\left[r_{\text{f}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}\right]\\ & -c_{\mathrm{2}}\left[r_{\text{g}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}-r_{\text{b}}{\mathit{\theta }}_{\text{b}}\right]+\dot{y_{\mathrm{1}}}\left(k_{\mathrm{1}}+k_{\mathrm{2}}\right)\\ & -k_{\mathrm{1}}\left[r_{\text{f}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}\right]\\ & -k_{\mathrm{2}}\left[r_{\text{g}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}-r_{\text{b}}\dot{{\mathit{\theta }}_{\text{b}}}\right]=\mathrm{0},\end{array}\text{(7)}& {\displaystyle }\begin{array}{rl}& \left(m_{\text{h}}{r}_{\text{h}}^{\mathrm{2}}+J_{\text{ch}}+m_{\text{f}}{r}_{\text{h}}^{\mathrm{2}}+J_{\text{cf}}+m_{\text{g}}{r}_{\text{h}}^{\mathrm{2}}+J_{\text{cg}}\right)\ddot{{\mathit{\theta }}_{\text{h}}}+\left(J_{\text{cf}}+J_{\text{cg}}\right)\ddot{{\mathit{\theta }}_{\text{f}}}\\ & +c_{\mathrm{1}}\left[{\mathit{\theta }}_{\text{h}}\left(r_{\text{f}}+r_{\text{h}}\right)+r_{\text{f}}{\mathit{\theta }}_{\text{f}}\right]\left(r_{\text{f}}+r_{\text{h}}\right)-c_{\mathrm{1}}{y}_{\mathrm{1}}\left(r_{\text{f}}+r_{\text{h}}\right)\\ & +c_{\mathrm{2}}\left[{\mathit{\theta }}_{\text{h}}\left(r_{\text{g}}+r_{\text{h}}\right)\right.\left.+r_{\text{g}}{\mathit{\theta }}_{\text{f}}-r_{\text{b}}{\mathit{\theta }}_{\text{b}}\right]\left(r_{\text{g}}+r_{\text{h}}\right)\\ & -c_{\mathrm{2}}{y}_{\mathrm{1}}\left(r_{\text{g}}+r_{\text{h}}\right)+k_{\mathrm{1}}\left[\dot{{\mathit{\theta }}_{\text{h}}}\left(r_{\text{f}}+r_{\text{h}}\right)+r_{\text{f}}\dot{{\mathit{\theta }}_{\text{f}}}\right]\left(r_{\text{f}}+r_{\text{h}}\right)\\ & -k_{\mathrm{1}}\dot{y_{\mathrm{1}}}\left(r_{\text{f}}+r_{\text{h}}\right)+k_{\mathrm{2}}\left[\dot{{\mathit{\theta }}_{\text{h}}}\left(r_{\text{g}}+r_{\text{h}}\right)\right.\\ & \left.+r_{\text{g}}\dot{{\mathit{\theta }}_{\text{f}}}-r_{\text{b}}\dot{{\mathit{\theta }}_{\text{b}}}\right]\left(r_{\text{g}}+r_{\text{h}}\right)-k_{\mathrm{2}}\dot{y_{\mathrm{1}}}\left(r_{\text{g}}+r_{\text{h}}\right)=M_{\text{h}},\end{array}\text{(8)}& {\displaystyle }\begin{array}{rl}& \left(J_{\text{cf}}+J_{\text{cg}}\right)\ddot{{\mathit{\theta }}_{\text{f}}}+\left(J_{\text{cf}}+J_{\text{cg}}\right)\ddot{{\mathit{\theta }}_{\text{h}}}+c_{\mathrm{1}}\left[r_{\text{f}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}\right]r_{\text{f}}\\ & -c_{\mathrm{1}}{y}_{\mathrm{1}}{r}_{\text{f}}+c_{\mathrm{2}}\left[r_{\text{g}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}-r_{\text{b}}{\mathit{\theta }}_{\text{b}}\right]r_{\text{g}}-c_{\mathrm{2}}{y}_{\mathrm{1}}{r}_{\text{g}}\\ & +r_{\text{g}}{k}_{\mathrm{1}}\left[r_{\text{f}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}\right]r_{\text{f}}-k_{\mathrm{1}}\dot{y_{\mathrm{1}}}{r}_{\text{f}}+k_{\mathrm{2}}\left[r_{\text{g}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)\right.\\ & \left.+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}-r_{\text{b}}\dot{{\mathit{\theta }}_{\text{b}}}\right]r_{\text{g}}-k_{\mathrm{2}}\dot{y_{\mathrm{1}}}{r}_{\text{g}}=\mathrm{0},\end{array}\text{(9)}& {\displaystyle }\begin{array}{rl}& J_{\text{cb}}\ddot{{\mathit{\theta }}_{\text{b}}}-c_{\mathrm{2}}{r}_{\text{b}}\left[r_{\text{g}}\left({\mathit{\theta }}_{\text{h}}+{\mathit{\theta }}_{\text{f}}\right)+r_{\text{h}}{\mathit{\theta }}_{\text{h}}-r_{\text{b}}{\mathit{\theta }}_{\text{b}}\right]+c_{\mathrm{2}}{y}_{\mathrm{1}}{r}_{\text{b}}\\ & -k_{\mathrm{2}}{r}_{\text{b}}\left[r_{\text{g}}\left(\dot{{\mathit{\theta }}_{\text{h}}}+\dot{{\mathit{\theta }}_{\text{f}}}\right)+r_{\text{h}}\dot{{\mathit{\theta }}_{\text{h}}}-r_{\text{b}}\dot{{\mathit{\theta }}_{\text{b}}}\right]+k_{\mathrm{2}}\dot{y_{\mathrm{1}}}{r}_{\text{b}}=\mathrm{0}.\end{array}\end{array}$$

Table 1 Basic parameters of the dynamical model.

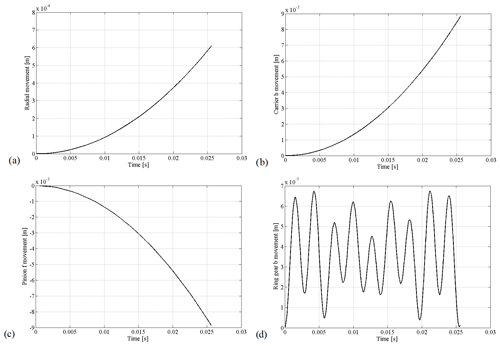
Figure 6 Displacement diagrams for $c_{\mathrm{1}}=\mathrm{1.67}\times {\mathrm{10}}^{\mathrm{10}}$ N m⁻¹, $c_{\mathrm{2}}=\mathrm{1.56}\times {\mathrm{10}}^{\mathrm{10}}$ N m⁻¹, k₁=3200 N s m⁻¹, and k₂=2400 N s m⁻¹: (a) y₁ direction, (b) θ_h direction, (c) θ_f direction, and (d) θ_b direction.

For the matrix form of the motion equations, the following equations apply (Eqs. 10–13):

$$\begin{array}{}\text{(10)}& {\displaystyle }M\left\{\ddot{q}\right\}=\left[\begin{array}{cccc}{m}_{\text{h}}+m_{\text{f}}+m_{\text{g}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& m_{\text{h}}{r}_{\text{h}}^{\mathrm{2}}+J_{\text{ch}}+m_{\text{f}}{r}_{\text{h}}^{\mathrm{2}}+J_{\text{cf}}+m_{\text{g}}{r}_{\text{h}}^{\mathrm{2}}+J_{\text{cg}}& J_{\text{cf}}+J_{\text{cg}}& \mathrm{0}\\ \mathrm{0}& J_{\text{cf}}+J_{\text{cg}}& J_{\text{cf}}+J_{\text{cg}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& J_{\text{cb}}\end{array}\right],\text{(11)}& {\displaystyle }B\left\{\dot{q}\right\}=\left[\begin{array}{cccc}{k}_{\mathrm{1}}+k_{\mathrm{2}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& k_{\mathrm{1}}{\left(r_{\text{f}}+r_{\text{h}}\right)}^{\mathrm{2}}+k_{\mathrm{2}}{\left(r_{\text{g}}+r_{\text{h}}\right)}^{\mathrm{2}}& k_{\mathrm{1}}{r}_{\text{f}}\left(r_{\text{f}}+r_{\text{h}}\right)+k_{\mathrm{2}}{r}_{\text{g}}\left(r_{\text{g}}+r_{\text{h}}\right)& -\left[k_{\mathrm{2}}{r}_{\text{b}}\left(r_{\text{g}}+r_{\text{h}}\right)\right]\\ \mathrm{0}& k_{\mathrm{1}}\left(r_{\text{f}}^{\mathrm{2}}+r_{\text{f}}{r}_{\text{h}}\right)+k_{\mathrm{2}}\left(r_{\text{g}}^{\mathrm{2}}+r_{\text{g}}{r}_{\text{h}}\right)& k_{\mathrm{1}}{r}_{\text{f}}^{\mathrm{2}}+k_{\mathrm{2}}{r}_{\text{g}}^{\mathrm{2}}& -k_{\mathrm{2}}{r}_{\text{b}}{r}_{\text{g}}\\ \mathrm{0}& -k_{\mathrm{2}}\left(r_{\text{b}}{r}_{\text{g}}+r_{\text{b}}{r}_{\text{h}}\right)& -k_{\mathrm{2}}{r}_{\text{b}}{r}_{\text{g}}& k_{\mathrm{2}}{r}_{\text{b}}^{\mathrm{2}}\end{array}\right],\text{(12)}& {\displaystyle }C\left\{q\right\}=\left[\begin{array}{cccc}{c}_{\mathrm{1}}+c_{\mathrm{2}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& c_{\mathrm{1}}{\left(r_{\text{f}}+r_{\text{h}}\right)}^{\mathrm{2}}+c_{\mathrm{2}}{\left(r_{\text{g}}+r_{\text{h}}\right)}^{\mathrm{2}}& c_{\mathrm{1}}{\left(r_{\text{f}}+r_{\text{h}}\right)}^{\mathrm{2}}+c_{\mathrm{2}}{\left(r_{\text{g}}+r_{\text{h}}\right)}^{\mathrm{2}}& -\left[c_{\mathrm{2}}{r}_{\text{b}}\left(r_{\text{g}}+r_{\text{h}}\right)\right]\\ \mathrm{0}& c_{\mathrm{1}}\left(r_{\text{f}}^{\mathrm{2}}+r_{\text{f}}{r}_{\text{h}}\right)+c_{\mathrm{2}}\left(r_{\text{g}}^{\mathrm{2}}+r_{\text{g}}{r}_{\text{h}}\right)& c_{\mathrm{1}}{r}_{\text{f}}^{\mathrm{2}}+c_{\mathrm{2}}{r}_{\text{g}}^{\mathrm{2}}& -c_{\mathrm{2}}{r}_{\text{b}}{r}_{\text{g}}\\ \mathrm{0}& -c_{\mathrm{2}}\left(r_{\text{b}}{r}_{\text{g}}+r_{\text{b}}{r}_{\text{h}}\right)& -c_{\mathrm{2}}{r}_{\text{b}}{r}_{\text{g}}& c_{\mathrm{2}}{r}_{\text{b}}^{\mathrm{2}}\end{array}\right],\text{(13)}& {\displaystyle }\left\{D\right\}=\left[\begin{array}{c}\mathrm{0}\\ M_{\text{h}}\\ \mathrm{0}\\ \mathrm{0}\end{array}\right].\end{array}$$

4 Solutions of the dynamic motion equations

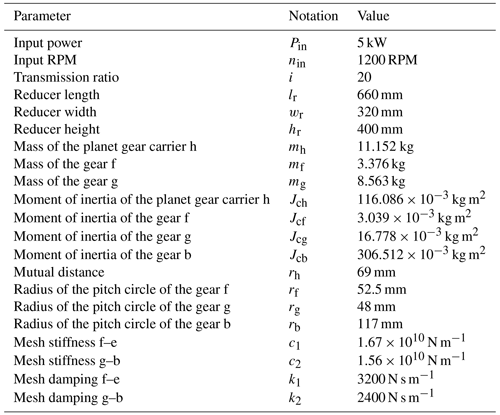
The values of the basic input parameters of the model and reducers working characteristics are given in Table 1. The geometric quantities, masses, and moments of inertia of certain planetary gear reducer elements are taken from the developed CAD model, while the stiffness and damping values are taken from the literature (Batinic, 2008, 2013).

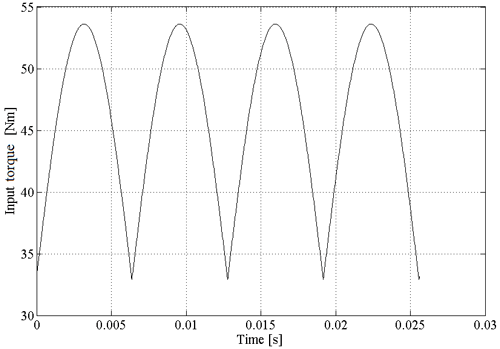
In order to get the simulation model initiated, it was necessary to define an initiation torque on the input shaft which is directly connected to the carrier h. The initiation torque function shape was obtained from literature (Batinic, 2008, 2013; Blagojević et al., 2018). The initiation torque graphic is shown in Fig. 3.

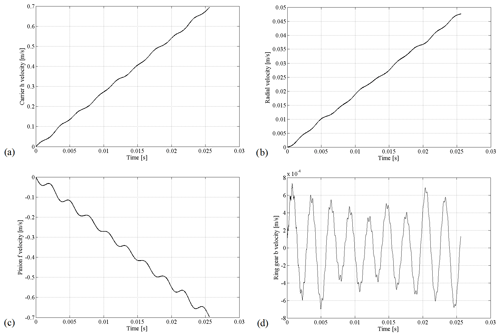
The dynamic motion equations are solved in the program MATLAB Simulink. Figure 4 shows acceleration diagrams for some directions, while Fig. 5 shows velocity diagrams.

Figure 6 shows displacement diagrams for certain directions, as the final results of this analysis.

5 Discussion

Oscillations of the analysed parameters are similar in form to the oscillation of the excitation torque, which is a periodic time function. The character of the displacement diagram is similar to the character of the velocity diagram. At first, oscillations of some parameters are very pronounced, but they calm down in time. The output degree of freedom on the gear b has the highest oscillation. The explanation for this phenomenon is that gear b is the last one in the chain, and it gets all of the vibrations from the other elements. The model is well configured. This can be noted from differences between diagrams of acceleration, velocity, and movement. The oscillations for acceleration are very pronounced, while for the velocities they are calmed. For the movement diagram, the curve is smooth.

6 Conclusions

This paper presents the dynamic behaviour of a planetary reducer with two planet gears. A complex dynamic model of the planetary reducer is made using Lagrange's equations of the second kind. The equation system is developed for all the degrees of freedom which describe the dynamical behaviour of the reducer gear in a high level of detail. The equations are solved in the math simulation software. Geometric quantities, masses, and moments of inertia for some of the elements are taken from the developed CAD model, while the stiffness and damping values are taken from the literature.

Based on the performed simulations, it can be concluded that the size of oscillations primarily depends on the way the dynamic model is set and on the values of the stiffness and the damping coefficients. The form of oscillations mostly depends on the excitation torque. Oscillations of velocities generally have a similar form as oscillations of displacements.

Further studies may include theoretical, analytical, and experimental investigations. However, the dynamic model needs to be further developed, and the stiffness and damping should be more precisely determined. The best way forward for further research is to manufacture the reducer with the same characteristics and to perform experimental measurements for the described phenomena.