Kinematics analysis of a four-legged heavy-duty robot with a force–position hybrid control servo actuator in a parallel-executed cylinder system

In this research, an electrohydraulic servo four-legged heavy-duty (FLHD) robot has been designed and developed. The study proposes an integration layout cylinder design scheme for a non-lightweight hydraulic servo four-legged robot with high loads and torques of hip joint and derives the mathematical element analysis model for a parallel-executed cylinder (PEC) system. The multiple inherent characteristics of the PEC integration system model are explored further. Based on the controllable functional requirements of interconnected joints, and to weaken the influence of internal force coupling, a force–position hybrid control scheme for the PEC is designed, and the force–position signal module design unit is used to solve the force–position hybrid control in reverse. Considering the inherent requirements of the servo-executed cylinder (SEC) force control unit module (CUM), the implementation process of magnetic flux compensation and speed compensation is discussed in detail. The minimum amplitude controller is applied to the SEC force CUM, and the proportional integrated controller has been determined in the SEC position CUM. A compound control strategy proposed in this paper is verified on a parallel hydraulic servo platform. The experimental verification results reveal that the values of position/force attenuation amplitude and lag phase are not greater than 9 % and 18^∘, respectively. The feasibility of the interconnected implementation of the hybrid control scheme proposed in this paper is further increased. The conclusions of this research will be useful for application in fields of four-legged heavy-load (FLHL) robot control systems.

1 Introduction

In recent years, many scholars have attached great importance to the research of heavy-load robots. The concept of a four-legged robot that could simulate ordinary animals has recently become a hot topic in bionics. Compared with unipedals and bipeds, hydraulic four-legged robots have a better ability and stability to carry heavy objects. And compared with hexapods and robots with more legs, redundancy in structural design is reduced. Therefore, extensive research and development have been conducted on hydraulic quadruped robots. A hydraulic four-legged robot is evolved and developed from multi-legged robots in many aspects (such as structure and motion form).

Many scholars have made achievements in the research of hydraulic four-legged robots. Their drive unit has the characteristics of a larger initial starting force, a precise position, a higher power density, a compact high-strength structure and so on. So far, many electrohydraulic servo actuators have been adopted in specialist engineering industries. The outstanding dynamic response characteristics of hydraulic four-legged robots have immediately attracted widespread attention in the field of electromechanical engineering applications. Boston Power Corporation (BPC) recently declared that it has begun researching and pre-developing lightweight hydraulic four-legged robots, such as Wildcat, Big Dog, Spot and LS3 (Elasswad et al., 2017).

So far, based on the background impact of this research topic, scientific research studies in the field of hydraulic servo four-legged heavy-load (FLHL) robots have been launched in many countries. Several brands of hydraulic four-legged robots have designed and developed the Advanced Robotics Division of Italian Industrial Robotics (IIT) (Barasuol et al., 2018), and a multifunctional robot system with hydraulic drive has been developed successively, such as HyQ, MiniHyQ and HyQ2Max, as shown in Fig. 1. A four-legged robot named Jinpoong has also successfully been developed and grandly launched by the Korea Institute of Science and Technology (Guo et al., 2021).

Figure 1 Physical images of a hydraulic four-legged robot. (a) In 2012, robot images with stereo cameras were not installed. (b) In 2012, robot images with stereo cameras were installed.

Many domestic universities and research institutions, such as Harbin Institute of Technology, Northeast Forestry University and Shandong University, have carried out research on topics related to hydraulic four-legged robots (Sarkar et al., 2016; Li et al., 2017; Bazeille et al., 2014; Khan et al., 2015).

To the author's knowledge, with the exception of the robot called LS3, the connection positions of the hip joints of the four-legged robot are controlled and driven by a single hydraulic actuator. Also HyQ uses a single electric motor, but the difference is that a single electrohydraulic servo actuator has been widely adopted by other robots. For the current research topic, a two-cylinder electrohydraulic actuator cylindrical transmission technology solution is proposed. The payload of the LS3 robot reaches 181 kg. Taking into account the special project background of Boston's dynamic characteristics, the report on the LS3 robot does not have much technical reference data (Shi et al., 2019). So far, hydraulic four-legged motion has always been a critical focus of discussion in current heavy-load robot research. A four-legged platform parallel servo cylinder transmission system with force–position control hydraulic integrated technology has rarely been studied in the current research field (Zhang et al., 2020).

Walking (or legged) robots have been an exciting area of research for the past few decades (Semini et al., 2015; Tian et al., 2016; Sharifi et al., 2016). A study of electrohydraulic servo-type four-legged robots found that the real-time control of the hip motion process is extremely complex; it is associated with elements from four rotating joints as well as hydraulic actuators for four symmetrical legs and a single leg to a hinged trunk with controllers and sensors (Iqbal et al., 2020). Next, many tasks in kinematics and dynamics simulation need to be studied, as well as the optimal design of the mechanical structure of the hydraulic actuated four-legged robot. A four-legged robot with 4 DOFs per supporting leg has motion redundancy to better adapt to rugged terrain (Andersen et al., 2017).

Similar to research on related topics, scholars mostly assume that the distance between the foot and the rolling axis of the hydraulic actuated four-legged robot studied in these subjects is larger, and the driving torque required by the design is larger under the same foot end force (Xu et al., 2019). Gor et al. (2018) analysed in detail the impact of supporting leg impedance on leg gait stability and efficiency. In this way, from the author's review of the literature, it is known that few researchers have actively contributed to the dynamic motion posture of four-legged robots. However, it is well known that tetrapods in nature usually twist, dive or bend their trunks to walk, run or crawl (Gonzalez-Luchena et al., 2016; Li et al., 2014; Gallant and Gosselin, 2018). The turning strategy of a four-legged robot based on leg gait was mentioned by Zhang and Dai (2018). The transition between a single supporting leg of the four-legged robot and a walking posture was studied by Pouya et al. (2016). In practical applications, these research results on leg gaits of twisted torso have been widely popularised. Undoubtedly, this will bring endless advantages to the movement of the inherent tripod structure, especially during fast and heavy-load hydraulic robot movements. Similarly, a twisted torso will also contribute to the leg gaits of a hydraulic four-legged robot. Huang et al. (2021) developed a sensory–motor fusion-based manipulation and grasping control strategy for a robotic hand–eye system, and an online neural dynamics optimisation solution was proposed and implemented. Therefore, the study of the torsional trunk gait of FLHL robots has high significance in practical applications.

Based on increasing the output pressure and effective equivalent area of an electrohydraulic servo execution cylinder, the required driving torque is achieved and obtained by means of adopting methods such as parallel multi-cylinders. The fuel supply pressure of a hydraulic system is restricted by the amplitude of the hydraulic components, which makes it difficult to increase further and indefinitely. The increase of the equivalent area of the electrohydraulic servo execution cylinder will inevitably add additional torque, but it is difficult to increase the design size due to structural limitations (the green parallel hydraulic larger cylinder has a small running space margin; green and red circles are shown in Fig. 4), which in turn limits the interchange cycle of the actuators and increases the electrohydraulic servo control function; the manufacturing cost will also be raised.

In view of the above factors, the design technology of the multi-cylinder electrohydraulic parallel structure shall be an ideal choice for achieving the torque output of heavy-load four-legged motors. Compared with wheeled robots in rough terrain, it has irreplaceable advantages. Therefore, FLHL robots have always been one of the most attractive research directions of focus in the field of multi-legged robots.

Considering the larger bearing loads and torque characteristics of the hip joints for a heavy-load hydraulic four-legged robot, a parallel servo cylinder driving element model is proposed in this study.

In view of the hybrid control performance of roller joint position and the output force used for driving, the numerical analysis model of a parallel servo-executed hydraulic cylinder system is proposed, the solution of mathematical theory model is explored and the decoupling algorithm of the parallel electrohydraulic SEC force–position hybrid control is constructed. Taking into account the force control model characteristics of an electrohydraulic parallel actuator, a minimal integrated controller is developed to optimise the design of driving force control. The semi-physical system with parallel cylinders is used to verify the hybrid force–position control strategy, and the feasibility of the proposed control scheme is checked by actual operating experiments.

2 Kinesiology modelling and parameter adjustable analysis of the robot mechanical system

2.1 Analysis of the transmission form of a double electrohydraulic cylinder

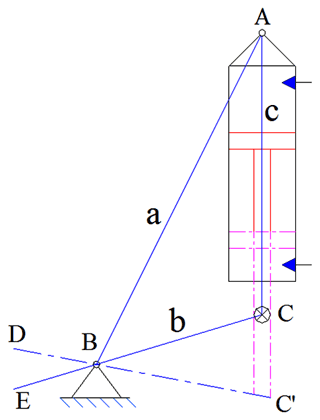
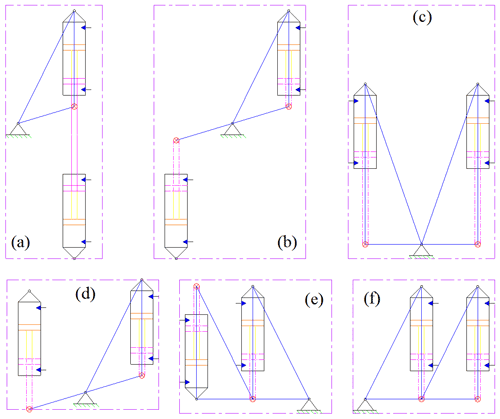
Most researchers only focus on the periodic and time-varying amplitude characteristics of joint angles but often ignore the force–position stability of continuous motion trajectories. The stable force–position hybrid control of a FLHL robot plays a vital role in the motion of a parallel servo execution cylinder transmission system, which is affected by the constraints of the electrohydraulic servo actuator. It is worth mentioning that the motion form of the four-legged robot is derived from the imitation of the animal's walking posture in nature. The motion forms of an electrohydraulic servo cylinder (ESC) are the representation of the gait of the FLHL robot. A joint illustration of a heavy-load four-legged robot driven by an electrohydraulic fuel pressure is shown in Fig. 2. In Fig. 2, the movement trajectory of the parallel actuator of the electrohydraulic servo cylinder is numerically simulated. The three connection points of the bottom of the electrohydraulic servo actuator cylinder, its associated axis and the end of the piston rod are expressed as A, B and C, respectively. For this point C^′, the position is described when the hydraulic cylinder is fully extended to ensure that the FLHL robot always moves in a preset direction. It can be seen from the above-mentioned figures that the torsional trajectory of the hydraulic cylinder of the four-legged robot is a prerequisite for the normal operation of the parallel actuator. As the driving mode is switched to a dual electric-hydraulic servo cylinder, the bottom active range of the other electrohydraulic servo cylinders must be located outside the sector area composed of DBE and CBC^′. At this time, a fixed centre exists in the transmission joint of the electric hydraulic cylinder, which makes it difficult to achieve its expected form of motion. As can be easily seen in the forms shown in Fig. 3a and b, the form of motion of the electrohydraulic cylinder has nothing to do with the twist of a FLHL manipulator body. It is known that the body translation of the FLHL robot has no effect on its horizontal coordinates. It can also be seen from the above analysis that another electrohydraulic servo actuating cylinder and its bottom end movement range should not exceed the sector area enclosed by C^′BE and CBD. Once the point A^′ is precisely controlled in the area C^′BE, the structural layout of a FLHL robot is described as in Fig. 3.

Figure 2 Structure diagram of an electrohydraulic servo actuator in parallel form.

Figure 3 Layout diagrams of a parallel electrohydraulic cylinder.

These methods can easily cause motion disturbance of the leg support structure of the FLHL robot in the internal and external pendulums. In Fig. 3a and b, the physical model has broken through the overall width limit of the FLHL robot, and it is concluded that the torso torsion behaviour is independent of the body motion of the robot in the horizontal coordinates. If using the design form of Fig. 3d, the two electrohydraulic cylinders are located on both sides of the joint axis. Assuming that this study adopts the layout design form shown in Fig. 3d, two electrohydraulic servo actuator cylinders are mounted on both sides of the joint axis. Herein, as can be seen from Fig. 3c, the two electrohydraulic actuators are set in the arrangement form of the same orientation of the articulated joint, thereby eliminating the existence of similar factors in Fig. 3d. In view of these issues, the structure form shown in Fig. 3c is selected and used for the current study. In Fig. 3d, the parallel arrangement form of a double electrohydraulic cylinder is pre-developed. Based on the above analysis, it can be seen that the force vector of the electrohydraulic actuator at the hinge joint is different in the positive and negative directions, as shown in Fig. 3e. The connection form in Fig. 3e is the best choice for this study. In view of the fact that the rotation angle of the rotary joint is set to exceed 45^∘, the electrohydraulic actuating cylinder must be connected to a fixed position at the hinge joint. If only the length of the supporting leg is increased, the effect of the angle-constraining effect of the articulated joint will promote the joint rotation angle, which is contrary to the original design requirements of the FLHL robot compact structure. For Fig. 3f, the positive and negative directions can ensure that the electrohydraulic cylinder at the hinge joint has an equivalent applied force, which is an ideal layout design form. The comprehensive influencing factors take into account the dynamic changes in the form of the link mechanism, which makes it difficult to perform the real-time replacement of electrohydraulic servo actuators.

2.2 Modelling of a servo actuator with an electrohydraulic function

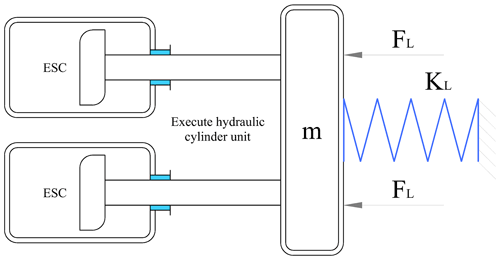
The posture stability of the force–position of the heavy-load hydraulic four-legged robot during the motion is further revealed and ensured. The strategy of electrohydraulic servo actuator control (ESAC) is launched, and the PD (deviation, P, and derivative, D) control method is selected to track the joint angles in real-time operating conditions. The feasibility of the technical solution of the current topic is analysed in detail, and the results have finally been verified by kinetic analysis simulations. In the movement of a heavy-load four-legged hydraulic robot, various forms of motion posture trajectories are planned by tracking the real-time changes of the joint angles to ensure smoothness, and in turn, the trajectory deviation of the torsional driving torque and the robot's movement posture is reduced. A 3D model of a quadruped robot driven by a parallel execution cylinder with a servo system is shown in Fig. 4. The four-legged robot with an electrohydraulic servo cylinder has active and passive degrees of freedoms, of which the active degrees of freedom are 12, and the passive degrees of freedom are 4. The robot system studied consists of 16 actuators of the same model with an electrohydraulic servo function. It is worth emphasising that the four-bar hinged connection rolling joint is driven by two actuators with an electrohydraulic servo system to increase the torsional driving torque of the connection position of its hinge joint. In further research, an equivalent analysis model of the required electrohydraulic servo actuator is proposed and captured. The authors propose the following assumptions: (1) the moment of inertia of a four-legged robot single-leg mechanism with an ESAC around its rolling axis is identified as J_L. (2) The torsional moment of the rolling axis is represented as T_L. (3) For the damping spring and joint axis, the equivalent characterisation of its stiffness is denoted as $K_{L_{\mathrm{1}}}$.

As shown in Fig. 5, an equivalent model of the actuator with an electrohydraulic servo function is established in view of the modular planning method and the controllable framework, which complies with the equivalent principle of load balancing of a parallel servo cylinder with an electrohydraulic system.

Figure 5 reveals a parallel electrohydraulic servo actuator for the scroll axis, which is a representative redundant driving system. It should be considered that the asynchronous operation of the two actuators will generate a greater internal force, which may also greatly weaken the necessary driving torque of the actuators.

Figure 4 An electrohydraulic servo four-legged robot model. (a) 3D configuration of a four-legged robot with an electrohydraulic system. (b) Single-leg 3D configuration of a four-legged robot.

Figure 5 System diagram of parallel form of electrohydraulic servo cylinders.

Herein, $m=J_{L_{\mathrm{0}}}/L_{\mathrm{0}}^{\mathrm{2}}$, $K_{L_{\mathrm{0}}}=K_{L_{\mathrm{1}}}/L_{\mathrm{0}}^{\mathrm{2}}$ and $F_{L_{\mathrm{0}}}=T_{L_{\mathrm{0}}}/L_{\mathrm{0}}$, where L₀ is defined as a distance parameter between the scroll axis and the joint loading of the parallel servo actuator with an electrohydraulic piston rod.

To avoid the interference of asynchronous motion, attention will be paid to the position of a servo actuator with an electrohydraulic function in its control mode. According to related research (Matta-Gómez et al., 2014; Wang et al., 2016; Gong et al., 2018; Wu and Bai, 2019), as shown in Eq. (1), the transfer function expression of the single-cylinder servo system with an electrohydraulic position can be derived.

$$\begin{array}{}\text{(1)}& y={\displaystyle \frac{\frac{K_{\mathrm{a}}{K}_{\mathrm{sv}}}{A_{\mathrm{p}}}u-\frac{K_{\mathrm{ce}}}{A_{\mathrm{p}}^{\mathrm{2}}}\left(\mathrm{1}+\frac{V_t}{\mathrm{4}{\mathit{\beta }}_{\mathrm{e}}{K}_{\mathrm{ce}}}s\right)f}{\left(\frac{s^{\mathrm{2}}}{{\mathit{\omega }}_{\mathrm{0}}^{\mathrm{2}}}+\frac{\mathrm{2}{\mathit{\zeta }}_{\mathrm{0}}}{{\mathit{\omega }}_{\mathrm{0}}}s+\mathrm{1}\right)\left(\frac{K_{\mathrm{ce}}K}{A_{\mathrm{p}}^{\mathrm{2}}}+\left(\mathrm{1}+\frac{K}{K_{\mathrm{h}}}\right)s\right)}}{\mathit{\omega }}_{\mathrm{0}}\end{array}$$

Among them, A_p represents the effective regions of the servo cylinder piston, K_a indicates the gain features for an amplifier with a servo function, K_sv indicates the parameter of flow gain, for a servo controllable regulating valve, ω₀ represents the integrated natural frequency of the system, ζ₀ indicates the comprehensive damping ratio of the system, K_h represents the stiffness parameter of the hydraulic equivalent spring, K represents the load equivalent spring stiffness variable of the aforementioned spring, K_ce expresses the total flux pressure coefficient of the cylinder, f represents an external comprehensive interference force of the system, which indicates both the externally applied loading force $F_{L_{\mathrm{0}}}$ and the internal inherent force based on the asynchronous movement of the hydraulic servo cylinder, β_e represents the volume parameter (elastic modulus) of a particular hydraulic oil and y indicates the displacement parameter output by the hydraulic servo cylinder.

2.3 Motion analysis of the double linear electrohydraulic servo cylinder

In view of the installation error of the linear servo actuator with an electrohydraulic function, the manufacturing of the displacement sensor and the measurement error and the dynamic performance difference make it difficult to ensure the synchronisation of servo actuators and electrohydraulic movements. Since the servo actuators and the joints are rigidly contacted, as the displacement amplitude deviation value of the servo actuator is smaller, the internal force generated by the servo actuator bearing load is larger, thereby resisting the actual output force of the electrohydraulic actuator with servo characteristics. Real-time controllable position and instantaneous drive force control are performed on two actuators; to put it simply, the hybrid form of the force–position control mode of the roll joint is directly completed. Herein, the preset torque index required in the design of the driving link of this subject has been checked, and the posture and position of the articulated joint space movement of the four-legged robot are also ensured. The motion strategy of a bilinear electrohydraulic servo cylinder should be traversed along a specific gait trajectory to accommodate the dynamic requirements of the FLHL robot. The linear electrohydraulic servo cylinder must alternately follow the specific rule during a position posture cycle. It can be seen from expression (1) that, focusing on models with motion posture/position control, for the electrohydraulic servo cylinder, the external excitation factor interference force is used as the output parameter of the electrohydraulic servo force control mode. Herein, it can be explained that there is an interconnection coupling relationship between the force–position control motion posture outputs of the electrohydraulic servo cylinder. Considering the mutual influence of the output of the FLHL robot system, the accuracy of the position/driving force servo will be reduced. Once the decoupling requirements are achieved, the force–position control accuracy required by the FLHL robot system can be obtained.

3 Decoupling analysis on hybrid mode of force–position control

The coupling interconnection relationship of the servo cylinder with force–position control hybrid mode is considered. The servo precision of the hydraulic cylinder is restricted by each direct input signal command, and each direct input signal should be accurately selected to achieve the decoupling analysis of the two hydraulic cylinders. Therefore, the coupling interconnection effects of the alternating movement of the two hydraulic cylinders are significantly eliminated, with a view to improving the control accuracy and quality of the FLHL robot system.

If

$$\begin{array}{rl}& V\left(s\right)={\displaystyle \frac{K_{\mathrm{a}}{K}_{\mathrm{sv}}}{A_{\mathrm{p}}\left(\frac{s^{\mathrm{2}}}{{\mathit{\omega }}_{\mathrm{0}}^{\mathrm{2}}}+\frac{\mathrm{2}{\mathit{\zeta }}_{\mathrm{0}}}{{\mathit{\omega }}_{\mathrm{0}}}s+\mathrm{1}\right)\left(\left(\mathrm{1}+\frac{K}{K_{\mathrm{h}}}\right)s+\frac{K_{\mathrm{ce}}K}{A_{\mathrm{p}}^{\mathrm{2}}}\right)}},\\ & {\displaystyle \frac{\mathrm{1}}{C_{\mathrm{a}}}}={\displaystyle \frac{K_{\mathrm{ce}}+\frac{V_t}{\mathrm{4}\mathit{\beta }e}s}{A_{\mathrm{p}}^{\mathrm{2}}\left(\frac{s^{\mathrm{2}}}{{\mathit{\omega }}_{\mathrm{0}}^{\mathrm{2}}}+\frac{\mathrm{2}{\mathit{\zeta }}_{\mathrm{0}}}{{\mathit{\omega }}_{\mathrm{0}}}s+\mathrm{1}\right)\left(\left(\mathrm{1}+\frac{K}{K_{\mathrm{h}}}\right)s+\frac{K_{\mathrm{ce}}K}{A_{\mathrm{p}}^{\mathrm{2}}}\right)}}.\end{array}$$

Hence Eq. (1) is expressed as

$$\begin{array}{}\text{(2)}& y={\displaystyle \frac{u}{s}}V\left(s\right)-{\displaystyle \frac{f_{\mathrm{0}}}{s{C}_{\mathrm{a}}}}.\end{array}$$

For servo cylinders 1 and 2, Eq. (2) is expressed by Eq. (3)

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& f_{\mathrm{1}}=C_{a\mathrm{1}}\left(V\right(s)u_{\mathrm{1}}-y_{\mathrm{1}})\\ & y_{\mathrm{2}}=-{\displaystyle \frac{\mathrm{1}}{C_{\mathrm{a}\mathrm{2}}}}{f}_{\mathrm{2}}+V\left(s\right)u_{\mathrm{2}}.\end{array}\end{array}$$

Obviously, for a four-legged robot with large self-weight loads, the correlation between the vectors of the displacement/force of the parallel execution cylinder electrohydraulic servo system can be expressed as

$$\begin{array}{}\text{(4)}& {\displaystyle }{y}_{\mathrm{2}}=y_{\mathrm{1}}\text{(5)}& {\displaystyle }{f}_{\mathrm{2}}=-f_{\mathrm{1}}.\end{array}$$

The matrix expression of Eq. (3) is derived as

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\left[\begin{array}{l}{f}_{\mathrm{1}}\\ y_{\mathrm{2}}\end{array}\right]& =V\left(s\right)\left[\begin{array}{ll}{C}_{a\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}\end{array}\right]\left[\begin{array}{l}{u}_{\mathrm{1}}\\ u_{\mathrm{2}}\end{array}\right]\\ & -\left[\begin{array}{ll}{C}_{\mathrm{a}\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& -\mathrm{1}/C_{\mathrm{a}\mathrm{2}}\end{array}\right]\left[\begin{array}{l}{f}_{\mathrm{1}}\\ y_{\mathrm{2}}\end{array}\right].\end{array}\end{array}$$

Equation (6) can be expressed as follows:

$$\begin{array}{}\text{(7)}& \left[\begin{array}{ll}\mathrm{1}& C_{\mathrm{a}\mathrm{1}}\\ -\mathrm{1}/C_{\mathrm{a}\mathrm{2}}& \mathrm{1}\end{array}\right]\left[\begin{array}{l}{f}_{\mathrm{1}}\\ y_{\mathrm{2}}\end{array}\right]=V\left(s\right)\left[\begin{array}{ll}{C}_{\mathrm{a}\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}\end{array}\right]\left[\begin{array}{l}{\mathit{\mu }}_{\mathrm{1}}\\ {\mathit{\mu }}_{\mathrm{2}}\end{array}\right],\end{array}$$

where Eq. (7) is rephrased as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\left[\begin{array}{l}{f}_{\mathrm{1}}\\ f_{\mathrm{2}}\end{array}\right]& =\left[\begin{array}{ll}{C}_{\mathrm{a}\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}\end{array}\right]\left[\begin{array}{l}{\mathit{\mu }}_{\mathrm{1}}\\ {\mathit{\mu }}_{\mathrm{2}}\end{array}\right]\\ & \times \left[\begin{array}{ll}\mathrm{1}& -\mathrm{1}/C_{\mathrm{a}\mathrm{1}}\\ \left(\mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}\right)/C_{\mathrm{a}\mathrm{2}}& \mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}\end{array}\right]\\ & \times {\displaystyle \frac{V\left(s\right)}{\mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}}}.\end{array}\end{array}$$

Equation (8) is written as

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\left[\begin{array}{l}{f}_{\mathrm{1}}\\ y_{\mathrm{2}}\end{array}\right]& ={\displaystyle \frac{V\left(s\right)}{\mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}}}\times \left[\begin{array}{l}{u}_{\mathrm{1}}\\ u_{\mathrm{2}}\end{array}\right]\\ & \times \left[\begin{array}{ll}{C}_{\mathrm{a}\mathrm{1}}& -\mathrm{1}/C_{\mathrm{a}\mathrm{1}}\\ C_{\mathrm{a}\mathrm{1}}\left(\mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}\right)/C_{\mathrm{a}\mathrm{2}}& \mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}\end{array}\right].\end{array}\end{array}$$

If

$$\begin{array}{}\text{(10)}& \left[\begin{array}{l}{u}_{\mathrm{1}}\\ u_{\mathrm{2}}\end{array}\right]=\left[\begin{array}{ll}\mathrm{1}& \mathrm{1}\\ -C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}& \mathrm{1}\end{array}\right]\left[\begin{array}{l}{u}_{\mathrm{1}}^{\prime }\\ u_{\mathrm{2}}^{\prime }\end{array}\right],\end{array}$$

then

$$\begin{array}{}\text{(11)}& \left[\begin{array}{l}{f}_{\mathrm{1}}\\ y_{\mathrm{2}}\end{array}\right]=V\left(s\right)\left[\begin{array}{ll}{C}_{\mathrm{a}\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}\end{array}\right]\left[\begin{array}{l}{u}_{\mathrm{1}}\\ u_{\mathrm{2}}\end{array}\right].\end{array}$$

The input signal decoupling process is achieved by Eq. (11), and the input signal is described as

$$\begin{array}{}\text{(12)}& \left[\begin{array}{l}{u}_{\mathrm{1}}\\ u_{\mathrm{2}}\end{array}\right]=\left[\begin{array}{ll}\mathrm{1}& \mathrm{1}\\ \mathrm{0}& \mathrm{1}\end{array}\right]\left[\begin{array}{l}{u}_{\mathrm{1}}^{\prime }\\ u_{\mathrm{2}}^{\prime }\end{array}\right].\end{array}$$

Then, Eq. (12) is characterised as

$$\begin{array}{}\text{(13)}& \begin{array}{rl}\left[\begin{array}{l}{f}_{\mathrm{1}}\\ y_{\mathrm{2}}\end{array}\right]& =V\left(s\right)\times \left[\begin{array}{l}{u}_{\mathrm{1}}^{\prime }\\ u_{\mathrm{2}}^{\prime }\end{array}\right]\\ & \times \left[\begin{array}{ll}{C}_{\mathrm{a}\mathrm{1}}/\left(\mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}\right)& \mathrm{0}\\ C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}& \mathrm{1}+C_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}}\end{array}\right].\end{array}\end{array}$$

Usually, the required driving force can be obtained with a smaller control signal. Herein, the parameter $u_{\mathrm{2}}^{\prime }$ is much larger than the parameter $u_{\mathrm{1}}^{\prime }$, and Eq. (13) is approximately described as

$$\begin{array}{}\text{(14)}& \left[\begin{array}{l}{f}_{\mathrm{1}}\\ y_{\mathrm{2}}\end{array}\right]\approx V\left(s\right)\times \left[\begin{array}{l}{u}_{\mathrm{1}}^{\prime }\\ u_{\mathrm{2}}^{\prime }\end{array}\right]\left[\begin{array}{ll}\frac{C_{\mathrm{a}\mathrm{1}}}{(\mathrm{1}+r^{\mathrm{2}}{C}_{\mathrm{a}\mathrm{1}}/C_{\mathrm{a}\mathrm{2}})}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}+\frac{r^{\mathrm{2}}{C}_{\mathrm{a}\mathrm{1}}}{C_{\mathrm{a}\mathrm{2}}}.\end{array}\right].\end{array}$$

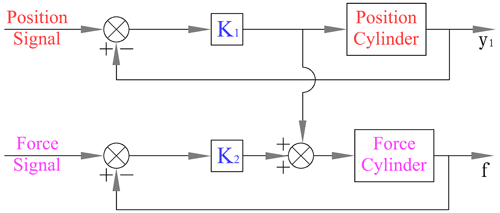
According to Eq. (14), the decoupling process analysis of the input signal is confirmed and completed by the parallel servo system with a dual electrohydraulic execution cylinder, so the force–position control mode of the servo cylinders will not affect each other. The principle diagram of the position/force control mode of a parallel system of with double electrohydraulic cylinders is proposed, as shown in Fig. 6.

Figure 6 Schematic diagram of force–position control parallel cylinders.

4 A comprehensive analysis of kinematics and dynamics of the FLHL robot designed in this study

In this study, the FLHL robot is mainly composed of three mechanical body structures and a joint structure with 12 DOFs; it is emphasised here that the abduction and hip joints intersect at a certain point on each supporting leg, and each liner hydraulic cylinder contains a single rod cylinder block, a servo control valve, a linear displacement sensor, two pressure sensors and other components.

Table 1 Main parameter symbols and specification values of the four-legged robot.

The robot support leg uses a spring to absorb the energy of the ground and to release energy during the lifting cycle. The main parameter symbols and specification values of the four-legged robot are presented in Table 1. Figure 7 reveals the geometric dimensions of a heavy-load hydraulic four-legged robot. Herein, l₀, l₁, l₂ and l₃ are expressed as length variables related to the hinge joint coupling links; q₀, q₁ and q₂ describe the related hinge joint angles; l_m0, l_m1 and l_m2 represent the centroid displacement variables of interconnected links; m₀, m₁ and m₂ represent the quality variables of correlation links; ε₀, ε₁ and ε₂ are the connection angles between quality centre and related links; and τ₀, τ₁ and τ₂ are the torque of corresponding joints.

As far as the authors know, the walking frequency of a four-legged robot decreases with an increase of body length and accelerates with a rapid walking speed. If the gait dynamic frequency is higher, then the walking response efficiency is lower. The target mass of the four-legged robot developed in this paper is no more than 125 kg (total weight), and the target speed is not less than 1.8 m/s. The optimal gait frequency of the four-legged robot is 1.0 to 2.0 Hz. The response frequency of the hydraulic servo cylinder must meet the gait dynamic frequency requirements.

4.1 Solving kinematics equations of a FLHL robot

The dynamic stability of a FLHL robot is characterised by its kinematics. Figure 7 defines the coordinate systems and kinematic vectors. With the view that the mechanical structure design forms of the spring–support legs are extremely similar, the four legs coordinate system and the transformation matrix are also similar. The posture of the rear legs and forelegs is the only difference. Referring to a four-legged animal walking posture, the displacement of the four-legged robot is achieved by the force control unit of the support legs. The expression equation at the end of the support leg is revealed as shown in Fig. 7.

$$\begin{array}{}\text{(15)}& \left\{\begin{array}{l}{x}_{\mathrm{f}}=-(l_{\mathrm{1}}\sin q_{\mathrm{1}}+l_{\mathrm{2}}\sin (q_{\mathrm{1}}+q_{\mathrm{2}}\left)\right)\\ y_{\mathrm{f}}=-(l_{\mathrm{0}}+l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{\mathrm{2}}\cos (q_{\mathrm{1}}+q_{\mathrm{2}}\left)\right)+l_{\mathrm{3}}\cos q_{\mathrm{0}}\\ z_{\mathrm{f}}=-(l_{\mathrm{0}}+l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{\mathrm{2}}\cos (q_{\mathrm{1}}+q_{\mathrm{2}})+l_{\mathrm{3}})\sin q_{\mathrm{0}}\end{array}\right.\end{array}$$

According to Eq. (16), the correlation between the displacement of the roller hinge joint actuator and the full-space rotation angle of the hip joints can be expressed as

$$\begin{array}{}\text{(16)}& \tan q_{\mathrm{0}}={\displaystyle \frac{z_{\mathrm{f}}}{y_{\mathrm{f}}}}\iff q_{\mathrm{0}}=\mathrm{arc}\tan {\displaystyle \frac{z_{\mathrm{f}}}{y_{\mathrm{f}}}}.\end{array}$$

Due to structural limitations, the coordinate value of the end of the support leg is y_f≠0; it can also be called and reflected in the expression in Eq. (16) as

Equation (16) coordinate values x_f and y_f are identified as

$$\begin{array}{}\text{(17)}& \left\{\begin{array}{l}{l}_{\mathrm{1}}\sin q_{\mathrm{1}}+l_{\mathrm{2}}\sin \left(q_{\mathrm{1}}+q_{\mathrm{2}}\right)-x_{\mathrm{f}}=\mathrm{1}\\ l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{\mathrm{2}}\cos \left(q_{\mathrm{1}}+q_{\mathrm{2}}\right)-\frac{y_{\mathrm{f}}}{\cos q_{\mathrm{0}}}=-(l_{\mathrm{0}}+l_{\mathrm{3}})\end{array}\right.,\end{array}$$

where the calculation values of cos q₂ and q₂ are defined as

$$\begin{array}{}\text{(18)}& {\displaystyle }\cos q_{\mathrm{2}}={\displaystyle \frac{x_{\mathrm{f}}^{\mathrm{2}}-l_{\mathrm{1}}^{\mathrm{2}}-l_{\mathrm{2}}^{\mathrm{2}}+{\left(\frac{y_{\mathrm{f}}}{\cos q_{\mathrm{0}}}+l_{\mathrm{0}}+l_{\mathrm{3}}\right)}^{\mathrm{2}}}{\mathrm{2}{l}_{\mathrm{1}}{l}_{\mathrm{2}}}}\text{(19)}& {\displaystyle }{q}_{\mathrm{2}}=\arccos {\displaystyle \frac{x_{\mathrm{f}}^{\mathrm{2}}-l_{\mathrm{1}}^{\mathrm{2}}-l_{\mathrm{2}}^{\mathrm{2}}+{\left(\frac{y_{\mathrm{f}}}{\cos q_{\mathrm{0}}}+l_{\mathrm{0}}+l_{\mathrm{3}}\right)}^{\mathrm{2}}}{\mathrm{2}{l}_{\mathrm{1}}{l}_{\mathrm{2}}}}.\end{array}$$

Then Eq. (17) is rewritten as

$$\begin{array}{}\text{(20)}& \left\{\begin{array}{l}\left(l_{\mathrm{1}}+l_{\mathrm{2}}\cos q_{\mathrm{2}}\right)\cos q_{\mathrm{1}}-l_{\mathrm{2}}\sin q_{\mathrm{2}}\sin q_{\mathrm{1}}\\ -\left(\frac{y_{\mathrm{f}}}{\cos q_{\mathrm{0}}}+l_{\mathrm{0}}+l_{\mathrm{3}}\right)=\mathrm{0}\\ \left(l_{\mathrm{1}}+l_{\mathrm{2}}\cos q_{\mathrm{2}}\right)\sin q_{\mathrm{1}}+l_{\mathrm{2}}\sin q_{\mathrm{2}}\cos q_{\mathrm{1}}-x_{\mathrm{f}}=\mathrm{0}.\end{array}\right.\end{array}$$

Herein, the calculation values of sin q₁ and q₁ are expressed as

$$\begin{array}{}\text{(21)}& {\displaystyle }\sin q_{\mathrm{1}}={\displaystyle \frac{\left(\frac{y_{\mathrm{f}}}{\cos q_{\mathrm{0}}}+l_{\mathrm{0}}+l_{\mathrm{3}}\right)l_{\mathrm{2}}\sin q_{\mathrm{2}}-x_{\mathrm{f}}\left(l_{\mathrm{1}}+l_{\mathrm{2}}\cos q_{\mathrm{2}}\right)}{l_{\mathrm{1}}^{\mathrm{2}}+\mathrm{2}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\cos q_{\mathrm{2}}+l_{\mathrm{2}}^{\mathrm{2}}}}\text{(22)}& {\displaystyle }{q}_{\mathrm{1}}=\arcsin {\displaystyle \frac{\left(\frac{y_{\mathrm{f}}}{\cos q_{\mathrm{0}}}+l_{\mathrm{0}}+l_{\mathrm{3}}\right)l_{\mathrm{2}}\sin q_{\mathrm{2}}-x_{\mathrm{f}}\left(l_{\mathrm{1}}+l_{\mathrm{2}}\cos q_{\mathrm{2}}\right)}{{\left(\frac{y_{\mathrm{f}}}{\cos q_{\mathrm{0}}}+l_{\mathrm{0}}+l_{\mathrm{3}}\right)}^{\mathrm{2}}+x_{\mathrm{f}}^{\mathrm{2}}}}.\end{array}$$

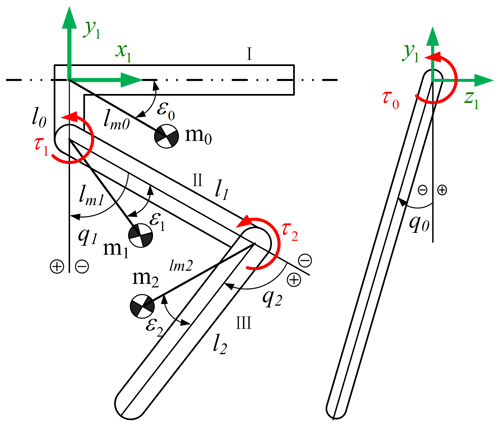
Figure 7 Geometric dimensions of the mechanical structure of a hydraulic four-legged robot support leg.

Taking the comprehensive structural limitations of the heavy-load hydraulic four-legged robot studied in this paper into consideration, the expressions q₂<π and $l_{\mathrm{1}}^{\mathrm{2}}+\mathrm{2}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\cos q_{\mathrm{2}}+l_{\mathrm{2}}^{\mathrm{2}}\ne \mathrm{0}$ are justified. That is, Eq. (22) is considered valid. The angle of the joint is solved by formula (16). As mentioned above, the mathematical correlation between the servo actuator displacement vector and full-space angle of the joint is described. Therefore, the specific requirement instruction signal of an electrohydraulic servo actuator is solved according to Eq. (16). Because the dynamic gait of the spring–support legs is a symmetrical form, the mass properties or inertial indicators of the support legs have little effect on the dynamics of the heavy-load robot, since the proportions of the two diagonal legs swinging together are arbitrary, and their dynamic effects almost counteract each other. Hence only the quality of the torso body is considered in the walking posture optimal design in the study.

4.2 Solving dynamics equations of a FLHL robot

From Fig. 7, the following conclusions are obtained. The kinematic equations are correct, and a FLHL robot has higher kinetic energy and potential energy than a light-loaded robot. On the basis of the above research, the system dynamics in Eq. (23) can be obtained from the Lagrangian equation.

$$\begin{array}{}\text{(23)}& \begin{array}{rl}\left[\begin{array}{l}{\mathit{\tau }}_{\mathrm{0}}\\ {\mathit{\tau }}_{\mathrm{1}}\\ {\mathit{\tau }}_{\mathrm{2}}\end{array}\right]& =\left[\begin{array}{lll}{A}_{\mathrm{11}}& A_{\mathrm{12}}& A_{\mathrm{13}}\\ A_{\mathrm{21}}& A_{\mathrm{22}}& A_{\mathrm{23}}\\ A_{\mathrm{31}}& A_{\mathrm{32}}& A_{\mathrm{33}}\end{array}\right]\left[\begin{array}{l}{\ddot{q}}_{\mathrm{0}}\\ {\ddot{q}}_{\mathrm{1}}\\ {\ddot{q}}_{\mathrm{2}}\end{array}\right]\\ & +\left[\begin{array}{lll}{B}_{\mathrm{11}}& B_{\mathrm{12}}& B_{\mathrm{13}}\\ B_{\mathrm{21}}& B_{\mathrm{22}}& B_{\mathrm{23}}\\ B_{\mathrm{31}}& B_{\mathrm{32}}& B_{\mathrm{33}}\end{array}\right]\left[\begin{array}{l}{\dot{q}}_{\mathrm{0}}\\ {\dot{q}}_{\mathrm{1}}\\ {\dot{q}}_{\mathrm{2}}\end{array}\right]\\ & +\left[\begin{array}{l}{g}_{\mathrm{11}}\\ g_{\mathrm{21}}\\ g_{\mathrm{31}}\end{array}\right],\end{array}\end{array}$$

where

$$\begin{array}{c}{\displaystyle }{A}_{\mathrm{12}}=A_{\mathrm{13}}=A_{\mathrm{21}}=A_{\mathrm{31}}=\mathrm{0}\\ {\displaystyle }\begin{array}{rl}{A}_{\mathrm{11}}& =m_{\mathrm{0}}{l}_{m\mathrm{0}}^{\mathrm{2}}{\cos }^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{0}}+m_{\mathrm{1}}[l_{\mathrm{0}}+l_{m\mathrm{1}}\cos (q_{\mathrm{1}}+{\mathit{\epsilon }}_{\mathrm{1}}){]}^{\mathrm{2}}\\ & +m_{\mathrm{2}}[l_{\mathrm{0}}+l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{m\mathrm{2}}\cos (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}){]}^{\mathrm{2}}\end{array}\\ {\displaystyle }{A}_{\mathrm{22}}=m_{\mathrm{1}}{l}_{m\mathrm{1}}^{\mathrm{2}}+m_{\mathrm{2}}{l}_{\mathrm{1}}^{\mathrm{2}}+m_{\mathrm{2}}{l}_{m\mathrm{2}}^{\mathrm{2}}+\mathrm{2}{m}_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{m\mathrm{2}}\cos (q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}})\\ {\displaystyle }{A}_{\mathrm{23}}=A_{\mathrm{32}}=m_{\mathrm{2}}{l}_{m\mathrm{2}}^{\mathrm{2}}+m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{m\mathrm{2}}\cos (q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}})\\ {\displaystyle }{A}_{\mathrm{33}}=m_{\mathrm{2}}{l}_{m\mathrm{2}}^{\mathrm{2}}\\ {\displaystyle }{B}_{\mathrm{13}}=B_{\mathrm{22}}=B_{\mathrm{33}}=\mathrm{0}\\ {\displaystyle }\begin{array}{rl}{B}_{\mathrm{11}}& =-\mathrm{2}{m}_{\mathrm{2}}[l_{\mathrm{0}}+l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{m\mathrm{2}}\cos (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}\left)\right]\\ & \times [l_{\mathrm{1}}{\dot{q}}_{\mathrm{1}}\sin q_{\mathrm{1}}+l_{m\mathrm{2}}({\dot{q}}_{\mathrm{1}}+{\dot{q}}_{\mathrm{2}}\left)\sin \right(q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}\left)\right]\end{array}\\ {\displaystyle }\begin{array}{rl}{B}_{\mathrm{21}}& =m_{\mathrm{1}}{l}_{m\mathrm{1}}[l_{\mathrm{0}}+l_{m\mathrm{1}}\cos (q_{\mathrm{1}}+{\mathit{\epsilon }}_{\mathrm{1}}\left)\right]\sin (q_{\mathrm{1}}+{\mathit{\epsilon }}_{\mathrm{1}}){\dot{q}}_{\mathrm{0}}\\ & +m_{\mathrm{2}}[l_{\mathrm{0}}+l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{m\mathrm{2}}\cos (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}\left)\right]\\ & \times [l_{\mathrm{1}}\sin q_{\mathrm{1}}+l_{m\mathrm{2}}\sin (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}\left)\right]{\dot{q}}_{\mathrm{0}}\end{array}\\ {\displaystyle }\begin{array}{rl}{B}_{\mathrm{31}}& =m_{\mathrm{2}}{l}_{m\mathrm{2}}[l_{\mathrm{0}}+l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{m\mathrm{2}}\cos (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}\left)\right]\\ & \times \sin (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}){\dot{q}}_{\mathrm{0}}\end{array}\\ {\displaystyle }{B}_{\mathrm{12}}=-\mathrm{2}{m}_{\mathrm{1}}{l}_{m\mathrm{1}}[l_{\mathrm{0}}+l_{m\mathrm{1}}\cos (q_{\mathrm{1}}+{\mathit{\epsilon }}_{\mathrm{1}}\left)\right]\sin (q_{\mathrm{1}}+{\mathit{\epsilon }}_{\mathrm{1}}){\dot{q}}_{\mathrm{0}}\\ {\displaystyle }{B}_{\mathrm{23}}=-m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{m\mathrm{2}}\sin (q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}})(\mathrm{2}{\dot{q}}_{\mathrm{1}}+{\dot{q}}_{\mathrm{2}})\\ {\displaystyle }{B}_{\mathrm{32}}=m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{m\mathrm{2}}\sin (q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}){\dot{q}}_{\mathrm{1}}\\ {\displaystyle }\begin{array}{rl}{g}_{\mathrm{11}}& =m_{\mathrm{0}}{l}_{m\mathrm{0}}\cos {\mathit{\epsilon }}_{\mathrm{0}}g\sin q_{\mathrm{0}}+m_{\mathrm{1}}[l_{\mathrm{0}}+l_{m\mathrm{1}}\cos (q_{\mathrm{1}}+{\mathit{\epsilon }}_{\mathrm{1}}\left)\right]g\sin q_{\mathrm{0}}\\ & +m_{\mathrm{2}}[l_{\mathrm{0}}+l_{\mathrm{1}}\cos q_{\mathrm{1}}+l_{m\mathrm{2}}\cos (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}\left)\right]g\sin q_{\mathrm{0}}\end{array}\\ {\displaystyle }\begin{array}{rl}{g}_{\mathrm{21}}& =m_{\mathrm{1}}{l}_{m\mathrm{1}}\sin (q_{\mathrm{1}}+{\mathit{\epsilon }}_{\mathrm{1}})g\cos q_{\mathrm{0}}\\ & +m_{\mathrm{2}}{l}_{m\mathrm{2}}\sin (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}})g\cos q_{\mathrm{0}}\\ & +m_{\mathrm{2}}{l}_{\mathrm{1}}\sin \left(q_{\mathrm{1}}\right)g\cos q_{\mathrm{0}}\end{array}\\ {\displaystyle }{g}_{\mathrm{31}}=m_{\mathrm{2}}g{l}_{m\mathrm{2}}\sin (q_{\mathrm{1}}+q_{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}})\cos q_{\mathrm{0}}.\end{array}$$

The desired planned trajectory is sought through the aforementioned kinematics equations, and the multiple joint torque required can also be obtained by these dynamic equations. In this study, the FLHL robot joint of this design is actuated by an electrohydraulic servo execution cylinder placed at the end of the spring–support legs. It is worth noting the design according to the variable length of the outrigger of the four-legged robot and the installation positions of the servo execution cylinder on the spring–support legs. Furthermore, the output decoupling of the FLHL robot with force–position hybrid controllable model is described, and the output variable decoupling process of the force–position control hybrid model is implemented in AMEsim software.

Figure 8 Curves of slope response decoupling.

Figure 9 Curves of step response decoupling.

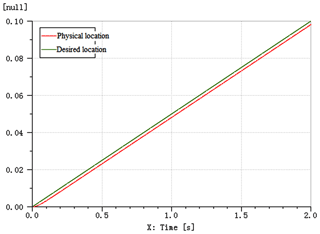
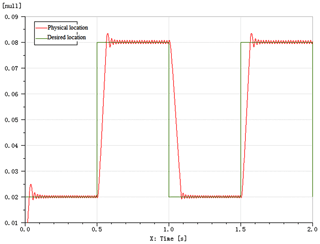
In this chapter, the time domain curves of the required position and physical position are drawn using AMEsim software, and the decoupling characteristics of the force–position hybrid control model are realised. Figure 8 is the time-domain curve of the decoupled slope response of the force–position hybrid control model. In Fig. 9, the time domain curve of the decoupled step response of the force–position control hybrid model is derived.

4.3 Effect of stiffness variable on the synchronisation performance of the servo controller

In this section, the effects of joint stiffness and system stiffness on the dynamic synchronisation characteristics of the servo controller are discussed under three typical loads: step load, alternating load and impact load. Among them, the system stiffness is $K_{\mathrm{1}}=\mathrm{1.80}\times {\mathrm{10}}^{\mathrm{5}}$ N m/rad, and the joint connection stiffness is $K_{\mathrm{2}}=\mathrm{2.32}\times {\mathrm{10}}^{\mathrm{7}}$ N m/rad. Figure 10 shows the influence curves of system stiffness on the synchronisation of the servo controller, and the influence curves of joint connection stiffness on the synchronisation of the servo controller are shown in Fig. 11.

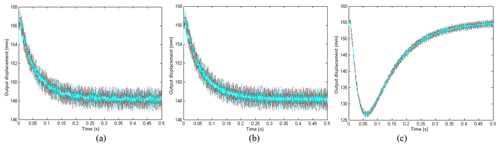
Figure 10 Influence curves of system stiffness on the synchronisation of the servo controller. Variation curves under (a) alternating load, (b) step load and (c) impact load.

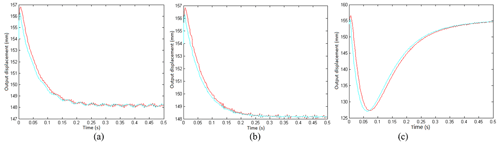
Figure 11 Influence curves of joint connection stiffness on the synchronisation of the servo controller. Variation curves under (a) alternating load, (b) step load and (c) impact load.

From the above simulation data, the following conclusions are drawn: the reduction of the objective system stiffness effectively increases the elastic buffer of FLHL robot and is beneficial to its protection; however, the change of joint stiffness has a great influence.

4.4 Optimal design of controller

The PD controller with the position control model is confirmed in the force control mode. This paper has proposed a compound strategy with minimum flow and speed compensation and servo control. For details, see Li et al. (2018) and Hu et al. (2019). The robotic planning path trajectory generator provides a reference joint angle through the servo controller with the PD strategy. Based on the research of this subject, a force control loop is added to deal with the joint force error, and the joint displacement value of the corresponding part is solved. Considering the time-varying disturbance of the joint angle reference value, the system provides the joint force feedback to realise the position tracking of the PD controller. Both the force vector control mode and the position vector control mode are always in the interconnected configuration operation; once the force is wrong and needs to be handled, the connection joint should become compliant. If there is no force error, the force–position control joint tracking is preferred. No matter how the force error changes, the joints of the key parts must guarantee their predetermined rigidity/softness for a long time. The connection modulation strategy between force feedback and active obedience is established.

4.5 Calculation model of supporting leg variable damping force

Based on the hybrid mode, the variable damper is the core component of the supporting leg. The damping force is regarded as the sum of multiple driving forces in the supporting leg controls. Herein, assuming that the effective leg diameter of the supporting leg control mode is equal to the diameter of its control valve, the tolerance area D_eπL_d is displayed during a specific calculation control process and set equal to the resistance area during actual operation variable Lb. The parameter D_eπL_d is used instead of Lb, and a mathematical calculation model for the supporting leg to control the damping force is performed. Its expression is

$$\begin{array}{}\text{(24)}& F_{\mathrm{d}}={\displaystyle \frac{\mathit{\pi }\mathit{\lambda }{D}_{\mathrm{e}}{L}_{\mathrm{d}}}{h_{\mathrm{d}}}}{v}_{\mathrm{s}}+\mathit{\pi }{D}_{\mathrm{s}}{L}_{\mathrm{d}}{\mathit{\gamma }}_y\mathrm{sgn}\left(v_{\mathrm{s}}\right).\end{array}$$

From the above discussion, it is shown that the damping force in the outrigger control is composed of two parts: The first part is related to the dynamic viscosity of lubricating oil, which generally reveals the viscous damping characteristics of the legs in the intelligent control technology. The second part shows that the force is related to the yield strength, which reveals that the yield strength is a quantitative parameter of Coulomb damping characteristics. The above damping force shows an exponential change trend with the control process. The expression of its change multiplier β_d can be written as

$$\begin{array}{}\text{(25)}& {\mathit{\beta }}_{\mathrm{d}}={\displaystyle \frac{{\mathit{\gamma }}_y{h}_{\mathrm{d}}}{\mathit{\lambda }\left|v_{\mathrm{s}}\right|}}.\end{array}$$

As far as the author knows, the analytical formula used to solve the flow pressure difference in the outrigger control mode is an algebraic equation, which reflects the valve unit force in the damping force control mode and presents the relationship between the external pressure difference and the yield strength. The simplified expression is described as

$$\begin{array}{}\text{(26)}& {\displaystyle }{P}_{\mathrm{0}}={\displaystyle \frac{b}{\mathrm{12}L}}{\displaystyle \frac{\mathrm{\Delta }p{h}_{\mathrm{d}}^{\mathrm{3}}}{Q\mathit{\lambda }}}\text{(27)}& {\displaystyle }{T}_{\mathrm{0}}={\displaystyle \frac{b}{\mathrm{12}}}{\displaystyle \frac{h_{\mathrm{d}}^{\mathrm{2}}{\mathit{\gamma }}_y}{Q\mathit{\lambda }}},\end{array}$$

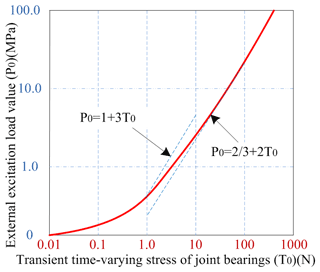
where P₀ represents the external excitation load pressure of the control valve, T₀ is the transient time-varying stress on supporting leg joints bearing and Δp is the differential pressure of the control valve.

Then, the correlation between the two parameters is

$$\begin{array}{}\text{(28)}& P_{\mathrm{0}}^{\mathrm{3}}-(\mathrm{1}+\mathrm{3}{T}_{\mathrm{0}})P_{\mathrm{0}}^{\mathrm{2}}+\mathrm{4}{T}_{\mathrm{0}}^{\mathrm{3}}=\mathrm{0}.\end{array}$$

The correlation time-varying curve between two parameters is shown in Fig. 12.

Figure 12 Correlation time-varying curve between two parameters P₀ and T₀.

With reference to the general actual environment, the outrigger is in a normal progress state when the value T₀ is not greater than 1.0 (that is T₀<1.0). Only if the mode control speed of the outrigger is lower may the value T₀ be less than 1.0 (that is, if T₀≥1.0, then $P_{\mathrm{0}}=\mathrm{2}{T}_{\mathrm{0}}+\mathrm{2}/\mathrm{3}$).

5 Experimental research and results

The compound strategy cannot only effectively reduce the internal force, but it can also enhance the actual driving force. The experimental prototype of this subject is validated on the test platform of the parallel electrohydraulic servo execution cylinder system. Figure 13 shows the prototype of the servo actuator with an electrohydraulic system of four-legged robot.

Figure 13 A four-legged robot with an electrohydraulic servo actuator. (1) Valve assembly. (2) Displacement vector sensor element. (3) Servo control valve with asymmetry. (4) Electrohydraulic servo execution cylinder. (5) Location marking device. (6) Force vector sensor element. (7) Articulated bearing with full-space rotation performance.

The experimental verification process is shown in Fig. 13. It is based on the use of a preset low-pass filter with a lower cut-off frequency of 250 rad/s to further improve and enhance the sensor signal quality, and the power supply pressure here is 7.0 MPa.

5.1 Response experiment of the position vector unit control mode

Considering the diagonally extended spatial state of the FLHL robot involved, the movement forms of the two legs on the diagonal are exactly the same, and the walking posture transition phase or the support dynamics phase is also in a time-varying period. The controllable method of spatial gait position has the advantages of lower energy loss, fast tempo and relatively stable constant stride in all directions. The dynamic response curves of hip joint position are shown in Fig. 14.

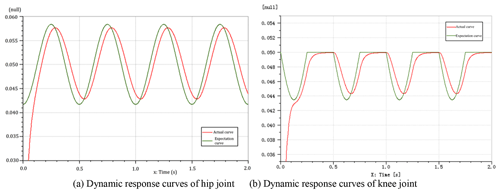
Figure 14 Comparison of dynamic response curves of actual and expected positions of hip and knee joints.

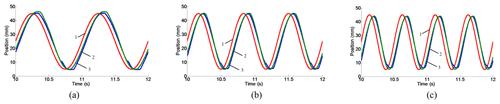
Figure 15 Position response curves at different frequencies. Response curves of (a) 1.0 Hz, (b) 1.5 Hz and (c) 2.0 Hz.

In this study, the parallel electrohydraulic servo system has zero-bound damping characteristics, and its steady-state error and speed asymmetry are manifested by the amplitude of attenuation and the asymmetric phase lag. Figure 15 shows the displacement response curves of 1.0, 1.5 and 2.0 Hz simulation systems. As shown in Fig. 15, curves 2 and 3 show that the dynamic response characteristics have too many similarities. The dynamic response curve 1 is indicated in the predetermined input command signal, and curves 2 and 3 are the one-to-one designated corresponding position dynamic real-time response curves of the servo cylinders 1 and 2, respectively.

Figure 16 Force curves. Response curves of (a) 1.0 Hz, (b) 1.5 Hz and (c) 2.0 Hz.

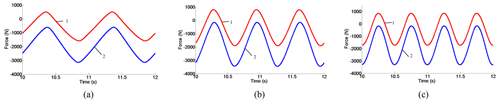
From Fig. 16, the force response curves of 1.0, 1.5 and 2.0 Hz systems are revealed. The response curve 1 and the response curve 2 are the corresponding force curves of the cylinder 1 and the cylinder 2, respectively. In Fig. 16, curves 1 and 2 have different functions under the dynamic real-time response characteristics of the same position. The dynamic response curve 2 always shows a negative trend, and curve 1 shows a positive and negative equilibrium state. Therefore, if the force value is shown as positive, the output forces of the actuator decrease.

5.2 Experiment for an internal force inhibition

The dynamic response curves of displacement and force variables for 1.0, 1.5 and 2.0 Hz systems are shown in Figs. 17–19. Panel (a) describes the change trend of the dynamic response curve of the driving force of the servo actuating cylinder, the signal amplitude is set to 2000 N. And panel (b) represents the time-varying law of the dynamic response curve of the displacement of the servo cylinder; here the signal amplitude is set to 20.0 mm. Curve 1 is the design request command signal, and curve 2 represents the corresponding dynamic real-time response process.

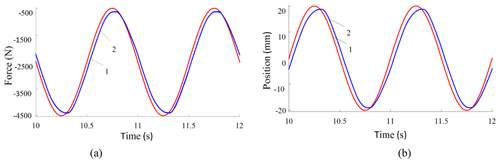
Figure 17 Real-time response curves of 1.0 Hz. Real-time change curves of (a) driving force and (b) position.

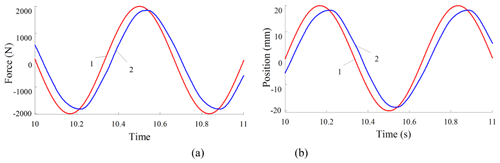
Figure 18 Real-time response curves of 1.5 Hz. Real-time change curves of (a) driving force and (b) position.

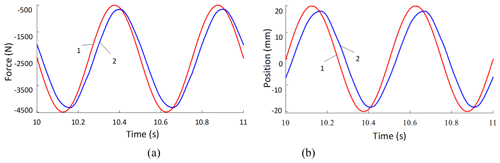
Figure 19 Real-time response curves of 2.0 Hz. Real-time change curves of (a) driving force and (b) position.

Based on the above relevant preconditions, the results show that under the given demand signal, the parallel double-cylinder hydraulic actuator system designed in this study has excellent servo tracking capability. Thereby the amplitude reduction and phase lag of the trajectory tracking signal in the dual-vector (force–position) hybrid control mode are close to each other. When the specific command signal frequency is 1.0, 1.5 and 2.0 Hz, the amplitude attenuation values are 5.52 %, 7.54 % and 8.53 %, and the phase lag values are 9.0, 13.0 and 18.0^∘, respectively.

In actual engineering applications, the adverse effect of the phase lag can be compensated by the front-feedback servo controller. As the frequency of the external excitation signal increases, the amplitude attenuation and phase lag of parallel electrohydraulic servo system are both increased. In conclusion, this research has proved the effectiveness of a parallel servo cylinder with a force–position hybrid control mode.

6 Conclusions

In this study, a scheme for a FLHL robot to reveal motion and a dual-vector (force–position) hybrid control mode of a parallel-executed cylinder (PEC) mechanical integration system has been proposed. First, the preliminary results validate a prototype of a proof-of-concept hydraulic four-legged robot. Then, the simulation results and the kinematics and dynamics of the relative force–position controller are analysed.

1. In view of the larger deadweight load and torsional moment of the supporting hip joints of a non-lightweight hydraulic servo four-legged robot, a parallel cylinder actuation scheme has been identified to improve the initial active torsional moment.

2. Based on the performances of the PEC mechanical integration system with a servo actuator with a dual-vector (force–position) hybrid control mode designed in this paper, by optimising the dual vectors of force signal and position signal, the decoupling analysis process of the force–position control mode is realised.

3. The compound optimisation strategy is verified on the simulation platform of the PEC mechanical integration system. The experimental results show that the dual-vector (force–position) hybrid control mode has excellent dynamic response characteristics, and the effectiveness of the proposed design scheme and control strategy is verified using the original sample model.

4. The scientific research results obtained in this paper may be applied in many specialist fields involving the hybrid control of industrial robot systems in the near future, especially in fields such as military and aerospace, flexible manufacturing, improved operation and remote control.

The upcoming studies take into account various optimisation conditions and are suitable for the analysis process inverse solution of the attitude or rotation torque in the multi-degree-of-freedom robot's instantaneous contact with a dual-vector (force–position) hybrid control mode. The real-time posture stability of the FLHL robot system has been overcome, and the credible results obtained in this paper will be used in forthcoming research.