A new method for isomorphism identification of planetary gear trains

Planetary gear trains (PGTs) are widely used in machinery such as vehicles, pulley blocks, wrist watches, machine tools, and robots. During the process of structural synthesis of PGTs using graph theory, isomorphism identification of graphs is an important and complicated problem. The reliability of the isomorphism detection method directly determines the accuracy of the synthesis result. In this paper, a novel isomorphism identification method for PGTs is proposed. First, a new weighted adjacent matrix is presented to describe the topological graph of PGTs, which has is unique in describing the structure of PGTs. Then, the weighted distance matrix is proposed and the sum of the matrix is obtained, which can determine whether the planetary gear trains is isomorphic or not. Eventually, the examples demonstrate that this new method can be accurately and effectively performed.

1 Introduction

Planetary gear trains (PGTs) include central gears and planetary gears rotating around them. A gear train mechanism has the advantages of high transmission efficiency, large transmission power range, accurate transmission ratio, and strong working reliability. It is the most widely used transmission mechanism at present. In particular, the planetary gear trains also take into account the advantages of small space, low weight, and high rotation efficiency. PGTs are widely used in machine transmissions, robot reducers, vehicle transmissions, gantry cranes, electric tools, and other transmissions. In the past 50 years, the concept of graph theory has been applied to synthesize PGTs (del Castillo, 2002; Hsu and Hsu, 1997; Ravisankar and Mruthyunjaya, 1985; Yan et al., 2006; Shanmukhasundaram et al., 2019b; Tsai, 1987; Tsai and Lin, 1989; Xie et al., 2015a, b; Yang and Ding, 2019), and the synthesis and analysis of planetary gear trains have become a hot topic in mechanism research. At present, the research on mechanism type synthesis mainly focuses on planar kinematic chains (Ding et al., 2010, 2011, 2012, 2013, 2016; Yang et al., 2018). The geometric axis of at least one gear in the planetary gear trains is rotated around the fixed axis of the other gear during transmission. Hsu and Lam (1992) proposed a new graph representation to represent the kinematic structure of a planetary spur gear train efficiently. Yang et al. (2018) proposed a novel displacement graph and a canonical displacement graph model to represent the structure of planetary gear trains. Shanmukhasundaram et al. (2019a, 2021) presented graph-theory-based methods for the detection of degenerate epicyclic gear trains (EGTs) graphs among the enumerated collection. Isomorphism identification of planetary gear trains is an essential step in type synthesis. Graph theory is often used to judge the isomorphism of simple joint and multiple joints kinematic chains, which are also used in planetary gear trains. The accuracy of the isomorphism determination method directly affects the accuracy of the structural synthesis result of planetary gear trains. The establishment of an efficient and accurate isomorphism determination method has always been a hot topic in the field of mechanism.

In the last few decades, a lot of research has been done on the isomorphism identification of planetary gear trains. Ravisankar and Mruthyunjaya (R and S, 1985) proposed the characteristic coefficients of the adjacency matrix method for isomorphism identification of planetary gear trains. Kim and Kwak (1990) introduced a mapping functions method to identify nonisomorphic graphs of epicyclic gear trains, which showed that the edge permutations are from the symmetric group of vertex permutations. Hsu (1994) proposed a structural code method for the identification of the displacement isomorphism of planetary gear trains which can represent the topological structure of planetary gear trains. del Castillo (2002) introduced a method for checking for isomorphisms based on the evaluation of a determinant. Rao (2003) proposed isomorphism identification methods for epicyclic gear trains based on hamming string and a genetic algorithm. Liu et al. (2004) proposed an novel kinematic fractionation concept for the determination of epicyclic gear trains. Yang et al. (2007) presented an algorithm for the identification of the isomorphisms of epicyclic gear mechanism, which improved the efficiency and reliability of the isomorphism identification method. Kamesh et al. (2017) proposed a novel and simple algorithm to eliminate isomorphism chains based on the graph theory. It has been tested on examples from planar kinematic chains with eight links and 1 DOF (degree of freedom), 10 links and 1 DOF, 12 links and 1 DOF, and 15 links and 4 DOF. Yang and Ding (2018a, b, 2019) proposed a fully automatic algorithm to detect and eliminate degenerate planetary gear trains. And the previous perimeter-loop-based isomorphism detection method has been improved to detect isomorphic planetary gear trains. It is applicable for linkage kinematic chains and has been proved to be reliable and efficient. Rai and Punjabi (2019) presented a simple algorithm of links labeling, which was used to find out a binary sequence that provides a maximum binary code. The maxi codes are generated, including binary sequence and binary code, to compare the isomorphisms of planetary gear trains. Xu et al. (2020) proposed a novel isomorphism detection method for the planetary gear transmission structure based on a matrix operation. The various components of the transmission structure and isomorphic structures of the numerous structures are classified.

In this paper, a distance matrix method for isomorphism identification of planetary gear trains is developed. First, a weighted adjacent matrix is proposed to represent the topological structure of planetary gear trains, which can uniquely represent the gear trains, including all information about them. Then, the weighted distance matrix is proposed by an iterative algorithm, and it can determine whether the planetary gear trains are isomorphic or not by sum of this matrix. This isomorphism identification method is simple and reliable and does not require complex computation. Finally, this new isomorphism identification method for PGTs proved to be accurately and effectively performed through a large number of examples.

2 Representation of the weighted adjacent matrix

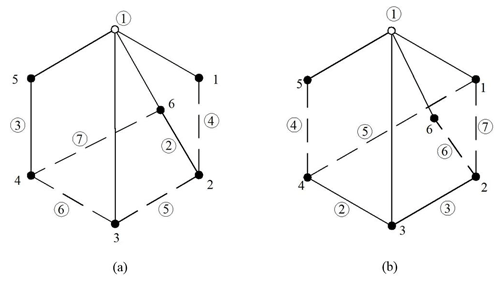
A 3D model of the famous Simpson gear drive system is shown in Fig. 1a. The gear drive system is a 6 bar 1 DOF planetary gear train. Figure 1b is the schematic diagram of a Simpson gear system. Its links and kinematic pairs (revolute pairs and higher pairs) are numbered, respectively. In this paper, the traditional representation of imaginary and real line topology (Hsu and Lam, 1992) is improved. Solid nodes are used to represent links. The real edges represent all the revolute pairs. The gear pairs are indicated by dotted lines. The corresponding topological graph can be obtained from the schematic diagram using the traditional dotted and solid line representation, as shown in Fig. 1c. Considering the planetary gear trains with multiple bars and multiple kinematic pairs, there are many imaginary and real lines represented. In order to simplify the graph, the lines with the same serial number of kinematic pairs in the topological graph are represented by a hollow node, as shown in Fig. 1d. Therefore, all solid nodes connected with the hollow node mean that their corresponding members have the same revolute pair.

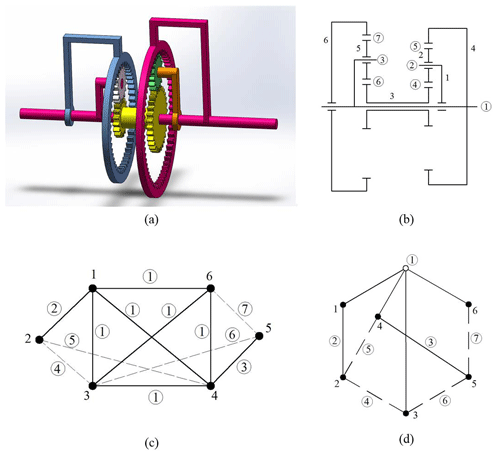
Figure 1 (a) A 3D model of the Simpson gear train, (b) a schematic diagram, (c) a graphic representation, and (d) bicolor topological graph a₁.

A gear train kinematic chain is a collection of links connected by joints, and this link and joint assemblage can be represented by the weighted adjacent matrix. The serial number of the links and kinematic pairs is not limited, and it only needs to be labeled in sequence. The size of the matrix is n×n, and n represents the number of links. The weighted adjacent matrix is expressed as follows:

$$\begin{array}{}\text{(1)}& a_{i,j}=\left\{\begin{array}{l}\mathrm{0},\text{if}i=j\\ \mathrm{\infty },\text{if link}i\text{is not connected to link }j,\\ \left(\mathrm{100}{d}_{max}+d_{min}\right)/\mathrm{1000},\text{if link}i\text{is connected}\\ \text{to link}j\text{by geared pair}\\ \mathrm{1}+\left(\mathrm{100}{d}_{max}+d_{min}\right)/\mathrm{1000},\text{if link}i\text{is connected}\\ \text{to link}j\text{by revolute pair}\end{array}\right.,\end{array}$$

where, $d_{max}=max\left\{d_i,d_j\right\}$, and $d_{min}=min\left\{d_i,d_j\right\}$. The symbol d_i is the degree of link i.

$$\begin{array}{}\text{(2)}& d_i=\left\{\begin{array}{l}{d}_k^{\prime }+\left(\mathrm{10}{n}_{\mathrm{r}}+n_{\mathrm{g}}\right)/\mathrm{10}-\mathrm{1},\text{if link}i\text{is connected}\\ \text{ to multiple joint}k\\ \left(\mathrm{10}{n}_{\mathrm{r}}+n_{\mathrm{g}}\right)/\mathrm{10},\text{if link }i\text{is not connected}\\ \text{ to multiple joint}k\end{array}\right.,\end{array}$$

where, n_r represents the number of revolute pairs in this link. n_g is the number of gear pairs in this link. For instance, the link 6 is connected multiple joint 1, and the degree of multiple joint 1 is 4, i.e., $d_{\mathrm{1}}^{\prime }=\mathrm{4}$. The numbers of revolute pairs and gear pairs are 0 and 1, respectively, i.e., n_r=0 and n_g=1. Thus, d₆=3.1.

The weighted adjacent matrix ${\mathbf{A}}_{a_{\mathrm{1}}}$ of the Simpson gear train a₁ is as follows:

$$\begin{array}{}\text{(3)}& {\mathbf{A}}_{a_{\mathrm{1}}}=\left[\begin{array}{cccccc}\mathrm{0}& \mathrm{1.4012}& \mathrm{1.4032}& \mathrm{1.4140}& \mathrm{\infty }& \mathrm{1.4031}\\ \mathrm{1.4012}& \mathrm{0}& \mathrm{0.3212}& \mathrm{0.4112}& \mathrm{\infty }& \mathrm{\infty }\\ \mathrm{1.4032}& \mathrm{0.3212}& \mathrm{0}& \mathrm{1.4132}& \mathrm{0.3212}& \mathrm{1.3231}\\ \mathrm{1.4140}& \mathrm{0.4112}& \mathrm{1.4132}& \mathrm{0}& \mathrm{1.4112}& \mathrm{1.4131}\\ \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.3212}& \mathrm{1.4112}& \mathrm{0}& \mathrm{0.3112}\\ \mathrm{1.4031}& \mathrm{\infty }& \mathrm{1.3231}& \mathrm{1.4131}& \mathrm{0.3112}& \mathrm{0}\end{array}\right].\end{array}$$

3 The shortest distance matrix

The shortest distance matrix corresponding to the topological diagram is denoted by the symbol E. The length of the shortest path among all the paths from joint to joint is represented by E(i,j). The iterative algorithm is utilized to obtain the shortest distance matrix. And the matrices ${\mathbf{E}}^{\left(\mathrm{0}\right)},{\mathbf{E}}^{\left(\mathrm{1}\right)},{\mathbf{E}}^{\left(\mathrm{2}\right)}\mathrm{\dots }{\mathbf{E}}^{\left(n\right)}$, and $\left({\mathbf{E}}^{\left(\mathrm{0}\right)}={\left(e_{ij}^{\left(\mathrm{0}\right)}\right)}_{n\times n}=\mathbf{A}\right)$ are constructed.

$$\begin{array}{}\text{(4)}& {\mathbf{E}}^{\left(n\right)}={\left(e_{ij}^{\left(n\right)}\right)}_{n\times n},e_{ij}^{\left(n\right)}=min\left\{e_{ij}^{\left(n-\mathrm{1}\right)},e_{in}^{\left(n-\mathrm{1}\right)}+e_{nj}^{\left(n-\mathrm{1}\right)}\right\},\end{array}$$

where, $e_{ij}^{\left(n\right)}$ represents the length of the shortest path from joint i to joint j. So, the final matrix E⁽ⁿ⁾ is the shortest distance matrix. The updating algorithm of the shortest distance matrix is as follows:

Step 1. Initialization, in which the improved adjacency matrix A is assigned to the initial improved shortest distance matrix E.

Step 2. The shortest distance matrix is updated as E(i,j). If $\mathbf{E}\left(i,k\right)+\mathbf{E}\left(k,j\right)<\mathbf{E}\left(i,j\right)$, then $\mathbf{E}\left(i,j\right)=\mathbf{E}\left(i,k\right)+\mathbf{E}\left(k,j\right)$.

Step 3. If k=n, stop. Otherwise, if $k=k+\mathrm{1}$, go to Step 2.

Through the corresponding operation, the shortest distance matrix ${\mathbf{E}}_{a_{\mathrm{1}}}$ of the gear train a₁ can be achieved as follows:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mathbf{E}}_{a_{\mathrm{1}}}=& \left[\begin{array}{cccccc}\mathrm{0}& \mathrm{1.4012}& \mathrm{1.4032}& \mathrm{1.4140}& \mathrm{1.7143}& \mathrm{1.4031}\\ \mathrm{1.4012}& \mathrm{0}& \mathrm{0.3212}& \mathrm{0.4112}& \mathrm{0.6424}& \mathrm{0.9536}\\ \mathrm{1.4032}& \mathrm{0.3212}& \mathrm{0}& \mathrm{0.7324}& \mathrm{0.3212}& \mathrm{0.6324}\\ \mathrm{1.4140}& \mathrm{0.4112}& \mathrm{0.7324}& \mathrm{0}& \mathrm{1.0536}& \mathrm{1.3648}\\ \mathrm{1.7143}& \mathrm{0.6424}& \mathrm{0.3212}& \mathrm{1.0536}& \mathrm{0}& \mathrm{0.3112}\\ \mathrm{1.4031}& \mathrm{0.9536}& \mathrm{0.6324}& \mathrm{1.3648}& \mathrm{0.3112}& \mathrm{0}\end{array}\right],\\ & \left[\begin{array}{c}\mathrm{7.3358}\\ \mathrm{3.7296}\\ \mathrm{3.4104}\\ \mathrm{4.9760}\\ \mathrm{4.0427}\\ \mathrm{4.6651}\end{array}\right].\end{array}\end{array}$$

The array of columns on the right-hand side of Eq. (5), which is the sum of the shortest distances from any joint to all other joints in the gear train, is denoted as the sum array. The sum of the shortest distance matrix is ${\mathbf{S}}_{a_{\mathrm{1}}}=\mathrm{28.1596}$.

4 Isomorphism identification

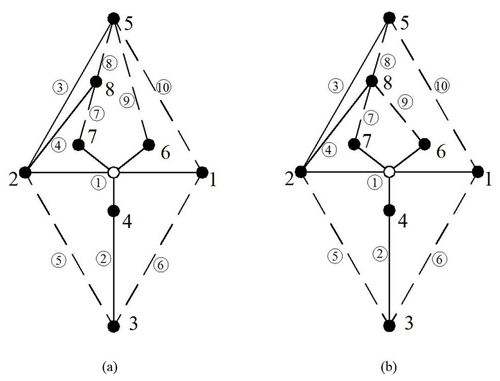
The process of isomorphism identification is as follows: first, the weighted adjacent matrixes of the planetary gear trains are obtained. If the size of the matrixes is not same, then the planetary gear trains are not isomorphic. Then, the sum array of the planetary gear trains are obtained by shortest distance matrix. If the information is different, the planetary gear trains are not isomorphic. If the information is same, then the planetary gear trains are isomorphic. A total of two 6 bar planetary gear trains are shown in Fig. 2. According to the description of the weighted adjacent matrix in Sect. 2, the expression of the 6 bar planetary gear trains a₂ and a₃ is carried out.

Figure 2 (a) Bicolor topological graph a₂ and (b) bicolor topological graph a₃.

The weighted adjacent matrix of the 6 bar planetary gear trains a₂ and a₃ are as follows:

$$\begin{array}{}\text{(6)}& {\mathbf{A}}_{a_{\mathrm{2}}}=\left[\begin{array}{cccccc}\mathrm{0}& \mathrm{1.4012}& \mathrm{1.4032}& \mathrm{1.4140}& \mathrm{\infty }& \mathrm{1.4031}\\ \mathrm{1.4012}& \mathrm{0}& \mathrm{0.3212}& \mathrm{0.4112}& \mathrm{\infty }& \mathrm{\infty }\\ \mathrm{1.4032}& \mathrm{0.3212}& \mathrm{0}& \mathrm{1.4132}& \mathrm{0.3212}& \mathrm{1.3231}\\ \mathrm{1.4140}& \mathrm{0.4112}& \mathrm{1.4132}& \mathrm{0}& \mathrm{1.4112}& \mathrm{1.4131}\\ \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.3212}& \mathrm{1.4112}& \mathrm{0}& \mathrm{0.3112}\\ \mathrm{1.4031}& \mathrm{\infty }& \mathrm{1.3231}& \mathrm{1.4131}& \mathrm{0.3112}& \mathrm{0}\end{array}\right],\end{array}$$

$$\begin{array}{}\text{(7)}& {\mathbf{A}}_{a_{\mathrm{3}}}=\left[\begin{array}{cccccc}\mathrm{0}& \mathrm{0.3212}& \mathrm{1.5032}& \mathrm{0.3212}& \mathrm{1.3231}& \mathrm{1.3231}\\ \mathrm{0.3212}& \mathrm{0}& \mathrm{1.5012}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.3112}\\ \mathrm{1.5032}& \mathrm{1.5012}& \mathrm{0}& \mathrm{1.5012}& \mathrm{1.5031}& \mathrm{1.5031}\\ \mathrm{0.3212}& \mathrm{\infty }& \mathrm{1.5012}& \mathrm{0}& \mathrm{0.3112}& \mathrm{\infty }\\ \mathrm{1.3231}& \mathrm{\infty }& \mathrm{1.5031}& \mathrm{0.3112}& \mathrm{0}& \mathrm{1.3131}\\ \mathrm{1.3231}& \mathrm{0.3112}& \mathrm{1.5031}& \mathrm{\infty }& \mathrm{1.3131}& \mathrm{0}\end{array}\right].\end{array}$$

The shortest distance matrix of the 6 bar planetary gear trains a₂ and a₃ are as follows:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\mathbf{E}}_{a_{\mathrm{2}}}=& \left[\begin{array}{cccccc}\mathrm{0}& \mathrm{1.4012}& \mathrm{1.4032}& \mathrm{1.4140}& \mathrm{1.7143}& \mathrm{1.4031}\\ \mathrm{1.4012}& \mathrm{0}& \mathrm{0.3212}& \mathrm{0.4112}& \mathrm{0.6424}& \mathrm{0.9536}\\ \mathrm{1.4032}& \mathrm{0.3212}& \mathrm{0}& \mathrm{0.7324}& \mathrm{0.3212}& \mathrm{0.6324}\\ \mathrm{1.4140}& \mathrm{0.4112}& \mathrm{0.7324}& \mathrm{0}& \mathrm{1.0536}& \mathrm{1.3648}\\ \mathrm{1.7143}& \mathrm{0.6424}& \mathrm{0.3212}& \mathrm{1.0536}& \mathrm{0}& \mathrm{0.3112}\\ \mathrm{1.4031}& \mathrm{0.9536}& \mathrm{0.6324}& \mathrm{1.3648}& \mathrm{0.3112}& \mathrm{0}\end{array}\right],\\ & \left[\begin{array}{c}\mathrm{7.3358}\\ \mathrm{3.7296}\\ \mathrm{3.4104}\\ \mathrm{4.9760}\\ \mathrm{4.0427}\\ \mathrm{4.6651}\end{array}\right],\end{array}\end{array}$$

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\mathbf{E}}_{a_{\mathrm{3}}}=& \left[\begin{array}{cccccc}\mathrm{0}& \mathrm{0.3212}& \mathrm{1.5032}& \mathrm{0.3212}& \mathrm{0.6324}& \mathrm{0.6324}\\ \mathrm{0.3212}& \mathrm{0}& \mathrm{1.5012}& \mathrm{0.6424}& \mathrm{0.9536}& \mathrm{0.3112}\\ \mathrm{1.5032}& \mathrm{1.5012}& \mathrm{0}& \mathrm{1.5012}& \mathrm{1.5031}& \mathrm{1.5031}\\ \mathrm{0.3212}& \mathrm{0.6424}& \mathrm{1.5012}& \mathrm{0}& \mathrm{0.3112}& \mathrm{0.9536}\\ \mathrm{0.6324}& \mathrm{0.9536}& \mathrm{1.5031}& \mathrm{0.3112}& \mathrm{0}& \mathrm{1.2648}\\ \mathrm{0.6324}& \mathrm{0.3112}& \mathrm{1.5031}& \mathrm{0.9536}& \mathrm{1.2648}& \mathrm{0}\end{array}\right],\\ & \left[\begin{array}{c}\mathrm{3.4104}\\ \mathrm{3.7296}\\ \mathrm{7.5118}\\ \mathrm{3.7296}\\ \mathrm{4.6651}\\ \mathrm{4.6651}\end{array}\right].\end{array}\end{array}$$

From Eqs. (5), (8), and (9), the sums of shortest distance matrixes are ${\mathbf{S}}_{a_{\mathrm{1}}}^T={\mathbf{S}}_{a_{\mathrm{2}}}^T=\mathrm{28.1596}$ and ${\mathbf{S}}_{a_{\mathrm{3}}}^T=\mathrm{27.7116}$. So, we can confirm the PGT a₁ and the PGT a₂ are isomorphic. The sum array of PGT a₃ is different. Therefore, PGT a₃ is not isomorphic.

The greatest advantage of this method is that it is more efficient than other methods without much additional computation. The time complexity of shortest distance matrix method is O(n²). The method implements a number to represent a numerical value of a planetary gear train.

Table 1 Isomorphism determination method of PGTs.

5 Case analysis

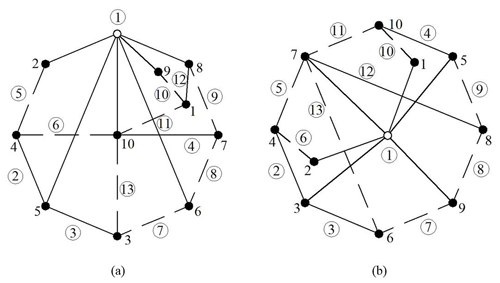
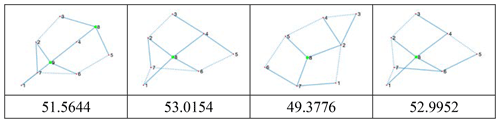
Case 1. Figure 3 shows the topological graph of two 8 bar planetary gear trains. They all contain six gear pairs.

Figure 3 (a) Bicolor topological graph b₁ and (b) bicolor topological graph b₂.

The weighted adjacent matrix of the 8 bar planetary gear trains b₁ and b₂ are as follows:

$$\begin{array}{}\text{(10)}& {\mathbf{A}}_{b_{\mathrm{1}}}=\left[\begin{array}{cccccccc}\mathrm{0}& \mathrm{1.6124}& \mathrm{0.4212}& \mathrm{1.5042}& \mathrm{0.4213}& \mathrm{1.4241}& \mathrm{1.4241}& \mathrm{\infty }\\ \mathrm{1.6142}& \mathrm{0}& \mathrm{0.6112}& \mathrm{1.6150}& \mathrm{1.6113}& \mathrm{1.6141}& \mathrm{1.6141}& \mathrm{1.6112}\\ \mathrm{0.4212}& \mathrm{0.6112}& \mathrm{0}& \mathrm{1.5012}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }\\ \mathrm{1.5042}& \mathrm{1.6150}& \mathrm{1.5012}& \mathrm{0}& \mathrm{\infty }& \mathrm{1.5041}& \mathrm{1.5041}& \mathrm{\infty }\\ \mathrm{0.4213}& \mathrm{1.6113}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0}& \mathrm{0.4113}& \mathrm{\infty }& \mathrm{0.1312}\\ \mathrm{1.4241}& \mathrm{1.6141}& \mathrm{\infty }& \mathrm{1.5041}& \mathrm{0.4113}& \mathrm{0}& \mathrm{1.4141}& \mathrm{\infty }\\ \mathrm{1.4241}& \mathrm{1.6141}& \mathrm{\infty }& \mathrm{1.5041}& \mathrm{\infty }& \mathrm{1.4141}& \mathrm{0}& \mathrm{0.4112}\\ \mathrm{\infty }& \mathrm{1.6112}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.1312}& \mathrm{\infty }& \mathrm{0.4112}& \mathrm{0}\end{array}\right],\end{array}$$

$$\begin{array}{}\text{(11)}& {\mathbf{A}}_{b_{\mathrm{2}}}=\left[\begin{array}{cccccccc}\mathrm{0}& \mathrm{1.6142}& \mathrm{0.4212}& \mathrm{1.5042}& \mathrm{0.4212}& \mathrm{1.4212}& \mathrm{1.4241}& \mathrm{\infty }\\ \mathrm{1.6142}& \mathrm{0}& \mathrm{0.6112}& \mathrm{1.6150}& \mathrm{1.6112}& \mathrm{1.6141}& \mathrm{1.6141}& \mathrm{1.6113}\\ \mathrm{0.4212}& \mathrm{0.6112}& \mathrm{0}& \mathrm{1.5012}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }\\ \mathrm{1.5042}& \mathrm{1.6150}& \mathrm{1.5012}& \mathrm{0}& \mathrm{\infty }& \mathrm{1.5041}& \mathrm{1.5041}& \mathrm{\infty }\\ \mathrm{0.4212}& \mathrm{1.6112}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.1312}\\ \mathrm{1.4241}& \mathrm{1.6141}& \mathrm{\infty }& \mathrm{1.5041}& \mathrm{\infty }& \mathrm{0}& \mathrm{1.4141}& \mathrm{0.4113}\\ \mathrm{1.4241}& \mathrm{1.6141}& \mathrm{\infty }& \mathrm{1.5041}& \mathrm{\infty }& \mathrm{1.4141}& \mathrm{0}& \mathrm{0.4113}\\ \mathrm{\infty }& \mathrm{1.6113}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.1312}& \mathrm{0.4113}& \mathrm{0.4113}& \mathrm{0}\end{array}\right].\end{array}$$

The shortest distance matrix of the 8 bar planetary gear trains b₁ and b₂ are as follows:

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{\mathbf{E}}_{b_{\mathrm{1}}}=& \left[\begin{array}{cccccccc}\mathrm{0}& \mathrm{1.0324}& \mathrm{0.4212}& \mathrm{1.5042}& \mathrm{0.4213}& \mathrm{0.8326}& \mathrm{0.9637}& \mathrm{0.5525}\\ \mathrm{1.0324}& \mathrm{0}& \mathrm{0.6112}& \mathrm{1.6150}& \mathrm{1.4537}& \mathrm{1.6141}& \mathrm{1.6141}& \mathrm{1.5849}\\ \mathrm{0.4212}& \mathrm{0.6112}& \mathrm{0}& \mathrm{1.5012}& \mathrm{0.8425}& \mathrm{1.2538}& \mathrm{1.3849}& \mathrm{0.9737}\\ \mathrm{1.5042}& \mathrm{1.6150}& \mathrm{1.5012}& \mathrm{0}& \mathrm{1.9154}& \mathrm{1.5041}& \mathrm{1.5041}& \mathrm{1.9153}\\ \mathrm{0.4213}& \mathrm{1.4537}& \mathrm{0.8425}& \mathrm{1.9154}& \mathrm{0}& \mathrm{0.4113}& \mathrm{0.5424}& \mathrm{0.1312}\\ \mathrm{0.8326}& \mathrm{1.6141}& \mathrm{1.2538}& \mathrm{1.5041}& \mathrm{0.4113}& \mathrm{0}& \mathrm{0.5937}& \mathrm{0.5425}\\ \mathrm{0.9637}& \mathrm{1.6141}& \mathrm{1.3849}& \mathrm{1.5041}& \mathrm{0.5424}& \mathrm{0.5937}& \mathrm{0}& \mathrm{0.4112}\\ \mathrm{0.5525}& \mathrm{1.5849}& \mathrm{0.9737}& \mathrm{1.9153}& \mathrm{0.1312}& \mathrm{0.5425}& \mathrm{0.4112}& \mathrm{0}\end{array}\right],\\ & \left[\begin{array}{c}\mathrm{5.7279}\\ \mathrm{9.5254}\\ \mathrm{6.9885}\\ \mathrm{11.4593}\\ \mathrm{5.7178}\\ \mathrm{7.1121}\\ \mathrm{7.3741}\\ \mathrm{6.1113}\end{array}\right],\end{array}\end{array}$$

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{\mathbf{E}}_{b_{\mathrm{2}}}=& \left[\begin{array}{cccccccc}\mathrm{0}& \mathrm{1.0324}& \mathrm{0.4212}& \mathrm{1.5042}& \mathrm{0.4212}& \mathrm{0.9637}& \mathrm{0.9637}& \mathrm{0.5524}\\ \mathrm{1.0324}& \mathrm{0}& \mathrm{0.6112}& \mathrm{1.6150}& \mathrm{1.4536}& \mathrm{1.6141}& \mathrm{1.6141}& \mathrm{1.5848}\\ \mathrm{0.4212}& \mathrm{0.6112}& \mathrm{0}& \mathrm{1.5012}& \mathrm{0.8424}& \mathrm{1.3849}& \mathrm{1.3849}& \mathrm{0.9736}\\ \mathrm{1.5042}& \mathrm{1.6150}& \mathrm{1.5012}& \mathrm{0}& \mathrm{1.9254}& \mathrm{1.5041}& \mathrm{1.5041}& \mathrm{1.9154}\\ \mathrm{0.4212}& \mathrm{1.4536}& \mathrm{0.8424}& \mathrm{1.9254}& \mathrm{0}& \mathrm{0.5425}& \mathrm{0.5425}& \mathrm{0.1312}\\ \mathrm{0.9637}& \mathrm{1.6141}& \mathrm{1.3849}& \mathrm{1.5041}& \mathrm{0.5425}& \mathrm{0}& \mathrm{0.8226}& \mathrm{0.4113}\\ \mathrm{0.9637}& \mathrm{1.6141}& \mathrm{1.3849}& \mathrm{1.5041}& \mathrm{0.5425}& \mathrm{0.8226}& \mathrm{0}& \mathrm{0.4113}\\ \mathrm{0.5524}& \mathrm{1.5848}& \mathrm{0.9736}& \mathrm{1.9154}& \mathrm{0.1312}& \mathrm{0.4113}& \mathrm{0.4113}& \mathrm{0}\end{array}\right],\\ & \left[\begin{array}{c}\mathrm{5.8588}\\ \mathrm{9.5252}\\ \mathrm{7.1194}\\ \mathrm{11.4694}\\ \mathrm{5.8588}\\ \mathrm{7.2432}\\ \mathrm{7.2432}\\ \mathrm{5.98}\end{array}\right].\end{array}\end{array}$$

From Eqs. (12) and (13), the sums of the shortest distance matrixes are ${\mathbf{S}}_{b_{\mathrm{1}}}^T=\mathrm{60.0164}$ and ${\mathbf{S}}_{b_{\mathrm{2}}}^T=\mathrm{60.298}$. Therefore, the two 8 bar planetary gear trains are non-isomorphic.

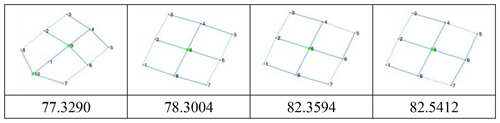
Case 2. There are a total of two 10 bar planetary gear trains as shown in Fig. 4. They all contain eight gear pairs.

Figure 4 (a) Bicolor topological graph c₁ and (b) bicolor topological graph c₂.

The weighted adjacent matrix of the 10 bar planetary gear trains c₁ and c₂ are as follows:

$$\begin{array}{}\text{(14)}& {\mathbf{A}}_{c_{\mathrm{1}}}=\left[\begin{array}{cccccccccc}\mathrm{0}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{1.6112}& \mathrm{0.5112}& \mathrm{0.6312}\\ \mathrm{\infty }& \mathrm{0}& \mathrm{\infty }& \mathrm{0.5112}& \mathrm{1.7051}& \mathrm{1.5251}& \mathrm{\infty }& \mathrm{1.6151}& \mathrm{1.5151}& \mathrm{1.6351}\\ \mathrm{\infty }& \mathrm{\infty }& \mathrm{0}& \mathrm{\infty }& \mathrm{1.7012}& \mathrm{1.5212}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.6312}\\ \mathrm{\infty }& \mathrm{0.5112}& \mathrm{\infty }& \mathrm{0}& \mathrm{1.7012}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.6312}\\ \mathrm{\infty }& \mathrm{1.7051}& \mathrm{1.7012}& \mathrm{1.7012}& \mathrm{0}& \mathrm{1.7052}& \mathrm{\infty }& \mathrm{1.7061}& \mathrm{1.7051}& \mathrm{1.7063}\\ \mathrm{\infty }& \mathrm{1.5251}& \mathrm{0.5212}& \mathrm{\infty }& \mathrm{1.7052}& \mathrm{0}& \mathrm{0.5212}& \mathrm{1.6152}& \mathrm{1.5251}& \mathrm{1.6352}\\ \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.5212}& \mathrm{0}& \mathrm{0.6112}& \mathrm{\infty }& \mathrm{1.6312}\\ \mathrm{1.6112}& \mathrm{1.6151}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{1.7061}& \mathrm{1.6152}& \mathrm{0.6112}& \mathrm{0}& \mathrm{1.6151}& \mathrm{1.6361}\\ \mathrm{0.5112}& \mathrm{1.5151}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{1.7051}& \mathrm{1.5251}& \mathrm{\infty }& \mathrm{1.6151}& \mathrm{0}& \mathrm{1.6351}\\ \mathrm{0.6312}& \mathrm{1.6351}& \mathrm{0.6312}& \mathrm{0.6312}& \mathrm{1.7063}& \mathrm{1.6352}& \mathrm{1.6312}& \mathrm{1.6361}& \mathrm{1.6351}& \mathrm{0}\end{array}\right],\end{array}$$

$$\begin{array}{}\text{(15)}& {\mathbf{A}}_{c_{\mathrm{2}}}=\left[\begin{array}{cccccccccc}\mathrm{0}& \mathrm{1.5151}& \mathrm{1.7051}& \mathrm{\infty }& \mathrm{1.6151}& \mathrm{\infty }& \mathrm{1.6351}& \mathrm{\infty }& \mathrm{1.5251}& \mathrm{0.5112}\\ \mathrm{1.5151}& \mathrm{0}& \mathrm{1.7051}& \mathrm{0.5112}& \mathrm{1.6151}& \mathrm{\infty }& \mathrm{1.6351}& \mathrm{\infty }& \mathrm{1.5251}& \mathrm{\infty }\\ \mathrm{1.7051}& \mathrm{1.7051}& \mathrm{0}& \mathrm{1.7012}& \mathrm{\infty }& \mathrm{1.7012}& \mathrm{1.7063}& \mathrm{\infty }& \mathrm{1.7052}& \mathrm{\infty }\\ \mathrm{\infty }& \mathrm{0.5112}& \mathrm{1.7012}& \mathrm{0}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.6312}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }\\ \mathrm{1.6151}& \mathrm{1.6151}& \mathrm{1.7061}& \mathrm{\infty }& \mathrm{0}& \mathrm{\infty }& \mathrm{1.6361}& \mathrm{0.6112}& \mathrm{1.6152}& \mathrm{1.6112}\\ \mathrm{\infty }& \mathrm{\infty }& \mathrm{1.7012}& \mathrm{\infty }& \mathrm{1.6361}& \mathrm{0}& \mathrm{0.6312}& \mathrm{\infty }& \mathrm{0.5212}& \mathrm{\infty }\\ \mathrm{1.6351}& \mathrm{1.6351}& \mathrm{1.7063}& \mathrm{0.6312}& \mathrm{0.6112}& \mathrm{0.6312}& \mathrm{0}& \mathrm{1.6312}& \mathrm{1.6352}& \mathrm{0.6312}\\ \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{1.6152}& \mathrm{\infty }& \mathrm{1.6312}& \mathrm{0}& \mathrm{0.5212}& \mathrm{\infty }\\ \mathrm{1.5251}& \mathrm{1.5251}& \mathrm{1.7052}& \mathrm{\infty }& \mathrm{1.6112}& \mathrm{0.5212}& \mathrm{1.6352}& \mathrm{0.5212}& \mathrm{0}& \mathrm{\infty }\\ \mathrm{0.5112}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0.6312}& \mathrm{\infty }& \mathrm{\infty }& \mathrm{0}\end{array}\right].\end{array}$$

The shortest distance matrix of the 10 bar planetary gear trains c₁ and c₂ are as follows:

$$\begin{array}{}\text{(16)}& \begin{array}{rl}{\mathbf{E}}_{c_{\mathrm{1}}}=& \left[\begin{array}{cccccccccc}\mathrm{0}& \mathrm{1.7736}& \mathrm{1.2624}& \mathrm{1.2624}& \mathrm{2.2163}& \mathrm{1.7836}& \mathrm{2.2224}& \mathrm{1.6112}& \mathrm{0.5112}& \mathrm{0.6312}\\ \mathrm{1.7736}& \mathrm{0}& \mathrm{1.7736}& \mathrm{0.5112}& \mathrm{1.7051}& \mathrm{1.5251}& \mathrm{2.0463}& \mathrm{1.6151}& \mathrm{1.5151}& \mathrm{1.1424}\\ \mathrm{1.2624}& \mathrm{1.7736}& \mathrm{0}& \mathrm{1.2624}& \mathrm{1.7012}& \mathrm{0.5212}& \mathrm{1.0424}& \mathrm{1.6536}& \mathrm{1.7736}& \mathrm{0.6312}\\ \mathrm{1.2624}& \mathrm{0.5112}& \mathrm{1.2624}& \mathrm{0}& \mathrm{1.7012}& \mathrm{1.7836}& \mathrm{2.2624}& \mathrm{2.1263}& \mathrm{1.7736}& \mathrm{0.6312}\\ \mathrm{2.2163}& \mathrm{1.7051}& \mathrm{1.7012}& \mathrm{1.7012}& \mathrm{0}& \mathrm{1.7052}& \mathrm{2.2264}& \mathrm{1.7061}& \mathrm{1.7051}& \mathrm{1.7063}\\ \mathrm{1.7836}& \mathrm{1.5251}& \mathrm{0.5212}& \mathrm{1.7836}& \mathrm{1.7052}& \mathrm{0}& \mathrm{0.5212}& \mathrm{1.1324}& \mathrm{1.5251}& \mathrm{1.1524}\\ \mathrm{2.2224}& \mathrm{2.0463}& \mathrm{1.0424}& \mathrm{2.2624}& \mathrm{2.2264}& \mathrm{0.5212}& \mathrm{0}& \mathrm{0.6112}& \mathrm{2.0463}& \mathrm{1.6312}\\ \mathrm{1.6112}& \mathrm{1.6151}& \mathrm{1.6536}& \mathrm{2.1263}& \mathrm{1.7061}& \mathrm{1.1324}& \mathrm{0.6112}& \mathrm{0}& \mathrm{1.6151}& \mathrm{1.6361}\\ \mathrm{0.5112}& \mathrm{1.5151}& \mathrm{1.7736}& \mathrm{1.7736}& \mathrm{1.7051}& \mathrm{1.5251}& \mathrm{2.0463}& \mathrm{1.6151}& \mathrm{0}& \mathrm{1.1424}\\ \mathrm{0.6312}& \mathrm{1.1424}& \mathrm{0.6312}& \mathrm{0.6312}& \mathrm{1.7063}& \mathrm{1.1524}& \mathrm{1.6312}& \mathrm{1.6361}& \mathrm{1.1424}& \mathrm{0}\end{array}\right],\\ & \left[\begin{array}{c}\mathrm{13.2743}\\ \mathrm{13.6075}\\ \mathrm{11.6216}\\ \mathrm{13.3143}\\ \mathrm{16.3729}\\ \mathrm{11.6498}\\ \mathrm{14.6098}\\ \mathrm{13.7071}\\ \mathrm{13.6075}\\ \mathrm{10.3044}\end{array}\right],\end{array}\end{array}$$

$$\begin{array}{}\text{(17)}& \begin{array}{rl}{\mathbf{E}}_{c_{\mathrm{2}}}=& \left[\begin{array}{cccccccccc}\mathrm{0}& \mathrm{1.5151}& \mathrm{1.7051}& \mathrm{1.7736}& \mathrm{1.6151}& \mathrm{1.7736}& \mathrm{1.1424}& \mathrm{2.0463}& \mathrm{1.5251}& \mathrm{0.5112}\\ \mathrm{1.5151}& \mathrm{0}& \mathrm{1.7051}& \mathrm{0.5112}& \mathrm{1.6151}& \mathrm{1.7736}& \mathrm{1.1424}& \mathrm{2.0463}& \mathrm{1.5251}& \mathrm{1.7736}\\ \mathrm{1.7051}& \mathrm{1.7051}& \mathrm{0}& \mathrm{1.7012}& \mathrm{1.7061}& \mathrm{1.7012}& \mathrm{1.7063}& \mathrm{2.2264}& \mathrm{1.7052}& \mathrm{2.2163}\\ \mathrm{1.7736}& \mathrm{0.5112}& \mathrm{1.7012}& \mathrm{0}& \mathrm{2.1263}& \mathrm{1.2624}& \mathrm{0.6312}& \mathrm{2.2624}& \mathrm{1.7836}& \mathrm{1.2624}\\ \mathrm{1.6151}& \mathrm{1.6151}& \mathrm{1.7061}& \mathrm{2.1263}& \mathrm{0}& \mathrm{1.6536}& \mathrm{1.6361}& \mathrm{0.6112}& \mathrm{1.1324}& \mathrm{1.6112}\\ \mathrm{1.7736}& \mathrm{1.7736}& \mathrm{1.7012}& \mathrm{1.2624}& \mathrm{1.6536}& \mathrm{0}& \mathrm{0.6312}& \mathrm{1.0424}& \mathrm{0.5212}& \mathrm{1.2624}\\ \mathrm{1.1424}& \mathrm{1.1424}& \mathrm{1.7063}& \mathrm{0.6312}& \mathrm{1.6361}& \mathrm{0.6312}& \mathrm{0}& \mathrm{1.6312}& \mathrm{1.1524}& \mathrm{0.6312}\\ \mathrm{2.0463}& \mathrm{2.0463}& \mathrm{2.2264}& \mathrm{2.2624}& \mathrm{0.6112}& \mathrm{1.0424}& \mathrm{1.6312}& \mathrm{0}& \mathrm{0.5212}& \mathrm{2.2224}\\ \mathrm{1.5251}& \mathrm{1.5251}& \mathrm{1.7052}& \mathrm{1.7836}& \mathrm{1.1324}& \mathrm{0.5212}& \mathrm{1.1524}& \mathrm{0.5212}& \mathrm{0}& \mathrm{1.7836}\\ \mathrm{0.5112}& \mathrm{1.7736}& \mathrm{2.2163}& \mathrm{1.2624}& \mathrm{1.6112}& \mathrm{1.2624}& \mathrm{0.6312}& \mathrm{2.2224}& \mathrm{1.7836}& \mathrm{0}\end{array}\right],\\ & \left[\begin{array}{c}\mathrm{13.6075}\\ \mathrm{13.6075}\\ \mathrm{16.3729}\\ \mathrm{13.3143}\\ \mathrm{13.7071}\\ \mathrm{11.6216}\\ \mathrm{10.3044}\\ \mathrm{14.6098}\\ \mathrm{11.6498}\\ \mathrm{13.2743}\end{array}\right].\end{array}\end{array}$$

From Eqs. (16) and (17), the sums of shortest distance matrixes are ${\mathbf{S}}_{c_{\mathrm{1}}}^T={\mathbf{S}}_{{\mathrm{c}}_{\mathrm{2}}}^T=\mathrm{132.0692}$. So, we can confirm the PGT c₁ and the PGT c₂ are isomorphic.

6 Conclusions

In this paper, the weighted adjacent matrix is introduced to describe the planetary gear train, which can uniquely represent the structure of the gear train. Then, a novel isomorphism identification method was proposed. This method is both reliable and simple. The time complexity of the shortest distance matrix method is O(n²). The greatest advantage of this method is that it is more efficient than other methods without much additional computation. The experimental results provided show the high performance.

Appendix A

Figure A1 A total of 81 displacement graphs of 6 bar 1 DOF planetary gear trains.

Figure A2 A total of four displacement graphs of 7 bar 2 DOF planetary gear trains.

Figure A3 A total of four displacement graphs of 8 bar 3 DOF planetary gear trains.