Structural synthesis of plane kinematic chain inversions without detecting isomorphism

A plane kinematic chain inversion refers to a plane kinematic chain with one link fixed (assigned as the ground link). In the creative design of mechanisms, it is important to select proper ground links. The structural synthesis of plane kinematic chain inversions is helpful for improving the efficiency of mechanism design. However, the existing structural synthesis methods involve isomorphism detection, which is cumbersome. This paper proposes a simple and efficient structural synthesis method for plane kinematic chain inversions without detecting isomorphism. The fifth power of the adjacency matrix is applied to recognize similar vertices, and non-isomorphic kinematic chain inversions are directly derived according to non-similar vertices. This method is used to automatically synthesize 6-link 1-degree-of-freedom (DOF), 8-link 1-DOF, 8-link 3-DOF, 9-link 2-DOF, 9-link 4-DOF, 10-link 1-DOF, 10-link 3-DOF and 10-link 5-DOF plane kinematic chain inversions. All the synthesis results are consistent with those reported in literature. Our method is also suitable for other kinds of kinematic chains.

1 Introduction

In the early stage of the creative design of mechanisms, the design work was accomplished mainly based on researchers' experience and inspiration, resulting in a low design efficiency. Moreover, the derived mechanism configurations were very limited. In order to resolve this problem, many systematic methods have been proposed since the 1960s to create novel mechanisms (Olson et al., 1985; Yan, 1992; Al-Dweiri, 2010; Yan and Chiu, 2014). An effective mechanism design method is based on the atlas of topological structures of kinematic chains (Rao, 1997; Butcher and Hartman, 2005; Sunkari and Schmidt, 2006; Ding et al., 2012, 2016).

A plane kinematic chain inversion refers to a plane kinematic chain with one link fixed (assigned as the ground link). When designing mechanisms based on kinematic chains, it is essential to select proper ground links. The structural synthesis of plane kinematic chain inversions plays an important role in the improvement of mechanism design efficiency. A cumbersome part of the structural synthesis process is to detect and eliminate isomorphic kinematic chain inversions. Meanwhile, kinematic chain components are represented by vertices in graph theory, and similarity analysis of kinematic chain components can be transformed into a similarity recognition problem of vertices in topological graphs. The similarity of kinematic chain components should be analyzed first to reduce redundant design schemes and improve the efficiency of innovative design.

In the early stage of research on the structural synthesis, the characteristic polynomial-based method was applied to synthesize 10-link 3-degree-of-freedom (DOF) and 11-link 2-DOF kinematic chain inversions (Mruthyunjaya, 1984; Mruthyunjaya and Balasubramanian, 1987). Subsequently, the hamming number technique was developed to detect isomorphic inversions of given kinematic chains (Rao and Prasad Raju Pathapati, 2000; Rao and Varada Raju, 1991). Chu and Cao (1994) utilized the link's adjacent-chain table to distinguish kinematic chain inversions and confirmed that there are 1834 10-link 1-DOF inversions. Vijayananda (1994) applied the representation set of links to detect isomorphism and enumerated a part of kinematic chain inversions with up to 13 links. Tuttle (1996) presented an isomorphism detection method based on the theory of finite symmetry groups and synthesized inversions from the corresponding non-fractionated kinematic chains.

An approach based on permutation groups was proposed to derive non-isomorphic inversions and mechanisms considering specific design constraints (Yan and Hwang, 1991; Yan and Hung, 2006; Hung et al., 2008). Based on genetic algorithms, Liu and McPhee (2007) studied the automatic kinematic synthesis of planar mechanisms with revolute joints by considering mechanism topology and geometric parameters. Simoni et al. (2009) applied the group theory technique to avoid the generation of isomorphic inversions and enumerated planar inversions with up to four independent loops. Dargar et al. (2013) and Rizvi et al. (2016) developed methods to determine structural invariants and identification numbers of kinematic chains to detect isomorphic kinematic chains inversions. Their methods were applied to synthesize kinematic chain inversions with up to 10 links. Mruthyunjaya (2003) and Simoni et al. (2011) reviewed the synthesis methods of kinematic chain inversions and analyzed the contradiction in the synthesis results. Yang et al. (2017) presented an automatic method to synthesize kinematic chain inversions, including those having complex topology. Ding and Huang (2007) improved the perimeter-loop-graph-based method to detect isomorphism. Sun et al. (2018) applied the joint–joint matrix to represent planar kinematic chains with multiple joints and studied the isomorphism detection of kinematic chains by comparing links, joints and matrices.

The literature review shows that the existing methods for structural synthesis of inversions involve isomorphism detection, which is cumbersome. This paper presents a simple and efficient structural synthesis method without detecting isomorphism. The fifth power of the adjacency matrix is applied to recognize similar vertices, and non-isomorphic kinematic chain inversions are directly derived according to non-similar vertices. This method is used to automatically synthesize 6-link 1-DOF, 8-link 1-DOF, 8-link 3-DOF, 9-link 2-DOF, 9-link 4-DOF, 10-link 1-DOF, 10-link 3-DOF and 10-link 5-DOF plane kinematic chain inversions. All the synthesis results are consistent with those reported in literature. The present method can also be applied to kinematic chain inversions with more links.

2 Graphic representation of kinematic chain inversion

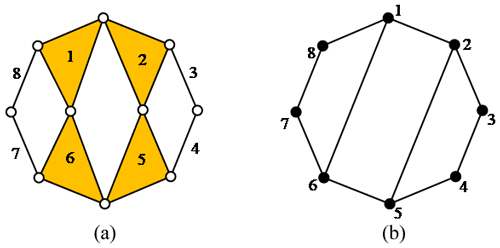
The concept of graph theory is frequently adopted to represent the topological structures of kinematic chains and mechanisms. In the graphic representation of kinematic chains, a vertex denotes a link, and an edge denotes a kinematic pair. For example, Fig. 1a shows an 8-link 1-DOF kinematic chain, and Fig. 1b shows its graphic representation. For convenience of developing computer-aided structural synthesis program, the graphic representation is further denoted by its adjacency matrix, which is defined as in Eq. (1). For example, the adjacency matrix of Fig. 1b is shown in Eq. (2).

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{AM}=[x_{i,j}{]}_{n\times n}=\left\{\begin{array}{ll}\mathrm{1},& \text{if vertex}i\text{is adjacent to vertex}j\\ \mathrm{0},& \mathrm{otherwise}\end{array}\right.\text{(2)}& {\displaystyle }\mathrm{AM}=\left[\begin{array}{cccccccc}\mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}\\ \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}\\ \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}\end{array}\right]\end{array}$$

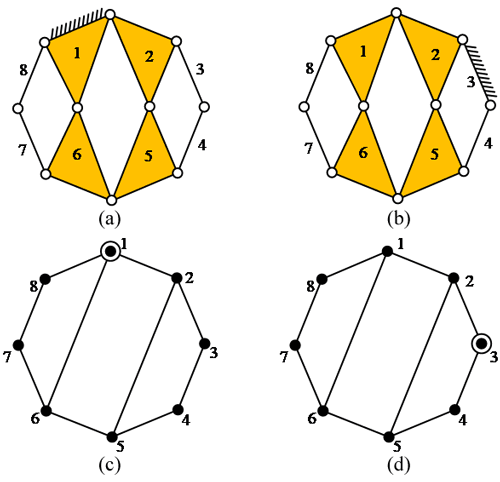
A kinematic chain inversion refers to a kinematic chain with one link fixed (assigned as the ground link). For example, two inversions derived from Fig. 1a are shown in Fig. 2a and b, where links 1 and 3 are assigned as ground links, respectively. Their graphic representations are shown in Fig. 2c and d, where the ground link is denoted by a vertex marked with a circle.

Figure 1 (a) An 8-link 1-DOF kinematic chain and (b) its graphic representation.

Figure 2 Inversions derived from Fig. 1a and their graphic representations.

3 Detection of similar vertices

Similar vertices in the graphic representation have the same topological attribution and characteristics. If similar vertices are assigned as ground links, the derived kinematic chain inversions are isomorphic. In other words, they have duplicate topological structures.

We developed a simple and efficient method to detect similar vertices based on the fifth power of the adjacency matrix. Given two matrices AM_a = [a_i,j]_n×n and AM_b = [b_i,j]_n×n, their multiplication is AM_c = AM_a ⋅ AM_b = [c_i,j]_n×n, and the element of matrix AM_c is $c_{i,j}={\sum }_{k=\mathrm{1}}^n{a}_{i,k}\cdot b_{k,j}$. In particular, the multiplication of matrix AM and itself is called the power of matrix and is denoted as AM${}^{\mathrm{2}}=\mathrm{AM}\cdot \mathrm{AM}=[c_{i,j}{]}_{n\times n}$, and its element is $c_{i,j}={\sum }_{k=\mathrm{1}}^n{a}_{i,k}\cdot a_{k,j}$. For example, the power of the matrix in Eq. (2) is shown in Eq. (3). Similarly, the third, fourth and fifth powers of the matrix in Eq. (2) are shown in Eqs. (4), (5) and (6), respectively.

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathrm{AM}}^{\mathrm{2}}=\mathrm{AM}\cdot \mathrm{AM}=\left[\begin{array}{cccccccc}\mathrm{3}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{2}& \mathrm{0}\\ \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{1}\\ \mathrm{1}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{2}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{2}\\ \mathrm{2}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{2}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{2}& \mathrm{0}& \mathrm{2}\end{array}\right]\text{(4)}& {\displaystyle }{\mathrm{AM}}^{\mathrm{3}}={\mathrm{AM}}^{\mathrm{2}}\cdot \mathrm{AM}=\left[\begin{array}{cccccccc}\mathrm{0}& \mathrm{6}& \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{7}& \mathrm{0}& \mathrm{5}\\ \mathrm{6}& \mathrm{0}& \mathrm{5}& \mathrm{0}& \mathrm{7}& \mathrm{0}& \mathrm{3}& \mathrm{0}\\ \mathrm{0}& \mathrm{5}& \mathrm{0}& \mathrm{4}& \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{1}\\ \mathrm{3}& \mathrm{0}& \mathrm{4}& \mathrm{0}& \mathrm{5}& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{7}& \mathrm{0}& \mathrm{5}& \mathrm{0}& \mathrm{6}& \mathrm{0}& \mathrm{3}\\ \mathrm{7}& \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{6}& \mathrm{0}& \mathrm{5}& \mathrm{0}\\ \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{5}& \mathrm{0}& \mathrm{4}\\ \mathrm{5}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{3}& \mathrm{0}& \mathrm{4}& \mathrm{0}\end{array}\right]\text{(5)}& {\displaystyle }\begin{array}{rl}{\mathrm{AM}}^{\mathrm{4}}& ={\mathrm{AM}}^{\mathrm{3}}\cdot \mathrm{AM}\\ & =\left[\begin{array}{rrrrrrrr}\mathrm{18}& \mathrm{0}& \mathrm{9}& \mathrm{0}& \mathrm{16}& \mathrm{0}& \mathrm{12}& \mathrm{0}\\ \mathrm{0}& \mathrm{18}& \mathrm{0}& \mathrm{12}& \mathrm{0}& \mathrm{16}& \mathrm{0}& \mathrm{9}\\ \mathrm{9}& \mathrm{0}& \mathrm{9}& \mathrm{0}& \mathrm{12}& \mathrm{0}& \mathrm{4}& \mathrm{0}\\ \mathrm{0}& \mathrm{12}& \mathrm{0}& \mathrm{9}& \mathrm{0}& \mathrm{9}& \mathrm{0}& \mathrm{4}\\ \mathrm{16}& \mathrm{0}& \mathrm{12}& \mathrm{0}& \mathrm{18}& \mathrm{0}& \mathrm{9}& \mathrm{0}\\ \mathrm{0}& \mathrm{16}& \mathrm{0}& \mathrm{9}& \mathrm{0}& \mathrm{18}& \mathrm{0}& \mathrm{12}\\ \mathrm{12}& \mathrm{0}& \mathrm{4}& \mathrm{0}& \mathrm{9}& \mathrm{0}& \mathrm{9}& \mathrm{0}\\ \mathrm{0}& \mathrm{9}& \mathrm{0}& \mathrm{4}& \mathrm{0}& \mathrm{12}& \mathrm{0}& \mathrm{9}\end{array}\right]\end{array}\text{(6)}& {\displaystyle }\begin{array}{rl}{\mathrm{AM}}^{\mathrm{5}}& ={\mathrm{AM}}^{\mathrm{4}}\cdot \mathrm{AM}\\ & =\left[\begin{array}{rrrrrrrr}\mathrm{0}& \mathrm{43}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{46}& \mathrm{0}& \mathrm{30}\\ \mathrm{43}& \mathrm{0}& \mathrm{30}& \mathrm{0}& \mathrm{46}& \mathrm{0}& \mathrm{25}& \mathrm{0}\\ \mathrm{0}& \mathrm{30}& \mathrm{0}& \mathrm{21}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{13}\\ \mathrm{25}& \mathrm{0}& \mathrm{21}& \mathrm{0}& \mathrm{30}& \mathrm{0}& \mathrm{13}& \mathrm{0}\\ \mathrm{0}& \mathrm{46}& \mathrm{0}& \mathrm{30}& \mathrm{0}& \mathrm{43}& \mathrm{0}& \mathrm{25}\\ \mathrm{46}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{43}& \mathrm{0}& \mathrm{30}& \mathrm{0}\\ \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{13}& \mathrm{0}& \mathrm{30}& \mathrm{0}& \mathrm{21}\\ \mathrm{30}& \mathrm{0}& \mathrm{13}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{21}& \mathrm{0}\end{array}\right]\end{array}\end{array}$$

For the fifth power of matrix AM⁵, its rearranged matrix RAM⁵ is acquired by arranging the elements of each row in descending order. For example, the rearranged fifth power of matrix RAM⁵ corresponding to Eq. (6) is shown in Eq. (7). If the elements in the ith row and the jth row of RAM⁵ are the same, vertices i and j in the corresponding graphic representation are detected to be similar vertices. For example, the elements in the first, second, fifth and sixth rows in Eq. (7) are (46, 43, 30, 25, 0, 0, 0, 0); hence vertices 1, 2, 5 and 6 in Fig. 1b are similar vertices. The elements in the third, fourth, seventh and eighth rows in Eq. (7) are (30, 25, 21, 13, 0, 0, 0, 0); hence vertices 3, 4, 7 and 8 in Fig. 1b are similar vertices. In fact, similar vertices in Fig. 1b can be directly detected by visual inspection. However, using visual inspection, it is very hard or impossible to precisely detect similar vertices in other complex cases. Our detection method based on the fifth power of the adjacency matrix AM⁵ is suitable for both simple and complex kinematic chains. Moreover, it is very easy to achieve automatic detection by developing a computer program.

$$\begin{array}{}\text{(7)}& {\mathrm{RAM}}^{\mathrm{5}}=\left[\begin{array}{cccccccc}\mathrm{46}& \mathrm{43}& \mathrm{30}& \mathrm{25}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{46}& \mathrm{43}& \mathrm{30}& \mathrm{25}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{30}& \mathrm{25}& \mathrm{21}& \mathrm{13}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{30}& \mathrm{25}& \mathrm{21}& \mathrm{13}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{46}& \mathrm{43}& \mathrm{30}& \mathrm{25}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{46}& \mathrm{43}& \mathrm{30}& \mathrm{25}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{30}& \mathrm{25}& \mathrm{21}& \mathrm{13}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{30}& \mathrm{25}& \mathrm{21}& \mathrm{13}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right]\end{array}$$

4 Structural synthesis of kinematic chain inversions

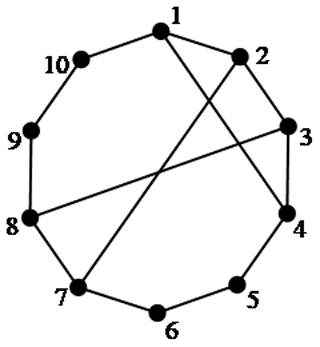
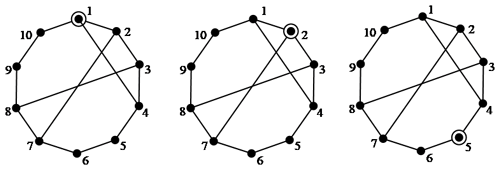
The existing methods for structural synthesis of kinematic chain inversions involve isomorphism detection, which is cumbersome. In this paper, the kinematic chain inversions are synthesized based on the information of similar vertices, without detecting isomorphism. If similar vertices are assigned as ground links, the derived kinematic chain inversions are isomorphic. Non-isomorphic kinematic chain inversions can be directly derived according to non-similar vertices. For example, vertices 1 and 3 in Fig. 1b are non-similar vertices. Only two non-isomorphic inversions can be derived from Fig. 1b, as illustrated in Fig. 2c and d. Another example 10-link 1-DOF kinematic chain is shown in Fig. 3. Its adjacency matrix, the fifth power of the adjacency matrix AM⁵ and the rearranged fifth power of the adjacency matrix RAM⁵ are shown in Eqs. (8)–(10), respectively. According to Eq. (10), vertices 1, 4, 7 and 8 are similar vertices, vertices 2 and 3 are similar vertices and vertices 5, 6, 9 and 10 are also similar vertices. Vertices 1, 2 and 5 are non-similar vertices, and three non-isomorphic inversions can be derived from Fig. 3, as shown in Fig. 4.

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathrm{AM}=\left[\begin{array}{cccccccccc}\mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\\ \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{1}\\ \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}\end{array}\right]\text{(9)}& {\displaystyle }{\mathrm{AM}}^{\mathrm{5}}=\left[\begin{array}{rrrrrrrrrr}\mathrm{0}& \mathrm{44}& \mathrm{0}& \mathrm{40}& \mathrm{0}& \mathrm{20}& \mathrm{0}& \mathrm{36}& \mathrm{0}& \mathrm{24}\\ \mathrm{44}& \mathrm{0}& \mathrm{51}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{44}& \mathrm{0}& \mathrm{25}& \mathrm{0}\\ \mathrm{0}& \mathrm{51}& \mathrm{0}& \mathrm{44}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{44}& \mathrm{0}& \mathrm{25}\\ \mathrm{40}& \mathrm{0}& \mathrm{44}& \mathrm{0}& \mathrm{24}& \mathrm{0}& \mathrm{36}& \mathrm{0}& \mathrm{20}& \mathrm{0}\\ \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{24}& \mathrm{0}& \mathrm{15}& \mathrm{0}& \mathrm{20}& \mathrm{0}& \mathrm{11}\\ \mathrm{20}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{15}& \mathrm{0}& \mathrm{24}& \mathrm{0}& \mathrm{11}& \mathrm{0}\\ \mathrm{0}& \mathrm{44}& \mathrm{0}& \mathrm{36}& \mathrm{0}& \mathrm{24}& \mathrm{0}& \mathrm{40}& \mathrm{0}& \mathrm{20}\\ \mathrm{36}& \mathrm{0}& \mathrm{44}& \mathrm{0}& \mathrm{20}& \mathrm{0}& \mathrm{40}& \mathrm{0}& \mathrm{24}& \mathrm{0}\\ \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{20}& \mathrm{0}& \mathrm{11}& \mathrm{0}& \mathrm{24}& \mathrm{0}& \mathrm{15}\\ \mathrm{24}& \mathrm{0}& \mathrm{25}& \mathrm{0}& \mathrm{11}& \mathrm{0}& \mathrm{20}& \mathrm{0}& \mathrm{15}& \mathrm{0}\end{array}\right]\text{(10)}& {\displaystyle }{\mathrm{RAM}}^{\mathrm{5}}=\left[\begin{array}{cccccccccc}\mathrm{44}& \mathrm{40}& \mathrm{36}& \mathrm{24}& \mathrm{20}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{51}& \mathrm{44}& \mathrm{44}& \mathrm{25}& \mathrm{25}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{51}& \mathrm{44}& \mathrm{44}& \mathrm{25}& \mathrm{25}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{44}& \mathrm{40}& \mathrm{36}& \mathrm{24}& \mathrm{20}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{25}& \mathrm{24}& \mathrm{20}& \mathrm{15}& \mathrm{11}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{25}& \mathrm{24}& \mathrm{20}& \mathrm{15}& \mathrm{11}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{44}& \mathrm{40}& \mathrm{36}& \mathrm{24}& \mathrm{20}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{44}& \mathrm{40}& \mathrm{36}& \mathrm{24}& \mathrm{20}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{25}& \mathrm{24}& \mathrm{20}& \mathrm{15}& \mathrm{11}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{25}& \mathrm{24}& \mathrm{20}& \mathrm{15}& \mathrm{11}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right]\end{array}$$

Figure 3 An example 10-link 1-DOF kinematic chain.

Figure 4 Non-isomorphic inversions derived from Fig. 3.

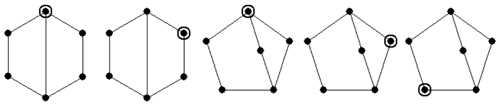
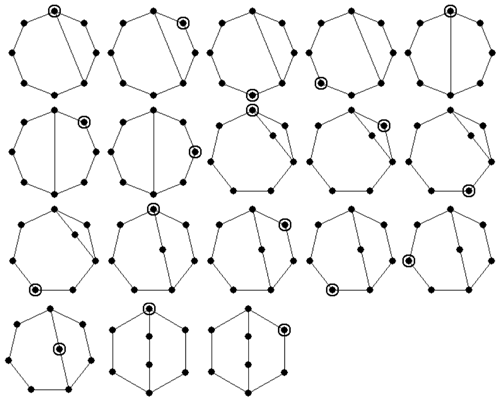
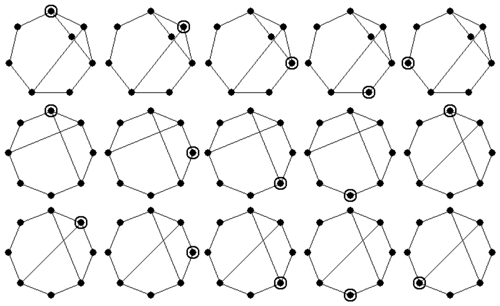
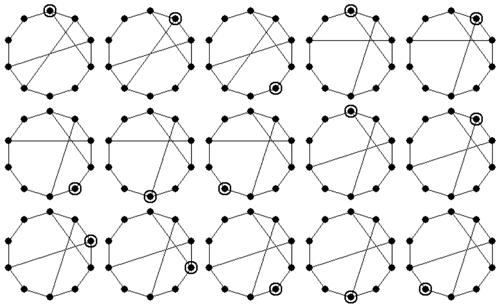
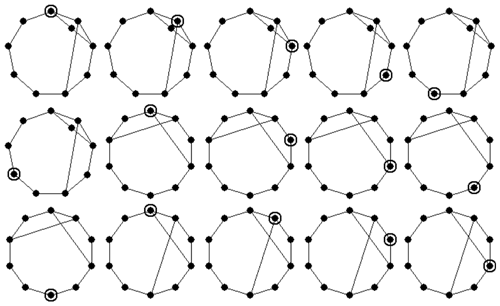
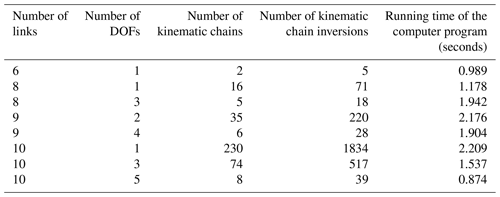
The atlas of plane non-fractionated kinematic chains can be derived using the existing method (Ding et al., 2016). Based on this atlas, plane kinematic chain inversions can be synthesized using the present method. For example, there are two 6-link 1-DOF kinematic chains, from which five non-isomorphic inversions can be synthesized, as shown in Fig. 5; there are five 8-link 3-DOF kinematic chains, from which 18 non-isomorphic inversions can be synthesized, as shown in Fig. 6. A part of the 8-link 1-DOF, 10-link 1-DOF and 10-link 3-DOF kinematic chain inversions are shown in Figs. 7–9, respectively. We have developed a computer program based on C$++$, and the synthesis process is fully automatic. All the numerical representations of kinematic chain inversions are generated automatically and stored in the database. For example, the complete database of 517 10-link 3-DOF kinematic chain inversions is shown in Appendix A. Taking the number string “1-100000011101000001000001100000100001000100100”, for instance, the first number “1” represents the ground link, and the remaining numbers are the upper triangular elements of the adjacency matrix of a 10-link 3-DOF kinematic chain. The detailed synthesis results of kinematic chain inversions are listed in Table 1. All the results are consistent with those reported in literature (Tuttle, 1996; Simoni et al., 2009; Yang et al., 2017). The running time of our computer program is also listed in Table 1, which is measured on a personal laptop Intel (R) Core (TM) i5-8265U CPU @ 1.60 GHz 8 GB RAM. It is clear that our method can be used to synthesize kinematic chain inversions efficiently.

Figure 5 The atlas of 6-link 1-DOF kinematic chain inversions.

Figure 6 The atlas of 8-link 3-DOF kinematic chain inversions.

Figure 7 A part of the 8-link 1-DOF kinematic chain inversions.

Figure 8 A part of the 10-link 1-DOF kinematic chain inversions.

Figure 9 A part of the 10-link 3-DOF kinematic chain inversions.

Table 1 Synthesis results of kinematic chain inversions.

5 Conclusions

The existing structural synthesis methods for plane kinematic chain inversions involve isomorphism detection, which is cumbersome. This paper proposes a simple and efficient synthesis method without detecting isomorphism. The fifth power of the adjacency matrix is applied to recognize similar vertices, and non-isomorphic kinematic chain inversions are directly derived according to non-similar vertices. We have developed a computer program based on C$++$, and the synthesis process is fully automatic. This method is used to synthesize 6-link 1-DOF, 8-link 1-DOF, 8-link 3-DOF, 9-link 2-DOF, 9-link 4-DOF, 10-link 1-DOF, 10-link 3-DOF and 10-link 5-DOF plane kinematic chain inversions. All the synthesis results are consistent with those reported in literature, demonstrating the reliability of our method. The present research is helpful for improving the efficiency of mechanism design.

Appendix A: Database of kinematic chain inversions

Table A1 The complete database of 517 10-link 3-DOF kinematic chain inversions.