Input Rationality Analysis of Three Degree of freedom Parallel Mechanism with Limbs of Embedding Structures

Three degrees of freedom (3-DoF) parallel mechanism (PM) with limbs of embedding structures is a kind of PM with a coupling relationship between limbs. In order to obtain a more desirable motion, the analysis of its actuated pairs shall be conducted. However, the fact that the existence of limbs coupling results in non-unique limb group, this mechanism has multiple limb groups. In this regard, the traditional input selection theory is not suitable for direct application in the input rationality analysis. Aiming to avoid this, a general extended input selection theory and limb group selection rule are proposed. The former tackles the traditional input selection theory which is not suitable for analyzing the input of PM with limbs of embedding structures since it does not take the influence of group into consideration, whereas the latter makes the calculation of the former easier. Based on the extended input selection theory and the limb group selection rule, the input and configuration of the 3-DoF PM with limbs of embedding structures are improved.

1 Introduction

A lower-mobility parallel mechanism (PM) is one PM with DoFs fewer than 6-DoF, which has advantages of simpler mechanical architecture, lower cost of design and manufacturing. For these reasons, lower-mobility PMs are suitable for many tasks requiring fewer than 6-DoF (Wei and Li, 2018; Yi and Kim, 2018; Li and Huang, 2003a). In lower-mobility PMs, 3-DoF PMs have been extensively studied (Wu et al., 2017; Sameer and Tsai, 2002). Therefore, many novel 3-DoF PMs have been proposed, and these PMs fall into four categories: This first category is the 3-DoF translational PM including the delta PM and Tasi's PM (Liu et al., 2018); The second category is the 3-DoF rotational PM, such as spherical PM (Essomba et al., 2016; Houssem et al., 2017), 3-RPS parallel pyramid mechanism (Mu and Huang, 2007); The third is the 3-DoF PM has two rotational DoFs and one translational DoF (2R1T), for example, 3-CRC PM (Hussein and Ernesto, 2016), 2-RPU&SPR PM (Li et al., 2016) and 3-UPU PM (Wang et al., 2016). The forth category has two translational DoFs and one rotational DoF (2T1R).

This paper focuses on the forth category PM, i.e., PM with 2T1R. This category PM with rotational-translational output characteristic has high practical value in industrial production. In 1996, Gosselin proposed a 3-RRR PM with 2T1R, but its outputs are planar motions which limit its application (Gosselin et al., 1996). Thus, the spatial PM with 2T1R attracts considerable attention and it has become the current trend in research community. Zhang and his colleagues established the motion synthesis ideas based on the screw theory and synthesis for the type spatial PM and proposed many novel architectures (Zhang and Ting, 2013; Wu et al., 2009). Since many type synthesis methods based on certain complicated theory, such as GF set, displacement group theory of Lie Group Algebra, geometrical analysis, they are difficult to widely apply. Liu et al. introduced a concise and visual type synthesis method and proposed a PRU&PRC PM with high rotational capability, and this PM was used in 3T2R-DoF hybrid mechanism (Xie et al., 2014). All of the above work promote the development of mechanism and support the engineering applications, and these architectures have greatly enriched the diversity of lower-mobility PM.

However, the above PMs suffer from the shortcoming of smaller workspace, and their workspace are mostly hemispherical or semi-cylindrical. There is lack of the architectures with larger workspace, such as the architecture with full cylindrical workspace. Workspace is one of the most important criteria in designing a PM. A good design is one in which a PM of small mechanical size possesses a large workspace volume (DibakarSen and Singh, 2008; Fu and Gao, 2016). In order to satisfy this requirement, one 3-DoF PM with limbs of embedding structures is proposed (Zhang, 2008).

This PM has a coupled limb structure, which means a common axis for different limbs is presented. Compared with other PMs, where the common axis is located on the fixed platform (Brogardh and Kock, 2003; Brogardh, 2000; Isaksson et al., 2012; Lou and Li, 2013; Bin et al., 2018; Huang et al., 2010; Ni et al., 2015), this PM shares advantages such as compacted structures and no limb interference. Meanwhile, this PM enables complete cylindrical workspace and is more suitable for transportation in space. Therefore, this PM is highly promising for industrial applications.

Due to the key role of selection of actuated pairs in obtaining desired motions by this PM, actuated pairs of this PM were investigated. The input selection theory proposed by Huang Zhen is a powerful tool for this issue (Zhao and Huang, 2000; Zhao et al., 2017; Li et al., 2010; Huang et al., 2007; Li and Huang, 2003b). Based on the screw theory, the input selection theory evaluates rationality of the actuated pairs by limb groups (twist systems of different limbs). However, physical crossing or embedding of limbs of the 3-DoF PM with limbs of embedding structures leads to the presence of multiple limb groups, while only one of them is rational. If an irrational limb group was selected, the analysis may be incorrect, resulting in wrong conclusion on the rationality of inputs (details are shown in Sect. 3 of this article). The input selection theory, however, cannot identify the rational limb group. Hence, traditional input selection theory is not suitable for analysis of 3-DoF PM with limbs of embedding structures as it doesn't consider the effects of multiple limb groups. Instead, it shall be extended.

This paper proposes extended input selection theory which is used to determine reasonable inputs and limb group, in the meantime, limb group selection rule is summarized. In order to verify their generality, the inputs of one 2-DoF PM with limbs of embedding structures (Qu et al., 2009) is analyzed in Sect. 4. The structure of this paper is organized as follows: Sect. 2 presents a detailed description about the two PMs, and analyses mobility. Section 3 proposes extended input selection theory. Section 4 determines the reasonable inputs and limb group of 3-DoF and 2-DoF PM with limbs of embedding structures. Section 5 concludes the paper.

2 Architecture and mobility analysis of 3-DoF and 2-DoF PM with limbs of embedding structures

2.1 Architecture description

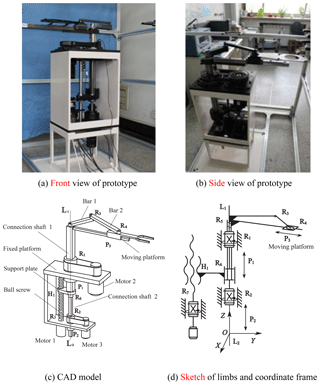
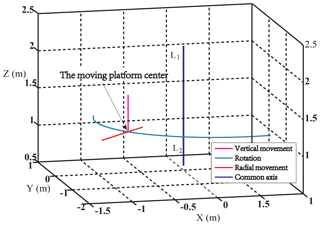
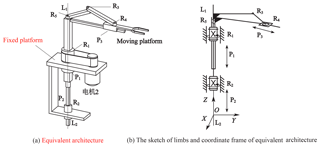
The CAD model and prototypes of 3-DoF PM with limbs of embedding structures are seen in Fig. 1a–c. The moving platform is connected with guideway and bar 2 by kinematic pair R₄ and P₃, respectively; the bar 2 is connected with bar 1 by R₃, and the guideway is fixed with connection shaft 1; the connecting shaft 2, being fixed to the bar 1, is connected to the connecting shaft 1 and the fixed platform through R₅ and P₂. Support plate is connected with ball screw and fixed platform by screw pair H₁ and revolute pair R₆, respectively. All the kinematic pairs mentioned above have the same axes except the prismatic pair P₃, which is indicated by L₁L₂. This PM has three motors, where the motor 1 drives moving platform to move along L₁L₂ axis by ball screw and connection shaft 1; the motor 2 drives the moving platform to rotate round L₁L₂ axis by belt and the connecting shaft 1; the motor drives moving platform to move along guideway, namely, radial movement centered on L₁L₂ axis. The workspace of this PM is complete cylindrical surface, and the motion trajectory is seen in Fig. 2.

Figure 1 The 3-DoF PM with limbs of embedding structures.

This coordinate of this PM is seen in Fig. 1d, where the origin is coincided with the middle point of revolute pair R₂; the Z axis is the axis of prismatic P₁, P₂, and is coincided with L₁L₂; the kinematic pair H₁, R₇ are both on the YZ plane, and is parallel to the Z axis.

Figure 2 The motion trajectory of moving platform.

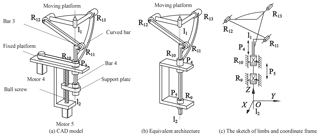
The CAD mode and equivalent architecture of 2-DoF decoupled PM with limbs of embedding structures are seen in Fig. 3a–c. The moving platform is connected by bar 3 and curved bar by revolute pair R₁₂ and R₁₃, respectively. Bar 3 and curved bar are connected with bar 4 and fixed platform by revolute pair R₁₁ and R₁₀, respectively. One end of bar 4 is connected with curved bar by prismatic P₄, and the other end is connected with support plate by revolute pair R₉. The ball screw is connected with support plate and fixed platform by screw pair H₂ and revolute pair R₈. The kinematic pairs H₂, R₈, R₉, R₁₀ and P₄ have the same axis l₁l₂. This PM has two motors, where the motor 4 drives the moving platform to rotate around axis l₁l₂; the motor 5 drives he moving platform to rotate with radial axis of l₁l₂.

In this PM, the component (ball screw and support plate) between R₈ and R₉ can be deemed to prismatic inputs. According to this characteristic, equivalent mechanism is obtained as Fig. 3b. The coordinate of equivalent mechanism is seen as Fig. 3c, where the P₄ and R₁₀ are inputs; the origin is coincided with the middle point of revolute pair R₁₀; Z axis is coincided with l₁l₂. Limbs and moving platform form closed chain structure.

Figure 3 The 3-DoF PM with limbs of embedding structures.

2.2 3-DoF and 2-DoF PM with limbs of embedding structures architecture analysis

Both of the previous PMs have coupled limbs, which embed each other, and the kinematics pairs included in the intersection of limbs have common axis L₁L₂ and l₁l₂. Limbs, moving platform and fixed platform in one PMs forms closed-loop structure by common axis. This coupled structure makes PM more compact, in the meanwhile avoids limbs interference and obtains larger workspace. However, this configuration also leads to uncertainties of the components or kinematic pairs included in limbs, such as in 3-DoF PM with limbs of embedding structures, the limbs from revolute pair R₇ to moving platform is either R₇H₁R₆P₁P₃ limb or R₇H₁R₆P₁R₅R₃R₄ limb. This problem will be discussed in Sect. 3.

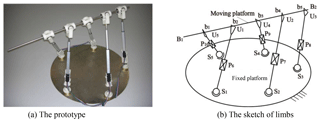
Besides PM with limbs of embedding structures, the extant PM (Borràs et al., 2014, 2011, 2009; Borràs and Thomas, 2008) also has common axis (common actuated axis), such as 5-DoF pentaponds (seen in Fig. 4).

This PM has five identical limbs, each of which has one spherical pair (S_i, i=1, …, 5), one prismatic pair (P_i, i=6, …, 10) and universal pair (U_i, i=1, …, 5). The moving platform can be deemed to one line, and this line is indicated as B₁B₂. B₁B₂ is coincided with one axis of U_i, and intersection at point b_i (i=1, …, 5) of the other axis. Therefore, B₁B₂ is the common axis (common actuated axis). Despite both 5-DoF pentaponds PM and PM with limbs of embedding structure have common axis, two mechanisms are disparate. The main distinction is as follows:

1. The limbs in 5-DoF pentaponds PM are independent of each other, and the limbs in PM with limbs of embedding structure exist coupling. Compared to the latter, 5-DoF pentaponds PM is more likely to have limb interference.

2. The axis B₁B₂ is located on the moving platform. However, with regards to 3-DoF PM with limbs of embedding structures, the moving platform is separated from the common axis (common actuated axis), thus increasing the structure's working space.

Figure 4 5-DoF pentapods PM.

3 Extended input selection theory

The input selection theory proposed by Huang Zhen is a powerful tool for analysis of rationality of inputs of PM. According to this theory, the rational actuated pairs of PM must lead to no remnant freedom singularity of this PM. In case of remnant freedom singularity, PM inputs are irrational and a new set of actuated pairs shall be selected. Actually, the remnant freedom singularity of PM is affected by the selection of the twist system of limbs and the actuated pairs. For PMs with determined twist system of limbs (PMs with one limb group only), irrational input selection is the only possible cause of remnant freedom singularity of PM. Hence, the input selection theory can be directly applied.

Nevertheless, for PM with limbs of embedding structures, the twist system of limbs is not determined and multiple limb groups are present. In this case, besides irrational input selection, irrational limb group can also lead to remnant freedom singularity of PM, if not errors in DoF calculations. Therefore, the input selection theory shall not be applied for judgment of 3-DoF PM with limbs of embedding structures without extension. The procedure of extended input selection theory can be stated as follows: (1) Select a limb group; (2) Calculate DoF based on twist systems of limb contained by this limb group; (3) If DoF calculation is correction, proceed to Step 4. Otherwise, return to Step 1; (4) Upon determination of correct calculation of PM, the remnant freedom of PM is analyzed: (a) Lock the actuated pairs, namely delete the actuated screws corresponding to the actuated pairs from twist systems of different limbs; (b) Calculate the limb reciprocal screw systems with inputs being locked of different limbs; (c) The mechanism constraint screw system after locking the inputs is gained from the limb reciprocal screw systems after locking inputs. To prevent input interference or invalid input in the same limb, the number of increased reciprocal in one limb after locking inputs must be equal to the number of locking inputs of this limb. (d) Calculate the rank (r) of the constraint screw system with inputs being locked of the mechanism. If r=6, no remnant freedom is presented; if r<6, remnant freedom and irrational input selection are present, a new limb group shall be selected and all steps above shall be repeated.

According to the extended input selection theory, for any actuated pair, if the DoF obtained by twists of different limbs of the limb group is correct, r=6, and the quantity of additional reciprocal systems on limbs with inputs being locked equals to that of actuated pairs, it can be concluded that the actuated pairs are rational. If any of these requirements is not met, it can be concluded that the input selection is irrational and a new set of actuated pairs shall be selected. Additionally, kinematic pairs near the fixed platform shall be preferred as the actuated pairs.

The extended input selection theory is suitable for 3-DoF PM with limbs of embedding structures and 2-DoF PM in the same category. Additionally, upon determination of rationality of the input kinematic pair, the rational limb group of PM with limb of embedding structures is determined, thus providing references for further studies of PM, including kinematic singularity analysis, instantaneous motion, and calculations of first-order influence coefficient.

4 Input rationality analysis of 3-DoF and 2-DoF PMs with limbs of embedding structures

4.1 Input rationality analysis of 3-DoF PM with limbs of embedding structures

4.1.1 The rationality analysis of the initial actuated pairs

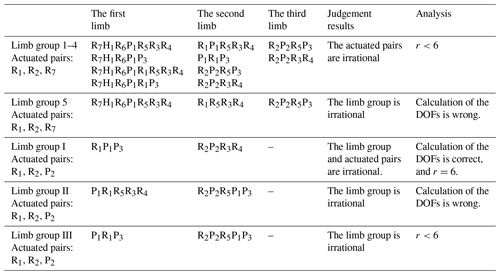
This coordinate of 3-DoF PM with limbs of embedding structures is seen in Fig. 1d, this PM has five limb groups (The actuated pairs are R₁, R₇ and R₂):

1. limb groups. 1: R₇H₁R₆P₁R₁R₅R₃R₄ limb, P₁R₁R₅R₃R₄ limb, R₂P₂R₅P₃ limb;

2. limb groups. 2: R₇H₁R₆P₁P₃ limb, P₁R₁P₃ limb, R₂P₂R₃R₄ limb;

3. limb groups. 3: R₇H₁R₆P₁R₁R₅R₃R₄ limb, R₂P₂R₅P₃ limb;

4. limb groups. 4: R₇H₁R₆P₁R₁P₃ limb, R₂P₂R₃R₄ limb;

5. limb groups. 5: R₇H₁R₆P₁R₅R₃R₄ limb, R₁R₅R₃R₄ limb, R₂P₂R₅P₃ limb.

In limb group 1, the first limb is R₇H₁R₆P₁R₅R₃R₄ limb, the second limb is P₁R₁R₅R₃R₄ limb, the third limb is R₂P₂R₅P₃ limb. The limb twist systems of the three limbs are as follows (the actuated screws are ${\mathit{\$}}_{\mathrm{11}}^{\mathrm{1}}$, ${\mathit{\$}}_{\mathrm{21}}^{\mathrm{1}}$ and ${\mathit{\$}}_{\mathrm{31}}^{\mathrm{1}}$):

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{11}};{\mathit{r}}_{\mathrm{11}}\times {\mathit{S}}_{\mathrm{12}})=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{7}}}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{12}};{\mathit{r}}_{\mathrm{12}}\times {\mathit{S}}_{\mathrm{12}}+h_{\mathrm{12}}{\mathit{S}}_{\mathrm{12}})=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{7}}}\mathrm{0}{h}_{\mathrm{12}})\\ & {\mathit{\$}}_{\mathrm{13}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{13}};\mathrm{0}\mathrm{0}\mathrm{0})=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{14}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};{\mathit{S}}_{\mathrm{14}})=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{15}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{1}};\mathrm{0}\mathrm{0}\mathrm{0})=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{16}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{1}};{\mathit{r}}_{\mathrm{16}}\times {\mathit{S}}_{\mathrm{16}})=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{3}}}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{17}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{1}};{\mathit{r}}_{\mathrm{17}}\times {\mathit{S}}_{\mathrm{17}})=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{4}}}-x_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\end{array}\text{(2)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};{\mathit{S}}_{\mathrm{21}})=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{22}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{22}};\mathrm{0}\mathrm{0}\mathrm{0})=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{23}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{23}};\mathrm{0}\mathrm{0}\mathrm{0})=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{24}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{24}};{\mathit{r}}_{\mathrm{24}}\times {\mathit{S}}_{\mathrm{24}})=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{3}}}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{25}}^{\mathrm{1}}=({\mathit{S}}_{\mathrm{25}};{\mathit{r}}_{\mathrm{25}}\times {\mathit{S}}_{\mathrm{25}})=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{4}}}-x_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\end{array}\end{array}$$

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{31}}^{\mathrm{3}}=({\mathit{S}}_{\mathrm{31}};\mathrm{0})=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{32}}^{\mathrm{3}}=(\mathrm{0};{\mathit{S}}_{\mathrm{32}})=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{33}}^{\mathrm{3}}=({\mathit{S}}_{\mathrm{33}};\mathrm{0}\mathrm{0}\mathrm{0})=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{34}}^{\mathrm{3}}=(\mathrm{0};{\mathit{S}}_{\mathrm{34}})=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{P}}_{\mathrm{3}}}-x_{{\mathrm{P}}_{\mathrm{3}}}\mathrm{0})\end{array}\end{array}$$

Where, is the twist associated with the jth kinematic pair in the ith limb of limb group M; ${\mathit{\$}}_{\mathrm{11}}^{\mathrm{1}}$ and ${\mathit{\$}}_{\mathrm{12}}^{\mathrm{1}}$ are in YZ plane, the axes of the two twists are parallel to Z axis; the vector $r_{\mathrm{16}}=r_{\mathrm{24}}=(x_{{\mathrm{R}}_{\mathrm{3}}}$, $y_{{\mathrm{R}}_{\mathrm{3}}}$, $z_{{\mathrm{R}}_{\mathrm{3}}})$ and $r_{\mathrm{17}}=r_{\mathrm{25}}=(x_{{\mathrm{R}}_{\mathrm{4}}},y_{{\mathrm{R}}_{\mathrm{4}}},z_{{\mathrm{R}}_{\mathrm{4}}})$, and $(x_{{\mathrm{R}}_{\mathrm{4}}},y_{{\mathrm{R}}_{\mathrm{4}}},z_{{\mathrm{R}}_{\mathrm{4}}})$ is the coordinate of the center of moving platform. The reciprocal screw systems of each limb in limb group 1 are as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{r\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{r\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\text{(5)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{r\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{22}}^{r\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\text{(6)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{31}}^{r\mathrm{1}}=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{32}}^{r\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{33}}^{r\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\end{array}$$

Where, a and b are determined by: $a{x}_{{\mathrm{R}}_{\mathrm{4}}}+b{y}_{{\mathrm{R}}_{\mathrm{4}}}=\mathrm{0}$. By Eqs. (4)–(6), the mechanism constraint screw system can be obtained as follows:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^r=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^r=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{13}}^r=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\end{array}\end{array}$$

By Eq. (7), the mechanism twist system $₁:

$$\begin{array}{}\text{(8)}& \begin{array}{lr}{\mathit{\$}}_{\mathrm{11}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})& \left(\mathrm{a}\right)\\ {\mathit{\$}}_{\mathrm{12}}=(\mathrm{0}\mathrm{0}\mathrm{0};x_{{\mathrm{R}}_{\mathrm{4}}}{y}_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})& \left(\mathrm{b}\right)\\ {\mathit{\$}}_{\mathrm{13}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})& \left(\mathrm{c}\right)\end{array}\end{array}$$

Equation (8) demonstrates this PM has three DoF as follows: (a) Moving platform rotates around Z axis, and indicated by $₁₁; (b) Moving platform translation along guideway, namely, radial translation centered on Z axis, and indicated by $₁₂; (c) Moving platform rotation along Z axis, and indicated by $₁₃.

It can be seemed from (a)–(c), this PM do not have parasitic motion, and the DoF is correct. The remnant-freedom analyzes as follows:

Delete the actuated screws in Eqs. (1)–(3), the limb twist systems of each limb after locking the inputs are as follows:

$$\begin{array}{}\text{(9)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{12}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{7}}}\mathrm{0}h)\\ & {\mathit{\$}}_{\mathrm{13}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{14}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{15}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{16}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{3}}}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{17}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{4}}}-x_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\end{array}\text{(10)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{23}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{24}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{3}}}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{25}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{4}}}-x_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\end{array}\text{(11)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{31}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{32}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{33}}^{\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{P}}_{\mathrm{3}}}-x_{{\mathrm{P}}_{\mathrm{3}}}\mathrm{0})\end{array}\end{array}$$

According to Eqs. (9)–(11), the three limb reciprocal screw systems after locking the inputs are as follows:

$$\begin{array}{}\text{(12)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{r{\mathrm{1}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{r{\mathrm{1}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\text{(13)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{r{\mathrm{1}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{22}}^{r{\mathrm{1}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\text{(14)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{31}}^{r{\mathrm{1}}^{\prime }}=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{32}}^{r{\mathrm{1}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{33}}^{r{\mathrm{1}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\end{array}$$

Based on Eqs. (12)–(14), the reciprocal screws in the three limbs after locking the inputs have not increased, so the inputs in limb group 1 are irrational. The mechanism constraint screw system after locking the inputs, namely, ${\mathit{\$}}_{\mathrm{1}}^{r^{\prime }}$ is:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{r^{\prime }}=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{13}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\end{array}$$

Equation (15) validates that, the rank of ${\mathit{\$}}_{\mathrm{1}}^{r^{\prime }}$ is less than six, so the PM has remnant-freedom at this time. Based on the same method, the limb groups 2–5 does not meet input rationality judgment condition, and the actuated pairs R₁, R₇ and R₂ are irrational.

It is worth noting that, in the analysis of limb group 2–4, this PM has remnant-freedom, but this PM appears miscalculation DoF when the limb 5 is selected. The process of analysis is as follows:

In limb group 5, the first limb is R₇H₁R₆P₁R₅R₃R₄ limb, the second limb is R₂P₂R₅P₃ limb, the third limb is R₁R₅R₃R₄ limb. The first and second limb twist systems are the same as Eqs. (1) and (3), the third limb twist system is as follows:

$$\begin{array}{}\text{(16)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{31}}^{\mathrm{5}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{32}}^{\mathrm{5}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{33}}^{\mathrm{5}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{3}}}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{34}}^{\mathrm{5}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{4}}}-x_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\end{array}\end{array}$$

The mechanism constraint screw system, namely, ${\mathit{\$}}_{\mathrm{5}}^r$:

$$\begin{array}{}\text{(17)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{51}}^r=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{52}}^r=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{53}}^r=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{54}}^r=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\end{array}\end{array}$$

The DoF obtained from limb group 5 is:

$$\begin{array}{}\text{(18)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{51}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{52}}=(\mathrm{0}\mathrm{0}\mathrm{0};x_{{\mathrm{R}}_{\mathrm{4}}}{y}_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\end{array}\end{array}$$

Obviously, the number of DoF is wrong. Contrast to limb group 1, the case of this problem is that lack of prismatic pair P₁ in R₁R₅R₃R₄ limb changes the mechanism constraint screw system. Prismatic pair P₁ indicates translation along Z axis, which is synchronous motion of each component, so the twist indicates this motion must be included in each limb twist system, or one twist has same axis. Therefore, one conclusion is obtained: in order to ensure correct DoF, the twist indicates this motion must be included in each limb twist system (conclusion 1 for short). Conclusion 1 is a necessary condition to ensure correct DoF, and this conclusion can delete irrational limb group to simplify the analysis process.

4.1.2 Reasonable justification after reselected actuated pairs

When the actuated pairs are R₇, R₁ and R₂, all the limb groups do not satisfy the judging conditions, so the actuated pairs need to be reselected. According to the principle that the kinematic pairs near the fixed platform are selected as the actuated pairs, the mechanism has two sets of kinematic pairs for actuated pairs, the first group is R₁, P₁, R₂, and the second group is R₁, P₂, R₂. In order to facilitate the transformation, the second sets of kinematic pairs are selected, and the motor 1 is changed to a linear motor at this time. After reselected inputs, the PM is seen in Fig. 5a, the sketch of limbs and actuated pairs coordinate frame of equivalent architecture are seen in Fig. 5b.

Figure 5 The 3-DoF PM with limbs of embedding structures after reselecting actuated pairs.

When actuated pairs are R₁, R₇ and R₂, the limb groups are as follows: (a) Limb group I: P₁R₁P₃ limb, P₂R₂R₃R₄ limb; (b) Limb group II: P₂R₅P₁R₁P₃ limb, R₂R₃R₄ limb; (c) Limb group III: P₁R₁R₅R₃R₄ limb, R₂P₂ R₅P₁P₃ limb.

The conclusion 1 mentioned above shows that the limb group II will lead to the error of the calculation of the DoF. For the irrational limb group, the rationality of the inputs is analyzed only through the remaining limb groups. The analysis process is as follows:

In limb group I, the first limb is P₁R₁P₃ limb and the second limb is P₂R₂R₃R₄ limb, the twist system of the first limb is:

$$\begin{array}{}\text{(19)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{\mathrm{I}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{\mathrm{I}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{13}}^{\mathrm{I}}=(\mathrm{0}\mathrm{0}\mathrm{0};x_{{\mathrm{P}}_{\mathrm{3}}}{y}_{{\mathrm{P}}_{\mathrm{3}}}{z}_{{\mathrm{P}}_{\mathrm{3}}})\end{array}\end{array}$$

The twist system of the second limb in limb group I:

$$\begin{array}{}\text{(20)}& \begin{array}{l}{\mathit{\$}}_{\mathrm{11}}^{\mathrm{I}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ {\mathit{\$}}_{\mathrm{12}}^{\mathrm{I}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{1})\\ {\mathit{\$}}_{\mathrm{13}}^{\mathrm{I}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{3}}}\mathrm{0})\\ {\mathit{\$}}_{\mathrm{14}}^{\mathrm{I}}=(\mathrm{0}\mathrm{0}\mathrm{1};y_{{\mathrm{R}}_{\mathrm{4}}}-x_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\end{array}\end{array}$$

Based on Eqs. (19)–(20), the reciprocal screw systems of each limb are as follows:

$$\begin{array}{}\text{(21)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{\mathrm{I}r}=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{\mathrm{I}r}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{13}}^{\mathrm{I}r}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\text{(22)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{\mathrm{I}r}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{22}}^{\mathrm{I}r}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\end{array}$$

Based on Eqs. (21)–(22), the mechanism twist system $_I is:

$$\begin{array}{}\text{(23)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{I}\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{I}\mathrm{2}}=(\mathrm{0}\mathrm{0}\mathrm{0};x_{{\mathrm{R}}_{\mathrm{4}}}{y}_{{\mathrm{R}}_{\mathrm{4}}}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{I}\mathrm{3}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\end{array}\end{array}$$

According to Eq. (23), the DoF is correct. The two limb reciprocal screw systems after locking the inputs are as follows:

$$\begin{array}{}\text{(24)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{r{\mathrm{I}}^{\prime }}=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{r{\mathrm{I}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{13}}^{r{\mathrm{I}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{14}}^{r{\mathrm{I}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\end{array}\text{(25)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{r{\mathrm{I}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{22}}^{r{\mathrm{I}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{23}}^{r{\mathrm{I}}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{24}}^{r{\mathrm{I}}^{\prime }}=(a_{\mathrm{1}}{b}_{\mathrm{1}}\mathrm{0};\mathrm{0}\mathrm{0}{c}_{\mathrm{1}})\end{array}\end{array}$$

In which, a₁, b₁ and b₁ are determined by the equation group $\left\{\begin{array}{c}{a}_{\mathrm{1}}{y}_{{\mathrm{R}}_{\mathrm{4}}}-b_{\mathrm{1}}{x}_{{\mathrm{R}}_{\mathrm{4}}}+c_{\mathrm{1}}=\mathrm{0}\\ a_{\mathrm{1}}(y_{{\mathrm{R}}_{\mathrm{4}}}-y_{{\mathrm{R}}_{\mathrm{3}}})+b_{\mathrm{1}}(x_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{4}}})=\mathrm{0}\end{array}\right.$. The quantity of additional reciprocal screw is equal to the number of actuated pairs, indicating that the inputs of each limb are reasonable. The mechanism constraint screw system after locking inputs, namely, ${\mathit{\$}}_{\mathrm{I}}^{r^{\prime }}$ is as follows:

$$\begin{array}{}\text{(26)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{I}\mathrm{1}}^{r^{\prime }}=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{I}\mathrm{2}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{I}\mathrm{3}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{I}\mathrm{4}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{I}\mathrm{5}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{I}\mathrm{6}}^{r^{\prime }}=(a_{\mathrm{1}}{b}_{\mathrm{1}}\mathrm{0};\mathrm{0}\mathrm{0}{c}_{\mathrm{1}})\end{array}\end{array}$$

The rank of Eq. (26) is six, namely, this PM loses all DoFs at this time. However, Eq. (25) only demonstrates one configuration, it is needed to analyze whether there is remnant-freedom in other configurations.

$$\begin{array}{}\text{(27)}& {\displaystyle }{c}_{\mathrm{1}}=\mathrm{0}\text{(28)}& {\displaystyle \frac{a_{\mathrm{1}}}{a}}={\displaystyle \frac{b_{\mathrm{1}}}{b}}\text{(29)}& {\displaystyle }\left\{\begin{array}{c}a{x}_{{\mathrm{R}}_{\mathrm{4}}}+b{y}_{{\mathrm{R}}_{\mathrm{4}}}=\mathrm{0}\\ a_{\mathrm{1}}(y_{{\mathrm{R}}_{\mathrm{4}}}-y_{{\mathrm{R}}_{\mathrm{3}}})+b_{\mathrm{1}}(x_{{\mathrm{R}}_{\mathrm{3}}}-x_{{\mathrm{R}}_{\mathrm{4}}})=\mathrm{0}\end{array}\right.\end{array}$$

Let r₁, r₂ and r₃ indicates vectors of guideway, bar 2 and bar 1, respectively. It can be obtained from Eqs. (27)–(29):

$$\begin{array}{}\text{(30)}& {\displaystyle }{r}_{\mathrm{1}}=(x_{{\mathrm{R}}_{\mathrm{4}}},y_{{\mathrm{R}}_{\mathrm{4}}},\mathrm{0})\text{(31)}& {\displaystyle }{r}_{\mathrm{2}}=(x_{{\mathrm{R}}_{\mathrm{4}}}-x_{{\mathrm{R}}_{\mathrm{3}}},y_{{\mathrm{R}}_{\mathrm{4}}}-y_{{\mathrm{R}}_{\mathrm{3}}},\mathrm{0})\text{(32)}& {\displaystyle }{r}_{\mathrm{3}}=(x_{{\mathrm{R}}_{\mathrm{3}}},y_{{\mathrm{R}}_{\mathrm{3}}},\mathrm{0})\text{(33)}& {\displaystyle }{\left|r_{\mathrm{3}}\right|}^{\mathrm{2}}={\left|r_{\mathrm{2}}\right|}^{\mathrm{2}}+{\left|r_{\mathrm{1}}\right|}^{\mathrm{2}}\end{array}$$

In order to avoid singularity, just meet the condition: |r₃|<|r₂|. In fact, this PM meets this condition, so dead point dose not present, namely, this PM dose not present remnant-freedom in any configuration, so the inputs are reasonable. Using the same method, the ${\mathit{\$}}_{\mathrm{III}}^{r^{\prime }}$ is as follows:

$$\begin{array}{}\text{(34)}& \begin{array}{r}{\mathit{\$}}_{\mathrm{III}\mathrm{1}}^{r^{\prime }}=(ab\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ {\mathit{\$}}_{\mathrm{III}\mathrm{2}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ {\mathit{\$}}_{\mathrm{III}\mathrm{3}}^{r^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\end{array}\end{array}$$

The rank of Eq. (34) is less than six, so the PM has remnant-freedom at this time. Contrast to limb group I and II, the case of this problem is excess kinematic pairs in limb group III, which leads to insufficient constraint of moving platform. Therefore, the other conclusion is obtained: in the process of input analysis, the limb group with fewer kinematic pairs should be preferred. Conclusion 1 and 2 can be called limb group selection rule.

According to analyze different inputs and limb groups (comparative analysis seen in Table 1), the reasonable inputs and limb group of 3-DoF PM with limbs of embedding structures are determined, and limb group selection rule is summarized. This research lays on a foundation for input rationality analysis for similar PM.

Table 1 Comparison of different inputs.

4.2 Reasonable justification of inputs of 2-DoF PM with limbs of embedding structures

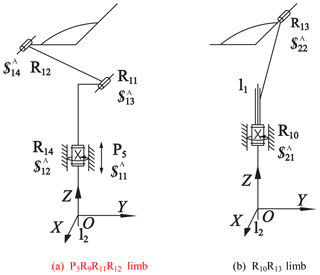
The coordinate system of 2-DoF PM with limbs of embedding structures is shown in Fig. 6, in which P₅, R₁₀ are the actuated pairs. There are two limb groups:

• Limb group A: P₅R₉R₁₁R₁₂ limb (Fig. 6a), R₁₀R₁₃ limb (Fig. 6b).

• Limb group B: P₅R₉P₄R₁₀R₁₃ limb, R₁₀P₄R₁₁R₁₂ limb.

Figure 6 The coordinate system of 2-DoF PM with limbs of embedding structures.

According to limb group selection rule, limb group A is selected to analyze input rationality. Let the first limb is P₅R₁₄R₁₁R₁₂ limb, the second limb is R₁₀R₁₃ limb. The limb twists systems are as follows:

$$\begin{array}{}\text{(35)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{12}}^{\mathrm{A}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{13}}^{\mathrm{A}}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};-z_{{\mathrm{R}}_{\mathrm{11}}}{y}_{{\mathit{S}}_{\mathrm{3}}}{z}_{{\mathrm{R}}_{\mathrm{11}}}{x}_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{11}}}{y}_{{\mathit{S}}_{\mathrm{3}}}-y_{{\mathrm{R}}_{\mathrm{11}}}{x}_{{\mathit{S}}_{\mathrm{3}}})\\ & {\mathit{\$}}_{\mathrm{14}}^{\mathrm{A}}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};-z_{{\mathrm{R}}_{\mathrm{12}}}{y}_{{\mathit{S}}_{\mathrm{3}}}{z}_{{\mathrm{R}}_{\mathrm{12}}}{x}_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{12}}}{y}_{{\mathit{S}}_{\mathrm{3}}}-y_{{\mathrm{R}}_{\mathrm{12}}}{x}_{{\mathit{S}}_{\mathrm{3}}})\end{array}\text{(36)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{\mathrm{A}}=({\mathit{S}}_{\mathrm{2}};\mathrm{0}\mathrm{0}\mathrm{0})=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{22}}^{\mathrm{A}}=({\mathit{S}}_{\mathrm{3}};{\mathit{r}}_{{\mathrm{R}}_{\mathrm{13}}}\times {\mathit{S}}_{\mathrm{3}})\\ & =(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};-z_{{\mathrm{R}}_{\mathrm{13}}}{y}_{{\mathit{S}}_{\mathrm{3}}}{z}_{{\mathrm{R}}_{\mathrm{13}}}{x}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0})\end{array}\end{array}$$

The reciprocal screw systems of each limb are as follows:

$$\begin{array}{}\text{(37)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}r}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{\mathrm{A}r}=(\mathrm{0}\mathrm{0}\mathrm{0};y_{{\mathit{S}}_{\mathrm{3}}}-x_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0})\end{array}\text{(38)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{21}}^{\mathrm{A}r}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{21}}^{\mathrm{A}r}=\left({\displaystyle \frac{x_{{\mathit{S}}_{\mathrm{3}}}}{z_{{\mathrm{R}}_{\mathrm{13}}}{y}_{{\mathit{S}}_{\mathrm{3}}}}}\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0}\right)\\ & {\mathit{\$}}_{\mathrm{21}}^{\mathrm{A}r}=\left({\displaystyle \frac{\mathrm{1}}{z_{{\mathrm{R}}_{\mathrm{13}}}}}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0}\right)\\ & {\mathit{\$}}_{\mathrm{21}}^{\mathrm{A}r}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\end{array}\end{array}$$

By Eqs. (37)–(38), the twist system of the mechanism is as follows:

$$\begin{array}{}\text{(39)}& \begin{array}{lr}{\mathit{\$}}_{\mathrm{A}\mathrm{1}}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})& \left(\mathrm{a}\right)\\ {\mathit{\$}}_{\mathrm{A}\mathrm{2}}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};-z_{{\mathrm{R}}_{\mathrm{13}}}{y}_{{\mathit{S}}_{\mathrm{3}}}{z}_{{\mathrm{R}}_{\mathrm{13}}}{x}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0})& \left(\mathrm{b}\right)\end{array}\end{array}$$

Where, (a) demonstrates a revolution DoF around Z axis; (b) demonstrates a revolution DoF around arbitrary axis in XY plane. According to Eq. (39), the workspace of this PM is sphere. The limb reciprocal screw systems after locking the inputs are as follows:

$$\begin{array}{}\text{(40)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}{r}^{\prime }}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{12}}^{\mathrm{A}{r}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};y_{{\mathit{S}}_{\mathrm{3}}}-x_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{13}}^{\mathrm{A}{r}^{\prime }}=\left(\right(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{11}}}-x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{12}}}-y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{11}}}+y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{12}}})/\\ & \left[y_{{\mathit{S}}_{\mathrm{3}}}\right(z_{{\mathrm{R}}_{\mathrm{12}}}-z_{{\mathrm{R}}_{\mathrm{11}}}\left)\right]\mathrm{0}-\mathrm{1};\\ & (x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{11}}}{z}_{{\mathrm{R}}_{\mathrm{12}}}-x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{12}}}{z}_{{\mathrm{R}}_{\mathrm{11}}}-y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{11}}}{z}_{{\mathrm{R}}_{\mathrm{12}}}\\ & +y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{12}}}{z}_{{\mathrm{R}}_{\mathrm{11}}})/[y_{{\mathit{S}}_{\mathrm{3}}}(z_{{\mathrm{R}}_{\mathrm{12}}}-z_{{\mathrm{R}}_{\mathrm{11}}})\left]\mathrm{0}\mathrm{0}\right)\end{array}\text{(41)}& {\displaystyle }\begin{array}{rl}& {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}{r}^{\prime }}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}{r}^{\prime }}=(x_{{\mathit{S}}_{\mathrm{3}}}/(z_{{\mathrm{R}}_{\mathrm{13}}}{y}_{{\mathit{S}}_{\mathrm{3}}})\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}{r}^{\prime }}=(\mathrm{1}/z_{{\mathrm{R}}_{\mathrm{13}}}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}{r}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{11}}^{\mathrm{A}{r}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\end{array}\end{array}$$

Based on Eqs. (40)–(41), the quantity of additional reciprocal screw is equal to the number of actuated screws, so the inputs in each limb are reasonable.

$$\begin{array}{}\text{(42)}& \begin{array}{rl}& {\mathit{\$}}_{\mathrm{1}}^{\mathrm{A}{r}^{\prime }}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{2}}^{\mathrm{A}{r}^{\prime }}=(x_{{\mathit{S}}_{\mathrm{3}}}/(z_{{\mathrm{R}}_{\mathrm{13}}}{y}_{{\mathit{S}}_{\mathrm{3}}})\mathrm{0}\mathrm{0};\mathrm{1}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{3}}^{\mathrm{A}{r}^{\prime }}=(\mathrm{1}/z_{{\mathrm{R}}_{\mathrm{13}}}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{1}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{4}}^{\mathrm{A}{r}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})\\ & {\mathit{\$}}_{\mathrm{5}}^{\mathrm{A}{r}^{\prime }}=(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})\\ & {\mathit{\$}}_{\mathrm{6}}^{\mathrm{A}{r}^{\prime }}=(x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{11}}}-x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{12}}}-y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{11}}}+y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{12}}})/\\ & \left[y_{{\mathit{S}}_{\mathrm{3}}}\right(z_{{\mathrm{R}}_{\mathrm{11}}}-z_{{\mathrm{R}}_{\mathrm{11}}}\left)\right]\mathrm{0}-\mathrm{1};\\ & (x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{11}}}{z}_{{\mathrm{R}}_{\mathrm{12}}}-x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathrm{R}}_{\mathrm{12}}}{z}_{{\mathrm{R}}_{\mathrm{11}}}-y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{11}}}{z}_{{\mathrm{R}}_{\mathrm{12}}}\\ & +y_{{\mathit{S}}_{\mathrm{3}}}{x}_{{\mathrm{R}}_{\mathrm{12}}}{z}_{{\mathrm{R}}_{\mathrm{11}}})/[y_{{\mathit{S}}_{\mathrm{3}}}(z_{{\mathrm{R}}_{\mathrm{11}}}-z_{{\mathrm{R}}_{\mathrm{11}}})\left]\mathrm{0}\mathrm{0}\right)\end{array}\end{array}$$

The rank of Eq. (42) is six, which indicates that the platform loses all DoFs, and the inputs of the mechanism are reasonable. At the same time, the limb group A can be determined as a reasonable limb group. For the limb group B, the constrained screw system of the moving platform only consists of three reciprocal screws, that is, the constraint of the moving platform is insufficient. According to the constraint screw system of the mechanism, the twist system of the mechanism is as follows:

$$\begin{array}{}\text{(43)}& {\mathit{\$}}_{\mathrm{dof}}^{\mathrm{B}}=\left\{\begin{array}{lr}(\mathrm{0}\mathrm{0}\mathrm{1};\mathrm{0}\mathrm{0}\mathrm{0})& \left(\mathrm{a}\right)\\ (x_{{\mathit{S}}_{\mathrm{3}}}{y}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0};-z_{{\mathrm{R}}_{\mathrm{13}}}{y}_{{\mathit{S}}_{\mathrm{3}}}{z}_{{\mathrm{R}}_{\mathrm{13}}}{x}_{{\mathit{S}}_{\mathrm{3}}}\mathrm{0})& \left(\mathrm{b}\right)\\ (\mathrm{0}\mathrm{0}\mathrm{0};\mathrm{0}\mathrm{0}\mathrm{1})& \left(\mathrm{c}\right)\end{array}\right.\end{array}$$

According to Eq. (36), the DoF of the mechanism is wrong, so the limb group B is irrational. Based on the analysis of this PM, the extended input selection theory and the limb group selection rule are verified to have generality.

5 Conclusion

According to analyze the characteristic of 3-DoF PM with limbs of embedding structures and the influence factor of remnant-freedom, the extended input selection theory is proposed. Through extended input selection theory, the reasonable inputs and limb group of 3-DoF PM with limbs of embedding structures is determined, and limb group selection rule is summarized. Based on the analysis of the inputs of 2-DoF PM with limbs of embedding structures, the extended input selection theory and limb group selection rule verified to have generality.