the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Mechanism design and parameter optimization of a new asymmetric translational parallel manipulator
Yi Yang
Yaqi Tang
Haijun Chen
Yan Peng
Huayan Pu
With the requirement of heavy load for pick-and-place operation, a new 3-DoF asymmetric translational parallel manipulator is invented in this paper. This manipulator is assembled by a kinematic limb with the parallel linear motion elements(PLMEs), and a single loop 2-UPR. Owning to the linear actuators directly connecting the moving and the fixed platforms, this parallel manipulator has high force transmission efficiency, and adapts to pick-and-place operation under heavy load. In this paper, the mobility and singularity are firstly analyzed by screw theory. And the simplified kinematic and dynamic model is established and solved. Secondly, the reaction forces of the prismatic joints in the PLMEs limb are investigated for the mechanism design. Also, the overall performance of the whole manipulator, such as the workspace, condition numbers of Jacobian matrices and motion transmission, etc, are discussed. Thirdly, a compound evaluation function, which involves the factors of workspace volume, transmission efficiency and reaction force, is proposed. In order to obtain a set of better design parameters, the optimization of the 3-DoF translational manipulator is conducted, for the object of maximum of the evaluation function. At last, the prototype is manufactured and experimented to validate the mobility and motion feasibility of this mechanism design.
- Article
(13709 KB) - Full-text XML
-
Supplement
(22668 KB) - BibTeX
- EndNote
As the need of the industry for 3-DoF translational parallel mechanisms(TPM) in the late 1990s, many these kinds of parallel mechanisms have been researched and developed. In academic, several approaches for the type synthesis of TPMs were investigated, such as methods based on screw theory (Mohamed et al., 1985; Lee et al., 1999; Zhao et al., 2002; Bonev et al., 2003; Huang and Li, 2003; Kong and Gosselin, 2004a; Dai, 2006, 2014; Dai et al., 2006; Wu et al., 2010; Zhao et al., 2017), displacement group theory (Hervé, 1999; Lee et al., 2009), position and orientation characteristic (POC) sets (Yang et al., 2009), generalized function (GF) sets (Gao et al., 2011) and etc. By these means, a number of novel TPMs were invented by Tsai and Joshi (2000); Chablat and Wenger (2003); Liu et al. (2003); Kong and Gosselin (2004b); Jin and Yang (2004); Gogu (2008); Yang et al. (2019) and et al. And the kinematics, dynamics, singularities, stiffness, workspaces for the 3-DOF TPMs were contributed by Carricato and Parenti-Castelli (2002); Li and Xu (2008); Liu et al. (2017); Kong and Gosselin (2002); Li et al. (2015); Zhang et al. (2017), amongst others.
The actuators among the above TPMs can be divided into 2 primitive types, i.e, rotational actuators and linear actuators. The well-known 3-DoF TPM, Delta robot, is driven by 3 rotational actuators located on the base (Pierrot et al., 1990). Due to its capacity of high speed and high accelerations, this robot has popular usage in picking and packaging in factories. In 1996, Tsai proposed a typical 3-UPU parallel robot, called Tsai manipulator (Tsai and Joshi, 2000). The prismatic joint in each leg is driven by one linear actuator. Compared with the rotational actuators, the linear actuators generally deliver large force at high efficiency due to the simple transmission structure, and are used in a wide range of application in industry, especially in heavy duty equipments. Therefore, in the design of the heavy-load translational parallel manipulator, we choose the linear actuators to drive the moving platform of TPM in this paper.
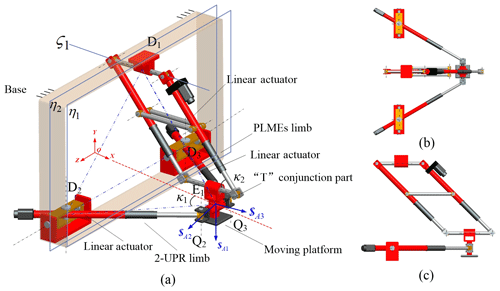
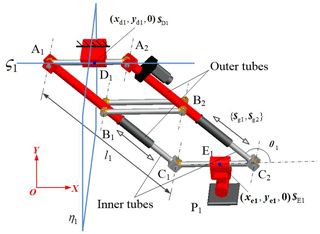
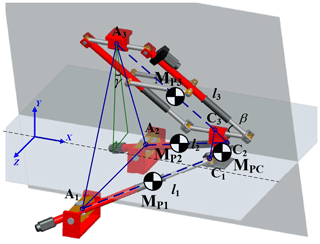
Figure 1A 3-DoF translational manipulator with PLMEs limb and single loop 2-UPR: (a) oblique view, (b) top view, (c) side view.
As aforementioned TPMs, Tsai manipulator can be driven by 3 linear actuators in each leg. Nevertheless, Han et al. (2002) showed that the small torsions in the legs of 3-UPU generated large deviations in the position of the moving platform. Thus, the applications of the Tsai's manipulator are limited in industry. The “Linear Deltas” has been developed from the standard Delta robot (Bouri and Clavel, 2010). The linear actuators move the parallelograms in each leg up or down, and then lead to the translating of the end platform. Furthermore, Yang et al. (2018) proposed a novel kind of kinematic chains with parallel linear motion elements(PLMEs), and synthesized a class of symmetrical 3T, 3T-1R, and 3R parallel mechanisms by these kinematic limbs. Different from “Linear Delta”, the linear actuators in these limbs directly connect the moving platform and the fixed base, which makes the parallel manipulators capable of higher transmission efficiency. Inspired by the above scholars' achievements, we propose a new 3-DoF translational manipulator by combining of PLMEs limb and single loop 2-UPR (Peng et al., 2018). This kind of manipulator has advantage of better transmission and simpler structure than other 3-DoF TPMs.
The rest of the paper is organized as follows. In Sect. 2, the structure is elaborated, and the mobility and singularity are analyzed. In Sect. 3, the kinematic and dynamic model is established and solved. In Sect. 4, the reaction forces of the prismatic joints in the PLMEs limb are studied. In Sect. 5, the overall performance of the whole manipulator, such as the workspace, condition numbers of Jacobian matrices and motion transmission, etc, are evaluated. In Sect. 6, a compound evaluation function is proposed. And the parameters of this manipulator are optimized. Finally, in Sect. 7, the prototypes are manufactured and validate the mobility and motion feasibility of this new manipulator.
The new 3-DoF manipulator is assembled by the parallel linear motion elements(PLMEs) limb and a single loop 2-UPR, as shown in Fig. 1. The moving platform is driven by 3 linear actuators, i.e., one actuator located in PLMEs limb and the other two actuators located in the single loop 2-UPR. To investigate the mobility and singularity of this new manipulator, we firstly analyze the PLMEs limb and the 2-UPR limb individually, by the utilization of screw theory. Secondly, we express the screws of the mechanism by Grassmann line geometry, and obtain the DoF space of the whole manipulator. Furthermore, we also discuss the controllability of the moving platform driven by the 3 selected linear actuators.
As an effective tool, screw theory is widely applied to analyze the mobility, singularity, transmission of mechanisms. A screw is usually represented by the form of Plucker homogeneous coordinates (L, M, N, P, Q, R). In mechanism research, the general term “screw” can be divided into twist $ and wrench $r. In twist $, the first three components denote an instantaneous angular velocity around an axis. And the last three components denote an instantaneous linear velocity along this axis. In wrench $r, The first three components denote the resultant force and the last three components denote the resultant moment. If the reciprocal product of the two screws, $ and $r, equals zero, these two screws are said to be reciprocal. The details can be found in Kong and Gosselin (2004a); Dai et al. (2006); Dai (2014), etc.
2.1 PLMEs limb
In Fig. 2, the PLMEs is constructed by two linear motion elements A1C1 and A2C2. The parallelogram A1B1A2B2 guarantees A1C1 and A2C2 be always parallel. The two inner tubes are able to slide along axes A1B1 and A2B2, respectively.
With reference (Yang et al., 2018), the moving link C1C2 generally has 2 translational DoFs without consideration of the revolute joints D1 and E1. The PLMEs linkage A1A2C1C2 can be regarded as a generalized kinematic pair, whose twist is denoted as {$g1,$g2}. Adding the revolute joints D1 and E1, the twist of the platform P1 is then written as in Eq. (1) if the PLMEs linkage is not in a singular configuration.
Its corresponding reciprocal screw can be obtained as
Equation (2) can be represented by the constraint space graph as shown in Fig. 5a. When , this configuration is a singularity. The Z axis rotational constraint is absent and the constraints reduce to only one. The kinematic limb has an extra instantaneous rotation about Z axis. Considering the rotating of this limb along X axis, this kind of singular configurations are all distributed on the plane η1 , as shown in Fig. 2. When θ1=0, π, the axes of the revolute joints D1 and E1 are collinear and the twists $D1 and $E1 are correlation. In this case, the moving platform has an additional instantaneous constraint to prevent it from translating along Z axis.This singular configuration is on the line ς1, as shown in Fig. 2.
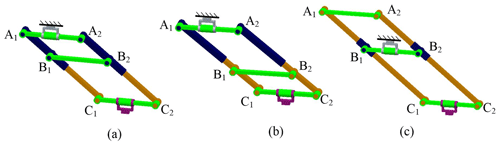
In the above PLMEs limb, the mid-link B1B2 connects the 2 outer tubes of the linear motion elements, as shown in Fig. 3a. In actual design, we can change the mid-link B1B2 from the outer tubes to the inner tubes, as shown in Fig. 3b. The parallelogram B1C1B2C2 guarantees A1C1 and A2C2 be always parallel. Thus, the mobility, constraint and singularity are as the same as the one in Fig. 3a. In another case, as shown in Fig. 3c, the mid-link B1B2 is fixed on the ground. The two sliders on the points B1 and B2 are jointed with the mid-link. The two linear guides A1C1 and A2C2 can slide on B1 and B2 . The linkage A1C1A2C2 is a parallelogram. Therefore, the PLMEs presented in Fig. 3c has also the same kinematic characteristics with the above two ones. From the kinematic point of view, these three PLMEs limbs presented in Fig. 3 are all equivalent.
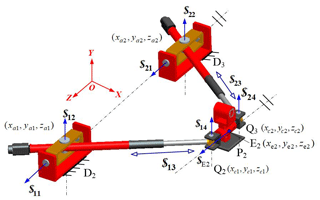
2.2 Single Loop 2-UPR
This single loop is constructed by 2 UPR limbs, as illustrated in Fig. 4. In Limb D2Q2 , one axis of the universal joint D2 is perpendicular with X–Y plane. The axis orientation is . The other axis is perpendicular with the plane formed by the vectors s1 and , where and are the coordinates of the points Q2 and D2. This axis orientation can be written as . The axis of another joint Q2 is parallel with the vector s2. The other Limb D3Q3 has the similar condition with D2Q2.
For Limb D2Q2, the twist of each kinematic pair can be written as
Through calculating the nullity of the above screws, the corresponding reciprocal screw of limb D2Q2 can be obtained as
In the same way, the wrench of limb D3Q3 is
If Q2Q3 and D2D3 are parallel with each other and both perpendicular with X–Y plane, the coordinates of the joints satisfy
Substituting the above condition into Eqs. (4) and (5), and using the algebra operation of reciprocal product, the twist of link Q2Q3 which is supported by the limbs D2Q2 and D3Q3 can be figured out. The results are as following
Within the consideration of the revolute pair E2 attached on the link Q2Q3, the twist of the platform P2 can then be expressed as
By solving the nullity of Eq. (8), the wrench of the moving platform P2 can be obtained.
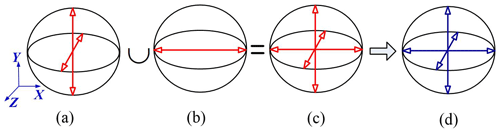
According to Eq. (9), the corresponding constraint space graph of the moving platform P2 is plotted as shown in Fig. 5b. Moreover, we substitute S-joint for U-joint. The single loop 2-SPR is instead of the loop 2-UPR. By repeating the above analysis process, it can be derived that the wrench of the moving platform P2 in this case still equals Eq. (9). This means that the loops 2-UPR and 2-SPR are equivalent and they can be swapped with each other for the requirements.
2.3 Whole manipulator
The PLMEs limb and the Loop 2-UPR are connected by a “T” shaped conjunction part, as shown in Fig. 1. The mobility of the whole manipulator can be deduced by Grassmann line geometry and the line-graph method. Grassmann line geometry is a systematic theory in mathematics, which can be used in the research on mechanism, especially on the DoFs and constraints of a mechanism. The line graph can be used to express an n-dimensional DoF space or constraint space in a mechanism. Blanding proposed a basic rule to uncover this dual relationship and mutual converse of the DoF spaces and constraint spaces through line graph. The basic rule was summarized by Blanding (1999); Yu et al. (2011), and etc. In this paper, we firstly plot the constraint space of the PLMEs limb and the single loop 2-UPR in one graph with Grassmann line geometry, as shown in Fig. 5c. Secondly, we apply the mutual conversion rule of DoF spaces and constraint spaces (Xie et al., 2013) for Fig. 5c. Then, the DoF space can be quickly obtained as shown in Fig. 5d. The result illustrates that the platform has 3 translational DoFs.
The manipulator has 2 kinds of singularities. One kind of singularity comes from the PLMEs limb. When or , the PLMEs limb is located on singular Plane η1 or Line ς1, as shown in Fig. 1. In this case, the constraints of the PLMEs limb are instantaneously changed. It results into the varying of the mobility of the manipulator. Another kind of singularity is that the 2-UPR limb are vertical, located on Plane η2. In this case, the constraints of the PLMEs limb and 2-URP limbs are all on Y–Z plane. The X axis rotational constraint is absent. The moving platform exists an extra instantaneous rotation about X axis.
In this manipulator, each limb is assumed to be driven by one linear actuator. Herein, we discuss whether the moving platform can be controlled by these 3 selected linear actuators. For the convenience of calculation, the moving platform is regarded as a link, without consideration of the actual geometric feature. Thus, the coordinates of the joints in the moving platform yield
In analysis, the two prismatic joints in the single loop 2-UPR are firstly fixed. The prismatic joint in PLMEs limb is free. In this case, the twist of the moving platform can be obtained as
Equation (11) illustrates that the moving platform has only one translational mobility under the above condition. The instantaneous velocity is perpendicular with the plane formed by D2Q2 and D3Q3.
Secondly, the prismatic joints in PLMEs and Limb D3Q3 are fixed and the prismatic joint in Limb D2Q2 is set to be free. The twist of the moving platform can be calculated as
Equation (12) illustrates that the moving platform has one translational mobility, which is perpendicular with the plane formed by D1E1 and D3Q3.
In the same way, the prismatic joints in PLMEs and Limb D2Q2 are fixed and the prismatic joint in Limb D3Q3 is set to be free. The twist of the moving platform is
Equation (13) illustrates that the only one translational mobility is perpendicular with the plane formed by D1E1 and D2Q2.
According to the above analysis, it can be summarized that the manipulator assembled by PLMEs and 2-UPR limbs generally has 3 pure translational DoFs. And the moving platform is controllable by 3 linear actuators.
According to the motion characteristics of this manipulator, the 3-DoF translational manipulator can be simplified as a 3-SPS mechanism without rotation mobilities. As shown in Fig. 6, , and are the initial positions of the points C1, C2 and C3 of the moving platform. , , are the initial positions of the points A1, A2 and A3 of the fixed platform, respectively. l1, l2 and l3 are the lengths of A1C1, A2C2 and A3C3, which can be regarded as the linear actuators of the manipulator.
3.1 Displacement equation
Let x, y, z be the displacements of the moving platform C1C2C3 from the initial position. The displacement equations can be derived as
If the displacement is known, the driving displacements of the linear actuators l1, l2 and l3 can be easily obtained by Eq. (14). Conversely, if the driving displacements l1, l2 and l3 are known, the forward displacement of the moving platform can be found by solving the above 3 equations. Let
and
Squaring both sides of Eq. (14), and subtracting the first formula to the second one, and the second one to the third one, Eq. (14) is transformed to
In this paper, the limbs A1A2 and C1C2 are always perpendicular with X–Y plane. The length projections of A1C1 and A2C2 on X-Y plane are equal. It yields
Through Eqs. (15) and (16), the displacement z can be quickly solved
Then, substituting Eq. (17) into Eqs. (14) and (15), and let
The displacements y and x can be solved by
Equation (17) and (18) give the analytic solution of the forward kinematics of the manipulator. Further, we can calculate the angle β (as shown in Fig. 6) in the PLMEs limb by the following formula.
And the angle γ between the PLMEs and the horizontal plane (as shown in Fig. 6) is calculated as
3.2 Velocity equation
Differentiating Eq. (14) leads to the velocity equation.
where the Jacobian matrix Jv is
In Eq. (22), each row of the matrix Jv represents the cosines of the angles between the corresponding SPS limb and the x, y, and z axes. The absolute value of the determinant of the third-order matrix Jv equals the volume of the parallelepiped spanned by each row vector of Jv. If the 3 SPS limbs are collinear or coplanar, the determinant of the Jacobian matrix equals zero. This mechanism is in singular configuration, which should be avoided in the motion planning. If an external force was exerted on the moving platform, the static driving forces of the linear actuators corresponding to limbs 1, 2 and 3 could be obtained through the Jacobian matrix.
3.3 Dynamic equation
In the manipulator, the moving platform is assumed to carry a heavy load. Taking the mass of 3 limbs as , and , each limb of the manipulator is simplified into a mass point for convenient calculation, which is located in the center of the limb as shown in Fig. 6. MPC is the mass of the moving platform with the heavy load. Based on these assumptions, the simplified dynamics equation can be written as
where I3×3 is the 3×3 identity matrix. Fx, Fy and Fz are the external force exerted on the moving platform. gx, gy and gz are the gravitational acceleration. And fi () are the driving forces of the 3 linear actuators. Let
Assume and ( be the velocity and acceleration of the actuators. Differentiating Eq. (21) and substituting the result into Eq. (24), it leads to
Considering
and substituting the above equation into Eq. (26), the equation can be rewritten as
where the derivative of Jacobian matrix is
Eq. (28) provides a simplified dynamic model for this translational parallel manipulator. It could be used into the control strategy, especially in the high speed pick-and-place operation.
In this manipulator, the PLMEs limb provides 2 rotational constraints to the moving platform. The varying of the reaction forces of the two prismatic joints in the PLMEs limb could reveal the performance of the manipulator, i.e., singularity, stiffness, etc. Thus, we mainly concern the reaction forces of the prismatic joints in the PLMEs limb in this section. We firstly study the reaction forces of the prismatic joints in the X–Y plane. Secondly, an external force is exerted on the moving platform. And then the reaction forces of the prismatic joints are investigated in the context of the whole manipulator. The results provide the basis for the design of the PLMEs limb in this new translational parallel manipulator.
4.1 Reaction forces in the planar PLMEs limb
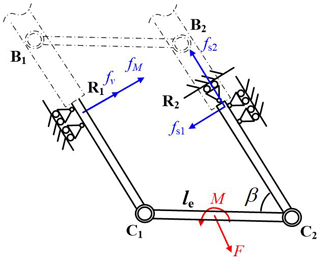
In the beginning, we only take the PLMEs limb into the analysis in the X–Y plane, without consideration of the Loop 2-UPR. As shown in Fig. 7, B1C1 and B2C2 are parallel. R1 and R2 are the two prismatic joints. Assumed the actuator is located on R2, B2C2 can be regarded to fix on the ground. An external force F and an external torque M are exerted on the middle of Link C1C2, as shown in Fig. 7. The length of Link C1C2 is le. The orientation of F is along with the PLMEs limb.
Taking fv as the reaction force corresponding to the force F, and fM as the reaction force corresponding to the torque M, the following equations are established by means of the virtual work principle.
Solving Eq. (30), we can obtain
By the sum of fv and fM, the total reaction force of the prismatic joint R1 can be calculated as the following equation. The orientation of is perpendicular with the prismatic joint.
The reaction force of the other prismatic joint R2 is decomposed into 2 directions. One direction force is perpendicular with Line B2C2 and opposite to . The other direction force is along with Line B2C2 and opposite to the actuator force F. Hence, the component forces and are written as
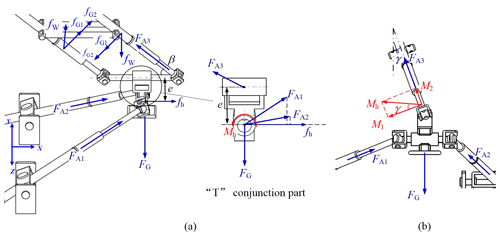
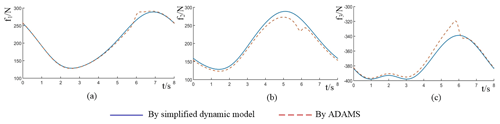
Figure 8Reaction forces of the prismatic joints in the context of the whole manipulator: (a) side view, (b) front view.
Observing Eqs. (32) and (33), it is noticed that and becomes infinite if . It indicates that the PLMEs limb with is in the singular configuration, which is consistent with the result derived in Sect. 2.
4.2 Reaction forces in the context of the whole manipulator
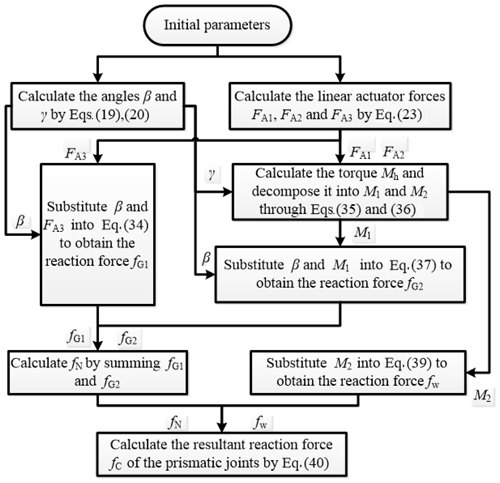
Based on the above results, we furthermore investigate the reaction forces of the PLMEs limb in the context of the whole manipulator. The moving platform bears a vertical force FG as shown in Fig. 8a. Through Eq. (23), the 3 linear actuator forces, denoted as , and , could be firstly calculated out. Secondly, by the utilization of and the first row of Eq. (31), one component reaction force of the prismatic joints, which is directly corresponding to the force , can be obtained as following.
As shown in Fig. 8a, there is a “T” shaped conjunction part connecting the PLMEs limb and the 2-UPR limb. If there is a small distance e between the two connections in the “T” conjunction part, the resultant force leads to a torque Mh exerted on the “T” conjunction part. The torque Mh can be obtained by
where fh is the resultant force of and projected on X axis. As shown in Fig. 8b, Mh can be decomposed into M1 and M2 by Eq. (36).
where M1 and M2 represent the torques be in and perpendicular to the plane of PLMEs, respectively. The angle γ between the PLMEs and the horizontal plane can be found by Eq. (20). According to the second row of Eq. (31), the reaction force corresponding to the torque M1 can be written as
Thus, the total reaction force fN perpendicular to the prismatic joint in the plane of PLMEs can be obtained by summing and .
In another way, the torque M2 would cause the other reaction force fW perpendicular to the plane of PLMEs. It can be figured out by Eq. (39).
Finally, through fN and fW, the resultant reaction force fc of the prismatic joint can be obtained as follows
All the above calculation procedure for the force of PLMEs limb is summarized in Fig. 9. It shows that the resultant reaction force of the prismatic joints is related to the Jacobian matrix of the manipulator and the configuration of the PLMEs limb. If the reaction force becomes large, it indicates the manipulator is in bad performance(e.g., in case of singularity), and vice versa. Through analyzing the force of the prismatic joints in the PLMEs limb, the performance of the manipulator can be revealed.
Based on the above-mentioned results, it is also found that the way of making the external load FG be closed to the actuator of PLMEs limb, or decreasing the distance e between PLMEs limb and 2-UPR limb could reduce the resultant reaction force of the prismatic joints. It is very helpful for the design of this new translational parallel manipulator.
Based on the aforementioned analysis, we discuss the workspace, condition numbers of Jacobian matrices, simplified dynamics and motion transmission of the new manipulator. And the reaction forces of the manipulator under the circumstance that the moving platform bearing a vertical force is also investigated.
5.1 Workspace and Jacobian matrices
We assume that the ranges of 3 linear actuators are , and for Limbs L1, L2 and L3 relative to the initial configuration. The joint positions of the initial configuration are listed in Table 1.
Considering the initial configuration, the absolute motion range of each limb is [467.0,1067.0], [467.0,1067.0] and [351.6,771.6], respectively. According to Eq. (14), the workspace of the moving platform is the intersection of the 3 hollow spheres, whose inner and outer radii are lmin and lmax. And the centers of the 3 spheres are respectively at , and . To avoid singularity and consider the actual usage, we just calculate the workspace in the range of y≤441.0 and , as shown in Fig. 10a. The workspace of the moving platform is plotted as shown in Fig. 10b–d. The volume of the workspace is calculated to be 1.9755×108 mm3.
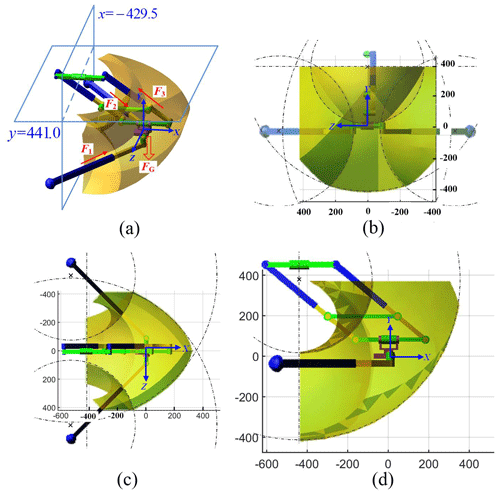
Figure 10Workspace of the moving platform: (a) oblique view, (b) front view, (c) top view, (d) side view.
Furthermore, the condition numbers of Jacobian matrices in the workspace is figured out to evaluate the kinematic performance of the manipulator. In Fig. 11, the condition numbers are plotted as the contour lines on the different layers which are respectively located on the planes and the plane z=0. The contour lines show that the condition numbers are large when the manipulator approaches the singular configurations, i.e., β=0 and . It illustrates that the kinematic property becomes bad when the moving platform is in these areas. In the proceeding of the motion planning, it is better to avoid these areas.
5.2 Simplified dynamics
In the dynamic analysis, the joint positions of the initial configuration are as the same as listed in Table 1. The mass of Limbs 1, 2 and 3 are 2.676, 2.676 and 5.35 kg, respectively. And the mass of the moving platform with the load is 11.237 kg. An external force N is exerted on the moving platform. The gravity is along the negative Y axis. We give the displacement equation dli of each linear actuator relative to the initial configuration as follows.
Adding the initial length of each limb , the absolute displacement equation of each limb is obtained as
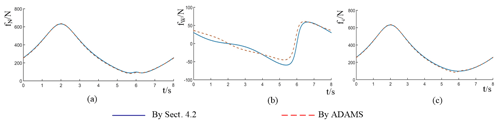
Substituting the above conditions into Eq. (28), the actuating force of each limb can be calculated out. To validate the effectiveness of the simplified model deduced in Sect. 3.3, the complete dynamic model is built and simulated in ADAMS software. Two results are presented in Fig. 12, where the solid lines represent the ones come from the simplified dynamic model, the dashed lines represent the ones come from ADAMS software. It shows that the two curves are generally consistent with each other, although some local errors are a bit of large. The errors come from the simplification of each limb into the mass point. It results in the decreasing of the model accuracy. Nevertheless, the simplified dynamic model still make sense to estimate the actuating force or make control strategy in the design of this manipulator.
Furthermore, the reaction forces of the prismatic joints are also calculated based on the method proposed in Sect. 4.2. The results are compared with the ones obtained by ADAMS software, as shown in Fig. 13. It is found that the two results are similar, which proves the correctness of the method proposed in Sect. 4.2.
5.3 Motion transmission
To evaluate the efficiency of the power transmission of the manipulator, the motion transmission indices of each leg are studied by screw theory (Wu et al., 2010; Zhao et al., 2017). For a given configuration, the transmission wrench screw(TWS), denoted , is defined as a unit screw that are reciprocal to all the twist screws except the actuated one in Limb i. The output twist screw(OTS), denoted , is the instantaneous movement of the moving platform when fixing all of its inputs except the one of the ith limb. The input twist screw(ITS), denoted , is the unit twist of the actuated joint in Limb i. And then, for the given configuration, the input transmission index (ITI) of each limb can be represented as
In this parallel manipulator, the translational direction of the prismatic actuator is along the limb. Thus, the input transmission index of the limb is constant and its value is always equal to 1. It means that this manipulator has high quality of input transmission.
Meanwhile, the output transmission index(OTI) of each limb can be represented as
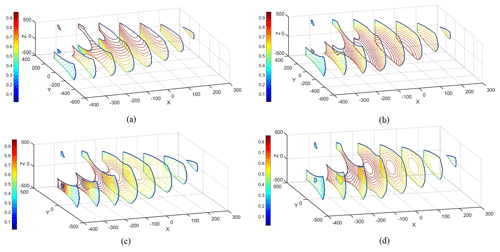
The output transmission index νi represents the cosine of the angle between the prismatic actuator of Limb i and the instantaneous movement of the moving platform. Considering ITI be always equal to 1 in this manipulator, we take the minimum value of νi as the local transmission index (LTI) of the whole manipulator at the given configuration, denoted as νm. Within the whole workspace, OTIs of each limb of this manipulator can be calculated by Eq. (44). The results are presented as shown in Fig. 14a–c. And the LTIs of the whole manipulator in the workspace are as shown in Fig. 14d. It is found that LTIs in the center of the workspace are generally larger than the ones of the other areas. It illustrates that there is higher efficiency of the motion transmission when the moving platform works in this area.
The above LTIs prescribe the quality of input and output transmission in a given configuration. To further evaluate the transmissibility of the manipulator within the whole workspace, a global transmission index(GTI) of this manipulator is defined as
where Ω is the workspace. For this manipulator, GTI over the whole workspace is 0.5664. For the purpose of making the moving platform work in the area of better transmissibility (GTI ≥0.7), we search for the maximum area Γ in the workspace where GTI ≥0.7, termed as the efficient workspace.
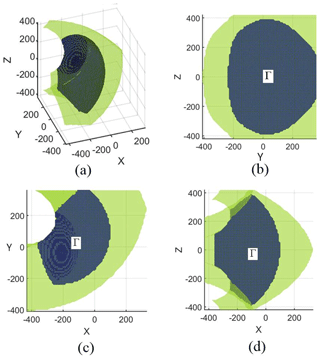
Through Genetic Algorithm (GA), the efficient workspace Γ can be obtained as shown in Fig. 15. The volume of the area Γ is 8.26×107 mm3, about 41.8 % of the whole workspace.
5.4 Reaction forces of the prismatic joints
A vertical force is exerted on the moving platform. By Eq. (23), the forces of the actuators in 3 limbs are calculated. By ratio of the results to the input force (100 N), the normalized reaction force of each limb is obtained. And the contour lines for them are drawn out as shown in Fig. 16a–c.
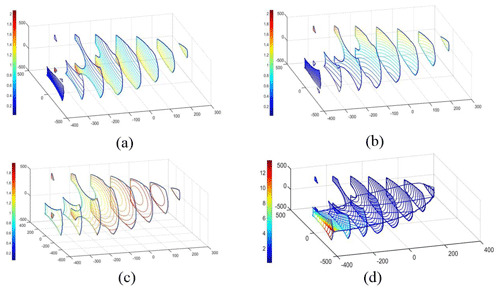
Figure 16Scale factors of the reaction forces: (a) Limb 1, (b) Limb 2, (c) limb 3, (d) Prismatic joints.
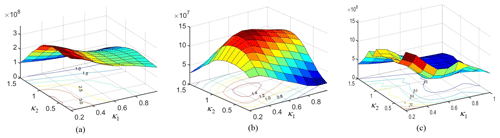
Figure 17Performance with respect to κ1 and κ2: (a) workspace volume, (b) transmission, (c) normalized reaction force.
Also, we calculate the normalized reaction forces of the prismatic joints in PLMEs limb under this circumstance. Given the small distance e between PLMEs limb and 2-UPR limb be 79 mm, the length le of the end link be 335 mm, the compound reaction force fc of the prismatic joints is figured out by Eq. (40). Similarly, by ratio of the results to 100 N, the scale factors are obtained and presented in Fig. 16d. Obviously, when the PLMEs limb approaches the singular configuration, i.e., , the reaction forces of the prismatic joints become larger which means the force performance gets worse.
Assumed the parameters of three limbs are given, the motion range of each limb are similar with the ones mentioned above. Through changing the angles κ1 and κ2 as shown in Fig. 1, we can obtain different initial configurations of the whole mechanism, which are symmetrical about x–y Plane. Each different initial configuration has its own workspace, transmissibility and force performance. The workspace is assumed in the range of and y<ς1 as presented in Fig. 1. To achieve the overall optimal performance, the designed parallel manipulator is expected to have large workspace, high transmission and low reaction forces.
Before optimized, we firstly draw out the workspace, transmission and normalized reaction force graphs with respect to the angles κ1 and κ2 within the range of [0,1] and , as shown in Fig. 17a–c. From Fig. 17a, it is found that the volume of the workspace becomes large when κ1 and κ2 approach to zero. On the contrary, Fig. 17b and c show that the transmission and the reaction force within this area are not so good.
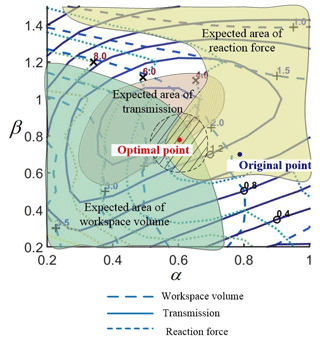
To make it clearly, we gathered all 3 contour maps in one graph, as show in Fig. 18, where the dashed lines represent the contour lines of the workspace volume, the solid lines represent the ones of the transmission, and the dotted lines represent the ones of the reaction force. According to the contour maps, we give the rough expected areas of workspace volume, transmission and reaction force. The overlap of the 3 areas(as shown the diagonal lines area in Fig. 18) can be regarded to be capable of optimal performance, i.e., large workspace, high transmission and low reaction force.
Based on the above analysis, a compound evaluation function Θ,which involves workspace volume, transmission efficiency and reaction force of the manipulator, is proposed as seen in Eq. (47).
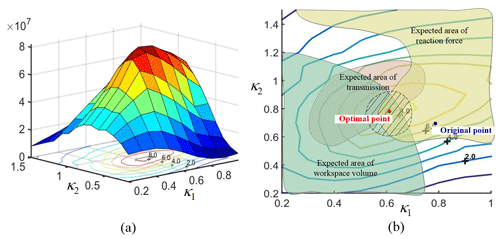
where Ω is the workspace of the manipulator. υm is the local transmission index (LTI), which is the non-dimensional parameter. fc is the normalized reaction force, which is also the non-dimensional parameter. Through varying the exponents r, s and t, we can change the weighting for certain variables to adjust the evaluation function. Usually , the exponents could be chosen as r=1, s=1 and t=1. In this case, the compound evaluation function with respect to κ1 and κ2 is calculated and drawn as shown in Fig. 19.
Figure 19 shows that Θ is a convex function, which obviously exists a maximum in the given range. Compared with the results of Fig. 18, it is found that the overlap almost locates in the region of the maximum of the compound evaluation function. Thus, it is feasible to obtain the optimal performance by searching the maximum of the compound evaluation function Θ. Given the range of optimization variables κ1 and κ2 in [0,1] and , the optimization is conducted by GA method. The results are obtained as κ1=0.605 and κ2=0.781. As shown in Figs. 18 and 19, the optimal point(red point) is located in the expected area. Compared with the original manipulator presented in Sect. 5 (as shown the blue point in Figs. 18 and 19), the workspace volume and transmission of the optimized manipulator are remarkably improved. Specifically, the workspace volume of the optimized manipulator is calculated as 2.1718×108 mm3, which is 9.9 % larger than the original one. The GTI of the optimized manipulator is 0.6252, which increase 10.3 %. And the volume of the efficient workspace Γ, where GTI ≥ 0.7, is 1.2427×108 mm3, i.e., 60 % of the whole workspace. Compared with the ones in Sect. 5, the volume of the efficient workspace of the optimized manipulator is expanded by 50 %, which is as shown in Fig. 20. In general, the manipulator with the optimized parameters has better overall performance than before.
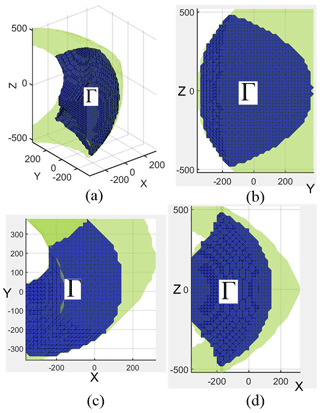
Figure 20Efficient workspace Γ of the optimized configuration: (a) oblique view, (b) front view, (c) top view, (d) side view.
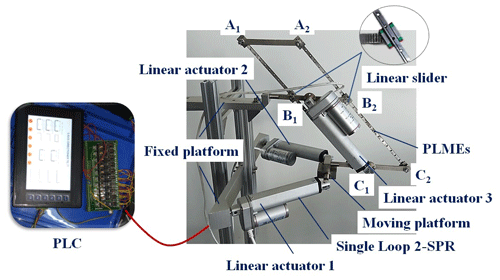
We manufacture the prototype of this new parallel manipulator in this paper. Since the loops 2-UPR and 2-SPR are equivalent, we choose Loop 2-SPR and PLMEs limb to assemble the parallel manipulator. As shown in Fig. 21, the PLMEs limb is constructed by 2 parallel linear guides and 2 sliders. The linkage A1C1A2C2 can slide on B1 and B2. And the middle link B1B2 is hinged with the fixed platform. The loop 2-SPR is constructed by 2 linear actuators. Through the “T” shaped moving platform, the PLMEs limb and 2-SPR limb are connected. The moving platform is driven by 3 electric linear actuators, which are controlled by the PLC(Programmable Logic Controller). Owning to the asymmetric structure, this prototype can be mounted on one side of the frame, as shown in Fig. 21.
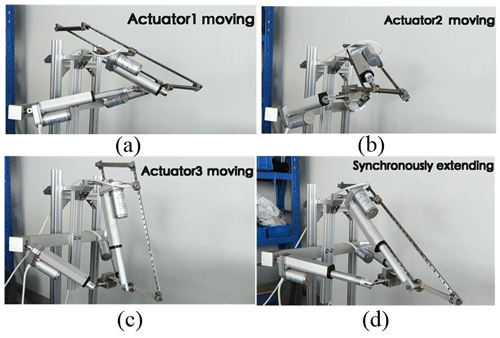
In the experiment, we firstly control each individual linear actuator to extend and retract sequentially, as shown in Fig. 22a–c. Secondly, we make all the 3 linear actuators to extend and retract synchronously, as shown in Fig. 22d. The experiment shows that the moving platform can translate into 3 different directions. The motion of the moving platform is smoothly and continuously under the driving of the linear actuators. It proves the correctness of the mobility and motion feasibility of this kind of mechanism.
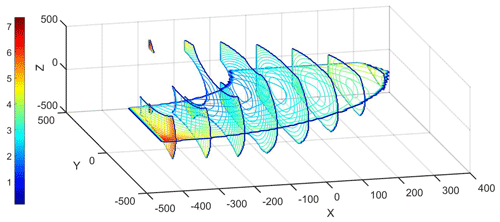
Furthermore, we plan a “⊂” shaped path for the moving platform. According to the given path points, the displacement of each linear actuator relative to the initial configuration is obtained by the method proposed in Sect. 3.1. Then, input the control parameters of the linear actuators into the PLC sequentially. Under the control of PLC, the moving platform achieves the expected trajectory, as shown the red lines in Fig. 23.
A new 3-DoF asymmetric translational parallel manipulator by combining of PLMEs limb and the single loop 2-UPR is proposed. By the utilization of the linear actuators directly connecting the moving platform and the fixed platform, this new manipulator has higher transmission efficiency than other 3-DoF TPMs, and adapts to pick-and-place operation under heavy load. In addition, owning to asymmetric structure, this manipulator can be installed aside of the workstation, e.g. as shown in Fig. 21. It provides more flexibility in its application. In this paper, the mobility of this parallel manipulator is analyzed by screw theory and the singularity is determined. Also, the simplified kinematic and dynamic models are established. And the analytic solution of the displacement and velocity equations are obtained. As the PLMEs limb is the key part of this kind of manipulator, the reaction forces of the prismatic joints in the PLMEs limb are investigated for the mechanism design. It is found that the varying of the reaction forces in the two prismatic joints are related to the Jacobian matrix of the manipulator and the configuration of the PLMEs limb, which can reveal the whole kinematic performance of the manipulator. Given an initial configuration, the workspace, condition numbers of Jacobian matrices, dynamics, motion transmission and reaction forces are discussed. Furthermore, we propose a compound evaluation function Θ, which involves the factors of workspace volume, motion transmission and reaction force. Aiming to the maximum of Θ, the optimization for the 3-DoF translational manipulator is conducted. After being optimized, the workspace volume enlarges 9.9 %, the GTI increases 10.3 %, and the volume of the efficient workspace is expanded by 50 %. At last, the prototype of this manipulator is manufactured, and the motion experiment validates the mobility and motion feasibility of the mechanism design.
All the data used in this manuscript can be obtained by Yi Yang (yiyangshu@shu.edu.cn) or Yan Peng (pengyan@shu.edu.cn).
The videos of the experiments are provided in the Supplement. The supplement related to this article is available online at: https://doi.org/10.5194/ms-10-255-2019-supplement.
YY conceived the overall idea of this paper and conducted the theoretical calculation as well as example studies. YT and HC performed the prototype fabrication and experiments. YP and HP verified the data and supervised the whole project. All authors discussed the results and conclusions contributing to the final manuscript.
The authors declare that they have no conflict of interest.
Preliminary versions of parts of this work were presented in June 2018 at 4th IEEE/IFToMM ReMAR2018 (Paper No. 33) in Delft, Netherlands, and in reference Peng et al. (2018).
This research has been supported by the National Natural Science Foundation of China (grant nos. 51675318 and 91648119)
This paper was edited by Guimin Chen and reviewed by two anonymous referees.
Blanding, D. L.: Exact Constraint: Machine Design Using Kinematic Principle, ASME Press, New York, 1999. a
Bonev, I. A., Zlatanov, D., and Gosselin, C. M.: Singularity analysis of 3-dof planar parallel mechanisms via screw theory, J. Mech. Des., 125, 573–581, https://doi.org/10.1115/1.1582878, 2003. a
Bouri, M. and Clavel, R.: The linear delta: Developments and applications[C]//Robotics (ISR), 2010 41st International Symposium on and 2010 6th German Conference on Robotics (ROBOTIK), VDE, 1–8, 2010. a
Carricato, M. and Parenti-Castelli, V.: Singularity-free fully-isotropic translational parallel mechanisms, Int. J. Rob. Res., 21, 161–174, https://doi.org/10.1177/027836402760475360, 2002, a
Chablat, D. and Wenger, P.: Architecture optimization of a 3-DOF translational parallel mechanism for machining applications, the orthoglide, IEEE. J. Robot., 19, 403–410, https://doi.org/10.1109/TRA.2003.810242, 2003. a
Dai, J. S.:Geometrical Foundations and Screw Algebra for Mechanisms and Robotics, Higher Education Press, ISBN: 9787040334838, 2014. a, b
Dai, J. S.: An historical review of the theoretical development of rigid body displacements from Rodrigues parameters to the finite twist, Mech. Mach. Theory., 41, 41–52, https://doi.org/10.1016/j.mechmachtheory.2005.04.004, 2006. a
Dai, J. S., Huang, Z., and Lipkin, H.: Mobility of overconstrained parallel mechanisms, J. Mech. Des., 128, 220–229, https://doi.org/10.1115/1.1901708, 2006. a, b
Gao, F., Yang, J. L., and Ge, Q. J.: Type synthesis of parallel mechanisms having the second class G(F) sets and two dimensional rotations, J. Mech. Robot., 3, 011003, https://doi.org/10.1115/1.4002697, 2011. a
Gogu, G.: Structural Synthesis of Parallel Robots, Part I: methodology, Springer, 2008. a
Han, C., Kim, J., Kim, J., and Park, F. C.: Kinematic sensitivity analysis of the 3-UPU parallel mechanism, Mech. Mach. Theory., 37, 787–798, https://doi.org/10.1016/S0094-114X(02)00021-6, 2002. a
Hervé,J. M.: The Lie group of rigid body displacements, a fundamental tool for mechanism design, Mech. Mach. Theory., 34, 719–-730, https://doi.org/10.1016/S0094-114X(98)00051-2, 1999. a
Huang, Z. and Li, Q.: Type synthesis of symmetrical lower-mobility parallel mechanisms using constraint synthesis method, Int. J. Rob. Res., 22, 59–-79, https://doi.org/10.1177/0278364903022001005, 2003. a
Jin, Q. and Yang, T. L.: Theory for topology synthesis of parallel manipulators and its application to three dimension-translation parallel manipulators, J. Mech. Des., 126, 625–-639, https://doi.org/10.1115/1.1758253, 2004. a
Kong, X. and Gosselin, C. M.: Kinematics and singularity analysis of a novel type of 3-CRR 3-DOF translational parallel manipulator, Int. J. Rob. Res., 21, 791–798, https://doi.org/10.1177/02783649020210090501, 2002. a
Kong, X. W. and Gosselin, C. M.: Type synthesis of 3T1R 4-DOF parallel manipulators based on screw theory, IEEE. J. Robot., 20, 181–190, https://doi.org/10.1109/TRA.2003.820853, 2004a. a, b
Kong, X. and Gosselin,C. M.: Type synthesis of 3-DOF translational parallel manipulators based on screw theory, J. Mech. Des., 126, 83-–92, https://doi.org/10.1115/1.1637662, 2004b. a
Lee, J., Duffy, J., and Keler, M.: The optimum quality index for the stability of in-parallel planar platform devices, J. Mech. Des., 121, 15–-22, https://doi.org/10.1115/1.2829417, 1999. a
Lee, C. C. and Herve, J. M.: Type synthesis of primitive Schoenflies-motion generators, Mech. Mach. Theory, 44, 1980-–1997, https://doi.org/10.1016/j.mechmachtheory.2009.06.001, 2009. a
Li, Y. and Xu, Q.: Stiffness analysis for a 3-PUU parallel kinematic machine, Mech. Mach. Theory, 43, 186–200, https://doi.org/10.1016/j.mechmachtheory.2007.02.002, 2008, a
Li, B., Li, Y. M., Zhao, X. H., and Ge, W. M.: Kinematic analysis of a novel 3-CRU translational parallel mechanism, Mech. Sci., 6, 57–64, https://doi.org/10.5194/ms-6-57-2015, 2015. a
Liu, X. J., Jay, J., and Kim, J.: A three translational DOFs parallel cube-manipulator, Robotica, 21, 645-–653, https://doi.org/10.1017/S0263574703005198, 2003. a
Liu, H., Huang, T., Chetwynd, D. G., and Kecskeméthy, A.: Stiffness modeling of parallel mechanisms at limb and joint/link levels, IEEE. J. Robot., 33, 734–741, https://doi.org/10.1109/TRO.2017.2654499, 2017. a
Mohamed, M. G. and Duffy, J.: A direct determination of the instantaneous kinematics of fully parallel robot manipulators, J. Mech. Trans. Automation, 107, 226–229, https://doi.org/10.1115/1.3258713, 1985. a
Peng, Y., Chen, H. J,, Lu, B. Z., and Yang, Y.: Design and Application of a 3-DoF Manipulator for Launch and Recovery System[C], 2018 International Conference on Reconfigurable Mechanisms and Robots (ReMAR), IEEE, 1–8, https://doi.org/10.1109/REMAR.2018.8449869, 2018. a, b
Pierrot, F., Reynaud, C., and Fournier, A.: DELTA: a simple and efficient parallel robot, Robotica, 8, 105–109, https://doi.org/10.1017/S0263574700007669, 1990. a
Tsai, L. W. and Joshi, S.: Kinematics and optimization of a spatial 3-UPU parallel manipulator, J. Mech. Des., 122, 439–446, https://doi.org/10.1115/1.1311612, 2000. a, b
Wu, C., Liu, X. J., Wang, L., and Wang, J.: Optimal design of spherical 5R parallel manipulators considering the motion/force transmissibility, J. Mech. Des., 132, 031002, https://doi.org/10.1115/1.4001129, 2010. a, b
Xie, F., Li, T., and Liu, X.: Type synthesis of 4-DOF parallel kinematic mechanisms based on Grassmann line geometry and atlas method, Chin. J. Mech. Eng-En., 26, 1073–1081, https://doi.org/10.3901/CJME.2013.06.1073, 2013. a
Yang, T. L., Liu, A. X., Jin, Q., Luo, Y. F., Shen, H. P., and Hang, L. B.: Position and orientation characteristic equation for topological design of robot mechanisms, J. Mech. Des., 131, 021001, https://doi.org/10.1115/1.2965364, 2009. a
Yang, Y., Peng, Y., Pu, H., and Cheng, Q.: Design of 2-Degrees-of- Freedom (Dof) Planar Translational Mechanisms With Parallel Linear Motion Elements for an Automatic Docking Device, Mech. Mach. Theory, 121, 398-–424, https://doi.org/10.1016/j.mechmachtheory.2017.11.005,2018, a, b
Yang, Y., Zhang, W., Pu, H., and Peng, Y.: A Class of Symmetrical 3T, 3T-1R, and 3R Mechanisms With Parallel Linear Motion Elements, J. Mech. Robot., 10, 051016, https://doi.org/10.1115/1.4040885, 2018.
Yang, Y., Peng, Y., Pu, H., Chen, H., Ding, X., Chirikjian, G. S., and Lyu, S.: Deployable parallel lower-mobility manipulators with scissor-like elements, Mech. Mach. Theory, 135, 226–250, https://doi.org/10.1016/j.mechmachtheory.2019.01.013, 2019. a
Yu, J., Li, S., Su, H. J., and Culpepper, M. L.: Screw theory based methodology for the deterministic type synthesis of flexure mechanisms, J. Mech. Robot., 3, 031008, https://doi.org/10.1115/1.4004123, 2011. a
Zhang, D., Xu, Y., Yao, J., Hu, B., and Zhao, Y. S.: Kinematics, dynamics and stiffness analysis of a novel 3-DOF kinematically/actuation redundant planar parallel mechanism, Mech. Mach. Theory, 116, 203–219, https://doi.org/10.1016/j.mechmachtheory.2017.04.011, 2017. a
Zhao, T. S., Dai, J. S., and Huang, Z.: Geometric Synthesis of Spatial Parallel Manipulators with Fewer Than Six Degrees of Freedom, P. I. Mech. Eng. C-JMEC, 216, 1175–1185, https://doi.org/10.1243/095440602321029418, 2002. a
Zhao, Y., Wang, J., Cao, Y., Liang, B., and Zhao, T.: Constant motion/force transmission analysis and synthesis of a class of translational parallel mechanisms, Mech. Mach. Theory, 108, 57–74, https://doi.org/10.1016/j.mechmachtheory.2016.10.008, 2017. a, b
- Abstract
- Introduction
- Structure and mobility of the new manipulator
- Simplified kinematic and dynamic model
- Reaction forces of the prismatic joints in the PLMEs limb
- Performance investigation
- Parameter optimization
- Prototype and Experiment
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Structure and mobility of the new manipulator
- Simplified kinematic and dynamic model
- Reaction forces of the prismatic joints in the PLMEs limb
- Performance investigation
- Parameter optimization
- Prototype and Experiment
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement