Design and hardware selection for a bicycle simulator

With the resurgence in bicycle ridership in the last decade and the continuous increase of electric bicycles in the streets a better understanding of bicycle rider behaviour is imperative to improve bicycle safety. Unfortunately, these studies are dangerous for the rider, given that the bicycle is a laterally unstable vehicle and most of the time in need for rider balance control. Moreover, the bicycle rider is very vulnerable and not easily protected against impact injuries. A bicycle simulator, on which the rider can balance and manoeuvre a bicycle within a simulated environment and interact with other simulated road users, would solve most of these issues. In this paper, we present a description of a recently build bicycle simulator at TU Delft, were mechanical and mechatronics aspects are discussed in detail.

1 Introduction

A number of recent studies have used recorded data of riders during naturalistic driving (Kovascova et al., 2016) and (Moore et al., 2011). However, behavioral studies for other vehicles often use simulators (Steen et al., 2011) as they afford more reproducible experiments over a range of riders in a safe environment. There have been a number of groups that have developed bicycle simulators for a variety of research goals. Schwab and Recuero (2013) designed and built a haptic steering interface for the control input of a bicycle simulator, a potentiometer was used to estimate the angular position of the handlebar and not an angular encoder, whereas the output feedback torque magnitude of the selected motor was insufficient for this application. He et al. (2005) and Yin and Yin (2007) describe the design of a simulator mounted on a Stewart platform with steering and pedaling subsystems, which was used to study rider-bicycle models, but use steer angular position measurements to estimate angular accelerations and consequently the input torques via the product of angular accelerations and shaft inertia. However, the estimation of input torques from inertia and angular acceleration data contains dynamic errors (Oliveira et al., 2015). Caro and Bernardi (2015), Herpers et al. (2008), Plumert et al. (2004) focus on rider behavior at a cognitive level and do not incorporate a realistic vehicle model. At TU Delft we have designed and built a fixed-base bicycle simulator with haptic feedback at the handlebars, which can be used for various applications, for example studying rider behavior in various infrastructures, studying rider interaction in traffic and performing rider training. The bicycle simulator includes a haptic steering device which generates feedback driven by an underlying bicycle computer model, an incremental encoder to measure handlebar angle and a torque sensor to measure handlebar applied torque. In this paper we present a step by step guide to build such a bicycle simulator. First, the design requirements of the simulator interfaces are examined. Then, the design of the mechanical structure is described. Afterwards, the hardware components selection and calibration procedure is analyzed. The article ends with a discussion and conclusion section presenting other factors that make such a design valid for rider behaviour studies.

2 Design requirements of bicycle simulator interfaces

The aim of this section is to examine all the necessary requirements needed to build a realistic bicycle simulator. This is achieved by understanding the role of each sensory system on rider control. The primary sensory systems used during the riding process are, the vestibular sensory system, the visual sensory system and the proprioceptive sensory system (Schwab et al., 2013). Secondary sensory systems such as the tactile and the auditory sensory system also contribute to the perception of information during the riding process. For example, Mclane and Wierwille (1975) found that additional auditory information and tactile vibratory information improved the humans' estimation of speed. In the first paragraph, of this section we describe the relation between the sensory systems and bicycle states. The second paragraph describes, the necessary requirements needed to be fulfilled in order to activate these sensory systems and build the simulator interfaces. We presume that the bicycle rider system is a closed loop control system, balancing the mostly unstable bicycle and manoeuvring in the environment using feedback from the vestibular sensory system, the visual sensory system and the proprioceptive sensory system (Schwab et al., 2013). The rider uses bicycle roll angle ϕ as part of the feedback control loops for the vestibular/visual sensory systems and handlebar steer angle δ as part of the feedback control loop for the proprioceptive sensory system. The rider processes each state individually in order to apply a steer torque Tδ to control the bicycle. A block diagram of the bicycle-rider system illustrating the relation between the primary sensory systems and bicycle states [ϕ,δ] the rider uses to control the bicycle by applying a steer torque Tδ is presented in Fig. 1.

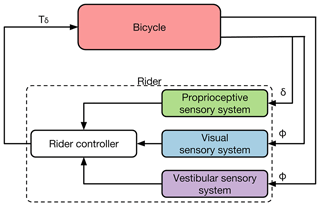
Figure 1 Block diagram of the bicycle-rider system illustrating the relation between the primary sensory systems and bicycle states [ϕ,δ] the rider uses to control the bicycle by applying a steer torque Tδ.

Due to the aforementioned it is necessary to design and build user interfaces able to activate at least the primary sensory systems of the rider. To activate the visual sensory system a virtual environment is built using Unity^® software. Projection of the virtual environment is achieved with a PC screen or with a head-mounted virtual reality display. To stimulate the proprioceptive sensory system a haptic steering device is designed and built. The steering device is able to generate torque feedback based on the equations of motion of a three degree of freedom bicycle model, the so-called Carvallo-Whipple bicycle model (Meijaard et al., 2007). The absence of a hexapod in the current implementation of the bike simulator does not allow the user to experience physical roll and thus, the vestibular sensory system remains inactive. Although, in naturalistic bicycle riding the rider uses both the vestibular and visual sensory systems to estimate roll angle. We think that visual roll of the horizon in the virtual environment might be an effective tool to compensate the vestibular loss. However, it should be noticed that the absence of vestibular input might have a negative effect on rider behavior in certain tasks, such as braking and lateral trajectory control. For this reason, the usage of such a simulator to study these tasks may be inappropriate (Shahar et al., 2014). The implementation of the equations of motions of the Carvallo-Whipple bicycle model used to drive the haptic steering device and Unity^® environment will be detailed in future publications.

Figure 2 TU Delft fixed base bicycle simulator.

3 Description of the mechanical structure

Several structural design considerations should be taken into account in case of building a bicycle simulator. Structural strength and required geometry are some of the most important aspects of the building process. The bicycle frame must be able to support the load of the rider during all operational conditions while having adjustable dimensions. Adjustable reach and stack dimensions are considered important mainly because it is suspected that body posture also influences the amount of applied torque. As stated in previous bicycle experiments conducted by Too (1988) the interaction of muscle length with muscle lever moment arm length is one of the factors which will dictate the amount of force or torque that can be produced by the rider during cycling. It should be noted that this statement does not describe the relationship between muscle length, muscle activity, and torque of the brachialis muscles however, it shows the influence of body posture to applied torque. On the other hand, the bicycle frame must be able to support all the functional subsystems used in bicycles. For instance, the rear wheel and derailleur, the seatpost and seat, the bottom bracket and pedal subsystem etc. In addition to the above, the simulator must be able to simulate the steering forces acting at the bicycle during the riding process. In the first section of this chapter we describe the design and building process of the main structure of the bicycle frame, next we present the design of the haptic steering device and overload protection mechanism.

The mechanical portion of the simulator consists of three main structural parts. A bicycle roller training base (600×400 mm), a square tube ($\mathrm{40}\times \mathrm{40}\times \mathrm{1000}$ mm) used as a steering column, and a rear half of a step-through bicycle frame (54 cm), see Fig. 2. To mount all the structural parts together the following modification are made. The front roller of the base is removed and a rectangular tube ($\mathrm{40}\times \mathrm{20}\times \mathrm{500}$ mm) is welded as a replacement. In addition, six metal foot pegs ($\mathrm{40}\times \mathrm{20}\times \mathrm{500}$ mm) two at the front, middle and rear are also mounted. The foot pegs are mainly used to increase the vertical distance of the base in respect to ground and also to distribute the load equally to specific areas of the frame. At the steering column a (25×500 mm) tube is welded at a 25^∘ angle and at a 40 mm distance from the end of the square tube. At the bicycle frame the headtube is removed two custom made clamps (AL 7075) are mounted to the upper and lower tubes respectively. The upper and lower clamps are connected with two metal straps one per each side. The combination of the upper frame clamp design together with the (25×500 mm) welded tube of the steering column create the first prismatic joint of the assembly, see Fig. 3a. This prismatic joint is used to mount the steering column to the bicycle frame. Steer and saddle height can be adjusted over a large range, and the steering assembly can be moved horizontally to accommodate a large range of body sizes and bike geometries.

Figure 3 Connection of the bicycle frame to the roller base using prismatic joints and mechanical arms.

To mount the steering column and bicycle frame to the roller base a combination of different types of adjustable blocks are used (blocks are provided from RK Rose Krieger). A hinge clamp block and a t-shape block (Gwv 40). First, the hinge clamp block is mounted to the column and tilted to create a bicycle headtube angle of 72^∘, since this is a common angle also adopted in the Carvallo-Whipple bicycle model (Meijaard et al., 2007). Afterwards, the hinge block is mounted to the t-shape block which is next mounted to the racks of the base with two addition square tubes ($\mathrm{40}\times \mathrm{40}\times \mathrm{380}$ mm) and two custom made c-shape clamps. Because the upper joint of the column is prismatic a second prismatic joint is also constructed at the base level. To construct the second joint an additional t-shape block is mounted to the base oppose to the first one. A square tube (40×40 mm) is mounted to the first clamp and sliding freely through the square hole of the second one, see Fig. 3b. These two prismatic joints together with the c shape clamps are used to adjust the reach dimensions of the bicycle frame. The mounting of the bicycle frame from the front end is now completed. To mount the bicycle frame from the rear end to the base two mechanical arms and a trapezoidal shape structure are combined. The mechanical arms are constructed from L-shape stripes and are used to mount the bike from the rear wheel axis to the base. The trapezoidal structure is constructed from aluminium tubes and a combination of hinge clamps (Gp 25, Kvr 25, W 25). This structure is used to mount the bicycle frame from the seatpost to the base, see Fig. 3c.

3.1 Description of haptic steering device

To allow the rider to interact with a virtual environment and receive realistic handlebar torque feedback from the simulation model a haptic steering device is required. The device must be able to generate realistic torque feedback in order to enhance rider control and prevent excessive rotation of the handlebars. The importance of haptic steering feedback on rider control is stated in previous bicycle experiments conducted by Lee et al. (2015). In this subsection we describe the components used to build such a device.

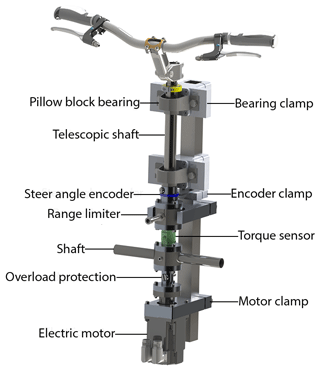
The haptic steering device consists of two sub-assemblies. The steering shaft assembly and the column mount assembly. The steering shaft assembly includes the components used to build the steering shaft, whereas the steering column assembly includes the components used to mount the steering shaft to the column. The steering shaft assembly consists mainly of eight components (not including the handlebar assembly and adaptors). Five of these components are mechanical and three of them are electromechanical. More specific, an overload protection mechanism is used for safety, a steer range limiter is used to restrict the rotational range to ±35^∘, a shaft is used to intersect with the actuators of the limit switches (limit switches are shown in Fig. 5) and turn of the electric motor when the maximum rotational range is reached. Two pillow block bearings are used to mount the telescopic shaft to the column. An electric motor is used to generate steering feedback, an incremental encoder is used to measure the steering angle and a torque sensor is used to measure the applied handlebar torque. The steer shaft assembly is mounted to the column with 3 additional custom made clamps, the electric motor clamp and two bearing clamps. An extra clamp is used to mount the reading head of the encoder. Material used for the shaft components is AL7075 excluding the telescopic shaft which is made from Steel 304. In Fig. 4 the steering shaft and column assembly is presented.

Figure 4 Steering column and shaft assembly exported from solidworks 2016.

3.2 Description of overload protection mechanism

Different methods can be used to protect a rotating shaft from torsional stress. On a software level torque and rotational range limits can be set in the parameter programming of the motor drive. However, in case of a sensor malfunction the software might be unable to recognize the torsional overload condition. For this reason, a mechanical solution is recommended as a second measure of protection. There are typically two mechanical mechanisms used to protect a rotation shaft, a torque limiter and a shear pin. From the above two mechanisms the usage of a torque limiter is not recommended for this application mainly because there is no clear indication of the operational speed the rated torques are measured at, as first noticed by Moore et al. (2004). Most of the available torque limiters list the rated torques but with no indication of the operating speed the torques are measured at. It turns out they are with respect to an 1800 rpm operating speed. The absence of this vital information together with the low steer rates make the selection of a limiter inappropriate, since it might lead to further adjustments and modifications to make the limiter operate properly. For this reason, a custom shear pin mechanism is designed and mounted inline with the steering shaft. The shear pin mechanism functions are to protect the steering shaft and the user by mechanically disengaging the feedback motor from the handlebars when the maximum torsional strength is reached. For the geometric design of the shaft-hub mechanism and selection of the proper pin size the following equations are used. For the shaft-hub combination the desired geometric relationship between the two diameters is D1=1.5D, where D1 is the hub, and D the shaft diameter, respectively. The diameter of the shear pin d, is calculated based on the shear strength τ, of the material, the service factor κ, the maximum breaking torque T, and the hub diameter D, as seen in Eq. (1) conforming to the requirements of ISO 8730-40 standards.

$$\begin{array}{}\text{(1)}& \mathit{\tau }=\mathit{\kappa }{\displaystyle \frac{\mathrm{4}T}{\mathit{\pi }{d}^{\mathrm{2}}D}}\end{array}$$

The shear strength of the selected pin is also tested in practice. The pin shears between 25–26 Nm which is 30 % lower from the steering shaft overload condition. The selected shear limit is considered adequate according to the aforementioned ISO standards.

4 Sensor and motor selection

There are three sensors and one actuator motor in the existing bicycle simulator. Two of the three sensors are located at the steering assembly. More specifically, an angular encoder, a torque sensor and an electric motor are mounted inline with the steering shaft, see Fig. 5, whereas a gearwheel encoder is mounted at the rear roller of the powertrain assembly as seen at Fig. 6.

Figure 5 Steering shaft assembly.

To select the proper motor and sensors a number of technical specifications need to be determined in advance. For the encoders, the type and resolution, for the torque sensor, the range and resolution, and for the electric motor the maximum and continuous torque. In this section we describe the procedure followed to determine these requirements. In the first two paragraphs, the encoders and torque sensor requirements are determined, whereas in the last paragraph the electric motor requirements.

Two types of encoders are found in literature, incremental and absolute. Incremental rotary encoders output the pulse corresponding to the rotation angle only while rotating, and the counting measurement method that adds up the pulse from the measurement beginning point. On the other hand, absolute rotary encoders output the signal of position corresponding to the rotation angle by coded elements. The incremental encoder does not output an absolute position and for this reason typically the internal structure is simpler and the cost lower. For both the steer angle and wheel speed measurements incremental encoders are selected. The resolution of the steer encoder in counts per turn (cpt), is determined based on the smallest steer angle increment Δδ, as seen at equation below (Fagor, 2013):

$$\begin{array}{}\text{(2)}& N={\displaystyle \frac{\mathrm{360}{}^{\circ }}{\mathrm{4}\mathrm{\Delta }\mathit{\delta }}}\end{array}$$

A steer encoder with 152 000 (cpt), and an additional index channel for accurate homing was selected (RLM2HDA001). For the wheel speed encoder the resolution is selected based on the resolution range of encoders used for similar systems, such as the anti-lock braking systems of motorcycles. A gearwheel encoder with 192 (cpt), is selected (reading head is from rls type is gts35, gearwheel from Ktm). The gearwheel and reading head are mounted directly to the rear roller and base respectively as seen at Fig. 6.

Figure 6 Gearwheel sensor mounted at base roller.

For the selection of the torque sensor the steer torque profile must be determined, not only for normal bicycle riding but also during perturbation tests. Measuring the steer torque profile can be achieved with modern torque sensors although the problem of crosstalk disturbance must be taken into account. Crosstalk occurs due to the large forces and moments applied to the fork and handlebars by the ground and the rider during bicycling. These forces and moments corrupt the relatively small torque measurements as they can be hundreds of times larger in magnitude. Few published studies attempt to estimate or directly measure steer torque. De Lorenzo and Hull (1999) instrumented a bicycle which could measure pedal, handlebar, and hub forces to characterize the in-plane structural loads during downhill mountain biking. The handlebar forces acting forward and parallel to the ground were used to estimate the steering torque. A maximum torque of about 7 Nm is shown in this study although crosstalk disturbance was not taken into account. Jackson and Dragovan (1998) attempted to estimate the torques acting on the front frame based on orientation, rate and acceleration data taken while riding a bicycle with no-hands. They estimated a steer torque under ±2.5 Nm. Cheng et al. (2003) attached a torque wrench to a bicycle and made left and right turns at speeds from 0–13 m s⁻¹. The torques were found to be under 5 Nm except for the 13 m s⁻¹ trial which read about 20 Nm. However, the torque wrench calibration range (0–84 Nm) was too large for the obtained torque measurements reducing the accuracy of his results. Iuchi and Murakami (2006) attached a steer motor and controller to the handlebars and tried to estimate steer torque from the motor current and handlebar moment of inertia. They are one of the few studies that takes into account some of the inertial effects of the handlebar. Cain and Perkins (2010) designed and fitted a custom torque sensor in the bicycle steer tube. They tried to remove crosstalk effects by applying an axial load on the sensor but they did not account for the dynamic inertial affects of the components above and below the sensor. Their measured steer torques during cornering were under ±2.4 Nm. From the above mention studies, none succeed to measure the actual applied rider torque since very few accounted crosstalk disturbance and even fewer the dynamic inertial effects of the components above or below the sensor. Moore et al. (2004) was the first who developed an experimental bicycle that can accurately extract rider applied torque. In his design a torque sensor (Futek 150, TFF350, ±15 Nm) is mounted inline with the handlebar and fork using a double universal joint isolating the handlebar and fork loads during bicycling. The instrumented bicycle he developed was used to measure steer torque responses during lateral force perturbation experiments (Schwab et al., 2013). A rider torque range between 0–10 Nm, is realized in these experiments. For that reason, a torque sensor with a range of ±25 Nm, and a resolution of 4 µNm, is selected (Kistler 9349A).

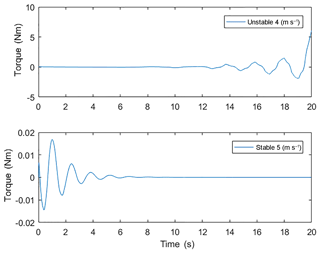
Figure 7 Estimated haptic steer feedback torque based on angular acceleration output $\ddot{\mathit{\delta }}$, of the benchmark bicycle model for a steer torque input of 5 Nm.

For the selection of the haptic steer feedback motor the Carvallo-Whipple bicycle model developed by Meijaard et al. (2007) is used to predict the maximum torque required within the stable and unstable speed. To obtain an estimation of the feedback motor torque a steer torque impulse of 5 Nm is given as an input to the model. The selected input torque is based on previous bicycle experiments conducted from Moore et al. (2004) and is considered the maximum steering torque measured for controlling a bicycle in normal maneuvers. To calculate the output feedback torque the steer angular acceleration $\ddot{\mathit{\delta }}$, and the moment of inertia I, of the steer axis of the bicycle simulator is used, see Eq. (3). The steer angular acceleration $\ddot{\mathit{\delta }}$, is given as an output of the Carvallo-Whipple bicycle model, whereas the steer shaft moment of inertia I, of the bicycle simulator is measured experimentally.

$$\begin{array}{}\text{(3)}& T=I\ddot{\mathit{\delta }}\left(t\right)\end{array}$$

As shown in Fig. 7 a maximum torque of almost 5.4 Nm is noticed at the unstable speed region, whereas at the stable speed region a torque of maximum 0.02 Nm is found. Combining a reduction gearhead with an electric motor to reduce its physical size and increase torque output is not optimal for the existing design. Backlash of the gearhead can distort torque sensor measurements and for this reason is excluded from the existing steering design. For this reason, an electric motor of 1410 W and drive combination able to deliver a stall torque of approximately 4 Nm, and a max.torque 11.5 Nm are selected for the steering actuation (Kollmorgen AKM42G and AKDP00606).

Figure 8 Block diagram of motor and motor drive configuration.

Figure 9 Ampere/torque analogy.

5 Calibration and testing of hardware components

To ensure that the selected components fulfill their specifications every component is tested and calibrated. It is important that all of the sensors and actuator behave in a consistent and predictable manner. For example, motor performance before and after tuning is compared not only with its own feedback but also with the torque sensor output. This way performance mismatch is analyzed in an early development stage and is avoided by either re-calibrating specific sensors or by re-tuning the motor drive control parameters.

To calibrate the torque sensor a table wrench, a digital torque wrench, an amplifier (Kistler 5030A2) and an oscilloscope are used. The torque sensor is mounted from one end to a table wrench and from the other end to a digital torque wrench. Next, the torque sensor is connected to an amplifier and an oscilloscope. For different torque magnitudes and amplification ranges the voltage output is measured. Amplification range 1 can measure torque magnitudes up to ±25 Nm, whereas range 2 only up to ±2.5 Nm. Expected rider torque is assumed within 0–10 Nm range and thus amplifier range 1 is selected as a configuration for the bicycle simulator.

Figure 10 Motor performance before and after tuning.

Figure 11 Experimental set-up to measure moment of inertia.

An analog signal is used to supply a reference command torque to the haptic feedback motor. There are three command modes that the motor drive can be set with the analog mode, position control, velocity control and torque control. Position and velocity control are typically used when precise tasks are required, for instance a welding task. On the other hand, torque control is used when compliant control is needed. Compliant here means that the rider is able to rotate the shaft at any angle required while receiving torque feedback from the motor. Since compliance is required the operation mode is set to analog torque mode.

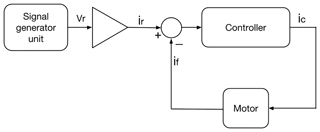
The analog torque control loop of the motor drive unit can be seen at Fig. 8, where (Vr) is the reference voltage, (ir) is the current reference, (ic) is the output current of the motor controller and (if) the feedback current of the electric motor. To convert the input reference voltage (Vr) to an input current reference (ir) a scaling constant must be set in Amp V⁻¹. This scaling constant is set based on the peak current of the drive and the maximum voltage range of the controller. For a peak motor current of 18 Amp and a maximum input voltage of 12 V the constant is set to 1.5 Amp V⁻¹.

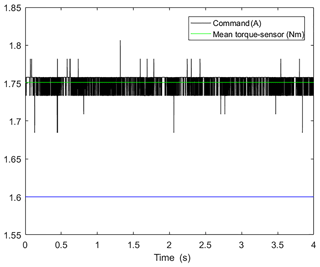
After the current scaling constant is set, the torque constant is determined by measuring the motor response for a given input command. For an input voltage command of 1.06 (Vr), which corresponds to a current of 1.6 (ir) a torque of 1.75 Nm is produced as an output from the motor, see Fig. 9. A linear torque/current relationship of 1.09 Nm Amp⁻¹ is set in the software for controlling the motor in torque mode. A maximum motor torque output of 10.92 Nm can be reached for this specific motor-drive configuration.

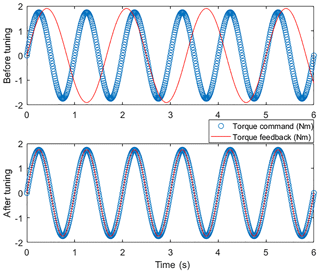
Once the motor is connected to the steering shaft the system is tested for given control tasks. A sinusoidal input signal with a frequency of 2 Hz and an amplitude of 1.6 Amp equivalent to 1.75 Nm is given as an input to capture the response of the system. The performance of the motor is tested before and after tuning. The methodology used to estimate the shaft inertia and tune the motor drive is described at next subsection. As it can be seen at Fig. 10 the torque commanded to the motor matches to the output feedback torque when the motor is tuned. On the other hand, overshooting and phase shift occurs when the motor is not properly tuned.

Estimation of steering shaft moment of inertia

The damping and inertia properties of the steering shaft must be estimated in case the torque that the rider applies is estimated from acceleration data and also in case position and velocity modes are used to control the motor and auto tuning can not be used for safety reasons. To estimate the moment of inertia different methods can be used. A first approach could be to extract the moment of inertia from the CAD model. A second approach could be to use system identification. A third approach could be to add two springs and calculate the moment of inertia from the oscillation period and the equation of motion of the system. The first method can not be used for the existing CAD model. In the CAD model of the steering shaft there are parts exported from suppliers which are represented as solid entities and are not modeled correctly. The assembly parts of these entities could not be separated and the moment of inertia of these components can not be calculated separately. For instance, the motor shaft moment of inertia can not be measured as a separate body of the motor. On the other hand, system identification can be used to estimate the moment of inertia of the steering shaft, however a more straightforward approach is the spring method. For the above reasons, the last approach is used to estimate the moment of inertia of the steering shaft. To oscillate the steering shaft two extension springs with a rate of k=317 N m⁻¹ and a length of 0.05 m are added perpendicular to the handlebars as shown in Fig. 11.

Figure 12 Oscillation of steering shaft using spring method.

The springs are pretensioned proportionally and set to idle around 0^∘. The springs are excited and the oscillation period is measured through the steering encoder. The oscillatory motion of the shaft can be seen in Fig. 12. The equation of motion of the steering shaft after attaching the springs is:

$$\begin{array}{}\text{(4)}& I\ddot{\mathit{\delta }}\left(t\right)+b\dot{\mathit{\delta }}\left(t\right)+\mathrm{2}k{a}^{\mathrm{2}}\mathit{\delta }\left(t\right)=\mathrm{0}\end{array}$$

The steering shaft equation of motion consists of the inertia I, viscous friction b, and spring stiffness k, and moment arm a. δ denotes the desired angle of the system, $\dot{\mathit{\delta }}$ and $\ddot{\mathit{\delta }}$ the desired angular velocity and acceleration respectively. Friction caused between bearings and electric motor components is neglected, thus b is considered zero. Thus the mass moment of inertia equals:

$$\begin{array}{}\text{(5)}& I={\displaystyle \frac{\mathrm{2}k{a}^{\mathrm{2}}}{{\mathit{\omega }}^{\mathrm{2}}}}\end{array}$$

The mass moments of inertia of the steering shaft assembly using the spring method and auto-tuner of the motor drive are I=0.0828 kg m² and I=0.0912 kg m² respectively. The comparison of the two methods is used to validate the spring method. The inertia difference between the two methods might be due to the fact that viscous friction b, is neglected in the spring method, whereas this is not the case when auto-tuning is used.

6 Discussions and conclusions

The objective of this study was to realize all the necessary steps needed to design and build a realistic bicycle simulator. The simulator prototype is the result of multiple design choices and constraints. Constraints, primarily time-wise, have resulted in a system wherein a mountain bike is placed on top of rollers and later fitted with a haptic steering device. There is still space for improvement regarding the mechanical structure and haptic steering device. For example, the prismatic joints of the mechanical structure can be equipped with linear bearings to allow friction-less motion when adjusting the stack and reach dimensions. The steering shaft assembly can be machined as a single part and from a light material in order to reduce both inertia weight and misalignment.