the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The computation of bending eigenfrequencies of single-walled carbon nanotubes based on the nonlocal theory
Jozef Bocko
Pavol Lengvarský
Róbert Huňady
Juraj Šarloši
In this work, a recently proposed nonlocal theory of bending is used in the analysis of eigenfrequencies of single-walled carbon nanotubes (SWCNTs). The nanotube vibration is analyzed in the form of a homogenized continuum. Classical treatment where a nanotube is approximated by standard beam theory, is replaced by the more sophisticated nonlocal method of material interactions where a nonlocal parameter is used. The eigenfrequencies are computed by the combination of analytical as well as numerical methods for four different carbon nanotube (CNT) supports. Various types of supports are considered for the analysis: fixed–simply supported, fixed–free, simply–simply supported and fixed–fixed. Due to the huge amount of computed data, only outcomes of eigenfrequency computations for the nanobeams of armchair type with fixed and simply supported ends, and different nonlocal parameters are represented in the form of graphs at the end of the article. The study shows how the nanotube eigenfrequencies depend on nonlocal parameters as well as on the length and diameter of CNTs. The obtained results are in good agreement with the results published in papers which were gained by different procedures.
- Article
(3641 KB) - Full-text XML
- BibTeX
- EndNote
Functional materials and nanomaterials are attracting a lot of attention in the areas of modern engineering. The internal structure of such materials is relatively simple but the determination of their properties is often associated with difficulties. In many cases, the theoretical treatments with indirect measurements of conjugated behavior lead to the solution of a stated problem. In our case, we will deal with the determination of eigenfrequencies of carbon nanotubes. The eigenfrequencies are very important parameters of these structures because their measurement can serve as a base for the determination of elastic properties, e.g., Young's modulus of homogenized materials.
The massive investigation of carbon nanotubes started after publishing well-known article (Iijima, 1991). CNTs are large macromolecules composed exclusively of carbon atoms. Nanotubes can be formally obtained by rolling up a single-walled plane sheet of graphite, called graphene, into a cylindrical shape. Nanotubes have remarkable mechanical properties. The most important task in the design of a machine is to find an adequate material for a particular structure. In principle, the aim is to use strength and lightweight material. Nowadays, in mechanical engineering, the carbon nanotubes are candidates that fulfill such demands as parts of composite materials (Wu and Chou, 2012; Yayli, 2014). Besides of mechanical properties, the scientists focus their research on electrical, thermal and optical properties of CNTs. Many applications of CNTs are oriented to the area of biology and medicine.
Depending on the scale, the simulation of SWCNTs is realized by several methods: atomistic scale simulation, simulation by molecular dynamic and the macroscale continuum treatment. In this paper, the third method is applied to describe the bending eigenfrequencies of CNTs. As the elements of nanostructure have special properties, the homogenized continuum of CNTs has to reflect such specific behavior. The standard theory of elasticity is built on the principle of local action, i.e. the response at a point depends on actions in its neighborhood. However, this is not the case of nanostructures. Here, nonlocal influences can occur and therefore, the nonlocal theory has to be used (Eringen, 2002). According to the underlying theory, strain in every point of a body influences a stress level at the investigated point.
Different applications of the nonlocal theory can be found in many research papers. A review on the application of the nonlocal continuum theory for static and dynamic loadings of carbon nanotubes and graphene sheets is presented in the paper of Arash and Wang (2012). The nonlocal elastic beam model, the elastic shell model and the elastic plate model is established for modeling carbon nanotubes and graphene sheets. The different loading states as bending under transverse loading of CNTs, buckling analysis of axial loaded CNTs and free vibration of CNTs are described. Using the nonlocal continuum mechanics in nonlinear stability analysis of graphene sheets is presented in paper (Asemi et al., 2014). The Galerkin method with the nonlocal parameter for the analysis of simply supported orthotropic graphene sheets is used. The paper reports that the nonlocal parameter has significant effect on the postbuckling behavior of graphene sheets. Kirchhoff's plate theory with the nonlocal parameter is used for eigenfrequency investigation of nanoplates with elastic (Winkler–Pasternak) boundary conditions in the research of Chakraverty and Behera (2015). The effect of the aspect ratio, the elastic boundary conditions and the nonlocal parameter is presented. A forced vibration of a single- and double-walled carbon nanotube under excitation of a moving harmonic load has been analyzed using nonlocal elasticity theory by Rahmani et al. (2017, 2018).
The vibrations of tensioned nanobeams using the nonlocal beam theory are investigated by Bagdatli (2015). The nonlinear frequencies for fixed–fixed and simply–simply supported Euler–Bernoulli nanobeams are presented. The vibration behavior of the nanobeams with small scale effects represented by the nonlocal parameter is studied in the research of Lim et al. (2010). The forced vibration of SWCNTs is investigated by the nonlocal theory in Şimşek (2010). The SWCNTs as nonlocal Euler–Bernoulli beams are modeled and the effects of aspect ratio and nonlocal parameter on vibration behavior of SWCNTs are discussed. The vibrational behavior of CNTs using wave propagation approach is studied by Hussain et al. (2017), Hussain and Nawaz (2017). Other applications of the nonlocal theory and the vibration behavior of carbon nanotubes with different boundary conditions can be found in papers (Narendar and Gopalakrishnan, 2012; Şimşek, 2011; Thongyothee et al., 2013; Wang et al., 2015; Yang et al., 2010). The properties of single-walled carbon nanotubes are well described in papers (Arash and Wang, 2012; Fu et al., 2012; Gupta and Batra, 2008; Harik, 2002; Karličić et al., 2015; Kumar and Srivastava, 2016; Lee and Chang, 2012).
In this paper, the bending frequencies of single-walled carbon nanotubes based on nonlocal stress theory are investigated. The carbon nanotubes are represented by the Euler–Bernoulli nanobeams with nonlocal parameter. The authors previously published bending eigenfrequencies for different types of boundary conditions and chirality (and corresponding diameters) in papers Bocko and Lengvarský (2014a, b, c). Novelty of paper lies in investigation of chirality effects to eigenfrequencies, comparision of semianalytical methods with the finite element method (FEM) for different nonlocal parameters for boundary condition of type fixed–free. Further, the eigenfrequencies are computed for four different supports (fixed–simply supported, fixed–free, simply–simply supported and fixed–fixed) of carbon nanotubes, the semianalytical results for fixed–simply supported armchair CNTs with different lengths and five nonlocal parameters are presented in graphical form at the end of the article. Finally, the comparison of the results with results from Imani Yengejeh et al. (2014), Lü et al. (2007), Zhang et al. (2009) is done.
The elasticity theory of continuum media is based on several fundamental assumptions: the principle of objectivity, determinism, material symmetry, equipresence, causality, local action, etc. The principle of local action represents the fact that stress at a material point is related exclusively to the deformations in its immediate surroundings. On the other hand, in the nonlocal continuum theory, this assumption is abandoned, and the stress tensor at the investigated part of continua is influenced by the movement of all points of continua (Eringen, 2002). The equation for nonlocal stress is written as:
Here, T(x) is the stress tensor at point x, C(x) is the fourth-order elasticity tensor, ϵ(x) is the strain tensor and relation is the nonlocal modulus defined by Eringen (2002). The material parameter τ is expressed by relation . Here, the so-called nonlocal parameter μ represents the influence of using very small distances. This parameter can be evaluated from relation . Here, e0 is a material constant, li is the internal characteristic length and l is the external characteristic length. More information about using the nonlocal parameter μ in connection with beams can be found in Reddy and Pang (2008). Simplified Eq. (1) can be written as:
where ∇2 is the Laplacian operator. The theory of homogeneous isotropic beam, together with above-mentioned premise, results in the equation relating normal strain εxx and normal stress σxx by Young's modulus E and parameter μ (Thongyothee et al., 2013):
Combination of the nonlocal theory and the theory of free vibration of a beam allows us to write the following relation (Thongyothee et al., 2013):
Here, u is the transverse displacement of the beam, mb is the mass of beam related to the unit length, J is the second moment of cross-section area. In the overall motions of the beam, the various parts will move in unison, the relative proportion of their displacements being unchanged with time. This leads to the separation of space and time variables. Finally, considering constant cross-section of the beam, we get the differential equation of fourth order with respect to the independent space variable x:
Here, ψ(x) is an eigenvector (eigenmode) and the parameter β is defined as:
The scalar quantity ω, in the above relation, is the angular frequency of vibrations of the free CNT. The substitution of β into the Eq. (6), results into the formula:
Here, B1, B2, B3, B4 are determined in accordance with the given support conditions of the nanobeam.
3.1 Geometry of carbon nanotubes
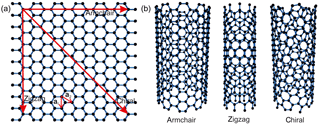
Rolling up of a graphene sheet (Fig. 1a) can be accomplished in many ways and in principle it can be described by a chiral vector ch or a chiral angle θ:
Having fixed vectors a1 and a2 the pairs of integers (n, m) specify the chirality of SWCNT. Two limit states of CNTs (n, 0) or (θ=0∘) and (n, n) or (θ=30∘) are called zigzag and armchair (Fig. 1b), respectively. The intermediate states of CNTs (n, m) or () define chiral nanotubes, (Fig. 1b).
Chirality influences the response of carbon nanotubes to external disturbances. Beside of chirality we will use another important characteristic parameter of the carbon nanotube, its length L.
3.2 Boundary conditions
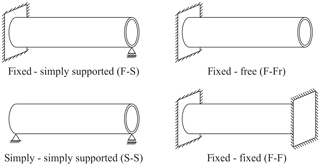
In this paper we have focused our attention on the CNTs with the following types of boundary conditions (Fig. 2): fixed–simply supported (F–S), fixed–free (F–Fr), simply–simply supported (S–S) and fixed–fixed (F–F).
3.3 Semianalytical solution
The application of boundary conditions to the differential equation results in the following characteristic equations:
and they finally lead to the relations:
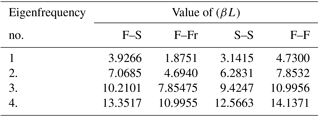
Because the nanotube is modeled as a continuum by homogenization method, the characteristic equations are transcendental ones. The roots (βL) of the equations for the prescribed supports were obtained using program MATLAB®. The first fourth values (βL) can be found in Table 1. The radian frequencies ω result from Eq. (7) and for the frequencies f we have formula .
The second moment of area J with respect to the axis which is perpendicular to the axial direction of the beam is related to the thickness of the nanotube shell. Because there is no certainty in the definition of this parameter, different values can be found in the literature. Here, we use relations from Swain et al. (2013):
where R is the radius of the nanotube. The chirality parameters (n, m) characterize the radius of CNT, and the radius is defined by equation:
where a0=0.1424 nm is the distance between two neighboring carbon atoms and the chirality parameters for our computations are m=n.
In this chapter, the nonlocal finite element formulation is presented. The mass and stiffness matrices of finite element are derived from Eq. (5).
The element stiffness matrix can be defined as:
and the nonlocal element mass matrix can be defined as:
Table 3The first eigenfrequency of carbon nanotubes for both methods with different nonlocal parameter.
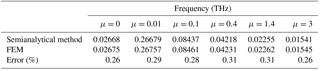
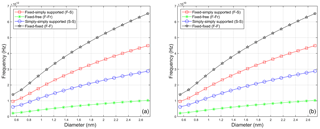
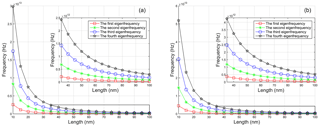
Figure 3The first eigenfrequencies of armchair nanotubes with the nonlocal parameter μ=0.01 and length (a) L=10 nm, (b) L=100 nm.
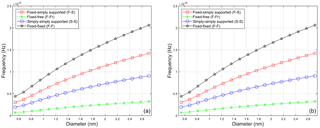
Figure 4The first eigenfrequencies of armchair nanotubes with the nonlocal parameter μ=0.1 and length (a) L=10 nm, (b) L=100 nm.
Table 4The first eigenfrequencies of armchair nanotubes with length L=10 nm for different boundary conditions and nonlocal parameters μ.
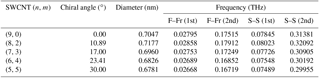
At first, the effect of chirality on the eigenfrequencies of CNTs is investigated. The chirality angle varies from 0 to 30∘. The semianalytical computations of the first two eigenfreqeuncies are accomplished for different types of CNTs but with approximately the same diameters. The length of the tubes is 10 nm and the following types of boundary conditions are used (Fig. 2): fixed–free (F–Fr) and simply–simply supported (S–S). From computations (Table 2) result that the chirality has effect on the change of CNTs eigenfrequencies due to the small change of tube diameter. The maximum difference in the eigenfrequencies is 7 %. Under otherwise identical conditions, the effect of the chirality of SWCNTs can be neglected. For this reason, only armchair CNTs are investigated in this paper.
The results for the tube chirality (5,5), length 10 nm and boundary condition of type F–Fr computed by the semianalytical as well as FEM are given in Table 3. The 100 elements are used for the FEM. It is clear from the results that both methods give almost the same results.
The semianalytical computations for armchair single-walled carbon nanotubes with F–S, F–Fr, S–S and F–F boundary conditions were accomplished in commercial program system MATLAB®. The chirality of armchair carbon nanotubes was changed from (4, 4) to (20, 20) which corresponds to the range of diameters from D=0.5424 nm to D=2.712 nm. The length of considered CNTs varies from L=10 nm to L=100 nm. The nonlocal parameter μ is chosen to be 0.01, 0.04, 0.1, 0.3 and 0.4, respectively. The minimal computed eigenfrequency f=0.9289 GHz was obtained for the fixed–free CNT with the diameter D=0.5424 nm, the length L=100 nm and the nonlocal parameter μ=0.4. The maximal computed eigenfrequency f=6.5223 THz is related to the fixed–free CNT with the diameter D=2.712 nm, the length L=10 nm and the nonlocal parameter μ=0.01. The dependence of the first eigenfrequencies of armchair SWCNTs with the nonlocal parameter μ=0.01 on the diameter for 10 nm long CNT is shown in Fig. 3a and for 100 nm in Fig. 3b. Similarly, Fig. 4 shows the results of computations for the nonlocal parameter μ=0.1, so that the dependence of the first eigenfrequencies of armchair SWCNTs with the nonlocal parameter on the diameter for 10 nm long CNT is shown in Fig. 4a and for 100 nm in Fig. 4b.
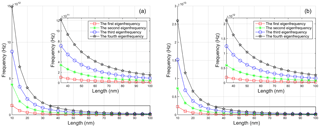
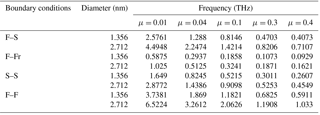
Figure 6The first four eigenfrequencies of fixed–simply supported armchair nanotubes with nonlocal parameter μ=0.04, (a) nanotube with chirality (n, m) = (10, 10) and diameter D=1.356 nm, (b) nanotube with and chirality (n, m) = (20, 20), diameter D=2.712 nm.
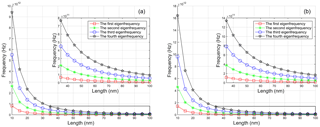
Figure 7The first four eigenfrequencies of fixed–simply supported armchair nanotubes with nonlocal parameter μ=0.1, (a) nanotube with chirality (n, m) = (10, 10) and diameter D=1.356 nm, (b) nanotube with and chirality (n, m) = (20, 20), diameter D=2.712 nm.
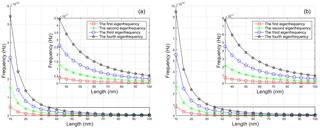
Figure 8The first four eigenfrequencies of fixed–simply supported armchair nanotubes with nonlocal parameter μ=0.3, (a) nanotube with chirality (n, m) = (10, 10) and diameter D=1.356 nm, (b) nanotube with and chirality (n, m) = (20, 20), diameter D=2.712 nm.
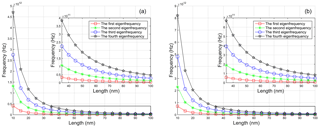
Figure 9The first four eigenfrequencies of fixed–simply supported armchair nanotubes with nonlocal parameter μ=0.4, (a) nanotube with chirality (n, m) = (10, 10) and diameter D=1.356 nm, (b) nanotube with and chirality (n, m) = (20, 20), diameter D=2.712 nm.
The graphs conclude that increasing diameter of the carbon nanotube leads to higher first eigenfrequency and the eigenfrequencies of ten times longer carbon nanotubes are hundred times lower. Comparison of Figs. 3 and 4 shows that ten times higher value of nonlocal parameter leads to approximately three times lower eigenfrequencies. The value of nonlocal parameter affects more the eigenfrequencies of the carbon nanotubes with a smaller diameter.
As there is a huge number of possible combinations of parameters, we have focused our attention on the first eigenfrequencies for the diameters nm for chirality (10, 10) and D=2.712 nm for chirality (20, 20). The comparison of the first eigenfrequencies for all considered boundary conditions of armchair nanotubes with the length L=10 nm is given in Table 4. It is clear from Table 4 that diameter, nonlocal parameter and boundary conditions have effect on the eigenfrequencies of nanotubes. In principle, the higher value of the nonlocal parameter the lower value of eigenfrequencies. Opposite tendency is seen for the diameter of CNTs. The highest first eigenfrequencies were computed for the fixed–fixed boundary conditions of CNTs and the lowest first eigenfrequencies for the fixed–free boundary conditions.
Due to complexity, the effect of the nonlocal parameter on only first four eigenfrequencies of armchair CNTs was studied. The graphs in Figs. 5–9 show relations between eigenfrequencies and length L of carbon nanotube with the F–S type boundary conditions. The nonlocal parameter was the same as above.
The graphs show that the eigenfrequencies decrease with increasing length and nonlocal parameter. The eigenfrequencies for the nonlocal parameter equal 0.01 are approximately three times lower than for the nonlocal parameter 0.1.
Because different authors use different parameters for nanotube description in the literature (density, Young's modulus, nominal thickness of nanotube, boundary conditions), we compared our results only with those where the authors used similar inputs. As a number of such inputs was published for the boundary conditions of type fixed–free, Table 5 gives the comparison of the first eigenfrequencies computed by different authors and methods with the result of method in the article. The biggest difference in this comparison does not exceed 15 %.
Table 5The comparison of the first eigenfrequencies with published results.
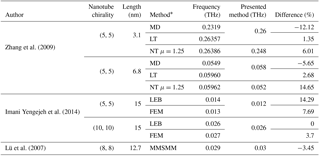
* MD: Molecular Dynamics, LT: Local Timoshenko beam, NT: Nonlocal Timoshenko beam, μ: nonlocal parameter, LEB: Local Euler–Bernoulli beam, FEM: Finite Element Method, MMSMM: Modified Molecular Structural MechanicsTables may have a footer.
We discussed the analytical computation of eigenfrequencies of SWCNTs based on nonlocal beam theory and the numerical results are given for armchair SWCNTs. In the nonlocal theory, the response of a structure at the point of a question is influenced by all particles of the structure. The small scale length effect of the CNTs was represented by the nonlocal parameter in the nonlocal beam theory. The transcendental frequency equations resulting from four different boundary conditions have been solved by computer system MATLAB® and parametric studies of results for the fixed–simply supported beam are given in the graphic form. Five different values of nonlocal parameter were used and its influence on the computed eigenfrequencies is shown.
It can be stated that:
-
The effect of the chirality of SWCNTs can be neglected.
-
The nanotube eigenfrequencies depend on nonlocal parameters, as well as on the length and diameter of CNTs.
-
Increase in the diameter of a carbon nanotube leads to higher eigenfrequencies and the eigenfrequencies of ten times longer carbon nanotubes are hundred times lower.
-
Higher nonlocal parameter leads to the smaller eigenfrequencies of CNTs. Ten times higher value of nonlocal parameter leads to approximately three times smaller eigenfrequencies.
-
The eigenfrequencies of shorter and, in general, smaller carbon nanotubes are more affected by the value of nonlocal parameter.
-
The presented results are in good agreement with the results published in other papers.
-
The experimentally measured eigenfrequencies can be used for the determination of Young's modulus of homogenized single-walled carbon nanotubes.
-
In the future work, the finite element method for modeling carbon nanotubes and the effects of boundary conditions, nonlocal parameters and vacancies on mechanical parameters will be investigated.
Data can be made available upon reasonable request. Please contact Pavol Lengvarský (pavol.lengvarsky@tuke.sk).
BJ formulated theoretical description of work and prepared analytical formulations; LP performed semianalytical computations; HR accomplished FEM computations; ŠJ wrote the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
The authors gratefully acknowledge the support
given by the Slovak Grant Agency VEGA under the grant no. 1/0731/16
Development of Modern Numerical and Experimental Methods of Mechanical System
Analysis. no. 1/0355/18 The use of experimental methods of mechanics for
refinement and verification of numerical models of mechanical systems with a
focus on composite materials and ITMS: 26220120060 supported by the Research
and Development Operational Programme funded by the ERDF.
Edited by: Anders Eriksson
Reviewed by: two
anonymous referees
Arash, B. and Wang, Q.: A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes, Comput. Mater. Sci., 51, 303–313, https://doi.org/10.1016/j.commatsci.2011.07.040, 2012.
Asemi, S. R., Mohammadi, M., and Farajpour, A.: A study on the nonlinear stability of orthotropic single-layered graphene sheet based on nonlocal elasticity theory, Lat. Am. J. Solids Struct., 11, 1515–1540, https://doi.org/10.1590/S1679-78252014000900004, 2014.
Bagdatli, S. M.: Non-linear transverse vibrations of tensioned nanobeams using nonlocal beam theory, Struct. Eng. Mech., 55, 281–298, https://doi.org/10.12989/sem.2015.55.2.281, 2015.
Bocko, J. and Lengvarský, P.: Bending vibrations of carbon nanotubes by using nonlocal theory, Procedia Eng., 96, 21–27, https://doi.org/10.1016/j.proeng.2014.12.093, 2014a.
Bocko, J. and Lengvarský, P.: The use of nonlocal theory for bending vibrations of single-walled carbon nanotubes, Appl. Mech. Mater., 611, 332–336, https://doi.org/10.4028/www.scientific.net/AMM.611.332, 2014b.
Bocko, J. and Lengvarský, P.: Vibration of single-walled carbon nanotubes by using nonlocal theory, Am. J. Mech. Eng., 2, 195–198, https://doi.org/10.12691/ajme-2-7-5, 2014c.
Chakraverty, S. and Behera, L.: Small scale effect on the vibration of non-uniform nanoplates, Struct. Eng. Mech., 55, 495–510, https://doi.org/10.12989/sem.2015.55.3.495, 2015.
Eringen, A. C.: Nonlocal Continuum Field Theories, Springer-Verlag, New York, 2002.
Fu, Y. M., Zhou, H. Q., and Zhang, P.: Nonlinear free vibration of nanowires including size effects, Micro Nano Lett., 7, 348–352, https://doi.org/10.1049/mnl.2011.0689, 2012.
Gupta, S. S. and Batra, R. C.: Continuum structures equivalent in normal mode vibrations to single-walled carbon nanotubes, Comput. Mater. Sci., 43, 715–723, https://doi.org/10.1016/j.commatsci.2008.01.032, 2008.
Harik, V. M.: Mechanics of carbon nanotubes: applicability of the continuum-beam models, Comput. Mater. Sci., 24, 328–342, https://doi.org/10.1016/S0927-0256(01)00255-5, 2002.
Hussain, M. and Naeem, M. N.: Vibration analysis of single-walled carbon nanotubes using wave propagation approach, Mech. Sci., 8, 155–164, https://doi.org/10.5194/ms-8-155-2017, 2017.
Hussain, M., Naeem, M. N., Shahzad, A., and He, M.: Vibrational behavior of single-walled carbon nanotubes based on cylindrical shell model using wave propagation approach, AIP Adv., 7, 045114, https://doi.org/10.1063/1.4979112, 2017.
Iijima, S.: Helical microtubules of graphitic carbon, Nat., 354, 56–58, https://doi.org/10.1038/354056a0, 1991.
Imani Yengejeh, S., Akbar Zadeh, M., and Öchsner, A.: Numerical modeling of eigenmodes and eigenfrequencies of hetero-junction carbon nanotubes with pentagon–heptagon pair defects, Comput. Mater. Sci., 92, 76–83, https://doi.org/10.1016/j.commatsci.2014.05.015, 2014.
Karličić, D., Murmu, T., Adhikari, S., and McCarthy, M.: Non-Local Structural Mechanics, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2015.
Kumar, D. and Srivastava, A.: Elastic properties of CNT- and graphene-reinforced nanocomposites using RVE, Steel. Comp. Struct., 21, 1085–1103, https://doi.org/10.12989/scs.2016.21.5.1085, 2016.
Lee, H. L. and Chang, W. J.: Frequency analysis of carbon-nanotube-based mass sensor using non-local Timoshenko beam theory, Micro Nano Lett., 7, 86–89, https://doi.org/10.1049/mnl.2011.0469, 2012.
Lim, C. W., Li, C., and Yu, J.: Free vibration of pre-tensioned nanobeams based on nonlocal stress theory, J. Zhejiang Univ. Sci. A, 11, 34–42, https://doi.org/10.1631/jzus.A0900048, 2010.
Lü, J., Chen, H., Lü, P., and Zhang, P.: Research of natural frequency of single-walled carbon nanotube, Chin. J. Chem. Phys., 20, 525, https://doi.org/10.1088/1674-0068/20/05/525-530, 2007.
Narendar, S. and Gopalakrishnan, S.: Nonlocal continuum mechanics formulation for axial, flexural, shear and contraction coupled wave propagation in single walled carbon nanotubes, Lat. Am. J. Solids Struct., 9, 497–514, https://doi.org/10.1590/S1679-78252012000400005, 2012.
Rahmani, O., Norouzi, S., Golmohammadi, H., and Hosseini, S. A. H.: Dynamic response of a double, single-walled carbon nanotube under a moving nanoparticle based on modified nonlocal elasticity theory considering surface effects, Mech. Adv. Mater. Struc., 24, 1274–1291, https://doi.org/10.1080/15376494.2016.1227504, 2017.
Rahmani, O., Shokrnia, M., Golmohammadi, H., and Hosseini, S. A. H.: Dynamic response of a single-walled carbon nanotube under a moving harmonic load by considering modified nonlocal elasticity theory, Eur. Phys. J. Plus., 133, 42, https://doi.org/10.1140/epjp/i2018-11868-4, 2018.
Reddy, J. N. and Pang, S. D.: Nonlocal continuum theories of beams for the analysis of carbon nanotubes, J. Appl. Phys., 103, 023511, https://doi.org/10.1063/1.2833431, 2008.
Şimşek, M.: Vibration analysis of a single-walled carbon nanotube under action of a moving harmonic load based on nonlocal elasticity theory, Physica E, 43, 182–191, https://doi.org/10.1016/j.physe.2010.07.003, 2010.
Şimşek, M.: Forced vibration of an embedded single-walled carbon nanotube traversed by a moving load using nonlocal Timoshenko beam theory, Steel. Comp. Struct., 11, 59–76, https://doi.org/10.12989/scs.2011.11.1.059, 2011.
Swain, A., Roy, T., and Nanda, B. K.: Vibration behaviour of single walled carbon nanotube using finite element, Int. J. Theor. Appl. Res. Mech. Eng., 2, 129–133, 2013.
Thongyothee, C., Chucheepsakul, S., and Li, T.: Nonlocal elasticity theory for free vibration of single-walled carbon nanotubes, Adv. Mat. Res., 747, 257–260, https://doi.org/10.4028/www.scientific.net/AMR.747.257, 2013.
Wang, Y.-G., Song, H.-F., Lin, W.-H., Wang, J.-K., Wang, Y.-G., Song, H.-F., Lin, W.-H., and Wang, J.-K.: Large amplitude free vibration of micro/nano beams based on nonlocal thermal elasticity theory, Lat. Am. J. Solids Struct., 12, 1918–1933, https://doi.org/10.1590/1679-78251904, 2015.
Wu, A. S. and Chou, T.-W.: Carbon nanotube fibers for advanced composites, Mat. Today, 15, 302–310, https://doi.org/10.1016/S1369-7021(12)70135-9, 2012.
Yang, J., Ke, L. L., and Kitipornchai, S.: Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory, Physica E, 42, 1727–1735, https://doi.org/10.1016/j.physe.2010.01.035, 2010.
Yayli, M. Ö.: On the axial vibration of carbon nanotubes with different boundary conditions, Micro Nano Lett., 9, 807–811, https://doi.org/10.1049/mnl.2014.0398, 2014.
Zhang, Y. Y., Wang, C. M., and Tan, V. B. C.: Assessment of Timoshenko beam models for vibrational behavior of single-walled carbon nanotubes using molecular dynamics, Adv. Appl. Math. Mech., 1, 89–106, 2009.