Study on the large-displacement behaviour of a spiral spring with variations of cross-section, orthotropy and prestress

This work is dedicated to the study of the large-displacement behaviour of a spiral spring. Parameters that influence the local torsion stiffness of the beam that constitutes the spiral are varied and their effect is studied. Cross-sectional shape, orthotropic material orientation and prestress are the three classes of parameters that are varied. The effect that the local change in torsional stiffness has on the overall behaviour is illustrated in a linearised way by comparing in-plane and out-of-plane stiffnesses, and nonlinearly, by inspecting a graphical representation of the potential energy field of the system. Several embodiments composed of multiple spirals are showed to illustrate how the understanding of the nonlinear behaviour could be exploited in conceptual design of compliant mechanisms.

1 Introduction

In the process of designing compliant mechanisms an important step is often the tailoring of the nonlinear stiffness behavior. Compliant mechanisms often work in a displacement range where their members undergo large deflections. In most cases the load response and the stiffness properties are not uniform across the motion range. It is thus challenging to thoroughly understand and exploit these properties. As such, innovative ideas that require this understanding may remain unexplored.

English (1999) shows the use of isopotential energy lines to visualize the endpoint stiffness of a 2-DoF robotic manipulator. The isopotential lines show that the commonly used stiffness ellipses give an insufficient representation for systems that are nonlinear. Herder (2001) employed the potential energy field (here PEF) of linear springs for the synthesis of mechanisms, especially statically balanced ones. Radaelli et al. (2011) employs potential energy fields for the synthesis of linkages with torsion springs, and later on for the synthesis of compliant mechanisms (Radaelli and Herder, 2017). The use of PEFs as visual aids enhances the understanding of the elastic behavior of systems with large deflections. This visualization gives the designer information on the size and direction of forces, stiffnesses, and on the (multi-)stability in the whole motion range, not just at a single configuration as is the case with e.g. the FACT method (Hopkins and Culpepper, 2010), or with the use of compliance and stiffness ellipsoids (Kim et al., 2008). It is possible to extend the PEF representation to 3-D motion by using colors for the 4th dimension, i.e. the energy scalar, and with isopotential surfaces instead of isopotential lines. No examples hereof have been found in literature.

To tailor the behavior of a curvilinear beam-based spring, it is worthwhile considering both the global shape of the curve and the local properties at cross-section level. Examples of compliant mechanisms where the global shape has been optimized for specific load responses can be found in Radaelli and Herder (2014, 2016); Vehar-Jutte (2008). In these examples the effect of the curved shape of the beam is clearly demonstrated. However, the examples are planar and the cross-sections are uniform and simple, i.e. rectangular or circular. In Lan and Cheng (2008); Xu and Ananthasuresh (2003); Zhou and Ting (2005) we find examples where in addition to the shape, also the cross-section is varied through the length of beam segments. Varying the shape and the cross-section is done as an additional step after obtaining a topology by means of topology optimization, in order to improve the performance in terms of stress concentration and strength. Nevertheless, the considered geometries are planar and have solid cross-section. Thin and open cross-sections, for instance, are left out of consideration.

Another means to tailor the global behavior is by changing the structure at a local level. Merriam et al. (2016) reduced the bending stiffness of flexures by changing the blade flexures into lattice flexures. He shows an increase of the torsional-to-bending stiffness ratio of up to 1.7 times higher than an equal aspect-ratio blade flexure, and an up to 6.5 times higher transversal-to-principal bending stiffness ratio. Integrated into a cross-axis flexural pivot joint he obtains a substantial stiffness reduction in the motion direction with respect to all other directions.

Lachenal et al. (2012) presents a multi-stable twisting structure based on two prestressed composite flanges combined using stiff connecting spokes. The concept is further devolped and analysed in Pirrera et al. (2013) and Lachenal et al. (2014b), eventually leading to the development of an I-beam with an unusually low torsional-to-bending stiffness ratio (Lachenal et al., 2014a). Besides the open cross-section of the I-beam that enhances the difference between torsional and bending stiffness, the carbon fibres that constitute the flanges are mostly placed in the longitudinal direction of the beam, pronouncing even further the contrast. By applying prestress on the flanges they even obtain a bi-stable twist behavior.

The open tube or split-tube concept can be found in different works, where the very low torsion-to-bending stiffness ratio is cleverly exploited. Goldfarb and Speich (1999, 2003) proposes a well-behaved revolute flexure joint and applies it in various embodiments. Well-behaved refers particularly to a fixed axis of rotation and high off-axis stiffnesses, properties that are non-typical in compliant mechanisms. Vos et al. (2010) employs the open tube geometry to twist a morphing wing. Moreover he controls the warping, and thus the twist, by actuating the relative position of the opposing sides of the slit. The CR joint introduced by Trease et al. (2004) has a cruciform cross-section. Also this open profile has a comparatively low torsion-to-bending stiffness ratio. These examples show that the cross-section shape, the material orientation and the application of prestress are ways to selectively increase compliance in certain directions in despite of other directions. It can be noticed, however, that in the given examples the goal is limited to a rotational motion about an axis, as fixed as possible.

It is worthwhile exploring alternative global shapes and combine them with various cross-sections, material orientation and prestress conditions. It becomes then possible to have combinations of selective compliance between other directions, including translational motions. This opens up the possibility to design, for instance, prismatic joints, cylindrical joints and other type of path following mechanisms.

Current work presents the results of an exploratory study on the effects of cross-sectional shape, material orientation and prestress on the large deflection elastic behavior of a given complex beam geometry. A spiral is chosen as global geometry because of the evident coupling between torsional deformation mode on a local level with the out-of-plane translational motion of the endpoint. A linearized stiffness measure is used to compare the out-of-plane stiffness with the in-plane stiffness. To analyze the behavior with large deflections the graphical representations of the PEF are used, which have been extended to 3-D for the occasion. It is the first time that such PEF representations are used for spatial mechanisms.

The remainder of the paper is structured as follows. Section 2 describes the concept of the spiral spring and the coupling between local and global deformation in further detail. Furthermore, the proposed variations in cross-section shape, material orientation and prestress are discussed. Section 3 contains the small displacement and large displacement analyzes. Section 4 gives some illustrative embodiments of multi-spring arrangements. The results are discussed in Sect. 5 and, finally, the conclusions are drawn.

2 Concept

The investigated concept consists of an initially planar spiral-shaped elastic body. The outer end of the spiral is fixed to ground. The inner end of the spiral is rigidly connected to a point that in undeformed configuration coincides with the origin (hereinafter endpoint), see Fig. 1. This point is treated as the end-effector throughout the remainder of the chapter. The spiral is defined in the yz-plane, (hereinafter main plane). In this concept it is interesting to analyze the effect of the global displacement of the endpoint on the local load-mode at cross-sectional level. If the endpoint of the spiral is loaded in the main plane the prevalent load-mode of the cross-section is bending. If the endpoint is loaded out of the plane instead, the prevalent load-mode of the cross-section is torsion. In this study we analyze the effect of altering the torsion stiffness in relation to the bending stiffness and its effect on the global behavior of the spiral. The torsional stiffness is altered through variations in the cross-section shape, orthotropic material orientation and prestress. It is expected that by lowering the torsional stiffness at the cross-section level, the global stiffness out-of-plane is reduced as well. Particular attention is given to the behavior at large displacements which is not obvious.

The spiral curve is defined as

$$\begin{array}{}\text{(1)}& r\left(t\right)=\left(\left(r_{\mathrm{in}}-r_{\mathrm{out}}\right)t+r_{\mathrm{out}}\right)\left(\begin{array}{l}\mathrm{0}\\ \cos \left(n\mathrm{2}\mathit{\pi }t\right)\\ \sin \left(n\mathrm{2}\mathit{\pi }t\right)\end{array}\right)\mathrm{0}<t<\mathrm{1},\end{array}$$

where n is the number of revolutions, r_in and r_out are the distance from the origin to the inner and the outer endpoint, respectively, see Fig. 1. The chosen parameter values are n=3, r_in=10 mm and r_out=100 mm.

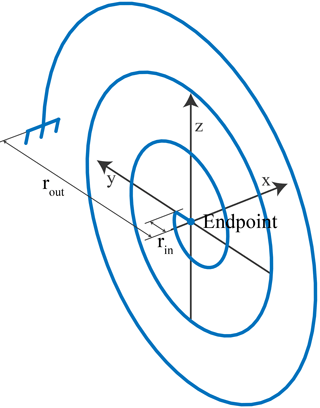
Figure 1 Basic shape of a spiral turning inward from radius r_out to r_in in three full revolutions. The curve defining the spiral is defined in the yz-plane. The inner end of the spiral is rigidly connected to the endpoint, considered the end-effector of the spring.

2.1 Variations

2.1.1 Cross-section shape

The first variation to be analyzed is related to the cross-sectional shape. In thin-walled open cross-sections it is quite easy to increase the bending stiffness, which is related to the material's distance to the centroidal axis of the shape. The torsional stiffness, on the other hand, is mainly related to the section wall length. For example, if a thin rectangular shape is bent into a curved section, the bending stiffness increases substantially while the torsional stiffness remains unaltered. There are many open thin-walled sections that would yield the sought behavior (I, T, L, Z, composed sections, etc.). To limit the number of variations and for a fair comparison this study is focussed on rectangular and curved sections that consist of a single branch with uniform thickness and length.

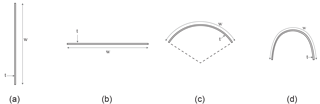
Figure 2 The four cross-sectional shapes that are considered are (a) a flat vertical in-plane strip, (b) a flat horizontal out-of-plane strip, (c) an arc and (d) a curved U-section. All shapes have the same thickness t=1 mm and length w=10 mm.

The four shapes that are considered are: a vertically oriented thin rectangle (flat in-plane), a horizontally oriented thin rectangle (flat out-of-plane), an arc with two radians arc-length and a curved U-section, see Fig. 2. The curve-length of all sections is kept constant, so that the amount of material is kept approximately constant between variants. The curve length w and the thickness t are set to 10 and 1 mm, respectively. The four geometries are shown in Fig. 3.

Figure 3 The four distinct cross-section shapes are swept uniformly over the spiral basic curve giving the spatial geometries of the springs.

2.1.2 Material orthotropy

An orthotropic material configuration also leads to differences of the stiffness ratio between bending and torsion. For example, a fibre reinforced material with the fibres mainly in diagonal (e.g. ±45^∘) direction creates additional resistance to torsion and diminished resistance to bending. On the contrary a composite with all fibres placed in the length direction of the beam has a relatively low resistance to torsion and high resistance to bending. The cases that are considered here are: quasi-isotropic [0^∘ 90^∘ 45^∘ $-\mathrm{45}{}^{\circ }$]_s, diagonal [±45^∘]_s and longitudinal [0^∘], where the angle is measured with respect to the longitudinal direction of the spiral curve. The material properties used in the model are those of a standard unidirectional (UD) carbon fibre and epoxy resin combination, cured at 120 ^∘C with a fibre volume fraction of 60 %. The used values for Young's modulus, the shear modulus, and Poisson's ratio are: E₁=135 GPa, E₂=10 GPa, G₁₂=5 GPa and ν₁₂=0.3.

2.1.3 Prestress

Prestress is another source of changes in the stiffness behavior of elastic systems. There are many ways to apply prestress, with different advantages and effects. We will consider a way that seems most viable in this practical embodiment. the prestress is introduced by applying a rotation θ at the endpoint in the positive x-direction. The angle is then hold constant throughout the rest of the analysis. This type of prestress causes a bending load at a local level that brings the structure towards or into lateral buckling. The result is a lowered or even negative out-of-plane stiffness.

3 Analysis and results

The variations on the concepts are analyzed and compared using two aids: a linearized stiffness measure at the undeformed configuration and the potential energy field (PEF). The first is favourable because it gives an easy to compare numeric value for each concept variation. The drawback is that it provides only insight at small displacements around the undeformed configuration. The second analysis aid is a visual representation of the potential energy on an finite space of possible displacements of the endpoint from its undeformed configuration. It is therefore much more appropriate to get understanding of the behavior at large displacements. The drawback is that the comparison among design alternatives is more open for interpretation.

3.1 linearized stiffness

The linearized stiffness measure κ is defined as the fraction of the out-of-plane stiffness over the minimum in-plane stiffness, as in

$$\begin{array}{}\text{(2)}& \mathit{\kappa }={\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{1}}}{min({\mathit{\lambda }}_{\mathrm{2}},{\mathit{\lambda }}_{\mathrm{3}})}},\end{array}$$

where λ₁ is the stiffness out-of-plane and λ_2,3 are the principal stiffnesses in the main plane. The three values are obtained by determining the eigenvalues of the stiffness matrix at the endpoint. In other words, they represent the length of the principal axes of the stiffness ellipsoid. Table 1 shows the values of κ for the concept variants of shape and material orientation without prestress.

Table 1 The linearized stiffness measure κ at the endpoint in de undeformed state is given for the four shape variants and the three material orientation variants. A low value indicates a low out-of-plane stiffness as compared to the in-plane stiffnesses.

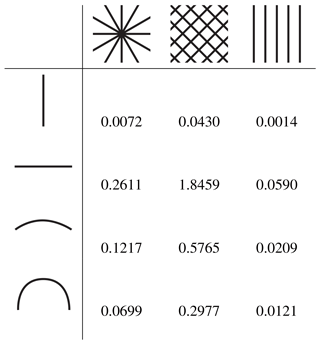
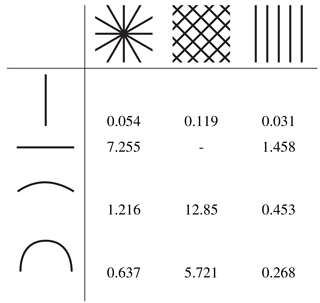
The effect of prestress on the linearized measure is indicated in Table 2 by the angle for which the stiffness measure becomes negative, the critical angle θ_c. It is clear that the angle at which the stiffness measure becomes negative is very much dependent on the other variables of geometry and material. This is comparable to the lateral buckling load of a beam loaded by a bending moment. For instance, the flat in-plane beam is very prone to lateral buckling, while the flat out-of-plane beam is not. No value (–) is assigned for the variant (flat out-of-plane, $\pm \mathrm{45}{}^{\circ }$) since a negative κ value is not reached within eight full revolutions (4π).

Table 2 To quantify the impact of the prestress rotation on the stiffness measure κ, the critical angle θ_c at which κ becomes negative is provided in this table. The critical angle is given for the four shape variants and the three material orientation variants. No value (–) is assigned to the variant where a negative κ is not reached within eight full revolutions.

Figure 4 The potential energy of the whole system is evaluated for a multitude of endpoint displacement locations. The set of points is ordered in a radial grid of 70 radial steps along 36 radial directions. This is repeated for a set of 100 equally spaced planes parallel to the yz-plane.

3.2 Potential energy fields

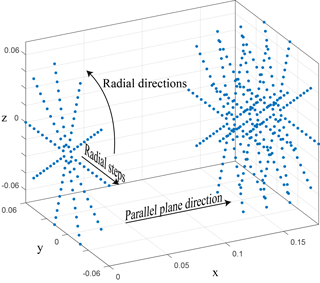
Visualisation of the potential energy field (PEF) is used for a broader comprehension of the elastic behavior. A PEF, namely, represents the potential energy of the whole system as a function of the endpoint location, also at large displacements. The values of the energy are visualised as color-mapped isopotential surfaces. That means that the endpoint of the structure can be positioned at all points on an isopotential surface without changing its potential energy. As a consequence the direction of the reaction force is at all times perpendicular to such isopotential surface and zero in any tangent direction. With this understanding a PEF gives an immediate insight on the global behavior of the system which is normally not achieved by other local methods. The PEFs are constructed by computing the elastic energy of the system for a set of endpoint displacements. This set of displacements is ordered in a radial grid in a series of planes parallel to the main plane, see Fig. 4. In the shown PEFs the grid consists of 70 steps on 36 radial directions on 100 planes, for a total number of 252 000 evaluated points. Finally, for plotting purposes, the points are interpolated linearly on a Cartesian grid of $\mathrm{100}\times \mathrm{100}\times \mathrm{100}$ points. Figure 5 shows an example of an obtained PEF. Note that displacements are applied only in the positive x-direction. Because the construction is symmetric in the yz-plane, the whole PEF can be mirrored in that plane. In applying the endpoint displacements, the orientation is kept fixed. This choice is motivated by the possibility to easily connect systems that are, for example, mirrored or with an x-offset, and have a common intermediate body. The assumption is that the moment of one spiral is cancelled by the moment of the opposing spiral(s). The stability of these equilibrating moments must then still be checked. In addition, the assumption of no rotation facilitates the calculations of the PEF of a spring with a rigid (intermediate) body at the endpoint. The PEF in that case, namely, shifts by the dimensions of the rigid link.

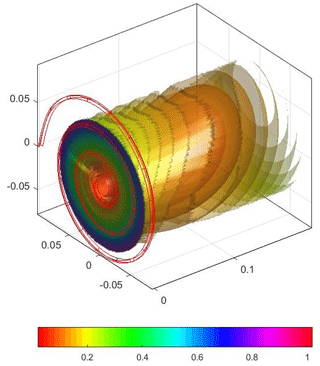
Figure 5 The energy values obtained at the points on the grid are interpolated to create isopotential surfaces. The isopotential surfaces are visualised with colors corresponding to the energy value. Since the system is symmetric in the yz-plane, the PEF at the side of the negative x-axis (not shown) is the mirrored replica of the shown PEF.

The analysis is performed with a finite element tool based on thin shell (Kirchhof-Love) elements, including geometrical nonlinearity and with a linear orthotropic material constitutive law. This is necessary to account for distorsion of the cross-sectional shape which would not be caught by most beam formulations. No contact model is implemented, meaning that the structure can freely intersect itself without affecting the behavior. This will oftentimes result in unrealistic situations. In a real implementation of this concept it must be checked if contact occurs in the desired range of motion.

Figure 6 shows the PEFs of all variants of shape and material with no prestress. The plots are sectioned at the xz-plane for a better view of the inner isopotential surfaces.

Figures 7 and 8 show the PEFs with a progression of presstress rotations on two chosen variants. The variants where the effect of prestress is most pronounced are chosen.

4 Embodiments

In this section we illustrate the possibility to combine and manipulate PEFs to obtain a desired behavior. A PEF can be manipulated (rotated, mirrored and translated) according to the rigid body motion of the element that it represents. Furthermore, the PEFs of multiple elements can be summed if the elements are rigidly connected in parallel. The connection consists of a rigid link between the ends of multiple spirals at a finite distance. This can be done in order to avoid physical contact between multiple elements.

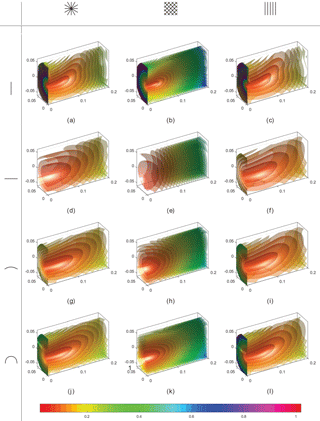
Figure 6 The PEFs of the variants of shape (flat in-plane, flat out-of-plane, arc, and U) and the variants of material orientation (quasi-isotropic, ±45, and 0^∘) are given. No prestress rotation is applied. The PEFs are sectioned at the xz-plane in order to improve the visibility of the isopotential surfaces.

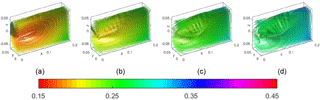
Figure 7 The PEFs of the variant arc-section and quasi-isotropic material, with a progressive prestress angle show that the lowest energy “bubble” drifts away from the main plane. The applied angle is (a) 1θ_c, (b) 1.1θ_c, (c) 1.2θ_c, and (d) 1.3θ_c. The critical angle in present variant is θ_c=1.216 rad, as can be found in Table 2.

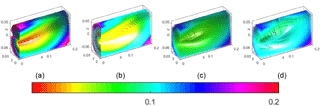
Figure 8 The PEFs of the variant U-section and 0^∘ material orientation, with a progressive prestress angle show that the lowest energy “bubble” drifts away from the main plane. The applied angle is (a) 0, (b) θ_c, (c) 1.5θ_c, and (d) 2θ_c. The critical angle in present variant is θ_c=0.268 rad, as can be found in Table 2.

Figure 9 shows the possibility to eliminate the asymmetric behavior of a single spiral by connecting mirrored replica of the same spiral. Namely, as will be discussed later, the preferred out-of-plane motion of many variants drifts away from the x-axis. The assembly consists of the chosen variant (U-section, quasi isotropic, no prestress) replicated three times by mirroring in the xy and the xz planes. Figure 9a shows an impression of how such system with connected spirals could look like. In a practical embodiment there would be an x-offset between the spirals to avoid physical contact. The effect of the offset on the rotational stability of the shuttle is neglected here. In an assembly with more replicas the moments can be balanced out. The obtained PEF is given in Fig. 9b. It can be noticed that the preferred out-of-plane motion is now following the x-axis.

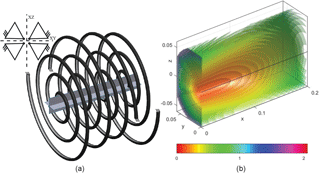
Figure 9 (a) A spiral with U-section and quasi-isotropic material is replicated four times by mirroring about the xy and xz planes. The endpoints are connected through a central shuttle. The spirals have an offset in the x direction to avoid contact. (b) The sum of the PEFs of the components gives the PEF of the whole system. The preferred out-of-plane motion direction exhibited a drift away from the x-axis in the separate components, but is corrected in the assembled system.

Figure 10 shows that two mirrored uni-stable spirals (flat in-plane section, 0^∘ material orientation, no prestress rotation) connected at the endpoint and subsequently preloaded can exhibit a bi-stable behavior. The spirals are mirrored in the horizontal xy-plane. Then the clamped outer-end of the original spiral is displaced downwards in z-direction by 20 mm down, and that of the replica by 20 mm upward. The result is that the “bubble” of lowest energy drifts away from the main plane and separates into two local minima, one in the positive x-direction (shown) and one in the negative x-direction (not shown). Again, the effect of the offset on the rotational stability is neglected in this illustrative embodiment.

An extreme case is shown in Fig. 11 where an octo-stable configuration is shown with the corresponding PEFs. A spiral that is bi-stable because of the applied rotation at the endpoint (arc-section, quasi-isotropic material, 1.3θ_c prestress) is connected to its three mirrored replicas, where the mirror planes are the xy and xz planes. Additionally, the outer clamps are displaced down by 5 mm for the upper two replica and 5 mm up for the other two, as shown in Fig. 11a. The result is a separation of the minimum energy “bubble” into four. Accounting for the symmetry about the main plane of the spiral (yz) there are other four stable equilibria in the negative x-direction (not shown) resulting in an octo-stable system. As before, the offset and its effect on the stability is neglected.

5 Discussion

We present a study on the effect of different types of parameters on the elastic behavior of a spiral shaped spring. In this section the results are discussed and compared. Also, some limitations and side-notes to this study and the results are discussed. The section ends with some thoughts on generalization and applicability of the study.

5.1 Observations

It was anticipated that a reduction in torsional stiffness with respect to the bending stiffness of the beam at a local level would result in a lowered out-of-plane to in-plane stiffness ratio of the endpoint of the spiral. This is indeed confirmed by the linearized stiffness measure κ (Table 1), and by the PEF graphs (Fig. 6). The longitudinal (0^∘) material orientation, where the contribution to the torsional stiffness is minimal, always gives a lower stiffness measure and an elongated energy field shape with respect to the quasi-isotropic cases. On the other hand, the diagonal ($\pm \mathrm{45}{}^{\circ }$) material orientation gives the opposite effect, i.e. higher stiffness measure and a shortened energy profile.

Looking at the cross-sectional shape it appears that the flat out-of-plane profile has in-plane and out-of-plane stiffnesses of the same order of magnitude. The out-of-plane stiffness is reduced in the arc section, and even more in the U-shaped section. The lowest ratio of stiffnesses is obtained with the in-plane flat strip. This is as expected, because every in-plane motion tends to bend the beam in its stiffest bending direction.

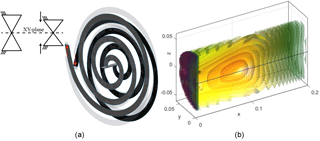
Figure 10 (a) Two mirrored flat in-plane spirals with 0^∘ material orientation are connected at their endpoints through a shuttle. Subsequently, the clamped outer ends of the spiral are moved apart by 20 mm each in the z-direction. (b) In the PEF of the obtained system the “bubble” of lowest energy drifts away from the main plane. Considering symmetry about the main plane, a bi-stable system is obtained.

Some of the PEFs in Fig. 6 (namely 6a, 6b, 6c and 6l) show a discontinuity of the energy near the main plane (yz). This is a result of the fact that the analysis is based on a geometry without imperfections. An applied displacement in the plane of symmetry of the geometry will not cause any point of the geometry to deviate from that plane. In reality, a small imperfection in the construction or in the application of the load can cause deviations from that plane, i.e. buckling can occur. Any displacement out of the main plane is in fact an asymmetric load-case and thus the deformed shape is a buckled one. Correspondingly, the energy value is normally much lower. Figure 12 shows a flat in-plane spiral on which an in-plane displacement is applied (Fig. 12a). Consecutively, a small out-of-plane displacement is applied (Fig. 12b) resulting in a buckled shape with relatively low energy level. This can be compared to the simple column buckling, where an analysis without imperfections will result in a straight compression of the beam with corresponding high energy values. A slight imperfection causes the column to bend asymmetrically, usually with lower energy values.

Since in reality a system without imperfections does not exist, the high energy gradients in the plane could be disregarded. However, they indicate another phenomenon. Namely, that crossing from one side of the main plane to the other side will most likely be accompanied by a snap-back, unless crossing through the channel of lowest energy. In the assembly of Fig. 10 it can be noted that due to the preload, the discontinuity forms a closed barrier. This means that crossing the main plane is accompanied by a snap-back. The spring variation was selected purposely to illustrate this effect. For a smoother transition through the main plane another variant (e.g. arc-section, 0^∘ material orientation) can be selected.

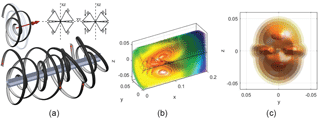
Figure 11 An octo-stable system is obtained by connecting four mirrored spirals (arc-section, quasi-isotropic material, 1.3θ_c prestress) to a central shuttle and by displacing the clamped outer ends. (a) An illustrative embodiment is shown. (b), (c) Four distinct energy minima are visible in the PEF of the total system that including their counterparts in the negative x-direction reveal an octo-stable system.

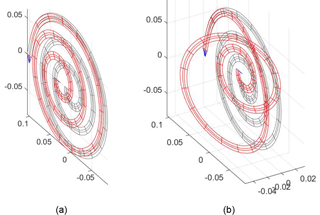
Figure 12 (a) An in-plane displacement is applied to a flat spiral. (b) An additional small out-of plane displacement brings the spiral in a post-buckling state.

Another conclusion related to this discontinuity can be drawn regarding the usability of a linearized stiffness based analysis. Namely that the stiffness between neighbouring points can sometimes change substantially. This compromises the validity of a linear analysis on a single point.

Figures 7 and 8 reveal that prestress, applied as a midpoint rotation, often causes a drift of the stable equilibrium out of the plane, giving rise to bi-stability. As further demonstrated in Table 2, the sensitivity of the cross-section and material variants to the critical angle is quite high. If the stiffness is to be adjusted by this prestress angle a compromise must be made between sensitivity and a practical angle range.

It is also shown that in an embodiment like the one of Fig. 11, all kind of multi-stability can be created. The other option shown to create multi-stability is by applying a displacement at the clamped outer-ends of the spirals. The prestress angle and the position of the clamped outer-ends can also be used to tune the positions of the equilibria.

From the PEFS in Fig. 6 it can be noticed that although initially the preferred out-of-plane direction is perpendicular to the main plane, further on the isopotential surfaces reveal a drift away from the x-axis. This drift is caused by the moments induced by fixing the orientations of the endpoints and the moment arm that separates both endpoints.

The drift is mainly in the positive y and z-directions. Presumably this has to do with the fact that the first quarter turn of the spiral is in that quadrant. This portion of the spiral is the one with largest distance to the endpoint. Therefore, because of the large moment arm, it feels the highest torsion. As a consequence the system tends to hinge about that portion of the spiral, causing the drift to be towards that quadrant.

An option to correct this drift is shown in the embodiment of Fig. 9. The straightening effect of this solution is quite obvious and clearly visible. A less obvious effect is that the isopotential surfaces of comparable width become shorter. This means that the achieved compliance out-of-plane is reduced on the long strokes. It can be explained as follows: All four component spirals are forced by symmetry to stay on the x-axis, while that is the preferred path to none of them. As a result they force each other on a relatively high energy state, thus increasing the resistance. An alternative solution to the drift can come from optimizing the basic shape of the spiral. The assumption, not unlikely, is that there exists a shape where this drift is self-correcting.

5.2 Notes

In this study the orientation of the inner endpoint is fixed. The practical assumption is that multiple springs are employed with an offset in x-direction to restrict the rotations about y and z. Using mirroring in either xy or xz plane further restrict the rotation in x direction. Enough replica of springs in the x-direction stabilizes the orientation of the shuttle. The resulting system could be a tubular straight-line mechanism with low stiffness in the direction of motion and with low friction. If miniaturised it could be suitable for e.g. laparoscopic tools, or as a substitute of high friction transmissions like bowden cables.

This fixed endpoint orientation condition may not be the most appropriate if the interest goes to, e.g., the free vibration of the spring. In such case constructing the PEFs with free endpoint condition would give a more appropriate representation.

The present study is limited by a specific set of choices to make the treatise compact and comprehensible. Certainly, every design choice has its influence on the resulting behavior. In design practice, specific behavior can be tuned and optimized according to the design requirements. The geometrical dimensions and material variants have been chosen such that the effects treated here are clearly visible such to convey the message. No effort has been undertaken to take the effects to extrema, such as to obtain, e.g., a minimum κ value.

An auxiliary goal of this work is to promote the use of PEFs for the analysis and synthesis of compliant mechanism. In this work it is shown that PEFs are a powerful tool, especially when dealing with very large deflections. It must be stressed that the visibility and thus the usability of a PEF (especially in 3-D) is very much compromised in a paper version. The full significance of this visualization method can be appreciated only in a virtual environment that allows for selective transparency of the isopotential surfaces, and for manipulation, reorientation and summation of the PEFs.

5.3 Outlook

The choice of the spiral as a basic shape for this study was motivated by the observation that a pure twist of the beam results in an out-of-plane displacement of the inner endpoint. There are many more shapes that would be worth investigating. One of them is the helix. By applying the same type of variations as in this study one could obtain helical springs with reduced resistance to compression and tension, especially compared to the torsion. Such spring could be used as a compliant replacement for a prismatic joint.

A smaller portion of the spiral could be more convenient in a practical embodiment. For example, multiple arcs configured with rotational symmetry, can result in a linear motion spring, similar to the one shown by Parise et al. (2001). The variations proposed in this study could enhance the out-of-plane compliance of such spring.

In general, by tailoring the global shape of the curve together with the local properties, e.g. reducing torsion stiffness, a multitude of preference path can be created. Thus it becomes possible to design a spatial curve which by allowing torsion and impeding bending traces a predefined trajectory. In such a case, a PEF representation would be a helpful instrument to analyze the behavior on the defined track and away from it.

6 Conclusions

This work describes an exploratory study on the elastic behavior of a spiral shaped spring and the effect of varying the cross-sectional shape, the material orientation and the prestress. It is shown that by lowering the torsion stiffness of the beam that constitutes the spiral with respect to its bending stiffness results in a reduced out-of-plane to in-plane stiffness ratio of the endpoint. By applying prestress as a rotation at the endpoint it becomes even possible to achieve a negative out-of-plane stiffness.

A measure for the linearized stiffness around the undeformed configuration is provided and gives a comprehensible overview of the behavior of the concept variations. Because the information is limited to a very confined working range, the graphic representation of the PEF is employed for a more complete understanding of the large deflection behavior. In the PEFs it is possible to grasp information about stability, equilibria, direction and magnitude of forces at every position of the displaced endpoint.

A few exemplary embodiments of multiple connected spirals are presented and their PEF is shown. The embodiments show a straightened out-of-plane preference path, a bistable, and a octo-stable behavior.

The study explores a new strategy to the design of compliant mechanisms with preference directions and/or paths. The resulting mechanism would typically be a slender spatial curvilinear beam with optimized local properties and global shape that follows a specific endpoint path.