Research on dynamic characteristics of motorized spindle based on comprehensive stiffness of angular contact ball bearing

In order to study the dynamic performance of a motorized spindle system more accurately and to consider the centrifugal effect, thermal effect of the angular contact ball bearing (ACBB) caused by high speed and influence of temperature rise on the dynamic viscosity of lubricating oil, a comprehensive stiffness model of a motorized spindle support bearing is established. Second, on this basis, combined with the Timoshenko beam theory and rotor dynamics, the dynamic model of the motorized spindle system is proposed using the finite element method. Finally, the influence of various factors on the dynamic characteristics of the high-speed motorized spindle system is studied and verified by experiments. The results show that the increase in the ball bearing preload and axial load could effectively improve the stability of the motorized spindle system, and the increase in the speed and thermal deformation of the ball bearing make the natural frequency and critical speed of the system decrease.

1 Introduction

A high-speed motorized spindle is the key functional component of computer numerical control (CNC) machine tools. This largely determines the high-speed motorized spindle, which is the core component that realizes the high speed and precision of the motorized spindle. Its stiffness in particular directly affects the overall stiffness of the motorized spindle system, which affects the stability and reliability of the system. Therefore, research on the stiffness of the angular contact ball bearing (ACBB) is the primary task when studying the dynamic characteristics of a motorized spindle. In the literature, when calculating the bearing stiffness, most scholars only equate the bearing stiffness to the contact stiffness, while ignoring the film stiffness (Noel et al., 2013; Wang et al., 2024; Li et al., 2020, 2024). Later, it was found that the order of magnitude of film stiffness under lubrication conditions is usually the same as that of contact stiffness, even higher than that of contact stiffness (Chen et al., 2013). Therefore, the contact stiffness and film stiffness should be considered simultaneously when studying the dynamic characteristics of a bearing. Wu (2011) proposed the concept and calculation idea of comprehensive stiffness of a rolling bearing and established an analytical calculation model of the comprehensive stiffness of a rolling bearing that considers lubricating film and the elastic deformation of the inner ring, outer ring and rolling element. However, the thermal effect was not considered. By considering the influence of the thermal effect and high-speed effect on the dynamics of the ACBB during rotation, the research group established the comprehensive stiffness calculation model of ball bearings (Lei et al., 2020, 2021; Li et al., 2020; Liu et al., 2023).

At the same time, scholars both domestic and abroad have some achievements in researching the dynamic characteristics of rotor-bearing systems. Nelson (1980) established the dynamic equation of a rotor system that considers the shear effect using the finite element method. Jorgensen and Shin (1998) built a dynamic model of the spindle-bearing system based on Timoshenko beam theory and carried out numerical calculation, verified by experiments. Fawzi (1998) used the finite element method to calculate the natural frequency, modal response and dynamic response of the rotor-bearing system, considering translational motion, moment of inertia, shear deformation, gyroscopic moment and system damping. Cao and Yusuf (2004) proposed a general method for calculating the dynamics of the spindle-bearing system based on Timoshenko beam theory. Li (2006) analyzed the internal dynamic state of the bearing, then proposed the dynamic model of the super-high-speed motorized spindle system using the finite element method and studied the factors influencing the dynamic performance of the system. Holkup and Cao (2011) systematically studied the dynamic performance of the spindle under different working conditions and different preloading. Cao et al. (2012) considered the centrifugal force and gyroscopic moment effect of rotating parts and presented the dynamic model of the spindle-bearing system using the finite element method. Fang et al. (2021) proposed a qualitative and quantitative analysis method for the rotor-bearing system supported by angular contact ball bearings. Lin et al. (2003) established a thermo-mechanical dynamic model of a high-speed spindle system and analyzed the influence of centrifugal effect and gyroscopic effect on the dynamic characteristics of the spindle when it rotates at high speed. Zhang and Chen (2016) established the thermal-dynamic models of bearings and rotating shafts, then analyzed the influencing factors. Cheng (2019) considered the influence of various factors on the deformation of the bearing and the spindle, and constructed a dynamic model of the motorized spindle system under the thermal-mechanical coupling condition. It can be seen from the above literature that when studying the dynamic characteristics of the motorized spindle system, some research has studied the thermal effect during the operation of the motorized spindle system. In addition, when calculating the total stiffness matrix of the motorized spindle system, the bearing contact stiffness is considered, while the influence of the film stiffness on the bearing is ignored. In this paper, the comprehensive stiffness model of the angular contact ball bearing of the motorized spindle system is established when the high-speed effect and the thermal effect are coupled. Based on the comprehensive stiffness, according to the structure of the motorized spindle unit and Timoshenko beam theory, the dynamic model of the motorized spindle system is established using the finite element method. The effects of different working conditions on the dynamic characteristics of the spindle system, such as natural frequency and critical speed, are investigated.

2 Calculation method of comprehensive stiffness of ACBB

2.1 Contact stiffness model of ACBB

To ensure the rationality of the modeling, the following assumptions are made:

1. The influence of the cage on the static balance of bearing is ignored, and the bearing is only subject to axial force.

2. The motion of the rolling element on the raceway is pure rolling.

3. The contact between the rolling body and the inner and outer raceways is the Hertz contact.

4. During high-speed operation, the interaction force between the cage and the rolling elements is very limited, so the role of the cage is ignored in the force analysis of the bearing.

The ACBB generates friction due to the contact of various parts during operation, which will cause friction heat generation. The higher the rotation speed, the more heat will be generated. The internal temperature of the bearing will gradually increase through heat conduction and heat convection, resulting in the thermal expansion of various parts of the bearing. When calculating the thermal deformation of the bearing inner ring, outer ring and rolling element, the calculation method proposed by Harris (1971) is generally adopted:

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}{u}_{\mathrm{i}}={\mathit{\alpha }}_{\mathrm{i}}{d}_{\mathrm{i}}\mathrm{\Delta }{T}_{\mathrm{i}}\\ u_{\mathrm{b}}={\mathit{\alpha }}_{\mathrm{b}}{d}_{\mathrm{b}}\mathrm{\Delta }{T}_{\mathrm{b}}\\ u_{\mathrm{o}}={\mathit{\alpha }}_{\mathrm{o}}{d}_{\mathrm{o}}\mathrm{\Delta }{T}_{\mathrm{o}},\end{array}\right.\end{array}$$

where u_i, u_o and u_b are the thermal deformation of the inner ring, outer ring and rolling element, respectively; and α_i, α_o and α_b are the thermal expansion coefficient of the inner ring, outer ring and rolling element materials, respectively. ΔT_i, ΔT_o and ΔT_b are the inner ring, outer ring and rolling temperature rise, respectively; and d_i, d_o and d_b are the diameters of the inner ring, outer ring and rolling element, respectively.

According to Eq. (1), the sum of the radial and axial thermal deformation δ_r and δ_a of the ACBB assembled face to face during high-speed operation due to temperature rise is respectively

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{l}{\mathit{\delta }}_{\mathrm{r}}=u_{\mathrm{i}}-\mathrm{2}{u}_{\mathrm{b}}-u_{\mathrm{o}}\\ {\mathit{\delta }}_{\mathrm{a}}=\frac{{\mathit{\alpha }}_h{L}_h\mathrm{\Delta }{T}_h-{\mathit{\alpha }}_s{L}_s\mathrm{\Delta }{T}_s}{\mathrm{2}}.\end{array}\right.\end{array}$$

When the bearing runs at high speed, the inner and outer rings and rolling elements of the bearing are subjected to centrifugal force, resulting in radial centrifugal deformation. Due to the bearing assembly, the bearing outer ring is installed in the bearing seat hole. Since the deformation of the bearing outer ring is small, the centrifugal deformation of the outer ring is ignored. The radial deformation of the inner ring due to the centrifugal effect δ₁ is (Li et al., 2020)

$$\begin{array}{}\text{(3)}& {\mathit{\delta }}_{\mathrm{1}}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}{\mathit{\omega }}^{\mathrm{2}}}{\mathrm{16}{E}_{\mathrm{i}}}}\left[\left(\mathrm{3}+{\mathit{\nu }}_{\mathrm{i}}\right)D_{\mathrm{i}}^{\mathrm{2}}+\left(\mathrm{1}-{\mathit{\nu }}_{\mathrm{i}}\right)d_{\mathrm{i}}^{\mathrm{2}}\right]D_{\mathrm{i}},\end{array}$$

where ρ_i is the material density of the bearing inner ring, E_i is the elastic modulus of the bearing inner ring material, D_i is the inner channel diameter and ν_i is the Poisson's ratio of the bearing inner ring material.

Considering the thermal deformation and centrifugal deformation of the ACBB, a modified quasi-static bearing model has been established. The contact stiffness of the ball bearing could then be obtained according to the relationship between the contact load and the contact deformation (Du et al., 2001).

$$\begin{array}{}\text{(4)}& K_{cj}={\displaystyle \frac{\mathrm{d}{Q}_j}{\mathrm{d}{\mathit{\delta }}_j}}=\mathrm{1.5}{\mathrm{\Gamma }}_j^{-\mathrm{1}}{\left[\left({\displaystyle \frac{\mathrm{9}}{\mathrm{2}{\mathit{\epsilon }}_j\mathrm{\Sigma }{\mathit{\rho }}_j}}\right){\left({\displaystyle \frac{\mathrm{1}}{\mathit{\pi }{\mathit{\kappa }}_{j}E}}\right)}^{\mathrm{2}}\right]}^{-\mathrm{1}/\mathrm{3}}{Q}_j^{\mathrm{1}/\mathrm{3}},\end{array}$$

where K_cj is the contact stiffness of the ball bearing; Q_j is the contact load of two contact objects; δ_j is the contact deformation of two contact objects; Γ and ε are complete elliptic integrals of the first and second kinds, respectively; and κ is an elliptic rate parameter.

$$\begin{array}{}\text{(5)}& {\displaystyle }\mathrm{\Gamma }=\underset{\mathrm{0}}{\overset{\frac{\mathit{\pi }}{\mathrm{2}}}{\int }}{\left[\mathrm{1}-\left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{{\mathit{\kappa }}^{\mathrm{2}}}}\right){\sin }^{\mathrm{2}}\mathit{\phi }\right]}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{d}\mathit{\phi }\text{(6)}& {\displaystyle }\mathit{\epsilon }=\underset{\mathrm{0}}{\overset{\frac{\mathit{\pi }}{\mathrm{2}}}{\int }}{\left[\mathrm{1}-\left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{{\mathit{\kappa }}^{\mathrm{2}}}}\right){\sin }^{\mathrm{2}}\mathit{\phi }\right]}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{d}\mathit{\phi }\end{array}$$

2.2 Film stiffness model of ACBB considering spinning and temperature

According to the motion form and characteristics of the spin motion of the ACBB, the motion form is equivalent to the motion of an ellipsoid on an infinite plane at the average speed u_b of the rolling element and raceway (Liu et al., 2023). Meanwhile, the plane rotates at the spin angular velocity ω_s. The velocity components at any point in the contact area are v_R and u_R, respectively. When the rolling element contacts the inner and outer raceways, the comprehensive elastic modulus is E, the equivalent radius of curvature is R_a and β is the attitude angle of bearing.

$$\begin{array}{}\text{(7)}& {\displaystyle }E=\mathrm{2}/\left({\displaystyle \frac{\mathrm{1}-{\mathit{\nu }}_{\mathrm{1}}^{\mathrm{2}}}{E_{\mathrm{1}}}}+{\displaystyle \frac{\mathrm{1}-{\mathit{\nu }}_{\mathrm{2}}^{\mathrm{2}}}{E_{\mathrm{2}}}}\right)\text{(8)}& {\displaystyle }{R}_{\mathrm{a}}={\displaystyle \frac{R_{\mathrm{1}}{R}_{\mathrm{2}}}{R_{\mathrm{1}}\pm R_{\mathrm{2}}}}\text{(9)}& {\displaystyle }\left\{\begin{array}{l}{u}_{{}_{{}_{\mathrm{R}}}}\left(x,y\right)=\frac{{\mathit{\omega }}_{\mathrm{s}}y}{\mathrm{2}}+u_{\mathrm{b}}\\ v_{{}_{{}_{\mathrm{R}}}}\left(x,y\right)=-\frac{{\mathit{\omega }}_{\mathrm{s}}x}{\mathrm{2}}\end{array}\right.\text{(10)}& {\displaystyle }{u}_{\mathrm{b}}=D_{\mathrm{b}}{\mathit{\omega }}_{\mathrm{r}}(\sin \mathit{\beta }\sin {\mathit{\alpha }}_{\mathrm{i}j}+\cos \mathit{\beta }\cos {\mathit{\alpha }}_{\mathrm{i}j})/\mathrm{2}\text{(11)}& {\displaystyle }\mathit{\beta }=\arctan (\sin {\mathit{\alpha }}_{\mathrm{0}}/(\cos {\mathit{\alpha }}_{\mathrm{0}}+\mathit{\gamma }\left)\right),\end{array}$$

where, according to the inner and outer rings of the bearing, ω_s is divided into ω_si and ω_so. The calculation formulas are as follows:

$$\begin{array}{}\text{(12)}& \left\{\begin{array}{l}{\mathit{\omega }}_{\mathrm{si}}={\mathit{\omega }}_{\mathrm{r}}\sin ({\mathit{\alpha }}_{\mathrm{i}j}-\mathit{\beta })-({\mathit{\omega }}_{\mathrm{i}}-{\mathit{\omega }}_{\mathrm{m}})\sin {\mathit{\alpha }}_{\mathrm{i}j}\\ {\mathit{\omega }}_{\mathrm{so}}={\mathit{\omega }}_{\mathrm{m}}\sin {\mathit{\alpha }}_{\mathrm{o}j}-{\mathit{\omega }}_{\mathrm{r}}\sin ({\mathit{\alpha }}_{\mathrm{o}j}-\mathit{\beta }),\end{array}\right.\end{array}$$

where $\mathit{\gamma }=\frac{D_{\mathrm{b}}}{d_{\mathrm{m}}}$; d_m is the pitch diameter of the ACBB; and E₁, E₂, v₁, v₂, R₁ and R₂ are the elastic modulus, Poisson's ratio and radius of curvature of the two contacts, respectively. Among them, “+” is the external contact and “−” the internal contact. ω_si and ω_so are the spinning angular speed of the bearing inner ring and outer ring, respectively; α_ij and α_oj are the contact angle of the inner and outer rings, respectively; ω_m is the orbital speed of the ball; ω_i is the inner ring angular speed of the bearing; and ω_r is the speed of the ball about its own axis. The calculation formulas are as follows:

$$\begin{array}{}\text{(13)}& {\displaystyle }{\mathit{\omega }}_{\mathrm{r}}={\displaystyle \frac{-{\mathit{\omega }}_{\mathrm{s}}}{\left(\frac{\cos {\mathit{\alpha }}_{\mathrm{o}j}+\tan \mathit{\beta }\sin {\mathit{\alpha }}_{\mathrm{o}j}}{\mathrm{1}+\frac{D_{\mathrm{b}}}{d_{\mathrm{m}}}\cos {\mathit{\alpha }}_{\mathrm{o}j}}+\frac{\cos {\mathit{\alpha }}_{\mathrm{i}j}+\tan \mathit{\beta }\sin {\mathit{\alpha }}_{\mathrm{i}j}}{\mathrm{1}-\frac{D_{\mathrm{b}}}{d_{\mathrm{m}}}\cos {\mathit{\alpha }}_{\mathrm{i}j}}\right)\left(\frac{D_{\mathrm{b}}}{d_{\mathrm{m}}}\right)\cos \mathit{\beta }}}\text{(14)}& {\displaystyle }{\mathit{\omega }}_{\mathrm{m}}={\displaystyle \frac{\mathrm{1}-\left(\frac{D_{\mathrm{b}}}{d_{\mathrm{m}}}\right)\cos {\mathit{\alpha }}_{\mathrm{i}j}}{\mathrm{1}+\cos \left({\mathit{\alpha }}_{\mathrm{i}j}-{\mathit{\alpha }}_{\mathrm{o}j}\right)}}{\mathit{\omega }}_{\mathrm{s}}.\end{array}$$

Considering the influence of spin motion, the Reynolds equation of point contact lubrication is described as follows:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial x}}& \left({\displaystyle \frac{\mathit{\rho }{h}^{\mathrm{3}}}{\mathit{\eta }}}\right.\left.{\displaystyle \frac{\partial p}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial y}}\left({\displaystyle \frac{\mathit{\rho }{h}^{\mathrm{3}}}{\mathit{\eta }}}\right.\left.{\displaystyle \frac{\partial p}{\partial y}}\right)=\mathrm{12}{\displaystyle \frac{\partial }{\partial x}}\left(u_R\mathit{\rho }h\right)\\ & +\mathrm{12}{\displaystyle \frac{\partial }{\partial x}}\left(v_R\mathit{\rho }h\right).\end{array}\end{array}$$

The boundary conditions are expressed by

$$\left\{\begin{array}{l}P(X_{\mathrm{0}},Y)=\mathrm{0}\\ P(X_e,Y)=\mathrm{0},\frac{\partial P\left(X_e,Y\right)}{\partial X}=\mathrm{0}\\ P\mathrm{|}Y=\pm \mathrm{1}=\mathrm{0}.\end{array}\right.$$

Considering the influence of temperature on lubricant viscosity, the viscosity pressure formula by Roelands (1966) and Wen and Yang (1992) is adopted.

$$\begin{array}{}\text{(16)}& \mathit{\eta }={\mathit{\eta }}_{\mathrm{0}}\exp \left\{\left(\ln {\mathit{\eta }}_{\mathrm{0}}+\mathrm{9.67}\right)\left[{\left(\mathrm{1}+p/p_{\mathrm{0}}\right)}^z{\left({\displaystyle \frac{T-\mathrm{138}}{T_{\mathrm{0}}-\mathrm{138}}}\right)}^{-\mathrm{1.1}}-\mathrm{1}\right]\right\},\end{array}$$

where η₀ is the dynamic viscosity of lubricating under normal pressure, p is the pressure, p₀ is the pressure coefficient and z is the viscous pressure coefficient.

The density-pressure-temperature equation of bearing under elastohydrodynamic lubrication (EHL) is shown in Eq. (17):

$$\begin{array}{}\text{(17)}& \mathit{\rho }={\mathit{\rho }}_{\mathrm{0}}\left(\mathrm{1}+{\displaystyle \frac{\mathrm{0.6}p}{\mathrm{1}+\mathrm{1.7}p}}+D(T-T_{\mathrm{0}})\right),\end{array}$$

where ρ is the density of lubricating oil, P is the pressure and ρ₀ is the density of lubricating oil under atmospheric pressure.

Figure 1 Finite element partition diagram of the rotor-bearing system.

Table 1 Bearing parameters.

Table 2 Comparison of calculated results and test results.

When the lubricating oil flows between the rolling element and the inner and outer ring, it will be affected by the contact load, and its balance equation is expressed by

$$\begin{array}{}\text{(18)}& w=\underset{x_{\mathrm{0}}}{\overset{x_e}{\int }}\underset{y_{\mathrm{0}}}{\overset{y_e}{\int }}p\mathrm{d}x\mathrm{d}y.\end{array}$$

According to the definition of stiffness, the basic formula for bearing film stiffness is shown in Eq. (19):

$$\begin{array}{}\text{(19)}& K_{\mathrm{film}}=\underset{\mathit{\delta }\to \mathrm{0}}{lim}{\displaystyle \frac{\mathrm{\Delta }w}{\mathit{\delta }}}=-{\displaystyle \frac{\mathrm{d}w}{\mathrm{d}{h}_{\min }}}.\end{array}$$

According to Formulas (15)–(18) and the minimum oil film thickness h_min formula (Gupta, 1979), considering spin and temperature, it can be derived that

$$\begin{array}{}\text{(20)}& {\displaystyle }\begin{array}{rl}{K}_{\mathrm{film}}& =-{\displaystyle \frac{\mathrm{d}{w}_{\mathrm{film}}}{\mathrm{d}{h}_{min}}}=\mathrm{13.6986}\left[{\displaystyle \frac{R_x}{\mathrm{3.63}{U}^{\mathrm{0.68}}{G}^{\mathrm{0.49}}\left(\mathrm{1}-e^{-\mathrm{0.68}k}\right)}}\right]\\ & \times E{R}_x^{\mathrm{2}}{\left[{\displaystyle \frac{h_{min}{R}_x}{\mathrm{3.63}{U}^{\mathrm{0.68}}{G}^{\mathrm{0.49}}\left(\mathrm{1}-e^{-\mathrm{0.68}k}\right)}}\right]}^{-\mathrm{14.6986}}\end{array}\text{(21)}& {\displaystyle }\begin{array}{rl}{K}_{\mathrm{films}}& =-{\displaystyle \frac{\mathrm{d}{w}_{\mathrm{films}}}{\mathrm{d}{h}_{\mathrm{mins}}}}=\mathrm{0.16219}E{R}_x^{\mathrm{3}}/\\ & \left[\mathrm{0.1077}\times {\mathrm{10}}^{\mathrm{3}}{R}_x{h}_{\mathrm{mins}}-\mathrm{0.9588}{G}^{\mathrm{0.8001}}\times \right.\\ & U^{\mathrm{0.72}}{k}^{\mathrm{1.616}}\left(\mathrm{1}+\mathrm{21.459}{e}^{-\mathrm{0.3}k}\right)\\ & \left.\times \left(\mathrm{1}-\mathrm{1.3101}\times {\mathrm{10}}^{\mathrm{10}}{\mathrm{\Omega }}_{\mathrm{s}}^{\mathrm{1.024}}\right)\right].\end{array}\end{array}$$

In the formula, U is the velocity parameter, G is the material parameter, k is ellipticity, Ω_s is spinning velocity parameter, K_film is the oil film stiffness without considering spin motion and K_films is the oil film stiffness when considering spin motion and temperature rise. The range of values for each parameter in the above equation can be found in Li et al. (2020).

2.3 Comprehensive stiffness model of ACBB

The contact stiffness and film stiffness of the ACBB are combined in series to establish the comprehensive stiffness model in this paper. The comprehensive stiffness between the jth rolling element and the inner and outer rings is as follows:

$$\begin{array}{}\text{(22)}& {\displaystyle \frac{\mathrm{1}}{K_{qij}}}={\displaystyle \frac{\mathrm{1}}{K_{\mathrm{ci}j}}}+{\displaystyle \frac{\mathrm{1}}{(K_{\mathrm{oil}}{)}_{ij}}}\text{(23)}& {\displaystyle \frac{\mathrm{1}}{K_{qoj}}}={\displaystyle \frac{\mathrm{1}}{K_{\mathrm{co}j}}}+{\displaystyle \frac{\mathrm{1}}{(K_{\mathrm{oil}}{)}_{oj}}},\end{array}$$

where (K_oil)_ij and (K_oil)_oj are the film stiffness between the jth rolling element and the inner ring and outer ring, respectively; and K_cij and K_coj are the contact stiffness between the jth rolling element and the inner and outer ring, respectively.

Figure 2 Calculation flowchart.

Figure 3 Schematic diagram of static hammering.

According to the calculation formula of bearing comprehensive stiffness, the comprehensive stiffness components K_rij and K_aij of the jth rolling element and inner ring in the radial and axial direction, and the comprehensive stiffness components K_roj and K_aoj of the outer ring in the radial and axial direction, are as follows:

$$\begin{array}{}\text{(24)}& {\displaystyle }{K}_{\mathrm{ri}j}=K_{qij}{\cos }^{\mathrm{2}}{\mathit{\alpha }}_{ij}\text{(25)}& {\displaystyle }{K}_{\mathrm{ai}j}=K_{qij}{\sin }^{\mathrm{2}}{\mathit{\alpha }}_{ij}\text{(26)}& {\displaystyle }{K}_{\mathrm{ro}j}=K_{qoj}{\cos }^{\mathrm{2}}{\mathit{\alpha }}_{oj}\text{(27)}& {\displaystyle }\begin{array}{l}{K}_{\mathrm{ao}j}=K_{qoj}{\sin }^{\mathrm{2}}{\mathit{\alpha }}_{oj}.\\ \end{array}\end{array}$$

For the ACBB, the entire comprehensive stiffness can be derived from the stiffness between the rolling element and the inner ring and outer ring:

$$\begin{array}{}\text{(28)}& {\displaystyle }\begin{array}{l}{K}_{\mathrm{a}}=\sum _{j=\mathrm{1}}^{j=Z}\frac{K_{\mathrm{ai}j}{K}_{\mathrm{ao}j}}{K_{\mathrm{ai}j}+K_{\mathrm{ao}j}}\\ \end{array}\text{(29)}& {\displaystyle }\begin{array}{l}{K}_{\mathrm{r}}=\sum _{j=\mathrm{1}}^{j=Z}\frac{K_{\mathrm{ri}j}{K}_{\mathrm{ro}j}}{K_{\mathrm{ri}j}+K_{\mathrm{ro}j}}{\cos }^{\mathrm{2}}\left[\frac{\mathrm{2}\mathit{\pi }}{Z}(j-\mathrm{1})\right]\\ \end{array}\text{(30)}& {\displaystyle }\begin{array}{l}{K}_{\mathit{\theta }}=\frac{d_m^{\mathrm{2}}}{\mathrm{4}}\sum _{j=\mathrm{1}}^{j=Z}\frac{K_{\mathrm{ai}j}{K}_{\mathrm{ao}j}}{K_{\mathrm{ai}j}+K_{\mathrm{ao}j}}{\cos }^{\mathrm{2}}\left[\frac{\mathrm{2}\mathit{\pi }}{Z}(j-\mathrm{1})\right],\\ \end{array}\end{array}$$

where K_a, K_r and K_θ are the comprehensive axial stiffness, comprehensive radial stiffness and comprehensive angular stiffness of the ACBB, respectively.

3 Dynamic model of motorized spindle system

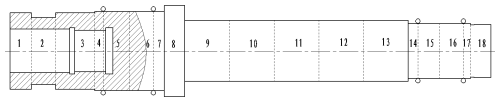
In order to study the dynamical characteristics of the motorized spindle system, the dynamical mathematical model of the system should first be established. In this paper, the dynamic model of the motorized spindle system is established by using the finite element method. The spindle unit is discretized, and each element is regarded as a Timoshenko beam element, which considers the shear effect. Figure 1 is the finite element partition diagram of the rotor-bearing system. The rotor is divided into 18 elements and 19 nodes, and each node has 4 degrees of freedom. Among them, nodes 5, 7, 15 and 17 are the location of the support bearing.

Figure 4 Response spectrum of the modal test.

Figure 5 Effect of rotational speed on natural frequency and critical speed of the system.

According to the structure and function characteristics of the motorized spindle, the motion equation of the motorized spindle system is established. Since the damping value of the motorized spindle is relatively small, its influence on the dynamics of the system is ignored, and the effect of the gyroscopic moment will cause the movement trajectory of the spindle to deviate from the central axis. Therefore, it is necessary to consider the influence of the gyroscopic matrix of the axis unit and additional unit on the system, and the system motion equation is

$$\begin{array}{}\text{(31)}& M_{\mathrm{T}}\ddot{x}+\mathrm{\Omega }{G}_{\mathrm{T}}\dot{x}+K_{\mathrm{T}}x=F,\end{array}$$

where M_T, G_T, K_T and F are the total mass matrix, total gyroscopic matrix, total stiffness matrix and total load column vector of the system, respectively.

$$\begin{array}{}\text{(32)}& {\displaystyle }{M}_{\mathrm{T}}=M_{\mathrm{t}}+M_{\mathrm{R}}+M_d\text{(33)}& {\displaystyle }{K}_{\mathrm{T}}=K_{\mathrm{S}}+K_{\mathrm{b}},\end{array}$$

where M_t and M_R represent the translational and rotational mass matrix of the spindle, respectively; M_d is the equivalent mass matrix of the additional parts; and K_S and K_b are the stiffness matrix of the spindle and the angular contact ball bearing, respectively. In this paper, the comprehensive stiffness matrix of the ball bearing is adopted to calculate the total stiffness matrix of the system.

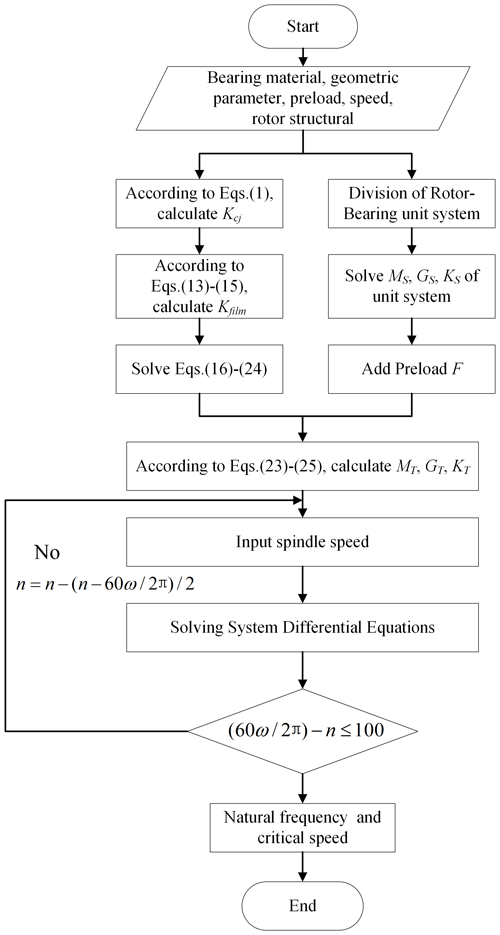
The steps to solve the dynamic model of the motorized spindle system are as follows: first, the spindle is discretized, and each element divided is regarded as a Timoshenko beam element. Then, the mass matrix, stiffness matrix, gyroscope matrix and load and displacement column vectors of each element are determined, and the total mass matrix, stiffness matrix, gyroscope matrix, total load and displacement column vectors of the system are superimposed and combined according to the method of matching. Finally, the dynamic parameters of the motorized spindle system are obtained by solving the differential equations of the system. After considering the comprehensive stiffness of the ACBB, the solution process for its overall dynamic characteristics is shown in Fig. 2, and the performance parameters of the bearing are shown in Table 1.

Figure 6 Effect of thermal deformation on natural frequency and critical speed of the system.

4 Test verification

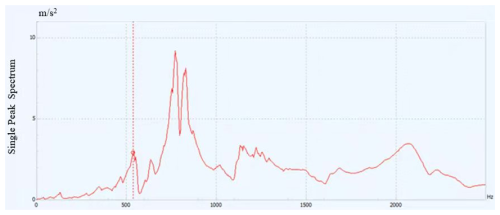
The dynamic characteristics of the motorized spindle system are measured by the static hammering method, as shown in Fig. 3. During measurement, the motorized spindle is in a free state, and the exciting force is applied on the spindle end by the force hammer. The excitation signal of the force sensor and the response signal measured by the acceleration sensor are transmitted to the computer, and the frequency response of the motorized spindle system is obtained by the analysis software, as shown in Fig. 4.

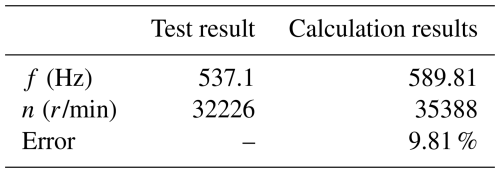
It can be seen from Fig. 4 that the first peak appears at 537.1 Hz, which could be judged as the first natural frequency of the system. The first critical speed can be calculated according to the formula n=60f. Table 1 shows the comparison between the calculated results and the experimental results.

There is a certain error between the test results and the calculation results in Table 2. This is because some structures of the spindle have been simplified in the process of establishing the dynamic model. However, the margin of error is within 10 %, which is relatively small. This shows the validity and reliability of the finite element dynamic model of the motorized spindle system established in this paper.

5 Dynamic characteristics analysis of motorized spindle based on comprehensive stiffness of ACBB

At high speed, the mechanical properties of the ACBB have an obvious influence on the dynamic characteristics of the motorized spindle system. The change of preload, axial external load and lubrication performance of the ACBB will greatly influence the comprehensive stiffness of the ACBB and then further affect the performance of the whole motorized spindle system. The influence of different factors such as bearing preload, bearing thermal deformation, external load and spindle speed on the dynamic characteristics of the motorized spindle system is studied in this paper, which considers the high-speed effect and thermal effect.

Figure 7 Effect of preload on natural frequency and critical speed of the system.

Figure 8 Effect of external load on natural frequency and critical speed of the system.

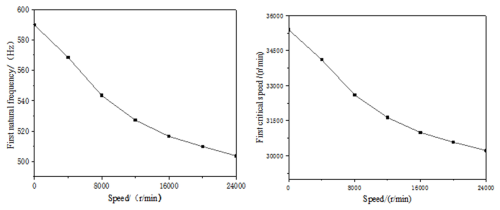
5.1 Effect of speed

When the ACBB preload Fa =500 N, the natural frequency and critical speed of the motorized spindle system at different ACBB speeds are given in Fig. 5. With the increase in the speed of the motorized spindle, the natural frequency and critical speed of the system show a downward trend. This is because the contact stiffness and film stiffness are in the same order of magnitude and decrease, and the comprehensive stiffness of the ACBB decreases under the action of the series, which results in a downward trend in the natural frequency and critical speed of the system.

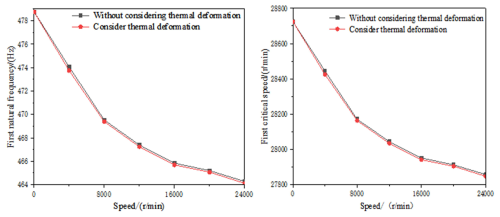
5.2 Effect of the thermal deformation of ACBB

When the motorized spindle rotates at high speed, the friction of the ACBB leads to an increase in the temperature and heat generation in the internal parts. This causes the thermal deformation of the ACBB and affects the dynamic characteristics of the system. Figure 6 shows the variation of the natural frequency and critical speed of the system when considering the thermal deformation of the ACBB at different speeds. It can be seen from Fig. 6 that the natural frequency and critical speed of the system are reduced when considering thermal deformation. This shows that the influence of thermal deformation on the dynamic characteristics of the ACBB should be considered when establishing a dynamic model of ball bearings, and the thermal deformation of the ACBB should be reduced as much as possible.

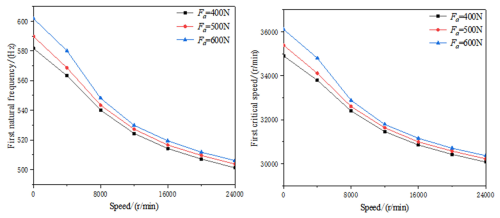
5.3 Effect of the preload of ACBB

As shown in Fig. 7, the natural frequency and critical speed of the system increase with increasing preload. The reason for this phenomenon is that the comprehensive stiffness of the bearing increases, and the total stiffness of the system increases with the increase in bearing preload. The increase in initial preload of the ACBB could improve the stability of the system, but the preload cannot be too large, which will reduce the service life of the bearing.

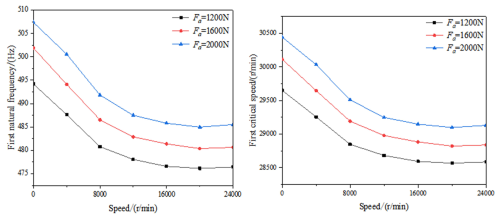
5.4 Effect of external load

When a constant axial external load is applied to the motorized spindle system, it will cause a change in the comprehensive stiffness of the supporting ACBB, thus affecting the dynamic performance of the system. As shown in Fig. 8, the natural frequency and critical speed of the system increase with the increase in the axial external load. The reason for this phenomenon is that the increase in the axial external load results in an increase in the comprehensive stiffness of the bearing, therefore the natural frequency and critical speed of the system increase. At the same time, with the increase in the speed of the motorized spindle, the natural frequency and critical speed of the system first decrease and then increase. This is because the speed increases, and the dynamic viscosity of the lubricating oil of the ACBB decreases due to the influence of temperature rise. The film stiffness then increases, which results in an increase in the comprehensive stiffness of the ACBB. Therefore, there is an inflection point in the figure.

6 Conclusions

In this paper, according to the characteristics of a high-speed motorized spindle, the comprehensive stiffness model of its support bearing is first established. On this basis, a dynamic model of a motorized spindle system is proposed using Timoshenko beam element theory and the finite element method. Subsequently, the dynamic characteristics of the high-speed motorized spindle system under the combined action of the high-speed effect and thermal effect are solved and verified by experiments. Finally, the influence of operating speed, thermal deformation of the ACBB, and preload and external load on the dynamic characteristics of the spindle system are studied. The following conclusions are obtained:

1. At high speed, the change of comprehensive stiffness of the ACBB directly affects the overall stiffness of the system and then influences the dynamic characteristics of the system, such as natural frequency and critical speed.

2. With the increase in motorized spindle speed, the comprehensive stiffness of the ACBB decreases, which leads to a decrease in the natural frequency and critical speed. At the same time, the ACBB will produce the thermal deformation during operation, which will reduce the natural frequency and critical speed of the system.

3. The increase in the ACBB preload increases the comprehensive stiffness of the ACBB, increases the natural frequency and critical speed of the motorized spindle system and effectively improves the stability of the system.

4. The axial external load acting on the motorized spindle system changes the comprehensive stiffness of the ACBB and changes the natural frequency and critical speed of the system.