An adaptive improved gray wolf optimization algorithm with dynamic constraint handling for mechanism-constrained optimization problems

To address constrained optimization problems in mechanical design, this study proposes an enhanced gray wolf optimization (GWO) algorithm. First, a novel individual memory optimization strategy is developed to expand the population's exploration scope and mitigate the risk of individuals pursuing misguided search trajectories. Second, a position update strategy incorporating differential variation is proposed to balance the local and global search capabilities of individual populations. Lastly, a discrete crossover strategy is proposed to promote information diversity across individual dimensions within the population. By integrating these three improvement strategies with the GWO, a novel improved gray wolf optimization (IGWO) algorithm is developed, which not only preserves robust global and local search capabilities but also demonstrates accelerated convergence performance. To validate the effectiveness, feasibility, and generalizability of the proposed algorithms, three representative mechanical design optimization cases and the Z3 parallel mechanism scale parameter optimization case were employed. Empirical findings reveal that the IGWO algorithm effectively resolves the targeted optimization problem, demonstrating superior performance relative to other benchmark algorithms in comparative analyses.

1 Introduction

Advancements in intelligent algorithms have facilitated the extensive application of diverse intelligent algorithms in addressing mechanical design optimization challenges. Mechanical design optimization problems are frequently formulated as constrained optimization tasks, which inherently involve both objective functions and constraints. These constraints, typically categorized into inequality constraints and equality constraints, further restrict the exploration scope of the feasible region. Consequently, constrained optimization problems typically manifest hybrid characteristics, discontinuous traits, discrete attributes, and nonlinear properties, rendering them arduous to resolve (Chen et al., 2022, Chakraborty et al., 2021). Two primary approaches for addressing constrained optimization problems are mathematical induction (Atta, 2024) and intelligent algorithms (Cheng et al., 2025). The mathematical induction-based solving approach can be characterized as a sequential exploration of the solution space, initiated from a predefined starting point and guided by gradient-derived information, progressing iteratively until either a local or global optimal state is reached. This method is plagued by two primary limitations: challenging gradient computation and a pronounced tendency to converge to local optima; furthermore, the efficacy of the solution process exhibits significant dependence on the selection of initial points. In contrast, intelligent algorithms exhibit resilience to initial point selection, with each agent evolving autonomously – a feature that endows them with advantages including structural simplicity, minimal control requirements, and robust generalization capacity. Consequently, population-based intelligent algorithms have demonstrated extensive applicability across diverse domains, such as optimal mechanism design (Ye et al., 2025), communication systems (Shuo et al., 2021), transportation planning optimization (Tang et al., 2024), and computer science research (Wen et al., 2025b).

Intelligent algorithms, a distinct category of computational methodologies, derive inspiration from biological intelligence, natural phenomena, or human cognitive processes. Their primary objective lies in addressing intricate challenges by emulating, extrapolating, and enhancing human cognitive capacities – including learning, reasoning, optimization, and adaptation. Intelligent algorithms typically manifest adaptability, self-learning capability, parallel processing, and global search proficiency, empowering them to pinpoint near-optimal solutions amid uncertain and dynamic milieus. Therefore, intelligent algorithms are widely employed to address real-world constrained optimization problems in engineering. The primary ones include the genetic algorithm (Wang et al., 2022), differential evolutionary algorithm (Li et al., 2023), gray wolf optimization algorithm (Zeng et al., 2025), gravitational search algorithm (Rashedi et al., 2009), artificial bee colony (ABC) algorithm (Gürcan et al., 2022), simulated annealing algorithm (Subrata et al., 2017), and teaching-learning-based optimization algorithm (Zhang et al., 2017), among others. Parsopoulos and Vrahatis (2012) addressed four classical benchmark problems in constrained mechanical design optimization – specifically, the spring optimization problem, pressure vessel optimization problem, welded beam optimization problem, and wheel train optimization problem – by employing standard particle swarm optimization (PSO) algorithms. Chen et al. (2024) proposed the accelerated teaching-learning-based optimization (ATLBO) algorithm to enhance the population update speed of the original teaching-learning-based optimization (TLBO) algorithm by integrating a differential evolution (DE)-based variation strategy. They further validated the effectiveness and feasibility of this improved strategy through typical benchmark test functions, mechanical optimization case studies, and parallel mechanism optimization examples. Sobia et al. (2024) proposed a novel meta-heuristic algorithm, termed the imitation-based cognitive learning optimizer (CLO), to address mechanical design optimization problems. Additionally, three representative mechanical optimization cases and 100 benchmark test functions were selected for experimental validation. The experimental results demonstrate that the CLO algorithm outperforms 12 state-of-the-art counterparts. Mridula and Tapan (2017) employed neutrosophic optimization (NSO) to optimize welded beam problem instances and experimentally demonstrated that the NSO algorithm outperforms other iterative methods.

The gray wolf optimization (GWO) algorithm, belonging to the category of intelligent algorithms, was proposed by Mirjalili et al. (2014) and draws inspiration from the population structure and hunting behavior of gray wolves. Twenty-nine classical test functions and three classical mechanical design optimization examples were employed in the experiments. The experimental results demonstrate that the GWO algorithm outperforms classical algorithms such as the PSO algorithm and the differential evolution algorithm. Meidani et al. (2022) proposed an adaptive GWO algorithm and verified its feasibility and validity through classical test functions. Wang et al. (2025) restructured the hierarchical architecture of the GWO, which enables direct information transmission from the alpha wolf to all subordinate wolves, thereby accelerating the population's convergence rate. Furthermore, they developed two novel learning strategies that synergistically reduce feature dimensionality while mitigating the risk of entrapment in local optima. Chen et al. (2025) incorporated an exponentially decreasing convergence factor, a per-generation elite reselection strategy, and a Cauchy mutation operator into the GWO algorithm, proposing the strengthened gray wolf optimization (SGWO). Singh et al. (2025) integrated a teaching-learning-based optimization (TLBO) algorithm into the GWO, enhancing its search capability, and proposed the hybrid GWO-TLBO algorithm.

The position update strategy of the traditional GWO algorithm is prone to falling into local optima and exhibits weak global search capability, whereas the search space accessible to individuals within the population remains relatively limited. This paper proposes an improved gray wolf optimization (IGWO) algorithm based on these analyses, which aims to address the aforementioned issues and is further applied to mechanical design optimization cases. The main contributions of this study are as follows:

1. The optimal individual memory strategy, the position update strategy incorporating differential variance, and the discrete crossover operation are integrated into the GWO algorithm to develop an improved variant, which simultaneously enhances local search capability, global search capability, and convergence speed.

2. Three classical mechanical optimization cases (welded beam optimization, spring optimization, and pressure vessel optimization), along with the optimization of scale parameters for the Z3 parallel mechanism, are employed as test functions. Experimental results demonstrate that the IGWO algorithm outperforms the other three comparator algorithms.

The remaining chapters of this paper are structured as follows: Sect. 2 presents the methodology for transforming constrained optimization problems into unconstrained optimization problems, along with the fundamental framework of the gray wolf optimization (GWO) algorithm; Sect. 3 details the improved GWO (IGWO) algorithm and its operational procedure; and Sect. 4 evaluates the performance of the IGWO algorithm through three classical mechanical design optimization cases and the dimensional parameter optimization problem of the Z3 parallel mechanism. Finally, Sect. 5 concludes the study and outlines future research directions.

2 Problem description and gray wolf optimizer

In this section, constrained optimization problems are introduced, along with methods for converting them into unconstrained formulations. The GWO algorithm for solving such problems is also presented.

2.1 Structural description

2.1.1 Constrained optimization problem

Without loss of generality, the constrained optimization problem can be formulated as

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}\text{min}f\left(x\right)\\ \text{s.t. }{g}_p\left(x\right)\le \mathrm{0},p=\mathrm{1},\mathrm{2},\mathrm{\dots },m\\ h_q\left(x\right)=\mathrm{0},q=\mathrm{1},\mathrm{2},\mathrm{\dots },n\\ x\in S_{\mathrm{0}}\end{array}\right.,\end{array}$$

where f(x) denotes the objective function; (x) denotes the decision variable; g_p(x) represents an inequality constraint; p denotes the number of inequality constraints, where $p=\mathrm{1},\mathrm{2},\mathrm{\dots },m$; h_q(x) represents an equational constraint; q denotes the number of equational constraints, where $q=\mathrm{1},\mathrm{2},\mathrm{\dots },n$; S₀ denotes the search space of decision variables, where $S_{\mathrm{0}}=\mathit{\{}x\in R_n\mathrm{|}{x}_{\text{min},i}\le x\le x_{\text{max},i}\mathit{\}}$; i denotes the decision variable in the ith dimension, where $i=\mathrm{1},\mathrm{2},\mathrm{\dots },D$; x_min,i denotes the minimum value of the decision variable in the ith dimension; and x_max,i denotes the maximum value of the decision variable in the ith dimension. The feasible domain, defined as the set of all points in the search space S for the decision variable that satisfy the constraints, is denoted as S (i.e., $S=\mathit{\{}x\in S_{\mathrm{0}},g_p(x)\le \mathrm{0}$, h_q(x)=0}). Points within this feasible domain are termed “feasible solutions”. For the inequality constraint g_p(x)≤0, if there exists a point x satisfying g_p(x)=0, then the point x is termed an “active constraint” of g_p(x). Similarly, a point x is said to be positively bounded by h_q(x) if there exists a point $y$ satisfying g_p(x)=0. Suppose that for some $x^{\ast }\in S_{\mathrm{0}}$, there exists a constant ε>0 such that $\forall x\in S_{\mathrm{0}}\cap \mathit{\{}x\mathrm{|}\mathrm{|}\mathrm{|}x-x^{\ast }\mathrm{|}\mathrm{|}<\mathit{\epsilon }\mathit{\}}$. Then, x^∗ is defined as a locally optimal solution of f(x) if it satisfies $f\left(x\right)\ge f\left(x^{\ast }\right)$ for all x in a neighborhood of x^∗. If the equality $f\left(x\right)\ge f\left(x^{\ast }\right)$ holds for all x∈S₀, then x^∗ is said to be a globally optimal solution of f(x).

2.2 Constrained optimization problem

It is inevitable that practical engineering optimization problems are inherently subject to constraints due to limitations such as those related to the environment, space, and other factors. Several types of constraint handling methods are commonly used, including the ε-constraint technique, the Deb criterion, and the penalty function method (also referred to as the feasibility rule). Among them, the ε-constrained processing technique is a process that introduces the parameter ε to control the weights of each objective function, aiming to find the technique's myopic optimal solution while ensuring constraint satisfaction. The penalty function method incorporates a corresponding penalty factor into individuals that violate the constraints, thereby reducing the probability of selecting infeasible individuals. Nevertheless, the relevance between the penalty factor and the optimization problem must be carefully considered during the design process. The feasibility rule, proposed by Deb (Wen et al., 2025a), which states that feasible solutions always outperform infeasible ones and thus results in the evolutionary population never accessing infeasible solutions, is one of the most classical constraint handling methods.

In summary, the Deb criterion is selected in this paper to address the inequality constraints. Therefore, the degree to which the candidate solution x violates the inequality constraint can be defined as follows:

$$\begin{array}{}\text{(2)}& f_{\text{ic}}\left(x\right)=\sum _{i=\mathrm{1}}^m\text{max}\mathit{\{}\mathrm{0},g_p(x\left)\mathit{\right\}}p=\mathrm{1},\mathrm{2},\mathrm{\dots },m,\end{array}$$

where g_p(x)≤0 indicates that the pth inequality constraint has not been violated; the opposite is indeed violated. f_ic(x) denotes the extent to which all inequality constraints are violated, with larger values indicating more severe violations.

In summary, Eq. (1) can be transformed into an unconstrained optimization problem by integrating the method proposed in Wen et al. (2025a) with the Deb criterion:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\text{min}F\left(x\right)=& -[\mathrm{1}-\text{sign}(f_{\text{ic}}\left(x\right)\left)\right]f\left(x\right)+\text{sign}\left(f_{\text{ic}}\right(x\left)\right)\\ & \times [\mathrm{\Phi }+f_{\text{ic}}(x\left)\right],\end{array}\end{array}$$

where sign (⋅) is the sign function and Φ is a sufficiently large constant; in this paper, we take Φ=10⁵.

2.3 Gray wolf optimizer algorithm

Mirjalili et al. (2014) proposed a gray wolf optimization (GWO) algorithm inspired by the population structure and hunting behavior of gray wolves, characterized by its simple architecture and minimal control parameters. The GWO algorithm primarily comprises three core components: social structure, prey herding, and prey capturing. Its main operational steps are detailed as follows:

1. Social structure: the population was hierarchically structured into α-wolves, β-wolves, and γ-wolves based on individual fitness values. During the evolutionary process, candidate wolves updated their positions by following the guidance of α-wolves, β-wolves, and γ-wolves.

2. Rounding up prey: during the hunting process, the Euclidean distance between the nth gray wolf and the α-wolf, β-wolf, and γ-wolf needs to be calculated, which is formulated as follows:

   $$\begin{array}{}\text{(4)}& \left\{\begin{array}{l}{D}_{\mathit{\alpha }}=C_{\mathit{\alpha }}\cdot x_{\mathit{\alpha }}-x_n\\ D_{\mathit{\beta }}=C_{\mathit{\beta }}\cdot x_{\mathit{\beta }}-x_n\\ D_{\mathit{\gamma }}=C_{\mathit{\gamma }}\cdot x_{\mathit{\gamma }}-x_n\end{array}\right.,\end{array}$$

   where D_α, D_β, and D_γ are the Euclidean distances between candidate gray wolves and α-wolves, β-wolves, and γ-wolves, respectively, and C_α, C_β, and C_γ are the swing factors corresponding to the α-wolf, β-wolf, and γ-wolf, respectively, where each parameter represents a random value uniformly sampled from the interval [0,2]. x_n denotes the position of the nth iteration in the GWO.

3. Prey hunting: gray wolves converge toward their prey, with a mathematical model describing this process formulated as follows:

   $$\begin{array}{}\text{(5)}& \left\{\begin{array}{l}{y}_{\mathit{\alpha }}=x_{\mathit{\alpha }}-A_{\mathit{\alpha }}\cdot D_{\mathit{\alpha }}\\ y_{\mathit{\beta }}=x_{\mathit{\beta }}-A_{\mathit{\beta }}\cdot D_{\mathit{\beta }}\\ y_{\mathit{\gamma }}=x_{\mathit{\gamma }}-A_{\mathit{\gamma }}\cdot D_{\mathit{\gamma }}\end{array}\right.,\end{array}$$

   where y_α, y_β, and y_γ denote the temporary positions generated by wolves x_α, x_β, and x_γ, respectively, and A_α, A_β, and A_γ are the convergence factors for the α-wolf, β-wolf, and γ-wolf, respectively.

The new position of the current gray wolf is determined by averaging the three temporary gray wolf positions generated by Eq. (5), which is calculated as follows:

$$\begin{array}{}\text{(6)}& x_n^{t+\mathrm{1}}={\displaystyle \frac{y_{\mathit{\alpha }}+y_{\mathit{\beta }}+y_{\mathit{\gamma }}}{\mathrm{3}}}.\end{array}$$

3 Improving the gray wolf optimization algorithm

In this section, the novel individual memory optimization strategy, position update strategy incorporating differential variation, and discrete crossover strategy are integrated into the GWO framework, with the IGWO algorithm flowchart illustrated subsequently.

3.1 Novel individual memory optimization strategy

As described in the previous section, GWO algorithms utilize the positions of the α-wolf, β-wolf, and γ-wolf to guide the swarm in pursuing the optimal solution, and such algorithms can be classified as elite optimization algorithms. According to Zhang et al. (2025), the search strategy of the elite optimization algorithm enhances the exploitation of its population while diminishing the exploration of the population. The GWO algorithm, on the other hand, relies solely on the current position information of the α-wolf, β-wolf, and γ-wolf during its position update process, without leveraging the historical optimal positions of individuals within the population. This limitation may consequently reduce the search range available to individuals in the swarm. To summarize, the historical optimal position during evolution is introduced not only to expand the population's search range but also to prevent individuals within the population from exploring in the wrong direction. Therefore, when the GWO algorithm evolves to generation t, the historical optimal position experienced by the $n$th gray wolf is denoted as $p_{\text{best},n}^{\left(t\right)}$, and the first three fitness function values within this historical optimal position are denoted as w_α, w_β, and w_γ. Meanwhile, a guide wolf w_g is introduced during a location update, which is closely associated with the historical optimal value of each updated individual. The guide wolf of the nth individual can be denoted as

$$\begin{array}{}\text{(7)}& x_{w_{\mathrm{g}},n}^t={\displaystyle \frac{\mathrm{2}{p}_{\text{best},n}^t+p_{\text{best},r}^t}{\mathrm{3}}},\end{array}$$

where $p_{\text{best},r}^{\left(t\right)}$ is the historical optimum of a random individual.

3.2 Position update strategy incorporating differential variation

During the evolutionary process of the GWO, individuals in the population require stronger global search capability in the early stages, whereas in the later stages, they demand enhanced local search ability and accelerated convergence speed. According to Zhang et al. (2025), the position update strategy presented in Eq. (6) exhibits favorable local search capability and rapid convergence speed; however, it tends to fall into local optima and demonstrates poor global search capability. According to Wen et al. (2022), the DEr1 mutation strategy is reported to exhibit strong global search capabilities while demonstrating relatively weak local exploitation capabilities. Based on this analysis, a three-stage velocity update formulation is proposed to fully exploit the complementary advantages of the GWO position update strategy and the DEr1 mutation strategy. In the early stage of the algorithm, individuals within the population exhibit strong global search capabilities; during the mid-stage, the algorithm demonstrates effective balancing between global search and local search capabilities. By the late stage, it further develops robust local search capability accompanied by accelerated convergence speed. In summary, the new location update strategy is presented below:

$$\begin{array}{}\text{(8)}& z_n^t=\left\{\begin{array}{ll}{x}_{w_{\mathrm{g}},n}^t& \mathrm{0}\le \mathit{\rho }<{\mathit{\kappa }}_{\mathrm{1}}\\ x_{w_{\mathrm{g}},n}^t+F\left(p_{\text{best},r_{\mathrm{1}}}^t-p_{\text{best},r_{\mathrm{2}}}^t\right)& {\mathit{\kappa }}_{\mathrm{1}}\le \mathit{\rho }<{\mathit{\kappa }}_{\mathrm{2}}\\ p_{\text{best},r_{\mathrm{1}}}^t+F\left(p_{\text{best},r_{\mathrm{2}}}^t-p_{\text{best},r_{\mathrm{3}}}^t\right)& {\mathit{\kappa }}_{\mathrm{2}}\le \mathit{\rho }<{\mathit{\kappa }}_{\mathrm{3}}\end{array}\right.,\end{array}$$

where $z_n^t$ denotes the position of the nth gray wolf subsequent to the mutation operation; r₁, r₂, and r₃ denote three distinct random integers sampled from the interval [1,NP]; F denotes the scale factor; and A is a random number uniformly distributed in the interval [0,1]. κ₁ and κ₂ denote random perturbation probabilities sampled uniformly from the interval [0,1]. In this study, we set κ₁=0.25 and κ₂=0.5.

3.3 Discrete crossover strategy

According to Mirjalili et al. (2014), the GWO addresses high-dimensional optimization problems by representing each wolf's position as a D-dimensional coordinate. As the dimensionality increases, the wolves' search efforts in individual dimensions gradually diminish, resulting in unbalanced exploration across different dimensions. Meanwhile, the linear decreasing strategy of the traditional GWO algorithm also struggles to adapt to high-dimensional search spaces, further diminishing the wolf pack's search efficiency. According to Wen et al. (2025b), the discrete crossover strategy can integrate the advantages of parent individuals, facilitate solution evolution, maintain population diversity, avoid premature convergence, balance exploration and exploitation, and enhance optimization efficiency. To summarize, a discrete crossover operation is performed between the mutated wolf position and the historical optimal position of the current wolf to generate the next-generation wolf position. The specific expression of this operation is provided below:

$$\begin{array}{}\text{(9)}& x_n^{t+\mathrm{1}}=\left\{\begin{array}{ll}{z}_{n,d}^t& \mathit{\varphi }<\text{CR}\\ p_{\text{best},n,d}^{t+\mathrm{1}}& \text{else if}\end{array}\right.,\end{array}$$

where CR denotes the crossover probability; in this study, we set CR=0.9. φ denotes a uniformly distributed random number within the closed interval [0,1]. $z_{n,d}^t$ denotes the d-dimensional variable corresponding to the position of the nth gray wolf. $p_{\text{best},n,d}^{t+\mathrm{1}}$ is the d-dimensional variable of the historically optimal position of the nth gray wolf.

3.4 Pseudocode of the IGWO

The IGWO algorithm is developed by integrating three key strategies – the optimal individual memory strategy, the position update strategy with differential variances, and the discrete crossover operation – into the baseline GWO algorithm presented in Sect. 2.3. The pseudocode of the IGWO algorithm is presented in Algorithm 1.

4 Mechanical optimization example

In this section, the IGWO, GWO, ABC, and PSO algorithms were employed to solve three classic mechanical optimization problems and the Z3 parallel mechanism scale parameter optimization problem.

4.1 Typical examples of mechanical optimization

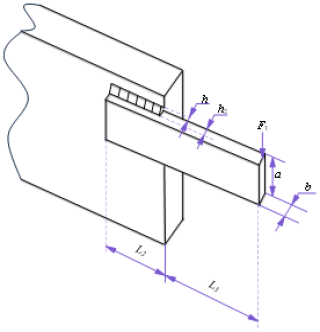
Case 1: welded beam optimization. The welded beam optimization problem aims to minimize the beam's fabrication cost under constraints such as shear stress, bending stress, buckling load on the rod, and end perturbations of the beam. The welded beam structure is schematically shown in Fig. 1, where the optimization variables are defined as $x=(x_{\mathrm{1}},x_{\mathrm{2}},x_{\mathrm{3}},x_{\mathrm{4}}{)}^{\mathrm{T}}=(h,l_{\mathrm{2}},a,b{)}^{\mathrm{T}}$. The mathematical model of the problem can be expressed as follows:

$$\begin{array}{}\text{(10)}& \text{min}f\left(x\right)=\mathrm{1.1047}{x}_{\mathrm{1}}^{\mathrm{2}}{x}_{\mathrm{2}}+\mathrm{0.04811}{x}_{\mathrm{3}}{x}_{\mathrm{4}}(\mathrm{14}+x_{\mathrm{2}}).\end{array}$$

Figure 1 Optimization of welded beams.

The constraints are

$$\begin{array}{}\text{(11)}& \left\{\begin{array}{l}{g}_{\mathrm{1}}\left(x\right)=\mathit{\tau }\left(x\right)-{\mathit{\tau }}_{\text{max}}\le \mathrm{0}\\ g_{\mathrm{2}}\left(x\right)=\mathit{\sigma }\left(x\right)-{\mathit{\sigma }}_{\text{max}}\le \mathrm{0}\\ g_{\mathrm{3}}\left(x\right)=x_{\mathrm{1}}-x_{\mathrm{4}}\le \mathrm{0}\\ g_{\mathrm{4}}\left(x\right)=\mathrm{0.10471}{x}_{\mathrm{1}}^{\mathrm{2}}+\mathrm{0.4811}{x}_{\mathrm{3}}{x}_{\mathrm{4}}(\mathrm{14.0}+x_{\mathrm{2}})-\mathrm{5}\le \mathrm{0}\\ g_{\mathrm{5}}\left(x\right)=\mathrm{0.125}-x_{\mathrm{1}}\le \mathrm{0}\\ g_{\mathrm{6}}\left(x\right)=\mathit{\delta }\left(x\right)-{\mathit{\delta }}_{\text{max}}\le \mathrm{0}\\ g_{\mathrm{7}}\left(x\right)=P-P_{\mathrm{c}}\left(x\right)\le \mathrm{0}\end{array}\right.,\end{array}$$

where $\mathit{\tau }\left(x\right)=\sqrt{({\mathit{\tau }}^{\prime }{)}^{\mathrm{2}}+\mathrm{2}{\mathit{\tau }}^{\prime }{\mathit{\tau }}^{\prime \prime }\frac{x_{\mathrm{2}}}{\mathrm{2}R}+({\mathit{\tau }}^{\prime \prime }{)}^{\mathrm{2}}},{\mathit{\tau }}^{\prime }=\frac{P}{\sqrt{\mathrm{2}}{x}_{\mathrm{1}}{x}_{\mathrm{2}}}$, ${\mathit{\tau }}^{\prime \prime }=\frac{MR}{J},M=P\left(L+\frac{x_{\mathrm{2}}}{\mathrm{2}}\right),R=\sqrt{\frac{x_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{4}}+{\left(\frac{x_{\mathrm{1}}+x_{\mathrm{3}}}{\mathrm{2}}\right)}^{\mathrm{2}}}$, $J=\mathrm{2}\left\{\frac{x_{\mathrm{1}}{x}_{\mathrm{2}}}{\sqrt{\mathrm{2}}}\left[\frac{x_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{12}}+{\left(\frac{x_{\mathrm{1}}+x_{\mathrm{3}}}{\mathrm{2}}\right)}^{\mathrm{2}}\right]\right\},\mathit{\delta }\left(x\right)=\frac{\mathrm{4}P{L}^{\mathrm{3}}}{E{x}_{\mathrm{3}}^{\mathrm{3}}{x}_{\mathrm{4}}},\mathit{\sigma }\left(x\right)=\frac{\mathrm{6}PL}{x^{\mathrm{4}}{x}_{\mathrm{3}}^{\mathrm{2}}}$, and $P_{\mathrm{c}}\left(x\right)=\frac{\mathrm{4.013}E\sqrt{\frac{a^{\mathrm{2}}{b}^{\mathrm{6}}}{\mathrm{36}}}}{L_{\mathrm{3}}^{\mathrm{2}}}\left(\mathrm{1}-\frac{a}{\mathrm{2}{L}_{\mathrm{3}}}\sqrt{\frac{E}{\mathrm{4}G}}\right).$

In the formula, each parameter is expressed in imperial units, with its value or the range of values specified. F₁ = 2761.6 kg, L₃ = 35.56 cm, E = 30 × 10⁶ psi, G = 12 × 10⁶ psi, τ_max = 13 600 psi, σ_max = 30 000 psi, and δ_max = 0.635 cm.

Here, the design variables have to be in the following ranges:

$$\mathrm{0.1}\le x_{\mathrm{1}}\le \mathrm{2.0};\mathrm{0.1}\le x_{\mathrm{2}}\le \mathrm{10};\mathrm{0.1}\le x_{\mathrm{3}}\le \mathrm{10};\mathrm{0.1}\le x_{\mathrm{4}}\le \mathrm{2.0}.$$

To verify the effectiveness and feasibility of the IGWO algorithm, the GWO, PSO, and ABC (Mridula and Tapan, 2017) algorithms are employed as comparative benchmarks.

Table 1 Statistical performance metrics of the four algorithms.

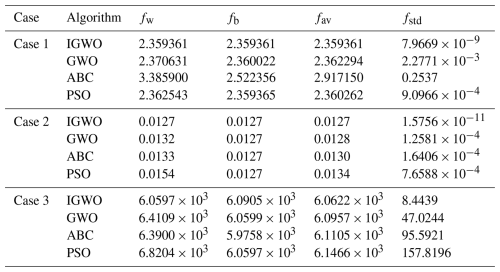
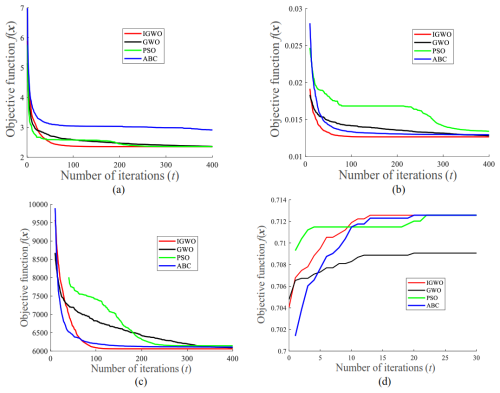
The control parameters of each algorithm are aligned with those reported in the original literature. To ensure the fairness of experimental outcomes, the population size NP and number of iterations T for all algorithms are set as follows: NP=100 and T=400. Equations (10) and (11) are first transformed into unconstrained optimization problems based on Eq. (3) and then solved separately using five algorithms. The four algorithms were run independently and randomly 50 times, and the average evolution curve of the objective function values was obtained, as shown in Fig. 4. The statistical results from 50 independent random runs of the five algorithms for solving the welded beam optimization problem are presented in Table 1. Here, f_w, f_av, f_b, and f_std denote the worst-case, mean, optimal, and standard deviation of the optimal objective function values across 50 independent algorithm runs, respectively.

As shown in Table 1, the IGWO algorithm yields the optimal values for f_w, f_av, f_b, and f_std, followed by the PSO, GWO, and ABC algorithms. Based on Fig. 4, it can be observed that during the pre-evolutionary algorithm period, the GWO and PSO algorithms converge faster than the IGWO algorithm. As the algorithm progresses to its later stages, the IGWO algorithm exhibits a superior convergence rate compared to other comparative algorithms. Moreover, the convergence accuracy of the IGWO algorithm is significantly better than that of several other comparative algorithms.

Figure 2 Schematic diagram of spring structure.

Case 2: spring optimization.

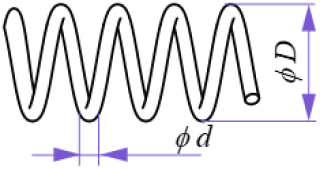
The spring optimization problem can be formulated as minimizing the spring weight subject to the constraints of minimum deflection, shear stress, surge frequency, and outside diameter limits. The optimization variables include the wire diameter d, average coil diameter D, and effective number of active coils N. The design variables can be mathematically represented as $x=(x_{\mathrm{1}},x_{\mathrm{2}},x_{\mathrm{3}}{)}^{\mathrm{T}}=(d,D,N{)}^{\mathrm{T}}$. A schematic diagram of the spring structure is illustrated in Fig. 1. The mathematical model of the problem can be expressed as follows:

$$\begin{array}{}\text{(12)}& \text{min}f\left(x\right)=(x_{\mathrm{3}}+\mathrm{2})x_{\mathrm{2}}{x}_{\mathrm{1}}^{\mathrm{2}}.\end{array}$$

The constraints are

$$\begin{array}{}\text{(13)}& \left\{\begin{array}{l}{g}_{\mathrm{1}}\left(x\right)=\mathrm{1}-\frac{x_{\mathrm{2}}^{\mathrm{3}}{x}_{\mathrm{3}}}{\mathrm{71785}{x}_{\mathrm{1}}^{\mathrm{4}}}\le \mathrm{0}\\ g_{\mathrm{2}}\left(x\right)=\frac{\mathrm{4}{x}_{\mathrm{2}}^{\mathrm{2}}-x_{\mathrm{1}}{x}_{\mathrm{2}}}{\mathrm{12566}\left(x_{\mathrm{2}}{x}_{\mathrm{1}}^{\mathrm{3}}-x_{\mathrm{1}}^{\mathrm{4}}\right)}+\frac{\mathrm{1}}{\mathrm{5108}{x}_{\mathrm{1}}^{\mathrm{2}}}-\mathrm{1}\le \mathrm{0}\\ g_{\mathrm{3}}\left(x\right)=\mathrm{1}-\frac{\mathrm{140.45}{x}_{\mathrm{1}}}{x_{\mathrm{2}}^{\mathrm{2}}{x}_{\mathrm{3}}}\le \mathrm{0}\\ g_{\mathrm{4}}\left(x\right)=\frac{x_{\mathrm{2}}+x_{\mathrm{1}}}{\mathrm{1.5}}-\mathrm{1}\le \mathrm{0}\end{array}\right.,\end{array}$$

where the design variables have to be in the following ranges:

$$\mathrm{0.05}\le x_{\mathrm{1}}\le \mathrm{2};\mathrm{0.25}\le x_{\mathrm{2}}\le \mathrm{1.3};\mathrm{2}\le x_{\mathrm{3}}\le \mathrm{15}.$$

Based on Eq. (3), Eqs. (12) and (13) were transformed into unconstrained optimization models and solved separately using four algorithms. The control parameters of the four algorithms were consistent with those in Case 1. Each algorithm was run 50 independent times, with the average evolutionary curve of the objective function presented in Fig. 4 and the performance metrics of the four algorithms shown in Table 1. Table 1 shows that the IGWO algorithm achieves optimal values in terms of f_w, f_av, f_b, and f_std, followed by the GWO, ABC, and PSO algorithms. Meanwhile, Fig. 4 illustrates that during the early evolutionary stage, the GWO algorithm exhibits faster convergence speed than the IGWO algorithm. However, in the late evolutionary stage, the IGWO algorithm demonstrates significantly superior convergence speed and convergence accuracy compared to several other benchmark algorithms.

Figure 3 Pressure vessel structure sketch.

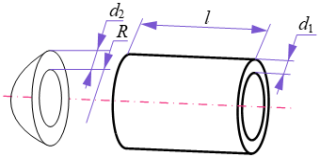
Case 3: pressure vessel optimization. The pressure vessel constrained optimization problem is described as a problem of minimizing the cost of a pressure vessel, subject to constraints on material cost, forming cost, welding cost, and shell thickness. The design variables are the shell thickness d₁, head thickness d₂, inner shell radius R, and cylindrical length l. These design variables can be mathematically represented as $x=(x_{\mathrm{1}},x_{\mathrm{2}},x_{\mathrm{3}},x_{\mathrm{4}}{)}^{\mathrm{T}}=(d_{\mathrm{1}},d_{\mathrm{2}},Rl{)}^{\mathrm{T}}$. A schematic diagram of the pressure vessel's structural configuration is shown in Fig. 1. The mathematical model of the problem can be expressed as follows:

$$\begin{array}{}\text{(14)}& \begin{array}{rl}\text{min}f\left(x\right)=& \mathrm{0.6224}{x}_{\mathrm{1}}{x}_{\mathrm{3}}{x}_{\mathrm{4}}+\mathrm{1.7811}{x}_{\mathrm{2}}{x}_{\mathrm{3}}^{\mathrm{2}}+\mathrm{3.166}{x}_{\mathrm{1}}^{\mathrm{2}}{x}_{\mathrm{4}}\\ & +\mathrm{19.84}{x}_{\mathrm{1}}^{\mathrm{2}}{x}_{\mathrm{3}}.\end{array}\end{array}$$

The constraints are

$$\begin{array}{}\text{(15)}& \left\{\begin{array}{l}{g}_{\mathrm{1}}\left(x\right)=-x_{\mathrm{1}}+\mathrm{0.0193}\le \mathrm{0}\\ g_{\mathrm{2}}\left(x\right)=-x_{\mathrm{2}}+\mathrm{0.00954}\le \mathrm{0}\\ g_{\mathrm{3}}\left(x\right)=-\mathit{\pi }{x}_{\mathrm{3}}^{\mathrm{2}}{x}_{\mathrm{4}}-\frac{\mathrm{4}}{\mathrm{3}}\mathit{\pi }{x}_{\mathrm{3}}^{\mathrm{2}}+\mathrm{129}\mathrm{600}\le \mathrm{0}\\ g_{\mathrm{4}}\left(x\right)=x_{\mathrm{4}}-\mathrm{240}\le \mathrm{0}\end{array}\right.,\end{array}$$

where the design variables have to be in the following ranges:

$$x_{\mathrm{1}}\ge \mathrm{0};x_{\mathrm{2}}\le \mathrm{99};x_{\mathrm{3}}\ge \mathrm{10};x_{\mathrm{4}}\le \mathrm{200}.$$

Equations (14) and (15) were first transformed into unconstrained optimization models based on Eq. (3) and then solved individually using four distinct algorithms. The control parameters of the four algorithms were consistent with those in Case  1. Each algorithm was independently run for 50 trials, with the average evolution curve of the objective function shown in Fig. 4 and the performance indexes of the four algorithms presented in Table 1. According to Table 1, the IGWO algorithm achieves the optimal values for f_w, f_av, f_b, and f_std, followed by the GWO, ABC, and PSO algorithms. Additionally, Fig. 4 illustrates that during the early stages of the algorithms, ABC and GWO exhibit faster convergence than IGWO. Conversely, in the later stages, IGWO demonstrates significantly superior convergence speed and accuracy compared to the other evaluated algorithms.

Figure 4 Average evolution curves of the algorithms. (a) Case 1, (b) case 2, (c) case 3, and (d) Z3 parallel mechanism.

4.2 Dimensional optimization for parallel mechanisms

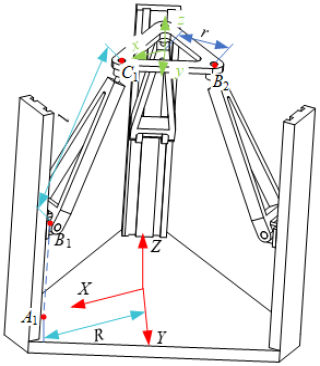
An example of scale parameter optimization for a Z3 parallel mechanism, reported in Wen et al. (2025a), is selected to further validate the generality of the IGWO algorithm. The structural diagram of the Z3 parallel mechanism is shown in Fig. 5, which primarily consists of three PRS (P: prismatic, R: revolute, S: spherical) pivot chains, along with movable and fixed platforms featuring identical structures and sizes. The P sub-axis intersects the fixed platform at point A_i, which lies on a circle with radius R centered at O, where the angles between A₁O, A₂O, and A₃O are each 120°. The length of the connecting rod B_iC_i is denoted by l. The center of the S-vice intersects the moving platform at point C_i, which lies on a circle with an outer radius r centered at o. Additionally, the angle among C₁P, C₂P, and C₃P is 120°.

Figure 5 Z3 parallel mechanism (Wen et al., 2025a).

In summary, the scale parameter optimization problem of the Z3 parallel mechanism can be succinctly formulated as follows: for a given scale parameter R, the optimal combination of the mechanism's scale parameters l and r enables the Z3 parallel mechanism to achieve an optimal effective transmission workspace. Therefore, the optimization variables in the scale parameter optimization problem for the Z3 parallel mechanism can be defined as

$$\begin{array}{}\text{(16)}& x=[x_{\mathrm{1}},x_{\mathrm{2}}{]}^{\mathrm{T}}=[r,l{]}^{\mathrm{T}}.\end{array}$$

According to Wen et al. (2025a), the objective function is defined as

$$\begin{array}{}\text{(17)}& \text{max}f\left(x\right)=\text{max}\mathit{\left\{}{\mathit{\kappa }}_{\text{ETW}}\right(r,l\left)\mathit{\right\}},\end{array}$$

where κ_ETW denotes the mathematical expression used to calculate the maximum radius of the internal tangent circle in the Z3 parallel mechanism via motion/force transfer metrics; specifically, ${\mathit{\kappa }}_{\text{ETW}}=\text{min}\mathit{\left\{}\mathit{\theta }\mathrm{|}{\mathit{\eta }}_{\text{LTI}}\right(\mathit{\phi },\mathit{\theta })=\mathrm{0.7},\forall \mathit{\phi }\in [\mathrm{0},\mathrm{2}\mathit{\pi }\left]\mathit{\right\}}$.

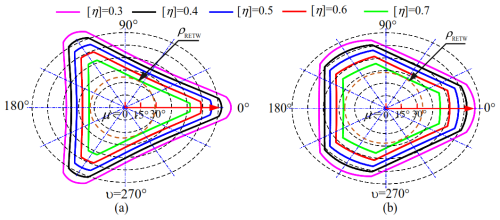
Figure 6 Performance comparison of the Z3 parallel mechanism before and after optimization. (a) Pre-optimization. (b) Optimization design.

The constraints can be expressed as follows:

$$\begin{array}{}\text{(18)}& \left\{\begin{array}{l}{g}_{\mathrm{1}}\left(x\right)=\mathrm{0.75}-{\mathit{\eta }}_{\text{GTI}}\le \mathrm{0}\\ g_{\mathrm{2}}\left(x\right)=\mathrm{0.05}-\frac{r}{l}\le \mathrm{0}\end{array}\right.,\end{array}$$

where η_GTI denotes the average of the transfer metrics for all attitudes (φ,θ) at a fixed altitude Z3, which is calculated as shown below:

$$\begin{array}{}\text{(19)}& {\mathit{\eta }}_{\text{GTI}}={\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{2}\mathit{\pi }}{\int }_{\mathrm{0}}^{{\mathit{\kappa }}_{\text{ETW}}}{\mathit{\eta }}_{\text{LTI}}(\mathit{\phi },\mathit{\theta })\sin \mathit{\theta }\mathrm{d}\mathit{\phi }\mathrm{d}\mathit{\theta }}{\mathrm{2}\mathit{\pi }(\mathrm{1}-\cos {\mathit{\kappa }}_{\text{ETW}})}}\mathrm{0.75}-{\mathit{\eta }}_{\text{GTI}}\le \mathrm{0}.\end{array}$$

Equal scaling of the mechanism's scale parameters does not affect its performance; therefore, the parameters of the Z3 parallel mechanism are set as R = 100 cm and Z_P = 100 mm. Equations (16) and (17) are transformed into the unconstrained optimization model presented in Eq. (3) and subsequently solved using four comparative algorithms – each employing identical parameter settings to those specified in Sect. 4.1. Each algorithm is run independently 50 times. The average evolution curve of the objective function is shown in Fig. 6. Meanwhile, based on the 50 optimization results obtained from the IGWO algorithm, a set of optimized mechanism scale parameters are selected as the mechanism parameters. The performance of these optimized scale parameters is then compared with that of the empirical scale parameters, and the ETW cross-section of the mechanism with fixed height is plotted, as shown in Fig. 6.

Figure 6 demonstrates that the optimized mechanism achieves significantly better performance than the pre-optimization state, aligning with the results reported by Wen et al. (2025a). As shown in Table 1, the optimization results of the IGWO, PSO, and ABC algorithms are consistent. However, Fig. 4 reveals that the IGWO algorithm exhibits a significantly faster convergence speed compared to the PSO and ABC algorithms. Meanwhile, the IGWO algorithm achieves significantly better optimization results than the GWO algorithm. However, as evidenced by Fig. 4, the GWO algorithm demonstrates a markedly faster convergence speed during the pre-evolutionary stage compared to IGWO. In the later stages of optimization, the GWO algorithm's position update mechanism tends to cause premature convergence to local optima. Conversely, the incorporation of the DE position update strategy effectively mitigates this issue, enabling the algorithm to escape local optima and converge more efficiently toward the global optimum. In summary, the proposed novel individual memory optimization strategy, differential-variation-based position update mechanism, and discrete crossover operator integrated with the GWO algorithm collectively enhance its global exploration capability, local exploitation efficiency, and convergence performance.

5 Conclusion

To enhance the convergence speed, convergence accuracy, and ability to solve high-dimensional constrained optimization problems of the traditional GWO algorithm, an IGWO algorithm is proposed. By integrating an optimal individual memory strategy, a position update strategy with differential variance, and a discrete crossover factor into the traditional GWO algorithm, the IGWO effectively balances local search capability, global search capability, and convergence speed. To validate the performance of the IGWO algorithm, three typical mechanical design optimization problems and the scale parameter optimization problem of the Z3 parallel mechanism were employed as test cases. The experimental results demonstrate that the IGWO algorithm outperforms the PSO, GWO, and ABC algorithms.

In future research, investigations on the IGWO algorithm can be extended to multi-objective optimization. To address its core challenges – including conflicting objectives and the need to balance convergence with solution set diversity – we propose designing a composite adaptive evaluation mechanism that integrates dominance relations, distribution indicators, and convergence metrics. Additionally, optimizing the rules for dynamic social hierarchy updating and group collaboration strategies is expected to mitigate the loss of solution set diversity caused by premature convergence. In addition, effective constraint processing techniques can be further integrated with the IGWO algorithm to expand its applicability to a broader range of practical engineering scenarios.