Bearing fault diagnosis method based on an improved particle swarm optimization–variational mode decomposition (PSO–VMD) multidimensional index and its application in a crane amplitude-changing mechanism

In the luffing mechanism of a crane, the bearing is one of the parts that bear the important load. If the bearing fails, the luffing mechanism of the crane will lose its steady state of operation and may even cause an accident. To identify the early characteristics of bearing failure in the crane luffing mechanism and prevent losses resulting from severe bearing damage, this paper proposes a bearing fault diagnosis method for the crane luffing mechanism based on improved particle swarm optimization–variational mode decomposition (PSO–VMD) multidimensional indicators. Firstly, the Metropolis algorithm was introduced into the PSO, and an improved PSO (IPSO) was proposed to solve the problems of poor global search ability and easy falling into local extreme values. The parameters of VMD are adapted through IPSO to decompose model components. Then, the three components with the largest kurtosis are selected for signal reconstruction, and the peak factor, margin factor, pulse factor, sample entropy, energy entropy, and power spectrum entropy of the reconstructed signal are used to form a multidimensional composite feature vector, and then the principal component analysis (PCA) method is used to extract its core components. Finally, the core components are used as input samples of the support vector machine (SVM) for training and testing, which can effectively detect the bearing fault of the crane luffing mechanism. Experimental data demonstrate that the proposed method not only reduces the training time of the classification model but also enhances the classification accuracy.

1 Introduction

The luffing mechanism of a crane is an important part of the crane and is used to control the position and direction of the hook. In the luffing mechanism of the crane, the bearing is one of the parts that bear the important load. If the bearing fails, it will cause the luffing mechanism of the crane to lose its stable running state and even cause an accident. Therefore, the bearing fault diagnosis of the luffing mechanism of the crane plays an important role in the maintenance of the crane (Qin et al., 2020; Wang et al., 2021, 2022a, b; Qin et al., 2023; Wang et al., 2023). Through the inspection and analysis of the bearing, the cause of the bearing failure can be found in time and corresponding maintenance and replacement measures can be taken to ensure the safe operation of the crane. At the same time, the maintenance of the bearing is also very important and can prolong its service life, reduce the possibility of failure, and improve the working efficiency and safety of the crane (Gao et al., 2015; Tao et al., 2023; Sun et al., 2023a; Wu et al., 2024; Zhao et al., 2023).

For the fault condition of the bearing of the luffing mechanism of the crane, the vibration signal on the surface of the bearing of the luffing mechanism of the crane can be collected. Vibration signals contain periodic shock signals, and the frequencies of shock signals generated by different health conditions are different, so the vibration signals are extracted and identified (Rodríguez Ramos et al., 2019; Chen et al., 2023). Dragomiretskiy and Zosso (2014) proposed a variational mode decomposition (VMD) method, which can effectively reduce problems such as mode aliasing compared with empirical mode decomposition (EMD). Jin et al. (2022) and Li et al. (2020, 2022) improved the VMD algorithm to improve the performance of the algorithm and solved the its local optimal problem. Recognizing the advantages of vibration signal anti-interference, Sun et al. (2024b) proposed a diagnostic method that combines VMD and multiscale wave dispersion entropy. Compared to methods such as empirical mode decomposition, this approach serves as a core effective feature selection tool. Dibaj et al. (2021) proposed a new end-to-end fault diagnosis method based on fine-tuning VMD and convolutional neural networks (CNNs). The optimization algorithm proposed by Dibaj et al. (2021) can optimize the VMD parameters so that the decomposition mode has the minimum bandwidth and noise interference.

This paper mainly studies difficult existing problems in the current fault diagnosis of rolling bearings, such as using singular value decomposition (SVD) to determine the delay step size k, create a Hankel matrix, and select effective singular values. By analyzing the principle of the SVD method, Qiao et al. (2021) proposed an adaptive singular value decomposition method based on correlation coefficients for singular value decomposition feature extraction of rolling bearing fault diagnosis. In order to select effective singular values more accurately, Cui et al. (2022) proposed a new singular value decomposition method based on energy graphs. For complex fault diagnosis of rolling bearings in complex industrial environments, Zhang et al. (2022) proposed an improved double-dictionary k singular value decomposition algorithm. Zhu et al. (2023) proposed an improved singular value decomposition grouping algorithm, which improves the ability of feature extraction by changing the structure of the Hankel matrix.

In order to solve problems such as large amounts of data and inaccurate and untimely fault diagnosis, Wen et al. (2021) proposed a hybrid fault diagnosis method based on relief, principal component analysis (PCA), and deep neural networks (DNNs), which can effectively solve the fault diagnosis problem of PCA. Zhu et al. (2020) regarded bearing fault diagnosis as a class of pattern classification problem and proposed an intelligent fault diagnosis method based on PCA and deep belief networks (DBNs). Addressing the limitations of traditional PCA linear dimensionality reduction, Sun et al. (2024a) introduced kernel functions to map features into high-dimensional space, thereby achieving nonlinear feature fusion and retaining fault-sensitive information while reducing feature dimensions. Guo et al. (2020) proposed a Gaussian mixture model (GMM)-based fault diagnosis strategy for variable refrigerant flow air conditioning systems. Cao et al. (2022) proposed a data-based method to improve the accuracy and speed of the fault diagnosis. Ye et al. (2021) proposed a method to improve the accuracy of rolling bearing fault detection. The method is based on VMD, multiscale permutation entropy (MPE), and PSO–SVMs (support vector machines) (Liu et al., 2023). Sun et al. (2023b) employed PSO to concurrently optimize the weights of multiscale fractional permutation entropy and hyperparameters of support vector machines, thereby proposing a synchronous optimization strategy.

The Metropolis algorithm was proposed in 1953 (Bhanot, 1988). The core idea of the Metropolis algorithm is to gradually approach the target probability distribution by randomly walking in the state space and deciding whether to accept the new state according to certain acceptance criteria. In traditional PSO, the update of particles mainly depends on their own speeds, historical optimal positions, and global optimal positions (Shenoy et al., 2020). After the introduction of the Metropolis algorithm, the factor of random disturbance is added. This randomness allows particles to escape the trap of local optimal solutions during the search process and have the opportunity to explore a wider solution space (Zhang et al., 2022).

On the basis of the above literature research, this paper solves the problems of adaptive selection of VMD parameters and the fact that the modal component of VMD is a series of disordered time series. It proposes a bearing fault diagnosis method based on an improved PSO–VMD multidimensional index and its application in a crane amplitude-changing mechanism. The Metropolis algorithm is introduced into PSO, and IPSO is proposed to solve the problems of poor global search ability and easy falling into local extreme values. IPSO is used to adapt the number of decomposition layers k and penalty factors α of VMD to decompose K modal components. The three components with the largest kurtosis are selected for signal reconstruction, and the peak factor, margin factor, pulse factor, sample entropy, energy entropy, and power spectrum entropy of the reconstructed signal are used to form a multidimensional composite feature vector, and then PCA is used to extract its core components. The core features are input into SVMs for training. In order to demonstrate the application effect of the proposed method, the method is used to perform diagnostic tests on the bearing fault data collected in the experiment. The main contributions and innovations of this paper are summarized as follows:

• 1.

  A crane luffing mechanism bearing fault diagnosis method utilizing improved PSO–VMD multidimensional indicators is proposed, with its application in crane luffing mechanisms.

• 2.

  The Metropolis algorithm is incorporated into PSO to enhance its global search capability, and a parameter adaptation method for IPSO–VMD is introduced.

• 3.

  The peak factor, margin factor, pulse factor, sample entropy, energy entropy, and power spectrum entropy within the VMD modal component are integrated to form a multidimensional composite feature vector.

• 4.

  The PCA dimensionality reduction algorithm is employed to extract the core components, which are then used as input samples for SVM training and testing.

The rest of this paper is organized as follows. In Sect. 2, the proposed method for crane luffing mechanism bearing fault diagnosis based on improved PSO–VMD multidimensional indicators is introduced. In Sects. 3 and 4, public datasets and real cases are used for analysis to verify the feasibility and advantages of the proposed method. Section 5 is the conclusion of this paper.

2 Research methods

2.1 Variational mode decomposition algorithm

In 2014, the VMD was proposed, which can perform custom decomposition on complex signals and decompose the signal into K modal components in different frequency domains (Dragomiretskiy and Zosso, 2014). This method can effectively solve a series of problems such as modal aliasing and endpoint effects in the decomposition of other time–frequency domain signals.

When obtaining the modal components, VMD introduces the original signal into the variational modal model for solution, and the constrained variational model is established as follows:

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{c}{min}_{\left\{u_k\right\}\left\{{\mathit{\omega }}_k\right\}}\left\{\sum _{k=\mathrm{1}}^K{∥\partial t\left[\left(\mathit{\delta }\left(t\right)+\frac{j}{\mathit{\pi }t}\right)\times u_k\left(t\right)\right]e^{-j{\mathit{\omega }}_{k}t}∥}_{\mathrm{2}}^{\mathrm{2}}\right\}\\ \text{s.t.}\sum _{k=\mathrm{1}}^K{u}_k\left(t\right)=f\left(t\right).\end{array}\right.\end{array}$$

In the formula, δ(t) is the unit pulse, x(t) is the input signal, and ω_k is the center frequency of the modal component u_k.

To solve the variational model established above, it is necessary to introduce the penalty factor α and the Lagrangian operator λ into the variational mode decomposition process. The augmented Lagrangian expression is as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{l}L\left(\left\{u_k\right\},\left\{w_k\right\},\mathit{\lambda }\right)\\ =\mathit{\alpha }\sum _k{∥{\partial }_t\left[\left(\mathit{\delta }\left(t\right)+\frac{j}{\mathit{\pi }t}\right)\times u_k\left(t\right)\right]e^{-j{w}_{k}t}∥}_{\mathrm{2}}^{\mathrm{2}}\\ +{∥x\left(t\right)-\sum _k{u}_k\left(t\right)∥}_{\mathrm{2}}^{\mathrm{2}}+〈\mathit{\lambda }\left(t\right),x\left(t\right)-\sum _k{u}_k\left(t\right)〉.\end{array}\end{array}$$

Finally, the alternating direction method of multipliers (ADMM) is employed to solve it.

2.2 IPSO-optimized VMD algorithm

Although the particle swarm algorithm has the advantages of fast convergence speed and few parameters, its global search ability is poor and it is easy to fall into local extreme values, which makes the algorithm unable to find the global optimum (Shenoy et al., 2020). The improved PSO generates a series of solutions to the combinatorial optimization problem through the Metropolis algorithm and then decides whether to exit the local search space according to the transition probability P_t corresponding to the criterion (Bhanot, 1988). The calculation method of P_t is as follows:

$$\begin{array}{}\text{(3)}& P_t=\left\{\begin{array}{l}\mathrm{1},E\left(x_{\mathrm{new}}\right)<E\left(x_{\mathrm{old}}\right)\\ \exp \left(-\frac{E\left(x_{\mathrm{new}}\right)-E\left(x_{\mathrm{old}}\right)}{T}\right),E\left(x_{\mathrm{new}}\right)⩾E\left(x_{\mathrm{old}}\right)\end{array}\right.,\end{array}$$

where E(x_new) and E(x_old) represent the new and old energy values, respectively, and T is the maximum number of iterations.

The numerical value of the kurtosis coefficient can represent the degree of dispersion of the sample data. It is very sensitive to the impact signal and is especially suitable for fault diagnosis research of rolling bearings. The mathematical expression of the kurtosis coefficient is

$$\begin{array}{}\text{(4)}& \text{KI}={\displaystyle \frac{\frac{\mathrm{1}}{N}{\sum }_{n=\mathrm{0}}^{N-\mathrm{1}}{x}^{\mathrm{4}}\left(n\right)}{{\left(\frac{\mathrm{1}}{N}{\sum }_{n=\mathrm{0}}^{N-\mathrm{1}}{x}^{\mathrm{2}}\left(n\right)\right)}^{\mathrm{2}}}},\end{array}$$

where x is the signal sequence. N is the length of the signal sequence and represents the kurtosis coefficient of the signal sequence.

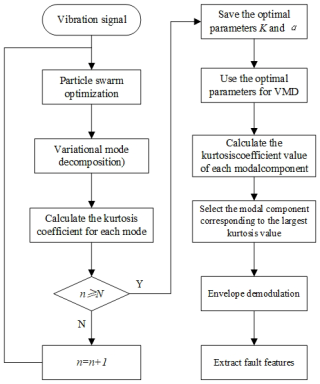
The kurtosis coefficient of a signal that obeys a normal distribution generally fluctuates around a fixed value of 3, and its kurtosis coefficient will become larger if the signal contains an impact signal. The flowchart of IPSO–VMD is shown in Fig. 1. In order to verify the effectiveness of this method, this paper also adds envelope demodulation to the process to extract the characteristics of the fault signal.

Figure 1 Flowchart of IPSO–VMD.

2.3 Fault feature extraction method

Time domain analysis of vibration signals usually refers to analysis based on the change in the number of vibration signals over time. It can show the vibration change in equipment more intuitively. In time domain analysis, there are some evaluation indicators that can be used to assist analysis. Entropy features are generally used to characterize the magnitudes of various energies contained in the signal. Sample entropy can reflect the complexity of the time series. The higher the complexity of the sequence, the greater the value of the sample entropy. Energy entropy will change with the energy distribution of the vibration signal. Power spectrum entropy can quantify the spectral complexity and irregularity of the signal. Therefore, this paper uses the peak factor, margin factor, pulse factor, sample entropy, energy entropy, and power spectrum entropy to extract multidimensional features (Richman et al., 2004; Yu et al., 2006; Zhang et al., 2008).

The higher the feature dimension of the feature sample, the more complex the mathematical model of SVM and the longer the model training time will be. It will also affect the classification accuracy of SVM. However, if the feature dimension of the feature sample is too small, some feature information will be lost, thus affecting the classification accuracy of SVM. Therefore, this paper introduces PCA, which can reduce the dimension of data without losing data information, and it uses the reduced feature matrix as the input of SVM (Wen et al., 2021).

2.4 The basic principle of SVM

The SVM algorithm is a supervised machine learning method that is widely used to solve complex multi-classification and regression problems (Liu et al., 2023). It can solve nonlinear, high-dimensional, and small sample machine learning problems and has good local and global search capabilities. The contour region segmentation of mature daily images can be regarded as a foreground and background classification problem. The foreground and background feature data are nonlinearly distributed in the sample space. In order to improve the robustness of the model, a relaxation variable is introduced to enable nonlinear mapping of samples from low-dimensional input space to high-dimensional space in order to make them linearly separable, so that the optimal classification hyperplane y(x) can be found in the feature space, as shown in Eq. (5):

$$\begin{array}{}\text{(5)}& y\left(x\right)={\mathit{\omega }}^{T}x+b,\end{array}$$

where ω represents the weight vector, x denotes the data point, and b is the threshold. The slack variable ζ_i is introduced to permit each sample to have a certain degree of misjudgment error. The constraint condition is presented in Eq. (6):

$$\begin{array}{}\text{(6)}& y\left({\mathit{\omega }}^T{x}_i+b\right)\ge \mathrm{1}-{\mathit{\zeta }}_i,\end{array}$$

where i = $\mathrm{1},\mathrm{2},\mathrm{\dots }n$, ζ_i ≥ 0, and x_i ∈ R. When determining the optimal segmentation hyperplane, the minimization of the squared norm ∥ω∥ of ω is utilized as the optimization objective function, as indicated in Eq. (7):

$$\begin{array}{}\text{(7)}& min{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{∥\mathit{\omega }∥}^{\mathrm{2}}+C\sum _{i=\mathrm{1}}^n{\mathit{\zeta }}_i,\end{array}$$

where C serves as the penalty coefficient; a larger C implies a higher fault tolerance. By introducing the Lagrangian multiplier a_i, the problem is transformed into solving the dual problem, as demonstrated in Eqs. (8) and (9):

$$\begin{array}{}\text{(8)}& {\displaystyle }min{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{i=\mathrm{1}}^n\sum _{j=\mathrm{1}}^n{\mathit{\alpha }}_i{\mathit{\alpha }}_{j}K\left(x,x_i\right)-\sum _{i=\mathrm{1}}^n{\mathit{\alpha }}_i,\text{(9)}& {\displaystyle }\left\{\begin{array}{l}K=\exp \left(-\frac{\mathrm{1}}{\mathrm{2}{\mathit{\delta }}^{\mathrm{2}}}{∥x-x_i∥}^{\mathrm{2}}\right)=\exp \left(g{∥x-x_i∥}^{\mathrm{2}}\right)\\ \text{s.t.}\sum _{i=\mathrm{1}}^n{y}_i{\mathit{\alpha }}_i=\mathrm{0},\mathrm{0}\le {\mathit{\alpha }}_i\le C,i=\mathrm{1},\mathrm{2},\mathrm{3}\mathrm{\dots },n\end{array}\right.,\end{array}$$

where K(x,x_i) is the inner product kernel function for addressing nonlinear problems, δ represents the bandwidth of the Gaussian radial basis kernel function, and g is the parameter of the Gaussian radial basis kernel function. Assuming that the optimal Lagrangian multiplier obtained by the solution is α^∗, the optimal hyperplanes ω^∗ and b^∗ can be inversely derived, and Eq. (10) represents the final classification decision function.

$$\begin{array}{}\text{(10)}& f\left(x\right)=\text{sgn}\left(\sum _{i=\mathrm{1}}^n{\mathit{\alpha }}^{\ast }{y}_{i}K\left(x,x_i\right)+b^{\ast }\right)\end{array}$$

Selecting parameters C and g in support vector machines is crucial. Parameter C influences the model's generalization ability, which relates to the predictability of unknown data. The value of the Gaussian radial basis kernel function parameter g affects the dispersion of the sample data. After conducting numerous experiments, this paper selects C as 6 and g as 1, employing 10-fold cross-validation.

2.5 Improved PSO–VMD multidimensional index fault diagnosis method

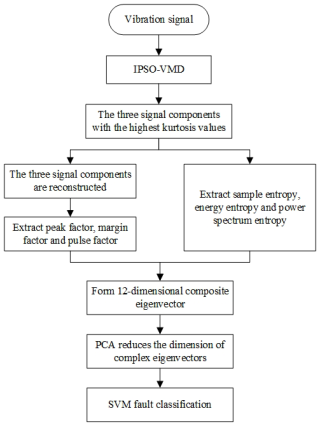
The proposed method flowchart is shown in Fig. 2. The specific steps are as follows:

• 1.

  Load the vibration signal.

• 2.

  Introduce the Metropolis criterion into PSO, optimize the K and α of VMD, and decompose the vectors.

• 3.

  The kurtosis of each component is calculated, and the three components with the highest kurtosis are obtained for signal reconstruction.

• 4.

  The peak factor, margin factor, and pulse factor of the reconstructed signal as well as the sample entropy, energy entropy, and power spectrum entropy of the three components are calculated to obtain a 12-dimensional composite feature vector.

• 5.

  Use PCA to reduce the composite eigenvector to three dimensions.

• 6.

  The feature samples are divided into a test set and a training set and are put into the SVM classification model for classification diagnosis. The classification accuracy of the test samples is used to verify the quality of the classification model.

Figure 2 Flowchart of the proposed method.

3 Signal analysis of public datasets

This paper uses the bearing test bench data of Western Reserve University to verify the method (Hou et al., 2018). Figure 3 shows a diagram of the experimental device. The motor spindle is supported by fan end (FE) and drive end (DE) bearings, respectively. The bearings are pitted by electrical discharge machining (EDM) to simulate common faults. The experiment uses the vibration signal of the SKF62052RS drive side bearing model collected by a 16-channel digital audio tape (DAT) recorder. The motor speed is 1797 r min⁻¹, the sampling frequency is 12 kHz, and the load is 0 hp. Vibration signals are collected in four states: normal (Normal), inner-race failure (IRF), outer-race failure (ORF), and ball failure (BF). In this study, 50 groups were sampled in each state and 200 groups were sampled in four states, with 8192 sampling points in each group.

Figure 3 Experimental device.

3.1 Public dataset analysis

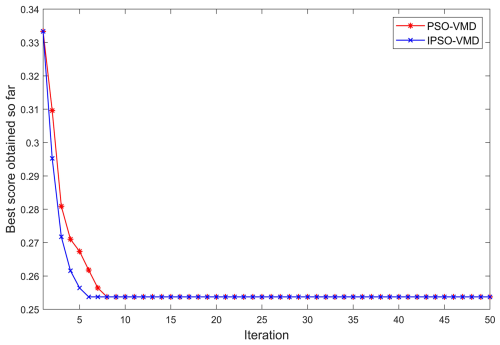
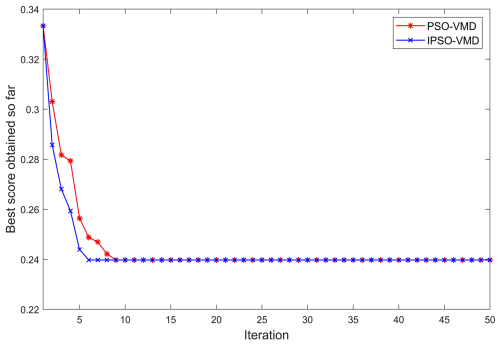
To determine the relevant parameters of VMD, the vibration signals collected in the laboratory are analyzed. After many experiments, the optimal particle swarm parameters are as follows: the particle swarm is 100, the weight factors are all set to 1.1, the particle speed is updated in the interval $[-\mathrm{30},\mathrm{30}]$, and the maximum number of iterations is set to 50. The fitness function value change curve of the training process is shown in Fig. 4. At the same time, in order to verify the effectiveness of the proposed algorithm, the particle swarm algorithm before and after the improvement is compared in the experiment. The convergence speed of the improved particle swarm algorithm is better than that of the algorithm before the improvement, and the obtained fitness value is also lower, which shows that the algorithm can achieve more ideal prediction results. According to the IPSO–VMD results, the final determined values of K and α are [3,3003].

Figure 4 Iterative curve of the public datasets IPSO–VMD and PSO–VMD.

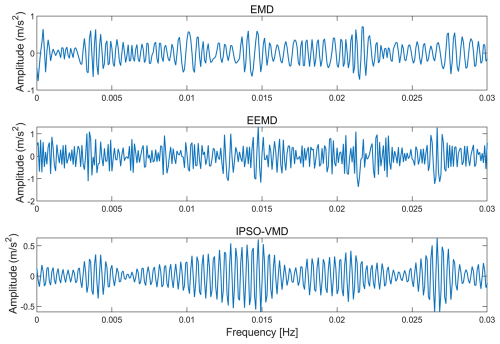
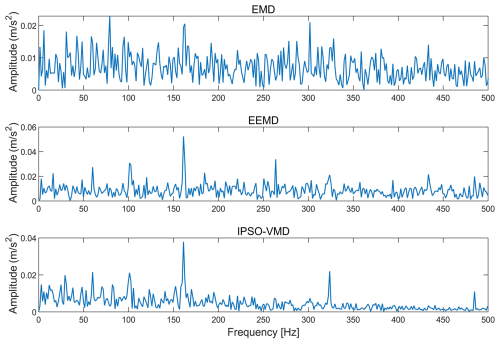
In order to verify the effectiveness of IPSO–VMD, the fault signals processed by EMD, ensemble empirical mode decomposition (EEMD), and VMD are compared. As shown in Figs. 5 and 6, the time domain signal processed by VMD is smoother than the signals of EMD and EEMD. The envelope spectrum of EMD and EEMD cannot clearly obtain the fault frequency and its frequency multiples, while the envelope spectrum of VMD can be seen clearly. As shown in Fig. 6, the characteristic frequency extracted by this method is 161 Hz, which is close to the actual fault characteristic frequency, although it is correct that the optimal number of decomposition layers for the inner-ring fault vibration signal is three layers. The peak factor, margin factor, pulse factor, sample entropy, energy entropy, and power spectrum entropy of the reconstructed signal are calculated to form a composite feature vector.

Figure 5 Three algorithms for time domain processing of public datasets.

Figure 6 Three algorithms for processing the public dataset envelope spectrum.

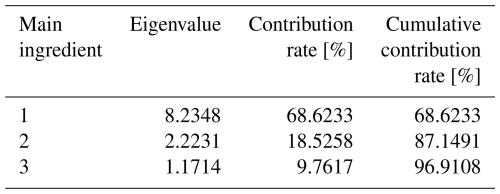
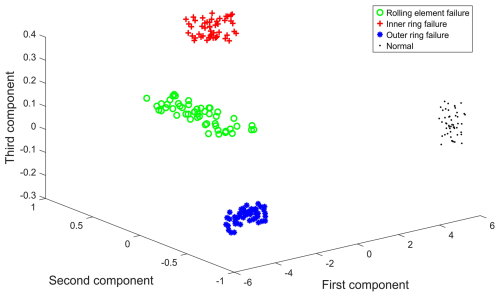
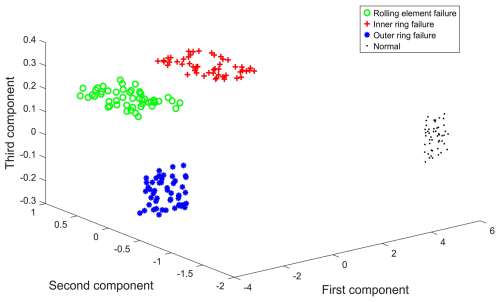
PCA is used to reduce the dimension of the fault feature matrix, retaining the principal component containing important feature information. The analysis results are shown in Table 1. The contribution rate of the first three principal components is 96.9108 % and contains most of the feature information. Therefore, this experiment uses the first three principal components as feature samples after dimensionality reduction, and the spatial distribution of the bearing state obtained by PCA is shown in Fig. 7. As can be seen from Fig. 7, each type of data is relatively concentrated and can be roughly distinguished, indicating that the PCA algorithm can extract feature information that can distinguish fault states.

Table 1 Cumulative contribution of the principal components of the public datasets.

Figure 7 Bearing state space diagram for dimensionality reduction by PCA (public datasets).

3.2 Realization of the bearing fault diagnosis method

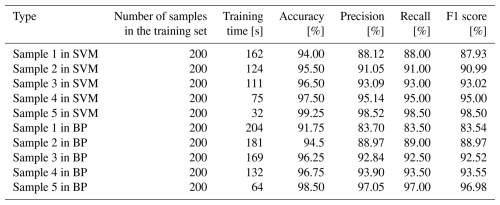
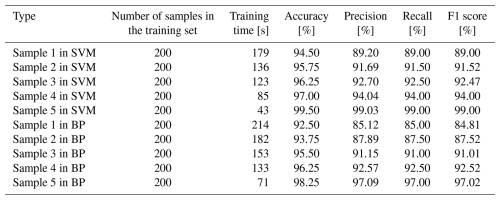
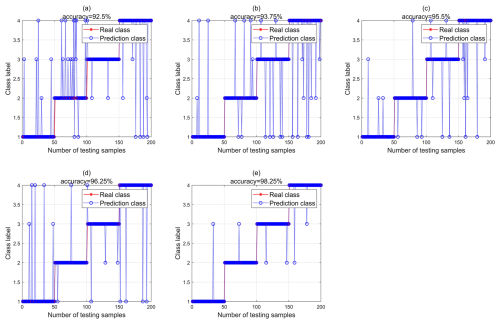
In order to reflect the superiority of the proposed method in fault diagnosis, this paper divides the test samples into five categories, as shown in Table 2. From the diagnosis results of Fig. 8a, b, c, and d, it can be seen that the recognition rate of sample 4 in SVM is 97.5 %, which is higher than that of samples 1, 2, and 3. The introduction of VMD–multidimensional composite features can effectively improve the accuracy of rolling bearing fault diagnosis, but the introduction of these features will increase the complexity of the classification model. In order to improve the accuracy, this paper uses PCA to reduce the dimension of the samples of VMD–multidimensional composite features. After the dimension reduction, the recognition accuracy of the samples in SVM is 99.25 %, as shown in Fig. 8e. In order to verify the superiority of SVM to similar algorithms, back propagation (BP) is used to classify and identify the test samples, as shown in Fig. 9. To conduct a comprehensive performance evaluation of the proposed method, this paper introduces metrics such as accuracy (Eq. 11), precision (Eq. 12), recall (Eq. 13), and F1 score (Eq. 14). The performance indicators of the public dataset diagnosis model are shown in Table 3.

$$\begin{array}{}\text{(11)}& {\displaystyle }\text{Accuracy}={\displaystyle \frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}}\text{(12)}& {\displaystyle }\text{Precision}={\displaystyle \frac{\text{TP}}{\text{TP}+\text{FP}}}\text{(13)}& {\displaystyle }\text{Recall}={\displaystyle \frac{\text{TP}}{\text{TP}+\text{FN}}}\text{(14)}& {\displaystyle }\text{F1 score}=\mathrm{2}\times {\displaystyle \frac{\text{precision}\times \text{recall}}{\text{precision}+\text{recall}}}\end{array}$$

TP stands for true positive, TN stands for true negative, FP stands for false positive, and FN stands for false negative. The F1 score is a metric used to evaluate the performance of classification models, particularly in scenarios involving imbalanced data. Its primary function is to integrate the precision and recall of the model, offering a balanced evaluation by harmonizing the mean.

Combined with Figs. 8 and 9 and Table 3, the recognition accuracy of SVM is better than that of BP for rolling bearing fault samples. The classification effect of VMD–multidimensional composite features combined with PCA samples in SVM is better, so this fault diagnosis method can be applied to rolling bearings.

Table 2 Test sample types.

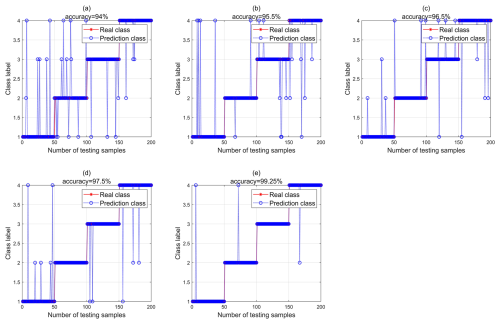
Figure 8 Public dataset samples identified in SVM: (a) Class 1, (b) Class 2, (c) Class 3, (d) Class 4, and (d) Class 5.

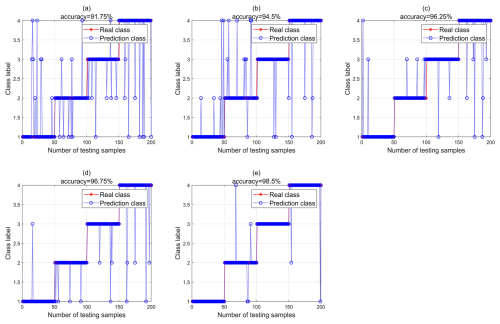
Figure 9 Public dataset samples identified in BP: (a) Class 1, (b) Class 2, (c) Class 3, (d) Class 4, and (d) Class 5.

Table 3 Public dataset diagnostic model performance indicators.

4 Experimental results and analysis

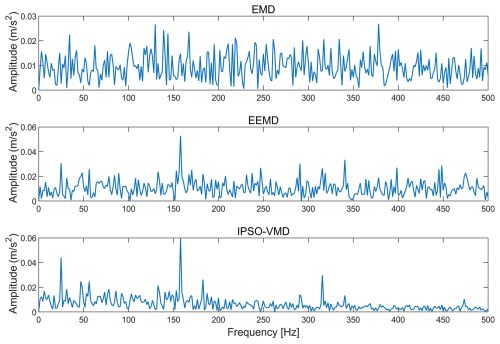
Figure 10 shows the inner-ring fault and outer-ring fault of the variable amplitude mechanism bearing. This paper collects the acceleration signal of the faulty bearing when it rotates through the bearing test bench. Four states, i.e., Normal, IRF, ORF, and BF, are collected. Fifty groups of samples are collected for each state, 200 groups of samples are collected for the four states, 8192 sampling points are collected for each group, and the collection frequency is 12 800 Hz. The fault signal of the luffing mechanism bearing is collected. Since the collected signal contains a high degree of noise, VMD processing is performed on the inner-ring fault signal. As shown in Fig. 11, IPSO is used to optimize the parameter combination [K,α] of VMD, and the optimization goal is to maximize the kurtosis of each component after decomposition. Here, we take a set of sampling point data as an example, and the optimal parameter combination is K = 3005 and α = 4. The 8192 data of each set of sampling points are subjected to variational mode decomposition to obtain four components.

Figure 10 Inner- and outer-ring faults of the luffing mechanism bearing.

Figure 11 Iteration curve of the actual signal IPSO–VMD and PSO–VMD.

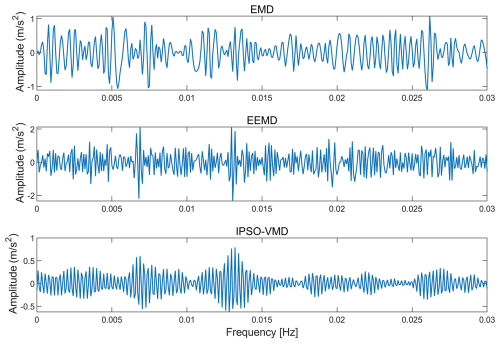
In order to verify whether IPSO–VMD is effective, EMD, EEMD, and IPSO–VMD process fault signals are compared. As shown in Figs. 12 and 13, the time domain signal of EMD is relatively chaotic, and the effect of extracting characteristic faults is not very good. Although traces of noise reduction can be seen in the EEMD time domain signal, there is still some noise interference. The time domain signal processed by IPSO–VMD is relatively smooth and smoother than the signals of EMD and EEMD. The envelope spectrum of EMD cannot clearly obtain the fault frequency and its frequency multiples. The fault frequency can be observed in the envelope spectrum of EEMD, but the frequency doubling is not obvious and there is noise interference. The envelope spectrum of VMD can clearly see the fault frequency and its double frequency.

Figure 12 Three algorithms for the actual signal time domain processing.

Figure 13 Three algorithms for the actual signal envelope spectrum.

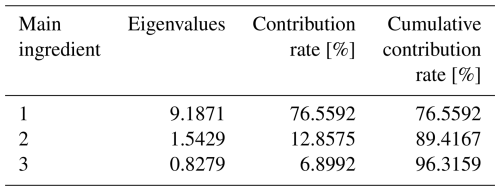
This paper uses IPSO–VMD to extract the fault frequency from the bearing inner-ring fault signal. However, although the fault frequency can be observed in the extracted signal, the signal after tripling the frequency is not very obvious. The peak factor, margin factor, pulse factor, sample entropy, energy entropy, and power spectrum entropy in the modal classification after IPSO–VMD are extracted to form a composite feature component. PCA is used to reduce the dimension of the vector. As shown in Table 4, after dimensionality reduction processing, these feature vectors retain the main components of important feature information and remove some components with low impact. The cumulative contribution rate of the first three main elements reaches 96.3159 %, indicating that most of the information has been included. As can be seen in Fig. 14, in the spatial distribution, there is no overlap between the four types of feature data after PCA dimensionality reduction, and each type of data is relatively concentrated. This shows that the PCA results extract the characteristics of the fault state.

Table 4 Cumulative contribution of the principal components of the actual signal.

Figure 14 Bearing state space diagram for dimensionality reduction by PCA (actual signal).

To demonstrate the advantages of the method proposed in this paper, we generated a total of five test samples to train the SVM and BP models. The relevant evaluation indicators are presented in Table 5. As shown in Fig. 15, the identification accuracy rates of the first, second, third, and fourth types of fault samples are 94.5 %, 95.75 %, 96.25 %, and 97 %. It can be concluded that VMD–multidimensional composite feature samples can effectively improve the accuracy of rolling bearing fault diagnosis. However, this sample will lengthen the SVM training time and also affect the SVM classification accuracy. Therefore, this paper uses VMD–multidimensional composite features combined with PCA samples as the input of the SVM model. As shown in Fig. 15e and Table 5, the recognition accuracy of the feature sample after PCA dimension reduction in SVM is 99.5 %, and the training time is 43 s. The recognition accuracy of the feature sample without dimension reduction is 97 %, and the training time is 85 s. Therefore, judging from the comprehensive classification results of the samples, the classification effect of the samples with VMD–multidimensional composite features combined with PCA in SVM is better. In order to verify that SVM is more effective than similar algorithms, we use BP to classify all of the samples. The results are shown in Fig. 16. It can be seen from Figs. 15 and 16 and Table 5 that SVM has better classification and recognition effects among the same types of algorithms.

Table 5 Actual signal diagnostic performance indicators.

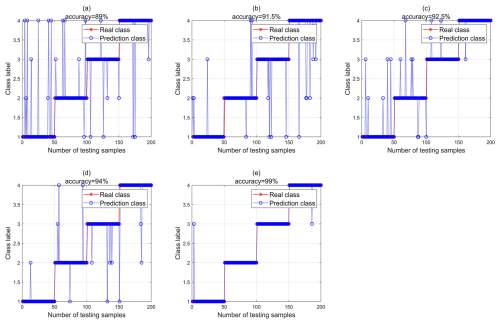
Figure 15 Actual signal samples identified in SVM: (a) Class 1, (b) Class 2, (c) Class 3, (d) Class 4, and (e) Class 5.

Figure 16 Actual signal samples identified in BP: (a) Class 1, (b) Class 2, (c) Class 3, (d) Class 4, and (e) Class 5.

5 Conclusions

In order to detect the fault condition of the bearing of the crane luffing mechanism, this paper proposes a kurtosis-based IPSO to optimize the penalty factor α and the number of decomposition levels k in VMD. Through simulation data and experimental data analysis, this method can obtain optimal parameter values. A method is also proposed to integrate time domain indicators with entropy features and extract their streamlined features through the PCA algorithm. Experimental data verification shows that this method not only reduces the training time of the classification model but also improves the classification accuracy.

Although this paper has achieved significant results in the detection technology of crane luffing mechanism bearings, certain limitations remain. The study focuses primarily on a single type of fault, whereas in real-world scenarios compound faults may occur. The paper lacks an in-depth discussion of compound faults, which restricts the method's applicability in complex real-world scenarios.