Design and analysis of a two-stage constant-torque flexure hinge (TS-CTFH) based on fixed-rotation constrained circular-arc segments

This study proposes a pseudo-rigid-body model (4bar-PRBM) for a fixed-rotation constrained circular-arc flexible segment and obtains characteristic parameters expressions using s as a variable. Then, the superposition principle of circular-arc segments is proposed, leading to the development of a novel two-stage constant-torque flexure hinge (TS-CTFH). With the dimension parameter s as a variable, TS-CTFH with different constant-torque output (T_id1 and T_id2) is optimized, which enhances the applicability of the hinge. The accuracy of theoretical analysis and the feasibility of the design scheme are ultimately validated through finite-element analysis (FEA) and testing. The novel TS-CTFH offers a proficient solution for design of grippers, joint rehabilitation devices, and assistive aids for human activities. Simultaneously, the four-bar PRBM offers a user-friendly tool for designing compliant constant-torque mechanisms (CCTMs) with circular-arc segments.

1 Introduction

Compliant mechanisms (CMs) facilitate the controlled elastic deformation of integrated flexure components to achieve precise force and motion transmission (Howell, 2001). The ability of flexure components to store energy allows for the creation/design of bistable/multistable compliant mechanisms (Howell et al., 2013), compliant constant force/torque mechanisms (Ling et al., 2022), and compliant parallel-guiding mechanisms (Culpepper et al., 2006). In recent years, the study of compliant constant-torque mechanisms (CCTMs) has gained significant attention due to their functional characteristics in rotational motion (Saerens et al., 2022). Within a specified range of operation, CCTMs are capable of delivering nearly constant torques, thereby eliminating the need for complex control structures and excessive sensor usage. The versatility of CCTMs is evident in their widespread application, including rotary positioning stages (Wang et al., 2018), functional joints (Hou and Lan, 2013), and medical robotics (Cheng et al., 2023).

Simultaneously, the mechanical structures and designs of CCTMs exhibit a remarkable diversity. The most commonly used design approach involves optimizing geometric shape parameters of curved beams (Reddy and Zhou, 2017), which necessitates the researcher to provide the initial position and shape function of deformed beams (i.e., to provide the initial value of the optimized variable). (Prakashah and Zhou, 2016). A different approach involves the integration of negative and positive stiffness mechanisms (Zhao et al., 2019; Liu et al., 2020), a commonly employed technique in the design of zero-torque compliant mechanisms (Bilancia et al., 2020). Additionally, precompression of beams can be utilized in the design of CCTMs (Thanaki and Zhou, 2018), effectively reducing the preloading region required for CCTMs (Gandhi and Zhou, 2019). This study enhances the existing pseudo-rigid-body models (PRBMs), offering a robust tool for the design and optimization of a two-stage constant-torque flexure hinge.

Previous research and design efforts have explored circular beam structures. Edwards et al. (2001) introduced a PRBM for initially curved pinned-pinned segments (Edwards et al., 2001). Venkiteswaran and Su (2016) developed a PRBM for circular-arc segments to effectively handle combined force and moment loads (Venkiteswaran and Su, 2016). Building upon this foundation, they proposed a versatile 3R PRBM capable of accurately capturing the behavior of initially curved and straight compliant beams (Venkiteswaran and Su, 2018). Compared to straight beams, the stress distribution of the circular-arc segment in large deformations exhibits greater uniformity (Phan et al., 2024). The design of circular-arc segments offers ease in terms of shape and structural parameters, making them suitable for application in compliant mechanisms (Roach and Howell, 2002). To facilitate the utilization of circular-arc segments in CCTM design, it is imperative to develop a user-friendly tool for their design and analysis.

Primarily, this study presents an innovative contribution through the introduction of an enhanced 4bar-PRBM, wherein the characteristic parameters are proposed using s as a variable in Sects. 2 and 3. Secondarily, a novel design concept for a two-stage constant-torque flexure hinge (TS-CTFH) is proposed. TS-CTFH is optimized with respect to s to achieve various constant-torque output values T_id1 and T_id2 in Sect. 4. Building on this foundation, a prototype of TS-CTFH was developed, exhibiting constant-torque output values of T_id1 and T_id2 at 44.08 and 82.50 N mm, respectively. Finally, finite-element analysis (FEA), theoretical analysis, and testing results are compared to validate the accuracy of 4bar-PRBM and demonstrate the effectiveness of TS-CTFH design in Sect. 5, thereby showcasing the practicality of utilizing 4bar-PRBM for optimizing TS-CTFH.

2 4bar-PRBM of a fixed-rotation constrained circular-arc segment

2.1 Problem formulation

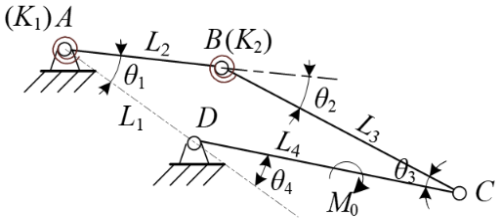
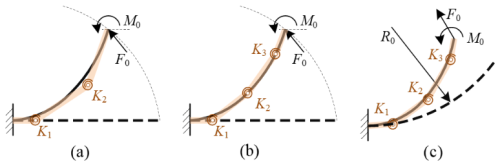
As depicted in Fig. 1, a flexible segment initially shaped as a circular arc exhibits a significant deflection. This kind of constraint of segment can be employed in design of the hinges, where the flexible segment is constrained as follows: one end (P) is fixed, while the other end (Q) moves along a trajectory of a circular arc under constraint of the link (OQ bar). The applied load is represented by the moment (M₀) on the OQ bar. To establish a relationship between the moment (M₀) and the angle (θ) of the OQ bar, a pseudo-rigid-body model, abbreviated as 4bar-PRBM, for the fixed-rotation constrained circular-arc segment was proposed, as illustrated in Fig. 2.

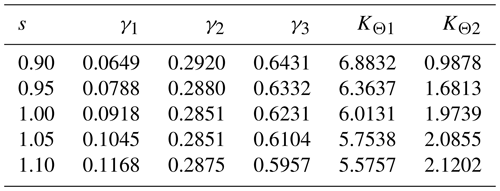
In Fig. 1, R₁ and α denote the radius and central angle of the circular-arc segment PQ. R₂ and θ denote the length and rotational angle of the OQ bar. β denotes the position angle of OQ bar, and M₀ represents the applied external load. In Fig. 2, K_Θ1, K_Θ2, γ₁, γ₂, and γ₃ represent the characteristic parameters of 4bar-PRBM, and l_i (i=1, 2, 3) represents the length of pseudo-rigid bars.

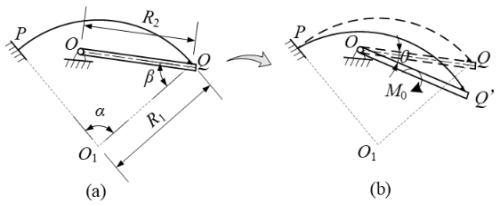
Figure 1 Fixed-rotation constrained circular-arc segment (a) prior to applying the load and (b) subsequent to applying the load.

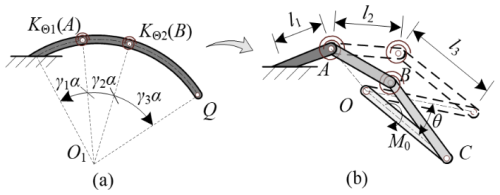
Figure 2 PRBM of fixed-rotation constrained circular-arc segment (4bar-PRBM): (a) characteristic parameters and (b) pseudo-rigid bars and pseudo-rigid joints.

The M₀–θ relationship of the fixed-rotation constrained circular-arc segment can be obtained by investigating the 4bar-PRBM and its equivalent four-bar linkage, as indicated in Fig. 3. The 4bar-PRBM uses five characteristic parameters to identify kinematic and torque-angle characteristics of the segment, namely, the stiffness coefficients (K_Θ1, K_Θ2) and the position factors (γ₁, γ₂, and γ₃).

Figure 3 Equivalent four-bar rigid linkage.

2.2 Determination of 4bar-PRBM characteristic parameters

The relation between spring stiffness K_i and stiffness coefficient K_Θi is as follows:

$$\begin{array}{}\text{(1)}& K_i=K_{\mathrm{\Theta }i}{\displaystyle \frac{EI}{L}},i=\mathrm{1},\mathrm{2},\end{array}$$

where

$$\begin{array}{}\text{(2)}& L=R_{\mathrm{1}}\mathit{\alpha },I={\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}w{t}^{\mathrm{3}}.\end{array}$$

E represents the elastic modulus of material; L denotes the length of circular-arc segment; I stands for the moment of inertia of the cross section; and w and t, respectively, indicate the width and thickness of circular-arc segment.

In Fig. 2, the lengths of each pseudo-rigid bar l_i, and in Fig. 3, the lengths of each rigid rod L_i, are as follows:

$$\begin{array}{}\text{(3)}& l_i=\mathrm{2}R\sin \left(\mathrm{0.5}{\mathit{\gamma }}_i\mathit{\alpha }\right),i=\mathrm{1},\mathrm{2},\mathrm{3},\end{array}$$

$$\begin{array}{}\text{(4)}& L_{\mathrm{1}}=\stackrel{\mathrm{‾}}{\mathrm{AD}},L_{\mathrm{2}}=l_{\mathrm{2}},L_{\mathrm{3}}=l_{\mathrm{3}},L_{\mathrm{4}}=R_{\mathrm{2}}.\end{array}$$

The initial values of angles (the values θ₁₀∼θ₄₀ are the initial values of θ₁∼θ₄) between the rods in Fig. 3 are as follows:

$$\begin{array}{}\text{(5)}& \left\{\begin{array}{c}{\mathit{\theta }}_{\mathrm{20}}=({\mathit{\gamma }}_{\mathrm{2}}+{\mathit{\gamma }}_{\mathrm{3}})\mathit{\alpha }/\mathrm{2},\\ {\mathit{\theta }}_{\mathrm{40}}=\arccos \frac{L_{\mathrm{2}}^{\mathrm{2}}+L_{\mathrm{3}}^{\mathrm{2}}-L_{\mathrm{1}}^{\mathrm{2}}-L_{\mathrm{4}}^{\mathrm{2}}+\mathrm{2}{L}_{\mathrm{2}}{L}_{\mathrm{3}}\cos {\mathit{\theta }}_{\mathrm{20}}}{\mathrm{2}{L}_{\mathrm{1}}{L}_{\mathrm{4}}},\\ {\mathit{\theta }}_{\mathrm{10}}=\frac{\mathit{\pi }-{\mathit{\gamma }}_{\mathrm{2}}\mathit{\alpha }}{\mathrm{2}}-\arccos \frac{R_{\mathrm{1}}^{\mathrm{2}}+L_{\mathrm{1}}^{\mathrm{2}}-{\stackrel{\mathrm{‾}}{{\mathrm{OO}}_{\mathrm{1}}}}^{\mathrm{2}}}{\mathrm{2}{R}_{\mathrm{1}}{L}_{\mathrm{1}}},\\ {\mathit{\theta }}_{\mathrm{30}}=\frac{\mathit{\pi }-{\mathit{\gamma }}_{\mathrm{3}}\mathit{\alpha }}{\mathrm{2}}-\arccos \frac{R_{\mathrm{1}}^{\mathrm{2}}+R_{\mathrm{2}}^{\mathrm{2}}-{\stackrel{\mathrm{‾}}{{\mathrm{OO}}_{\mathrm{1}}}}^{\mathrm{2}}}{\mathrm{2}{R}_{\mathrm{1}}{R}_{\mathrm{2}}}.\end{array}\right.\end{array}$$

When the CD bar rotates by θ under the influence of M₀, the angles between the rods in Fig. 3 are as follows:

$$\begin{array}{}\text{(6)}& \left\{\begin{array}{c}{\mathit{\theta }}_{\mathrm{4}}={\mathit{\theta }}_{\mathrm{40}}-\mathit{\theta },\\ {\mathit{\theta }}_{\mathrm{2}}=\arccos \frac{L_{\mathrm{1}}^{\mathrm{2}}+L_{\mathrm{4}}^{\mathrm{2}}-L_{\mathrm{2}}^{\mathrm{2}}-L_{\mathrm{3}}^{\mathrm{2}}+\mathrm{2}{L}_{\mathrm{1}}{L}_{\mathrm{4}}\cos {\mathit{\theta }}_{\mathrm{4}}}{\mathrm{2}{L}_{\mathrm{2}}{L}_{\mathrm{3}}},\\ {\mathit{\theta }}_{\mathrm{1}}=\arcsin \frac{L_{\mathrm{4}}\sin {\mathit{\theta }}_{\mathrm{4}}}{\stackrel{\mathrm{‾}}{AC}}+\arcsin \frac{L_{\mathrm{3}}\sin {\mathit{\theta }}_{\mathrm{2}}}{\stackrel{\mathrm{‾}}{AC}},\\ {\mathit{\theta }}_{\mathrm{3}}=\arccos \frac{L_{\mathrm{3}}^{\mathrm{2}}+L_{\mathrm{4}}^{\mathrm{2}}-L_{\mathrm{1}}^{\mathrm{2}}-L_{\mathrm{2}}^{\mathrm{2}}+\mathrm{2}{L}_{\mathrm{1}}{L}_{\mathrm{2}}\cos {\mathit{\theta }}_{\mathrm{1}}}{\mathrm{2}{L}_{\mathrm{3}}{L}_{\mathrm{4}}}.\end{array}\right.\end{array}$$

The torques generated by the pseudo-hinges A and B are as follows:

$$\begin{array}{}\text{(7)}& M_i=K_i\mathrm{\Delta }{\mathit{\theta }}_i,i=\mathrm{1},\mathrm{2}.\end{array}$$

Using the principle of virtual work, an expression for the output torque M₀ in terms of the included angle θ₄ can be obtained as follows:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& M_{\mathrm{0}}\left({\mathit{\theta }}_{\mathrm{4}}\right)=M_{\mathrm{0}}({\mathit{\theta }}_{\mathrm{40}}-\mathit{\theta })\\ & =M_{\mathrm{1}}{\displaystyle \frac{L_{\mathrm{4}}\left[L_{\mathrm{1}}\sin {\mathit{\theta }}_{\mathrm{4}}+L_{\mathrm{2}}\sin ({\mathit{\theta }}_{\mathrm{1}}-{\mathit{\theta }}_{\mathrm{4}})\right]}{L_{\mathrm{2}}\left[L_{\mathrm{1}}\sin {\mathit{\theta }}_{\mathrm{1}}+L_{\mathrm{4}}\sin ({\mathit{\theta }}_{\mathrm{1}}-{\mathit{\theta }}_{\mathrm{4}})\right]}}\\ & +M_{\mathrm{2}}{\displaystyle \frac{L_{\mathrm{1}}{L}_{\mathrm{4}}\sin {\mathit{\theta }}_{\mathrm{4}}}{L_{\mathrm{1}}{L}_{\mathrm{2}}\sin {\mathit{\theta }}_{\mathrm{1}}+L_{\mathrm{2}}{L}_{\mathrm{4}}\sin ({\mathit{\theta }}_{\mathrm{1}}-{\mathit{\theta }}_{\mathrm{4}})}}.\end{array}\end{array}$$

M₀ approximation error e₁ is defined as sum of the squared differences between the predicted and actual torques at each loading step. (The angle of each loading step is uniform, and there are altogether N loading steps.)

$$\begin{array}{}\text{(9)}& e_{\mathrm{1}}=\sum _{j=\mathrm{1}}^N{\left(M_{\mathrm{0}Pj}-M_{\mathrm{0}Qj}\right)}^{\mathrm{2}},\end{array}$$

where M_0Pj is the value calculated using Eq. (8) and M_0Qj is the FEA values. In FEA, a fixed constraint is imposed at the P end, and rotational displacement is set at the Q end, with the adoption of automatic mesh, program-controlled solver type, and large deflection setting. Then, the torque (M_0Qj) data can be obtained in post-processing.

A fitness function can be formulated as a minimization objection function as follows:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& min\mathrm{fitness}=e_{\mathrm{1}}\\ & \mathrm{so}\mathrm{that}{K}_{\mathrm{\Theta }\mathrm{1}}>\mathrm{0},K_{\mathrm{\Theta }\mathrm{2}}>\mathrm{0},{\mathit{\gamma }}_{\mathrm{1}}>\mathrm{0},{\mathit{\gamma }}_{\mathrm{2}}>\mathrm{0},\\ & {\mathit{\gamma }}_{\mathrm{3}}>\mathrm{0},{\mathit{\gamma }}_{\mathrm{1}}+{\mathit{\gamma }}_{\mathrm{2}}+{\mathit{\gamma }}_{\mathrm{3}}=\mathrm{1}.\end{array}\end{array}$$

Finally, specific values of the characteristic parameters γ₁, γ₂, γ₃, K_Θ1, and K_Θ2 of the 4bar-PRBM are ultimately determined using MATLAB based on Eq. (10).

3 Expressions of the characteristic parameters of 4bar-PRBM with respect to dimension parameters

3.1 Determination of the constant-torque output region and dimensions of the circular-arc segment

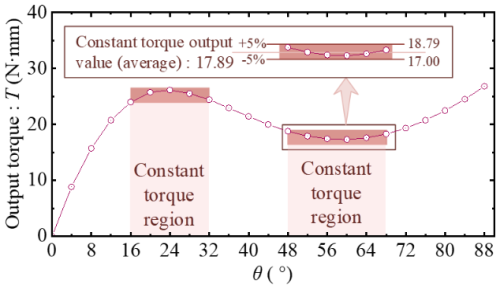
The determination of the constant-torque output region is as follows: if the torque output value does not deviate from the mean by more than 5 % within a certain angular region (usually greater than 10°), the region is set as the constant-torque output region, and the mean torque value in region is the constant-torque output value, as shown in Fig. 4.

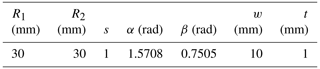
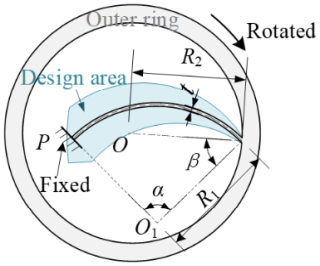
It is necessary to study the relationship between the characteristic parameters (γ₁, γ₂, γ₃, K_Θ1, and K_Θ2) and dimensions (R₁, R₂, α, and β). As shown in Fig. 5, the rotational radius R₂ determines the size of the hinge, radius and angle (R₁ and α) determine the length of the circular-arc segment, and β determines the relative position of the circular-arc segment. Additionally, the width (w) and thickness (t) of the circular-arc beam primarily affect the spring stiffness K_i (as per Eq. 1) and hence the torque output. The initial dimensions of circular-arc segment are given in Table 1. The definition of the ratio s is as follows: here:

$$\begin{array}{}\text{(11)}& s=R_{\mathrm{1}}/R_{\mathrm{2}}.\end{array}$$

Table 1 Initial dimensions of circular-arc segment.

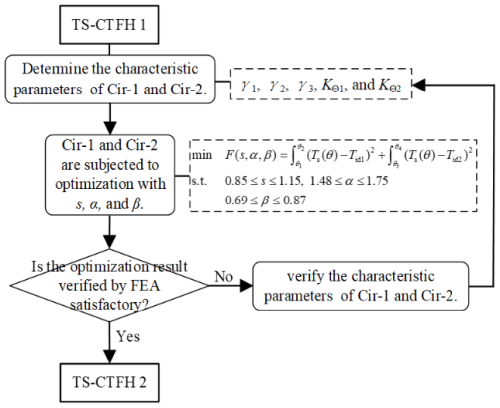
Ratio s determines the magnitude of circular-arc segment relative to the hinge. To achieve desired large deformation, it is recommended that α lies within the range of 1.48 to 1.75, β lies within the range of 0.69 to 0.87, s lies within the range of 0.85 to 1.15.

Figure 4 Determination of the constant-torque output value and region.

Figure 5 Dimensions of the circular-arc segment.

In FEA, modeling can be conducted based on Fig. 5 and Table 1. A fixed constraint is imposed at the P end, and rotational displacement is set on the outer surface of the outer ring. Then, the torque–angle data of the outer ring can be obtained in post-processing.

In order to improve the accuracy and versatility of the 4bar-PRBM, it is necessary to obtain the characteristic parameter expressions of the 4bar-PRBM under different sizes (s), which enables the 4bar-PRBM to be used for related structural design and serves as a basis for subsequent constant-torque flexure hinge design.

3.2 4bar-PRBM characteristic parameters in terms of the variable s

According to Eq. (10), the MATLAB software is employed for the solution with s(R₁) as the variable, and the characteristic parameters, as presented in Table 2, can be obtained. Subsequently, under the condition of a goodness of fit greater than 0.95 and the lowest number of polynomial terms, polynomial fitting is conducted. The relationship between the characteristic parameters and the variable s obtained by fitting is as follows:

$$\begin{array}{}\text{(12)}& \left\{\begin{array}{l}{\mathit{\gamma }}_{\mathrm{1}}\to f_{\mathrm{1}}\left(s\right)=\mathrm{0.259}s-\mathrm{0.1676},\\ {\mathit{\gamma }}_{\mathrm{2}}\to f_{\mathrm{2}}\left(s\right)=-\mathrm{0.0234}s+\mathrm{0.3109},\\ {\mathit{\gamma }}_{\mathrm{3}}\to f_{\mathrm{3}}\left(s\right)=-\mathrm{0.2352}s+\mathrm{0.8563},\\ K_{\mathrm{\Theta }\mathrm{1}}\to f_{\mathrm{4}}\left(s\right)=\mathrm{22.117}{s}^{\mathrm{2}}-\mathrm{50.684}s+\mathrm{34.574},\\ K_{\mathrm{\Theta }\mathrm{2}}\to f_{\mathrm{5}}\left(s\right)=\mathrm{220}{s}^{\mathrm{3}}-\mathrm{703.16}{s}^{\mathrm{2}}+\mathrm{749.81}s\\ -\mathrm{264.67}.\end{array}\right.\end{array}$$

Table 2 Characteristic parameters of corresponding to different svalues.

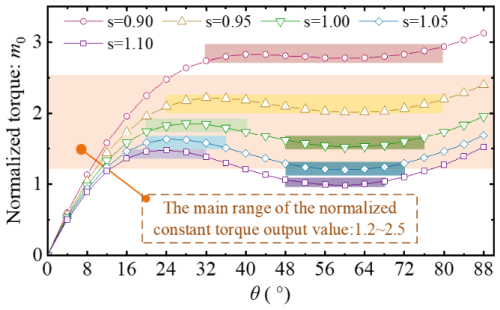
The load torque M₀ (derived via FEA and computation) is normalized as $m_{\mathrm{0}}=M_{\mathrm{0}}L/EI$, and the m₀–θ curve displayed in Fig. 6 is obtained. It is known from Fig. 6 that the ratio s affects the amplitude of the overall curve but has a limited influence on the trend of the curve. Specifically, the constant-torque regions are mostly within 20–40° and 48–76°, and the range of the constant-torque output value (normalized) m₀ is approximately from 1.2 to 2.5. Therefore, the constant-torque output value T_id of a single circular-arc segment is selected as follows:

$$\begin{array}{}\text{(13)}& T_{\mathrm{id}}=m_{\mathrm{0}}{\displaystyle \frac{EI}{L}}=(\mathrm{1.2}-\mathrm{2.5}){\displaystyle \frac{EI}{L}}.\end{array}$$

Figure 6 m₀–θ curve for different s values.

4 Design of a two-stage constant-torque flexure hinge (TS-CTFH)

4.1 Superposition principle and mechanical design

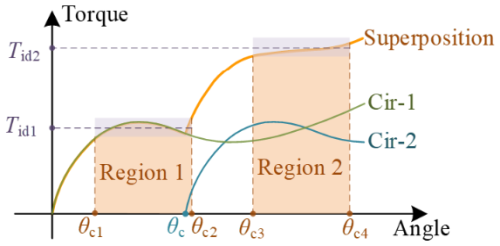
Figure 7 illustrates the superposition of two circular-arc segments (Cir-1 and Cir-2), where one segment (Cir-1) initially rotates by θ_c and then synchronously rotates with the other segment (Cir-2), resulting in a two-stage constant-torque output.

Figure 7 Superposition principle.

After superposition, the region θ_c1–θ_c2 exhibits a constant-torque output of T_id1, while the region θ_c3–θ_c4 demonstrates a constant-torque output of T_id2. The curve expression of T_s–θ for the segments after superposition is as follows:

$$\begin{array}{}\text{(14)}& T_s\left(\mathit{\theta }\right)=\left\{\begin{array}{ll}{n}_{\mathrm{1}}{M}_{\mathrm{01}}\left(\mathit{\theta }\right),& \mathrm{0}<\mathit{\theta }<{\mathit{\theta }}_{\mathrm{c}},\\ n_{\mathrm{1}}{M}_{\mathrm{01}}\left(\mathit{\theta }\right)+n_{\mathrm{2}}{M}_{\mathrm{02}}(\mathit{\theta }-{\mathit{\theta }}_{\mathrm{c}}),& {\mathit{\theta }}_{\mathrm{c}}<\mathit{\theta }.\end{array}\right.\end{array}$$

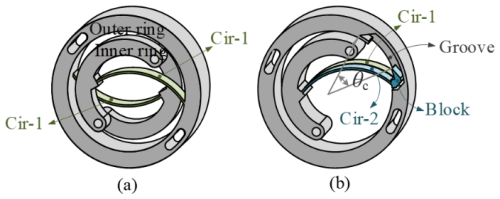
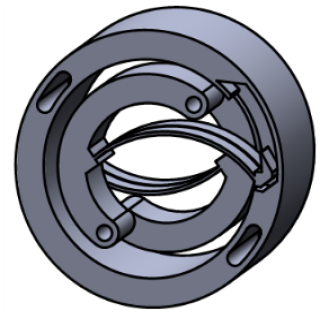
M₀₁ and M₀₂ represent torque outputs of the individual Cir-1 segment and Cir-2 segment, respectively. The number of Cir-1 segments (n₁) and Cir-2 segments (n₂) determines the circular-arc trajectory of the end of circular-arc segments. To ensure this trajectory, a circular array distribution is required for the Cir-1 segment; thus, n₁ should be greater than or equal to 2, as depicted in Fig. 8a. Additionally, as displayed in Fig. 8b, the groove and block are structured in a way that allows both Cir-2 and Cir-1 to turn and deform together after an outer-ring rotation of θ_c. When $n_{\mathrm{1}}=n_{\mathrm{2}}=\mathrm{2}$, a two-stage constant-torque flexure hinge that is displayed in Fig. 9 is obtained. In this study, the quantities of Cir-1 and Cir-2 are both taken as minimum values (namely, $n_{\mathrm{1}}=n_{\mathrm{2}}=\mathrm{2}$).

Figure 8 Mechanical design of superimposed circular-arc segments: (a) Cir-1 and Cir-1 and (b) Cir-1 and Cir-2.

Figure 9 Two-stage constant-torque flexure hinge (TS-CTFH).

4.2 Optimization for the two-stage constant-torque output with s as variable

It can be known from Sect. 3.2 that the ratio s has a minor influence on the trend of the m₀–θ curve but that it has an impact on the overall amplitude of the curve. Thus, the same dimension parameters can be chosen for Cir-1 and Cir-2, and the desired ratio of constant-torque output can be selected as T_id1 : $T_{\mathrm{id}\mathrm{2}}=\mathrm{1}:\mathrm{2}$. The value range of T_id1 can be selected as follows:

$$\begin{array}{}\text{(15)}& T_{\mathrm{id}\mathrm{1}}=\mathrm{2}(\mathrm{1.2}-\mathrm{2.5}){\displaystyle \frac{EI}{L}}.\end{array}$$

The objective function is to minimize the difference between a chosen constant-torque value T_id1 and T_id2 and output torque T_s (θ), which can be expressed as

$$\begin{array}{}\text{(16)}& \begin{array}{rl}& minF\left(s\right)=\underset{{\mathit{\theta }}_{\mathrm{c}\mathrm{1}}}{\overset{{\mathit{\theta }}_{\mathrm{c}\mathrm{2}}}{\int }}\left(T_s\right(\mathit{\theta })-T_{\mathrm{id}\mathrm{1}}{)}^{\mathrm{2}}+\underset{{\mathit{\theta }}_{\mathrm{c}\mathrm{3}}}{\overset{{\mathit{\theta }}_{\mathrm{c}\mathrm{4}}}{\int }}(T_{\mathrm{s}}\left(\mathit{\theta }\right)-T_{\mathrm{id}\mathrm{2}}{)}^{\mathrm{2}}\\ & \mathrm{so}\mathrm{that}\mathrm{0.85}\le s\le \mathrm{1.15}.\end{array}\end{array}$$

This equation can be solved using MATLAB.

The material used for TS-CTFH is PA12, Poisson's ratio μ is 0.34, and the bending modulus E is 2.0 GPa. The bending strength of PA12 is capable of reaching 100 MPa. Its dimension parameters are presented in Table 3.

Table 3 Parameters of TS-CTFH.

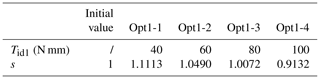
According to the parameters specified in Eq. (15) and Table 3, the range of T_id1 is calculated to be 43.46–90.55 N mm, and the range 40–100 N mm is selected here. Subsequently, for optimization analysis based on Eq. (16), different constant-torque output targets for T_id1 are selected, resulting (Opt1) in the findings presented in Table 4. The value of θ_c is established at 40°. The values of θ_c1 and θ_c2 are determined, based on the constant-torque output regions in the first half of the m₀–θ curve in Fig. 6 (primarily concentrated within 16–40°), to be 12 and 40°, respectively. The constant-torque output region in the second half of the curve is supposed to be 40–88°. Considering the 16° loading region, ultimately, θ_c3 and θ_c4 are chosen to be 56 and 88°, respectively.

Table 4 Optimization results of Opt1.

Figure 10 T_s–θ curves for different optimization results (regard s as variable).

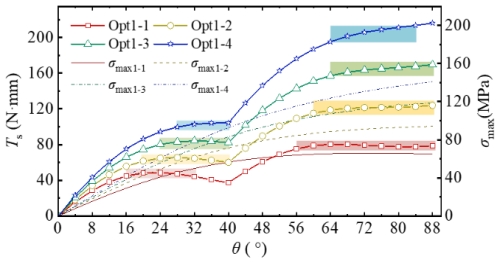
Based on the results of Table 4 and Eqs. (8) and (14), the T_s–θ curve can be derived, as depicted in Fig. 10. The respective constant-torque output regions are indicated thereon. Additionally, the T_id1–T_id2 for Opt1-1 to 1-4 is, respectively, 46.71–78.54 N mm, 63.21–120.82 N mm, 82.82–164.48 N mm, and 102.84-206.08 N mm. The maximum stresses of circular-arc segments are 65.18, 94.17, 118.79, and 141.0 MPa, respectively. Opt1-1 and 1-2 possess a relatively large constant-torque output region and do not exceed the bending strength of the material. Therefore, the two-stage constant-torque output functionality of TS-CTFH has been essentially accomplished.

5 Experimental testing

5.1 Prototype and experimental platform

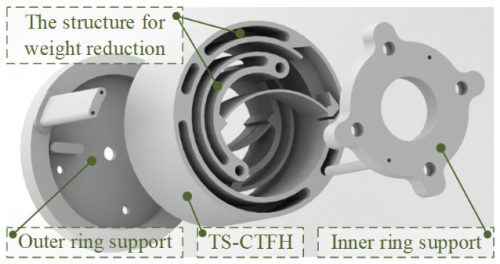
In this section, a confirmatory experiment on Opt1-1 is performed. The TS-CTFH, designed based on parameters optimized by Opt1-1, incorporates weight reduction structures on both the outer and inner rings along with through holes for installing the outer-ring support and inner-ring support as depicted in Fig. 11. Utilizing laser sintering technology, a 3D printed prototype of the TS-CTFH was fabricated, as shown in Fig. 12.

Figure 11 Structure of TS-CTFH and supports.

Figure 12 Prototype of TS-CTFH.

The test platform is depicted in Fig. 13. When outer-ring support rotates at a specific angle, driven by a precision angle measuring turntable, the torque output of inner-ring support can be measured using a torque sensor.

Figure 13 Test platform for TS-CTFH.

5.2 Experimental results

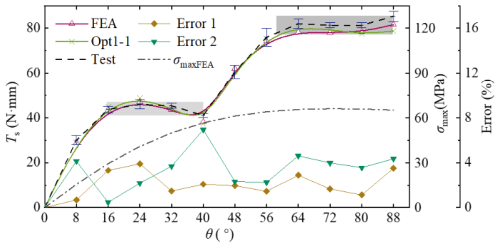
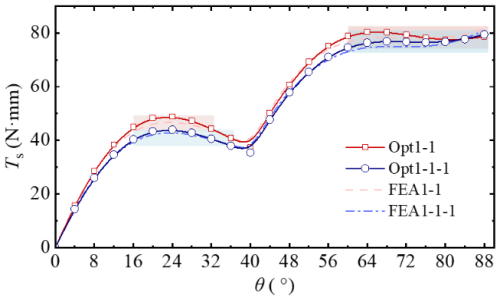
After Opt1-1 optimization, the circular-arc segments obtained are subjected to FEA analysis, and the T_s–θ curve of TS-CTFH is calculated using the 4bar-PRBM and the principle of superposition. Finally, experimental testing is conducted on the prototype. The results obtained from Opt1-1, including the theoretical, FEA, and test results, are presented in Fig. 14. Error 1 represents the discrepancy between the theory and FEA, with an average error of 2.00 % and a maximum error of 3.90 %. Error 2 indicates the deviation between the test and FEA, with an average error of 3.20 % and a maximum error of 6.93 %. Error 3 is the difference between FEA and theoretical values of the maximum stress in Cir-1, with a maximum error of 3.67 %.

In the experiment, a value was measured every 8°, and the average of three measurements was taken. Experimental results indicate that the constant-torque output regions are 16–40° and 56–88° (which have been marked in Fig. 14). Subsequently, the average torque output within the regions of 16–40° and 56–88° was computed, thereby obtaining the constant-torque output values T_id1 and T_id2 (namely 44.08 and 82.50 N mm). The experimental results demonstrate that the TS-CTFH possesses a two-stage constant-torque output function. These findings validate the accuracy of the 4bar-PRBM and affirm the effectiveness of the optimization strategy.

Figure 14 FEA, theoretical, and test results of TS-CTFH optimized by Opt1-1.

Furthermore, when the rotation angle was 40°, a notable deviation emerged in experimental results. Its primary cause lies in the fact that roughness of prototype surface led to premature contact between the block and the groove. However, this contact was not firm (with an existing gap), as depicted in Fig. 15. When the rotation angle increased, the gap narrowed, and contact became more stable, thereby reducing the errors.

Figure 15 Contact gap between the block and the groove.

6 Discussion

6.1 Comparison of TS-CTFH and other compliant constant-torque mechanisms

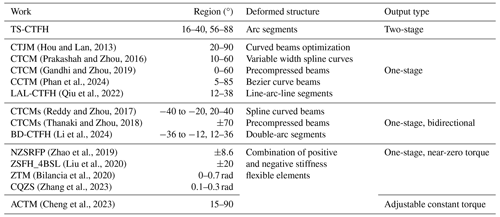
TS-CTFH exhibits the characteristics of a two-stage constant-torque output, thereby enhancing the functionality of CTFH and presenting a novel approach to its design. Table 5 presents a comparison between TS-CTFH and existing CCTMs in terms of their constant-torque regions, deformation structure, and torque output type.

Some CCTMs are characterized by large strokes, enabling their application in specific functional joints. CCTMs with zero-torque output characteristics have demonstrated applicability in shock absorption systems and bearing replacement applications, as identified by Bilancia et al. (2020) Furthermore, adjustable constant force/torque mechanisms can be applied well in the medical field.

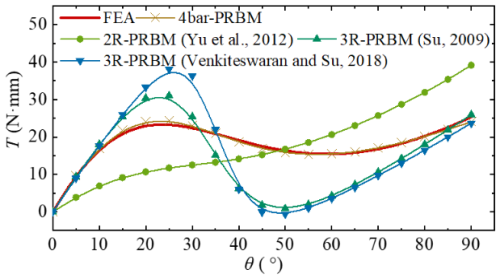
The 2R PRBM (Yu et al., 2012) and 3R PRBM (Su, 2009) were proposed, as depicted in Fig. 16a and b, to capture the deformation and end-point trajectory of a flexible cantilever beam subjected to free-end force and moment loading. Furthermore, a 3R PRBM (Venkiteswaran and Su, 2018) specifically designed for initially curved beams was introduced. The T–θ curves of CTFH obtained by directly utilizing these PRBM parameters are illustrated in Fig. 17. It is evident that the existing PRBMs exhibit significant inaccuracies and fail to accurately fit the T–θ characteristics of the constrained flexible beam shown in Fig. 1. Therefore, the four-bar PRBM proposed in this study introduces an innovative approach for the design of CCTMs with circular-arc segments while serving as a user-friendly tool for their implementation.

Figure 16 Existing PRBMs in references: (a) 2R PRBM (Yu et al., 2012), (b) 3R PRBM (Su, 2009), and (c) 3R PRBM (Venkiteswaran and Su, 2018).

Figure 17 T–θ curves of Opt1-1 for existing PRBM.

Table 5 Comparison of TS-CTFH and constant-torque mechanisms.

6.2 The further optimization of TS-CTFH

When contemplating the further optimization of Opt1-1, dimension parameters (s, α, and β) can be concurrently regarded as design variables. The optimization procedure is depicted in Fig. 18. Based on Opt1-1, identical dimension parameters are selected for Cir-1 and Cir-2, and dimension parameters (s, α, and β) are regarded as design variables to optimize the output torques T_id1 and T_id2. The expression is

$$\begin{array}{}\text{(17)}& \begin{array}{r}minF\left(s\right)={\sum }_{{\mathit{\theta }}_{\mathrm{c}\mathrm{1}}}^{{\mathit{\theta }}_{\mathrm{c}\mathrm{2}}}\left(T_s\right(\mathit{\theta })-T_{\mathrm{id}\mathrm{1}}{)}^{\mathrm{2}}+{\sum }_{{\mathit{\theta }}_{\mathrm{c}\mathrm{3}}}^{{\mathit{\theta }}_{c\mathrm{4}}}(T_s\left(\mathit{\theta }\right)-T_{\mathrm{id}\mathrm{2}}{)}^{\mathrm{2}}\\ \mathrm{so}\mathrm{that}\mathrm{0.85}\le s\le \mathrm{1.15},\mathrm{1.48}\le \mathit{\alpha }\le \mathrm{1.75},\mathrm{0.69}\le \mathit{\beta }\le \mathrm{0.87}.\end{array}\end{array}$$

The ultimate optimization outcome (Opt1-1-1) is presented in Table 6. By conducting the simulation of the optimized circular-arc segments, the result shown in Fig. 19 is obtained. It can be concluded that the simulation results of T_id1 and T_id2 for Opt1-1-1 are 40.92 and 76.35 N mm, respectively. Moreover, the torque output of the first stage of Opt1-1-1 is smoother, attaining a more desirable two-stage constant-torque output effect.

Figure 18 The further optimized flowchart of TS-CTFH.

Table 6 Optimization results of Opt1-1-1.

Figure 19 T_s–θ curves after further optimization.

7 Conclusions

Primarily, this study introduces the 4bar-PRBM for a fixed-rotation constrained circular-arc segment and provides the corresponding characteristic parameters for different s values. Based on this, expressions of the characteristic parameters are derived using the ratio s as a variable.

Secondarily, the superposition principle is employed to design circular-arc segments, resulting in the development of a two-stage constant-torque flexure hinge (TS-CTFH). Based on the optimized parameters of Opt1-1, a prototype of TS-CTFH was fabricated using 3D printing technology.

Finally, an experimental test is conducted to compare the FEA, theoretical analysis, and testing results. The maximum error between theory and FEA is determined to be 3.90 %, while the maximum error between the test and FEA is found to be 6.93 %. These findings validate the accuracy of the 4bar-PRBM model and confirm the effectiveness of optimization outcomes. The constant-torque output regions of the TS-CTFH prototype are identified as 16–40° and 56–88°, with the torque values T_id1 and T_id2 determined to be 44.08 and 82.50 N mm, respectively, thereby achieving the functionality of a two-stage constant-torque output.