Inverse dynamics and inertia coupling analysis of a parallel mechanism with parasitic motions and redundant actuations

In this paper, a bio-inspired masticatory mechanism has been developed to reproduce the chewing behaviors of human beings. It is a natural spatial parallel mechanism constrained directly by the base at its end effector. These constraints form two point-contact higher kinematic pairs, producing parasitic motions and redundant actuations simultaneously. To facilitate the model-based control, a rigid-body inverse dynamic model is built and the inertia coupling is analyzed. Firstly, by virtue of a dynamic method, the Hessian matrices of the constraint equations and the kinetic energy are derived. The modeling process is straightforward, and the correctness is validated by virtue of the classical Lagrange equations. However, from the comparison between the technique in this method and a classical method in computing the first time derivative of the Jacobian matrices and the Coriolis–centrifugal force matrix, the former is more time-consuming. Secondly, the inertia coupling is analyzed via the inertia matrix in the joint space, showing that the first, third, and fourth active joints are the most strongly coupled. Finally, by comparing both the inverse dynamics and inertia coupling of the target mechanism and its counterpart, the foregoing constraints raise the computational cost of the inverse dynamics extraordinarily but greatly alleviate the inertia coupling.

1 Introduction

The food industry is very interested in evaluating the time-varying textures and properties of newly developed foods during the entire masticatory process, which can contribute to the development of healthy and widely accepted food products (B. Chen et al., 2021). Nevertheless, generally, different from the real complicated three-dimensional (3D) masticatory behaviors of human beings, the current instruments available can only perform simple one-dimensional crushing. Thus, the time-varying properties of newly developed foods during the chewing process cannot be discovered accurately or completely (Sun et al., 2014), and a robotic device that can replicate the chewing motions and forces with high fidelity will no doubt facilitate the development of new food textures in this industry. Nature is a great source of inspiration that enhances technological innovations, and a great variety of bionic robots have been designed to imitate various animals (Chen et al., 2023, 2024; Wang et al., 2024). In this regard, a human-like parallel chewing robot has been designed according to the layout of the muscles of mastication and the physiological jaw structure of human beings, mimicking the masticatory system of human beings faithfully (Cheng et al., 2015): the base attached to the skull is the fixed upper jaw; the end effector is the lower moving jaw; and the six kinematic chains working in parallel mimic the primary mouth-closing chewing muscle groups, i.e., the temporalis, masseter, and pterygoid at the two sides of the masticatory system, since these muscles work in parallel to drive the mandible in the three-dimensional space (Xu et al., 2008​​​​​​​a, b). The large temporalis muscles are attached from the side of the skull to the top of the lower jaw behind the teeth and consist of vertical and horizontal muscle fibers. The masseter muscles are attached between the cheek on the skull and the lower rear section of the lower jaw. The pterygoid muscles are attached between the skull and the lower jaw in a horizontal fashion. Further, to model the two temporomandibular joints (TMJs) between the temporal bone of the skull and the condyles of the lower jaw, direct constraints from the base to the end effector are implemented, forming two point-contact higher kinematic pairs (HKPs). A detailed description of the masticatory system of human beings and chewing robotics can be found in Koolstra (2002) and Chap. 1 of Xu and Bronlund (2010).

Compared to open-loop serial-chain mechanisms, there are many closed loops in parallel mechanisms (PMs). Due to this topology, PMs display greater stiffness (Sun et al., 2024; Song et al., 2020), a better motion accuracy (Han et al., 2021; Qiancheng et al., 2022), a larger acceleration capability (Corbel et al., 2010), a larger payload capacity (Chen and Liao, 2016), and better elastodynamic performance (Germain et al., 2015) than their serial-chain counterparts. Therefore, these mechanisms are widely employed in a variety of fields where these strengths are greatly needed, such as machine tools (Zhang et al., 2022; Guo et al., 2022; Hernández et al., 2020), and telescope applications (Díaz-Rodríguez et al., 2016).

Before our robotic device can be commanded to replicate the chewing behaviors of human beings, and even further employed in the food industry as a well-established commercial product, it is very necessary to implement the model-based motion and/or force control in real time. In addition, since the inverse kinematics of the target PM has already been analyzed in Cheng et al. (2015), it is natural to extend the study to inverse dynamics. However, it is a challenging job as there are so many constraints in the mechanism: the end effector is not only constrained by the six chains, but also by the base directly at two HKPs. As such, we are strongly motivated to seek a computationally efficient methodology to establish an inverse dynamic model.

Many a method has been devoted to formatting the equations of motion (EOMs) of a wide variety of PMs, for instance, Newton–Euler's law (Bi and Kang, 2014; Gosselin, 1996; M. Chen et al., 2021; Yan et al., 2022), the Lagrangian formulation (Mohan and Corves, 2017; Hernández et al., 2020; Li et al., 2009), the principle of virtual work (Carbonari et al., 2013; Liu et al., 2019; Carricato and Gosselin, 2008), the Jourdain principle of virtual power (Yang et al., 2019), the natural orthogonal complement (Wang et al., 2019; Eskandary and Angeles, 2018), Kane's equations (Cibicik and Egeland, 2019), and the method based on Screw and Lie group theory (Müller, 2022, 2019). However, these spatial or planar PMs are all composed of lower kinematic pairs; that is, HKPs are probably uncommon in PMs.

On the other hand, since PMs are typical multi-input and multi-output mechanical systems, generally, it is very difficult to derive forward kinematics that can be calculated in real time, which is of great significance in motion control in the task space. Meanwhile, exteroceptive vision devices that can directly measure the motions of end effectors in real time as in Bellakehal et al. (2011) increase the expenditure and the intricacy of the experimental setup. In this regard, the motion control in the active joint space of PMs is much easier to be implemented. However, the existence of many closed loops usually produces strong couplings among active joints: one active joint burdens not only the inertia from its own kinematic chain, but also the coupling inertias from the other ones. Mathematically, the inertia coupling is from the non-diagonal terms of the inertia matrix, which can be found in the dynamic model. The coupled inertias can be viewed as disturbances to the active joint, increasing motion control difficulties. Henceforth, this property is a significant reference to design convenient motion control strategies in the joint space. In addition, this dynamic performance is also an important reference for motor sizing and resonance frequency analysis (Shao et al., 2012). Finally, from the publications, the study on this property is mainly composed of only lower kinematic pairs in PMs. Thus, this property in PMs with direct constraints from the base like the one under study is unclear. In this regard, the inertia coupling is analyzed after the dynamic model is built in this paper.

From the literature, an index judging the inertia coupling among different active joints was proposed and applied in a 3-UPS PM in Guo et al. (2022), where U, P, and S mean universal, prismatic, and spherical joints, respectively. This index takes both the diagonal and off-diagonal elements of the inertia matrix into consideration, evaluating the inertia coupling among different chains. In Liu et al. (2014), the eigenvalues of the inertia matrix of a Stewart platform were decomposed, and the largest one was adopted to judge the inertia-decoupling characteristic. The matching issue between the inertias of the actuator and the load on the kinematic chain in the Stewart platform was studied in Shao et al. (2012), where an index named joint-reflected inertia was developed based on the coupling analysis of the joint-space inertia matrix. This index used the average value of the principal diagonal elements of the inertia matrix in the joint space; however, it cannot reflect the imbalance of the inertia property among chains. To this end, a coefficient of variation of the joint-space inertia index equaling the coefficient of variation of the principal diagonal elements of the inertia matrix was proposed and employed in a pick-and-place PM with 4 degrees of freedom (DOFs) in Mo et al. (2017). A minor value of this index promises a better inertia isotropy for all chains. In Zou et al. (2022), two indices from both Mo et al. (2017) and Shao et al. (2012) were employed to compare the dynamic performance of two PMs with 3 translational DOFs. In addition, two new indices based on the off-diagonal elements of the inertia matrix, i.e., the branch-coupling absolute inertia index and the variation in the branch-coupling inertia index, were designed to study the inertia couplings among different chains.

According to these publications on inverse dynamics and inertia coupling, studies on dynamic modeling have made considerable achievements in PMs, but inertia coupling analyses are relatively rare (Guo et al., 2022), and the works on these two fields are primarily about PMs composed of lower kinematic pairs. Meanwhile, a dedicated study in PMs constrained by the base directly like the one under study is rather limited. That is probably because this sort of PM is very uncommon. As a result, it is a challenging job to establish a cost-effective inverse dynamic model for the PM under study and analyze its coupling performance. Among the publications, the inverse dynamic model in Abo-Shanab (2020) for PMs using the Hessian matrix under the framework of the Lagrange–D'Alembert principle provokes our interest. The first time derivative of the Jacobian matrices and the Coriolis–centrifugal force matrix can be derived by the Hessian matrices of the constraint equations and the overall kinetic energy of a mechanism, respectively. The derivation of the EOMs is simple and straightforward, and the final model is rather well-structured and compact. As such, it is particularly attractive to develop inverse dynamic models for PMs with complex topologies by virtue of these strengths. Nevertheless, so far, this method has only been applied in a simple planar PM in Abo-Shanab (2020), and no further attempt has been made to evaluate its computational efficiency yet. Due to these, it is to be employed to build the inverse dynamic model of our target PM, and its correctness will be verified by the model built by the Lagrange formulation. The method of deriving these foregoing matrices will be compared with a classical one from Liang et al. (2017), concerning the computational cost. Meanwhile, the index from Guo et al. (2022) which uses both the diagonal and off-diagonal elements of the inertia matrix is to be applied to evaluate the inertia coupling property of this uncommon PM.

In this study, it is assumed that there are no link deformations, and joints are free of clearances or friction effects. These are all complicated subjects and are left for future developments. In the following, at first, a detailed description of the target PM is provided in Sect. 2, and then the derivations of parasitic motions and redundant actuations are given in Sect. 3. The derivation of the constraint Jacobian matrices and their first time derivatives by Hessian matrices is presented in Sect. 4. The dynamic models under the framework of the Lagrange–D'Alembert principle by the Hessian matrices and under the classical Lagrangian equations are both derived in Sect. 5. In Sect. 6, the inertia coupling of the target PM is performed. In Sect. 7, the correctness of the dynamic method is verified by comparing the numerical results from the classical Lagrange formulation. The computational efficiency to derive the first time derivative of the Jacobian matrices and the Coriolis–centrifugal force matrix in the Hessian matrix approach is studied, by comparing the mathematical method from Liang et al. (2017) to obtain these matrices. Moreover, the effects of direct constraints from the base to the end effector in terms of both computational demands in inverse dynamics and inertia coupling are further explored by making a comparative study between the target PM and a 6-Revolute-Spherical-Spherical (RSS) PM, where the italic letter R means it is the active joint in the kinematic chain. Finally, some conclusions are given in Sect. 8.

The contributions of this paper are as follows:

1. The rigid-body inverse dynamics of a novel spatial PM featuring direct constraints from the base to the end effector at the HKPs is addressed by the Hessian matrix method in Abo-Shanab (2020). Further, from the comparison between the mathematical techniques in Abo-Shanab (2020) and Liang et al. (2017) to derive the first time derivatives of constraint Jacobian matrices and the Coriolis–centrifugal force matrix, the computational efficiency of this approach is discovered.

2. The inertia coupling property of the target PM is revealed numerically.

3. The influence brought by the direct constraints from the base in inverse dynamics and inertia coupling is identified clearly by comparing these two features between the target PM and a 6RSS PM.

2 The robotic mechanism

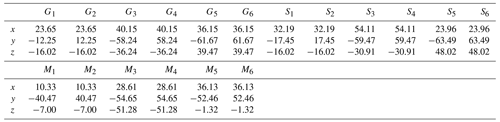
The scheme of the mechanism is illustrated in Fig. 1. The maxilla (i.e., the base) is fixed on the ground, and the movable mandible (i.e., the end effector) is connected to the base by six independent kinematic chains. The primary part of the maxilla is not shown for a clear illustration of the movable bodies, except for the upper articular surfaces of the TMJs as ③ and ④ for the sake of the illustration of the point-contact HKPs between the condyles and the maxilla. The inertia coordinate system {S} is assigned to the maxilla. This system consists of a horizontal X_S–Y_S plane perpendicular to the vertical Z_S axis. A coordinate system {M} is established at the mass center O_M of the end effector. The origins and orientations of {S} and {M} overlap when the mechanism is at the home position; that is, the maxilla and the mandible are in the occlusal state. The position of the origin O_M in {S} is used as the reference to describe the mandibular translations, and its orientations with respect to {S} are expressed by X–Y–Z Euler angles. In each chain, the crank G_iS_i (i=1, …, 6) is driven by a base-mounted rotary actuator with a revolute joint at G_i, and the coupler S_iM_i joins the crank and the end effector via two spherical joints at its two ends S_i and M_i, respectively. The rotation of the ith actuator with respect to {S} is described by the actuator frame {C_i} attached at G_i. In this {C_i} frame, the $X_{C_i}$ axis is directed from G_i to S_i; the $Z_{C_i}$ axis runs through the driving shaft of the actuator; and the $Y_{C_i}$ axis completes the frame, obeying the right-hand rule. The numbers of the chains are given in the subscripts of G, S, and M. With centers at T_i (i=L, R), the condyles of the mandible are modeled as two balls as ① and ②, which are always touching ③ and ④, respectively, forming two HKPs. These contacts play the role of TMJs in the chewing system of human beings. As clearly shown in this figure, the end effector is driven by six chains at spherical joints M_i and constrained by the base at two HKPs simultaneously. At the initial time, the coordinates of G_i and S_i (i=1, …, 6) in frame {S} and M_i in frame {M} are given in Table 1.

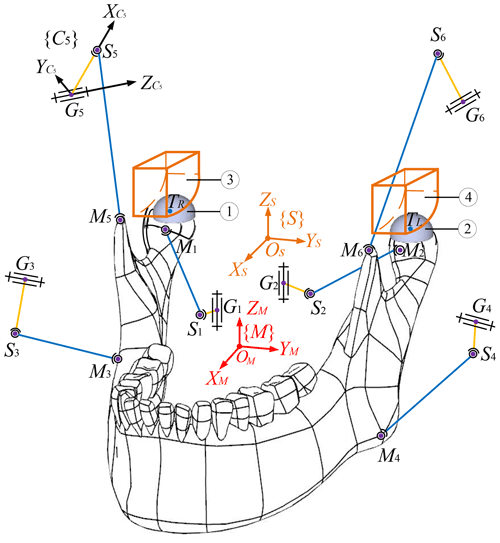
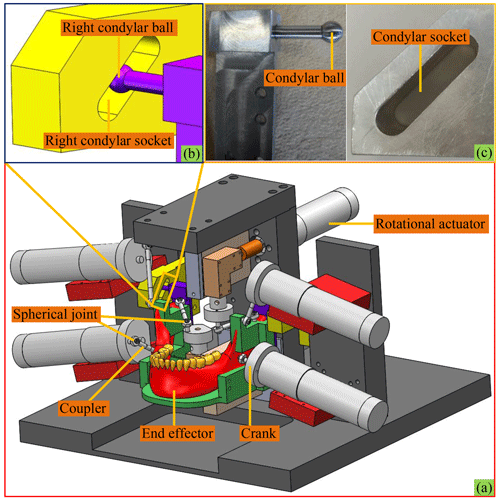
Figure 1 Schematic diagram of the PM constrained by the base at two point-contact HKPs, where ① and ② are condylar balls, and ③ and ④ are articular surfaces of TMJs.

Table 1 Coordinates of G_i and S_i (i=1, …,6) in frame {S} and M_i in frame {M} (unit: mm).

A closer observation of Fig. 1 reveals that the point-contact HKPs between the condylar balls and articular surfaces of TMJs are only schematic, since condylar balls only receive unilateral constraints from the articular surfaces of TMJs. As such, in practical manipulations of the PM, due to errors in manufacturing, assembling, or motion control, condylar balls easily lose contact with the articular surfaces. Thus, the nature of the mechanism is changed. In this regard, the computer-aided design (CAD) model of the HKPs and related mechanical parts in engineering practice are designed as in Fig. 2. The condylar ball slips along a condylar socket, with the width being equal to its diameter. Thus, the two point-contact HKPs during the arbitrary movements of the end effector can be guaranteed satisfactorily.

Figure 2 The target PM: (a) CAD model, (b) magnification of the right HKP, and (c) prototype of the HKP-related mechanical parts.

3 Derivations of parasitic motions and redundant actuations

How parasitic motions and redundant actuations are generated in the target PM is presented in this section. In frame {S}, the mathematical functions of surfaces where the left and right condylar ball centers are situated are

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& p_{\mathrm{1}}\cdot X_S+Z_S+p_{\mathrm{2}}=\mathrm{0},p_{\mathrm{3}}\le X_S\le p_{\mathrm{4}},\\ & p_{\mathrm{5}}\le Y_S^L\le p_{\mathrm{6}},-p_{\mathrm{6}}\le Y_S^R\le -p_{\mathrm{5}}\\ & p_{\mathrm{1}}=\mathrm{1.1},p_{\mathrm{2}}=-\mathrm{13.215},p_{\mathrm{3}}=-\mathrm{10},p_{\mathrm{4}}=\mathrm{5},\\ & p_{\mathrm{5}}=\mathrm{69},p_{\mathrm{6}}=\mathrm{75},\end{array}\end{array}$$

where $Y_S^i$ (i=L, R) denotes the coordinates along the Y_S axis of the left and right surfaces, respectively; p₁ is a dimensionless parameter; and the unit of p₂–p₆ is millimeters.

The coordinates of the condylar ball centers T_i (i=L, R) in {S} are

$$\begin{array}{}\text{(2)}& {\mathbf{O}}_S{\mathbf{T}}_i={\mathbf{O}}_S{\mathbf{O}}_M+{}_M^S\mathbf{R}\cdot {}^M{\mathbf{O}}_M{\mathbf{T}}_i,\end{array}$$

where O_SO_M=[X Y Z]^T denotes the 3 × 1 position vector of the mass center O_M in {S}, ^MO_MT_i is the constant position vector of T_i in {M}, and ${}_M^S\mathbf{R}$ is the rotation matrix from {S} to {M} in terms of X–Y–Z Euler angles and is computed as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{}_M^S\mathbf{R}& ={\mathbf{R}}_X\left(\mathit{\alpha }\right)\cdot {\mathbf{R}}_Y\left(\mathit{\beta }\right)\cdot {\mathbf{R}}_Z\left(\mathit{\gamma }\right)\\ & =\left[\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{c}\mathit{\alpha }& -s\mathit{\alpha }\\ \mathrm{0}& \mathrm{s}\mathit{\alpha }& \mathrm{c}\mathit{\alpha }\end{array}\right]\cdot \left[\begin{array}{ccc}\mathrm{c}\mathit{\beta }& \mathrm{0}& \mathrm{s}\mathit{\beta }\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\mathrm{s}\mathit{\beta }& \mathrm{0}& \mathrm{c}\mathit{\beta }\end{array}\right]\\ & \cdot \left[\begin{array}{ccc}\mathrm{c}\mathit{\gamma }& -\mathrm{s}\mathit{\gamma }& \mathrm{0}\\ \mathrm{s}\mathit{\gamma }& \mathrm{c}\mathit{\gamma }& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\\ & =\left[\begin{array}{ccc}\mathrm{c}\mathit{\beta }\mathrm{c}\mathit{\gamma }& -\mathrm{c}\mathit{\beta }\mathrm{s}\mathit{\gamma }& \mathrm{s}\mathit{\beta }\\ \mathrm{s}\mathit{\alpha }\mathrm{s}\mathit{\beta }\mathrm{c}\mathit{\gamma }+\mathrm{c}\mathit{\alpha }s\mathit{\gamma }& -\mathrm{s}\mathit{\alpha }\mathrm{s}\mathit{\beta }\mathrm{s}\mathit{\gamma }+\mathrm{c}\mathit{\alpha }\mathrm{c}\mathit{\gamma }& -\mathrm{s}\mathit{\alpha }\mathrm{c}\mathit{\beta }\\ -\mathrm{c}\mathit{\alpha }\mathrm{s}\mathit{\beta }\mathrm{c}\mathit{\gamma }+\mathrm{s}\mathit{\alpha }\mathrm{s}\mathit{\gamma }& \mathrm{c}\mathit{\alpha }\mathrm{s}\mathit{\beta }\mathrm{s}\mathit{\gamma }+\mathrm{s}\mathit{\alpha }\mathrm{c}\mathit{\gamma }& \mathrm{c}\mathit{\alpha }\mathrm{c}\mathit{\beta }\end{array}\right]\end{array},\end{array}$$

where R_X(α), R_Y(β), and R_Z(γ) are the rotation matrices around the X_M, Y_M, and Z_M axes by α, β, and γ, respectively, and s and c are short for sin (⋅) and cos (⋅), respectively.

Substituting Eqs. (2) and (3) into Eq. (1) produces the geometric constraint equation at two HKPs as

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& p_{\mathrm{1}}\cdot \left(X+{}_M^S{\mathbf{R}}_{\left(\mathrm{1},:\right)}\cdot {}^M{\mathbf{O}}_M{\mathbf{T}}_j\right)+Z+{}_M^S{\mathbf{R}}_{\left(\mathrm{3},:\right)}\cdot {}^M{\mathbf{O}}_M{\mathbf{T}}_j\\ & +p_{\mathrm{2}}=\mathrm{0},\left(j=L,R\right),\end{array}\end{array}$$

where ${}_M^S{\mathbf{R}}_{\left(i,:\right)}$ is the ith (i=1, 3) row of ${}_M^S\mathbf{R}$. Considering the left-right symmetry of ^MO_MT_L and ^MO_MT_R in {M}, a summation and a subtraction of the two equations in Eq. (4) sidewise yield

$$\begin{array}{}\text{(5)}& \begin{array}{rl}Z& =-\left(p_{\mathrm{1}}X+p_{\mathrm{2}}+\left(p_{\mathrm{1}}\cdot {}_M^S{\mathbf{R}}_{(\mathrm{1},:)}+{}_M^S{\mathbf{R}}_{(\mathrm{3},:)}\right)\right.\\ & \left.\cdot \left[\begin{array}{c}{}^M{\mathbf{O}}_M{\mathbf{T}}_{L\left(\mathrm{1}\right)}\\ \mathrm{0}\\ {}^M{\mathbf{O}}_M{\mathbf{T}}_{L\left(\mathrm{3}\right)}\end{array}\right]\right)\\ \mathit{\gamma }& =\mathbf{atan}{\displaystyle \frac{s\mathit{\alpha }}{p_{\mathrm{1}}\mathrm{c}\mathit{\beta }+c\mathit{\alpha }s\mathit{\beta }}},\end{array}\end{array}$$

where ^MO_MT_L(j) (j=1, 3) is the jth term of ^MO_MT_L. As a consequence, these constraints at HKPs change 1 translational DOF Z and one Euler angle γ into parasitic motions, which are the functions of 4 DOFs, i.e., 2 translational DOFs, X and Y, and two Euler angles, α and β. In fact, from the Kutzbach–Grübler criterion, the mechanism has 4 DOFs, but it does not tell us which 4 and cannot judge whether parasitic motions exist or not. From this rigorous computation, not only the 4 DOFs but also two parasitic motions in the mechanism can be found. As such, the target mechanism can still perform motions in six directions in the 3D space. Because there are still six actuators, it is redundantly actuated. Thus, parasitic motions and redundant actuations are explicitly brought by the direct constraints from the base to the end effector. By contrast, generally, parasitic motions in PMs are caused by the constraints in the chains (Carretero et al., 2000; Nayak et al., 2018), and the conventional ways to form actuation redundancy as stated in Gosselin and Schreiber (2018) are to raise the number of actuators in the chains. That is to say, both parasitic motions and actuation redundancy are usually rooted in the kinematic chains. The above mathematical derivation of the constraints at the HKPs shows that the manner of producing these two features in the target mechanism is very unconventional.

To conveniently build the dynamic model in the following, a 4 × 1 vector grouping the 4 DOFs of the mechanism is defined as

$$\begin{array}{}\text{(6)}& {\mathbf{q}}_{\mathrm{EE}}={\left[\begin{array}{cccc}X& Y& \mathit{\alpha }& \mathit{\beta }\end{array}\right]}^T.\end{array}$$

Meanwhile, to characterize the instantaneous configuration of the mechanism, a 6 × 1 vector is denoted as

$$\begin{array}{}\text{(7)}& {\mathbf{X}}_{\mathrm{EE}}={\left[\begin{array}{cccccc}X& Y& Z& \mathit{\alpha }& \mathit{\beta }& \mathit{\gamma }\end{array}\right]}^T.\end{array}$$

From this section, the mechanism in Fig. 1 can be generated by imposing direct constraints from the maxilla to the condylar balls ① and ② of the 6RSS PM with 6 DOFs as in Chap. 4 of Xu and Bronlund (2010). In other words, by deleting these constraints, the 6RSS PM is recovered. Mathematically, for the target PM, the six variables in X_EE contain 4 DOFs and two parasitic motions. Meanwhile, in the 6RSS PM, its six motion variables can also be expressed in the form of X_EE, but they are all DOFs.

4 Constraint Jacobian matrices and their first time derivatives

By following the procedure of the Hessian matrix method in Abo-Shanab (2020), this section is mainly to derive the Jacobian matrices between the constraint equations and generalized coordinates and their first time derivatives. They serve as fundamental elements in the dynamic model in Sect. 5.1.

As shown in Fig. 1, a constraint equation in each chain can be defined as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{h}_i\left({\mathit{\theta }}_i,{\mathbf{q}}_{\mathrm{EE}}\right)& ={∥{\mathbf{O}}_S{\mathbf{G}}_i+{\mathbf{G}}_i{\mathbf{S}}_i-\left({\mathbf{O}}_S{\mathbf{O}}_M+{\mathbf{O}}_M{\mathbf{M}}_i\right)∥}^{\mathrm{2}}\\ & -{∥{\mathbf{S}}_i{\mathbf{M}}_i∥}^{\mathrm{2}}=\mathrm{0}\left(i=\mathrm{1},\mathrm{\dots },\mathrm{6}\right),\end{array}\end{array}$$

where θ_i is the rotational displacement of the ith actuator around the $Z_{C_i}$ axis of frame {C_i} and has been calculated in inverse kinematics from Eq. (7) of Cheng et al. (2015). O_SG_i is a constant vector for G_i, which is a fixed point, and

$$\begin{array}{}\text{(9)}& {\mathbf{G}}_i{\mathbf{S}}_i={}_{C_{i\mathrm{0}}}^S\mathbf{R}\cdot {\mathbf{R}}_Z\left({\mathit{\theta }}_i\right)\cdot \left[\begin{array}{c}∥{\mathbf{G}}_i{\mathbf{S}}_i∥\\ {\mathrm{0}}_{\mathrm{2}\times \mathrm{1}}\end{array}\right],\end{array}$$

where ${}_{C_{i\mathrm{0}}}^S\mathbf{R}$ is the rotation matrix from {S} to {C_i} at the initial configuration of the mechanism, R_Z(θ_i) is the rotation matrix around the $Z_{C_i}$ axis by the angle θ_i, and ∥G_iS_i∥ is the length of the ith crank. The numerical values of ${}_{C_{i\mathrm{0}}}^S\mathbf{R}$ (i=1, …, 6) are

$$\begin{array}{rl}& {}_{C_{\mathrm{10}}}^S\mathbf{R}=\left[\begin{array}{ccc}\mathrm{0.8541}& \mathrm{0.5201}& \mathrm{0}\\ -\mathrm{0.5201}& \mathrm{0.8541}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right],\\ & {}_{C_{\mathrm{20}}}^S\mathbf{R}=\left[\begin{array}{ccc}\mathrm{0.8541}& \mathrm{0.5201}& \mathrm{0}\\ \mathrm{0.5201}& -\mathrm{0.8541}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& -\mathrm{1}\end{array}\right],\\ & {}_{C_{\mathrm{30}}}^S\mathbf{R}=\left[\begin{array}{ccc}\mathrm{0.9310}& \mathrm{0.3651}& \mathrm{0}\\ -\mathrm{0.0822}& \mathrm{0.2096}& \mathrm{0.9743}\\ \mathrm{0.3558}& -\mathrm{0.9071}& \mathrm{0.2251}\end{array}\right],\\ & {}_{C_{\mathrm{40}}}^S\mathbf{R}=\left[\begin{array}{ccc}\mathrm{0.9310}& -\mathrm{0.3651}& \mathrm{0}\\ \mathrm{0.0822}& \mathrm{0.2096}& -\mathrm{0.9743}\\ \mathrm{0.3558}& \mathrm{0.9071}& \mathrm{0.2251}\end{array}\right],\\ & {}_{C_{\mathrm{50}}}^S\mathbf{R}=\left[\begin{array}{ccc}-\mathrm{0.8127}& \mathrm{0.5827}& \mathrm{0}\\ -\mathrm{0.1215}& -\mathrm{0.1694}& \mathrm{0.9780}\\ \mathrm{0.5699}& \mathrm{0.7948}& \mathrm{0.2085}\end{array}\right],\\ & {}_{C_{\mathrm{60}}}^S\mathbf{R}=\left[\begin{array}{ccc}-\mathrm{0.8127}& -\mathrm{0.5827}& \mathrm{0}\\ \mathrm{0.1215}& -\mathrm{0.1694}& -\mathrm{0.9780}\\ \mathrm{0.5699}& -\mathrm{0.7948}& \mathrm{0.2085}\end{array}\right].\end{array}$$

For the displacement of the end effector, the term O_SO_M in Eq. (8) is the position vector of the mass center O_M in {S} and has been defined under Eq. (2), and

$$\begin{array}{}\text{(10)}& {\mathbf{O}}_M{\mathbf{M}}_i={}_M^S\mathbf{R}\cdot {}^M{\mathbf{O}}_M{\mathbf{M}}_i,\end{array}$$

where ^MO_MM_i is the constant 3 × 1 position vector of M_i in {M}. Their coordinates are given in the last three lines of Table 1. Finally, in Eq. (8), ∥S_iM_i∥ is the length of the ith coupler S_iM_i. The lengths of the six cranks and couplers are given as (unit: mm)

$$\begin{array}{rl}& ∥{\mathbf{G}}_{\mathrm{1}}{\mathbf{S}}_{\mathrm{1}}∥=∥{\mathbf{G}}_{\mathrm{2}}{\mathbf{S}}_{\mathrm{2}}∥=\mathrm{10},\\ & ∥{\mathbf{S}}_{\mathrm{1}}{\mathbf{M}}_{\mathrm{1}}∥=∥{\mathbf{S}}_{\mathrm{2}}{\mathbf{M}}_{\mathrm{2}}∥=∥{\mathbf{S}}_{\mathrm{3}}{\mathbf{M}}_{\mathrm{3}}∥=∥{\mathbf{S}}_{\mathrm{4}}{\mathbf{M}}_{\mathrm{4}}∥=\mathrm{33}\\ & ∥{\mathbf{G}}_{\mathrm{3}}{\mathbf{S}}_{\mathrm{3}}∥=∥{\mathbf{G}}_{\mathrm{4}}{\mathbf{S}}_{\mathrm{4}}∥=∥{\mathbf{G}}_{\mathrm{5}}{\mathbf{S}}_{\mathrm{5}}∥=∥{\mathbf{G}}_{\mathrm{6}}{\mathbf{S}}_{\mathrm{6}}∥=\mathrm{15},\\ & ∥{\mathbf{S}}_{\mathrm{5}}{\mathbf{M}}_{\mathrm{5}}∥=∥{\mathbf{S}}_{\mathrm{6}}{\mathbf{M}}_{\mathrm{6}}∥=\mathrm{52}.\end{array}$$

Henceforth, a 6 × 1 constraint vector can be defined as

$$\begin{array}{}\text{(11)}& \mathbf{H}\left(\mathbf{q}\right)=\left[\begin{array}{c}{h}_{\mathrm{1}}\left({\mathit{\theta }}_{\mathrm{1}},{\mathbf{q}}_{\mathrm{EE}}\right)\\ \mathrm{⋮}\\ h_{\mathrm{6}}\left({\mathit{\theta }}_{\mathrm{6}},{\mathbf{q}}_{\mathrm{EE}}\right)\end{array}\right]={\mathrm{0}}_{\mathrm{6}\times \mathrm{1}},\end{array}$$

where $\mathbf{q}=\left[\begin{array}{c}\mathit{\theta }\\ {\mathbf{q}}_{\mathrm{EE}}\end{array}\right]$ is the generalized coordinate vector, and $\mathit{\theta }=\left[\begin{array}{c}{\mathit{\theta }}_{\mathrm{1}}\\ \mathrm{⋮}\\ {\mathit{\theta }}_{\mathrm{6}}\end{array}\right]$. Differentiating H with respect to time produces

$$\begin{array}{}\text{(12)}& {\mathbf{J}}_{\mathit{\theta }}\cdot \dot{\mathit{\theta }}+{\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}}={\mathrm{0}}_{\mathrm{6}\times \mathrm{1}},\end{array}$$

where J_θ and ${\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}$ are the Jacobian matrices of H with respect to θ and q_EE, respectively. In this paper, symbols with one and two dots above indicate their first and second time derivatives, respectively.

Because h_i(θ_i,q_EE) does not contain the terms θ_j where j≠i, explicitly, J_θ is a diagonal matrix. From Eq. (12) one can derive

$$\begin{array}{}\text{(13)}& \dot{\mathit{\theta }}={\mathbf{J}}_{\mathit{\theta }\mathrm{1}}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}},\end{array}$$

where

$$\begin{array}{}\text{(14)}& {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}=-{\mathbf{J}}_{\mathit{\theta }}^{-\mathrm{1}}\cdot {\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}},\end{array}$$

and ${\mathbf{J}}_{\mathit{\theta }}^{-\mathrm{1}}$exists when the mechanism is not at its singular configuration. Differentiating Eq. (12) with respect to time and putting Eq. (13) into the result gives rise to

$$\begin{array}{}\text{(15)}& {\mathbf{J}}_{\mathit{\theta }}\cdot \ddot{\mathit{\theta }}+\left({\dot{\mathbf{J}}}_{\mathit{\theta }}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}+{\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}\right)\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}}+{\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}\cdot {\ddot{\mathbf{q}}}_{\mathrm{EE}}={\mathrm{0}}_{\mathrm{6}\times \mathrm{1}}.\end{array}$$

Thereby, the accelerations of the active revolute joints are

$$\begin{array}{}\text{(16)}& \ddot{\mathit{\theta }}={\mathbf{J}}_{\mathit{\theta }\mathrm{2}}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}}+{\mathbf{J}}_{\mathit{\theta }\mathrm{1}}\cdot {\ddot{\mathbf{q}}}_{\mathrm{EE}},\end{array}$$

where

$$\begin{array}{}\text{(17)}& {\mathbf{J}}_{\mathit{\theta }\mathrm{2}}=-{\mathbf{J}}_{\mathit{\theta }}^{-\mathrm{1}}\cdot \left({\dot{\mathbf{J}}}_{\mathit{\theta }}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}+{\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}\right).\end{array}$$

As a result, the first and the second time derivatives of q are

$$\begin{array}{}\text{(18)}& \begin{array}{rl}& \dot{\mathbf{q}}={\mathbf{J}}_{\mathit{\theta }\mathrm{3}}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}}\\ & \ddot{\mathbf{q}}={\mathbf{J}}_{\mathit{\theta }\mathrm{3}}\cdot {\ddot{\mathbf{q}}}_{\mathrm{EE}}+{\mathbf{J}}_{\mathit{\theta }\mathrm{4}}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}},\end{array}\end{array}$$

where

$$\begin{array}{}\text{(19)}& {\mathbf{J}}_{\mathit{\theta }\mathrm{3}}=\left[\begin{array}{c}{\mathbf{J}}_{\mathit{\theta }\mathrm{1}}\\ {\mathbf{I}}_{\mathrm{4}}\end{array}\right],{\mathbf{J}}_{\mathit{\theta }\mathrm{4}}=\left[\begin{array}{c}{\mathbf{J}}_{\mathit{\theta }\mathrm{2}}\\ {\mathrm{0}}_{\mathrm{4}}\end{array}\right],\end{array}$$

with I₄ and 0₄ being 4 × 4 identity and zero matrices, respectively. In this paper, I_n, where n is a positive integer, is an n × n identity matrix. To compute ${\dot{\mathbf{J}}}_{\mathit{\theta }}$ in J_θ2, one can find that

$$\begin{array}{}\text{(20)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial h_i}{\partial {\mathit{\theta }}_i}}\right)={\dot{\mathbf{q}}}^T\cdot {\mathbf{H}}_{i\left(:,i\right)}(i=\mathrm{1},\mathrm{\dots },\mathrm{6}),\end{array}$$

where H_i is the Hessian matrix of h_i with respect to q, and the subscript $(:,i)$ represents its ith column. In this regard,

$$\begin{array}{}\text{(21)}& {\dot{\mathbf{J}}}_{\mathit{\theta }}=\left({\mathbf{I}}_{\mathrm{6}}\otimes {\dot{\mathbf{q}}}^T\right)\cdot \mathrm{diag}\left(\begin{array}{ccc}{\mathbf{H}}_{\mathrm{1}\left(:,\mathrm{1}\right)}& \mathrm{\cdots }& {\mathbf{H}}_{\mathrm{6}\left(:,\mathrm{6}\right)}\end{array}\right),\end{array}$$

where ⊗ is the Kronecker product. Identically, to compute ${\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}$, one can see that

$$\begin{array}{}\text{(22)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial h_i}{\partial {\mathbf{q}}_{\mathrm{EE}\left(j\right)}}}\right)={\dot{\mathbf{q}}}^T\cdot {\mathbf{H}}_{i\left(:,j+\mathrm{6}\right)}\\ & (i=\mathrm{1},\mathrm{\dots },\mathrm{6};j=\mathrm{1},\mathrm{\dots },\mathrm{4}),\end{array}\end{array}$$

where q_EE(j) (j=1, …, 4) is the jth entry of q_EE, and ${\mathbf{H}}_{i\left(:,j+\mathrm{6}\right)}$ is the (j+6)th column of H_i. Consequently, it can be found that

$$\begin{array}{}\text{(23)}& {\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}=\left({\mathbf{I}}_{\mathrm{6}}\otimes {\dot{\mathbf{q}}}^T\right)\cdot \left[\begin{array}{c}{\mathbf{H}}_{\mathrm{1}\left(:,\mathrm{7}:\mathrm{10}\right)}\\ \mathrm{⋮}\\ {\mathbf{H}}_{\mathrm{6}\left(:,\mathrm{7}:\mathrm{10}\right)}\end{array}\right],\end{array}$$

where the subscript ($:,\mathrm{7}:\mathrm{10}$) indicates the 7th to the 10th columns of H_i. From the definition of J_θ and ${\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and Eqs. (14), (21), and (23), J_θ2 can be computed; thus, Eq. (18) can be calculated.

5 Dynamic modeling of the mechanism

5.1 Hessian matrix method

In this section, the inverse dynamic model of the target PM is built using the Hessian matrix method under the Lagrange–D'Alembert principle from Abo-Shanab (2020). Thus, the kinetic and potential energies of the entire mechanism are derived prior to use of the Hessian matrix method.

5.1.1 Kinetic energy

Because the ith (i=1, …, 6) crank can only rotate around the $Z_{C_i}$ axis, for the six cranks, their kinetic energy is

$$\begin{array}{}\text{(24)}& T_{\mathbf{GS}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\dot{\mathit{\theta }}}^T\cdot {\mathbf{M}}_{\mathbf{GS}}\cdot \dot{\mathit{\theta }},\end{array}$$

where ${\mathbf{M}}_{\mathbf{GS}}=\mathrm{diag}\left(\begin{array}{ccc}{I}_{{\mathbf{G}}_{\mathrm{1}}{\mathbf{S}}_{\mathrm{1}}}& \mathrm{\cdots }& I_{{\mathbf{G}}_{\mathrm{6}}{\mathbf{S}}_{\mathrm{6}}}\end{array}\right)$, and $I_{{\mathbf{G}}_i{\mathbf{S}}_i}$ is the rotational inertia of the ith crank. Their values are (unit: g mm²)

$$\begin{array}{rl}& I_{{\mathbf{G}}_{\mathrm{1}}{\mathbf{S}}_{\mathrm{1}}}=I_{{\mathbf{G}}_{\mathrm{2}}{\mathbf{S}}_{\mathrm{2}}}=\mathrm{3510}\\ & I_{{\mathbf{G}}_{\mathrm{3}}{\mathbf{S}}_{\mathrm{3}}}=I_{{\mathbf{G}}_{\mathrm{4}}{\mathbf{S}}_{\mathrm{4}}}=\mathrm{6630}\\ & I_{{\mathbf{G}}_{\mathrm{5}}{\mathbf{S}}_{\mathrm{5}}}=I_{{\mathbf{G}}_{\mathrm{6}}{\mathbf{S}}_{\mathrm{6}}}=\mathrm{17}\mathrm{628}.\end{array}$$

For the ith (i=1, …, 6) coupler, the distance from S_i to an arbitrary point P_i on S_iM_i is set as x. As a result,

$$\begin{array}{}\text{(25)}& {\mathbf{O}}_S{\mathbf{P}}_i={\mathbf{O}}_S{\mathbf{S}}_i+{\mathbf{S}}_i{\mathbf{P}}_i={\mathbf{O}}_S{\mathbf{S}}_i+x\cdot {\displaystyle \frac{{\mathbf{S}}_i{\mathbf{M}}_i}{∥{\mathbf{S}}_i{\mathbf{M}}_i∥}}.\end{array}$$

Further, one can obtain that

$$\begin{array}{}\text{(26)}& {\mathbf{S}}_i{\mathbf{M}}_i={\mathbf{O}}_S{\mathbf{M}}_i-{\mathbf{O}}_S{\mathbf{S}}_i.\end{array}$$

Putting Eq. (26) into Eq. (25) gives rise to

$$\begin{array}{}\text{(27)}& {\mathbf{O}}_S{\mathbf{P}}_i=\left(\mathrm{1}-{\displaystyle \frac{x}{∥{\mathbf{S}}_i{\mathbf{M}}_i∥}}\right)\cdot {\mathbf{O}}_S{\mathbf{S}}_i+x\cdot {\displaystyle \frac{{\mathbf{O}}_S{\mathbf{M}}_i}{∥{\mathbf{S}}_i{\mathbf{M}}_i∥}}.\end{array}$$

The velocity of point P_i is

$$\begin{array}{}\text{(28)}& {\mathbf{V}}_{P_i}={\mathbf{J}}_{P_i}\cdot \dot{\mathbf{q}},\end{array}$$

where ${\mathbf{J}}_{P_i}$ is the Jacobian matrix between O_SP_i and q, namely, ${\mathbf{J}}_{P_i}=\mathrm{Jacobian}\left(\begin{array}{cc}{\mathbf{O}}_S{\mathbf{P}}_i,& \mathbf{q}\end{array}\right)$. Thus, the kinetic energy of the ith coupler is

$$\begin{array}{}\text{(29)}& T_{{\mathbf{S}}_i{\mathbf{M}}_i}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\dot{\mathbf{q}}}^T\cdot {\mathbf{M}}_{{\mathbf{S}}_i{\mathbf{M}}_i}\cdot \dot{\mathbf{q}},\end{array}$$

where

$$\begin{array}{}\text{(30)}& {\mathbf{M}}_{{\mathbf{S}}_i{\mathbf{M}}_i}=\underset{\mathrm{0}}{\overset{∥{\mathbf{S}}_i{\mathbf{M}}_i∥}{\int }}{\mathbf{J}}_{P_i}^T\cdot {\mathit{\rho }}_i\cdot A_i\cdot {\mathbf{J}}_{P_i}\cdot \mathrm{d}x\end{array}$$

is the inertia matrix of the ith coupler. In it, ρ_i=7.8 g mm⁻³ and A_i=17.3494 mm² are its density and cross-section area, respectively.

The 6 × 1 twist of the end effector is

$$\begin{array}{}\text{(31)}& {\mathbf{T}}_{\mathrm{EE}}={\mathbf{M}}_{\mathrm{0}a}\cdot {\dot{\mathbf{X}}}_{\mathrm{EE}},\end{array}$$

where

$${\mathbf{M}}_{\mathrm{0}a}=\mathrm{diag}\left(\begin{array}{cc}{\mathbf{I}}_{\mathrm{3}}& {\mathbf{R}}_{\mathit{\omega }}\end{array}\right),{\mathbf{R}}_{\mathit{\omega }}=\left[\begin{array}{ccc}\mathrm{1}& \mathrm{0}& s\mathit{\beta }\\ \mathrm{0}& c\mathit{\alpha }& -s\mathit{\alpha }c\mathit{\beta }\\ \mathrm{0}& s\mathit{\alpha }& -c\mathit{\alpha }c\mathit{\beta }\end{array}\right].$$

Note that Z and γ in X_EE are parasitic motions which are functions of q_EE, and ${\dot{\mathbf{X}}}_{\mathrm{EE}}$ can be further written using ${\mathbf{q}}_{\mathrm{EE}},{\dot{\mathbf{q}}}_{\mathrm{EE}}$ as

$$\begin{array}{}\text{(32)}& {\dot{\mathbf{X}}}_{\mathrm{EE}}={\mathbf{M}}_J\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}},\end{array}$$

where M_J is the Jacobian matrix of X_EE with respect to q_EE. Upon putting Eq. (32) into Eq. (31), one can find that

$$\begin{array}{}\text{(33)}& {\mathbf{T}}_{\mathrm{EE}}={\mathbf{M}}_{\mathrm{0}b}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}},\end{array}$$

where ${\mathbf{M}}_{\mathrm{0}b}={\mathbf{M}}_{\mathrm{0}a}\cdot {\mathbf{M}}_J$.

By virtue of Eq. (33), the kinetic energy of the end effector is

$$\begin{array}{}\text{(34)}& T_{\mathrm{EE}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\mathbf{T}}_{\mathrm{EE}}^T\cdot \mathrm{diag}\left(\begin{array}{cc}{m}_{\mathrm{EE}}\cdot {\mathbf{I}}_{\mathrm{3}}& {\mathbf{I}}_{\mathrm{EE}}\end{array}\right)\cdot {\mathbf{T}}_{\mathrm{EE}},\end{array}$$

where m_EE=340.22 g and ${\mathbf{I}}_{\mathrm{EE}}={}_M^S\mathbf{R}\cdot {}^M{\mathbf{I}}_{\mathrm{EE}}\cdot {}_M^S{\mathbf{R}}^T$ are the mass and the inertia tensor of the end effector with respect to {S}, respectively, and

$${}^M{\mathbf{I}}_{\mathrm{EE}}=\left[\begin{array}{ccc}\mathrm{820091.15}& -\mathrm{26.57}& -\mathrm{137019.15}\\ -\mathrm{26.57}& \mathrm{423459.18}& -\mathrm{88.60}\\ -\mathrm{137019.15}& -\mathrm{88.60}& \mathrm{818784.7}\end{array}\right]{\mathrm{g}\mathrm{mm}}^{\mathrm{2}}$$

is the inertia tensor with respect to {M}.

Putting Eq. (33) into Eq. (34) gives rise to

$$\begin{array}{}\text{(35)}& T_{\mathrm{EE}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}}^T\cdot {\mathbf{M}}_{\mathrm{EE}}\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}},\end{array}$$

where

$$\begin{array}{}\text{(36)}& {\mathbf{M}}_{\mathrm{EE}}={\mathbf{M}}_{\mathrm{0}b}^T\cdot \mathrm{diag}\left(\begin{array}{cc}{m}_{\mathrm{EE}}\cdot {\mathbf{I}}_{\mathrm{3}}& {\mathbf{I}}_{\mathrm{EE}}\end{array}\right)\cdot {\mathbf{M}}_{\mathrm{0}b}\end{array}$$

is the inertia matrix of end effector. In this regard, the overall kinetic energy is

$$\begin{array}{}\text{(37)}& T=T_{\mathbf{GS}}+\sum _{i=\mathrm{1}}^{\mathrm{6}}{T}_{{\mathbf{S}}_i{\mathbf{M}}_i}+T_{\mathbf{EE}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\dot{\mathbf{q}}}^T\cdot \mathbf{M}\cdot \dot{\mathbf{q}},\end{array}$$

where

$$\begin{array}{}\text{(38)}& \mathbf{M}=\mathrm{diag}\left(\begin{array}{cc}{\mathbf{M}}_{\mathbf{GS}}& {\mathbf{M}}_{\mathrm{EE}}\end{array}\right)+\sum _{i=\mathrm{1}}^{\mathrm{6}}{\mathbf{M}}_{{\mathbf{S}}_i{\mathbf{M}}_i}\end{array}$$

is the inertia matrix of the entire robotic mechanism.

5.1.2 Potential energy

It is noted that in the ith chain, the revolute joint center G_i is a fixed point in the inertia frame {S}, and it is also the mass center of the ith crank. Thus, the potential energy $V_{{\mathbf{G}}_i{\mathbf{S}}_i}$ of the crank is a constant.

The potential energy of the ith coupler S_iM_i is

$$\begin{array}{}\text{(39)}& V_{{\mathbf{S}}_i{\mathbf{M}}_i}=m_{{\mathbf{S}}_i{\mathbf{M}}_i}\cdot g\cdot {\mathbf{O}}_S{\mathbf{E}}_{i\left(\mathrm{3}\right)},\end{array}$$

where $m_{{\mathbf{S}}_i{\mathbf{M}}_i}$ is the mass of S_iM_i, g=9800 mm s⁻² is the gravitational acceleration, E_i is the mass center, and O_SE_i(3) is the third term of O_SE_i that is computed as

$$\begin{array}{}\text{(40)}& {\mathbf{O}}_S{\mathbf{E}}_i={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot \left({\mathbf{O}}_S{\mathbf{S}}_i+{\mathbf{O}}_S{\mathbf{M}}_i\right).\end{array}$$

The potential energy of the end effector is

$$\begin{array}{}\text{(41)}& V_{\mathrm{EE}}=m_{\mathrm{EE}}\cdot g\cdot Z.\end{array}$$

From Eqs. (5), (31)–(33), and (41), parasitic motions are clearly taken into the dynamic model by virtue of ${\mathbf{q}}_{\mathrm{EE}},{\dot{\mathbf{q}}}_{\mathrm{EE}}$.

The potential energy of the mechanism is

$$\begin{array}{}\text{(42)}& V=\sum _{i=\mathrm{1}}^{\mathrm{6}}\left(V_{{\mathbf{G}}_i{\mathbf{S}}_i}+V_{{\mathbf{S}}_i{\mathbf{M}}_i}\right)+V_{\mathrm{EE}}.\end{array}$$

5.1.3 Dynamic model

Based on the derived kinetic and potential energies of the mechanism, the dynamic model can be built. From the Lagrange–D'Alembert principle, one can write that

$$\begin{array}{}\text{(43)}& \mathit{\delta }{\mathbf{q}}^T\cdot \left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial T}{\partial \dot{\mathbf{q}}}}\right)-{\displaystyle \frac{\partial T}{\partial \mathbf{q}}}+{\displaystyle \frac{\partial V}{\partial \mathbf{q}}}-\mathbf{F}\right)=\mathrm{0},\end{array}$$

where $\mathit{\delta }\mathbf{q}=\left[\begin{array}{c}\mathit{\delta }\mathit{\theta }\\ \mathit{\delta }{\mathbf{q}}_{\mathrm{EE}}\end{array}\right]$ is the virtual displacement vector of q, and $\mathbf{F}=\left[\begin{array}{c}\mathit{\tau }\\ {\mathbf{F}}_{\mathrm{EE}}\end{array}\right]$ is the 10 × 1 generalized force vector corresponding to the 10 elements of q. In it, τ is the 6 × 1 actuating torque vector, and F_EE is the 4 × 1 generalized force vector formed by the reacted bite force on the end effector. By virtue of the expression of q and F, Eq. (43) can be rewritten as

$$\begin{array}{}\text{(44)}& \begin{array}{rl}& \mathit{\delta }{\mathit{\theta }}^T\cdot \left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial T}{\partial \dot{\mathit{\theta }}}}\right)-{\displaystyle \frac{\partial T}{\partial \mathit{\theta }}}+{\displaystyle \frac{\partial V}{\partial \mathit{\theta }}}-\mathit{\tau }\right)\\ +& \mathit{\delta }{\mathbf{q}}_{\mathrm{EE}}^T\cdot \left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial T}{\partial {\dot{\mathbf{q}}}_{\mathrm{EE}}}}\right)-{\displaystyle \frac{\partial T}{\partial {\mathbf{q}}_{\mathrm{EE}}}}+{\displaystyle \frac{\partial V}{\partial {\mathbf{q}}_{\mathrm{EE}}}}-{\mathbf{F}}_{\mathrm{EE}}\right)=\mathrm{0}.\end{array}\end{array}$$

From Eq. (13), one can obtain

$$\begin{array}{}\text{(45)}& \mathit{\delta }\mathit{\theta }={\mathbf{J}}_{\mathit{\theta }\mathrm{1}}\cdot \mathit{\delta }{\mathbf{q}}_{\mathrm{EE}}.\end{array}$$

Putting this into Eq. (44), deleting the free term δq_EE, and rewriting the result gives rise to

$$\begin{array}{}\text{(46)}& {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\cdot \mathit{\tau }={\mathbf{J}}_{\mathit{\theta }\mathrm{3}}^T\cdot \left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial T}{\partial \dot{\mathbf{q}}}}\right)-{\displaystyle \frac{\partial T}{\partial \mathbf{q}}}+{\displaystyle \frac{\partial V}{\partial \mathbf{q}}}\right)-{\mathbf{F}}_{\mathrm{EE}},\end{array}$$

from which one can derive that

$$\begin{array}{}\text{(47)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial T}{\partial \dot{\mathbf{q}}}}\right)=\mathbf{M}\cdot \ddot{\mathbf{q}}+\dot{\mathbf{M}}\cdot \dot{\mathbf{q}}.\end{array}$$

To compute the matrix $\dot{\mathbf{M}}$, a vector $\mathbf{U}={\left[\begin{array}{cc}{\dot{\mathbf{q}}}^T& {\mathbf{q}}^T\end{array}\right]}^T$ is set. Then, a 20 × 20 Hessian matrix of the kinetic energy T of the mechanism with respect to U can be obtained as

$$\begin{array}{}\text{(48)}& \mathbf{H}=\mathrm{Hessian}\left(\begin{array}{cc}T,& \mathbf{U}\end{array}\right).\end{array}$$

Then, the first time derivative of M is

$$\begin{array}{}\text{(49)}& \dot{\mathbf{M}}={\mathbf{H}}_{\left(\mathrm{1}:\mathrm{10},\mathrm{11}:\mathrm{20}\right)},\end{array}$$

where ${\mathbf{H}}_{\left(\mathrm{1}:\mathrm{10},\mathrm{11}:\mathrm{20}\right)}$ is the submatrix of H containing its first 10 rows and second 10 columns. Additionally,

$$\begin{array}{}\text{(50)}& {\displaystyle \frac{\partial T}{\partial \mathbf{q}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\dot{\mathbf{M}}}^T\cdot \dot{\mathbf{q}}.\end{array}$$

These computational details are not described in this paper for the sake of brevity, and interested readers can find how they are derived in Abo-Shanab (2020). Consequently, one can obtain

$$\begin{array}{}\text{(51)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial T}{\partial \dot{\mathbf{q}}}}\right)-{\displaystyle \frac{\partial T}{\partial \mathbf{q}}}+{\displaystyle \frac{\partial V}{\partial \mathbf{q}}}=\mathbf{M}\cdot \ddot{\mathbf{q}}+\mathbf{C}\cdot \dot{\mathbf{q}}+{\displaystyle \frac{\partial V}{\partial \mathbf{q}}},\end{array}$$

where

$$\begin{array}{}\text{(52)}& \mathbf{C}=\dot{\mathbf{M}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\dot{\mathbf{M}}}^T\end{array}$$

is the Coriolis–centrifugal force matrix. From Eqs. (18), (46), and (51), this results in the dynamic model expressed by the independent generalized coordinates q_EE as

$$\begin{array}{}\text{(53)}& {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\cdot \mathit{\tau }={\mathbf{M}}_f\cdot {\ddot{\mathbf{q}}}_{\mathrm{EE}}+{\mathbf{C}}_f\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}}+{\mathbf{G}}_f+{\mathbf{F}}_{\mathrm{EE}},\end{array}$$

which has four equations and six unknowns in τ, indicating the mechanism is redundantly actuated. In it,

$$\begin{array}{rl}& {\mathbf{M}}_f={\mathbf{J}}_{\mathit{\theta }\mathrm{3}}^T\cdot \mathbf{M}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{3}},\\ & {\mathbf{C}}_f={\mathbf{J}}_{\mathit{\theta }\mathrm{3}}^T\cdot \left(\mathbf{M}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{4}}+\mathbf{C}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{3}}\right),\text{ and}\\ & {\mathbf{G}}_f={\mathbf{J}}_{\mathit{\theta }\mathrm{3}}^T\cdot {\displaystyle \frac{\partial V}{\partial \mathbf{q}}}\end{array}$$

are the 4 × 4 inertia matrix, the 4 × 4 Coriolis–centrifugal force matrix, and the 4 × 1 gravitational vector, respectively. Theoretically, there are infinite solutions in Eq. (53), since there are more unknowns than equations. In general, the minimum norm of the actuating torques is used as a feasible solution in redundantly actuated PMs (Han et al., 2021; Hernández et al., 2020; Yan et al., 2022; Wang et al., 2019). Regarding this, the actuating torques are computed as

$$\begin{array}{}\text{(54)}& \mathit{\tau }={\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\cdot \left({\mathbf{M}}_f\cdot {\ddot{\mathbf{q}}}_{\mathrm{EE}}+{\mathbf{C}}_f\cdot {\dot{\mathbf{q}}}_{\mathrm{EE}}+{\mathbf{G}}_f+{\mathbf{F}}_{\mathrm{EE}}\right),\end{array}$$

where $({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T{)}^{+}={\mathbf{J}}_{\mathit{\theta }\mathrm{1}}\cdot ({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}{)}^{-\mathrm{1}}$ is the Moore–Penrose pseudo-inverse matrix of ${\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T$, which clearly satisfies the four Moore–Penrose conditions:

$$\begin{array}{rl}& {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\cdot {\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T={\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T,\\ & {\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\cdot {\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\right)}^T={\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\cdot {\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\\ & {\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\cdot {\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}={\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+},\\ & {\left({\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^T={\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T.\end{array}$$

5.2 Lagrangian equations

The software at hand, i.e., Simscape Multibody in MATLAB, does not support inverse dynamic analysis in a rigid multibody system with actuation redundancy. As a consequence, software simulation is not performed to verify the correctness of the dynamic model in Sect. 5.1. Considering its kinetic energy and potential energy have already been derived, the Lagrange equations of the first type (Tsai, 1999) are applied to build a second theoretical model to validate the correctness.

The first set of Lagrangian equations is

$$\begin{array}{}\text{(55)}& {\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}^T\cdot \mathit{\lambda }={\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial L}{\partial {\dot{\mathbf{q}}}_{\mathrm{EE}}}}\right)-{\displaystyle \frac{\partial L}{\partial {\mathbf{q}}_{\mathrm{EE}}}}-{\mathbf{F}}_{\mathrm{EE}},\end{array}$$

where $L=T-V$, and λ is the 6 × 1 vector of Lagrangian multipliers.

The second set of Lagrangian equations is

$$\begin{array}{}\text{(56)}& {\mathbf{J}}_{\mathit{\theta }}^T\cdot \mathit{\lambda }+{\displaystyle \frac{\partial L}{\partial \mathit{\theta }}}-{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial L}{\partial \dot{\mathit{\theta }}}}\right)=\mathit{\tau }.\end{array}$$

From Eqs. (55) and (56), by eliminating λ, one can derive that the minimum norm solution of the actuating torques is

$$\begin{array}{}\text{(57)}& \mathit{\tau }=-{\left({\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^T\right)}^{+}\cdot \left({\mathbf{J}}_{\mathit{\theta }\mathrm{3}}^T\cdot \left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\partial L}{\partial \dot{\mathbf{q}}}}\right)-{\displaystyle \frac{\partial L}{\partial \mathbf{q}}}\right)-{\mathbf{F}}_{\mathrm{EE}}\right).\end{array}$$

6 Inertia coupling analysis

To discover the inertia coupling property among the active joints in the target PM, an inertia matrix in the active joint space must be obtained. Firstly, from Eq. (13), one can derive that

$$\begin{array}{}\text{(58)}& {\dot{\mathbf{q}=J}}_{\mathit{\theta }\mathrm{5}}\cdot \dot{\mathit{\theta }},\end{array}$$

where ${\mathbf{J}}_{\mathit{\theta }\mathrm{5}}=\left[\begin{array}{c}{\mathbf{I}}_{\mathrm{6}}\\ {\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^{+}\end{array}\right]$ and ${\mathbf{J}}_{\mathit{\theta }\mathrm{1}}^{+}$ is the pseudo-inverse matrix of J_θ1. By virtue of this, the kinetic energy of the mechanism in Eq. (37) can be rewritten as

$$\begin{array}{}\text{(59)}& T={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cdot {\dot{\mathit{\theta }}}^T\cdot {\mathbf{M}}_A\cdot \dot{\mathit{\theta }},\end{array}$$

where ${\mathbf{M}}_A={\mathbf{J}}_{\mathit{\theta }\mathrm{5}}^T\cdot \mathbf{M}\cdot {\mathbf{J}}_{\mathit{\theta }\mathrm{5}}$ is the 6 × 6 inertia matrix in the joint space. To judge the inertia coupling among different active joints, the index MCI_i (i=1, …, 6) from Guo et al. (2022) as

$$\begin{array}{}\text{(60)}& {\mathrm{MCI}}_i=\ln \left({\displaystyle \frac{\sum _{k=\mathrm{1},k\ne i}^{\mathrm{6}}\left|{\mathbf{M}}_{A\left(i,k\right)}\right|}{\mathrm{5}\left|{\mathbf{M}}_{A\left(i,i\right)}\right|}}+\mathrm{1}\right)\end{array}$$

is resorted to, where M_A(i,k) is the element at the ith row and kth column of M_A, M_A(i,i) is the ith diagonal element, and |⋅| means the absolute value of the specific element. From this definition, a larger MCI_i indicates that the coupling to the ith active joint from the other ones is stronger; on the contrary, the smaller the MCI_i is, the weaker the coupling.

7 Numerical results and discussions

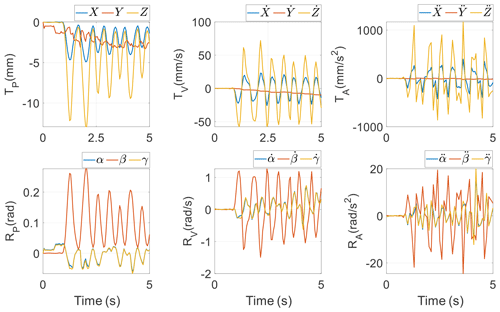
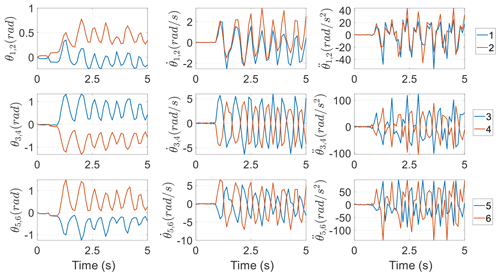
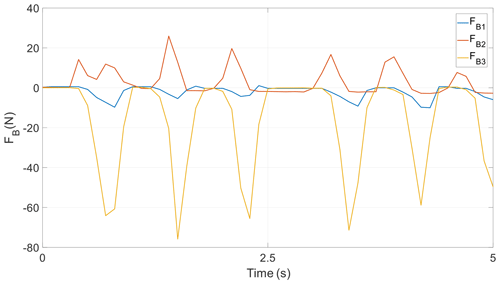
To justify the dynamic model and analyze the inertia coupling numerically, the mechanism is commanded to follow a real incisor trajectory of a healthy human subject, which lasts 5 s. Detailed techniques of capturing the chewing trajectories of human subjects are given in Chap. 6 of Xu and Bronlund (2010). The corresponding six variables in X_EE in the time history are provided with their first and second time derivatives in Fig. 3, where T and R represent the translational and rotational variables in X_EE, respectively, and D, V, and A represent the displacements, velocities, and accelerations, respectively. Clearly, the mechanism exhibits a rhythmic chewing motion, with a larger translation along the Z_S axis than that along the X_S and Y_S axes and a larger rotation around the Y_M axis than that around the X_M and Z_M axes. This comparison shows that mouth-opening and mouth-closing movements play an important role in chewing motions. The corresponding angular displacements, velocities, and accelerations of the six active revolute joints are given in Fig. 4, by virtue of the inverse kinematics from Cheng et al. (2015). One can find that the motions between the ith and (i+1)th (i=1, 3, 5) active joints on the left and right sides are nearly symmetric. Clearly, Figs. 3 and 4 show the motions of the target PM in the task space and the joint space, respectively. They have roughly the same trend, meaning the motions of the mechanism in these two spaces are synchronous. The numerical values in these two figures are used as fundamental elements in inverse dynamics. An experimentally measured 3D reacted bite force in {S} on peanuts by a healthy human subject on a left molar as in Fig. 5 is exerted onto the end effector as a time-varying payload. It clearly shows that the chewing force has five bursts and is dominated by the vertical component, and the lateral component has a smallest amplitude around the zero line.

Figure 3 Motions of the end effector.

Figure 4 Motions of the six active revolute joints.

Figure 5 Reaction forces to a left molar in frame {S} from chewing on peanuts.

7.1 Inverse dynamics

The symbolic procedures above are implemented in programs formatted and calculated numerically in MATLAB, using a personal computer with an Intel^® Core™ i7-8700K CPU at 3.70 GHz and 32 GB of RAM. The time series of actuating torques from Eq. (54) are shown in the first column of Fig. 6, from which the bursts over time tightly follow those in Fig. 5, rather than those in Figs. 3 and 4, indicating that to output the predefined chewing force via the mechanism, much more actuating torques are needed than those to run the mechanism itself; i.e., the inertia of the mechanism is much smaller relatively. Meanwhile, the six actuators output torques synchronously, and specifically, these three subplots roughly illustrate a left–right symmetry of output torques in the mechanism. The differences in the actuating torques from corresponding actuators over time between the two methods in Sect. 5.1 and 5.2 are given in the second column of Fig. 6. These values are very tiny, demonstrating the correctness and accuracy of the dynamic model. To make a comparative study about chewing actions, the same chewing forces from Fig. 5 are exerted on a symmetrically right molar. The actuating torques via the Hessian matrix method are exhibited in the third column of Fig. 6. From the comparison in the first and third columns, the magnitudes of τ₁ and τ₂ are changed, but their profiles vary little. The amplitudes of the torques from the fourth and fifth active joints are larger, while those from the third and sixth active joints are smaller. This comparison explicitly shows that the actuating torques are tightly related to the position where the external forces are acted. What is not changed is that the five bursts still follow those in Fig. 5. In addition, when the right-side chewing is performed, the differences of the actuating torques between the two methods in Sect. 5.1 and 5.2 are also as tiny as those in the second column; they are not shown for reasons of space.

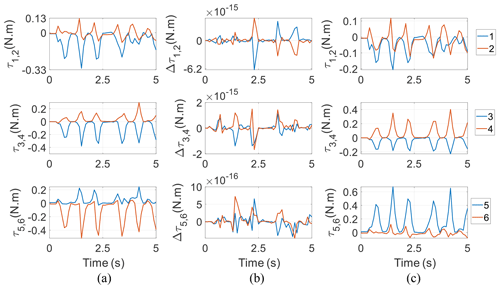
Figure 6 (a) Actuating torques with the left-side chewing, (b) their differences under two dynamic methods from Sect. 5.1 and 5.2, and (c) actuating torques with the right-side chewing.

The correctness of the model is important, and the computational cost is also critical, especially in the model-based motion and/or force control if the model can be computed in real time using an embedded micro-controller; thus, a desktop computer which can raise the expenditure is not needed. After the careful study of the method from Abo-Shanab (2020), it is not about the Lagrange–D'Alembert principle; instead it uses the Hessian matrix of the constraint equations to compute the first time derivatives of the Jacobian matrices ${\dot{\mathbf{J}}}_{\mathit{\theta }}$ and ${\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}$ in Sect. 3 and the Hessian matrix of the kinetic energy to obtain the Coriolis–centrifugal force matrix C in Eq. (52), respectively. Meanwhile, in Liang et al. (2017), there is also classical mathematical access to compute these matrices. Thus, it is necessary to determine which method is more computationally economic. To make a fair comparison, under the framework of the Lagrange–D'Alembert principle, a third inverse dynamic model of the target PM is also built as the procedure in Sects. 4 and 5.1, except that the first time derivatives of J_θ, ${\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and the Coriolis–centrifugal force matrix C are computed using the method in Liang et al. (2017), as

$$\begin{array}{}\text{(61)}& \begin{array}{rl}& {\dot{\mathbf{J}}}_{\mathit{\theta }}={\displaystyle \frac{\partial {\mathbf{J}}_{\mathit{\theta }}}{\partial {\mathbf{q}}^T}}\cdot \left(\dot{\mathbf{q}}\otimes {\mathbf{I}}_{\mathrm{6}}\right)\\ & {\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}={\displaystyle \frac{\partial {\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}}{\partial {\mathbf{q}}^T}}\cdot \left(\dot{\mathbf{q}}\otimes {\mathbf{I}}_{\mathrm{4}}\right)\\ & \mathbf{C}={\displaystyle \frac{\partial \mathbf{M}}{\partial {\mathbf{q}}^T}}\cdot \left(\dot{\mathbf{q}}\otimes {\mathbf{I}}_{\mathrm{10}}\right)-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\mathbf{I}}_{\mathrm{10}}\otimes \dot{\mathbf{q}}\right)}^T\cdot {\displaystyle \frac{\partial \mathbf{M}}{\partial \mathbf{q}}},\end{array}\end{array}$$

where $\frac{\partial {\mathbf{J}}_{\mathit{\theta }}}{\partial {\mathbf{q}}^T}$, $\frac{\partial {\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}}{\partial {\mathbf{q}}^T}$, and $\frac{\partial \mathbf{M}}{\partial {\mathbf{q}}^T}$ are the partial derivatives of J_θ, ${\mathbf{J}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and M with respect to the row vector q^T, respectively, and $\frac{\partial \mathbf{M}}{\partial \mathbf{q}}$ is the partial derivative of M with respect to the column vector q. That is to say, a third dynamic model is built by following the procedures in Sect. 5.1, but ${\dot{\mathbf{J}}}_{\mathit{\theta }}$, ${\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and C are replaced using the values in Eq. (61).

In the comparative study, on the one hand, the numerical differences of the actuating torques from these two methods under the Lagrange–D'Alembert principle are as minor as those in the second column of Fig. 6. In this regard, these numerical differences are not described for the sake of brevity, and the correctness of the method in Abo-Shanab (2020) to compute ${\dot{\mathbf{J}}}_{\mathit{\theta }}$, ${\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and the Coriolis–centrifugal force matrix C can be verified. On the other hand, the computational time of the model in Sect. 5.1 and the third model using Eq. (61) to compute ${\dot{\mathbf{J}}}_{\mathit{\theta }}$, ${\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and the Coriolis–centrifugal force matrix C is 27.87 and 21.79 s, respectively. The computational resources as mentioned in the first paragraph of this section are still used for this comparison. The result explicitly shows that the method proposed in Abo-Shanab (2020) to calculate ${\dot{\mathbf{J}}}_{\mathit{\theta }}$, ${\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and the Coriolis–centrifugal force matrix C is 21.82 % slower than the classical method in Liang et al. (2017).

7.2 Inertia coupling property

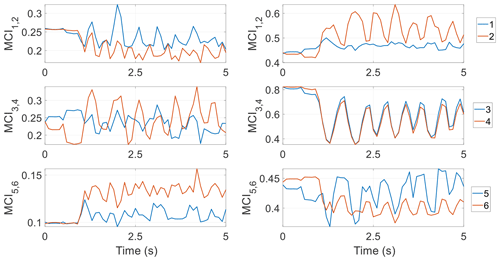
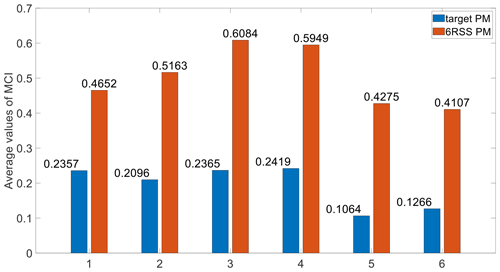
The evolution of the numerical values of the inertia coupling indices MCI_i (i=1, …, 6) in the target PM through the predefined mandibular motions is plotted in the first column of Fig. 7. It clearly shows that they fluctuate roughly with the peaks and valleys of the displacement variables of the end effector as in Fig. 3, meaning that inertia coupling is strongly configuration-dependent. Specifically, during the first second, the mechanism is almost stationary as shown in Fig. 3, and MCI_i varies little at this stage; however, MCI_i is not zero, which indicates that the inertias are coupled near the initial configuration of the mechanism. Specifically, MCI₁ fluctuates around 0.23 and is larger than MCI₂; MCI₃ and MCI₄ fluctuate around 0.23 and 0.25, respectively, and clearly MCI₄ has a larger amplitude, though MCI₆ is larger than MCI₅; both of them are evidently smaller than MCI₁–MCI₄. To better evaluate the inertia coupling among different active joints, their average values are shown as the heights of the blue bars in Fig. 8. From Figs. 7 and 8, one can observe that the first, third, and fourth active joints are more strongly coupled than the other joints, and the coupling effects on the fifth and sixth joints are the weakest. As such, one may predict that the actuating torques from the first, third, and fourth actuators can be reduced if the coupling effects to them are alleviated, whilst the peak values of the torques from the sixth actuator can be further raised if these effects to it are enhanced. This discovery may be of interest to the biomechanical community to find the relationship between the chewing forces and coupling effects in the chewing muscles of the masticatory system of human beings. To reduce the inertia coupling, the optimal design of the end effector, which has an intricate shape and large inertias, and the trajectory planning of the mechanism could be performed in future work.

Figure 7 MCI_i of six active joints in the target PM and the 6RSS PM.

Figure 8 Average values of each MCI_i in the target PM and the 6RSS PM.

It is noted that from Sect. 6, the inertia coupling is only relevant to the inertia matrix of the mechanism itself and is independent of external forces acting at the end effector. Therefore, no matter where the reaction forces in Fig. 5 act at the end effector, it does not influence MCI_i.

7.3 Inverse dynamics and inertia coupling of the 6RSS PM

From the viewpoint of theoretical study, how the direct constraints from the base influence the dynamic model and inertia coupling is still an unknown problem; thus, it is to be resolved in this section.

The procedure in Sects. 4 and 5.1 is also applied to obtain the inverse dynamic model of the 6RSS PM with 6 DOFs as in Chap. 4 of Xu and Bronlund (2010). This mechanism can be recovered by deleting the direct constraints from the base to the end effector of the target mechanism in Fig. 1. The same modeling process is not listed for the sake of brevity. The built inverse dynamic model contains six scalar equations and six unknown actuating torques. The numerical displacements, velocities, and accelerations of its 6 DOFs are completely identical to X_EE, ${\dot{\mathbf{X}}}_{\mathrm{EE}}$, and ${\ddot{\mathbf{X}}}_{\mathrm{EE}}$ in Fig. 3, and the reacted bite force from Fig. 5 is also exerted on the same right molar of its end effector. Its actuating torques experience similar profiles to those in the first column of Fig. 6 but with a larger magnitude, since it is well-known that redundant actuation(s) can reduce the magnitudes of actuating torques in PMs. Thus, for the sake of brevity, they are not described in the paper.

Under the Lagrange–D'Alembert principle, the time consumption by the model in Sect. 5.1 and the third model using the mathematical method in Eq. (61) to compute ${\dot{\mathbf{J}}}_{\mathit{\theta }}$, ${\dot{\mathbf{J}}}_{{\mathbf{q}}_{\mathrm{EE}}}$, and C is 2.64 and 2.44 s, respectively. It can be observed that from this comparison, the method in Eq. (61) is also clearly more efficient, even though the rise is not as remarkable as that in the target PM. Furthermore, one can see that from the comparison between the target PM and the 6RSS PM, as expected, the direct constraints from the base at the two HKPs significantly raise the computational demands. The time cost in the target PM is 9.56 and 7.93 times larger than that of the 6RSS PM using the two methods, respectively. Why it is computationally more intensive in the model of the target PM can be explicitly explained by two reasons: firstly, the two parasitic motion variables Z and γ are the complicated functions of 4 DOFs, as shown in Eq. (5). Secondly, the calculation of Eq. (54) involves the pseudo-inverse of a 4 × 6 matrix due to actuation redundancy, which is more complex than calculating the inverse of a 6 × 6 matrix. However, in the 6RSS PM, neither parasitic motions nor redundant actuations exist, which greatly facilitate the computation.

The inertia coupling property of the 6RSS PM is also investigated by virtue of the index in Eq. (60), to find the role of direct constraints from the base to the end effector in this property. The distributions of the indices over time are given in the second column of Fig. 7, displaying a similar profile as those in the target PM but with larger magnitudes. Specifically, MCI₁ is much smoother than MCI₂; the curves of MCI₃ and MCI₄ are approximately identical, owning a larger amplitude than the other four indices; and MCI₅ is experiencing more drastic changes than MCI₆. Additionally, the average values of MCI_i (i=1, …, 6) are displayed in Fig. 8 as the heights of the red bars. These two figures also clearly show that the third and the fourth active joints are mostly coupled by inertias from the other four joints, and the fifth and sixth joints are least coupled. Moreover, the average values of MCI_i in the target PM are only 50.67 %, 40.60 %, 38.87 %, 40.66 %, 24.89 %, and 30.83 % of those of the 6RSS PM, respectively. This means the inertia coupling is significantly alleviated by the direct constraints from the base, being rather against intuition.

8 Conclusion

In this work, firstly, under the framework of the Lagrange–D'Alembert principle, a method from Abo-Shanab (2020) has been used to build an inverse dynamic model of an uncommon spatial PM. The modeling procedure is well-structured and straightforward, and the correctness has been verified by comparing the numerical results with those from the classical Lagrange equations. However, the method for deriving the first time derivatives of the constraint Jacobian matrices and the Coriolis–centrifugal force matrix in this method is computationally less efficient than the method from Liang et al. (2017) in both the target PM and the 6RSS PM. Secondly, through the inertia coupling analysis, one can find that the first, third, and fourth active joints are more strongly coupled than the other ones, and the fifth and sixth active joints are the least coupled. In addition, from the comparison between the target PM and the 6RSS PM, as expected, the direct constraints from the base considerably increase the computational cost in the dynamic model; on the contrary, interestingly, the inertia couplings are greatly alleviated, behaving differently than expected.