A miniaturized statically balanced compliant mechanism for on-chip ultralow wide-bandwidth vibrational energy harvesting

This research demonstrates a miniaturized statically balanced compliant mechanism (SBCM) at the micro-electromechanical systems (MEMS) scale. The primary objective is to integrate the MEMS-scale SBCM on chip as the fundamental structure of vibrational energy harvesters for powering low-energy-cost sensors and circuits. The static and dynamic characteristics of the micro-scale SBCM are investigated based on a 2D finite element analysis (FEA) model in COMSOL Multiphysics^®. Static balancing is achieved by finely tuning the geometric parameters of the FEA SBCM model. The analytical, numerical, and FEA results confirm that the MEMS-scale SBCM is sensitive to ultralow wide-bandwidth excitation frequencies with weak accelerations. This micro-scale SBCM structure provides a structural solution to effectively lower the working frequencies of MEMS vibrational energy harvesters to ultralow ranges within a wide bandwidth. It overcomes the working frequency limit imposed by the size effect. This would significantly improve the dynamic performance of vibrational energy harvesters at the MEMS scale. In addition, a conceptual structure of the MEMS-scale SBCM is preliminary proposed for the integration of piezoelectric materials by MEMS technologies for vibrational energy harvesting.

1 Introduction

Energy in the form of mechanical vibrations ubiquitously exists in our ambient environment. The concept of harvesting vibrational energy provides an ideal solution for powering numerous sensors in the Internet of Things (IoTs) project (Kamalinejad et al., 2015). The research area of vibrational energy harvesting has attracted increasing attention in the past decades (Liang et al., 2021; Liu et al., 2021). The frequencies of most accessible vibrational sources, such as ocean waves, anthropogenic activities, and bridge vibrations, are normally between 10⁰–10¹ Hz (Li et al., 2014). Thus, the mechanical structures of vibrational energy harvesters are expected to be sensitive to ultralow wide-bandwidth vibrations for more efficient energy-harvesting performance. The design of such mechanical structures responding to ultralow wide-bandwidth vibrations is one of the main tasks for researchers in this area.

One ultimate goal for powering low-energy-cost sensors and electronics is that the vibrational energy harvesters can be integrated on a single chip (Todaro et al., 2017). This requires the vibrational energy harvesters to be miniaturized significantly and fabricated using micro-electromechanical systems (MEMS) technologies. MEMS vibrational energy harvesters have been reported in the literature (Feng et al., 2023; Hossain et al., 2023); however, these micro-oscillators normally have narrow working bandwidths and high natural frequencies due to their linear stiffness and the size effect, i.e. smaller sizes lead to higher resonant frequencies (Deng et al., 2014). These drawbacks lead to poor energy-harvesting performance and make the traditional MEMS-scale vibrational energy harvester less attractive in practical applications.

Statically balanced compliant mechanisms (SBCMs) are special compliant mechanisms (CMs) with zero force and zero stiffness over a certain displacement range (Liang et al., 2022). They can remain in equilibrium in a continuous finite displacement range, while the nonlinear static curve is observed over the wider displacement range. This novel force–displacement relationship results in SBCMs having a unique dynamic characteristic under base excitations. The SBCM responds to ultralow frequencies (theoretically starting from 0 Hz) with a wide bandwidth. In addition, the advantages of SBCMs include highly alleviated friction, low or no assembling complexity, reduced mass, low cost, and good scalability and compatibility with respect to MEMS techniques (Maamer et al., 2019; Paul et al., 2021). These features make the SBCMs scalable. Both the static and dynamic characteristics are independent of the fabrication size of the structure. Therefore, SBCMs provide practical structural solutions for vibrational energy harvesters at the MEMS scale.

Typical SBCMs are designed based on the stiffness compensation principle: the stiffness of a positive-stiffness components is balanced by the stiffness of the negative-stiffness components; thus, zero stiffness is achieved. However, zero stiffness only determines that the integrated CM has content force (not necessary to be zero) in a certain displacement. A further requirement to achieve static balancing is that the force–displacement curves of the positive- and negative-stiffness components should be symmetric about the horizontal axis (Liang et al., 2022). These requirements can be described with the following two equations:

$$\begin{array}{}\text{(1)}& {\displaystyle }{k}_{+}\left(x\right)+k_{-}\left(x\right)=\mathrm{0},\text{(2)}& {\displaystyle }{F}_{+}\left(x\right)+F_{-}\left(x\right)=\mathrm{0}.\end{array}$$

Here, k₊(x) and k₋(x) represent the stiffness equations of the positive- and negative-stiffness compliant components, respectively, and F₊(x) and F₋(x) are force–displacement equations of the positive- and negative-stiffness compliant components, respectively.

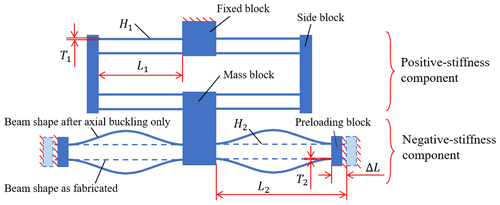
Figure 1 Schematic structure of the SBCM proposed for the piezoelectric vibrational energy harvesting (Liang et al., 2022).

A specific SBCM has been reported in our previous research (Liang et al., 2022), as shown in Fig. 1. This SBCM design consists of a pair of double parallelograms (positive-stiffness component) and a pair of post-buckled fixed guided beams (negative-stiffness component). Based on its good scalability and manufacturability in a single plane, the SBCM structure is miniaturized at the MEMS scale in this research as the main structure of an on-chip vibrational energy harvester. The design of the miniaturized SBCM with well-designed geometric parameters is first introduced in Sect. 2. The dynamic performance of the MEMS-scale SBCM is then investigated based on finite element analysis (FEA) simulations in Sect. 3. A preliminary structural concept of the MEMS-scale SBCM considered from the aspects of MEMS techniques is proposed in Sect. 4. Conclusions are drawn in the final section.

2 Design of the miniaturized SBCM

The miniaturized SBCM structure at the MEMS scale is composed of a pair of double parallelograms and a pair of post-buckled fixed guided beams. As both the adopted positive- and negative-stiffness components remain in equilibrium in the original position, i.e. $F_{+}\left(\mathrm{0}\right)=F_{-}\left(\mathrm{0}\right)=\mathrm{0}$, Eq. (2) is the only requirement to meet. The linearized stiffness equation of the positive-stiffness component (two double parallelograms connected in parallel) with slight nonlinearity neglected (Awtar et al., 2007) is given in Eq. (3). Based on Dijksman (1979), the stiffness equation of the negative-stiffness component (a pair of post-buckled fixed guided beams) can be described with the approximate closed-form equation (Eq. 4).

$$\begin{array}{}\text{(3)}& {\displaystyle }{k}_{+}={\displaystyle \frac{\mathrm{24}E{I}_{\mathrm{1}}}{L_{\mathrm{1}}^{\mathrm{3}}}}\text{(4)}& {\displaystyle }{k}_{-}=-{\displaystyle \frac{\mathrm{16}{\mathit{\pi }}^{\mathrm{2}}E{I}_{\mathrm{2}}}{L_{\mathrm{2}}^{\mathrm{3}}}}\end{array}$$

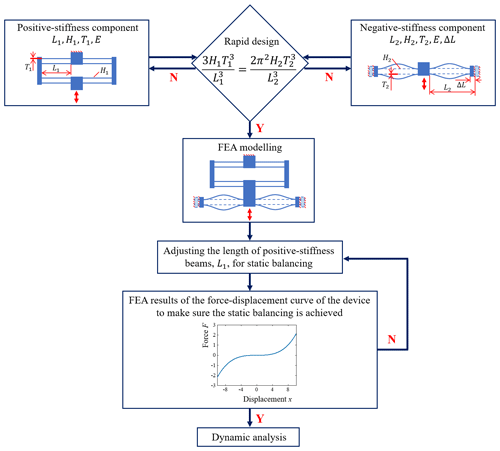
A rapid design equation of the SBCM is then obtained by substituting the stiffness equations of the positive- and negative-stiffness equations (Liang et al., 2022), as given in Eq. (5). This equation helps to narrow down the possible geometric parameters to create the desired SBCM. However, errors exist due to the approximation in Eqs. (3) and (4). Further refinement of the geometric parameters is required with the assistance of the FEA models. A design guideline for the SBCM (Liang et al., 2022) is summarized in the form of a flow chart in Fig. 2.

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{3}{H}_{\mathrm{1}}{T}_{\mathrm{1}}^{\mathrm{3}}}{L_{\mathrm{1}}^{\mathrm{3}}}}={\displaystyle \frac{\mathrm{2}{\mathit{\pi }}^{\mathrm{2}}{H}_{\mathrm{2}}{T}_{\mathrm{2}}^{\mathrm{3}}}{L_{\mathrm{2}}^{\mathrm{3}}}}\end{array}$$

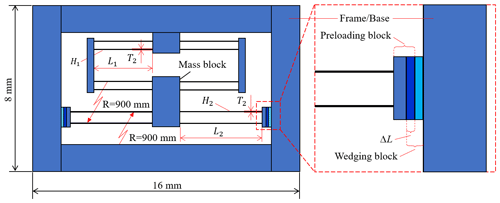
The key geometric parameters of the 2D FEA model of the MEMS-scale SBCM created in COMSOL Multiphysics^® are illustrated in Fig. 3 and are determined following the design guideline. The footprint size of the SBCM is 16 mm × 8 mm, which is 128 mm². The thickness of the model is set as 0.5 mm. Silicon is chosen as the structural material of the MEMS-scale SBCM model. This MEMS-scale SBCM can then be fabricated using a silicon wafer with a standard thickness of 525 µm. Static balancing is finally achieved by finely adjusting the geometric parameters of the compliant beams. These geometric parameters are listed in Table 1. Note that this set of geometric parameters is one example of the many possible geometric solutions to achieve static balancing of the MEMS-scale SBCM device. The geometric parameters can be determined based on the specific application conditions. The following analysis is carried out based on the static balancing achieved corresponding to the geometric parameters listed in Table 1.

Figure 2 Design guideline of the SBCM (modified based on a previous study – Liang et al., 2022).

Figure 3 The 2D FEA model of the miniaturized SBCM at the MEMS scale and key geometric parameters.

Table 1 Geometric parameters of the MEMS-scale SBCM with static balancing achieved.

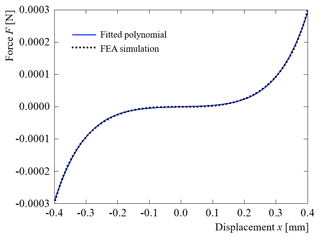
The force–displacement curve of the MEMS-scale SBCM can be obtained based on the static FEA simulation. The targeted displacement range in this simulation is from −0.4 to 0.4 mm. The force–displacement curve in the FEA results is shown in Fig. 4. The fitted fifth-order polynomial of the force–displacement curve is obtained using the polyfit function in MATLAB^® and is given in Eq. (6). The R² coefficient of determination is 99.97 %, indicating a high fitting accuracy. The fitted polynomial curve is also plotted in Fig. 4 for direct comparison. The maximum stress, σ_max, happens at the central and clamped positions of the buckled negative-stiffness beams when the mass block stays at its origin point. The σ_max is calculated as 155 MPa based on the geometric parameters listed in Table 1. It is smaller than the maximum allowable stress of 200 MPa of silicon (Farhadi Machekposhti et al., 2019). The dynamic performance of the SBCM at the MEMS scale under harmonic base excitation is analysed based on the force–displacement character obtained.

$$\begin{array}{}\text{(6)}& F_{\mathrm{SBCM}}\left(x\right)=\mathrm{0.00002656}x+\mathrm{0.001574}{x}^{\mathrm{3}}+\mathrm{0.01771}{x}^{\mathrm{5}}\end{array}$$

Figure 4 Force–displacement curves of the SBCM at the MEMS scale based on the FEA simulations and fitted fifth-order polynomial equation.

3 Dynamic characteristic of the MEMS-scale SBCM

The dynamic displacement response of the proposed MEMS-scale SBCM (as shown in Fig. 3) can be theoretically predicted based on the dynamic model (Eq. A3 in Appendix A) and the force–displacement polynomial (Eq. 6). In addition, the numerical model is obtained using the ode45 Runge–Kutta method in MATLAB^®. The H–f curves of the SBCM under different excitation accelerations, A₀ = 0.1, 0.2, and 0.3 g, are obtained based on the analytical and numerical models and plotted in Fig. 5. A close agreement between the analytical and numerical results is observed in the overall frequency range, as shown in Fig. 5. Both the theoretical and numerical results show that the SBCM at the MEMS scale responds to weak excitations (A₀ = 0.1, 0.2, and 0.3 g) at ultralow frequencies (theoretically any frequencies above 0 Hz) in a wide range. The maximum error percentage between the two theoretical methods is 22.8 %, which happens around 8.3 Hz at 0.2 g. The errors are caused due to the superharmonic oscillation phenomenon (Kronauer and Musa, 1966; Liang et al., 2022); this phenomenon is predicted by the numerical analysis, whereas it cannot be predicted by the dynamic analytical model.

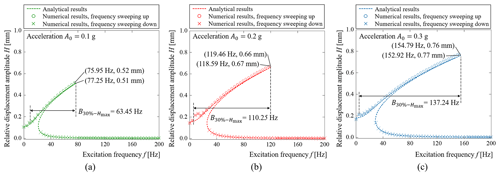
Figure 5 Relative displacement amplitude–excitation frequency curves of the SBCM at the MEMS scale based on analytical and numerical results at different accelerations: (a) A₀ = 0.1 g, (b) A₀ = 0.2 g, and (c) A₀ = 0.3 g.

The 30 %-H_max bandwidth is introduced to evaluate the working frequency range of the SBCM. It refers to the frequency range in which the oscillator has a relative displacement amplitude larger than 30 % of the maximum relative displacement amplitude, H_max. As shown in Fig. 5, both the 30 %-H_max bandwidth and H_max of the micro-scale SBCM increase as the acceleration increases. H_max reaches 0.76 and 0.77 mm at the jumping-down frequency, f_Jumping-down, of 154.79 and 152.92 Hz at 0.3 g according to the analytical and numerical results, respectively. The 30 %-H_max bandwidth is about 137.24 Hz under these conditions, as shown in Fig. 5c. It is noteworthy that the 30 %-H_max bandwidth is about 63.45 Hz when the acceleration is only 0.1g. H_max is 0.51 and 0.52 mm at the respective jumping-down frequencies of 77.25 and 75.95 Hz at 0.1 g, as shown in Fig. 5a.

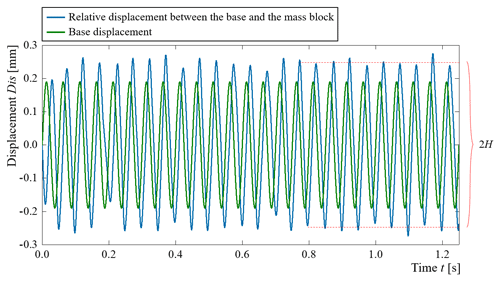
Figure 6 The relative displacement curve between the base and mass block of the SBCM at the MEMS scale corresponding to the excitation condition of 20 Hz and 0.3 g (blue and green curves).

The dynamic displacement response of the MEMS-scale SBCM under harmonic base excitations is further studied using the FEA method. In each FEA simulation, the micro-scale SBCM model is base-excited by harmonic vibrations with discrete frequencies. The frequency range of 0.25–50 Hz and the excitation acceleration of 0.3 g are selected for demonstration. The jumping-up frequency, f_Jumping-up, with a significant change in the relative displacement amplitude lies in this frequency range. The relative displacement between the mass block and the frame is obtained from the FEA results and recorded. One example of the relative displacement curve corresponding to the base excitation condition of 20 Hz and 0.3 g is plotted in Fig. 6.

The relative displacement amplitude, H, is calculated based on the last 10 oscillations which are regarded as steady-state oscillations. The relative displacement amplitude, H, corresponding to the discrete frequencies, f, in the targeted frequency range are obtained and summarized in Table 2 based on the FEA simulations. The H–f relationship based on Table 2 is represented as discrete data points connected by a solid curve, as shown in Fig. 7.

Table 2 Dynamic displacement response of the MEMS-scale SBCM under harmonic base excitations with discrete frequencies from 0.25 to 50 Hz in FEA simulations (acceleration of 0.3 g).

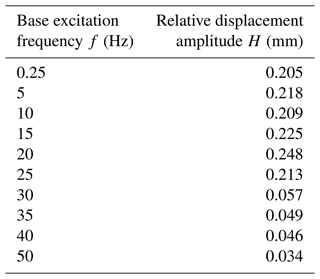
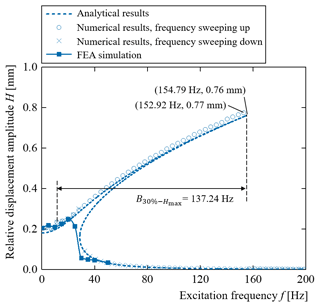
Figure 7 Relative displacement amplitude–excitation frequency curves of the SBCM at the MEMS scale based on the FEA, analytical, and numerical results.

A close agreement between the FEA, analytical, and numerical results is observed in the frequency range from 0.25 to 25 Hz in Fig. 7. In the frequency range higher than 25 Hz, the relative displacement amplitude, H, from the FEA simulations did not reach larger values. This is because no vibrational energy is imported into the oscillation system with the initial condition. Therefore, vibrations with larger amplitudes cannot be stimulated. The close agreement among the FEA, analytical and numerical results, as depicted in Fig. 7, further validates that the SBCM at the MEMS scale is sensitive to a wide range of ultralow frequencies with weak accelerations.

Damping has been considered in the FEA simulations via the COMSOL settings of “Rayleigh damping”. The damping ratio is set as 0.02 based on our previous experimental research using a macro-SBCM prototype (Liang, 2022). In real applications, air damping can be one of the critical factors impacting the vibration amplitude of the micro-scale energy harvester and, consequently, its energy-generation performance. This issue can be tackled by housing the device in a micro-scale vacuum chamber fabricated using MEMS techniques (Pu et al., 2022; Choa, 2005). It has been experimentally verified using a macro-SBCM prototype that the central mass only vibrates in the vertical direction with a single degree of freedom under base excitation (Liang, 2022). This is because other degrees of freedom have been restricted by the specially designed positive-stiffness component. Higher-order resonance modes with rotational or twisting motions of the SBCM structure may happen at high excitation frequencies. These motions will also contribute the energy harvesting when the compliant beams are either compressed or stretched, which generates stress inside the piezoelectric materials attached to the beams. In this research, vertical vibration of the mass block at ultralow wide-bandwidth frequencies is focused.

4 A preliminary structural concept of the MEMS-scale SBCM

The MEMS-scale SBCM structure (as shown in Fig. 1) is particularly fabrication-friendly with respect to MEMS technologies due to its in-plane and monolithic structure. In the application of the MEMS-scale SBCM in vibrational energy harvesting based on piezoelectric effect, the piezoelectric materials, e.g. AlN (Jackson et al., 2013) and ZnO (Tao et al., 2019), and electrode materials, e.g. titanium and aluminium (Jackson et al., 2014, 2017), should be attached to the beams' surfaces perpendicular to the bending direction for the best energy-generation performance. However, these surfaces of the SBCM structure (as shown in Fig. 3) are vertical in the MEMS fabrication process. It is challenging to deposit the piezoelectric and electrode materials in the designated order and with the desired crystal orientation on the lateral walls. Targeting this problem, an SBCM structure concept based on the stiffness compensation principle is preliminarily proposed and schematically illustrated in Fig. 8. This SBCM structure would be suitable for the deposition of piezoelectric and electrode materials on the beam surfaces in MEMS fabrication process for better energy generation performance.

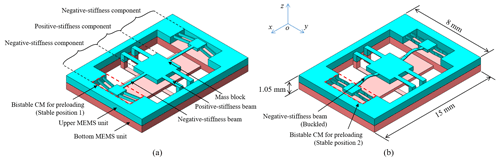
Figure 8 The preliminary structural concept of the micro-scale SBCM for fabrication with MEMS technologies: (a) the MEMS-scale SBCM structure before preloading; (b) the MEMS-scale SBCM structure after preloading.

In addition, the approach of preloading on the negative-stiffness beams should be carefully considered in the MEMS-scale SBCM structures. Several preloading methods used in MEMS devices have been reported in the literature (Barel et al., 2018; Kuppens et al., 2019; De Laat et al., 2016). These techniques include thermal actuation, electrostatic actuation, and piezoelectric actuation. However, they require extra energy input, have a relatively large footprint, and increase the fabrication complexity (De Laat et al., 2016). Negative stiffness can also be obtained through the exploitation of residual stress from thermal oxidation of silicon (Kuppens et al., 2019), while an ultrahigh processing temperature limits the general applicability of this method. Bistable CMs have also been widely adopted for stiffness adjustment of MEMS devices (Alqasimi et al., 2014; Li et al., 2022; De Laat et al., 2016). Their applicability in preloading the negative-stiffness beams has been experimentally verified in the literature (Kuppens et al., 2021). Bistable CMs present benefits in three different ways. Firstly, bistable CMs have good adaptability to MEMS techniques (Wilcox and Howell, 2005; Wang et al., 2021). Secondly, the switch between preloading and unloading on the negative-stiffness beams can be easily achieved by the reversible snapping-through behaviour of bistable CMs. This consequently leads to the switch between the static-balancing mode and mono-stable mode of the MEMS-scale SBCM structure. When the external excitations are severe, the negative-stiffness beam can be unloaded in advance by manual operations. Alternatively, unloading of the negative-stiffness beams can be achieved automatically via the violent base excitations due to its high vibrational energy. The overall oscillator then has a higher stiffness and higher resonant frequency. This provides an overload protection and helps to avoid breaking the slim beams and the failure of the oscillating device.

Lastly, a one-off external energy input is only required at the preloading procedure, i.e. a one-off manual push of the bistable mechanism, instead of the whole working process. This makes bistable CMs outperform other prestressing methods (e.g. thermal actuation) and avoids continuous energy input for preloading. Based on these advantages, preloading on negative-stiffness beams using bistable CMs is adopted in the schematic MEMS-scale SBCM structure, as presented in Fig. 8.

It is noteworthy that, in some application scenarios, such as energy-harvesting devices implanted into human bodies, this autonomous reverse snapping-through behaviour (snapping-through in the direction opposite to the direction of preloading) may be not desired. More stable and durable static balancing can be maintained in two ways. The first solution features creating a higher energy barrier between the two energy wells. Robust bistable CMs with higher energy barriers are available via well-designed geometric parameters (Hao, 2018; Chen and Ma, 2015). In the second method, permanent preloading on the negative-stiffness beam can be achieved by wedging and fixing a preloading block between the central shuttle of bistable CMs and the outer frame. The fixed preloading block stops the bistable CM snapping through backwards and keeps it in the desired position.

The conceptual SBCM structure for MEMS fabrication is composed of positive- and negative-stiffness components, which are connected by the central sharing movable mass block. The positive-stiffness component consists two double parallelogram mechanisms in parallel. The positive-stiffness beams are located in two planes of two MEMS units instead of the identical plane. The structure of the positive-stiffness component allows vibration in the vertical direction only and restricts other undesired motions. The negative-stiffness component consists of two fixed-guided post-buckled beams in parallel. Preloading on the negative-stiffness beams is achieved by the snapping-through behaviour of the bistable CMs from stable position 1 (as shown in Fig. 8a) to stable position 2 (as shown in Fig. 8b). Static balancing is then obtained with well-designed geometric parameters of the positive- and negative-stiffness components. Depositing piezoelectric and electrode materials on the beam surfaces with the most stress generation is then feasible with MEMS technologies for vibrational energy harvesting based on the piezoelectric effect. However, one drawback of this conceptual structure is that some basic MEMS assembling operations are required in the fabrication process.

It should be noted that the preliminary structural concept of the MEMS-scale SBCM proposed in this section is demonstrated for the integration of piezoelectric materials for vibrational energy harvesting. Its structural details are still not fully considered or optimized for MEMS fabrication. It is one of many possible MEMS structures of SBCM-based piezoelectric vibrational energy harvesting. The structure can vary when the SBCM concept is utilized in vibrational energy harvesting combined with other energy conversion mechanisms, such as electromagnetic, electrostatic, and triboelectric mechanisms.

5 Conclusions

A miniaturized SBCM structure at the MEMS scale is demonstrated in this research. It is aimed at the future integration of the MEMS-scale SBCM on chip as the main structure of vibrational energy harvesters for powering low-energy-cost sensors and circuits. Both the static and dynamic characteristics of the micro-scale SBCM are investigated based on a 2D FEA model in COMSOL Multiphysics^®. Static balancing is achieved by finely tuning the geometric parameters of the FEA SBCM model. The analytical, numerical, and FEA results verify that the MEMS-scale SBCM is sensitive to ultralow wide-bandwidth excitation frequencies with a weak acceleration. This micro-scale SBCM structure provides a structural solution for effectively lowering the working frequencies of MEMS oscillators to the ultralow-frequency range. It breaks the working frequency limit imposed by the size effect. This would significantly improve the dynamic performance of the vibrational energy harvesters at the MEMS scale. In addition, a conceptual structure of the MEMS-scale SBCM is proposed for the integration of piezoelectric materials by MEMS technologies for vibrational energy harvesting.

Appendix A

The motion equation for the proposed SBCM structure under harmonic base excitation can be described with the equation below:

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}-m\ddot{z}& =m\ddot{x}+c\dot{x}+F_{\mathrm{SBCM}}\left(x\right)\\ & =m\ddot{x}+c\dot{x}+\mathit{\alpha }x+\mathit{\beta }{x}^{\mathrm{3}}+\mathit{\gamma }{x}^{\mathrm{5}},\end{array}\end{array}$$

where m is the mass of the central mass block; c represents the damping ratio of the oscillating system; x is the steady-state relative displacement between the mass block and the base; α, β, and γ represent the respective coefficients of the odd-order terms of the force–displacement equation; and $\ddot{z}$ is the harmonic base excitation acceleration, which is assumed to be $\ddot{z}=A_{\mathrm{0}}\cos \left(\mathrm{\Omega }t\right)$. The motion equation Eq. (A1) is further normalized to facilitate analysis as follows:

$$\begin{array}{}\text{(A2)}& -A_{\mathrm{0}}\cos \left(\mathrm{\Omega }\mathit{\tau }\right)=\ddot{X}+\mathrm{2}\mathit{\zeta }\dot{X}+k_{\mathrm{1}}X+k_{\mathrm{2}}{X}^{\mathrm{3}}+k_{\mathrm{3}}{X}^{\mathrm{5}}.\end{array}$$

In Eq. (A2), the introduced normalized constant and variables are as follows:

$$\begin{array}{rl}& {\mathrm{\Omega }}_n=\sqrt{{\displaystyle \frac{k_{+}}{m}}},A_{\mathrm{0}}={\displaystyle \frac{a_{\mathrm{0}}}{{\mathrm{\Omega }}_n^{\mathrm{2}}{L}_{\mathrm{1}}}},\mathrm{\Omega }={\displaystyle \frac{\mathit{\omega }}{{\mathrm{\Omega }}_n}},X={\displaystyle \frac{x}{L_{\mathrm{1}}}},\\ & \mathit{\zeta }={\displaystyle \frac{c}{\mathrm{2}\sqrt{m{k}_{+}}}},\mathit{\tau }={\mathrm{\Omega }}_{n}t,k_{\mathrm{1}}={\displaystyle \frac{\mathit{\alpha }}{k_{+}}},k_{\mathrm{2}}={\displaystyle \frac{\mathit{\beta }{L}_{\mathrm{1}}^{\mathrm{2}}}{k_{+}}},\\ & k_{\mathrm{3}}={\displaystyle \frac{\mathit{\gamma }{L}_{\mathrm{1}}^{\mathrm{4}}}{k_{+}}}.\end{array}$$

Here, Ω_n represents the resonant frequency of the equivalent linear oscillator; A₀ is the normalized excitation acceleration amplitude; Ω is the normalized excitation frequency; X is the normalized relative displacement; ζ is the damping ratio; τ is the normalized time; k₁, k₂, and k₃ represent the respective normalized stiffness coefficients of the odd-order terms; k₊ is the stiffness of the positive-stiffness compliant component; and L₁ is the effective beam length of the positive-stiffness compliant components. Using the averaging method (Liang et al., 2022; Liu and Yu 2020), the steady-state relative displacement amplitude, H, with respect to the excitation frequency, Ω, can be described with the equation below:

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}{H}^{\mathrm{2}}& [k_{\mathrm{1}}^{\mathrm{2}}+\mathrm{4}\left({\mathit{\zeta }}^{\mathrm{2}}-\mathrm{2}{k}_{\mathrm{1}}\right){\mathrm{\Omega }}^{\mathrm{2}}+{\mathrm{\Omega }}^{\mathrm{4}}+{\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}{k}_{\mathrm{2}}\left(k_{\mathrm{1}}-{\mathrm{\Omega }}^{\mathrm{2}}\right)H^{\mathrm{2}}\\ & +\left({\displaystyle \frac{\mathrm{5}}{\mathrm{4}}}{k}_{\mathrm{1}}{k}_{\mathrm{3}}+{\displaystyle \frac{\mathrm{9}}{\mathrm{16}}}{k}_{\mathrm{2}}^{\mathrm{2}}-{\displaystyle \frac{\mathrm{5}}{\mathrm{4}}}{k}_{\mathrm{3}}{\mathrm{\Omega }}^{\mathrm{2}}\right)H^{\mathrm{4}}+{\displaystyle \frac{\mathrm{15}}{\mathrm{16}}}{k}_{\mathrm{2}}{k}_{\mathrm{3}}{H}^{\mathrm{6}}\\ & +{\displaystyle \frac{\mathrm{25}}{\mathrm{64}}}{k}_{\mathrm{3}}^{\mathrm{2}}{H}^{\mathrm{8}}]=A_{\mathrm{0}}^{\mathrm{2}}.\end{array}\end{array}$$

The detailed derivation process has been presented in Liang et al. (2022).