Modular configuration design of a special machine tool for variable hyperbolic circular-arc-tooth-trace cylindrical gears

In this paper, the machining principle of variable hyperbolic circular-arc-tooth-trace (VH-CATT) cylindrical gears is analysed, and a modular configuration design of this special machine tool is carried out. Based on the importance of parameter and knowledge dependence of rough set theory, the degree of influence of the index hidden in the data on the decision-making results is mined, and an algorithm for calculating the objective weight of the index is given. The comprehensive weight of the index is then obtained, combining the analytic hierarchy process. After obtaining the results of the index's comprehensive weight and module attribute classification, a module retrieval strategy is formulated using the fuzzy similarity priority ratio algorithm. Based on the modular division of this special gear-making machine tool, the modular configuration sequence of the machine tool using the depth-first search algorithm is determined. According to the module retrieval strategy and configuration sequence, a traversal of module instances is carried out, and a variety of modular configuration schemes of the machine tool is obtained, which provides a practical and efficient method for the rapid design of a special machine tool for VH-CATT cylindrical gears.

1 Introduction

A variable hyperbolic circular-arc-tooth-trace (VH-CATT) cylindrical gear is a new type of transmission form. Its tooth profile consists of a spatial arc in the tooth's width direction, the middle section of the tooth profile is involute and the other sections comprise envelopes of the hyperbolic family that uniformly change. The new gear transmission has the advantages of good meshing performance, large coincidence coefficient, large bearing capacity, high transmission efficiency, no additional axial force, long service life, high stability and low noise.

Because of the particularities of its gear tooth geometry, its specific processing equipment needs to be improved. The manufacture of VH-CATT cylindrical gears is inefficient, time-consuming and expensive, so their large-scale applications in the industrial field are limited. Therefore, it is urgent to research and develop the special machine tool for VH-CATT cylindrical gears. Product modularization and modular configuration are the relevant key technologies and enabling means to realize rapid product customization (Liu, 2008; Luo, 2011). Product configuration is based on modularization and standardization, and personalized products meeting customer needs are realized through different selections and reasonable matchings of modules (Luo, 2011). Therefore, the research on the key technologies of the modular configuration design of a special machine tool for VH-CATT cylindrical gears has important theoretical value for enhancing the market competitiveness of new gears, shortening the product design and development cycle, reducing the product production costs and improving the production capacity of enterprises.

Scholars have conducted extensive research on all aspects of product configuration. Fujita (2002) studied a method of configuring products with modules, where the number of instance libraries was determined jointly by the characteristic parameters of the modules and number of combinations, so the configuration problem was transformed into a problem consisting of the characteristic parameters and number of combinations. Lou et al. (2006) proposed that product configuration design could be considered a product design process to meet customers' personalized needs through reasonable matchings and combinations based on a predefined product configuration model of each component set and mutual constrained relationship. Xu et al. (2011) proposed a modular configuration design method for a numerical control machine tool with multi-domain interoperability and developed a modular configuration design prototype system. Mourtzis et al. (2015) used simulated annealing and tabu search algorithms to model and solve product configuration problems. Badurdeen et al. (2018) proposed a product configuration design optimization method based on multiple life cycles. Yuan (2020) built a personalized product configuration network based on data mining technology, constructing a multi-objective product configuration optimization model aimed at customer satisfaction and product sustainability. He et al. (2021) proposed a product family design and product configuration method based on system data mining, and divided the module instances into optional modules, general modules and special modules, then a product platform was established based on the general modules. In general, the process of configuration design is essentially a process of concreting and instancing the modules in the configuration model, which is a process of knowledge reasoning (Wang, 2016). The module retrieval algorithm and the determination of the module configuration sequence are the key technical problems in the process of configuration design.

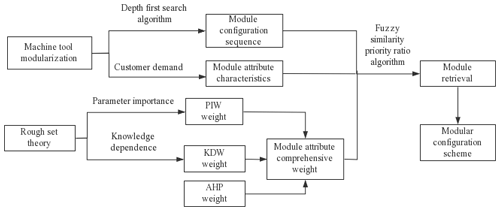
This paper takes a special machine tool for VH-CATT cylindrical gears as the research object. On the premise of machine tool modularization, the module configuration sequence for the machine tool is determined based on the depth-first search algorithm. The modules are retrieved based on rough set theory and the fuzzy similarity priority ratio algorithm, instanced and traversed according to the configuration sequence and then a machine tool module configuration scheme is obtained. The flow chart of the modular configuration scheme is shown in Fig. 1.

Figure 1 Flow chart of the modular configuration scheme for a special machine tool for VH-CATT cylindrical gears.

2 Determining of the index weight based on rough set theory

As a data analysis and processing theory, rough set theory was founded by Polish scientist Pawlak Zdzistaw in 1982 (Pawlak, 1982); it is a mathematical tool that deals with fuzzy and uncertain systems. All the information it needs is provided by the given data without additional information or parameters (Das et al., 2021). From the perspective of rough set theory, this paper proposes an algorithm to calculate the objective weight of each indicator according to parameter importance and knowledge dependence, which is then combined with an analytic hierarchy process (AHP) to obtain a more ideal comprehensive weight, which can greatly improve the accuracy of the weight calculation (Sun, 2013; Wu, 2007) and improve the universality of this method.

2.1 Objective weight calculation of the index based on parameter importance

The main idea of calculating the objective weight of index based on a parameter of importance weight (PIW) is as follows. According to the upper and lower approximations of rough set theory, the importance of each system parameter is calculated, so that the degree of influence of index parameters hidden in data on decision-making and judgement results can be analysed (Zhu, 2018). Then the index weight can be calculated according to the importance of each parameter (Tan, 2012).

Assuming that the knowledge base is $K=(U,R)$, R∈IND(K) represents one or more system parameters of system characteristics (Hadrani et al., 2020). The subset X in discourse domain U is X(X∈U), the partition of discourse domain U with respect to system parameter R is $\mathit{\pi }\left(U\right)=\mathit{\{}{X}_{\mathrm{1}},X_{\mathrm{2}},\mathrm{\dots },X_n\mathit{\}}$, the lower approximation of subset X with respect to knowledge R is $\underset{\mathrm{¯}}{R}\left(X\right)$, the upper approximation is $\stackrel{\mathrm{‾}}{R}\left(X\right)$, the boundary domain is bn_R(X), the upper approximation contains all elements that may belong to X and the lower approximation contains all elements that can be accurately classified to X using knowledge R. The upper and lower approximations and boundary fields of X with respect to knowledge R are as follows:

$$\begin{array}{ll}{\displaystyle }\stackrel{\mathrm{‾}}{R}\left(X\right)& {\displaystyle }=\left\{x\mathrm{|}(\forall x\subseteq U)\wedge ({\left[x\right]}_R\cap X\ne \mathrm{\varnothing })\right\}\\ \text{(1)}& {\displaystyle }& {\displaystyle }=\cup \left\{Y\mathrm{|}(Y\in U/R)\wedge (Y\cap X\ne \mathrm{\varnothing }\right\}{\displaystyle }\underset{\mathrm{¯}}{R}\left(X\right)& {\displaystyle }=\left\{x\mathrm{|}(\forall x\subseteq U)\wedge ({\left[x\right]}_R\subseteq X)\right\}\\ \text{(2)}& {\displaystyle }& {\displaystyle }=\cup \left\{Y\mathrm{|}(Y\in U/R)\wedge (Y\subseteq X\right\}\text{(3)}& {\displaystyle }{\text{bn}}_R\left(X\right)& {\displaystyle }=\stackrel{\mathrm{‾}}{R}\left(X\right)-\underset{\mathrm{¯}}{R}\left(X\right).\end{array}$$

For any set X∈U, the amount of information provided by X relative to the system parameter R is called the importance of X. Then the calculation equations of the importance sig_R(X) of set X with respect to the system parameter R and the importance sig_R(π(U)) of partition with respect to the parameter R are as follows:

$$\begin{array}{l}{\displaystyle }{\text{sig}}_R\left(X\right)={\displaystyle \frac{\left|U-{\text{bn}}_R\left(X\right)\right|}{U}}\\ \text{(4)}& {\displaystyle }{\text{sig}}_R\left[\mathit{\pi }\right(U\left)\right]={\displaystyle \frac{\left|U-{\text{bn}}_R\left(X\right)\right|}{n\left|U\right|}}.\end{array}$$

In the above equations, $\mathrm{0}\le {\text{sig}}_R\left(X\right)\le \mathrm{1}$, if sig_R(X)=1, and set X can fully represent the system parameter R; if sig_R(X)=0, set X cannot represent the system parameter R. With an increase of importance of X relative to R, the degree of using set X to represent system parameter R will also increase. |⋅| represents the cardinal number of the set, that is, the number of elements in the set.

Next we calculate the weighted value of each index according to the parameter importance following Eq. (5):

$$\begin{array}{}\text{(5)}& {\mathit{\omega }}_{\mathrm{1}i}={\displaystyle \frac{{\text{sig}}_{a_i}\left(X\right)}{{\sum }_{i=\mathrm{1}}^n{\text{sig}}_{a_i}\left(X\right)}},(i=\mathrm{1},\mathrm{2},\mathrm{\cdots },n).\end{array}$$

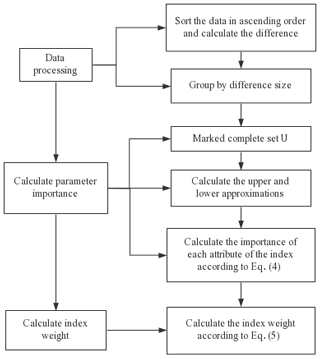
The algorithm flow chart of calculating the objective weight according to parameter importance is shown in Fig. 2.

Figure 2 Flow chart of the objective weight calculation algorithm according to parameter importance.

2.2 Objective weight calculation of the index based on knowledge dependence

The main idea of calculating index weights based on knowledge dependence weight (KDW) is to research the knowledge dependence theory according to rough set theory (Bai et al., 2021; Naouali et al., 2020). First, calculate the knowledge dependence of each index, and then calculate the weight of index parameters. Assuming that knowledge base $K=(U,R)$, ∀P, and Q∈IND(K), the equation of the knowledge dependence γ_P(Q) of knowledge Q that depends on P is as follows:

$$\begin{array}{}\text{(6)}& {\mathit{\gamma }}_P\left(Q\right)=k={\displaystyle \frac{\left|{\text{pos}}_P\left(Q\right)\right|}{\left|U\right|}}={\displaystyle \frac{\left|{\bigcup }_{X\in \frac{U}{Q}}\underset{\mathrm{¯}}{P}\left(X\right)\right|}{\left|U\right|}},\end{array}$$

which is abbreviated as P⇒kQ, where

$${\text{pos}}_P\left(Q\right)={\bigcup }_{X\in \frac{U}{Q}}\underset{\mathrm{¯}}{P}\left(X\right)$$

is the P positive field of knowledge Q, which is the set of all information classified by $U/P$ that can be accurately divided into Q equivalence classes.

In the above equation, $\mathrm{0}\le {\mathit{\gamma }}_P\left(Q\right)\le \mathrm{1}$. If γ_P(Q)=1, it means that P contains all the information of Q, and the dependence of Q on P is complete. If γ_P(Q)=0, P does not contain any Q information at all, and Q and P are completely independent; if, however $\mathrm{0}<{\mathit{\gamma }}_P\left(Q\right)<\mathrm{1}$, P contains only part of the information of Q, and it can also be said that Q depends on P to the degree of k.

Next we calculate the weighted value of each index according to the knowledge dependence following Eq. (7):

$$\begin{array}{}\text{(7)}& {\mathit{\omega }}_{\mathrm{2}i}={\displaystyle \frac{{\mathit{\gamma }}_i\left(Q\right)}{{\sum }_{i=\mathrm{1}}^n\left({\mathit{\gamma }}_i\right(Q\left)\right)}},(i=\mathrm{1},\mathrm{2},\mathrm{\cdots },n).\end{array}$$

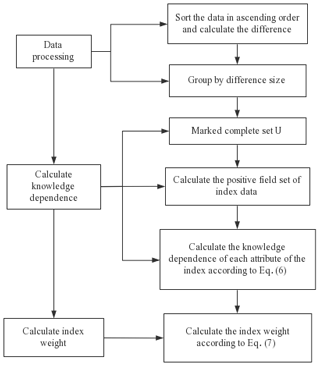
The algorithm flow chart of calculating the objective weight according to knowledge dependence is shown in Fig. 3.

Figure 3 Flow chart of the objective weight calculation algorithm according to knowledge dependence.

2.3 Calculation of the comprehensive weight of the index

The comprehensive weight is obtained by combining the objective weight determined by rough set theory with the index weight determined by AHP (Foteinopoulos et al., 2019), which is combined with the prior knowledge of the evaluator, thus realizing the unification of subjective and objective. The AHP method combines quantitative methods with qualitative methods, which decomposes the original complex problems, systematizes people's thinking process and is more convenient for people to accept and apply.

We record ω_i as the comprehensive weight of the i index, given as

$$\begin{array}{}\text{(8)}& {\mathit{\omega }}_i=\mathit{\alpha }{\mathit{\omega }}_{\mathrm{1}i}+\mathit{\beta }{\mathit{\omega }}_{\mathrm{2}i}+(\mathrm{1}-\mathit{\alpha }-\mathit{\beta }){\mathit{\omega }}_{\mathrm{3}i},i=\mathrm{1},\mathrm{2},\mathrm{\cdots },n,\end{array}$$

where ω_3i is the index weight determined by the AHP (Rajput et al., 2021), and $\mathrm{1}-\mathit{\alpha }-\mathit{\beta }$ is an empirical factor $(\mathrm{0}\le \mathit{\alpha }+\mathit{\beta }\le \mathrm{1})$, where the smaller $\mathrm{1}-\mathit{\alpha }-\mathit{\beta }$ is, the more attention it pays to the objective weight.

3 Module retrieval based on the fuzzy similarity priority ratio method

In the process of product configuration design, module retrieval and matching are key points (Song, 2014), where expression of the module attributes is the primary premise of module retrieval. Attributes are used to describe the parameters in the module that can be expressed in words or values (such as structural form or size or specification) (Zhang, 2012). According to the weighted value of each attribute of the machine tool module, various attribute factors are comprehensively considered, to achieve the purpose of retrieving the nearest module instance.

During module retrieval, we set the target module as M_t. The module library of such module has n modules, which are set as $M=\mathit{\{}{M}_{\mathrm{1}},M_{\mathrm{2},}\mathrm{\cdots },M_n\mathit{\}}$. Then we calculate the fuzzy priority similarity ratio between the module attribute of the target module and the corresponding attribute of the optional module in the module library.

The fuzzy similarity priority ratio is a method for comparing the samples with a fixed sample to determine which one is more similar to the fixed sample, so as to select the one with the greatest similarity to the fixed sample (Wei et al., 2017). Each module of the machine tool has multiple unique attributes.

There is a certain attribute set $X=\mathit{\{}{x}_{\mathrm{1}},x_{\mathrm{2}},\mathrm{\cdots },x_n\mathit{\}}$ of module to be compared, and compare any $x_i,x_j\in X$ with the fixed sample x_k, i, $j=\mathrm{1},\mathrm{2},\mathrm{\cdots },n;$ $i,j\ne k$. Here r_ij is assumed to indicate the degree of superiority of x_i compared to x_j or x_j compared to x_i when x_i and x_j are compared with fixed samples x_k. If $r_{ij}\in [\mathrm{0.5},\mathrm{1}]$, x_i is prior to x_j; if $r_{ij}\in [\mathrm{0},\mathrm{0.5}]$, x_j is prior to x_i. The priority ratio meets the following conditions:

$$\begin{array}{}\text{(9)}& {\displaystyle }\left\{\begin{array}{l}{r}_{ii}=\mathrm{1}\\ r_{ij}\in [\mathrm{0},\mathrm{1}]\\ r_{ij}+r_{ji}=\mathrm{1}\end{array}\right.i\ne j.\end{array}$$

The above conditions show that when making comparisons, there is no priority, and x_i and x_j are equivalent, which is denoted as r_ii=1. When comparing, each has its own advantages and combines the priorities of the two; that is $r_{ij}+r_{ji}=\mathrm{1}$. When x_i has obvious advantages over x_j, but x_j has no advantages over x_i, r_ij=1 and r_ji=0; when x_i and x_j are compared regardless of their advantages and disadvantages, $r_{ij}=r_{ji}=\mathrm{0.5}$.

Matrix $R=(r_{ij}{)}_{n\times n}$ is a fuzzy similarity priority ratio matrix, where r_ij is defined as the Hamming distance (Taheri et al., 2020):

$$\begin{array}{}\text{(10)}& r_{ij}={\displaystyle \frac{d_{kj}}{d_{ki}+d_{kj}}},\end{array}$$

where $d_{ki}=|x_k-x_i|$ and $d_{kj}=|x_k-x_j|$.

After the matrix is established, we take the lowest definite bound of the elements in the non-diagonal of each row and then get the highest priority object according to the row where the maximum value in the lowest definite bound is located. Then, we remove the column and row of this object to form a new matrix. This operation is repeated for the new matrix to obtain the good and bad sequence of samples in X. Finally, we number each sequence with a natural number.

If there are m attributes that need to be compared, each attribute needs to be processed separately. The method of determining the index weight based on rough set theory and AHP in the previous section is applied to give a weight to the importance of each attribute, and the weighted average method is used for fuzzy comprehensive evaluation. The equations are as follows:

$$\begin{array}{}\text{(11)}& S=\sum _{i=\mathrm{1}}^m{p}_i{S}_i\sum _{i=\mathrm{1}}^m{p}_i=\mathrm{1},\end{array}$$

where S represents the total similar sequence number, where the smaller the S value of the comparison sample, the more similar it is to the fixed sample, which is the target module.

4 Design of the machine tool module configuration sequence based on the depth-first search algorithm

The depth-first search algorithm is similar to the pre-order traversal of the tree (Fu et al., 2019; Cao et al., 2020), which searches the depth direction as much as possible (Nimmanterdwong, 2018). The basic idea is to visit the starting point V firstly and mark it as visited, then start from V and search each adjacent point W of V in turn. If W has not been accessed, start from W and continue to traverse the other nodes in the way of a depth-first search until all vertices connected to the source node V in the graph are accessed. At this time, if there are any points that have not been accessed, we need to select another one as the new source node and repeat the above access process until all the nodes in the figure are accessed.

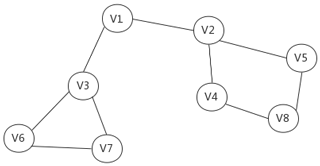
For example, Fig. 4 shows an undirected graph. The process of traversing the graph using the depth-first search algorithm is as follows:

Figure 4 Undirected graph.

1. First, find a vertex randomly that has not been traversed. For example, starting from V1, since V1 has been visited first, it is necessary to mark the state of V1 as visited.

2. Then traverse the adjacency point of V1. For example, access V2 and mark it, and then access the adjacency point of V2, for example, V4 (mark), then V8 and then V5.

3. When continuing to traverse the adjacency points of V5, all adjacency points have been accessed according to the previous marks. At this time, go back from V5 to V8 to see if there are any unreachable adjacency points of V8. If not, continue to go back to V4, V2 and V1.

4. By looking at V1, find a vertex V3 that has not been accessed, continue to traverse and then access V3's adjacency points, V6, then V7.

5. Since there are no unreachable adjacency points of V7, go back to V6, then continue to go back to V3 and finally reach V1. Continue until there are no unreachable adjacency points.

6. The last step is to determine whether all vertices are accessed. If there are still unreachable vertices, take the unreachable vertex as the first vertex and continue to traverse according to the above steps.

According to the above steps, the traversal sequence of the vertices obtained by the depth-first search algorithm in Fig. 4 is as follows:

$$\text{V1}\to \text{V2}\to \text{V4}\to \text{V8}\to \text{V5}\to \text{V3}\to \text{V6}\to \text{V7}.$$

When configuring the machine tool, there is a sequence for every module. The depth-first search algorithm is used to traverse and solve, so as to determine the modular configuration sequence of the machine tool.

5 Modular configuration design of the special machine tool for VH-CATT cylindrical gears

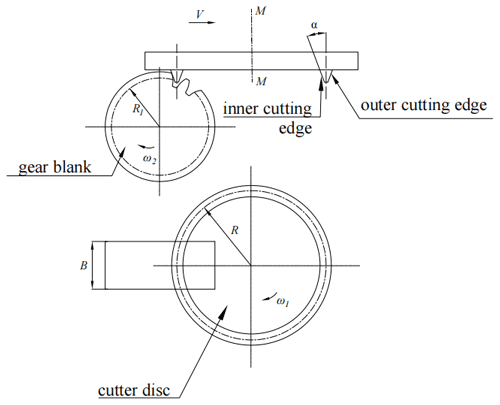
A VH-CATT cylindrical gear is machined by double edges cutters with rotating cutter disc (Zhao, 2016), and its processing principle is shown in Fig. 5. When using a double edges cutter, the rotary cutter disc for processing VH-CATT cylindrical gears is installed on the machine tool's main shaft and rotates at an angular speed of ω₁ around its own axis M–M. The cutters are fixed on the cutter disc and rotate synchronously with it. The angles between the inner or outer edge of the cutter and cutter axis or axis of the rotary cutter disc are both α (i.e. pressure angle). The cutter edge rotates with the cutter disc to form two conical surfaces, where the outer cutting edge is a positive cone (machining a concave surface), and the inner cutting edge is an inverted cone (machining a convex surface). During cutting, the gear blank rotates around its own axis as it moves back and forth along the horizontal direction, forming a close generative movement with the cutters. During the machining process, the cutters cut out the concave convex tooth surface of the gear tooth at the same time. After machining a pair of tooth surfaces, it is necessary to pitch then start machining the next pair of tooth surfaces until the machining of the whole gear is completed.

During the machining process, the cutter disc rotates around the main shaft, and the gear blank rotates around its own axis at an angular speed of ω₂. At the same time, the gear blank moves horizontally close to the cutter disc at a speed of V. The relationship between the two is

$$\begin{array}{}\text{(12)}& V={\mathit{\omega }}_{\mathrm{2}}\times R_{\mathrm{1}},\end{array}$$

where R₁ is the gear pitching circle radius, R is the cutter disc's radius and B is the width of the gear blank.

Figure 5 Processing principle of VH-CATT cylindrical gears.

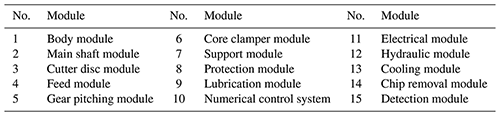
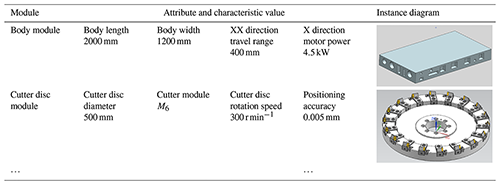
To realize the rapid customization of the special machine tool for VH-CATT cylindrical gears, the machine tool is divided into modules, where each type of module has different types and models from which to choose, as shown in Table 1.

Table 1 Modules of the special machine tool for VH-CATT cylindrical gears.

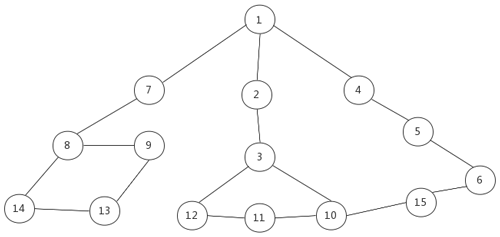
Considering the machining principle of VH-CATT cylindrical gears and the assembly relationship between the modules, the final undirected graph is shown in Fig. 6.

Figure 6 Modular configuration sequence of the special machine tool for VH-CATT cylindrical gears.

The configuration sequence solved by the depth-first search algorithm is

$$\begin{array}{ll}{\displaystyle }\mathrm{1}& {\displaystyle }\to \mathrm{4}\to \mathrm{5}\to \mathrm{6}\to \mathrm{15}\to \mathrm{10}\to \mathrm{11}\to \mathrm{12}\to \mathrm{3}\to \mathrm{2}\to \mathrm{7}\\ {\displaystyle }& {\displaystyle }\to \mathrm{8}\to \mathrm{9}\to \mathrm{13}\to \mathrm{14}.\end{array}$$

According to the configuration sequence, we select the no. 1 body module as the first module for retrieval and retrieve the fully matched module or similar module of this module. The module attributes of the module and other related modules are taken as the attributes of related modules. After the module is retrieved, the associated attributes can be taken as its qualitative attributes. Then, instance search traversal is carried out according to the configuration sequence until all module attributes are instanced. After the final instance, the scheme meeting the requirements can be obtained.

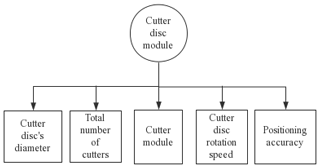
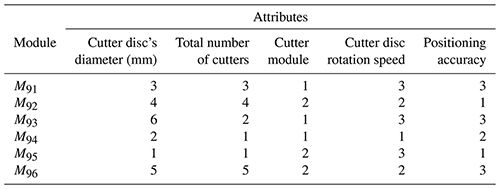
Let us take the no. 3 cutter disc module, i.e. the 9th retrieval module, as an example to illustrate the module retrieval process. The corresponding attributes of the cutter disc module are shown in Fig. 7.

Figure 7 Cutter disc module attributes.

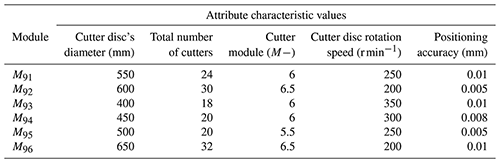
The attribute characteristic values of the cutter disc's target module are obtained through the customer demand analysis, as shown in Table 2.

Table 2 Attribute characteristic values of target module.

The attribute characteristic values of the cutter disc module are obtained from the cutter disc module library of the machine tool, as shown in Table 3, where M_9i represents the ith module in the 9th type module, and M_9t is the target module of the 9th type module.

Table 3 Attribute characteristic values of the cutter disc module.

Next we calculate the parameter importance of each attribute according to Eq. (4), as shown in Table 4.

Table 4 Parameter importance of the cutter disc module attributes.

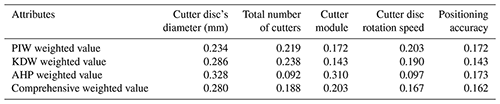
Then we calculate the weighted value of each attribute according to Eq. (5), as shown in Table 5.

Table 5 PIW weighted values of the cutter disc module attributes.

Based on Eqs. (6) and (7), we calculate the dependence and weight of each attribute of the cutter disc module according to the knowledge dependence. Finally, we combine the AHP with Eq. (8) and assign greater weight to the objective taking $\mathit{\alpha }=\mathit{\beta }=\mathrm{0.35}$ to obtain the comprehensive weight of each attribute, as shown in Table 6.

Table 6 Comprehensive weighted values of the cutter disc module attributes.

Figure 8 Comparison of the attribute weighted values calculated by the four methods.

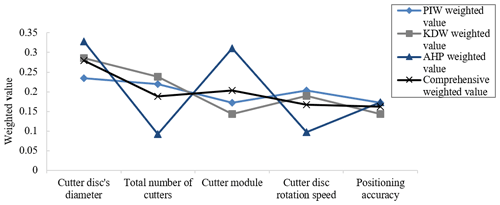
We used a line chart to compare the weighted values calculated by the above four methods, the results of which are shown in Fig. 8. According to the parameter importance and knowledge dependence, the objective weight of the index is obtained, which is combined with the AHP algorithm to obtain its comprehensive weight. This approach improves upon the deficiencies of each single assignment method to a certain extent, improves the rationality of the weight calculation and makes the final decision more accurate.

On the basis of Eqs. (9) and (10), the fuzzy similarity priority ratio matrices R₁, R₂, R₃, R₄ and R₅, respectively describing the cutter disc's diameter, total number of cutters, cutter module, cutter disc rotation speed and positioning accuracy, are calculated according to the fuzzy similarity priority ratio algorithm, as follows:

$$R_{\mathrm{1}}=\left[\begin{array}{cccccc}\mathrm{1.000}& \mathrm{0.667}& \mathrm{0.667}& \mathrm{0.500}& \mathrm{0.000}& \mathrm{0.750}\\ \mathrm{0.333}& \mathrm{1.000}& \mathrm{0.500}& \mathrm{0.333}& \mathrm{0.000}& \mathrm{0.600}\\ \mathrm{0.333}& \mathrm{0.500}& \mathrm{1.000}& \mathrm{0.333}& \mathrm{0.000}& \mathrm{0.600}\\ \mathrm{0.500}& \mathrm{0.667}& \mathrm{0.667}& \mathrm{1.000}& \mathrm{0.000}& \mathrm{0.750}\\ \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}\\ \mathrm{0.250}& \mathrm{0.400}& \mathrm{0.400}& \mathrm{0.250}& \mathrm{0.000}& \mathrm{1.000}\end{array}\right]$$

$$R_{\mathrm{2}}=\left[\begin{array}{cccccc}\mathrm{1.000}& \mathrm{0.714}& \mathrm{0.333}& \mathrm{0.000}& \mathrm{0.000}& \mathrm{0.750}\\ \mathrm{0.286}& \mathrm{1.000}& \mathrm{0.167}& \mathrm{0.000}& \mathrm{0.000}& \mathrm{0.545}\\ \mathrm{0.667}& \mathrm{0.833}& \mathrm{1.000}& \mathrm{0.000}& \mathrm{0.000}& \mathrm{0.857}\\ \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{0.500}& \mathrm{1.000}\\ \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{0.500}& \mathrm{1.000}& \mathrm{1.000}\\ \mathrm{0.250}& \mathrm{0.455}& \mathrm{0.143}& \mathrm{0.000}& \mathrm{0.000}& \mathrm{1.000}\end{array}\right]$$

$$R_{\mathrm{3}}=\left[\begin{array}{cccccc}\mathrm{1.000}& \mathrm{1.000}& \mathrm{0.500}& \mathrm{0.500}& \mathrm{1.000}& \mathrm{1.000}\\ \mathrm{0.000}& \mathrm{1.000}& \mathrm{0.000}& \mathrm{0.000}& \mathrm{0.500}& \mathrm{0.500}\\ \mathrm{0.500}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{0.500}& \mathrm{1.000}& \mathrm{1.000}\\ \mathrm{0.500}& \mathrm{1.000}& \mathrm{0.500}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}\\ \mathrm{0.000}& \mathrm{0.500}& \mathrm{0.000}& \mathrm{0.000}& \mathrm{1.000}& \mathrm{0.500}\\ \mathrm{0.000}& \mathrm{0.500}& \mathrm{0.000}& \mathrm{0.000}& \mathrm{0.500}& \mathrm{1.000}\end{array}\right]$$

$$R_{\mathrm{4}}=\left[\begin{array}{cccccc}\mathrm{1.000}& \mathrm{0.667}& \mathrm{0.500}& \mathrm{0.000}& \mathrm{0.500}& \mathrm{0.667}\\ \mathrm{0.333}& \mathrm{1.000}& \mathrm{0.333}& \mathrm{0.000}& \mathrm{0.333}& \mathrm{0.000}\\ \mathrm{0.500}& \mathrm{0.667}& \mathrm{1.000}& \mathrm{0.000}& \mathrm{0.500}& \mathrm{0.667}\\ \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{0.000}& \mathrm{1.000}\\ \mathrm{0.500}& \mathrm{0.667}& \mathrm{0.500}& \mathrm{0.000}& \mathrm{1.000}& \mathrm{0.667}\\ \mathrm{0.333}& \mathrm{1.000}& \mathrm{0.333}& \mathrm{0.000}& \mathrm{0.333}& \mathrm{1.000}\end{array}\right]$$

$$R_{\mathrm{5}}=\left[\begin{array}{cccccc}\mathrm{1.000}& \mathrm{0.000}& \mathrm{0.500}& \mathrm{0.375}& \mathrm{0.000}& \mathrm{0.500}\\ \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{0.500}& \mathrm{1.000}\\ \mathrm{0.500}& \mathrm{0.000}& \mathrm{1.000}& \mathrm{0.375}& \mathrm{0.000}& \mathrm{0.500}\\ \mathrm{0.625}& \mathrm{0.000}& \mathrm{0.625}& \mathrm{1.000}& \mathrm{0.000}& \mathrm{0.625}\\ \mathrm{1.000}& \mathrm{0.500}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}& \mathrm{1.000}\\ \mathrm{0.500}& \mathrm{0.000}& \mathrm{0.500}& \mathrm{0.375}& \mathrm{0.000}& \mathrm{1.000}\end{array}\right].$$

According to the method described above, the order of the M₉₅ module corresponding to the attribute “cutter disc's diameter” should be 1. By then deleting its row and column, we can calculate the next order. We then sort the attributes of the module with natural numbers and finally get the priority of the attributes of the cutter disc module, as shown in Table 7.

Table 7 Priority of the cutter disc module attributes.

According to the comprehensive weighted values of the attributes of the cutter disc module obtained in Table 6, the data obtained in Table 7 are weighted and summed according to Eq. (11) to obtain the corresponding similarity of each module, where the smaller the value, the higher the similarity. As shown in Table 8, it can be seen that the ideal module is the one closest to the target module.

Table 8 Similarity of each cutter disc module.

It can be seen that the module M₉₄ and the module M₉₅ are similar to the target module. We search and match each module of the machine tool in turn, and the search results are shown in Table 9.

Table 9 Search results of the machine tool module.

The module combination obtained after the final retrieval and matching is taken as the product scheme, and six configuration schemes of the special machine tool for VH-CATT cylindrical gears are obtained through the module combination $\mathrm{1}\times \mathrm{1}\times \mathrm{2}\times \mathrm{1}\times \mathrm{1}\times \mathrm{1}\times \mathrm{1}\times \mathrm{1}\times \mathrm{2}\times \mathrm{2}\times \mathrm{1}\times \mathrm{1}\times \mathrm{1}\times \mathrm{1}\times \mathrm{1}=\mathrm{6}$. After module selection and variant design, the final machine tool configuration scheme is obtained, as shown in Table 10.

Table 10 Configuration result of the main modules of the special machine tool for VH-CATT cylindrical gears.

6 Conclusions

In this paper, research on module retrieval and configuration of a special machine tool for VH-CATT cylindrical gears is carried out. This approach provides a foundation for the rapid design of machine tool. It is also suitable for other complex electromechanical products. The conclusions of this study are summarized as follows:

1. According to the parameter importance and knowledge dependence of rough set theory, this paper proposes an algorithm to calculate the objective weight of the index, and its comprehensive weight is obtained by combining the AHP method. Our approach complements the traditional subjective weight calculation method, which can not only greatly improve the accuracy and rationality of the calculated weighted value, but also improve the universality of the method.

2. Based on the processing principle of the special machine tool for VH-CATT cylindrical gears, the divided machine tool modules are searched and solved based on the depth-first search algorithm to determine their configuration sequences.

3. Applying the fuzzy priority similarity ratio algorithm, each module of the machine tool is retrieved and matched according to the configuration sequence, and various attribute factors are comprehensively considered according to the weight value of each attribute of the machine tool module. This allowed us to achieve the purpose of retrieving the most similar module examples and finally obtain a variety of machine tool module configuration schemes.