Optimization and active control of internal gearing power honing process parameters for better gear precision

Optimization and active control of internal gearing power honing (IGPH) process parameters for excellent and stable gear precision were carried out using the engagement theory of a conjugate curved face, the Box–Behnken design of experiments method, and the artificial immune clone selection algorithm (AICSA). Optimization and active control were carried out in four stages. In the first stage, the second-order models of tooth profile deviations were developed considering the nonlinear influence of IGPH process parameters on tooth profile deviations based on the Box–Behnken design. In the second stage, a method for solving the multi-objective optimization of the IGPH process was presented based on building the synthetic tooth profile deviation model, which considered the different weighting factors of different tooth profile deviation indexes. In the third stage, excellent gear precision was obtained by importing the ranges of synthetic tooth profile deviation and parameters into the AICSA. In the fourth stage, based on the optimized process parameters, the active control of IGPH process parameters was realized based on the constant cutting speed on the fixed position of the gear tooth surface. The total gear profile error reached a minimum value at the optimal parameters of 1270.4 rpm for spindle speed, 60 mm min⁻¹ for axis feed velocity, 2.4 µm per oscillation for radial feed velocity, and 2.4 spark-out times. The gear accuracy test results show that the total gear profile error value from the above active control method is more stable and lower than that without active control, indicating that the proposed method is effective.

1 Introduction

Internal gearing power honing (IGPH) is a gear finishing process via abrasion that can improve gear tooth surface quality; it is thus widely used in the field of advanced automobile gearbox systems. The special mechanism of the IGPH process can form a kind of curved orientation texture and high compressive residual stress on workpiece gear tooth surfaces (Karpuschewski et al., 2008). Moreover, these good tooth surface characteristics can reduce the meshing noise and prolong the service life of gear transmission systems. Compared with the worm wheel gear grinding process, the IGPH process is irreplaceable in stepped gear finishing, and its lower cutting velocity can avoid high thermal load and burns on the tooth surface. However, the gear precision of the IGPH process ranges in the GB4–GB6 level, while the worm wheel gear grinding process can reach the GB4–GB5 level, which is the limitation of the IGPH process. Process parameters have a significant effect on gear precision, and, thus, in this paper, several experiments on the optimization of IGPH process parameters for better and more stable gear precision were carried out.

Recently, many studies have focused on the improvement of gear finishing with abrasive processes. For instance, Teixeira et al. (2019) reported the influence of the grains' characteristics and process parameters on the material removal behavior and gear grinding energy model based on modeling of the normal force. Through the use of high-order topology expression and analysis of the numerical loaded tooth contact area, Ding and Tang (2020) proposed a target grinding flank modeling method to improve the tooth flank geometric topography and loaded contact performance. Furthermore, Giacomo et al. (2019) analyzed the relationship between the thermal damage and gear grinding process parameters on a new dry-grinding machine and found that the gear module and radial feed rate were the most significant factors affecting the thermal damage. Yoshikoto et al. (2018) developed a high-precision, high-efficiency internal gear grinding method by setting a large crossed-axis angle between the grinding wheel spindle and workpiece gear axis and conducted a series of actual grinding experiments to verify the new proposed grinding model.

With the wide application of the IGPH process, several studies were carried out to explore the mechanism and improve the gear tooth surface quality of the IGPH process. By adding three axes' additional motions, i.e., the honing wheel spindle axis, swivel axis, and workpiece spindle axis in the internal gearing power honing machine, Vanquyet and Yuren (2020) built a numerical model of the closed-loop topology modification for the double-crowned and anti-twist gear tooth surfaces and verified the validity of the proposed method. A series of preliminary research works were carried out by our team based on traditional roughness theory and the internal engagement theory of conjugate curved surfaces. For example, Han et al. (2017) performed a contrastive analysis of tooth surface quality between the IGPH process and gear grinding process. So far, the main point of the IGPH process is ensuring the microscopic qualities of the tooth surface. In the present work, therefore, to improve the macroscopic quality of the tooth surface for IGPH gears, three main gear tooth profile errors and four input IGPH process parameters were chosen as the factors and indexes of the optimization experiment. The Box–Behnken design of experiments (DOE) method and artificial immune clone selection algorithm (AICSA) were the main optimization methods used to find the predicted model of gear tooth profile deviations and achieve the best gear precision for the IGPH process. Finally, an active control method was proposed to deal with the unstable gear precision caused by the variable IGPH crossed-axis angle parameter.

2 Basic gear profile error model

Design of experiments (DOE) is an important branch of mathematical statistics which has been widely used to find the influence rule between factors (x₀, x₁, x₂, ..., x_n) and responses (y₀, y₁, y₂, ..., y_n) in scientific research and industry. Response surface methodology is one of the DOE methods, which was proposed by Box and Wilson in 1951 (Korra et al., 2014). Generally, the purpose of response surface methodology is to find the optimal process through building the approximation surface model. If factors have a linear effect on responses, the approximation surface model between responses and factors can be expressed by the first-order Taylor series expansion:

$$\begin{array}{}\text{(1)}& y\left(x\right)={\mathit{\beta }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{1}}{x}_{\mathrm{1}}+{\mathit{\beta }}_{\mathrm{2}}{x}_{\mathrm{2}}+\mathrm{\dots }+{\mathit{\beta }}_k{x}_k+\mathit{\epsilon }.\end{array}$$

If there are some nonlinear factors in the system, the first-order Taylor series expansion cannot express the system model accurately, and mostly the system model will be comprised of second-order Taylor series expansion:

$$\begin{array}{}\text{(2)}& y\left(x\right)={\mathit{\beta }}_{\mathrm{0}}+\sum _{i=\mathrm{1}}^k{\mathit{\beta }}_i{x}_i+\sum _{i=\mathrm{1}}^k{\mathit{\beta }}_{ii}{x}_i^{\mathrm{2}}+\sum _{i<j}^k\sum {\mathit{\beta }}_{ij}{x}_i{x}_j+\mathit{\epsilon },\end{array}$$

where y(x) is the response target function; k is the number of factors; β_i, β_ii, and β_ij are the influence coefficient of each factor; x_i and x_j are the values of each factor; and ε is the additive constant.

Figure 1 Diagrams of gear profile errors.

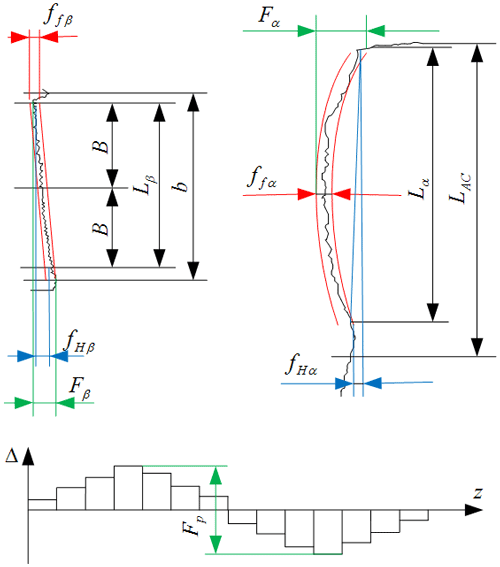
This study aims at achieving minimum gear profile errors. According to the standards of gear accuracy, a high-precision gear will have a good tooth profile accuracy, lead accuracy, and rotation accuracy. In the actual production, the total profile deviation (F_α), the total helix deviation (F_β), and the total cumulative pitch deviation (F_P) embody these three kinds of gear accuracies, as shown in Fig. 1. In this figure, L_β is the measurement range along tooth longitudinal direction, b is the tooth width, B is the central position of the range, L_α is the measurement range of tooth profile, and L_AC is the measuring range of tooth profile. The input parameters of honing process include the spindle speed S_W (rpm), the axis feed velocity f_z (mm min⁻¹), the radial feed velocity f_x (µm per oscillation), and the spark-out times t_s. Thus, there are four factors and three responses in this study, and the basic model of the total profile deviation (F_α), the total helix deviation (F_β), and the total cumulative pitch deviation (F_P) were built as in Eq. (3):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}y\left(x\right)& ={\mathit{\beta }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{1}}{x}_{\mathrm{1}}+{\mathit{\beta }}_{\mathrm{2}}{x}_{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{3}}{x}_{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{4}}{x}_{\mathrm{4}}+{\mathit{\beta }}_{\mathrm{11}}{x}_{\mathrm{1}}^{\mathrm{2}}\\ & +{\mathit{\beta }}_{\mathrm{22}}{x}_{\mathrm{2}}^{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{33}}{x}_{\mathrm{3}}^{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{44}}{x}_{\mathrm{4}}^{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{12}}{x}_{\mathrm{1}}{x}_{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{13}}{x}_{\mathrm{1}}{x}_{\mathrm{3}}\\ & +{\mathit{\beta }}_{\mathrm{14}}{x}_{\mathrm{1}}{x}_{\mathrm{4}}+{\mathit{\beta }}_{\mathrm{23}}{x}_{\mathrm{2}}{x}_{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{24}}{x}_{\mathrm{2}}{x}_{\mathrm{4}}+{\mathit{\beta }}_{\mathrm{34}}{x}_{\mathrm{3}}{x}_{\mathrm{4}}+\mathit{\epsilon }\end{array}.\end{array}$$

The left hand of y(x) is a polynomial which is the approximate value of reality, and the coefficients of the model were estimated by the least-squares method in matrix form. The estimated coefficients of the model depend on the minimum error, and it can be expressed by Eq. (4):

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& Q\left({\mathit{\beta }}_{\mathrm{0}},{\mathit{\beta }}_{\mathrm{1}},\mathrm{\cdots },{\mathit{\beta }}_{\mathrm{13}},{\mathit{\beta }}_{\mathrm{23}}\right)=\sum _{i=\mathrm{0}}^n\\ & {\left(y_i-{\mathit{\beta }}_{\mathrm{0}}-{\mathit{\beta }}_{\mathrm{1}}{x}_{\mathrm{1}}-{\mathit{\beta }}_{\mathrm{2}}{x}_{\mathrm{2}}-\mathrm{\cdots }-{\mathit{\beta }}_{\mathrm{13}}{x}_{\mathrm{1}}{x}_{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{23}}{x}_{\mathrm{2}}{x}_{\mathrm{3}}\right)}^{\mathrm{2}}\to min\end{array}.\end{array}$$

The extreme value of $Q({\mathit{\beta }}_{\mathrm{0}},{\mathit{\beta }}_{\mathrm{1}},\mathrm{\cdots },{\mathit{\beta }}_{\mathrm{13}},{\mathit{\beta }}_{\mathrm{23}}$) can be expressed by Eq. (5):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\displaystyle \frac{\partial Q}{\partial {\mathit{\beta }}_{ij}}}=-\mathrm{2}\sum _{i=\mathrm{0}}^n(y_i& -{\mathit{\beta }}_{\mathrm{0}}-{\mathit{\beta }}_{\mathrm{1}}{x}_{\mathrm{1}}-{\mathit{\beta }}_{\mathrm{2}}{x}_{\mathrm{2}}-\mathrm{\cdots }\\ & -{\mathit{\beta }}_{\mathrm{13}}{x}_{\mathrm{1}}{x}_{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{23}}{x}_{\mathrm{2}}{x}_{\mathrm{3}})x_i{x}_j=\mathrm{0}\end{array}.\end{array}$$

Equation (5) can be expressed in matrix form by Eq. (6):

$$\begin{array}{}\text{(6)}& X^{\mathbf{T}}X\mathit{\beta }=X^{\mathbf{T}}y,\end{array}$$

and the value of β can be calculated by Eq. (7):

$$\begin{array}{}\text{(7)}& \mathit{\beta }=(X^{\mathbf{T}}X{)}^{-\mathrm{1}}{X}^{\mathbf{T}}y.\end{array}$$

After solving the coefficient of the model, it is necessary to verify the accuracy of the model. The multiple correlation coefficient (R) can be calculated by Eq. (8–10):

$$\begin{array}{}\text{(8)}& {\displaystyle }R=\sqrt{{\mathrm{SS}}_R/{\mathrm{SS}}_Y}=\sqrt{({\mathrm{SS}}_Y-{\mathrm{SS}}_E)/{\mathrm{SS}}_Y}\text{(9)}& {\displaystyle }{\mathrm{SS}}_Y=\sum _{i=\mathrm{1}}^m(y_i-\overline{y}{)}^{\mathrm{2}}\text{(10)}& {\displaystyle }{\mathrm{SS}}_E=\sum _{i=\mathrm{1}}^m(y_i-{\stackrel{\mathrm{̃}}{y}}_i{)}^{\mathrm{2}},\end{array}$$

where SS_Y is the total sum of squares for error, SS_E is the total sum of squares for regression, SS_R is the regression sum of the square, $\overline{y}$ is the mean of response, ${\stackrel{\mathrm{̃}}{y}}_i$ is the value of the response, and R represents the accuracy of the model; the larger the value, the more accurate.

To screen out the significant factors, the associated F value or p value to the factors can solve this problem:

$$\begin{array}{}\text{(11)}& F={\displaystyle \frac{R^{\mathrm{2}}/m}{(\mathrm{1}-R^{\mathrm{2}})/(n-m-\mathrm{1})}}.\end{array}$$

Such a calculated F value will be compared with the critical value F^′. If F>F^′, it means that the associated factor is significant, or this factor is insignificant. The other way is to look at the p value of the result, which is calculated by design expert software; if the p value is smaller than 0.05, it indicates the model has 95 % confidence level, which means that the model is statistically significant.

3 Experimental work

3.1 Pilot experiments

The IGPH experiments were conducted on the HMX-400 IGPH machine. Gear profile errors were measured on the gear measuring center (Klingelnberg P40), as shown in Fig. 1. Table 1 shows the processing parameter range of the IGPH machine and the measuring range of the gear measuring center. Table 2 shows the parameters of the work piece gear and the honing wheel.

Figure 2 HMX-400 IGPH machine and Klingelnberg P40 gear measuring center.

Table 1 The main technological parameters of the experiment equipment.

Table 2 Basic parameters of workpiece gear and honing wheel.

3.2 IGPH experiments based on the Box–Behnken DOE method

British biostatistician Ronald Aylmer Fisher first proposed and established the concept of the DOE (design of experiments) method in the 1920s (Fisher, 1954). The DOE and ANOVA (analysis of variance) methods have been successfully used in agricultural and biological tests since then. A good DOE can exclude most of the interference from non-experimental factors and improve the accuracy of the predicted model and experiment efficiency. Normally, DOE is composed of input factors, unavoidable random factors, and subject and output indexes. In this paper, the input factors are the four input IGPH process parameters; the random factors are the abrasive wear, the cooling and lubrication conditions of machine tools, and so on; the subject is the IGPH process; and the output indexes are the three main gear profile deviations.

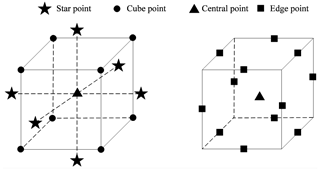
Common response surface methodology (RSM) includes the Box–Behnken design, the central composite design (CCD), the central composite inscribed design (CCI), and the central composite face-centered design (CCF) method. The Box–Behnken design method is a statistical method which is usually used to model the relationship between the factors and responses for s nonlinear system. Compared with the other three methods, the Box–Behnken design method possesses the advantage of a fewer number of tests, and it can avoid exceeding the allowable process parameters. Figure 3 shows the comparison of experiment points between the CCD and Box–Behnken DOE method. It is shown that the star points would exceed the setting process parameter range, and the Box–Behnken DOE method can avoid this problem. Thus, the Box–Behnken DOE method is the most suitable method for this study considering the cost and safety of the experiment.

Figure 3 Comparison of experiment points between the CCD and Box–Behnken DOE method.

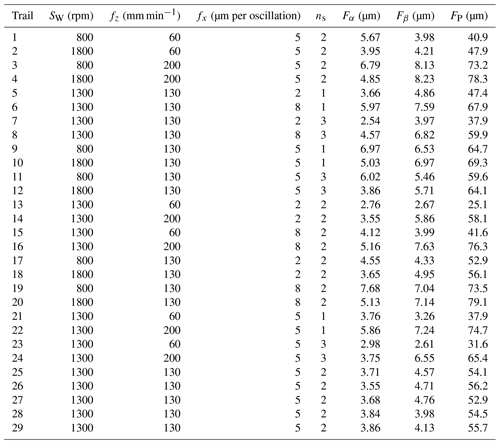
In this study, the main IGPH process parameters were the spindle speed S_W (rpm), the axis feed velocity f_z (mm min⁻¹), the radial feed velocity f_x (µm per oscillation), and the spark-out times n_s. The main gear profile deviations were the total profile deviation (F_α), the total helix deviation(F_β), and the total cumulative pitch deviation (F_p). Based on the principle of the Box–Behnken DOE method and the input IGPH process parameters, the experiment levels were carried out as shown in Table 3. The common spindle speed ranged from 800 to 1800 (rpm), the axis feed velocity ranged from 60 to 200 (mm min⁻¹), the radial feed velocity ranged from 2 to 8 (µm per oscillation), and the spark-out times ranged from 1 to 3.

Table 3 Box–Behnken level of the IGPH experiment.

According to the different combinations of IGPH process parameter levels in Table 3, 29 IGPH processing and gear measuring experiments in total were carried out using the experimental equipment. Figure 4 shows the 29 workpiece gears from 29 IGPH experiments, and Table 4 shows the measured gear profile errors for each IGPH experiment.

Figure 4 Workpiece gears of IGPH experiments.

Table 4 IGPH experiments and measurement results based on the Box–Behnken DOE method.

4 Mathematical model

After conducting 29 IGPH experiments (Fig. 3), analysis of variance (ANOVA) was carried out to verify the confidence of the gear profile error models based on the response surface methodology (RSM). Equations (12)–(14) show the gear profile error models, and the adjusted R-squared value of the model summary statistics was below 0.9762, 0.9587, and 0.9902; the closer to 1 the adjusted R-squared value was, the more accurate the statistical model.

$$\begin{array}{}\text{(12)}& {\displaystyle }\begin{array}{rl}{F}_{\mathit{\alpha }}& =(\mathrm{4.181}-\mathrm{3.678}\times {\mathrm{10}}^{-\mathrm{3}}\times S_{\mathrm{W}}+\mathrm{2.287}\times {\mathrm{10}}^{-\mathrm{3}}\\ & \times f_Z-\mathrm{0.102}\times f_X-\mathrm{0.192}\times n_{\mathrm{S}}-\mathrm{6.983}\times {\mathrm{10}}^{-\mathrm{8}}\\ & \times S_{\mathrm{W}}\times f_Z-\mathrm{4.729}\times {\mathrm{10}}^{-\mathrm{5}}\times S_{\mathrm{W}}\times f_X+\mathrm{4.578}\times {\mathrm{10}}^{-\mathrm{5}}\\ & \times S_{\mathrm{W}}\times n_{\mathrm{S}}+\mathrm{2.258}\times {\mathrm{10}}^{-\mathrm{5}}\times f_Z\times f_X-\mathrm{7.492}\times {\mathrm{10}}^{-\mathrm{5}}\\ & \times f_Z\times n_{\mathrm{S}}+\mathrm{1.148}\times {\mathrm{10}}^{-\mathrm{3}}\times f_X\times n_{\mathrm{S}}+\mathrm{1.390}\times {\mathrm{10}}^{-\mathrm{6}}\\ & \times S_{\mathrm{W}}^{\mathrm{2}}-\mathrm{2.020}\times {\mathrm{10}}^{-\mathrm{6}}\times f_Z^{\mathrm{2}}+\mathrm{3.281}\times {\mathrm{10}}^{-\mathrm{3}}\\ & \times f_X^{\mathrm{2}}+\mathrm{0.036}\times n_{\mathrm{S}}^{\mathrm{2}}{)}^{\mathrm{2}}\end{array}\text{(13)}& {\displaystyle }\begin{array}{rl}{F}_{\mathit{\beta }}& =\mathrm{11.419}-\mathrm{0.012}\times S_{\mathrm{W}}+\mathrm{0.017}\times f_Z-\mathrm{0.140}\\ & \times f_X-\mathrm{2.655}\times n_{\mathrm{S}}-\mathrm{9.286}\times {\mathrm{10}}^{-\mathrm{7}}\times S_{\mathrm{W}}\times f_Z\\ & -\mathrm{8.667}\times {\mathrm{10}}^{-\mathrm{5}}\times S_{\mathrm{W}}\times f_X+\mathrm{9.500}\times {\mathrm{10}}^{-\mathrm{5}}\\ & \times S_{\mathrm{W}}\times n_{\mathrm{S}}+\mathrm{5.357}\times {\mathrm{10}}^{-\mathrm{4}}\times f_Z\times f_X-\mathrm{1.429}\times {\mathrm{10}}^{-\mathrm{4}}\\ & \times f_Z\times n_{\mathrm{S}}+\mathrm{0.01}\times f_X\times n_{\mathrm{S}}+\mathrm{4.858}\times {\mathrm{10}}^{-\mathrm{6}}\times S_{\mathrm{W}}^{\mathrm{2}}\\ & -\mathrm{3.563}\times {\mathrm{10}}^{-\mathrm{5}}\times f_Z^{\mathrm{2}}+\mathrm{0.054}\times f_X^{\mathrm{2}}+\mathrm{0.576}\times n_{\mathrm{S}}^{\mathrm{2}}\end{array}\text{(14)}& {\displaystyle }\begin{array}{rl}{F}_{\mathrm{p}}& =\mathrm{61.297}-\mathrm{0.099}\times S_{\mathrm{W}}+\mathrm{0.460}\times f_Z+\mathrm{2.885}\\ & \times f_X-\mathrm{3.057}\times n_{\mathrm{S}}-\mathrm{1.357}\times {\mathrm{10}}^{-\mathrm{5}}\times S_{\mathrm{W}}\times f_Z\\ & -\mathrm{4.000}\times {\mathrm{10}}^{-\mathrm{4}}\times S_{\mathrm{W}}\times f_X-\mathrm{5.000}\times {\mathrm{10}}^{-\mathrm{5}}\times S_{\mathrm{W}}\\ & \times n_{\mathrm{S}}+\mathrm{2.024}\times {\mathrm{10}}^{-\mathrm{3}}\times f_Z\times f_X-\mathrm{0.011}\times f_Z\times n_{\mathrm{S}}\\ & +\mathrm{0.125}\times f_X\times n_{\mathrm{S}}+\mathrm{3.987}\times {\mathrm{10}}^{-\mathrm{5}}\times S_{\mathrm{W}}^{\mathrm{2}}-\mathrm{7.361}\\ & \times {\mathrm{10}}^{-\mathrm{4}}\times f_Z^{\mathrm{2}}-\mathrm{0.056}\times f_X^{\mathrm{2}}+\mathrm{0.068}\times n_{\mathrm{S}}^{\mathrm{2}}\end{array}\end{array}$$

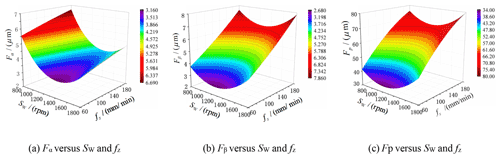
Figure 5a–c show parts of the response surface of the main gear profile deviation models, while the other two process parameters are set as the common constant, i.e., the radial feed velocity f_x=5 (µm per oscillation) and the spark-out times n_s=2. Based on these response surface results, the roles each IGPH process parameter plays in influencing the gear profile deviations can be obtained. These three main gear profile deviations decrease with increasing S_W before the peak value and then increase with increasing S_W because the honing wheel spindle vibration is becoming increasingly more intense with increasing S_W. Once a certain value is exceeded, these three main gear profile deviations all increase with increasing f_z because the cutting amount per revolution increases. Finally, the comprehensive influence orders were F_α (f_x>S_W>f_z>n_s), F_β (f_z>f_x>n_s>S_W), and F_p (f_z>f_x>n_s>S_W).

Figure 5 The influence roles of each IGPH process parameter on the gear profile deviations.

5 Optimization

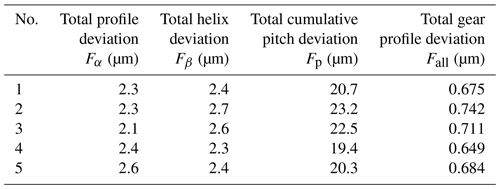
After building the gear profile error models, the optimization studies were carried out based on the AICSA. First, a total gear profile deviation model is needed before the optimization process. Because these three profile deviations have different levels, the results cannot arrive at optimal values when using a simple addition of three profile deviation functions. In this work, a total gear profile deviation model F_all was proposed based on different weighted coefficients of the three gear profile deviation models according to the same precision as from the Chinese Standard No. GBT 10095.1-2008.

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{F}_{\mathrm{all}}& ={\displaystyle \frac{\mathrm{1}}{\mathrm{SD}\left(F_{\mathit{\alpha }}\right)}}{F}_{\mathit{\alpha }}+{\displaystyle \frac{\mathrm{1}}{\mathrm{SD}\left(F_{\mathit{\beta }}\right)}}{F}_{\mathit{\beta }}+{\displaystyle \frac{\mathrm{1}}{\mathrm{SD}\left(F_{\mathrm{p}}\right)}}{F}_{\mathrm{p}}\\ & ={\displaystyle \frac{\mathrm{1}}{\mathrm{18}}}{F}_{\mathit{\alpha }}+{\displaystyle \frac{\mathrm{1}}{\mathrm{18}}}{F}_{\mathit{\beta }}+{\displaystyle \frac{\mathrm{1}}{\mathrm{50}}}{F}_{\mathrm{p}}\end{array}\end{array}$$

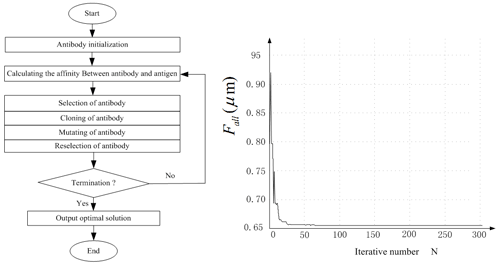
AICSA is a learning algorithm based on the artificial immunity system which performs the autoimmune mechanism of antigen and antibody combination. The AICSA optimization procedure was executed using MATLAB in a Windows operating system, and the optimization process started with a population number of 40, a scale of 10 antibody libraries, and an inhibitory factor of 0.5 that evolved up to 500 iterations. The flowchart and calculation processes of the optimization are shown in Fig. 6. The optimization line stabilized after 75 iterations. The optimal combination of IGPH process parameters based on the AICSA method is shown in Table 5. The comparison experiment of IGPH process between the optimization IGPH process parameters and actual production experience parameters was carried out. Table 6 shows the repeated IGPH process based on the optimization IGPH process parameters, and the result shows that the total profile deviation F_α is approximately flat, and the total helix deviation (F_β) and the total cumulative pitch deviation (F_p) reduced 39.5 % and 59.5 % compared with the original parameters, which achieved the target of improving the gear precision.

Figure 6 The flowchart and the interactions process of AICSA method.

Table 5 The optimal combination of IGPH process parameters based on the AICSA method.

Table 6 Five repeated IGPH experimental results based on the optimization process parameters.

6 Active control of IGPH process parameters focuses on different crossed-axis angles

In the IGPH process, the tooth profile precision of the honing wheel would be reduced with increasing abrasive wear; therefore, a low-precision honing wheel could increase the rejection rate of workpiece gears. Thus, when a certain amount of a workpiece gear is honed or the radial force and torque of a honing wheel are changed abnormally, it is necessary to use a diamond dressing tool to dress the worn honing wheel during the dressing process. Changing the helix angle of the honing wheel is usually carried out to increase the repair number and service life of the honing wheel. The crossed-axis angle between the honing wheel and workpiece gear also changes when honing various batches of workpiece gears. However, such a change of crossed-axis angle could influence the stability of IGPH process quality. Different IGPH process parameters finally reflect the relative velocity between the honing wheel and the workpiece gear tooth surface. Thus, the relationship between the honing relative velocity, crossed-axis angle, and IGPH spindle speed was built and analyzed in this paper. Machine operators just need to input a suitable honing speed parameter and the basic parameters of workpiece gear and honing wheel, and the rotation speed of the workpiece gear or honing wheel that is needed for the numerical control program can be obtained by the active control algorithm.

Figure 7 The coordinate systems of the IGPH machine and the relative velocity on the contact point.

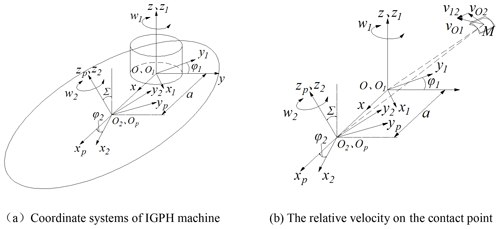
Figure 7a shows the coordinate system of the IGPH process built through analyzing the structure of the IGPH machine and the motion relationship between the honing wheel and the workpiece gear, whereby S_O ($O-x-y-z$) and $S_{\mathrm{P}}(O_{\mathrm{P}}-x_{\mathrm{P}}-y_{\mathrm{P}}-z_{\mathrm{P}}$) are the fixed coordinate systems of the workpiece gear and honing wheel, which can be viewed as the initial position of the meshing movement between the workpiece gear and the honing wheel; S₁($O_{\mathrm{1}}-x_{\mathrm{1}}-y_{\mathrm{1}}-z_{\mathrm{1}}$) and S₂($O_{\mathrm{2}}-x_{\mathrm{2}}-y_{\mathrm{2}}-z_{\mathrm{2}}$) are the following rotation coordinate systems of the workpiece gear and honing wheel; a is the center distance between the workpiece gear and honing wheel; φ₁ and φ₂ are the rotation angle of the workpiece gear and honing wheel; w₁ and w₂ are the angular velocities of the workpiece gear and honing wheel; and Σ is the crossed-axis angle between the workpiece axis and honing wheel axis. At a certain moment, the teeth surface of the workpiece gear and honing wheel come into a random point M, as shown in Fig. 7b, where ${\mathit{v}}_{{\mathrm{O}}_{\mathrm{1}}}$ is the linear velocity vector of point M on the workpiece gear tooth surface, and ${\mathit{v}}_{{\mathrm{O}}_{\mathrm{2}}}$ is the velocity of point M on the honing wheel tooth surface. Thus, the relative velocity between the honing wheel abrasive and the workpiece gear tooth surface v₁₂ can be shown as Eq. (16) in the coordinate system S${}_{\mathrm{O}}(O-x-y-z$).

$$\begin{array}{}\text{(16)}& {\mathit{v}}_{\mathrm{12}}={\mathit{v}}_{{\mathrm{O}}_{\mathrm{1}}}-{\mathit{v}}_{{\mathrm{O}}_{\mathrm{2}}}={\mathit{w}}_{{\mathrm{O}}_{\mathrm{1}}}\times {\mathit{r}}_{{\mathrm{O}}_{\mathrm{1}}}-{\mathit{w}}_{{\mathrm{O}}_{\mathrm{2}}}\times {\mathit{r}}_{{\mathrm{O}}_{\mathrm{2}}},\end{array}$$

where ${\mathit{w}}_{{\mathrm{O}}_{\mathrm{1}}}$ is the angular velocity vector of the workpiece gear and ${\mathit{w}}_{{\mathrm{O}}_{\mathrm{2}}}$ is the angular velocity vector of the honing wheel in the coordinate system S_O($O-x-y-z$), and ${\mathit{r}}_{{\mathrm{O}}_{\mathrm{1}}}$ and ${\mathit{r}}_{{\mathrm{O}}_{\mathrm{2}}}$ are the position vector of contact points on the workpiece gear tooth surface and honing wheel tooth surface in the coordinate system S_O($O-x-y-z$). The final calculated value of the relative velocity v₁₂ can be expressed as Eq. (17).

$$\begin{array}{}\text{(17)}& {\mathit{v}}_{\mathrm{12}}=\left(\begin{array}{c}-{\mathit{\omega }}_{\mathrm{1}}y+{\mathit{\omega }}_{\mathrm{2}}\left(y\cos \mathrm{\Sigma }+z\sin \mathrm{\Sigma }\right)\\ {\mathit{\omega }}_{\mathrm{1}}x-{\mathit{\omega }}_{\mathrm{2}}\left(x+a\right)\cos \mathrm{\Sigma }\\ -{\mathit{\omega }}_{\mathrm{2}}\left(x+a\right)\sin \mathrm{\Sigma }\end{array}\right)\end{array}$$

For the convenience of calculation, the relationship between the relative velocity value v₁₂(M₀) of point M₀ and the spindle speed value (S_W) of the workpiece gear at a certain crossed-axis angle (Σ) can be obtained as Eq. (18):

$$\begin{array}{}\text{(18)}& S_{\mathrm{W}}={\displaystyle \frac{\mathrm{30}\times {\mathit{v}}_{\mathrm{12}}}{\mathit{\pi }\times \left|\begin{array}{c}-y+\left(y\cos \mathrm{\Sigma }+z\sin \mathrm{\Sigma }\right)/i_{\mathrm{12}}\\ x-{\mathit{\omega }}_{\mathrm{2}}\left(x+a\right)\cos \mathrm{\Sigma }/i_{\mathrm{12}}\\ -\left(x+a\right)\sin \mathrm{\Sigma }/i_{\mathrm{12}}\end{array}\right|}},\end{array}$$

where i₁₂ is the transmission ratio between the workpiece gear and honing wheel.

In Sect. 4, the optimized spindle speed (S_W=1270 rpm) was obtained at the crossed-axis angle (Σ=8.722^∘), and the relative velocity value at point M₀ can be calculated (v_12op=2650 mm s⁻¹) at this fixed crossed-axis angle. Based on the relationship between the relative velocity value v₁₂(M₀) of point M₀ and the spindle speed value (S_W) of the workpiece gear at a certain crossed-axis angle (Σ), the adaptable active control of the spindle speed value (S_W) can be realized at different crossed-axis angles. Figure 8 shows the active control matched the curve of spindle speed value (S_W) with the change of the crossed-axis angle (Σ) from 0 to 20^∘. It can be seen that the spindle speed (S_W) of the workpiece gear is 8328.8077 rpm which can be translated to the spindle speed of the honing wheel, S_H=4943.1135 rpm. But the maximum honing wheel spindle speed is 1500 rpm, which cannot support the needed spindle speed; thus, when choosing the initial design parameters of the honing wheel, low-speed crossed-axis angle zones need to be considered as an important effect factor.

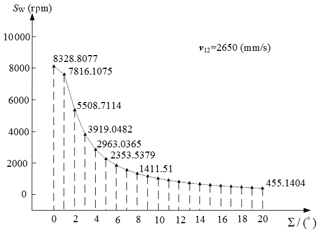
Figure 8 Rotation speed of the workpiece gear versus the crossed-axis angle for stable relative velocity.

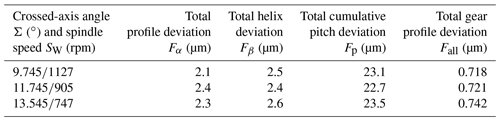
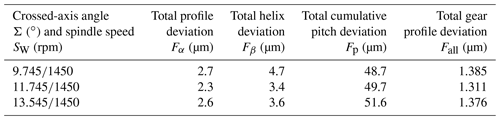
To verify the effect of this active control method, IGPH experiments were carried out. When the crossed-axis angle arrived at 9.745, 11.745, and 13.745^∘, if using the method of keeping the stable honing velocity, the workpiece spindle speed should be suitable for the crossed-axis angle; the adaptive honing wheel spindle speed was 669.1476 rpm, 537.2859 rpm, and 443.5825 rpm. Table 7 shows the results of the gear profile errors based on the active control method.

Table 7 The gear profile error results of IGPH experiments based on the active control method.

Table 8 The gear profile error results of IGPH experiments without the active control method.

The stable spindle speed of 1450 rpm was used when the crossed-axis angle was changing. The results of the gear profile errors are shown in Table 8. It can be seen that the total gear profile error value from the active control method is more stable and lower than that without the active control method. In addition, a lower spindle speed is needed for the IGPH process when the crossed-axis angle is used, which has the advantage of reducing the power consumption and production cost.

7 Conclusion

In order to improve the machining precision and stability for IGPH gear, this paper proposed a theoretical and experimental strategy for IGPH process parameter optimization. Simultaneously, the research results of this paper have an important theoretical basis and engineering application value to guide the development of the gear finishing process. The following conclusions are drawn from the experimental results:

1. The influences of the input IGPH parameters on the gear profile deviation were obtained based on the Box–Behnken DOE method through 29 IGPH experiments. The comprehensive influence orders were F_α(f_x>S_W>f_z>n_s), F_β(f_z>f_x>n_s>S_W), and F_p (f_z>f_x>n_s>S_W), which could provide a theoretical basis for the improvement of gear honing quality.

2. A novel total gear profile deviation modeling method was presented considering different weight coefficients on each IGPH process parameter, which could give a new method for multi-objective optimization for the gear honing process.

3. An active control method of IGPH parameters was proposed for stable relative velocity to solve the problem of the crossed-axis angle changing throughout the total life cycle, which could give the suitable IGPH process parameters and honing wheel basic parameters for different situations.