the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Discrete element method investigation of the milling characteristic in a rice mill
Yan Zhang
Quan Han
Chunlin Xun
Gongtan Zhang
A milling chamber consisting of a rice sieve and a rotating roller plays critical roles in modulating the milling performance of rice grains. However, the mechanism of how the geometries of the rice sieve and rotating roller affect the particle collisions and the interaction time remains not fully understood. Our experimental results show that the milling degree and rate of broken rice of the octagonal rice sieve are largest among the hexagonal sieve, octagonal sieve, and circular sieve. Through the discrete element method, we illustrate that the peak milling degree at the octagonal sieve is attributed to the competition between the decreasing force and increasing milling time with the increase in edges. In addition, the geometries of the convex ribs of the rotating roller are investigated to optimize the structure of the milling chamber. In the left-hand spiral or right-hand spiral of the convex ribs, the rice particles are accumulated in the inlet or outlet regions, respectively, which leads to an uneven milling degree in the axial direction. The uniformity of a milling process can be promoted by increasing the number of convex ribs, which will reduce the milling degree on the other hand.
- Article
(4113 KB) - Full-text XML
- BibTeX
- EndNote
A rice mill machine plays crucial roles in processing unhusked rice and improving its utilization rate. Generally, a modern rice milling machine consists of different functional parts, including a rice huller, a bran remover, and a rice polisher. During the milling process, bran removal occurs in a milling chamber which usually comprises a stationary rice sieve and a rotating roller, where the brown rice is milled by the friction force between itself with other rice grains, the rotating roller, and the sieve (Lim et al., 2013). However, the rice grains tend to be broken under greater friction force (Liang et al., 2008). In order to improve the rate of broken rice, the mechanical characteristic of rice grains in the milling chamber must be figured out first to optimize the structure design of the milling chamber.
In experiments, the characteristics of milling degree, broken rate, and vibration are explored to promote the design of the rice mill machine. Satake (1995) and Seto et al. (2015) developed vertical and horizontal rice milling machines with iron roller grinding, equipped with pressure-regulating devices to adjust the milling pressure and milling degree. Shitanda et al. (2001) investigated the effects of rice varieties, rotating speed, and clearances between rollers and rice sieves on the performance of rice milling. Cho et al. (2017) studied the influence of different spindle speeds on rice temperature rise, milling degree, broken rate, and energy dissipation, and the results showed that the optimal spindle speed should be 1000–1100 rpm. All the experimental works have promoted the development of rice milling machines to obtain the required milling characteristics. However, many milling details of each rice particle are not available due to the limitations of experimental methods. In fact, the dynamics of rice clusters in the milling chamber are part of the granular system problems, which are widely investigated based on the discrete element method (DEM) (Zhu et al., 2007; Wang et al., 2012; Tahvildarian et al., 2013). Recently, Cao et al. (2018) and Han et al. (2016) studied the effects of rotation speed and rice sieve geometry on the turbulent motion of particles in a vertical rice mill through the DEM simulations. In their works, the average turbulent kinetic energy was proposed to understand the mechanisms of particle collisions and energy dissipation, which are directly determined by the cross-section shape of the rice sieve. No doubt the milling degree of rice grains is closely related to the average force, particle speed, milling time, and energy dissipation during the particle collisions (Bian et al., 2017; Delaney et al., 2015). However, the mechanism of how the geometries of the milling chamber affect the particle collisions and finally affect the milling degree needs further study, especially for the combined effects of the parameters above.
In this work, the milling degrees and broken rates of rice grains are discussed by implementing the experiments under different shapes of rice sieve. Through the DEM simulations, effects of the geometry of the milling chamber on the milling performance, including the average compressive force, axial velocity, and energy dissipation, are investigated. Finally, the structure of convex ribs of the rotating rollers is optimized to modulate the milling process.
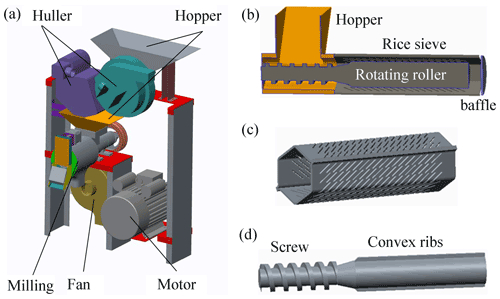
Figure 1(a) Diagram of a rice mill machine. (b) The cross-section profile of the milling chamber. (c) A hexagonal rice sieve. (d) A rotating roller consisting of a screw and two symmetrical convex ribs.
2.1 Geometry models
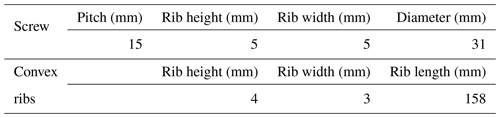
In a rice mill machine, the rice grains directly interact with the hopper, rotating roller, rice sieve, and baffle, as shown in Fig. 1a, b. In the previous works, it indicates that the geometry of the rice sieve and the rotating speed were critical to the milling process, but few studies focused on the geometry of the rotating roller. Thus, we will explore the effects of both the rice sieve and the rotating roller on the milling performance. Figure 1c represents a hexagonal sieve made of two identical sheet metal plates through laser drilling, bending, and welding. A rotating roller consisting of a screw and two symmetrical convex ribs is shown in Fig. 1d, in which the screw is used to convey the rice grains to the milling areas formed by the rice sieve and the convex ribs. The detailed size parameters of the rotating roller in our rice mill machine are shown in Table 1. During a milling process, the rice bran can be removed from a single rice grain by contact with other grains and with the geometry, and then the bran is blown away through the holes in the rice sieve to obtain the milled rice.
2.2 DEM models
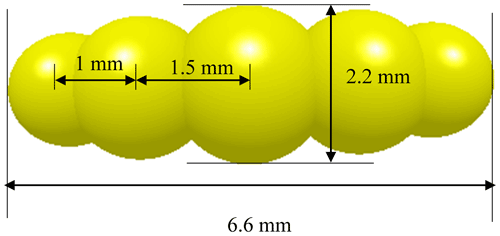
The rice grain model used in the DEM simulations is based on the soft-sphere model. An irregular particle is composed of many small spheres, such as the approximately ellipsoidal rice particles studied in the reference Meng et al. (2021). As shown in Fig. 2, the symmetrical rice particle model is made up of five spheres arranged in a straight line with different spherical diameters of 1.6, 2, 2.2, 2, and 1.6 mm, respectively. The distances between every two spheres are displayed in Fig. 2, and the overall size of a rice particle is 2.2 mm × 2.2 mm × 6.6 mm. In the simulation, the interaction between the spheres in each rice particle is bonded.
In order to precisely simulate the motions of rice particles, the contact model for calculating friction forces between rice particles with each other and the geometric boundary should be considered prudently (Hu et al., 2014). The Hertz–Mindlin contact model is used in the DEM simulation (Hertz, 1882; Mindlin, 1953; Cleary and Sawley, 2002; Gao et al., 2020), where the forces of each particle are decomposed into the normal and tangential directions of the contact point, and the forces in each direction are simplified into the elastic or damping forces. For the tangential force, in addition to the elastic and damping forces, the Coulomb friction should be taken into account. Finally, the normal and tangential forces are coupled to calculate the spatial force of particles, which is used to calculate the particle motions by Newton's second law of motion. Thus, the trajectory, rotation, velocity, and force of each particle in the system can be obtained in the DEM simulation. The equations for the translational and rotational motions of each particle are
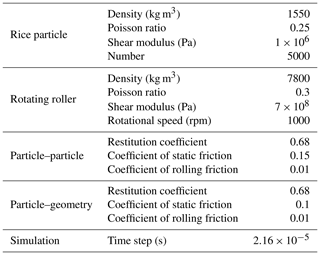
where mi, vi, ωi, and Ii are the mass, translational velocity, angular velocity, and moment of inertia of particle i. ni is the number of particles in contact with particle i. Fn is the normal contact force and is the normal damping force. Analogously, Ft is the tangential contact force and is the tangential damping force. The torque Tt and Tr are contributed by the tangential force and the rolling friction force, respectively. Various parameters (Cao et al., 2018) are set as shown in Table 2, including the material properties of rice particles and rotating rollers and contact conditions of the particle–particle and particle–geometry. The time step is set as s.
3.1 Circumferential characteristic of a milling chamber
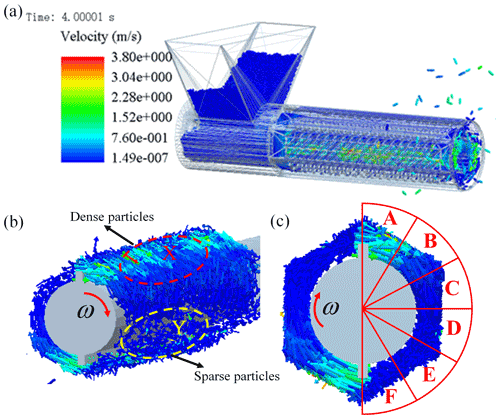
As the rice particles put into the hopper and the screw start to rotate, the rice particles are conveyed to the milling region between the rice sieve and rotating roller. In the DEM simulation, the total simulation time is set as 5 s and the particle system tends to be stable after 4 s. Figure 3a shows a snapshot of the velocity of all rice particles in the stable situation. Moreover, Fig. 3b and c show a distribution diagram of these rice particles at different views. It can be seen clearly in Fig. 3b that the particles are quite dense in region X due to the clockwise rotation and the influence of a convex rib. By contrast, the bottom convex rib near region Y rotates more quickly than the rice particles, causing a sparse-particle region Y. The distribution of rice particles in the milling chamber is highly consistent with the experimental results of Baker (2014), indicating that the convex ribs lead to a non-uniform distribution and several different circumferential milling areas. Half of the symmetrical milling chamber is divided into six portions in the circumferential direction as shown in Fig. 3c, and the velocity of rice particles in region A is largest, while the velocity is smallest in region F.
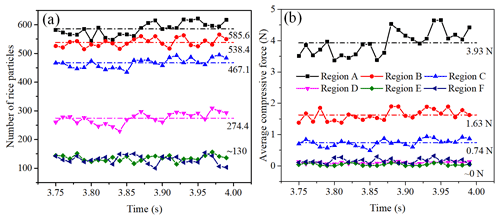
Figure 4The number of particles (a) and the average compressive force (b) within different regions changing with time.
According to Fig. 3c, the interaction condition of rice particles in different circumferential areas of the chamber is quite different. It is worth investigating the number of particles and the average compressive force in the different regions to understand the milling characteristic. Figure 4a and b represent the number of particles and average compressive force of different circumferential regions in a rotating cycle of the roller of 0.24 s. In a milling chamber, each rice particle is subjected to the forces from all the directions, so the algebraic sum of all the subjected forces of a rice particle is defined as its compressive force. The average compressive force within a region is defined as the total compressive forces of all the rice particles over the number of particles.
It is clear that the number of rice particles in Fig. 4a decreases from regions A to F, with a drop of about 4.5 times. In regions A, B, and C, the numbers of particles are relatively larger, while the number in region D goes down dramatically until it reaches a convergent minimum in regions E and F. An analogical tendency of these regions is shown by the average compressive force in Fig. 4b, which can be seen by the forces in regions A, B, and C being greater than zero, while the forces of the other regions are almost zero. That is, regions A, B, and C are the effective rice milling areas; however, the milling degree in regions D, E, and F is very low.
3.2 Milling characteristic under different milling chambers
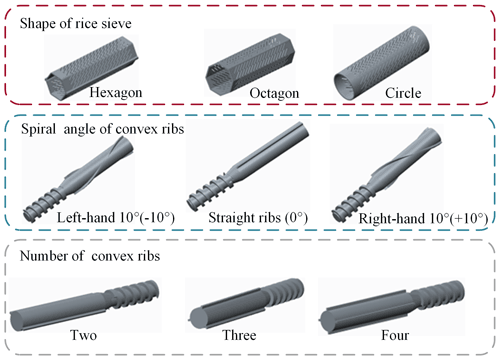
In a milling chamber, the main geometries influencing the milling performance include the shape of the rice sieve, spiral angles of convex ribs, and the number of convex ribs, as indicated in Fig. 5. In this section, based on the original milling chamber in Fig. 1 (hexagonal rice sieve, straight ribs, and two convex ribs), the three variables are studied by the DEM simulation and milling experiments. Since the milling process almost always takes place in the interacting regions between the rice sieve and the rotating roller, we divide the rice sieve into 20 equal sections in the axial direction. Besides the average compressive force, the average axial velocity and energy dissipation during the particle collisions can also be used to evaluate the milling degree since that part of the dissipated energy is used to grind out the bran from a rice particle in addition to vibration and noise (Weerasekara et al., 2016).
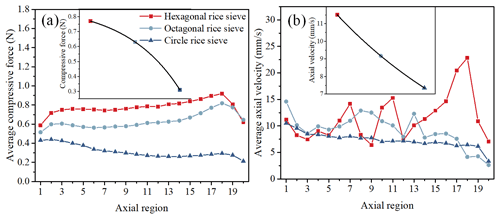
Figure 7(a) Average compressive force under different shapes of rice sieves. (b) Average axial velocity under different shapes of rice sieves.
3.2.1 Experimental results under different rice sieves
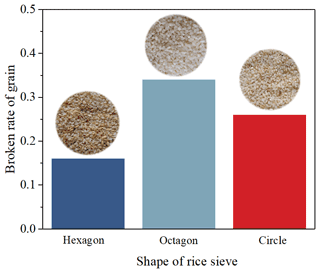
In order to facilitate the installation and replacement of a rice sieve in the application of a rice mill machine, the circumcircle size of the hexagonal and octagonal shapes of the cross section is set to be consistent with the circle sieve. The milling experiments in our rice mill machine are implemented to investigate the influence of different rice sieve shapes on the milling degree. In the experiments, the unhusked rice grains are put into the upper hopper in Fig. 1a, and then the grains are hulled in the huller unit and finally enter the milling chamber. The shapes of the rice sieve in the milling chamber are shown in Fig. 5, and the outlet pressure of the milling chamber is constant. Other parameters are consistent with Table 2. After the milling process, the circular pictures of milled rice grains are represented in Fig. 6, where the whiter rice grains indicate the milled rice, while the brown rice grains are the unpolished rice. Results show that the milling degree of the octagonal rice sieve is the largest of the three rice sieves. Also, the milled rice under different rice sieves is sampled to calculate the rice broken rate, which indicates that the broken rate is consistent with the milling degree.
3.2.2 Simulation results under different rice sieves
In the DEM simulations, the average compressive force in different axial regions is extracted from the last steady 1 s, with the results under different shapes of rice sieves shown in Fig. 7a. Note that the compressive forces in regions 1, 2, 19, and 20 are obviously smaller than the other regions because of the shorter convex ribs compared with the rice sieve. Under the hexagonal, octagonal, and circle rice sieves, the average compressive forces in the whole milling chamber are 0.77, 0.63, and 0.31 N, respectively. The compressive force decreases with the increase in the edge number of rice sieves and encounters a large decrease in the circle rice sieve, indicating that the rice particles suffer from the greater milling degree in the hexagonal and octagonal rice sieves. In fact, the cross-section area in the hexagonal rice sieve is the smallest, so that its density of rice particles is largest, causing the largest compressive force. Besides, the uneven clearance between the hexagonal rice sieve and the convex ribs will result in a violent axial motion of the rice particles, as shown in Fig. 7b. The average axial velocities in the whole milling chamber under the hexagonal, octagonal, and circle rice sieves are 11.51, 9.17, and 7.35 mm s−1, respectively. To sum up, as the edges of regular polygon sieves increase, the decreasing compressive force causes a slighter milling degree and a decreasing axial velocity, which means that longer milling times in the chamber will enhance the milling degree. Due to the competition of the compressive force and the axial average velocity, the milling degree and broken rate under the octagonal rice sieve are the largest, which has been illustrated in the experiments.
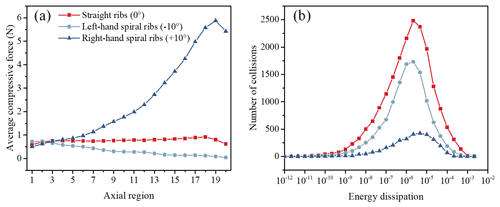
Figure 9(a) Average compressive force under different spiral angles of convex ribs. (b) The distribution of energy dissipation during the particle collisions.
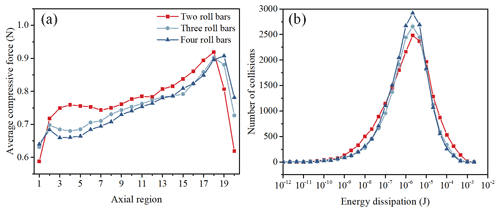
Figure 10(a) Average compressive force under different numbers of convex ribs. (b) The distribution of energy dissipation during the particle collisions.
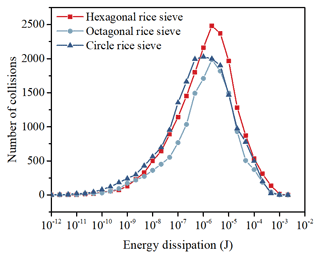
The number of collisions under different energy dissipation during the particle collisions is counted to further explore the influence of a rice sieve on the particle interactions. The energy dissipation is defined as the kinetic energy loss during each collision. Figure 8 is drawn from the collision events of all particles in the whole milling chamber within 1 s in the steady state. The curves are approximate to the Maxwell distribution centered at the energy dissipation of about 10−6 J. It is apparent that the energy dissipation corresponding to the curve peak obviously decreases with the increase in the edge of the rice sieve, indicating that larger energy transfer occurs during the collision events in the hexagonal rice sieve and that more energy can be utilized to remove the rice bran. In addition, the number of collision events in the hexagonal rice sieve is the largest, while the number in the octagonal rice sieve is the smallest. The possible reason is that the collisions between the rice particles and the collisions between the particle and geometry are changing with the variation of cross-section area and perimeter of the rice sieve.
3.2.3 Spiral angle and number of convex ribs
Similarly, the average compressive force and the energy dissipation distribution are discussed under different spiral angles and numbers of convex ribs. The geometry diagrams are also represented in Fig. 5, including the straight ribs (0∘), left-hand spiral ribs (−10∘), right-hand spiral ribs (+10∘), two ribs, three ribs, and four ribs. Three different tendencies of the curves in Fig. 9a are shown: the force fluctuates under the straight ribs, while it decreases under the left-hand spiral ribs and increases under the right-hand spiral ribs as the axial region increases. In the inlet of the milling regions (region 1), the average compressive force in the left-hand spiral ribs is largest and the force in the right-hand spiral ribs is smallest. The reason is that the screw of the rotating roller for conveying the rice particles is a right-hand spiral; the left-hand spiral ribs impede the transfer of particles, causing the accumulation of particles in the inlet regions. By contrast, the right-hand spiral ribs promote the transfer of particles causing the accumulation of particles in the outlet regions. Therefore, both the left-hand and right-hand spiral ribs are not conducive to the stability of the compressive force in the milling chamber and affect the uniformity of milling. Figure 9b shows the number of collision events under different energy dissipation. The results indicate that the numbers of collision events under left-hand spiral ribs and right-hand spiral ribs are both decreased compared with the straight ribs, due to the accumulation of rice particles in the inlet or outlet reducing the probability of collisions. In general, the convex ribs are not recommended for choosing the right-hand spiral when the screw is a right-hand spiral, and the straight ribs can facilitate the formation of a uniform rice milling chamber.
It has been shown that the rice particles are quite dense in the region towards the convex ribs in Sect. 3.1. In fact, the increase in convex ribs in a rotating roller can divide the rice milling chamber into several regions in the circumferential direction to improve the uniformity of rice particles. Figure 10a shows that the average compressive force decreases with the increase in the number of convex ribs in almost all the axial regions. This means that the increase in the number of convex ribs is beneficial to the uniformity of milling but not to the improvement of milling degree. The energy dissipation distribution under different numbers of convex ribs in Fig. 10b illustrates that the energy dissipation is more concentrated in the larger number of ribs, indicating a better milling uniformity.
In summary, the DEM simulations are carried out to study the milling performance of the rice particles in the milling chamber. By analyzing the circumferential distribution of rice particles, we confirmed that the DEM simulation can well describe the milling process compared with the previous experimental results. Results show that the regions in front of the rotating convex ribs are the main milling regions with larger particle density and compressive force. When changing the shape of the rice sieve in the milling chamber, the milling experiments illustrate that the milling degree and rate of broken rice under the octagonal sieve are larger than that under the hexagonal and circle sieves. To further explore the factors influencing milling degree, the DEM simulations are conducted with the same conditions of the experiments. This shows that when the edges of regular polygon sieves increase, the decreasing compressive force causes a slighter milling degree and the decreasing axial velocity indicates a longer milling time in the chamber, which will enhance the milling degree. Due to the combined effect of the compressive force and the axial velocity, the milling degree and broken rate under the octagonal rice sieve are the largest. The energy dissipation during particle collisions is calculated to index the strength of interactions in the collisions. The peak of the energy dissipation curve obviously decreases with the increase in the edge of the rice sieve, indicating that larger energy transfer occurs during the collision events in the hexagonal rice sieve and that more energy can be utilized to remove the rice bran. In addition, the geometries of the convex ribs of the rotating roller are investigated. We find that the left-hand spiral and right-hand spiral of the convex ribs accumulate the particles in the inlet and outlet regions, respectively, causing an uneven distribution of particles in the axial direction. With the increase in the number of convex ribs, the uniformity of milling increases, while the milling degree decreases.
All the code/data used in this paper can be obtained upon request to the corresponding author.
YZ provided ideas, reviewed the overall process for the work, and wrote the majority of the paper. QH provided the simulation method, made the figures, and revised the paper. CX and GZ performed the simulations and experiments.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the National Natural Science Foundation of China (grant no. 51575104) and the Natural Science Foundation of Jiangsu Province (grant no. BK20140627).
This work was supported by the National Natural Science Foundation of China (grant no. 51575104) and the Natural Science Foundation of Jiangsu Province (grant no. BK20140627).
This paper was edited by Xichun Luo and reviewed by two anonymous referees.
Baker, A. J.: A Study of Tribological Processes During the Milling of Rice, University of Sheffield, 140–141, 2014.
Bian, X., Wang, G., Wang, H., Wang, S., and Lv, W.: Effect of lifters and mill speed on particle behaviour, torque, and power consumption of a tumbling ball mill: Experimental study and DEM simulation, Miner. Eng., 105, 22–35, 2017.
Cao, B., Jia, F., Zeng, Y., Han, Y., Meng, X., and Xiao, Y.: Effects of rotation speed and rice sieve geometry on turbulent motion of particles in a vertical rice mill, Powder Technol., 325, 429–440, 2018.
Cho, B.-H., Han, C.-S., Kang, T.-H., Lee, D.-I., Won, J.-H., and Lee, H.-S.: Milling characteristics of cutting-type rice milling machine according to the rotating speed of the main shaft, Korean Journal of Agricultural Science, 44, 416–423, 2017.
Cleary, P. W. and Sawley, M. L.: DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge, Appl. Math. Model., 26, 89–111, 2002.
Delaney, G., Morrison, R., Sinnott, M., Cummins, S., and Cleary, P.: DEM modelling of non-spherical particle breakage and flow in an industrial scale cone crusher, Miner. Eng., 74, 112–122, 2015.
Gao, X., Zhou, Z., Xu, Y., Yu, Y., Su, Y., and Cui, T.: Numerical simulation of particle motion characteristics in quantitative seed feeding system, Powder Technol., 367, 643–658, 2020.
Han, Y., Jia, F., Zeng, Y., Jiang, L., Zhang, Y., and Cao, B.: Effects of rotation speed and outlet opening on particle flow in a vertical rice mill, Powder Technol., 297, 153–164, 2016.
Hertz, H.: Ueber die Berührung fester elastischer Körper, De Gruyter, in: Band 92, edited by: Crelle, A. L., Borchardt, C. W., and Schellbach, De Gruyter, 156–171, 1882.
Hu, J., Guo, K., Zhou, C., and Hou, C.: Simulation and experiment of supplying seeds in box of magnetic precision cylinder-seeder, Nongye Jixie Xuebao, Transactions of the Chinese Society for Agricultural Machinery, 45, 61–65, 2014.
Liang, J., Li, Z., Tsuji, K., Nakano, K., Nout, M. J. R., and Hamer, R. J.: Milling characteristics and distribution of phytic acid and zinc in long-, medium- and short-grain rice, J. Cereal Sci., 48, 83–91, https://doi.org/10.1016/j.jcs.2007.08.003, 2008.
Lim, J. S., Abdul Manan, Z., Hashim, H., and Wan Alwi, S. R.: Towards an integrated, resource-efficient rice mill complex, Resour. Conserv. Recycling, 75, 41–51, https://doi.org/10.1016/j.resconrec.2013.04.001, 2013.
Meng, X., Han, Y., Jia, F., Chen, P., Xiao, Y., Bai, S., and Zhao, H.: Numerical simulation approach to predict the abrasion rate of rice during milling, Biosyst. Eng., 206, 175–187, 2021.
Mindlin, R. D.: Elastic spheres in contact under varying oblique forces, J. Appl. Mech., 20, 327–344, 1953.
Satake, S.: Vertical milling machine, U.S. Patent No. 5,419,252, 30 May 1995.
Seto, Y., Kajihara, K., Nonaka, K., Koike, Y., and Yamamoto, K.: Grinding type vertical grain milling machine, U.S. Patent No. 9,114,400, 25 Aug. 2015.
Shitanda, D., Nishiyama, Y., and Koide, S.: Performance analysis of impeller and rubber roll husker using different varieties of rice, Agricultural Engineering International: CIGR Journal, Journal of Scientific Research and Development, Manuscript FP 01 001, Vol. III, 0–19, 2001.
Tahvildarian, P., Ein-Mozaffari, F., and Upreti, S. R.: Circulation intensity and axial dispersion of non-cohesive solid particles in a V-blender via DEM simulation, Particuology, 11, 619–626, 2013.
Wang, M., Yang, R., and Yu, A.: DEM investigation of energy distribution and particle breakage in tumbling ball mills, Powder Technol., 223, 83–91, 2012.
Weerasekara, N., Liu, L., and Powell, M.: Estimating energy in grinding using DEM modelling, Miner. Eng., 85, 23–33, 2016.
Zhu, H. P., Zhou, Z. Y., Yang, R. Y., and Yu, A. B.: Discrete particle simulation of particulate systems: Theoretical developments, Chem. Eng. Sci., 62, 3378–3396, https://doi.org/10.1016/j.ces.2006.12.089, 2007.