the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel mathematical model for the design of the resonance mechanism of an intentional mistuning bladed disk system
Xuanen Kan
Tuo Xing
Bladed disk systems with advanced functions are widely used in turbo-machineries. However, there are always deviations in physical dynamic properties between blades and blades due to the tolerance and wear in operation. The deviations will lead to vibration localization, which will result in high cycle fatigue and accelerate the damage of the bladed disk system. Therefore, many intentional mistuning patterns are proposed to overcome this larger local vibration. Previous studies show that intentional mistuning patterns can be used to reduce the vibration localization of the bladed disk. However, the determination of the resonance mechanism of the intentional mistuning bladed disk system is still an unsolved issue. In this paper, a novel mathematical model of resonance of an intentional mistuning bladed disk system is established. Mistuning of blades and energy resonance are included in this theoretical model. The method of the mechanical power of the rotating blade for one cycle is applied to obtain the resonance condition. By using this theoretical model, the resonance mechanism of an intentional mistuning bladed disk is demonstrated. The results suggest that the ideal results can be obtained by adjusting the intentional mistuning parameter. This paper will guide the design of the dynamic characteristics of the intentional mistuning bladed disk.
- Article
(621 KB) - Full-text XML
- BibTeX
- EndNote
Bladed disk systems are the key component for energy conversion in turbo-machinery, and it forms the largest number of components. Therefore, bladed disk systems with advanced functions are widely used. In general, in the tuned bladed disk system, the blades are designed to be identical to each other. The physical properties of each blade are universal. The vibration energy can be able to transmit uniformly in the tuned bladed disk systems. The vibration characteristics of the rotating bladed disk are complicated (Khorasany and Hutton, 2012a, b; Picou et al., 2020), and the research shows that frequency characteristics are significantly influenced by the magnitudes of forced displacements. The resonance of the tuned bladed disk satisfies specific conditions (Huang, 1981).
However, in operation, there are deviations between the blade and others due to tolerance and wear. These deviations from the physical properties of blades may lead to a larger forced vibration response in some blades (Bai et al., 2020; Li et al., 2019; Ma et al., 2016; Nikolic et al., 2007). This will result in vibration localization, and it will accelerate the high cycle fatigue of the bladed disk and the damage to the blades. Therefore, the dynamic characteristics and the energy transmission of the mistuned bladed disk are widely conducted. A dynamic model with centrifugal stiffening, Coriolis force, and other critical factors is proposed (Guo et al., 2021), and their results show that friction between adjacent shrouds can result in the complex nonlinear vibration. The altering load's effect on the vibration behaviors of cracked blades is investigated (Liu et al., 2015), and this research shows that the critical frequency is affected due to the coupling effect of the rotating speed and alternating loads. The dynamic characteristics of twisted shrouded blades are researched (Xie et al., 2017), and the mechanism of impact-caused vibration is revealed in their research. An enhanced dynamic model is proposed by considering the coupling effects of bending stretching and torsion (Yutaek et al., 2018), and their results show that the stretch variable is key for the coupling effects between stretching, bending, and torsion. The issue of the coupling effect between blade shafting and the shell is investigated in structure vibration (Liu et al., 2019), and this research shows that the natural frequency has a great influence on the acoustic radiation characteristics. The characteristics of a mistuned bladed disk with friction interfaces are researched (Pourkiaee et al., 2022; Ferhatoglu and Zucca, 2021). The coupling vibration behaviors of flexible shaft disk blades are investigated (She et al., 2018), and their result indicates that shaft and disk flexibility can influence the critical rotational speeds greatly.
In order to control the level of vibration localization of the forced response caused by mistuning, the intentional mistuning bladed disk is proposed (Han et al., 2014; Yoo et al., 2017; Martel et al., 2008; Chen et al., 2019; Beirow et al 2018, 2019). The results show that intentional mistuning has a great effect on the vibration localization. Intentional mistuning of the bladed disk is used to reduce the larger forced response (Corral et al., 2018; Martel and Sanchez-Alvarez, 2018; Gao et al., 2020; Joachim et al., 2021; Repetckii, 2020). An intentional mistuning bladed disk changes the vibration localization by designing the structure parameter (Nakos et al., 2021; Picou et al., 2018; Beirow et al., 2021; Biagiotti et al., 2018; Schlesier et al., 2018). The robust design concept is proposed to control the vibration level by the parameter design in the bladed disk systems (Chan et al., 2010). The method of using bladed packets to reduce the vibration localization of the mistuned bladed disk is researched (Kan and Zhao, 2021), and the results show that the design of the bladed packets is an alternative method to reduce the larger forced response of the mistuned bladed disk system. Di Paolo et al. (2021) introduced a friction-based passive method to reduce the vibration of a rotating structure (Di Paolo et al., 2021), and their research indicates that the dry friction can be used to reduce the vibration localization. Our previous work investigated the Coriolis effect on the intentional mistuning bladed disk. The results show that the Coriolis effect has an effect on the dynamic characteristics of the intentional mistuning bladed disk (Kan et al., 2017).
Despite the previous effort, it remains an unclear issue how to design intentional mistuning parameters in the bladed disk in theory. Therefore, the aim of this paper is to propose a theoretical model of resonance to solve this issue in the intentional mistuning bladed disk system. Mistuning of blades and energy resonance are included in this theoretical model. By using this novel model, the critical resonance mechanism of an intentional mistuning bladed disk is demonstrated. The results of this paper can provide guidance for the dynamic control of the mistuned bladed disk.
In general, the bladed disk is subjected to a periodic force. This periodic force can be decomposed into a series of harmonic engine order forces. Harmonic forces are
where fk(θ,t) is the harmonic force along the circumferential direction, fk is the amplitude of the external force of each blade, k is the engine order of the external force, ω is the frequency, and θ is the phase.
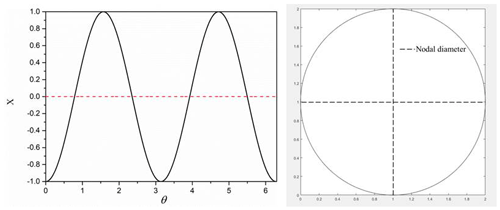
The vibration mode of the mth nodal diameter of the tuned bladed disk is depicted as
where Xm is the mth nodal diameter and Am is the amplitude of the mth nodal diameter. The nodal diameter is that the amplitude of vibration is zero in the bladed disk system as shown in Fig. 1. It shows the second nodal diameter of the bladed disk system in Fig. 1.
However, there are deviations between the blade and others due to tolerance and wear. These deviations in the physical properties of blades may lead to a larger forced vibration response in some blades. This will result in vibration localization, which may accelerate the high cycle fatigue of the bladed disk and the damage to the blades.
An intentionally mistuned bladed disk is used to change the mistuning parameter to reduce the vibration localization of the mistuned bladed disk. Therefore, the intentional mistuning bladed disk attracts much attention. For example, harmonic intentional mistuning is one of the intentional mistuning bladed disks. Mistuning is introduced by changing Young's modulus as below (Hou and Cross, 2005; Castanier and Pierre, 2006).
Ei is Young's modulus of the mistuned blade. E0 is Young's modulus of the tuned blade. For example, the harmonic intentional mistuning value of blade i is defined as
A is the mistuning strength, N is the total number of blades, and h is the harmonic order.
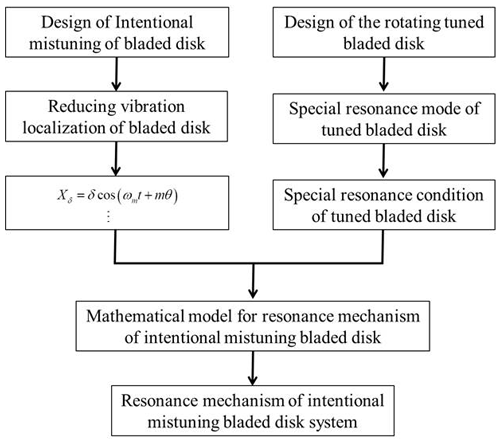
The idea of this mathematical model of the intentional mistuning bladed disk is shown in Fig. 2. First, the main dominant mode shape of the bladed system is calculated under its rated conditions. Second, the dominant mode shape obtained in the first step is brought into the theoretical model of active detuned resonance proposed in this paper. From the work done in a single cycle, according to the needs of your own working conditions, you can choose the theoretical design of your corresponding parameters.
An intentional mistuning bladed disk is used to change the vibration localization by designing the structure parameter. When the blade is intentional mistuning, the mistuning can be adjusted as the design. In this paper, the vibration mode of the mth nodal diameter is depicted as
where δ is the mistuning parameter.
When the blade goes though one period, the power of the blade is depicted:
where W is the power and T is the period of the blade:
In order to describe the energy transfer of the mistuned part, the idea of describing the energy transfer based on different parts is proposed. The power of the blade is divided into two parts, the tuning part and the mistuned part. The tuning part and the mistuned part are
where W1 is the power of the tuned part and W2 is the power of the mistuned part. In this paper, the aim is to establish the bridge between the intentional bladed disk and the vibration localization. The indicators W1 and W2 will be able to describe the energy transfer separately.
The power of the tuned part is
Taking Eqs. (1) and (2) into Eq. (9),
when
The result of Eq. (11) is depicted as
when
The result of Eq. (9) is
The power of the intentional mistuning part is depicted as
Substituting Eqs. (1) and (2) into Eq. (15), the power of the mistuned part is depicted as
when
The power of the intentional mistuning part is obtained. The result of Eq. (16) is
when
The power of the intentional mistuning part is obtained. The result of Eq. (16) is
The power of the tuned and intentional mistuning parts is obtained in different situations. Summing up the above,
From Eq. (21), the different situations can be able to produce a different result. We can adjust the different mistuning parameter δ, and we will obtain an ideal result, as the designer expects.
In our paper, the proposed mathematical model is not applied to all bladed disk systems. From Eqs. (9) and (15) we can see that friction is not considered in this proposed mathematical model of the bladed disk system. The friction will produce some power in the bladed disk system, when the bladed disk system contains friction. Some blade disk systems do have friction, and the blades are connected with each other through a shroud or shoulder. In this way, there is friction at the interface. Friction is very complex. Friction is related to the roughness, contact area, contact angle and positive contact pressure of the interface. When the blade is out of tune, the friction of each interface is different, and the work done by the friction is also different. Therefore, this mathematical model is not applied to bladed disks with friction.
Bladed disk systems are the key component for energy conversion in turbo-machineries. The power is important for the design of the bladed disk system. From the power of the blade, it shows that we can adjust a different mistuning parameter δ, and we will obtain an ideal result, as the designer expects.
when the mistuning parameter is
In this paper, the aim is to adjust the mistuning parameters to control the vibration localization of the mistuned bladed disk. Based on the proposed mathematical model, the power will be less than the tuned bladed disk system, and this illustrates that the proposed mathematical model is useful for reducing the vibration localization of a mistuned bladed disk system. The intentional mistuning is used to reduce some power of the bladed disk. Then the level of the forced response is less than the tuned bladed disk system.
The power will be less than the tuned bladed disk system, and it means that
From Eq. (24), we can get that we can adjust the intentional mistuning parameter for obtaining a small resonance in the bladed disk system. Based on the proposed mathematical model, the power will be less than the tuned bladed disk system, and this shows that the proposed mathematical model is valid for reducing the vibration localization of the mistuned bladed disk system. This is a vital value for the dynamic characteristics of the intentional mistuning bladed disk.
When the mistuning parameter is
the power will exceed the tuned bladed disk system, and it means that
From Eq. (26), we can get that if we want to avoid a larger resonance in a bladed disk and we can adjust the intentional mistuning parameter.
When the mistuning parameter is
the power will be equal to the tuned bladed disk, and it means that
From the discussion, we can design the intentional mistuning parameter to get a different target.
In this part, in order to illustrate the validity of the proposed model, we can suppose the intentional mistuning parameter and Am=1. Based on the proposed model, Eq. (24) in this paper, we can get the power of the intentional bladed disk.
When the intentional mistuning parameter and Am=1, the power of the intentional bladed disk decreases by 1 % compared with the tuned system. Based on the proposed mathematical model, in some situations, we can get the ideal power by adjusting the intentional mistuning parameters. It suggests that we can change deliberate detuning parameters to get the aim of reducing the forced response. First, the main dominant mode shape of the bladed system is calculated under its own rated conditions. Second, the dominant mode shape obtained in the first step is brought into the theoretical model of active detuned resonance proposed in this paper. From the work done in a single cycle, according to the needs of your own working conditions, you can choose the theoretical design of your own corresponding parameters.
Many methods are used to reduce forced response localization. One of the methods is using piezoelectric networking to reduce vibration localization (Zhang et al., 2003; Tang and Wang, 2003; Yu et al., 2006). Previous studies show that intentional mistuning patterns can be used to reduce the vibration localization of bladed disks. However, the determination of the resonance mechanism of the intentional mistuning bladed disk system is still an unsolved issue. In this paper, a novel mathematical model of the resonance of the intentional mistuning bladed disk system is established. Based on the proposed novel model, the vibration localization can be adjusted by using intentional mistuning parameters.
In this paper, the determination of the critical resonance mechanism of the intentional mistuning bladed disk system is studied. Many new conclusions are obtained as follows.
-
A novel mathematical model of the resonance of the intentional mistuning bladed disk system is established based on mechanisms of the tuned system.
-
The method of the mechanical power of the rotating blade for one cycle is used to obtain the resonance condition.
-
The results suggest that we can obtain the ideal results by adjusting the intentional mistuning parameter. This is a vital value for the design of the intentional bladed disk system.
The above findings of this paper will give some advice for the design of an intentional mistuning bladed disk and provide guidance for the dynamic vibration control of the mistuned bladed disk.
All the data used to support the findings of this study are included within the article.
XK conducted the research and wrote the paper, and TX was responsible for editing.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the Natural Science Basic Research Plan in Shaanxi Province of China (grant no. 2021JQ-462), the State Key Laboratory for Strength and Vibration of Mechanical Structures (grant no. SV2018-KF-34) and the China Postdoctoral Science Foundation (grant no. 2022MD723836).
This research has been supported by the Natural Science Basic Research Plan in Shaanxi Province of China (grant no. 2021JQ-462), the State Key Laboratory for Strength and the Vibration of Mechanical Structures (grant no. SV2018-KF-34), China Postdoctoral Science Foundation (grant no. 2022MD723836).
This paper was edited by Daniel Condurache and reviewed by five anonymous referees.
Bai, B., Li, H., Zhang, W., and Cui, Y.: Application of extremum response surface method-based improved substructure component modal synthesis in mistuned turbine bladed disk, J. Sound Vibrat., 472, 115210, https://doi.org/10.1016/j.jsv.2020.115210, 2020
Beirow, B., Figaschewsky, F., Kühhorn, A., and Bornhorn, A.: Modal analyses of an axial turbine blisk with intentional mistuning, J. Eng. Gas Turb. Power, 140, 012503, https://doi.org/10.1115/1.4037588, 2018.
Beirow, B., Kühhorn, A., Figaschewsky, F., Bornhorn, A., and Repetckii, O. V.: Forced response reduction of a blisk by means of intentional mistuning, J. Eng. Gas Turb. Power, 141, 011008, https://doi.org/10.1115/1.4040715, 2019.
Beirow, B., Kühhorn, A., Weber, R., and Popig, F.: Vibration Analyses of an Axial Turbine Wheel with Intentional Mistuning, J. Eng. Gas Turb. Power, 143, 061027, https://doi.org/10.1115/1.4049449, 2021.
Biagiotti, S., Pinelli, L., Poli, F., Vanti, F., and Pacciani, R.: Numerical study of flutter stabilization in low pressure turbine rotor with intentional mistuning, Energy Proc., 148, 98–105, https://doi.org/10.1016/j.egypro.2018.08.035, 2018.
Castanier, M. P. and Pierre, C.: Modeling and analysis of mistuned bladed disk vibration: current status and emerging directions, J. Propul. Power, 22, 384–396, https://doi.org/10.2514/1.16345, 2006.
Chan, Y.-J. and Ewins, D. J.: Management of the variability of vibration response levels in mistuned bladed discs using robust design concepts. part 1: parameter design, Mechan. Syst. Signal Proc., 24, 2777–2791, https://doi.org/10.1016/j.ymssp.2010.06.005, 2010a.
Chan, Y. J. and Ewins, D. J.: Management of the variability of vibration response levels in mistuned bladed discs using robust design concepts. Part 2, Mechan. Syst. Signal Proc., 24, 2792–2806, https://doi.org/10.1016/j.ymssp.2010.06.005, 2010b.
Chen, Y., Wu, H., Zhai, J., Chen, H., Zhu, Q., and Han, Q.: Vibration reduction of the blisk by damping hard coating and its intentional mistuning design, Aerospace Sci. Technol., 84, 1049–1058, https://doi.org/10.1016/j.ast.2018.11.043, 2019.
Corral, R., Khemiri, O., and Martel, C.: Design of mistuning patterns to control the vibration amplitude of unstable rotor blades, Aerospace Sci. Technol., 80, 20–28, https://doi.org/10.1016/j.ast.2018.06.034, 2018.
Di Paolo, M., Nuzzo, I., Caterino, N., and Georgakis, C. T.: A friction-based passive control technique to mitigate wind induced structural demand to wind turbines, Eng. Struc., 232, 111744, https://doi.org/10.1016/j.engstruct.2020.111744, 2021.
Ferhatoglu, E. and Zucca, S.: On the Non-Uniqueness of Friction Forces and the Systematic Computation of Dynamic Response Boundaries for Turbine Bladed Disks with Contacts, Mechan. Syst. Signal Process., 160, 107917, https://doi.org/10.1016/j.ymssp.2021.107917, 2021.
Gao, J., Gao, Y., Yan, X., Jiang, J., Xu, K., and Sun, W.: Damping mistuning effect of the hard-coating-based intentional mistuning techniques on mistuned blisks and its mechanism, Aerospace Sci. Technol., 101, 105848, https://doi.org/10.1016/j.ast.2020.105848, 2020.
Guo, X. M., Ni, K. X., Ma, H., Zeng, J., Wang, Z. L., and Wen, B. C.: Dynamic response analysis of shrouded blades under impact-friction considering the influence of passive blade vibration, J. Sound Vib., 503, 116112, https://doi.org/10.1016/j.jsv.2021.116112, 2021.
Han, Y., Murthy, R., Mignolet, M. P., and Lentz, J.: Optimization of intentional mistuning patterns for the mitigation of the effects of random mistuning, J. Eng. Gas Turb. Power, 136, 062505, https://doi.org/10.1115/1.4026141, 2014.
Hou, J. and Cross, C.: Minimizing blade dynamic response in a bladed disk through design optimization, AIAA J., 43, 406–412, https://doi.org/10.2514/1.11526, 2005.
Huang, W. H.: Free and Forced Vibration of Closely Coupled Turbo-machinery Blades, AIAA J., 918–924, https://doi.org/10.2514/3.51020, 1981.
Joachim, J., Nyssen, F., and Batailly, A.: Numerical Investigation of a Mistuned Academic Bladed Disk Dynamics with Blade/Casing Contact, J. Eng. Gas Turb. Power, 143, 041028, https://doi.org/10.1115/1.4047780, 2021.
Kan, X. and Zhao, B.: A New Method of Reducing the Vibration Localization of the Multi-packet Whole Mistuned Bladed Disk System Using Bladed Packets, Int. J. Aeronaut. Space Sci., 22, 857–865, https://doi.org/10.1007/s42405-021-00369-9, 2021.
Kan, X., Xu, Z., Zhao, B., and Zhong, J.: Effect of Coriolis force on forced response magnification of intentionally mistuned bladed disk, J. Sound Vib., 399, 124–136, https://doi.org/10.1016/j.jsv.2017.03.002, 2017.
Khorasany, R. and Hutton, S. G.: Vibration characteristics of rotating thin disks – part i: experimental results, J. Appl. Mechan., 79, 1–11, https://doi.org/10.1115/1.4005539, 2012a.
Khorasany, R. M. H. and Hutton, S. G.: Vibration Characteristics of Rotating Thin Disks – Part II: Analytical Predictions, J. Appl. Mechan., 79, 1–11, https://doi.org/10.1115/1.4005810, 2012b.
Li, C. F., She, H. X., Tang, Q. S., Wen, B. C.: The coupling vibration characteristics of a flexible shaft – disk-blades system with mistuned features, Appl. Mathe. Modell. 67, 557–572, https://doi.org/10.1016/j.apm.2018.09.041, 2019.
Liu, C., Jiang, D. X., and Chu, F. L.: Influence of alternating loads on nonlinear vibration characteristics of cracked blade in rotor system, J. Sound Vib., 353, 205–219, https://doi.org/10.1016/j.jsv.2015.05.007, 2015.
Liu, Y., Han, J. Y., Xue, Z. Y., Zhang, Y., and Yang, Q.: Structural vibrations and acoustic radiation of blade–shafting–shell coupled system-sciencedirect, J. Sound Vib., 463, 114961, https://doi.org/10.1016/j.jsv.2019.114961, 2019.
Ma, H., Lu, Y., Wu, Z. y., Tai, X. y., and Wen, B. C.: Vibration response analysis of a rotational shaft-disk-blade system with blade-tip rubbing, Int. J. Mechan. Sci., 107, 110–125, https://doi.org/10.1016/j.ijmecsci.2015.12.026, 2016.
Martel, C. and Sanchez-Alvarez, J. J.: Intentional mistuning effect in the forced response of rotors with aerodynamic damping, J. Sound Vib., 433, 212–229, https://doi.org/10.1016/j.jsv.2018.07.020, 2018.
Martel, C., Corral, R., and Llorens, J. M.: Stability increase of aerodynamically unstable rotors using intentional mistuning, J. Turbo., 130, 011006, https://doi.org/10.1115/1.2720503, 2008.
Mehrdad Pourkiaee, S., Zucca, S., and Parker, R. G.: Relative cyclic component mode synthesis: A reduced order modeling approach for mistuned bladed disks with friction interfaces, Mechan. Syst. Signal Process., 163,108197, https://doi.org/10.1016/j.ymssp.2021.108197, 2022.
Nakos, A., Beirow, B., and Zobel, A.: Mistuning and Damping of a Radial Turbine Wheel. Part 1: Fundamental Analyses and Design of Intentional Mistuning Pattern, J. Eng. Gas Turb. Power, GT2021-59283, https://doi.org/10.1115/GT2021-59283, 2021.
Nikolic, M., Petrov, E. P., and Ewins, D. J.: Coriolis forces in forced response analysis of mistuned bladed disks, J. Turbomachin.-Trans. ASME, 129, 730–739, https://doi.org/10.1115/1.2720866, 2007.
Picou, A., Capiez-Lernout, E., Soize, C., and Mbaye, M.: Effects of geometrical nonlinearities for a rotating intentionally mistuned bladed-disk, in: Conference on Noise and Vibration Engineering (ISMA 2018), https://www.researchgate.net/publication/355029599 (last access: 16 December 2022), 2018.
Picou, A., Capiez-Lernout, E., Soize, C., and Mbaye, M.: Robust dynamic analysis of detuned-mistuned rotating bladed disks with geometric nonlinearities, Comput. Mechan., 65, 711–730, https://doi.org/10.1007/s00466-019-01790-4, 2020.
Repetckii, O. V.: Numerical Research of Vibrational Characteristics for Compressor Bladed Disks of an Energy Turbomachine with Intentional Mistuning of Blades, in: 2020 International Multi-Conference on Industrial Engineering and Modern Technologies IEEE, 1–6 pp., 6–9 October, Vladivostok, Russia, https://doi.org/10.1109/FarEastCon50210.2020.9271444, 2020.
Schlesier, K. D., Panning-von Scheidt, L., and Wallaschek, J.: Investigations on transient amplitude amplification by applying intentional mistuning, in: Turbo Expo: Power for Land, Sea, and Air Vol. 51159, V07CT35A011, https://doi.org/10.1115/GT2018-75514, 2018.
She, H. X., Li, C. F., Tang, Q. S., and Wen, B. C.: The investigation of the coupled vibration in a flexible-disk blades system considering the influence of shaft bending vibration, Mechan. Syst. Signal Process., 111, 545–569, https://doi.org/10.1016/j.ymssp.2018.03.044, 2018.
Tang, J. and Wang, K. W.: Vibration delocalization of nearly periodic structures using coupled piezoelectric networks, J. Vib. Acoust., 125, 95–108, https://doi.org/10.1115/1.1521951, 2003.
Xie, F. T., Ma, H., Cui, C., and Wen, B. C.: Vibration response comparison of twisted shrouded blades using different impact models, J. Sound Vib., 397, 171–191, https://doi.org/10.1016/j.jsv.2017.02.056, 2017.
Yoo, D., Lee, I., and Tang, J.: Reliability-oriented optimal design of intentional mistuning for a bladed disk with random and interval uncertainties, Eng. Optim., 49, 796–814, https://doi.org/10.1080/0305215X.2016.1206538, 2017.
Yu, H., Wang, K. W., and Zhang, J.: Piezoelectric networking with enhanced electromechanical coupling for vibration delocalization of mistuned periodic structures—theory and experiment, J. Sound Vib., 295, 246–265, https://doi.org/10.1016/j.jsv.2006.01.006, 2006.
Yutaek, O. and Hong Hee, Y.: Vibration analysis of a rotating pre-twisted blade considering the coupling effects of stretching, bending, and torsion, J. Sound Vib., 431, 20–39, https://doi.org/10.1016/j.jsv.2018.05.030, 2018.
Zhang, J., Wang, K. W., and Yu, H.: Active coupling enhancement of piezoelectric networks for vibration delocalization of nearly periodic structures. Proc. SPIE – The Int. Soc. Opt. Eng., 5056, 151–162, https://doi.org/10.1117/12.483441, 2003.
- Abstract
- Introduction
- Model of vibration of the tuned bladed disk
- Intentional mistuning of the bladed disk
- Novel model of the intentional mistuning bladed disk
- Results and discussions
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Model of vibration of the tuned bladed disk
- Intentional mistuning of the bladed disk
- Novel model of the intentional mistuning bladed disk
- Results and discussions
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References