the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Identification of eccentricity of a motorized spindle-tool system with random parameters
Qingqing Tang
Dan Feng
In order to improve the efficiency of identifying parameters using the maximum likelihood method and to avoid the sensitivity of initial values, a proposed method that combines the micro-genetic algorithm with the advance and retreat method is presented in order to identify the eccentricity of the spindle-tool system with random input and output parameters, which obey a certain probability distribution. Eccentricity without prior information is determined through an iterative procedure. The initial value starts from zero, and the interval is determined by the advance and retreat method. Then, the optimal value is searched in the corresponding interval, utilizing the micro-genetic algorithm. The initial value and interval at each of iterations are changed to ensure a fast and stable convergence. Eventually, a numerical example with three kinds of random deviations verifies the feasibility and validity of the proposed method.
- Article
(4093 KB) - Full-text XML
- BibTeX
- EndNote
The spindle system, which is mainly composed of the motor and the spindle and realizes “zero transmission” between the variable frequency motor and the machine tool spindle, is the core component of a precision grinding machine, and its dynamic performance directly determines the overall performance of the grinding machine. The imbalance is the main factor causing vibration of the spindle-tool system (Keiichi et al., 2009; Elhaj et al., 2019), where a tiny unbalance of the grinding wheel and spindle system can result in a severe vibration response of the supporting bearings during the high-speed grinding process. Unbalanced mass, resulting in eccentricity due to the center of the disc parts deviating from the centerline of the shaft, makes the unbalanced excitation proportional to the square of the speed. The unbalanced mass is the main source of vibration during the operation of the grinding machine. Identifying the eccentricity of the spindle-tool system can effectively eliminate the mass imbalance of the machine tool by utilizing online dynamic balance technology (Zhan and Wei, 2017; Pan et al., 2019; Xul et al., 2017). The technique of eccentricity parameter identification solves an inverse problem aiming at estimating inputs via given outputs, where the concerned structure parameters are treated as unambiguous values. However, due to the complexity of the processing and running environment and the change of material properties, the motorized spindle-tool system is a random system, and the parameters are uncertain; that is, the eccentricity identification problem is uncertain. The accuracy of identified results can hardly be evaluated using traditional deterministic inverse problem methods. Therefore, how to deal with the random factors and quickly identify eccentricity has become a research hotspot in the field of precision grinding machines. It is also a significant problem in the process of eccentricity recognition. According to the difference in the sources of uncertainties and the amount of available information, Meng et al. (2020) and Liu et al. (2018, 2020) developed a probability method and evidence theory model for quantifying uncertainties to convert the uncertainty propagation into multiple deterministic calculations. For the spindle-tool system, the uncertainties coming from random parameters can be modeled with the probability method.
The imbalance fault is the coupling effect of multiple eccentricities, such as the unbalanced magnetic pulling force caused by the motor eccentricity and the unbalanced excitation force caused by the grinding wheel eccentricity. The a priori information of each eccentricity is difficult to know. The eccentricity identification problem without a prior information and the given input and output parameters with random factors can be dealt with using the maximum likelihood method to transform the recognition problem into an iterative problem. The iterative technique, aiming at estimating inputs via a process of constantly updating old values with the new values of input variables, has received increasing attention due to its efficiency and accuracy (Yang et al., 2014; Xia, 2019; Feng et al., 2018). Zhang (2013) obtain the explicit increment by utilizing the sensitivity matrix method (SMM); the explicit method avoids complicated mathematical processing, but the iterative efficiency is low. Mao et al. (2020) adjusts the iterative increment to reduce the objective function value by utilizing the advance–retreat method in the iterative process, but the “sawtooth” phenomenon approaching the optimal solution affects its accuracy and efficiency. A commonly encountered difficulty with the iterative algorithm is that it is often difficult to converge and easy to diverge due to the sensitivity of the initial value resulting from nonlinear characteristics (Liang et al., 2013). As for the eccentricity identification problem, another difficulty is that the eccentricity search interval required in the conventional iterative method cannot be specified because there is no a priori information.
In accordance with the present problem, a proposed method is presented by combining the advance and retreat method (ARM) (Ma et al., 2017) with the micro-genetic algorithm (uGA) (Liu et al., 2012; Harbrecht and Loos, 2016) in this paper. In the iterative procedure, the initial value starts from zero, the iterative increment is obtained by the explicit method (Zhang, 2013), the search interval in each iterative step is obtained by ARM, and the initial value of eccentricity is updated by the local optimal solution searched in the corresponding search interval by the uGA. In the iterative procedure, the initial value, the iterative increment, and the search interval are gradually changed until the error between the calculated and observed unbalanced response is within the specified toleration.
2.1 Theoretical background
Eccentricity identification of the motorized spindle-tool system with random factors aims at estimating the unknown eccentricity Xu from the observed unbalanced response Yk, together with the known input parameter Xk and the established solver T, as shown in Fig. 1.
In Fig. 1, is the output unbalanced response; denotes the input parameters causing the unbalanced response; and T is a forward problem solver for calculating the output Y from the input X (as shown in Eq. 1) using the finite element analysis method (FEA) (Kong et al., 2020). The subscripts k and u respectively denote the known and unknown parts. The uncomplete known parameter vector Xk and Yk obey the probability density distribution.
where , , and q respectively represent the acceleration, velocity, and displacement vector of the rotor; M, K, and C respectively represent the mass, stiffness, and damping matrix of the motorized spindle-tool system; and the force vector F is composed of the mass unbalanced exciting force caused by the shaft rotational speed ω with eccentricity.
Presently, the inverse problem with random parameters is solved using the maximum likelihood method and the Markov chain Monte Carlo method (MCMC) (Zhang, 2013). In the maximum likelihood method, by introducing the sensitive matrix S (Liu et al., 2001), the random information of the uncomplete known parameters Xk and Yk can be transformed into the explicit solvable form (Zhang, 2013); that is, the eccentricity increment B, as shown in Eq. (2), can be solved in the iterative process.
where , , , , and . and are the deviations of the ith known parameter vector Xk and Yk. is the variation of the output unbalanced response q, is the variation of X, respectively, and m and n are the number of q and X, respectively.
However, the explicit method can avoid the high-dimensional integral problem in the uncertainty inverse problem using the sensitive matrix together with the similar least-squares form; it is still difficult to search the for optimal value of unknown parameters in many cases. This is because such an unbalanced response Y may not be linear to the input unknown eccentricity to produce divergence due to the unknown eccentricity interval and difficulty to converge due to the sensitivity of the initial value problem (Triet et al., 2020). To effectively overcome the problem, it has been proposed to introduce the micro-genetic algorithm and advance and retreat method to the maximum likelihood method in this paper, so that the initial value and interval in each iteration are variable, and the initial value starts from zero.
2.2 The advance and retreat method
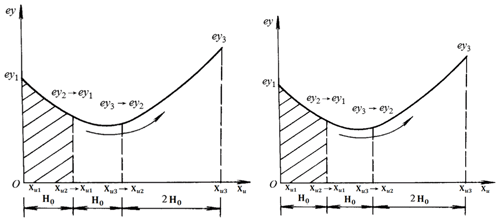
The eccentricity in the maximum likelihood is identified by repeated iterations until the error between the calculated unbalanced response and the observed unbalanced response is within the specified toleration. Selecting the information includes the search interval due to the unknown bounds of eccentricity in engineering practice, and the initial eccentricity will greatly influence the efficiency and precision in the search of a total solution to the problem. The advance and retreat method can obtain a search interval based on a “high–low–high” morphology, as shown in Fig. 2.
This procedure is conducted by comparing the mean square error ey1, ey2 with ey3 between the observed unbalanced response and the calculated unbalanced response Y from the solution T(Xui, Xk) together with three eccentricities: the initial point Xu1, the middle point Xu2, and the end point Xu3. The interval problem can be mathematically represented as Eq. (3).
The unknown eccentricity increment B from the solution the Eq. (2) is the initial step H0. Assuming the initial eccentricity Xu1, , the corresponding unbalanced response {Y1, Y2} to {Xu1, Xu2} can be calculated through the forward solver T(Xu, Xk) with the known parameters Xk. Calculating the mean square error ey1, ey2 centering on the present parameters , the end point Xu3 can be constructed based on the mean square error ey1, ey2. The mean square error ey3 is calculated again using the newly obtained Xu3. The lower bound and the upper bound of the search interval are found by comparing ey2 with ey3.
2.3 Micro-genetic algorithm
Once the forward solver and search interval are determined, the eccentricity identification problem is transferred to an optimization problem, shown as follows:
-
find eccentricity, Xu,
-
for given conditions and
-
by .
The optimization problem aims at finding the optimal solution of eccentricity which can meet this condition that the errors eY between the observed unbalanced response with the calculated unbalanced response Y is within the specified toleration through constantly updating input parameters to correct the solution T(Xu,Xk). Updating the input parameters to find the optimal solution with high efficiency and precision is key in iterative algorithms. The micro-genetic algorithm updates the input parameters starting with a small sample, and the “precocious” phenomenon in the search interval can be avoided (Liu et al., 2012).
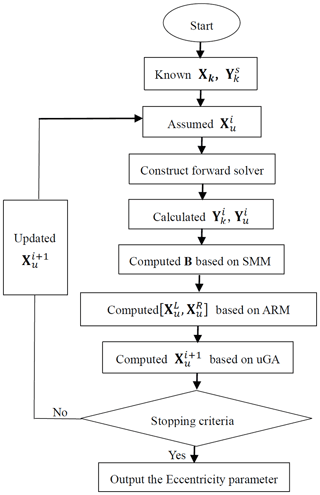
As mentioned above, the computational procedure of obtaining eccentricity of the motorized spindle-tool system with random distribution (normal distribution) can be described in Fig. 3:
-
Step 1. Specify toleration ε and the probability density distribution , , and get known output parameters .
-
Step 2: Assume the initial eccentricity . Combine them together with the mean value of the known parameter Xk into the forward solver T(Xu,Xk) of the motorized spindle-tool system to calculate the corresponding unbalanced response .
-
Step 3: Compute the eccentricity increment vector B using Eq. (2), and find the corresponding search interval , combining and B using the advance and retreat method.
-
Step 4: Obtain a new set of eccentricity in the search interval using the micro-genetic algorithm, and combine them with the mean value of the known parameter Xk into the forward solver T(Xu,Xk) of the motorized spindle-tool system to calculate the corresponding output . Compare the errors eY between the calculated and the known ; if the error is within the predefined toleration, this parameter value is considered to be the total optimal solution of the problem. The iterative process ends. Otherwise, , and go back to step (2) to compute the new output , together with the updated .
4.1 Recognition model
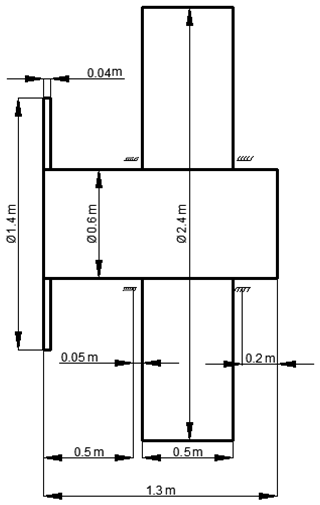
The motorized spindle-tool system (Mao et al., 2020), shown in Fig. 4, is considered to verify the proposed method, and details of the numerical model are listed in Table 1. When the rotor is not eccentric, the average air gap length is 8 mm, the air magnetic conductivity coefficient is , and the fundamental MMF (magneto-motive force) coefficient of the air gap is 5.2. The rotation frequency of the unit is 100 Hz.
If eccentricity (e1,e2) can be provided completely, the unbalanced response can easily be obtained by FEA using the Euler–Bernoulli beam theory as a reference (Michael et al., 2010). For testing the proposed algorithms, eccentricity (e1,e2) is assumed as the unknown parameter, consistent with the model in the literature (Mao et al., 2020). It is difficult to identify eccentricity based on the conventional maximum likelihood method due to the lack of necessary search interval (see Fig. 3). According to the proposed approach, we first treat this problem as an identification of eccentricity with random parameters, where the unbalanced responses (d1,d2) at the grinding wheel and shaft end are experimentally obtainable. These parameters are set up as follows: , , , , , . The mass, damping, and stiffness matrices of the motorized spindle-tool system based on Eq. (1) are established using the Euler–Bernoulli beam theory as a reference (Michael et al., 2010). FEA is used to deal with the forward problem.
The true values of eccentricity (e1,e2) are assumed as [20, 100 µm], and the true unbalanced responses (d1,d2) corresponding to [20, 100 µm] are easily calculated to be 33.0594 and 23.0366 µm through FEA, respectively. In order to compared with the literature (Mao et al., 2020), taking the measurement deviation of 1 % as a random deviation, the length and diameter of motor are expressed as L ∼ N(0.5,0.0052) m and m, respectively. And the unbalanced responses are µm and µm, respectively, in which the symbol “∼” means “obey on”, and d1 represents the random distribution, with 33.0594 µm as the mean and 0.3306 µm as the deviation.
4.2 Solving process
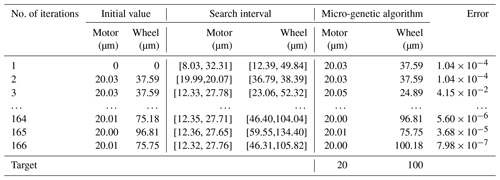
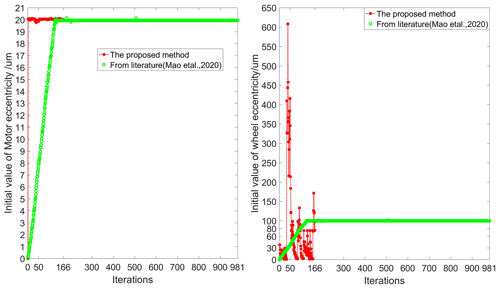
In this example, the stop criterion constant is set to , and the parameters used by the uGA are as follows: the size of the population is 5, the maximum number of iterations is 300, the crossover probability is 0.9, and the mutation probability is 0.05. The initial value of eccentricity {e1,e2} is {0,0 µm}, which is combined with the forward solver FEA. The eccentricity increment B is calculated from Eq. (2). The corresponding eccentricity intervals of the motor and wheel are calculated to be [8.03, 32.31] µm and [12.39, 49.84] µm, respectively, according to ARM. In this interval, the eccentricity {20.03,37.59 µm} with the minimum error corresponding to is obtained by the micro-genetic algorithm, as shown in the third row of Table 2. The error is larger than the predefined toleration. Substituting the initial value of eccentricity {e1,e2} with the updated values of {20.03,37.59 µm}, and combining them together with the forward solver FEA once again, the corresponding eccentricity increment B and a new eccentricity {20.03,37.59 µm} are calculated, as shown in the fourth row of Table 2. After 166 iteration steps, the error between the calculated and the known unbalanced response is within the predefined toleration ; the eccentricity {20.00,100.18 µm} is considered to be the global optimal solution of the problem. The corresponding solution procedures are listed in Table 2. The comparison results of the iterative process of initial eccentricity in Fig. 5 show that, using the method from the literature (Mao et al., 2020), the sawtooth phenomenon occurs approaching the optimal solution; that is, in the method from the literature (Mao et al., 2020), the zigzag route is taken when the iterative point approaches the optimal point, which leads to slower convergence. In general, compared with other algorithms (Mao et al., 2020), this proposed method improves the computational efficiency of the maximum likelihood method and avoids the sensitivity of the initial value.
4.3 Discussion under different random deviations
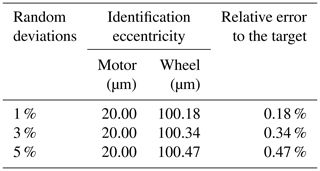
In the section, three different random deviations of 1 %, 3 %, and 5 % are provided to verify the robustness of the proposed method. The convergence history of the corresponding solution procedure is shown in Fig. 6. The initial value starts from zero. Fig. 6a and b show linear parameters (motor eccentricity to affect linearly the unbalance) can be quickly identified, and the interval and updated initial value of the nonlinear parameters (wheel eccentricity to affect the unbalance nonlinearly) are close to the real situation at about 150 steps. It shows the proposed method is suitable not only for linear parameters, but also for nonlinear parameters by introducing the uGA for finding the optimal value in the corresponding interval obtained by ARM at each of the iterations. Figure 6c shows that the uGA can gain the local optimal solution of the corresponding interval in 200 iterative steps. The maximum iterative step of the uGA is the main factor affecting the convergence speed of this proposed method, which can be adjusted according to the situation. However, according to MCMC, a commonly used probability method that deals with randomness uncertainty, MCMC sampling with 106 samples (Zhang, 2013) must be carried out to compute all possible marginal probability densities in each interval in order to validate the accuracy of the identified results. So, the proposed method improves its efficiency. It is known from Fig. 6 that the identification results are less affected by the Gaussian noise deviation; that is, the robustness of the proposed method is good. The identification results are summarized in Table 3. It is also shown that the identification results are accurate and robust when random deviations are considered. Even when the random deviation is up to 5 %, the identification results are still satisfactory.
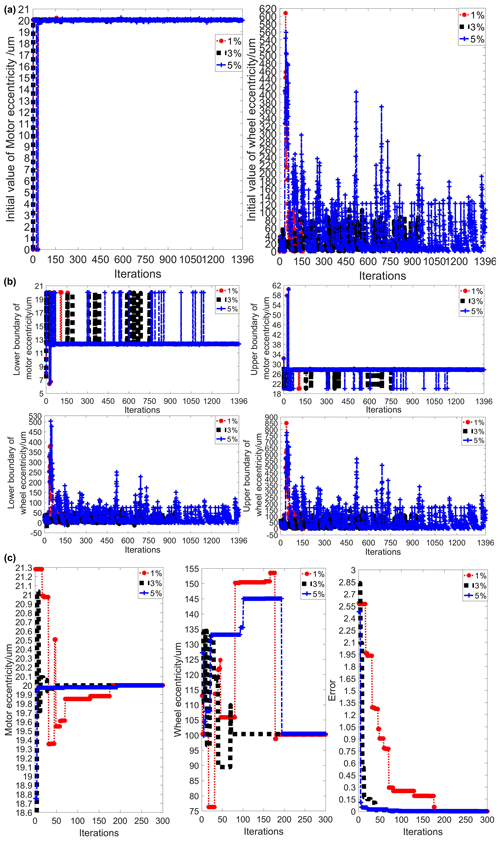
Figure 6The convergence process of the corresponding solution at each of the iterations. (a) Iterative process of initial eccentricity. (b) Iterative process of interval search. (c) Iterative process of the uGA in the last interval.
In the present paper, a proposed method that combines ARM and the uGA is presented to identify the eccentricity of a motorized spindle-tool system with random parameters. A numerical example is studied and used to illustrate the feasibility and validity of the proposed method. The following novelties and conclusions can be derived from this study:
-
The unknown uncertain input and output parameters are characterized as random variables.
-
The proposed method allows the initial value, the iterative increment, and the search interval to be gradually changed at each of the iterations, and the initial value starts from zero, which avoids the sensitivity of the initial value and ensures a stable convergence of the solution procedure.
-
It can be used as a reference for dealing with the inverse problem of random uncertainty in engineering.
The authors confirm that the data supporting the conclusions of the article are shown in the relevant figure and tables in the article.
WM established an overall research framework, QT conducted detailed optimization and data experiments for the overall paper, and DF carried out paper revisions and organized financial support of the paper.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research has been supported by the National Natural Science Foundation of China (grant no. 51775180) and the Hunan Provincial Natural Science Foundation of China (grant no. 2019JJ60036).
This paper was edited by Dario Richiedei and reviewed by two anonymous referees.
Elhaj, A. I. A., Li, S. S., and Mohammed, N.: Optimization of Factors Affecting Vibration Characteristics of Unbalance Response for Machine Motorized Spindle Using Response Surface Method, Math. Probl. Eng., 2019, 1–12, https://doi.org/10.1155/2019/1845056, 2019.
Feng, H. H., Wang, Y. R., and Jiang, X. H.: A Maximum Likelihood Method for Estimating Probabilistic Strain Amplitude-Fatigue Life Curves, Acta Mech. Solida Sin., 31, 80–93, https://doi.org/10.1007/s10338-018-0002-1, 2018.
Harbrecht, H. and Loos, F.: Optimization of current carrying multicables, Comput. Optim. Appl., 63, 237–271, https://doi.org/10.1007/s10589-015-9764-2, 2016.
Keiichi, N., Shinya, M., Kazuhiko, A., and Keiichi, S.: A Machine Tool Spindle Achieving Real-Time Balancing Using Magnetic Fluid, International Journal of Automation Technology, 3, 193–198, https://doi.org/10.20965/ijat.2009.p0193, 2009.
Kong, Q. S., Yu, Z. H., Mao, X. Y., Zhou, J., Li, F., Li, H., and Tang, J.: Rotation error modeling and compensation of spindle based on Clarke transformation in straightness error measurement of regular hexagon section shaft, Measurement, 166, 1–10, https://doi.org/10.1016/j.measurement.2020.108233, 2020.
Liang, X. W., Gong, W., Fu, W. L., and Qi, J.: Research on the Initial Value of the Simulated Annealing, Adv. Mat. Res., 2586, 1770–1773, https://doi.org/10.4028/www.scientific.net/AMR.774-776.1770, 2013.
Liu, G. P., Han, X., and Jiang, C.: An efficient multi-objective optimization approach based on the Micro genetic algorithm and its application, Int. J. Mech. Mater. Des., 8, 37–49, https://doi.org/10.1007/s10999-011-9174-2, 2012.
Liu, G. R., Xu, Y. G., and Wu, Z. P.: Total solution for structure mechanics problems, Comput. Method. Appl. M., 19, 1989–1012, https://doi.org/10.1016/S0045-7825(01)00314-0, 2001.
Liu, J., Meng, X. H., Xu, C., Zhang, D. Q., and Jiang, C.: Forward and inverse structural uncertainty propagations under stochastic variables with arbitrary probability distributions, Comput. Method. Appl. M., 342, 287–320, https://doi.org/10.1016/j.cma.2018.07.035, 2018.
Liu, J., Cao, L. X., Jiang, C., Ni, B. Y., and Zhang, D. Q.: Parallelotope-formed evidence theory model for quantifying uncertainties with correlation, Appl. Math. Model., 77, 32–48, https://doi.org/10.1016/j.apm.2019.07.017, 2020.
Ma, K., Bai, Y., Yang, J., Yu, Y. Q., and Yang, Q. X.: Demand-Side Energy Management Based on Nonconvex Optimization in Smart Grid, Energies, 10, 1–17, https://doi.org/10.3390/en10101538, 2017.
Mao, W. G., Hu, C. L., Li, J. H., Huang, Z. H., and Liu, G. P.: Eccentricity Parameters Identification for a Motorized Spindle System Based on Improved Maximum Likelihood Method, Shock Vib., 2020, 1–10, https://doi.org/10.1155/2020/5491957, 2020.
Meng, X. H., Liu, J., Cao, L. X., Yu, Z. B., and Yang, D. M.: A general frame for uncertainty propagation under multimodally distributed random variables, Comput. Method. Appl. M., 367, 1–21, https://doi.org/10.1016/j.cma.2020.113109, 2020.
Michael, F., John, E. T. P., and Seamus, D. G.: Dynamics of Rotating Machines, Cambridge university press, ISBN 9-7805-117805-09, https://doi.org/10.1017/CBO9780511780509, 2010.
Pan, X., He, X. T., Wei, K. Z., Wu, H. Q., Gao, J. J., and Jiang, Z. N.: Performance Analysis and Experimental Research of Electromagnetic-Ring Active Balancing Actuator for Hollow Rotors of Machine Tool Spindles, Applied Sciences, 9, 1–19, https://doi.org/10.3390/app9040692, 2019.
Triet, N. A., Binh, T. T., Phuong, N. D., Baleanu, D., and Can, N. H.: Recovering the initial value for a system of nonlocal diffusion equations with random noise on the measurements, Math. Method. Appl. Sci., 44, 5188–5209, https://doi.org/10.1002/mma.7102, 2020.
Xia, L. G.: Study of constraint and impact of a nuisance parameter in maximum likelihood method, J. Phys. G Nucl. Partic., 46, 1–22, https://doi.org/10.1088/1361-6471/ab02c0, 2019.
Xul, J., Zheng, X. H., Zhang, J. J., and Liu, X.: Vibration Characteristics of Unbalance Response for Motorized Spindle System, Proced. Eng., 174, 331–340, https://doi.org/10.1016/j.proeng.2017.01.148, 2017.
Yang, X., Xiong, W., Huang, B., and Gao, H.: Identification of Linear Parameter Varying Systems with Missing Output Data Using Generalized Expectation-Maximization Algorithm,IFAC-Papers OnLine, 47, 9364–9369, https://doi.org/10.3182/20140824-6-ZA-1003.00527, 2014.
Zhan, W. and Wei, T.: Online Dynamic Balance Detection Method of High Speed Motorized Spindle Based on LabVIEW, Appl. Mech. Mater., 868, 369–374, https://doi.org/10.4028/www.scientific.net/AMM.868.369, 2017.
Zhang, W.: The research on engineering inverse problems under uncertainty based on probability and interval, doctoral thesis, Hunan University, Changsha, 2013 (in Chinese).