Denim-fabric-polishing robot size optimization based on global spatial dexterity

This paper presents a novel method to make denim-fabric-polishing robots perform their primary task flexibly and efficiently within a limited workspace. Link lengths are optimized based on an adaptive fireworks algorithm to improve the comprehensive dexterity index. A forward kinematics analysis of the denim-fabric-polishing robot is conducted via the D–H method; the workspace is analyzed according to the needs at hand to determine the range of motion of each joint. To solve the movement condition number of the Jacobian matrix, the concept of low-condition-number probability is established, and a comprehensive dexterity indicator is constructed. The influence of the robot's size on the condition number and comprehensive dexterity index is determined. Finally, the adaptive fireworks algorithm is used to establish the objective optimization function by integrating the dexterity index and other performance indicators. The optimization results show that when the comprehensive dexterity index is taken as the optimization objective, the dexterity comprehensive index and other performance indices of the robot are the lowest; that is, the robot is more flexible. Compared with the traditional genetic algorithm and particle swarm algorithm, the adaptive fireworks algorithm proposed in this paper has better solving speed and solving precision. The optimized workspace of the robot meets the requirements of the polishing task. The design also yields a sufficiently flexible, efficient, and effective robot.

1 Introduction

Recent years have seen notable advancements in robotics technology and an increase in the popularity of robotics applications in various industries. Textile and clothing enterprises have gradually begun to replace human beings with robots to reduce the cost of labor. Robots may be utilized to polish denim fabric (Liu et al., 2014), for example. These robots must be designed for high flexibility, high efficiency, and high precision.

It is crucial that robots be designed with sufficient flexibility in order to properly adapt to various working environments. Many scholars target the size of the robot to this effect, as size markedly influences flexibility. Luo et al. (2020) and Ning et al. (2015), for example, used computer-aided engineering (CAE) software to optimize their robots' sizes for enhanced performance. They used the finite-element method, however, which only optimizes the size of the fixed pose of the robot. Shen et al. (2013) defined workspace flexibility on the basis of a service ball and then redesigned the structural parameters of a cotton fiber sorting robot accordingly. Sun et al. (2019, 2020a) proposed a generalized inverse description method based on the finite instantaneous screw theory, which improved the accuracy of the manipulator. Considering the uncertainty of parameters, they proposed a design method to minimize vibration and deformation to optimize the manipulator. Jia et al. (2015) established the posture maneuverability concept, which can be used as an index to optimize the size of a given machine. However, this requires solving highly complex inverse kinematics problems.

There have been many other valuable contributions to the literature. Gosselin and Angeles (1988, 1991) took the condition number of a Jacobian matrix as the main factor to design a robot structure. Li et al. (2013), Gan et al. (2014), and Tian et al. (2013) optimized the structural parameters of a robot with the workspace as a constraint. Gao et al. (2011) established flexible polishing point and flexible polishing space concepts under which the position and size of a robot can be optimized relative to the workpiece. Deng et al. (2017) proposed workspace, static stiffness, and global velocity fluctuation indices for optimizing the size and quality of a robot arm. Sun et al. (2020b) and Sun and Lian (2018) proposed a probabilistic safety factor, which takes the probability density function as the constraint condition to optimize a new type of parallel machine tool. Quan et al. (2017) optimized a set of robot parameters by covering the minimum workspace, connecting the link lengths, and establishing comprehensive optimization indices. Most of the above methods for size optimization are genetic algorithms, which have the disadvantages of relatively low accuracy and slow convergence (Aghazadeh Heris and Oskoei, 2014; Tinós et al., 2018).

The fireworks algorithm (FWA) is an intelligent optimization algorithm first proposed by Tan and Zhu (2010) in 2010. It has become a popular research topic as per its simple parameters and strong solution performance. Xue et al. (2017) applied FWA to discretize an optimization field and effectively solved a multidimensional knapsack problem. Li et al. (2015) improved the FWA for precise parameter estimation in a chaos control system. Li et al. (2018) applied the improved FWA to multiprocessor task scheduling and achieved good results. Babu et al. (2016) used the improved FWA to solve unknown parameters in the dual diode model of a photovoltaic (PV) module. Reddy et al. (2016) used FWA to solve the scheduling problem in a smart power grid.

The denim-fabric-polishing robot should be designed for maximum flexibility and stability to effectively complete its task. The “low-condition-number probability” concept was developed in this study; a comprehensive evaluation index and mean space condition number indicator were also used to finalize the proposed robot design. The influence of link length on the condition number of the robot was calculated to determine the target link to be optimized. The adaptive FWA was then used to optimize the target function and optimize the robot's size for the given task.

2 Kinematics and workspace analysis of denim-fabric-polishing robot

2.1 2.1 kinematics analysis

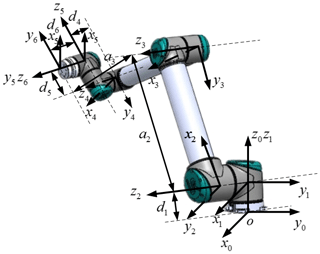
The mechanical body of the denim-fabric-polishing robot discussed here is composed of a Universal Robots (UR) robot and grinding head. The kinematic model of the robot is an important theoretical basis for workspace analysis, motion planning, and parameter optimization. The forward kinematics model of this robot was established via the D–H method. The kinematic coordinate system is shown in Fig. 1, and the link parameters are given in Table 1.

Figure 1 Joint coordinate system of jean-fabric-grinding robot.

Table 1 D–H parameter table of jean-fabric-grinding robot.

The transformation matrix ${}_i^{i-\mathrm{1}}\mathbf{T}$ of the ith link of the robot is

$$\begin{array}{}\text{(1)}& {}_i^{i-\mathrm{1}}\mathbf{T}=\left[\begin{array}{cccc}\cos {\mathit{\theta }}_i& -\sin {\mathit{\theta }}_i\cos {\mathit{\alpha }}_i& \sin {\mathit{\theta }}_i\sin {\mathit{\alpha }}_i& a_i\cos {\mathit{\theta }}_i\\ \sin {\mathit{\theta }}_i& \cos {\mathit{\theta }}_i\cos {\mathit{\alpha }}_i& -\cos {\mathit{\theta }}_i\sin {\mathit{\alpha }}_i& a_i\sin {\mathit{\theta }}_i\\ \mathrm{0}& \sin {\mathit{\alpha }}_i& \cos {\mathit{\alpha }}_i& d_i\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right].\end{array}$$

According to the D–H parameter, the transformation matrix ${}_{\mathrm{1}}^{\mathrm{0}}\mathbf{T}$ of the first link is

$$\begin{array}{}\text{(2)}& {}_{\mathrm{1}}^{\mathrm{0}}\mathbf{T}=\left[\begin{array}{cccc}\cos {\mathit{\theta }}_{\mathrm{1}}& \mathrm{0}& \sin {\mathit{\theta }}_{\mathrm{1}}& \mathrm{0}\\ \sin {\mathit{\theta }}_{\mathrm{1}}& \mathrm{0}& -\cos {\mathit{\theta }}_{\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& d_{\mathrm{1}}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right].\end{array}$$

${}_{\mathrm{2}}^{\mathrm{1}}\mathbf{T}$, ${}_{\mathrm{3}}^{\mathrm{2}}\mathbf{T}$, ${}_{\mathrm{4}}^{\mathrm{3}}\mathbf{T}$, ${}_{\mathrm{5}}^{\mathrm{4}}\mathbf{T}$, and ${}_{\mathrm{6}}^{\mathrm{5}}\mathbf{T}$ can be obtained similarly. The transformation matrix of the links can be multiplied to obtain the transformation matrix ${}_{\mathrm{6}}^{\mathrm{0}}\mathbf{T}$ of the end of the denim-fabric-polishing robot relative to the base coordinates:

$$\begin{array}{ll}\text{(3)}& {}_{\mathrm{5}}^{\mathrm{4}}{\mathbf{T}}_{{}_{\mathrm{6}}^{\mathrm{0}}\mathbf{T}}& {\displaystyle }={}_{\mathrm{1}}^{\mathrm{0}}\mathbf{\text{T}}{}_{\mathrm{2}}^{\mathrm{1}}\mathbf{\text{T}}{}_{\mathrm{3}}^{\mathrm{2}}\mathbf{\text{T}}{}_{\mathrm{4}}^{\mathrm{3}}\mathbf{\text{T}}{}_{\mathrm{5}}^{\mathrm{4}}\mathbf{\text{T}}{}_{\mathrm{6}}^{\mathrm{5}}\mathbf{\text{T}}{\displaystyle }& {\displaystyle }=\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\\ {\displaystyle }& {\displaystyle }=\left[\begin{array}{cc}R& P\\ \mathrm{0}& \mathrm{1}\end{array}\right].\end{array}$$

2.2 Workspace analysis of denim-fabric-polishing robot

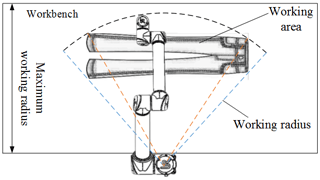
In the process of denim polishing, site space and actual polishing space restrictions limit the range of joint corners and link size. A diagram of the polishing workspace is shown in Fig. 2.

Figure 2 Schematic workspace diagram of denim-polishing process.

The worktable length is 2 m, and the worktable width (maximum working radius) is $r_{max}=\mathrm{1}$ m. To maximize the working range of the robot, it is placed in the middle of the 2 m side of the worktable edge. The maximum length and width of the denim fabric piece are l=1.1 m and d=0.5 m, so its working radius is smallest (r_min) when it is near the robot side:

$$\begin{array}{}\text{(4)}& r_{min}=\sqrt{{\left({\displaystyle \frac{l}{\mathrm{2}}}\right)}^{\mathrm{2}}+d^{\mathrm{2}}}=\mathrm{0.7434}\mathrm{m}.\end{array}$$

The Monte Carlo method can be used to determine the workspace of the robot at different time points across the turning angle range. According to the working requirements of the robot, the turning angle range of each joint is determined by trial and error:

$$\begin{array}{}\text{(5)}& \left\{\begin{array}{l}{\mathit{\theta }}_{\mathrm{1}}=\left[-\mathit{\pi }/\mathrm{2},\mathit{\pi }/\mathrm{2}\right]\\ {\mathit{\theta }}_{\mathrm{2}}=\left[\mathrm{0},\mathit{\pi }/\mathrm{2}\right]\\ {\mathit{\theta }}_{\mathrm{3}}=\left[-\mathit{\pi }/\mathrm{2},\mathrm{0}\right]\\ {\mathit{\theta }}_{\mathrm{4}}=\left[-\mathit{\pi }/\mathrm{2},\mathrm{2}\mathit{\pi }/\mathrm{2}\right]\\ {\mathit{\theta }}_{\mathrm{5}}=\left[-\mathit{\pi }/\mathrm{2},\mathrm{2}\mathit{\pi }/\mathrm{2}\right]\\ {\mathit{\theta }}_{\mathrm{6}}=\left[\mathrm{0},\mathit{\pi }/\mathrm{2}\right].\end{array}\right.\end{array}$$

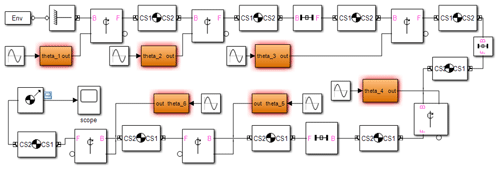
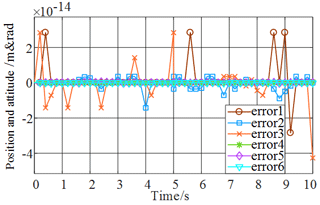
The mechanism model of the denim-fabric-polishing robot was established in SimMechanics as is shown in Fig. 3. The end position of the robot was obtained given the same joint angle input of the SimMechanics mechanism model and the mathematical model (Eqs. 1–3). The error of the end position of the two models, which validates the mathematical model presented above, is shown in Fig. 4.

Figure 3 Model drawing of denim-fabric-polishing robot mechanism.

Figure 4 End position error.

Randomly taking the values in each joint range as the angle input value, the position of the end of the robot in the workspace can be obtained according to Eqs. (1)–(3). A workspace with 15 000 cycles was obtained here under the initial link size condition as shown in Fig. 5.

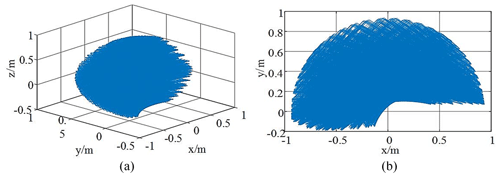
Figure 5 Schematic workspace with initial link size. (a) Three-dimensional workspace. (b) Workspace XY plane projection.

According to the projection of the XY plane of the workspace in Fig. 5b, the maximum motion radius of the denim-fabric-polishing robot is 0.9117 m. The robot's motion radius is between 0.7434 and 1 m, so its workspace meets the polishing requirements in this case.

3 Flexibility index of denim-fabric-polishing robot

Flexibility is one of the most widely used indices for evaluating the motion performance of robots. “Flexibility” in this context refers to the number of postures that can be obtained by the end tool when the end reference point of the robot is located at a certain point in the workspace. The condition number of the Jacobian matrix indicates the robot's level of dexterity; the matrix itself represents the linear mapping between the operating space velocity and the joint space velocity of the end of the robot. The Jacobian matrix can be solved directly by a predefined method, The robot has six rotating joints, so only differential rotations were considered. The ith column of the Jacobian matrix representative of the rotating joints is

$$\begin{array}{}\text{(6)}& {\mathit{J}}_i=\left[\begin{array}{c}{\left(\mathit{p}\times \mathit{n}\right)}_z\\ {\left(\mathit{p}\times \mathit{o}\right)}_z\\ {\left(\mathit{p}\times \mathit{a}\right)}_z\\ n_z\\ o_z\\ a_z\end{array}\right]=\left[\begin{array}{c}{p}_x{n}_y-p_y{n}_x\\ p_x{o}_y-p_y{o}_x\\ p_x{a}_y-p_y{a}_x\\ n_z\\ o_z\\ a_z\end{array}\right],\end{array}$$

where n, o, a, and p denote the four column vectors of the transformation matrix ${}_{\mathrm{6}}^i\mathbf{T}$.

The expression of the transformation matrix ${}_{\mathrm{6}}^i\mathbf{T}$ can be obtained by the following formula.

$$\begin{array}{}\text{(7)}& {}_{\mathrm{6}}^i\mathbf{T}={}_{i+\mathrm{1}}^i\mathbf{T}\cdot {}_{i+\mathrm{2}}^{i+\mathrm{1}}\mathbf{T}\cdot \mathrm{\dots }\cdot {}_{\mathrm{6}}^{\mathrm{5}}\mathbf{T}=\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\end{array}$$

The condition number is defined as the ratio of the maximum singular value to the minimum singular value of a Jacobian matrix, that is

$$\begin{array}{}\text{(8)}& K={\displaystyle \frac{{\mathit{\sigma }}_{max}\left(\mathbf{J}\right)}{{\mathit{\sigma }}_{min}\left(\mathbf{J}\right)}}.\end{array}$$

Variables σ_max(J) and σ_min(J) represent the maximum and minimum singularities of the Jacobian matrix, respectively, and J is the Jacobian matrix. The range of condition numbers is $[\mathrm{1},+\mathrm{\infty }]$. A smaller condition number indicates a more flexible robot with better performance.

Because the condition number is only related to the turning angle and structure size of the robot joint, which reflects the ability of the robot to move in the specified position and posture (but not in the task space), a global spatial condition number mean (GCI) index was established in this study. The condition number was averaged in the whole motion space to build an indicator that reflects the flexibility of the robot's kinematics in the whole motion space:

$$\begin{array}{}\text{(9)}& \text{GCI}={\displaystyle \frac{{\int }_{W}K\mathrm{d}w}{{\int }_W\mathrm{d}w}},\end{array}$$

where K is the condition number under the specified position and W is the global workspace.

A new dexterity index was established based on the mean of the spatial condition number to reflect the fluctuations discussed above: low condition probability (LCP), the percentage α of the number of locations with condition numbers lower than the mean of the spatial condition number b in the space location number n after discretizing the points in the reachable operation space of the task space. When α=0.5, the condition number distribution is uniform and there are no large fluctuations. As α approaches 0, the condition number fluctuates greatly but the overall condition value is high. When α approaches 1, the condition number fluctuates greatly, but the overall condition value is low. A larger LCP value indicates the overall operability of the robotic arm better.

$$\begin{array}{}\text{(10)}& \mathit{\alpha }={\displaystyle \frac{b}{n}}\end{array}$$

The effects of the above two indicators on the dexterity of the robot must be unified to be interpreted properly. The LCP is $\mathit{\alpha }=[\mathrm{0},\mathrm{1}]$, so weighting it directly has little effect on the results. To increase the order of the LCP, weighting was applied to form the comprehensive flexibility index (CFI):

$$\begin{array}{}\text{(11)}& \text{CFI}=k_{\mathrm{1}}\text{GCI}+k_{\mathrm{2}}\mathit{\delta }(\mathrm{1}-\text{LCP}),\end{array}$$

where k₁ and k₂ are the weighting factors for the corresponding items, and δ is the parameter that raises the order of magnitude.

3.1 Influence of link size on condition number

The joint angle and link size ranges are key factors in the kinematic performance of the robot. The joint angle range is mainly determined by the size and placement of the denim fabric, so it was not analyzed in detail in this study; the effects of link size were prioritized as per their effects on the kinematic performance index. The relationship between link size and condition number was determined by analyzing the relationship between each link size and condition number via the control variable method. When the joint angle is −70^∘, 10^∘, −30^∘, 10^∘, 10^∘, and 0^∘, the effect of each link size on the condition number of the robot is as shown in Fig. 6.

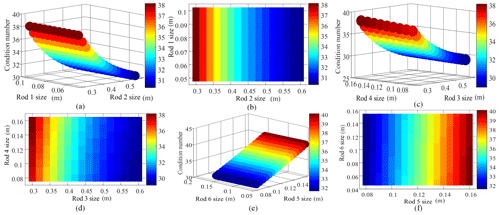
Figure 6 Effect of each link size on condition number. (a) The effect of rod 1 and rod 2. (b) Top view of the effect of rod 1 and rod 2. (c) The effect of rod 3 and rod 4. (d) Top view of the effect of rod 3 and rod 4. (e) The effect of rod 5 and rod 6. (f) Top view of the effect of rod 5 and rod 6.

As is shown in Fig. 6a and b, the condition number decreases as the second dimension of the link increases when the first dimension of the link remains unchanged. When the size of Link 2 is unchanged, changes in the size of Link 1 have no effect on the condition number.

As is shown in Fig. 6c and d, the condition number increases as link Size 4 increases while Size 3 remains unchanged. However, the condition number decreases as Size 3 increases when Size 4 remains unchanged.

Figure 6e and f indicate that the condition number decreases as link Size 6 increases while Size 5 remains unchanged; the condition number increases with Size 5; however, when the size of Link 6 is unchanged. In summary, the size of Link 1 has no effect on the CFI, i.e., the comprehensive dexterity evaluation index. The dimensions of Links 2–6 were selected to optimize the robot size in this study accordingly.

4 Robot dimension optimization based on adaptive FWA

4.1 Adaptive FWA

The FWA is a swarm intelligence optimization algorithm inspired by the explosion of fireworks and sparks across a certain range. It is mainly composed of an explosion operator, mutation operator, mapping rule, and selection strategy. It is operated in the following step-wise process.

The first step is initialization, the generation of fireworks at any N locations in the solution space; the explosion operator generates S_i new sparks in the explosion range A_i, where A_i and S_i are

$$\begin{array}{}\text{(12)}& {\displaystyle }& {\displaystyle }{A}_i=\widehat{A}{\displaystyle \frac{f\left(x_i\right)-Y_{min}+\mathit{\epsilon }}{{\sum }_{i=\mathrm{1}}^N\left(f\left(x_i\right)-Y_{min}\right)+\mathit{\epsilon }}},\text{(13)}& {\displaystyle }& {\displaystyle }{S}_i=m{\displaystyle \frac{Y_{max}-f\left(x_i\right)+\mathit{\epsilon }}{{\sum }_{i=\mathrm{1}}^N\left(Y_{max}-f\left(x_i\right)\right)+\mathit{\epsilon }}},\end{array}$$

where $\widehat{A}$ and m are the maximum explosion radius and the maximum number of sparks caused by the explosion, respectively; Y_min and Y_max are the fitness values of the individuals with the best and worst fitness. f(x_i) is the fitness value of individual x_i, and ε is the minimum constant. To prevent uneven spark numbers from affecting performance, S_i can be changed to

$$\begin{array}{}\text{(14)}& S_i=\left\{\begin{array}{ll}\text{round}\left(am\right),& S_i<am\\ \text{round}\left(bm\right),& S_i>bm,a<b<\mathrm{1}\\ \text{round}\left(S_i\right),& \text{else},\end{array}\right.\end{array}$$

where round() is an integer function, and a and b are given constants.

To increase the spark diversity, the following displacement and Gauss variation can be imposed:

$$\begin{array}{}\text{(15)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{x}_i^k=x_i^k+\text{rand}\left(\mathrm{0},A_i\right),\text{(16)}& {\displaystyle }& {\displaystyle }{x}_i^k=x_i^{k}g,\end{array}$$

where rand(0,A_i is the uniform random number generated in the explosion range, $x_i^k$ is the position of the ith individual in the kth dimension, and g is a random number in a Gaussian distribution with a mean variance of 1.

To avoid spark locations from crossing the boundary, the following mapping rules are used:

$$\begin{array}{}\text{(17)}& x_i^k=x_{min}^k+\left|x_i^k\right|\mathit{\%}\left(x_{max}^k-x_{min}^k\right),\end{array}$$

where $x_{max}^k$ and $x_{min}^k$ are upper and lower bounds on the kth dimension, respectively, and % denotes redundancy.

An elite retention strategy is used to directly retain the best-fit sparks with a roulette to filter the remaining sparks. The probability that each spark will be selected is

$$\begin{array}{}\text{(18)}& p\left(x_i\right)={\displaystyle \frac{R\left(x_i\right)}{{\sum }_{j=\mathrm{1}}^{H}R\left(x_j\right)}},\end{array}$$

where R(x_i) represents the sum of the distances of an individual x_i to other sparks; H is the total number of sparks. The FWA has a prematurity problem; its performance is poor and its operations are time-consuming when the optimal solution is far from the origin. The adaptive FWA is an improvement over the FWA that enables the explosion radius to be automatically adjusted, changes the mutation mode, maps the rules and selection strategies, and improves the performance of the algorithm.

The adaptive radius is calculated by selecting among values that meet several criteria. The fitness value must be lower than this generation of fireworks, the distance to the optimum individual must be the shortest among the individuals satisfying Eq. (1), and the distance between the individual and the optimum fireworks must be considered the subsequent explosion radius. The initialization radius is the entire solution range. To strike a balance between local and global searches, a weight λ (usually 1.3) is multiplied by the adaptive radius.

The Gauss sparks for the new Gauss variant operator are calculated as follows:

$$\begin{array}{}\text{(19)}& x_i^k=x_i^k+\left(x_b^k-x_i^k\right)\times e,\end{array}$$

where e is a random number with a mean of 0 and a variance of 1; $x_b^k$ is the position of the most suitable firework in the k-dimension of the current population. Next, new mapping rules are established at random:

$$\begin{array}{}\text{(20)}& x_i^k=x_{min}^k+U\left(\mathrm{0},\mathrm{1}\right)\cdot \left(x_{max}^k-x_{min}^k\right),\end{array}$$

where U(0,1) is a uniformly distributed random number on the [0,1] interval. Finally, an elite-random selection strategy is operated by selecting the most suitable individual in the population and then using a random strategy for the selection of other fireworks to minimize the computation time.

4.2 Fitness function selection

The link size of the robot affects its dexterity. To satisfy the workspace requirements of the polishing process, the dexterity index was used here as the objective function. Only the link size was optimized in this case, so the structure of the robot did not change. The sum of the dimensions of Links 2, 3, and 5 is the radius of motion of the robot. Changes in size affect the farthest distance the robot can reach, so the length of the link is a restrictive element. The fitness function is

$$\begin{array}{}\text{(21)}& {\displaystyle }& {\displaystyle }min\left(\text{CFI}\right)=k_{\mathrm{1}}\text{GCI}+k_{\mathrm{2}}\mathit{\delta }(\mathrm{1}-\text{LCP}),\text{(22)}& {\displaystyle }& {\displaystyle }{r}_{min}\le l_{\mathrm{2}}+l_{\mathrm{3}}+l_{\mathrm{5}}\le r_{max},\end{array}$$

where l₂, l₃, and l₅ are the lengths of Links 2, 3, and 5, respectively.

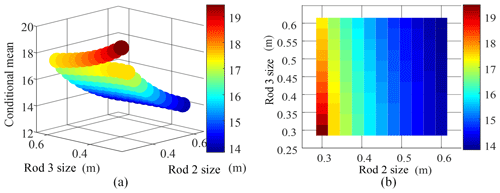
Figure 7 Effect of bar size on mean of spatial condition number. (a) The effect of rod 2 and rod 3. (b) The top view of the effect of rod 2 and rod 3.

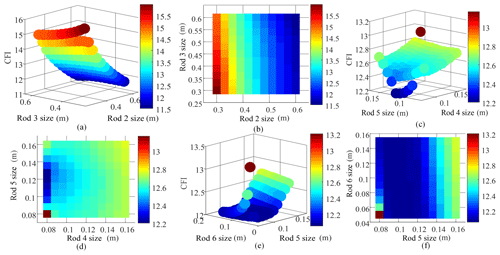
Figure 8 Effect of each link size on the comprehensive dexterity index. (a) The influence of rod 2 and rod 3. (b) The top view of the influence of rod 2 and rod 3. (c) The influence of rod 4 and rod 5. (d) The top view of the influence of rod 4 and rod 5. (e) The influence of rod 5 and rod 6. (f) The top view of the influence of rod 5 and rod 6.

4.3 Algorithmic steps

The denim-fabric-polishing robot was optimized in this study based on the adaptive FWA via the following step-wise process.

1. Initialize population. Determine the number of fireworks N, which are generated anywhere in the link size search space.

2. Solve polynomial coefficients. Solve the dexterity evaluation index by substituting N-group link size Q into Eqs. (5)–(9).

3. Verify constraints. Determine whether the link size obtained in Step 2 meets the constraint of Eq. (20).

4. Calculate fitness values. The result of Step 3 is filtered. If the link size does not meet the constraint, the fitness value of the fireworks is increased to increase the explosion amplitude and expand the search range. If the link size meets the constraint, the adaptive FWA is iterated with Eq. (19) as the objective function.

5. Adaptive FWA generates new population.

6. Judge final conditions. If the number of iterations is reached or the fitness value meets the requirements, the algorithm ends; otherwise, return to Step 2.

5 Simulation verification and analysis

To set the value in the comprehensive dexterity index, it was necessary to first analyze the condition number mean value of the workspace. Taking the effect of the change of secondary and tertiary dimensions of the link on the condition number mean value of the workspace as an example, the effect of the link size on the condition number mean value of the workspace is as shown in Fig. 7.

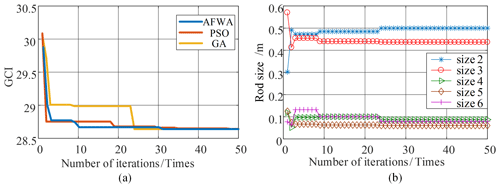
Figure 9 Particle evolution diagram with GCI as optimization target. (a) GCI index evolution diagram. (b) Particle evolution diagram for each link size.

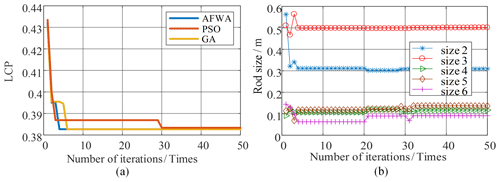
Figure 10 Particle evolution diagram with LCP as optimization target. (a) LCP index evolution diagram. (b) Particle evolution diagram for each link size.

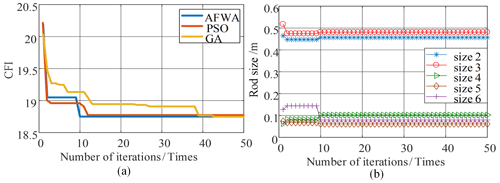
Figure 11 Particle evolution diagram with CFI as optimization target. (a) CFI index evolution diagram. (b) Particle evolution diagram for each link size.

As shown in Fig. 7, the mean value of the condition number in the workspace (14, 20) varies as the link size changes within the given joint angle range. Because GCI and LCP have the same degree of influence on the dexterity of the robot, in order to make the range of both changes equal in magnitude, their weights were set here to k₁=0.5, k₂=0.5, and δ=20.

Table 2 Dimensions of links obtained by different optimization objectives.

Table 3 Optimized objective function values.

Because the optimum range of each link size needed to be determined artificially in this case, in order to illustrate how we take into account the effects of the dimensions of the various links, we take Link 2 and Link 3 as an example, several groups of different sizes of other links were selected (in each group combination, Link 2 and Link 3 joints were variables). Combined with the results of several groups of simulation experiments, the value ranges of Link 2 and Link 3 were selected according to the comprehensive index (the simulation in this paper is just an example). The same idea is used to get the initial dimensions of the other links. We have also added the illustrations in the paper.

The influence of each link's size on the comprehensive dexterity index was obtained by writing an M-file (Fig. 8) to make the optimum range as accurate as possible. As shown in Fig. 8a and b, the robot appears to be more flexible with a smaller comprehensive dexterity index when Links 2 and 3 have larger dimensions. These dimensions must satisfy the limitations of the working site, however. The optimal values were found to be [0.3, 0.6]. As shown in Fig. 8c and d, the dimensions of Links 4 and 5 affect the comprehensive dexterity index within the range of [0.08, 0.16]. The comprehensive dexterity index is smaller when Link 4 is smaller and reaches its minimum around 0.12 m. The optimal range of Link 4 size was determined to be [0.05, 0.12]. As shown in Fig. 8e and f, the comprehensive dexterity index is minimal when the size of Link 5 is within the range [0.096, 0.14]; the optimal size was determined to be [0.06, 0.14]. Finally, as shown in Fig. 8e and f, the comprehensive dexterity index remains relatively stable when Link 6 ranges in size from [0.05, 0.15]. The optimal range of Link 6 was determined to be [0.05, 0.15].

The adaptive FWA, particle swarm algorithm, and genetic algorithm were used to optimize GCI, LCP, and CFI, respectively. The number of fireworks N was set to 5; the number of sparks generated was 50; the number of variant sparks was 5; the initial positions of fireworks were any random number of $l_{\mathrm{2}}=l_{\mathrm{3}}=[\mathrm{0.3},\mathrm{0.6}]$, $l_{\mathrm{5}}=[\mathrm{0.06},\mathrm{0.14}]$, $l_{\mathrm{4}}=[\mathrm{0.05},\mathrm{0.12}]$, or $l_{\mathrm{6}}=[\mathrm{0.05},\mathrm{0.15}]$; the number of explosions was limited to a=0.8 and b=0.04; and the number of iterations was 50. The results are shown in Figs. 9–11.

Algorithmic evolution curve of the three optimization indices was obtained based on the adaptive fireworks algorithm (AFWA), particle swarm optimization (PSO), and GA shown in Figs. 9a, 10a, and 11a. Compared with the other two algorithms (PSO and GA), the adaptive AFWA has better solution accuracy and convergence speed than the other two algorithms (PSO and GA). So, the AFWA is used to optimize the size of the robot rod.

The dimensions of the robot links were obtained by the three optimization indices based on the AFWA; the results are shown in Figs. 9b, 10b, and 11b. The sum of the optimized link dimensions and the dimensions of Links 2, 3, and 5 are listed in Table 2. The sum of dimensions of Links 2, 3, and 5 is 0.9999, 0.9465, and 0.9999 m, respectively. The sum of the dimensions of the optimized Links 2, 3, and 5 falls between the minimum working radius of 0.7434 m and the maximum working radius of 1 m, which meets the working requirements of the denim-fabric-polishing robot.

GCI and LCP can be calculated simultaneously when the objective function value has been optimized and the comprehensive flexibility index is taken as the optimization target based on the optimized robot link size. The optimized objective function values are shown in Table 3. The GCI and LCP obtained with the comprehensive flexibility index as the optimization target are lower than those obtained with the GCI and LCP as the optimization target.

When the link size is not optimized, the GCI is 32.88, the LCP is 56.78 %, and the comprehensive flexibility index is 20.76. The overall flexibility index was reduced by 9.68 % after optimization. It can be found that the link size obtained by taking the comprehensive flexibility as the index mostly meets the requirements, and the motion performance of the robot is improved. From the above analysis, it can be seen that the comprehensive index (CFI) proposed in this paper has obvious advantages.

6 Conclusions

A comprehensive evaluation index based on the mean of the space condition number and weighted low probability condition number is proposed in this paper for judging the dexterity of a denim-fabric-polishing robot. The adaptive FWA can be used to optimize the size of the robot links to meet the requirements of the polishing task while achieving the optimal dexterity index. The results of an optimization experiment show that the proposed adaptive FWA has better solution accuracy and convergence speed than traditional algorithms, and the technique remits a substantial improvement in the robot's motion performance as well as a slight increase in the available workspace while meeting the given working radius requirements. The optimized robot is sufficiently flexible and precise for completing the denim-fabric-polishing task effectively.

Appendix A: Character definition

Number	Character	Explanation
1	ai	Link length
2	di	Offset  distance
3	αi	Twist angle
4	θi	Joint angle
5	${}_i^{i-\mathrm{1}}\mathbf{T}$	The transformation matrix of the two adjacent links
6	rmax	Maximum working radius
7	l	The length of the denim fabric piece
8	d	The width of the denim fabric piece
9	rmin	Minimum working radius
10	Ji	the ith column of the Jacobian matrix J
11	n, o, a, P	The four column vectors of the transformation matrix, where n, o, and a are the attitude vectors and P is the position vector
12	K	The condition number
13	σmax(J)	The maximum singularities of the Jacobian matrix
14	σmin(J)	The minimum singularities of the Jacobian matrix
15	GCI	The global spatial condition number mean index
16	K	The condition number under the specified position
17	W	global working space
18	b	The number of points where condition numbers are lower than the mean of the spatial condition number
19	n	The total space location number
20	CFI	Comprehensive flexibility index
21	k1, k2	The weighting factor for the corresponding items
22	δ	The parameter that raises the order of magnitude
23	LCP	The low condition probability
24	Ai	The explosion range
25	Si	New sparks
26	$\widehat{A}$	The maximum explosion radius
27	m	The maximum number of sparks
28	Ymin	The fitness values of the individuals with the best fitness
29	Ymax	The fitness values of the individuals with the worst fitness
30	f(xi)	The fitness value of individual xi
31	ε	The minimum constant
32	$x_i^k$	The position of the ith individual in the kth dimension
33	g	Gaussian random number whose mean square error is 1
34	$x_{max}^k$	Upper bounds on the kth dimension
35	$x_{min}^k$	Lower bounds on the kth dimension
36	p(xi)	The probability that each spark will be selected
37	R(xi)	The sum of the distances of an individual xi to other sparks
38	H	The total number of sparks
39	e	A random number with a mean of 0 and a variance of 1
40	$x_b^k$	The position of the most suitable firework in the k-dimension of the current population
41	l2, l3, l4, l5, l6	the lengths of Links 2, 3, 4, 5, and 6, respectively
42	U(0,1)	Random number in the range (0,1)